Как найти давление на лед

Плотность льда 0,9167 кг/дм^3 (кг/л). При замерзании воды объём образующегося льда на 9 % больше, чем исходный объём воды. При этом создаются огромные давления. Если заполнить водой (без остатков воздуха) металлическую бочку, закрыть герметично крышку и выставить на мороз, то лёд разорвёт бочку по шву или выдавит дно. Когда-то в юности я, обучаясь в техникуме, проходил практику на химическом предприятии. Там, в частности был трубопровод с горячим маслом. Чтобы масло не остывало, масляная труба была заключена в другую трубу большего диаметра. По образующемуся кольцевому пространству подавался водяной пар. Однажды зимой предприятие остановили на ремонт (аварийно). При этом никто не подумал о том масляном трубопроводе “труба в трубе”. Во время ремонта пар, естественно, не подавался. Арматура на входе пара и выходе конденсата была закрыта. на горизонтальном участке этого трубопровода был прогиб (естественно, вниз). Так вот вода, образовавшаяся при конденсации пара, собралась в этой низине, и замёрзла. При этом создалось такое давление, что внутреннюю трубу (диаметром около 50 мм и толщиной около 3 мм) просто сплющило так, что по ней не могло проходить масло.

А в природе, попавшая в трещины камней или скал вода при замерзании раскалывает их.

Условие задачи:

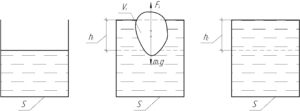
В стакане, наполненном до краев водой, плавает кусок льда. Как изменится давление на дно сосуда, когда лед растает?

Задача №3.3.7 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

(frac{P_2}{P_1}-?)

Решение задачи:

По третьему закону Ньютона с какой силой жидкость выталкивает льдину, с такой же силой льдина давит на воду (и на дно). Значит льдина увеличивает силу давления на дно на величину силы Архимеда. Сила давления на дно равно:

[{P_1} = {P_0} + {F_А}]

Здесь (P_0) – это вес изначально находившейся в стакане воды.

Льдина плавает, поэтому запишем условие плавание тела:

[{F_А} = {m_л}g;;;;(1)]

Значит:

[{P_1} = {P_0} + {m_л}g]

Теперь заметьте, что когда лёд растает, то масса образовавшейся воды (m_в) будет такой же, как и масса льда (m_л).

[{m_л} = {m_в}]

Эта масса воды будет увеличивать силу давления на дно на величину своего веса, то есть:

[{P_2} = {P_0} + {m_в}g]

Так как (m_л=m_в), то (P_1=P_2). Получается, что сила давления на дно не изменится!

Некоторые могут возразить, что при плавлении льда часть воды может вылиться из стакана, поскольку изначально стакан был наполнен до краев. Покажем, что уровень жидкость не изменится. Для этого на схеме покажем три состояния.

Тело вытесняет объем воды, равный по объему части тела, погруженную в воду, поэтому:

[S{h_1} = {V_п}]

[{h_1} = frac{{{V_п}}}{S}]

Распишем ранее приведенное условие плавания льда (формула (1)):

[{rho _в}g{V_п} = {m_л}g]

[{V_п} = frac{{{m_л}}}{{{rho _в}}}]

Тогда:

[{h_1} = frac{{{m_л}}}{{{rho _в}S}}]

Когда лёд растает, то уровень повысится на (h_2) по сравнению с начальным (когда лёд еще не погрузили в стакан):

[S{h_2} = {V_в}]

[{h_2} = frac{{{V_в}}}{S}]

Так как (m_л=m_в), то объем воды (V_в), получившийся при таянии льда, равен:

[{V_в} = frac{{{m_л}}}{{{rho _в}}}]

Тогда:

[{h_2} = frac{{{m_л}}}{{{rho _в}S}}]

Видно, что (h_1=h_2), поэтому никакая часть воды не выльется, значит сомнений в правильности решения более не осталось.

Ответ: не изменится.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

3.3.6 В воде плавает шар, погрузившись на 2/3 объема. Определите плотность
3.3.8 В цилиндрический сосуд с водой, с площадью дна 150 см2, опускают тело массой 1 кг
3.3.9 Вес куска железа в воде 1,67 Н. Найти его объем

Подробности

Обновлено 30.01.2019 17:15

Просмотров: 291

Назад в «Оглавление»

Так нет ли здесь нужной вам задачи?
Обязательно найдется!

1. Bыразите в пасналях давления: 5 гПа; 0,02 Н/см2; 0,4 кПа, 10Н/см2.
Выразите в гектопаскалях и килопаскалях давление: 10 000 Па; 5800 Па.

1 гПа = 100 Па
1 кПа = 1000 Па
1 см² = 0,0001 м²

2. Гусеничный трактор ДТ-75М массой 6610 кг имеет опорную площадь обеих гусениц – 1,4 м2. Определите давление этого трактора на почву. Во сколько раз оно больше давления, производимого мальчиком (см. пример в §33)?

3. Человек нажимает на лопату с силой 600 Н. Какое давление оказывает лопата на почву, если ширина ее лезвия 20 см, а толщина режущего края 0,5 мм?
Зачем лопаты остро затачивают?

4. Мальчик массой 45 кг стоит на лыжах. Длина каждой лыжи 1,5 м, ширина 10 см. Какое давление оказывает мальчик на снег?
Сравните его с давлением, которое производит мальчик, стоящий без лыж.

—————————-

1. Рассмотрите устройство плоскогубцев и клещей. При помощи какого инструмента можно произвести большее давление на зажатое тело, действуя одинаковой силой?

2. Зачем при бороновании плотных почв на бороны кладут тяжелые предметы?

Назад в «Оглавление»

КОРАБЛЕСТРОЕНИЕ. Теория корабля и строительная механика

DOI.org/10.5281/zenodo.2578675 УДК 629.128

А.И. Мамонтов

МАМОНТОВ АНДРЕЙ ИГОРЕВИЧ – к.т.н., доцент, e-mail: mamontov.ai@dvfu.ru Кафедра кораблестроения и океанотехники Инженерной школы Дальневосточный федеральный университет Суханова ул., 8, Владивосток, 690091

Определение давления динамического разрушения льда на основе предельной модели материала

Аннотация: Рассматривается пиковое давление льда на корпус судна, определяется зависимость давления льда от угла наклона разрушающей плоскости. Представлен эксперимент по сбросу инденторов на поверхность льда, каждый индентор представляет собой две наклонные плоскости (их наклон различен), образующие острый клин. В месте контакта индентора со льдом в результате удара лёд динамически разрушался (сминался). Давление при ударе определено по глубине отпечатка.

Предельная модель материала создана по экспериментальной зависимости давления разрушения льда от угла наклона плоскостей. На основе предельной модели выполнен теоретический расчёт давления разрушения льда. Результат расчёта представлен в виде зависимости давления от угла наклона плоскостей. Полученная функция полностью совпадает с экспериментальной. Ключевые слова: прочность льда при смятии, локальное ледовое давление, динамическое разрушение, предельная модель.

Введение

Испытаниям льда на прочность посвящен ряд работ. В [4], где обобщены основные экспериментальные данные, рассмотрены районы проведения испытаний, площади образцов льда, солёности и температура, при этом относительно смятия льда указано лишь, что напряжение зависит от времени приложения нагрузки.

В ряде работ последних лет особое внимание уделяется времени приложения нагрузки. Так, в [2], где обобщён опыт отечественных исследований, указывается на значительное влияние скорости разрушения льда на значение давления. Теме влияния скорости разрушения льда на давление при осевом сжатии посвящены также обширные исследования зарубежных коллег [6].

Для исследования давления разрушения на больших скоростях в разное время проводились эксперименты по сбросу шаров-инденторов на поверхность льда [1, 5]. Сферическая форма индентора не позволяет объяснить эксперименты с позиции теории плоского предельного равновесия, в рамках которой решены многие задачи разрушения твердых тел [3].

Взаимодействие корпуса судна со льдом можно условно разделить на два типа. Первый – раздвижение льдин, погружение и поворот, второй тип – удар. При ударе небольшая часть льдины сминается, что приводит к началу её последующего движения. В статье представлена оценка давления при смятии (разрушении), которое является результатом динамического воздействия наклонной плоскости. Это давление локальное и пиковое, так как оно действует до нескольких секунд на небольшой площади.

© Мамонтов А.И., 2019

О статье: поступила: 04.05.2018; финансирование: бюджет ДВФУ.

Цель настоящей статьи – определение давления разрушения морского льда во время удара; зависимости давления разрушения от наклона плоскости; формы и параметров предельной модели.

Для определения давления применялся баланс работы, затраченной на разрушение льда, и потенциальной энергии до сброса; исходные данные: вес груза, высота сброса, глубина отпечатка.

Для определения зависимости давления разрушения от наклона плоскости менялся угол установки плоскости, после чего серия сбросов клина с грузом повторялась.

Для определения формы и параметров предельной модели по данным эксперимента построена зависимость давления от угла наклона плоскости. Рядом с этой зависимостью построена теоретическая зависимость, в основе расчёта которой – параметры модели материала льда. Расчет производится в рамках плоской задачи теории предельного равновесия. Если графики этих зависимостей совпадут, то параметры модели материала будут считаться определёнными.

Предельная модель материала – это зависимость касательных напряжений от нормальных на площадке текучести. Она позволит нам узнать, под каким сочетанием внутренних напряжений материал разрушается до состояния смятия. Модель, в общем случае, определяет границу упругости и состояние, в котором наблюдается значительное увеличение деформации при небольшом изменении нагрузки. Такая модель покажет нам, как зависит давление от формы объекта, который разрушает лёд. Это максимально возможное давление, так как, когда оно достигается, тело перестает существовать как единое целое.

Порядок эксперимента

1. Прежде всего мы фиксируем высоту сброса индентора и его вес (постоянен в данном эксперименте) с нагрузкой в 22 кг. Затем измеряем глубину вмятины после удара и по этим данным определяем давление смятия. Следующий шаг: меняем угол в вершине инден-тора и повторяем эксперименты. По этим данным строим графики зависимости давления смятия от угла в вершине индентора.

2. Ориентировочно принимаем параметры модели предельного материала и вычисляем теоретическую зависимость давления. После этого меняем параметры так, чтобы теоретическая зависимость совпала с экспериментальной.

Описание эксперимента

Эксперимент проводился в феврале 2018 г. в бухте Новик Приморского края при температуре льда -6 °С. В начале эксперимента поверхность льда была очищена от верхнего слоя. В результате очистки в плане сформирована круглая выемка, в центре которой – небольшое отверстие от машины, которая очищает лед.

-Индснтор

ВЫСОТА СБРОСА

ПОВЕРХНОСТЬ ЛЬДА

ГН

Рис. 1. Схема эксперимента.

Индентор представляет собой клин массой 2 кг с грузом 20 кг для увеличения глубины отпечатка. Перед падением индентор закрепляется под грузом.

Каждый индентор был сброшен три раза на поверхность очищенного льда с высоты 1.5-1.8 м (рис. 1). Вертикальная скорость в момент касания льда составила 5.5-6 м/с (10-11 узлов). Всего проведено 8 удачных сбросов с тремя разными углами в вершине индентора. Схема эксперимента представлена на рис. 1, фото индентора и вмятины – на рис. 2 и рис. 3.

Рис. 2. Индентор с нагрузкой

в подвешенном состоянии. Рис. 3. Отпечаток.

Экспериментальное определение давления

Для определения давления льда мы используем равенство потенциальной энергии подвешенного индентора работе при торможении. Введем следующие обозначения: давление льда на индентор – р, глубина отпечатка – D, длина индентора между концами – Ь = 0.15 м, высота сброса – ^ угол в вершине индентора, отсчитываемый от вертикали, – в, вертикальное суммарное усилие при торможении – Fz.

Сила Fz представляет собой сумму давления льда на поверхности индентора в проекции на вертикальную ось. Зависимость силы Fz (О) от глубины:

Fz(D) = 2 • р • tan(P) • D • Ь. (1)

Работа давления, затраченная на торможение:

П П Т”)2

Ш = /0 Fz(D) • dD = 2 • /0 р • tan(P) • D • Ь • dD = 2 • р • tan(P) • ^ • Ь. (2)

Потенциальная энергия до падения:

Е = т • g • (h + D) « т • g • h. (3)

Давление льда равно, Ш = Е.

Р = ‘¿ап(Р>П2Ь. ( )

Результаты расчета давления льда по экспериментальным данным приведены в таблице. Зависимость давления льда от угла в вершине индентора показана на рис. 4.

Результат расчета давления по экспериментальным данным

№ Угол в вершине индентора, в Масса индентора с нагрузкой, т Высота падения, Ь Глубина погружения, Б Давление, Р

град. кг м м МПа

1 63.4 22 1.7 0.012 8.505872

2 63.4 22 1.75 0.0115 9.533992

3 63.4 22 1.5 0.0116 8.031704

4 25.1 22 0.924 0.025 4.540919

5 25.1 22 1.63 0.036 3.863086

6 25.1 22 1.61 0.0427 2.712201

7 44.4 22 1.53 0.022 4.644543

8 44.4 22 1.37 0.022 4.158839

* у !

/ /Л

/

5 Т =10 (ЛГ?) ‘(6)1.925 =0.81 91 РеМО.О! 2^ (

< Э” * У

V

“С

у-1Ц”(Ь] Кл(2)=0 5152

О 10 20 30 40 50 60 70

р,

Рис. 4. Зависимость давления льда от угла индентора.

Синяя линия – теоретический расчёт. Коричневые линии регрессии с коэффициентами 0.82 и 0.52; точками отмечены экспериментальные данные.

Теоретическое определение давления разрушения льда

Предположим, что предельная модель является кривой второй степени. Это означает, что для определения коэффициентов кривой мы должны проводить минимум три независимых эксперимента.

В нашей модели индентор представляет собой клин с углом 2-р в вершине (рис. 1). Мы сбрасываем инденторы с тремя разными углами р. Таким образом, мы 3 раза изменяем тангенциальные и нормальные напряжения в областях разрушения льда.

По экспериментальным данным была построена зависимость давления льда от угла в вершине индентора и найдено уравнение регрессии (рис. 4). Теоретическая зависимость давления льда от угла строилась по формулам (12) и обозначалась синим цветом на рис. 4. Рассмотрим плоскую задачу теории предельного равновесия [3].

Предположим, что модель предельного материала является уравнением (5). Мы вводим обозначения в соответствии с рис. 5:

Т = Ъп(р) • ^ + Но), (5)

где S и T – нормальные и касательные напряжения на границе предельного состояния или координаты предельной модели материала.

р, Ис – константы или параметры предельной модели, которые должны быть определены экспериментально.

На рис. 5 показан круг Мора и предельная модель – прямая под углом р.

Рис. 5. Круг Мора и предельная модель.

Рис 6. Ориентация линии скольжения в декартовой системе координат.

Когда материал измельчается, каждая линия скольжения ориентируется так, чтобы соответствовать минимальной внешней нагрузке. Эти линии отклоняются от декартовых осей, как показано на рис. 6. Они отклоняются от направления основного нормального напряжения на угол 8 (рис. 1 и рис. 7).

Ориентация линии скольжения в декартовой системе координат определяется углом ф ± 8, где ф – наклон максимального напряжения к оси OX. Вся область разрушения образована из таких линий скольжения.

Лед разрушается и выдавливается на поверхность, когда индентор нажимает на нее (см. рис. 7). В зависимости от ориентации линий скольжения область разрушения может быть разделена на 3 части: 0А0Аь 0АхА2, 0А2А3.

Рис. 7. Индентор и области разрушения.

При увеличении в-угла увеличивается область 0А0А1 (см. рис. 7), напряжение меняется, а давление увеличивается.

о – напряжение в области ОА]^ зависит от угла ф, который изменяется от 0А0А1 к 0А2А3:

а = С • ехр(—2 • ф • ^п(р)). (6)

Давление удержания в области 0А2А3

q = а ■ (1 – зт(р)) – Но. (7)

Давление раздавливания в области 0А0А1 составляет

р = а ■ (1 + зт(р)) – Н0. (8)

Произвольная константа C в (6) определяется следующим образом. Известно, что в области 0А0А1 ф = п / 2, а в области 0А2А3 ф = п / 2 + в.

ехр(—2 ■ п/2 ■ tan(p)) = С ■ ехр(-2 ■ (п/2 + в) ■ ^п(р)), С = ехр(2 ■ в ■ tan(p)). (9)

Перепишем (8) с учетом (9): р = (1 + зт(р)) • ехр(2 • в ” tan(p)) • а — Н0. Из (7) известно, что

Ч+Но

а

(1^т(р))”

(10)

(11)

Поверхность льда вблизи индентора не находится под давлением. Следовательно, удерживающее давление равно нулю, т.е. q = 0.

Подставим (11) в (10). Мы получаем окончательную формулу для расчета давления раздавливания как функцию угла в вершине индентора.

Р = (Г+Ш ^ Но ^ еХР(2 • в • ^П(Р)) – Но. (12)

iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

Уравнение (12) связывает угол в вершине индентора и давление разрушения через параметры предельной модели р, Ио, указанные на рис. 5.

Пример расчета давления на корпус судна

от разрушения льда

Мы рассматриваем удар корпуса о край льда. Свойства льда мы берем как в (14). Угол наклона борта равен Р-0.523 рад.

Определим давление льда по уравнению (12).

Н0 = 940000, р = 0.504.

Р = (1+^(0504)) • 940000 • exp(2 • 0.523 • tan(0.504)) – 940000 = 3.86МПа. (13)

В статье давление определяется для случая, когда лед имеет статическое положение. На практике льдины начинают двигаться и меняют положение по отношению к развалу корпуса (см. рис. 8). Для более точного определения давления необходимо интегрировать уравнение движения льдины. Для интеграции необходимо знать давление в каждый бесконечно малый момент времени, это возможно на основе исследований, аналогичных тем, которые представлены в этой работе.

0 тУ

Судно / /-Лёд

/ / –

— — — — — — _/ V/А/- • -vV/V^Vv-

—-u ~ ———-

Рис. 8. Воздействие льда на корпус судна.

Заключение

Всего в работе выполнено 8 удачных сбросов инденторов с углами в = 63.4, в = 44.4 и в = 25.1.

Поведение льда во время динамического разрушения можно описать с использованием предельной модели (которая определялась на основе зависимости давления льда от угла в вершине индентора), представленной уравнением (14):

T = tan (0.504) • (S+940000). (14)

Это уравнение определяет следующие параметры модели: угол внутреннего трения р = 0.504rad, H0 = 0.94 МПа.

Если подставить в уравнение (12) значения р = 0.504rad. и H0 = 0.94 МПа, то расчет давления совпадает с линией регрессии, построенной на экспериментальных данных с коэффициентом R2= 0.8191.

Если же использовать другие параметры, например, р = 0.772 rad и Ho = 0.202 МПа, то коэффициент регрессии уменьшается, он равен R2 = 0.5152, т.е. когда коэффициент регрессии снижается на 30%, параметры модели могут меняться в несколько раз.

Максимальный коэффициент регрессии, который может быть получен на экспериментальных данных, равен R2 = 0.8191.

Коэффициент регрессии зависит от количества сбросов и количества углов в вершине индентора.

Особенностью эксперимента является тот факт, что результаты получены для фиксированных углов в вершине индентора. Увеличение количества сбросов приводит к увеличению числа значений давления для каждого фиксированного угла, но число углов остается постоянным. Увеличение числа значений относительно оси ординат не увеличивает разброс значений по оси абсцисс, поэтому коэффициент регрессии может быть увеличен только за счет совместного увеличения количества сбросов и увеличения числа углов в вершине индентора.

Давление разрушения зависит от нормальной скорости и угла в вершине индентора. В этой работе угол и скорость изменяются.

Максимальное давление при скорости разрушения льда 5 м/с составило 9.5 МПа для угла 63.4 град, а минимальное давление при скорости разрушения льда 3 м/с – 2.75 МПа для угла 25.1 град.

Предельная модель, полученная в этой работе, соответствует разным скоростям разрушения, поэтому в будущем планируется получить предельную модель, основанную на данных, полученных при постоянной скорости разрушения льда с переменным углом в вершине ин-дентора. Для этого необходимо изменить высоту сброса при соответствующем изменении угла в вершине индентора, чтобы нормальная скорость разрушения оставалась постоянной. Мы считаем, что необходимо повторить эксперименты для разных скоростей. Это позволит исследовать влияние скорости дробления на давление для разных углов в вершине индентора.

Обработка большого количества экспериментальных данных должна дать нам модель материала и её параметры для каждой фиксированной скорости. Такая модель должна связывать давление при ударе с углом наклона борта и скоростью судна. Сейчас правила не связывают в явном виде пиковое давление льда со скоростью. Нет разделения на пиковое давление при динамическом смятии кромки льдины и на общее давление льда.

Автор выражает благодарность МНОЦ «Арктика» Инженерной школы ДВФУ за помощь в проведении эксперимента.

СПИСОК ЛИТЕРАТУРЫ

1. Гомольский С.Г., Храпатый Н.Г., Цуприк В.Г. Исследование удара твёрдого тела о лёд // Ледо-термические явления и их учёт при возникновении и эксплуатации гидроузлов и гидротехнических сооружений: материалы конференций и совещаний по гидротехнике. Л.: Энергия, 1979. С.73-76.

2. Лобанов В.А. Моделирование льда в задачах с конечноэлементной постановкой // Дифференциальные уравнения и процессы управления. 2008. № 4. С. 20-24.

URL: http://docplayer.ru/3 8501220-Modelirovanie-lda-v-zadachah-s-konechnoelementnoy-postanovkoy-v-a-lobanov.html (дата обращения: 28.04.2018).

3. Соколовский В.В. Теория пластичности. Изд. 3. М.: Высшая школа, 1969. 80 с.

4. Степанюк И.А. Технологии испытаний и моделирования морского льда // Федеральная целевая программа «Государственная поддержка интеграции высшего образования и фундаментальной науки на 1997- 2000 годы». СПб.: Гидрометеоиздат, 2001. 78 с.

5. Хейсин Д.Е., Черепанов Н.В. Изменение структуры льда в зоне удара твёрдого тела о поверхность ледяного покрова // Проблемы Арктики и Антарктики. 1970. № 34. С. 79-84.

6. Chunfeng Qia, Jijian Liana, Qunan Ouyanga, Xin Zhaoa. Dynamic Compressive Strength and Failure of Natural Lake Ice Under Moderate Strain Rates at Near Melting Point Temperature. Latin American Journal of Solids and Structures. 2017(14);9. URL: http://dx.doi.org/10.1590/1679-782539.07.-02.04.2018.

Theory of the Ship and Construction Mechanics www.dvfu.ru/en/vestnikis

DOI.org/10.5281/zenodo.2578675

Mamontov A.

ANDREY MAMONTOV, Candidate of Engineering Sciences, Associate Professor, Department of Shipbuilding & Ocean Engineering, School of Engineering, e-mail: mamontov.ai@dvfu.ru Far Eastern Federal University 8 Sukhanova St., Vladivostok, 690091, Russia

Determination of ice dynamic crush pressure based on the limit material model

Abstract: The article analyzes the pressure of ice on a ship’s hull, and determines the ice pressure dependent on the angle of inclination of the crush plane. An experiment of dropping the indenters on the ice surface has been performed; where each indenter has the form of two inclined planes (their inclination is different) forming a sharp wedge. At the contact point of the indenter with ice, as a result of the impact, the ice was dynamically squashed (crushed). The impact pressure is determined by the depth of indentation.

The limit model of the material has been developed by the experimental dependence of the ice crushing pressure on the angle of inclination of the planes. On the basis of the limit model, a theoretical calculation of the ice crushing pressure has been made. The result of the calculation is presented as the dependence of pressure on the angle of inclination of the planes. The obtained function completely coincides with the experimental one.

Keywords: crush strength of ice, local ice pressure, dynamic crush, limit model. REFERENCES

1. Gomolsky S.G., Khrapatyi N.G., Tsuprik V.G. Investigation of the impact of a solid body on ice. Ice-thermal phenomena and their registration in the event of the emergence and operation of hydroschemes and hydraulic structures. Proceedings of conferences and meetings on hydraulic engineering. Leningrad, Energy, 1979, p. 73-76.

2. Lobanov V.A. Modeling of ice in problems with finite element setting. Differential equations and control processes. 2008; 4:20-24. URL: http://docplayer.ru/38501220-Modelirovanie-lda-v-zadachah-s-ko-nechnoelementnoy-postanovkoy-v-a-lobanov.html – 28.04.2018.

3. Sokolovsky V.V. Theory of plasticity. M., Higher School, 1969, 80 p.

4. Stepaniuc I.A. Technology testing and modeling of sea ice. Federal Target Program State Support for the Integration of Higher Education and Fundamental Science for 1997-2000. Saint Petersburg, Gidrometeoizdat, 2001, 78 p.

5. Kheysin D.E., Cherepanov N.V. Changes in the structure of ice in the zone of impact of a solid body on the surface of the ice cover. Problems of the Arctic and Antarctic. 1970;34:79-84.

6. Chunfeng Qia, Jijian Liana, Qunan Ouyanga, Xin Zhaoa. Dynamic Compressive Strength and Failure of Natural Lake Ice Under Moderate Strain Rates at Near Melting Point Temperature. Latin American Journal of Solids and Structures. 2017(14);9. URL: http://dx.doi.org/10.1590/1679-782539.07.-02.04.2018.

Определите, какое давление оказывает на лед человек массой 65 кг стоя, если площадь его опоры в ботинках равна 0,07 м², и лежа, если площадь его опоры равна 0,7 м².

Ответ

Дано

m = 65 кг
S₁ = 0,7 м²
S₂ = 0,07 м²

Найти

p₁ = ?
p₂ = ?

Решение

p = F/S

F = P
P = mg
F = mg = 9,8 Н/кг ⋅ 65 кг = 637 Н

p₁ = F/S₁ = 637 Н / 0,7 м² = 910 Па

p₂ = F/S₂ = 637 Н / 0,07 м² = 9100 Па

Ответ:
p₁ = 910 Па
p₂ = 9100 Па

Опубликовано: 26.03.2023
Обновлено: 26.03.2023