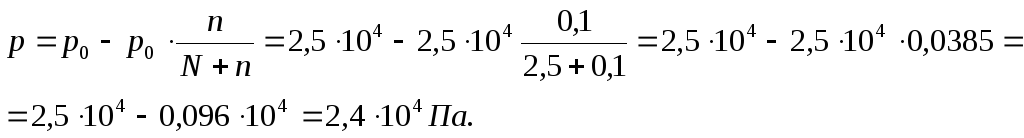Как найти давление пара раствора - Сайт, где вы сможете решить свои вопросы

Download Article

Have you ever left a bottle of water out in the hot sun for a few hours and heard a slight “hissing” noise when you opened it? This is caused by a principle called vapor pressure. In chemistry, vapor pressure is the pressure that is exerted on the walls of a sealed container when a substance in it evaporates (converts to a gas).^[1] To find the vapor pressure at a given temperature, use the Clausius-Clapeyron equation: ln(P1/P2) = (ΔH_vap/R)((1/T2) – (1/T1)). You could also use Raoult’s Law to find the vapor pressure: P_solution=P_solventX_solvent.

1
Write the Clausius-Clapeyron equation. The formula used for calculating vapor pressure given a change in the vapor pressure over time is known as the Clausius-Clapeyron equation (named for physicists Rudolf Clausius and Benoît Paul Émile Clapeyron).^[2] This is the formula you’ll use to solve the most common sorts of vapor pressure problems you’ll find in physics and chemistry classes. The formula looks like this: ln(P1/P2) = (ΔH_vap/R)((1/T2) – (1/T1)). In this formula, the variables refer to:
- ΔH_vap: The enthalpy of vaporization of the liquid. This can usually be found in a table at the back of chemistry textbooks.
- R: The real gas constant, or 8.314 J/(K × Mol).
- T1: The temperature at which the vapor pressure is known (or the starting temperature.)
- T2: The temperature at which the vapor pressure is to be found (or the final temperature.)
- P1 and P2: The vapor pressures at the temperatures T1 and T2, respectively.
2
Plug in the variables you know. The Clausius-Clapeyron equation looks tricky because it has so many different variables, but it’s actually not very difficult when you have the right information. The most basic vapor pressure problems will give you two temperature values and a pressure value or two pressure values and a temperature value — once you have these, solving is a piece of cake.
- For example, let’s say that we’re told that we have a container full of liquid at 295 K whose vapor pressure is 1 atmosphere (atm). Our question is: What is the vapor pressure at 393 K? We have two temperature values and a pressure, so we can solve for the other pressure value with the Clausius-Clapeyron equation. Plugging in our variables, we get ln(1/P2) = (ΔH_vap/R)((1/393) – (1/295)).
- Note that, for Clausius-Clapeyron equations, you must always use Kelvin temperature values. You can use any pressure values as long as they are the same for both P1 and P2.
Advertisement
3
Plug in your constants. The Clausius-Clapeyron equation contains two constants: R and ΔH_vap. R is always equal to 8.314 J/(K × Mol). ΔH_vap (the enthalpy of vaporization), however, depends on the substance whose vapor pressure you are examining. As noted above, you can usually find the ΔH_vap values for a huge variety of substances in the back of chemistry or physics textbooks, or else online.
- In our example, let’s say that our liquid is pure liquid water. If we look in a table of ΔH_vap values, we can find that the ΔH_vap is roughly 40.65 kJ/mol. Since our H value uses joules, rather than kilojoules, we can convert this to 40,650 J/mol.
- Plugging our constants in to our equation, we get ln(1/P2) = (40,650/8.314)((1/393) – (1/295)).
4
Solve the equation. Once you have all of your variables in the equation plugged in except for the one you are solving for, proceed to solve the equation according to the rules of ordinary algebra.^[3]
- The only difficult part of solving our equation (ln(1/P2) = (40,650/8.314)((1/393) – (1/295))) is dealing with the natural log (ln). To cancel out a natural log, simply use both sides of the equation as the exponent for the mathematical constant e. In other words, ln(x) = 2 → e^ln(x) = e² → x = e².
- Now, let’s solve our equation:
- ln(1/P2) = (40,650/8.314)((1/393) – (1/295))
- ln(1/P2) = (4,889.34)(-0.00084)
- (1/P2) = e^(-4.107)
- 1/P2 = 0.0165
- P2 = 0.0165^-1 = 60.76 atm. This makes sense — in a sealed container, increasing the temperature by almost 100 degrees (to almost 20 degrees over the boiling point of water) will create lots of vapor, increasing the pressure greatly

1
Write Raoult’s Law. In real life, it’s rare to work with a single pure liquid — usually, we deal with liquids that are mixtures of several different component substances. Some of the most common of these mixtures are created by dissolving a small amount of a certain chemical called a solute in a large amount of a chemical called a solvent to create a solution. In these cases, it’s useful to know an equation called Raoult’s Law (named for physicist François-Marie Raoult),^[4] which looks like this: P_solution=P_solventX_solvent. In this formula, the variables refer to;
- P_{solution_:} The vapor pressure of the entire solution (all of the component parts combined)
- P_solvent: The vapor pressure of the solvent
- X_solvent: The mole fraction of the solvent.
- Don’t worry if you don’t know terms like “mole fraction” — we’ll explain these in the next few steps.
2
Identify the solvent and solute in your solution. Before you calculate the vapor pressure of a mixed liquid, you need to identify the substances with which you are working. As a reminder, a solution is formed when a solute is dissolved in a solvent — the chemical that dissolves is always the solute and the chemical that does the dissolving is always the solvent.
- Let’s work through a simple example in this section to illustrate the concepts we’re discussing. For our example, let’s say that we want to find the vapor pressure of simple syrup. Traditionally, simple syrup is one part sugar dissolved in one part water, so we’ll say that sugar is our solute and water is our solvent.
- Note that the chemical formula for sucrose (table sugar) is C₁₂H₂₂O₁₁. This will be important soon.
3
Find the temperature of the solution. As we saw in the Clausius-Clapeyron section above, a liquid’s temperature will affect its vapor pressure. In general, the higher the temperature, the greater the vapor pressure — as the temperature increases, more of the liquid will evaporate and form vapor, increasing the pressure in the container.^[5]
- In our example, let’s say that the simple syrup’s current temperature is 298 K ( about 25 C).
4
Find the solvent’s vapor pressure. Chemical reference materials usually have vapor pressure values for many common substances and compounds, but these pressure values are usually only for when the substance is at 25 C/298 K or at its boiling point. If your solution is at one of these temperatures, you can use the reference value, but if not, you’ll need to find the vapor pressure at its current temperature.^[6]
- The Clausius-Clapeyron can help here — use the reference vapor pressure and 298 K (25 C) for P1 and T1 respectively.
- In our example, our mixture is at 25 C, so we can use our easy reference tables. We find that water at 25 C has a vapor pressure of 23.8 mm HG ^[7]
5
Find the mole fraction of your solvent. The last thing we need to do before we can solve is to find the mole fraction of our solvent. Finding mole fractions is easy: just convert your components to moles, then find what percentage of the total number of moles in the substance each component occupies. In other words, each component’s mole fraction equals (moles of component)/(total number of moles in the substance.)^[8]
- Let’s say that our recipe for simple syrup uses 1 liter (L) of water and 1 liter of sucrose (sugar.) In this case, we’ll need to find the number of moles in each. To do this, we’ll find the mass of each, then use the substance’s molar masses to convert to moles.
- Mass (1 L of water): 1,000 grams (g)
- Mass (1 L of raw sugar): Approx. 1,056.7 g^[9]
- Moles (water): 1,000 grams × 1 mol/18.015 g = 55.51 moles
- Moles (sucrose): 1,056.7 grams × 1 mol/342.2965 g = 3.08 moles (note that you can find sucrose’s molar mass from its chemical formula, C₁₂H₂₂O₁₁.)
- Total moles: 55.51 + 3.08 = 58.59 moles
- Mole fraction of water: 55.51/58.59 = 0.947
6
Solve. Finally, we have everything we need to solve our Raoult’s Law equation. This part is surprisingly easy: just plug your values in for the variables in the simplified Raoult’s Law equation at the beginning of this section (P_solution = P_solventX_solvent).^[10]
- Substituting our values, we get:
- P_solution = (23.8 mm Hg)(0.947)
- P_solution = 22.54 mm Hg. This makes sense — in mole terms, there’s only a little sugar dissolved in a lot of water (even though in real-world terms the two ingredients have the same volume), so the vapor pressure will only decrease slightly.

1
Be aware of Standard Temperature and Pressure conditions. Scientists frequently use a set of temperature and pressure values as a sort of convenient “default”. These values are called Standard Temperature and Pressure (or STP for short). Vapor pressure problems frequently make reference to STP conditions, so it’s handy to have these values memorized. STP values are defined as:^[11]
- Temperature: 273.15 K / 0 C / 32 F
- Pressure: 760 mm Hg / 1 atm / 101.325 kilopascals
2
Rearrange the Clausius-Clapeyron equation to find other variables. In our example in Section 1, we saw that the Clausius-Clapeyron equation is very useful for finding the vapor pressures of pure substances. However, not every question will ask you to find P1 or P2 — many will ask you to find a temperature value or even sometimes an ΔH_vap value. Luckily, in these cases, getting the right answer is simply a matter of rearranging the equation so that the variable you’re solving for is alone on one side of the equals sign.^[12]
- For instance, let’s say that we have an unknown liquid with a vapor pressure of 25 torr at 273 K and 150 torr at 325 K and we want to find this liquid’s enthalpy of vaporization (ΔH_vap). We could solve like this:
- ln(P1/P2) = (ΔH_vap/R)((1/T2) – (1/T1))
- (ln(P1/P2))/((1/T2) – (1/T1)) = (ΔH_vap/R)
- R × (ln(P1/P2))/((1/T2) – (1/T1)) = ΔH_vap Now, we plug in our values:
- 8.314 J/(K × Mol) × (-1.79)/(-0.00059) = ΔH_vap
- 8.314 J/(K × Mol) × 3,033.90 = ΔH_vap = 25,223.83 J/mol
3
Account for the vapor pressure of the solute when it produces vapor. In our Raoult’s Law example above, our solute, sugar, doesn’t produce any vapor on its own at normal temperatures (think — when was the last time you saw a bowl of sugar evaporate on your counter top?) However, when your solute does evaporate, this will affect your vapor pressure.^[13] We account for this by using a modified version of the Raoult’s Law equation: P_solution = Σ(P_componentX_component) The sigma (Σ) symbol means that we just need to add up all of the different components’ vapor pressures to find our answers.
- For example, let’s say that we have a solution made from two chemicals: benzene and toluene. The total volume of the solution is 120 milliliters (mL); 60 mL of benzene and 60 of toluene. The temperature of the solution is 25 C and the vapor pressures of each of these chemicals at 25 C is 95.1 mm Hg for benzene 28.4 mm Hg for toluene. Given these values, find the vapor pressure of the solution. We can do this as follows, using standard density, molar mass, and vapor pressure values for our two chemicals:
- Mass (benzene): 60 mL = .060 L &times 876.50 kg/1,000 L = 0.053 kg = 53 g
- Mass (toluene): .060 L &times 866.90 kg/1,000 L = 0.052 kg = 52 g
- Moles (benzene): 53 g × 1 mol/78.11 g = 0.679 mol
- Moles (toluene): 52 g × 1 mol/92.14 g = 0.564 mol
- Total moles: 0.679 + 0.564 = 1.243
- Mole fraction (benzene): 0.679/1.243 = 0.546
- Mole fraction (toluene): 0.564/1.243 = 0.454
- Solve: P_solution = P_benzeneX_benzene + P_tolueneX_toluene
- P_solution = (95.1 mm Hg)(0.546) + (28.4 mm Hg)(0.454)
- P_solution = 51.92 mm Hg + 12.89 mm Hg = 64.81 mm Hg

Add New Question

Question

How is vapor pressure affected by temperature?

As the temperature of a liquid or solid increases, its vapor pressure also increases. Conversely, vapor pressure decreases as the temperature decreases.
Question

How can I solve this problem? “The vapor pressure of pure water is 760mm at 25 degree Celsius. The vapor pressure of a solution containing 1 m of solution of glucose will be what?”

I suggest you study colligative properties. The pressure lowering of the water is PX’ as P stands for the pressure of pure solvent and X’ is the molar fraction of the solute. 1L of water has 1000g of water, so there are 1000/18 mols of water ~ 55.6 mols. So, there’s 56.6 mols of molecules for every 1L of solution (one comes from glucose and 55.6 from water as calculated). So, the solute molar fraction is 1/56.6 ~ 1.768.10^-2. So the pressure lowering is 760mmHg times 1.768.10^-2, which is ~ 13.44 mmHg. Finally, the vapor pressure of the solution is 760mmHg-13.44mmHg = 746.56mmHg.
Question

At an ambient temperature, what would be the vapor pressure of water?

You can use the Antoine’s equation to calculate the vapor pressure of any substance and any temperature. At an ambient pressure of 25 degrees Celsius, the vapor pressure of water is 23.8 torr.

See more answers

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

To use the Clausius Clapeyron equation above, temperature must be measured in Kelvin (denoted as K). If you have the temperature in Centigrade, then you need to convert it with the following formula: T_k = 273 + T_c
The methods above work because energy is directly proportional to the amount of heat supplied. The temperature of the liquid is the only environmental factor upon which the vapor pressure depends.

References

About This Article

Article SummaryX

To calculate vapor pressure, use the Clausius-Clapeyron equation, which includes the variables for the enthalpy of the liquid, the real gas constant, the starting and final temperatures, and the starting and final vapor pressures. Plug all of the known variables and constants into the equation, and isolate the unknown variable, which will be the pressure. Solve the equation for the pressure by following the order of operations. Be sure to label your final answer in atmospheres! For information on how to find the vapor pressure of dissolved solutions, read on!

Did this summary help you?

Thanks to all authors for creating a page that has been read 578,736 times.

Reader Success Stories

Noah Franklin

Dec 6, 2018

“I was helping my friend with a chemistry problem about vapor pressure and mole fractions. I couldn’t figure it…” more

Did this article help you?

Источник

Пример 1.
Вычислите давление пара над раствором,
содержащим 34,23 г сахара C₁₂H₂₂O₁₁
в 45,05 г воды при 65 ºС, если давление паров
воды при этой температуре равно 2,5·10⁴
Па.

Решение: Давление
пара над раствором нелетучего вещества
в растворителе всегда ниже давления
пара над чистым растворителем при той
же температуре. Относительное понижение
давления пара растворителя над раствором
согласно закону Рауля выражается
соотношением

где p₀– давление
пара над чистым растворителем;

p
– давление пара растворителя над
раствором;

n
– количество растворенного вещества,
моль;

N
– количество растворителя, моль.

M
(C₁₂H₂₂O₁₁)
= 342,30 г/моль;

M
(H₂O)
= 18,02 г/моль.

Количество
растворенного вещества и растворителя:
n=34,23/342,30=0,1
моль; N
= 45,05/18,02= 2,5моль.

Давление пара над
раствором:

Пример 2.
Рассчитайте молекулярную массу
неэлектролита, если 28,5 г этого вещества,
растворенного в 785 г воды, вызывают
понижение давления пара воды над
раствором на 52,37 Па при 40 °С. Давление
водяного пара при этой температуре
равно 7375,9 Па.

Решение:
Относительное
понижение давления пара растворителя
над раствором равно

Находим:

здесь m_x– масса
нэлектролита, молярная масса которого
M_x
г/моль.

0,309M_x+ 0,202=28,5;

0,309M_x
=28,298;

M_x=91,58
г/моль.

Молекулярная масса
неэлектролита равна ~ 92 г/моль.

1 Давление пара
эфира при 30⁰С
равно 8, 64∙10⁴
Па. Сколько молей неэлектролита надо
растворить в 50 молях эфира, чтобы понизить
давление пара при данной температуре
на 2666 Па? Ответ: 1,6 моля.

2 Понижение давления
пара над раствором, содержащим 0,4 моля
анилина в 3,04 кг сероуглерода, при
некоторой температуре, равно 1003,7 Па.
Давление пара сероуглерода при той же
температуре 1,0133∙10⁵
Па. Вычислите молекулярную массу
сероуглерода. Ответ: 76,0.

3 При некоторой
температуре давление пара над раствором,
содержащим 62 г фенола С₆H₅ОН
в 60 молях эфира, равно 0,507∙10⁵
Па. Найдите давление пара эфира при этой
температуре. Ответ: 0,513∙10⁵
Па.

4 Давление пара
воды при 50⁰С
равно 12334 Па. Вычислите давление пара
раствора, содержащего 50 г этиленгликоля
С₂Н₄(ОН)₂
в 900 г воды. Ответ: 12140 Па.

5 Определите
давление пара над раствором, содержащим
1,212∙10²³
молекул неэлектролита в 100 г воды при
100⁰С.
Давление пара воды при 100 °С равно
1,0133∙10⁵
Па. Ответ: 0,98∙10⁵
Па.

6 Давление водяного
пара при 65⁰С
равно 25003 Па. Определите давление пара
над раствором, содержащим 34,2 г сахара
С₁₂H₂₂O₁₁
в 90 г воды при этой температуре. Ответ:
24512 Па.

7 Вычислите
молекулярную массу глюкозы, если давление
водяного пара над раствором 27 г глюкозы
в 108 г воды при 100⁰С
равно 98775,3 Па. Ответ: 180.

8 Давление пара
воды при 100⁰С
равно 1,0133∙10⁵Па. Вычислите
давление водяного пара над 10%-ным
раствором мочевины СО(NН₂)₂
при этой температуре. Ответ:
0,98∙10⁵
Па.

9 Давление пара
над раствором 10,5 г неэлектролита в 200 г
ацетона (СН₃)₂CO
равно 21854,4 Па. Давление пара ацетона при
этой температуре равно 23939,35 Па. Найдите
молекулярную массу неэлектролита.
Ответ:32,0.

10 Рассчитайте
молекулярную массу неэлектролита, если
при 20⁰С
давление водяного пара над 63%-ным водным
раствором этого неэлектролита равно
1399,40 Па. Давление паров воды при этой
температуре равно 2335,42Па. Ответ: 46, 0.

11 Давление пара
воды при 25⁰С
составляет 3167 Па. Вычислить для этой
температуры давление пара раствора, в
450 г которого содержится 90 г глюкозы
С₆Н₁₂0₆.
Ответ: 3090 Па.

12 Давление пара
воды при 20⁰С
составляет 2338 Па. Сколько граммов сахара
C₁₂H₂₂O₁₁
следует
растворить в 720 г воды для получения
раствора, давление пара которого на
18,7 Па меньше давления пара воды? Вычислить
процентное содержание сахара в растворе.
Oтвет:
109 г; 13,5%.

13 При 0⁰С
давление пара эфира (C₂H₅)₂O
составляет 2465 Па. Найдите для той же
температуры: а) давление пара 5%-ного
раствора анилина С₆Н₅NH₂
в эфире; б) давление пара 10%-ного раствора
бензойной кислоты С₆Н₅СООН
в эфире. Ответ: а) 23,65 кПа; б) 23,09 Па.

14При 32⁰С
давление пара водного раствора некоторого
неэлектролита составляет 4721 Па, а
давление пара воды при той же температуре
4753 Па. Вычислить осмотическое давление
при той же температуре, приняв плотность
раствора равной единице. Ответ: 622 кПа.

15 Осмотическое
давление водного раствора глицерина
С₃Н₈О₃
составляет при 0⁰С
567,3 кПа. Приняв плотность раствора равной
единице, вычислить давление пара раствора
при 0⁰С,
если давление пара воды при той же
температуре составляет 610,5 Па. Ответ:
608 Па.

16 Чему равно
давление пара раствора, содержащего 46
г глицерина С₃Н₈0₃
в 900 г воды при 40⁰С,
если давление пара воды при той же
температуре 55,32 мм рт. ст. Ответ: 55,1 мм
рт.ст.

17 Давление пара
раствора 27 г неэлектролита в 108 г воды
при 75⁰С
равно 270,1 мм рт.ст. Вычислить молекулярную
массу неэлектролита, если
давление
пара воды при 75⁰С
равно 289,1 мм рт.ст. Ответ: 68,5.

18 Давление пара
раствора 8,89 г неэлектролита в 100 г воды
при 0⁰С
равно 4,54 мм рт.ст. Вычислить молекулярную
массу неэлектролита, если давление пара
воды при 0⁰С
равно 4,58 мм рт.ст. Ответ: 183,2.

19 Давление пара
водного раствора глюкозы С₆Н₁₂О₆
при 75⁰С
равно 250 мм рт.ст. Вычислить процентную
концентрацию раствора, если давление
пара воды при 75 °С равно 289,1 мм рт.ст.
Ответ: 58,3%.

20 Давление пара
чистого ацетона (СН₃)₂СO
при 20⁰С
равно 179,6 мм рт.ст. Вычислить давление
пара раствора 2,5 г камфоры С₁₀Н₁₆О
в 100 г ацетона
при той же температуре. Ответ: 177,9 мм
рт.ст.

21 Давление пара
раствора глицерина С₃Н₈О₃
в воде при 40⁰С
равно 50мм рт.ст. Сколько приблизительно
молекул воды приходится на одну молекулу
глицерина в указанном растворе? Давление
пара воды при 40⁰С
равно 55,32 мм рт.ст. Ответ: ~11.

22 Давление пара
эфира (С₂Н₅)₂O
при 30⁰С
равно 647,9 мм рт.ст.; давление пара раствора
3,1 г анилина в 370 г эфира при той же
температуре равно 643,58 мм рт.ст. Вычислить
молекулярную массу анилина. Ответ: 93.

23 Давление пара
воды при 40⁰С
равно 55,32 мм рт.ст. Вычислить понижение
давления пара при растворении 0,2 моль
вещества в 540 г воды. Ответ: 334 мм рт.ст.

24 Давление пара
эфира при 30⁰С
равно 648 мм рт.ст. Сколько молей вещества
надо растворить в 40 моль эфира, чтобы
понизить давление пара при данной
температуре на 10 мм рт.ст.? Ответ: 0,627
моль.

25 Давление пара
воды при 75⁰С
равно 289,1 мм рт. ст. В скольких молях воды
нужно растворить 0,4 моль вещества, чтобы
при данной температуре понизить давление
пара на 9 мм рт.ст.? Ответ: 12,45 моль.

26 Давление пара
воды при 55⁰С
равно 633,9 мм рт.ст. Вычислить давление
пара раствора, содержащего 29 г фенола
С₆Н₅ОH
в 900 г воды. Ответ: 630,7 мм рт.ст.

27 Давление пара
воды при 100 °С равно 760 мм рт.ст. Вычислить
давление пара над 4%-ным раствором
мочевины СО(NН₂)₂
при этой температуре. Ответ: 750,6 мм
рт.ст.

28
При некоторой
температуре давление пара над раствором,
содержащим 31 г анилина С₆H₅NH₂
в 30 моль эфира, равно 540,8 мм рт.ст. Вычислить
давление пара эфира при этой температуре.
Ответ: 546,8 мм рт.ст.

29 Над раствором,
содержащим 5,59 маннозы в 180 г воды,
давление пара при 80⁰С
равно 354 мм рт.ст., а давление пара воды
при этой температуре 355,1 мм рт.ст.
Вычислить молекулярную массу маннозы.
Ответ: 180.

30 При некоторой
температуре давление пара над раствором,
содержащим 2,44 г бензойной кислоты в
370,0 г эфира С₄Н₁₀О,
равно 917,5 мм рт.ст. Давление пара эфира
при этой температуре 921,2 мм рт.ст.
Вычислить молекулярную массу бензойной
кислоты. Ответ: 122.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

…

Любому раствору характерны те или иные физические свойства, к которым относятся и коллигативные свойства растворов. Это такие свойства, на которые не оказывает влияние природа растворенного вещества, а зависят они исключительно от количества частиц этого растворенного вещества.

К коллигативным свойствам растворов относятся:

Понижение давление паров
Повышение температуры кипения
Понижение температуры затвердевания (кристаллизации)
Осмотическое давление раствора.

Рассмотрим подробнее каждое из перечисленных свойств.

Понижение давления паров

Давление насыщенного пара (т.е. пара, который пребывает в состоянии равновесия с жидкостью) над чистым растворителем называется давлением или упругостью насыщенного пара чистого растворителя.

Если в некотором растворителе растворить нелетучее вещество, то равновесное давление паров растворителя при этом понижается, т.к. присутствие какого – либо вещества, растворенного в этом растворителе, затрудняет переход частиц растворителя в паровую фазу.

Экспериментально доказано, что такое понижение давления паров напрямую зависит от количества растворенного вещества. В 1887 г. Ф.М. Рауль описал количественные закономерности коллигативных свойств растворов.

Первый закон Рауля

Первый закон Рауля заключается в следующем:

Давление пара раствора, содержащего нелетучее растворенное вещество, прямо пропорционально мольной доле растворителя в данном растворе:

p = p₀ · χ_р-ль

p = p₀ · n_р-ля/(n_в-ва + n_р-ля), где

p — давление пара над раствором, Па;

p₀ — давление пара над чистым растворителем, Па;

χ_р-ль — мольная доля растворителя.

n_в-ва и n_р-ля – соответственно количество растворенного вещества и растворителя, моль.

Иногда Первому закону Рауля дают другую формулировку:

относительное понижение давления насыщенного пара растворителя над раствором равно мольной доле растворенного вещества:

(p₀ – p)/p₀ = χ_в-ва

(p₀ – p)/p₀ = n_в-ва/(n_в-ва + n_р-ля)

При этом принимаем, что χ_в-ва + χ_р-ль= 1

Изотонический коэффициент Вант-Гоффа

Для растворов электролитов данное уравнение приобретает несколько иной вид, в его состав входит изотонический коэффициент i:

p₀ – p = Δр

Δp = i · p₀ · χ_в-ва, где

Δp — изменение давления паров раствора по сравнению с чистым растворителем;

χ_в-ва — мольная доля вещества в растворе

i – изотонический коэффициент.

Изотонический коэффициент (или фактор Вант-Гоффа) — это параметр, не имеющий размерности, который характеризует поведение какого – либо вещества в растворе.

То есть, изотонический коэффициент показывает, разницу содержания частиц в растворе электролита по сравнению с раствором неэлектролита такой же концентрации. Он тесно связан связан с процессом диссоциации, точнее, со степенью диссоциации и выражается следующим выражением:

i = 1+α(n-1), где

n – количество ионов, на которые диссоциирует вещество.

α – степень диссоциации.

Повышение температуры кипения или понижение температуры затвердевания (кристаллизации). Второй закон Рауля

Равновесное давление паров жидкости имеет тенденцию к увеличению с ростом температуры, жидкость начинает кипеть, при уравнивании давления ее паров и внешнего давления.

При наличии нелетучего вещества, давление паров раствора снижается, и раствор будет закипать при более высокой температуре, по сравнению с температурой кипения чистого растворителя.

Температура замерзания жидкости также определяется той температурой, при которой давления паров жидкой и твердой фаз уравниваются.

Ф.М. Рауль доказал, что повышение температуры кипения, так же как и понижение температуры замерзания разбавленных растворов нелетучих веществ, прямо пропорционально моляльной концентрации раствора и не зависит от природы растворённого вещества. Это правило известно как Второй закон Рауля:

ΔT_кип= E· m_в-ва,

ΔT_крист= K·m_в-ва, где

E—эбулиоскопическая константа,

K — криоскопическая константа,

m_в-ва — моляльность вещества в растворе.

Растворы электролитов не подчиняются Законам Рауля. Но для учёта всех несоответствий Вант-Гофф предложил ввести в приведённые уравнения поправку в виде изотонического коэффициента i, учитывающего процесс распада на ионы молекул растворённого вещества:

ΔT_кип= i·E·m_в-ва

ΔT_крист= i·К·m_в-ва

Осмотическое давление раствора

Некоторые материалы имеют способность к полупроницаемости, т.е. им свойственно пропускать частицы определенного вида и не пропускать частицы другого вида.

Перемещение молекул растворителя (но не растворенного, в нем вещества), через полупроницаемую мембрану в раствор с большей концентрацией из более разбавленного представляет собой такое явление как осмос.

ОСМОС

Представим два таких раствора, которые разделены полупроницаемой мембраной, как показано на рисунке выше. Растворы стремятся к выравниванию концентраций, поэтому вода будет проникать в раствор, тем самым уменьшая его концентрацию.

Для того, чтобы осмос приостановить, необходимо приложить внешнее давление к раствору. Такое давление, которое требуется приложить, называется осмотическим давлением.

Осмотическое давление и концентрацию раствора неэлектролита позволяет связать уравнение Вант — Гоффа, которое напоминает уравнение идеального газа Клапейрона – Менделеева:

π = C·R·T,

где C — молярная концентрация раствора, моль/м³,

R — универсальная газовая постоянная (8,314 Дж/моль·К);

T — абсолютная температура раствора.

Преобразуем уравнение следующим образом:

C = n/V = m/(M·V)

π = т·R·T / M·V или

π·V = m·R·T /M

Для растворов электролитов осмотическое давление определяется уравнением, в которое входит изотонический коэффициент:

π^` = i·C·R·T ,

где i — изотонический коэффициент раствора.

Для растворов электролитов i > 1, а для растворов неэлектролитов i = 1.

Если полупроницаемой перегородкой разделены два раствора, имеющие одинаковое осмотическое давление, то перемещение растворителя через перегородку отсутствует. Такие растворы называются изотоническими.

Раствор, с меньшим осмотическим давлением, по сравнению с более концентрированным раствором, называют гипотоническим, а раствор с большей концентрацией – гипертоническим.

Источник

Загрузить PDF

Вы когда-нибудь оставляли бутылку воды на несколько часов под палящим солнцем и слышали «шипящий» звук, открывая ее? Этот звук вызван давлением пара. В химии давление пара – это давление, оказываемое парами жидкости, которая испаряется в герметично закрытом сосуде.^[1] Чтобы найти давление пара при данной температуре, воспользуйтесь уравнением Клапейрона-Клаузиуса: ln(P1/P2) = (ΔH_vap/R)((1/T2) – (1/T1)).

1
Запишите уравнение Клапейрона-Клаузиуса, которое используется для расчета давления пара при его изменении с течением времени.^[2] Эту формулу можно использовать в большинстве физических и химических задач. Уравнение выглядит следующим образом: ln(P1/P2) = (ΔH_vap/R)((1/T2) – (1/T1)), где:
- ΔH_vap – энтальпия испарения жидкости. Ее, как правило, можно найти в таблице в учебниках по химии.
- R – газовая постоянная, равная 8,314 Дж/(K×моль)^[3]
- T1 – начальная температура (при которой давление пара известно).
- T2 – конечная температура (при которой давление пара неизвестно).
- P1 и P2 – давление пара при температуре T1 и T2, соответственно.
2
Подставьте в уравнение Клапейрона-Клаузиуса данные вам значения величин. В большинстве задач даются два значения температуры и значение давления или два значения давления и значение температуры.
- Например, в сосуде находится жидкость при температуре 295 К, а давление ее паров равно 1 атмосфере (1 атм). Найдите давление паров при температуре 393 K. Здесь вам даны два значения температуры и значение давления, поэтому вы можете найти другое значение давления при помощи уравнения Клапейрона-Клаузиуса. Подставив данные вам значения в формулу, вы получите: ln(1/P2) = (ΔH_vap/R)((1/393) – (1/295)).
- Обратите внимание, что в уравнении Клапейрона-Клаузиуса температура всегда измеряется в кельвинах, а давление в любых единицах измерения (но они должны быть одинаковыми для Р1 и Р2).
3
Подставьте константы. Уравнение Клапейрона-Клаузиуса содержит две константы: R и ΔH_vap. R всегда равна 8,314 Дж/(К×моль). Значение ΔH_vap (энтальпия испарения) зависит от вещества, давление паров которого вы пытаетесь найти; эту константу, как правило, можно найти в таблице в учебниках по химии или на сайтах (например, здесь).^[4]
- В нашем примере допустим, что в сосуде находится вода. ΔH_vap воды равна 40,65 кДж/моль или равна 40650 Дж/моль.
- Подставьте константы в формулу и получите: ln(1/P2) = (40650/8314)((1/393) – (1/295)).
4
Решите уравнение при помощи алгебраических операций.
- В нашем примере неизвестная переменная находится под знаком натурального логарифма (ln). Для избавления от натурального логарифма превратите обе стороны уравнения в степень математической константы «е». Другими словами, ln(x) = 2 → e^ln(x) = e² → x = e².
- Теперь решите уравнение:
- ln(1/P2) = (40650/8,314)((1/393) – (1/295))
- ln(1/P2) = (4889,34)(-0,00084)
- (1/P2) = e^(-4,107)
- 1/P2 = 0,0165
- P2 = 0.0165^-1 = 60,76 атм. Это имеет смысл, так как повышение температуры в герметично закрытом сосуде на 100 градусов приведет к увеличению парообразования, что значительно увеличит давление пара.
Реклама

1
Запишите закон Рауля. В реальной жизни чистые жидкости встречаются редко; зачастую мы имеем дело с растворами. Раствор получается при добавлении небольшого количества определенного химического вещества, называемого «растворенное вещество», в большее количество другого химического вещества, называемого «растворитель». В случаях растворов пользуйтесь законом Рауля:^[5]P_{раствор} = P_{растворитель}X_{растворитель}, где:
- P_{раствор} – давление паров раствора.
- P_{растворитель} – давление паров растворителя.
- X_{растворитель} – мольная доля растворителя.
- Если вы не знаете, что такое «мольная доля», читайте дальше.
2
Определите, какое вещество будет растворителем, а какое – растворенным веществом. Напомним, что растворенное вещество – это вещество, растворяемое в растворителе, а растворитель – это вещество, растворяющее растворенное вещество.
- Рассмотрим пример сиропа. Для получения сиропа одну часть сахара растворяют в одной части воды, поэтому сахар – это растворенное вещество, а вода – это растворитель.^[6]
- Обратите внимание, что химическая формула сахарозы (обыкновенного сахара): C₁₂H₂₂O₁₁. Она понадобится нам в дальнейшем.
3
Найдите температуру раствора, так как она будет влиять на давление его пара. Чем выше температура, тем выше давление паров, так как с ростом температуры растет парообразование.
- В нашем примере допустим, что температура сиропа равна 298 K (около 25˚С).
4
Найдите давление паров растворителя. В справочниках по химии приводятся значения давления паров многих распространенных химических веществ, но, как правило, такие значения даны при температуре веществ в 25°С/298 К или при их температурах кипения. Если в задаче вам даны такие температуры, используйте значения из справочников; в противном случае вам необходимо вычислить давление паров при данной температуре вещества.
- Для этого воспользуйтесь уравнением Клапейрона-Клаузиуса, подставив в него давление паров и температуру 298 К (25˚С) вместо P1 и T1, соответственно.
- В нашем примере температура раствора равна 25°С, поэтому пользуйтесь значением из справочных таблиц – давление паров воды при 25°С равно 23,8 мм ртутного столба.^[7]
5
Найдите мольную долю растворителя. Для этого найдите отношение числа молей вещества к общему числу молей всех веществ, имеющихся в растворе. Другими словами, мольная доля каждого вещества равна (число молей вещества)/(общее число молей всех веществ).
- Допустим, что для приготовления сиропа вы использовали 1 л воды и 1 л сахарозы (сахара). В этом случае необходимо найти число молей каждого вещества. Для этого нужно найти массу каждого вещества, а затем использовать молярные массы этих веществ, чтобы получить моли.
- Масса 1 л воды = 1000 г
- Масса 1 л сахара = 1056,7г^[8]
- Моль (вода): 1000 г×1 моль/18,015 г = 55,51 моль
- Моль (сахароза): 1056,7 г×1 моль/342,2965 г = 3,08 моль (обратите внимание, что вы можете найти молярную массу сахарозы из ее химической формулы C₁₂H₂₂O₁₁).
- Общее число молей: 55,51 + 3,08 = 58,59 моль
- Мольная доля воды: 55,51/58,59 = 0,947.
6
Теперь подставьте данные и найденные значения величин в уравнение Рауля, приведенное в начале этого раздела (P_{раствор} = P_{растворитель}X_{растворитель}).
- В нашем примере:
- P_{раствор} = (23,8 мм рт. ст.)(0,947)
- P_{раствор} = 22,54 мм рт. ст. Это имеет смысл, так как в большом количестве воды растворено небольшое количество сахара (если измерять в молях; в литрах их количество одинаково), поэтому давление паров незначительно уменьшится.
Реклама

1
Определение стандартных условий. Зачастую в химии используются значения температуры и давления как своего рода значения «по умолчанию». Такие значения называются стандартными температурой и давлением (или стандартными условиями). В задачах на давление пара часто упоминаются стандартные условия, поэтому лучше запомнить стандартные значения:^[9]
- Температура: 273,15 K/0˚C/32 F
- Давление: 760 мм рт.ст./1 атм./101,325 кПа
2
Перепишите уравнение Клапейрона-Клаузиуса так, чтобы найти другие переменные. В первом разделе этой статьи было показано, как вычислять давления паров чистых веществ. Однако не во всех задачах требуется найти давление P1 или P2; во многих задачах нужно вычислить температуру или значение ΔH_vap. В таких случаях перепишите уравнение Клапейрона-Клаузиуса, обособив неизвестную величину на одной стороне уравнения.
- Например, дана неизвестная жидкость, давление пара которой равно 25 торр при 273 К и 150 Торр при 325 К. Нужно найти энтальпию испарения этой жидкости (то есть ΔH_vap). Решение этой задачи:
- ln(P1/P2) = (ΔH_vap/R)((1/T2) – (1/T1))
- (ln(P1/P2))/((1/T2) – (1/T1)) = (ΔH_vap/R)
- R × (ln(P1/P2))/((1/T2) – (1/T1)) = ΔH_vap Теперь подставьте данные вам значения:
- 8,314 Дж/(K × моль) × (-1,79)/(-0,00059) = ΔH_vap
- 8,314 Дж/(K × моль) × 3033,90 = ΔH_vap = 25223,83 Дж/моль
3
Учтите давления пара растворенного вещества. В нашем примере из второго раздела этой статьи растворенное вещество – сахар – не испаряется, но если растворенное вещество производит пар (испаряется), давление такого пара следует учесть. Для этого воспользуйтесь модифицированным видом уравнения Рауля: P_{раствор} = Σ(P_{вещество}X_{вещество}), где символ Σ (сигма) означает, что необходимо сложить значения давлений паров всех веществ, из которых состоит раствор.
- Например, рассмотрим раствор, состоящий из двух химических веществ: бензола и толуола. Общий объем раствора 120 миллилитров (мл); 60 мл бензола и 60 мл толуола. Температура раствора равна 25°С, а давление паров при 25°С равно 95,1 мм рт.ст. для бензола и 28,4 мм рт.ст. для толуола. Необходимо вычислить давление паров раствора. Мы можем сделать это при помощи плотностей веществ, их молекулярных масс и значений давления паров:
- Масса (бензол): 60 мл = 0,06 л × 876,50 кг/1000 л = 0,053 кг = 53 г
- Масса (толуол): 0,06 л × 866,90 кг/1000 л = 0,052 кг = 52 г
- Моль (бензол): 53 г × 1 моль/78,11 г = 0,679 моль
- Моль (толуол): 52 г × 1 моль/92,14 г = 0,564 моль
- Общее число молей: 0,679 + 0,564 = 1,243
- Мольная доля (бензол): 0,679/1,243 = 0,546
- Мольная доля (толуол): 0,564/1,243 = 0,454
- Решение: P_{раствор} = P_бензолX_бензол + P_толуолX_толуол
- P_{раствор} = (95,1 мм рт. ст.)(0,546) + (28,4 мм рт. ст.)(0,454)
- P_{раствор} = 51,92 мм рт. ст. + 12,89 мм рт. ст. = 64,81 мм рт. ст.
Реклама

Советы

Для использования уравнения Клапейрона Клаузиуса температура должна быть указана в градусах Кельвина (обозначается К). Если у вас дана температура по Цельсию, необходимо конвертировать ее при помощи следующей формулы: T_k = 273 + T_c
Описанный выше метод работает, потому что энергия прямо пропорциональна количеству тепла. Температура жидкости является единственным фактором окружающей среды, от которой зависит давление паров.

Об этой статье

Эту страницу просматривали 27 712 раз.

Была ли эта статья полезной?

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 24 сентября 2021 года; проверки требуют 4 правки.

Зако́ны Рау́ля — общее название открытых французским химиком Ф. М. Раулем в 1887 году количественных закономерностей, описывающих некоторые коллигативные (зависящие от концентрации, но не от природы растворённого вещества) свойства растворов.

Первый закон Рауля[править | править код]

Первый закон Рауля связывает давление насыщенного пара над раствором с его составом; он формулируется следующим образом:

Парциальное давление насыщенного пара компонента раствора прямо пропорционально его мольной доле в растворе, причём коэффициент пропорциональности равен давлению насыщенного пара над чистым компонентом.

Для бинарного раствора, состоящего из компонентов А и В (компонент А считаем растворителем), удобнее использовать другую формулировку:

Относительное понижение парциального давления пара растворителя над раствором не зависит от природы растворённого вещества и равно его мольной доле в растворе.

${{{rm{(}}P^o _A - P_A {rm{)}}} over {P^o _A }} = X_B$

На поверхности оказывается меньше молекул растворителя, способных испаряться — ведь часть места занимает растворённое вещество.

Растворы, для которых выполняется закон Рауля, называются идеальными. Идеальными при любых концентрациях являются растворы, компоненты которых очень близки по физическим и химическим свойствам (оптические изомеры, гомологи и т. п.), и образование которых не сопровождается изменением объёма и выделением либо поглощением теплоты. В этом случае силы межмолекулярного взаимодействия между однородными и разнородными частицами примерно одинаковы, и образование раствора обусловлено лишь энтропийным фактором.

Отклонения от закона Рауля[править | править код]

Растворы, компоненты которых существенно различаются по физическим и химическим свойствам, подчиняются закону Рауля лишь в области очень малых концентраций; при больших концентрациях наблюдаются отклонения от закона Рауля. Случай, когда истинные парциальные давления паров над смесью больше, чем вычисленные по закону Рауля, называют положительными отклонениями, а противоположные случаи — отрицательными отклонениями.

Причиной отклонений от закона Рауля является то обстоятельство, что однородные частицы взаимодействуют друг с другом иначе, чем разнородные (сильнее в случае положительных и слабее в случае отрицательных отклонений).

Реальные растворы с положительными отклонениями от закона Рауля образуются из чистых компонентов с поглощением теплоты (ΔН_раств > 0); объём раствора оказывается больше, чем сумма исходных объёмов компонентов (ΔV > 0). Растворы с отрицательными отклонениями от закона Рауля образуются с выделением теплоты (ΔН_раств < 0); объём раствора в этом случае будет меньше, чем сумма исходных объёмов компонентов (ΔV < 0).

Второй закон Рауля[править | править код]

Отличие давления паров над раствором от давления паров над чистым растворителем существенно влияет на процессы кристаллизации и кипения. Из первого закона Рауля выводятся два следствия, касающиеся понижения температуры замерзания и повышения температуры кипения растворов, которые в объединённом виде известны как второй закон Рауля.

Понижение температуры кристаллизации растворов[править | править код]

См. также: понижение точки замерзания (англ. Freezing-point depression)

Условием кристаллизации является равенство давления насыщенного пара растворителя над раствором давлению пара над твёрдым растворителем. Поскольку давление пара растворителя над раствором всегда ниже, чем над чистым растворителем, это равенство всегда будет достигаться при температуре более низкой, чем температура замерзания растворителя. Так, океанская вода начинает замерзать при температуре около −2 °C.

Разность между температурой кристаллизации растворителя T°_fr и температурой начала кристаллизации раствора T_fr есть понижение температуры кристаллизации.

Понижение температуры кристаллизации бесконечно разбавленных растворов не зависит от природы растворённого вещества и прямо пропорционально моляльной концентрации раствора.

$T_{fr}^o - T_{fr} = Delta T_{fr} = Km$

Поскольку по мере кристаллизации растворителя из раствора концентрация последнего возрастает, растворы не имеют определённой температуры замерзания и кристаллизуются в некотором интервале температур.

Повышение температуры кипения растворов[править | править код]

Жидкость кипит при той температуре, при которой общее давление насыщенного пара становится равным внешнему давлению. Если растворённое вещество нелетуче (то есть давлением его насыщенных паров над раствором можно пренебречь), то общее давление насыщенного пара над раствором равно парциальному давлению паров растворителя. В этом случае давление насыщенных паров над раствором при любой температуре будет меньше, чем над чистым растворителем, и равенство его внешнему давлению будет достигаться при более высокой температуре. Таким образом, температура кипения раствора нелетучего вещества T_b всегда выше, чем температура кипения чистого растворителя при том же давлении T°_b.

Повышение температуры кипения бесконечно разбавленных растворов нелетучих веществ не зависит от природы растворённого вещества и прямо пропорционально моляльной концентрации раствора

$T_{b} - T_{b}^o = Delta T_{b} = Em$

Криоскопическая и эбулиоскопическая константы[править | править код]

Коэффициенты пропорциональности К и Е в приведённых выше уравнениях — соответственно, криоскопическая и эбулиоскопическая постоянные растворителя, имеющие физический смысл понижения температуры кристаллизации и повышения температуры кипения раствора с концентрацией 1 моль/кг. Для воды они равны 1,86 и 0,52 K·моль⁻¹·кг, соответственно. Поскольку одномоляльный раствор не является бесконечно разбавленным, второй закон Рауля для него в общем случае не выполняется, и величины этих констант получают экстраполяцией зависимости из области малых концентраций до m = 1 моль/кг.

Для водных растворов в уравнениях второго закона Рауля моляльную концентрацию иногда заменяют молярной. В общем случае такая замена неправомерна, и для растворов, плотность которых отличается от 1 г/см³, может привести к существенным ошибкам.

Второй закон Рауля даёт возможность экспериментально определять молекулярные массы соединений, неспособных к диссоциации в данном растворителе; его можно использовать также для определения степени диссоциации электролитов.

Растворы электролитов[править | править код]

Законы Рауля не выполняются для растворов (даже бесконечно разбавленных), которые проводят электрический ток — растворов электролитов. Для учёта этих отклонений Вант-Гофф внёс в приведённые выше уравнения поправку — изотонический коэффициент i, неявно учитывающий диссоциацию молекул растворённого вещества:

${displaystyle Delta T_{fr}=iKm}$

;

${displaystyle Delta T_{b}=iEm}$

Неподчинение растворов электролитов законам Рауля и принципу Вант-Гоффа послужили отправной точкой для создания С. А. Аррениусом теории электролитической диссоциации.

Литература[править | править код]

Стромберг А. Г., Семченко Д. П. Физическая химия — М. : Высшая школа, 1999. — 527 с.
Даниэльс Ф., Олберти Р. Физическая химия — М. : Мир, 1978. — 645 с.

Источник

References

About This Article

Reader Success Stories

Did this article help you?

Понижение давления паров

Первый закон Рауля

Изотонический коэффициент Вант-Гоффа

Повышение температуры кипения или понижение температуры затвердевания (кристаллизации). Второй закон Рауля

Осмотическое давление раствора

Советы

Об этой статье

Была ли эта статья полезной?

Первый закон Рауля[править | править код]

Отклонения от закона Рауля[править | править код]

Второй закон Рауля[править | править код]

Понижение температуры кристаллизации растворов[править | править код]

Повышение температуры кипения растворов[править | править код]

Криоскопическая и эбулиоскопическая константы[править | править код]

Растворы электролитов[править | править код]

Литература[править | править код]

Вам также может понравиться

Как исправить залипающую кнопку

Как найти силу для трех зарядов

Как найти входящие звонки на мтс

Добавить комментарий Отменить ответ