Давление поршня, Гидравлический пресс
Если на жидкость действует внешнее давление, то вследствие
подвижности молекул это давление передается одинаково во все стороны.
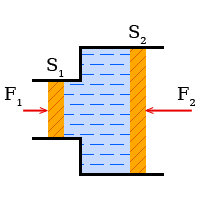
В гидравлическом прессе на все поршни действует одинаковое давление. Однако, вследствие того,
что площади поршней различны, силы действующие на них, не одинаковы.
Согласно формуле:
Гидравлический пресс уравновешивает давление в ступенях.
Силы относятся друг к другу как площади поршней, т.е. как квадраты диаметров поршней:
[
p = frac{F_1}{S_1} = frac{F_2}{S_2}
]
или
[
frac{F_1}{F_2} = frac{S_1}{S_2} = frac{d_1^2}{d_2^2}
]
Это соотношение лежит в основе действия различных подъемных механизмов (домкрат, подъемник),
гидравлических тормозов, преобразователей давления и т.д.
Давление поршня, Гидравлический пресс |
стр. 500 |
|---|
Асламазов Л. Гидростатика // Квант. – 1995. – № 1. – С. 51-55.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
Давление и силы давления
Жидкость оказывает давление на стенки сосуда, в котором она находится, или на любую другую поверхность, соприкасающуюся с ней. Давление – величина скалярная. Оно измеряется абсолютной величиной нормальной (перпендикулярной поверхности) силы, действующей со стороны жидкости на единицу площади поверхности:
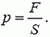
Давление в различных точках поверхности может быть разным. Поэтому площадь S мы должны брать достаточно маленькой.
По закону Паскаля давление жидкости не зависит от ориентации поверхности. Как бы ни была расположена поверхность в данном месте жидкости, давление на нее будет одним и тем же.
Сила давления всегда перпендикулярна поверхности. В обычных условиях она направлена так, как если бы жидкость стремилась расшириться.
Задача 1. В сосуд, имеющий форму куба с ребром a, налита доверху жидкость плотностью ρ. Определите силы давления жидкости на дно и стенки сосуда.
Давление жидкости на дно сосуда равно весу столба жидкости высотой a с площадью основания, равной единице: 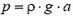 , где g – ускореннее свободного падения. (Для простоты здесь и в других задачах, где это специально не оговорено, предполагается, что атмосферное давление отсутствует). Сила давления на дно сосуда (рис. 1, а)
, где g – ускореннее свободного падения. (Для простоты здесь и в других задачах, где это специально не оговорено, предполагается, что атмосферное давление отсутствует). Сила давления на дно сосуда (рис. 1, а)
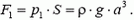
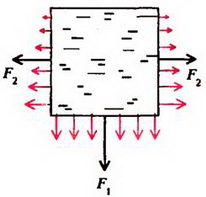
а

б
Рис. 1
Давление на боковую грань куба будет зависеть от расстояния до поверхности жидкости. На глубине h давление 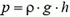 . Так как давление изменяется с глубиной по линейному закону (рис. 1. б), для определения силы давления мы должны среднее давление
. Так как давление изменяется с глубиной по линейному закону (рис. 1. б), для определения силы давления мы должны среднее давление
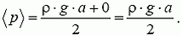
умножить на площадь боковой грани
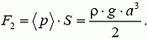
Задача 2. В цилиндрический сосуд диаметром D = 0,7 м вставлен поршень с длинной вертикальной трубкой диаметром d = 0,05 м (рис. 2). Максимальная сила трения между поршнем и стенками сосуда Fтp = 100 Н. Через трубку в сосуд наливают воду. При каком уровне воды в трубке H поршень начнет двигаться? Чему будет равна при этом сила давления воды на дно сосуда? Поршень расположен на высоте h = 0,2 м от дна сосуда. Плотность воды ρ = 103 кг/м3. Массой поршня с трубкой пренебречь.
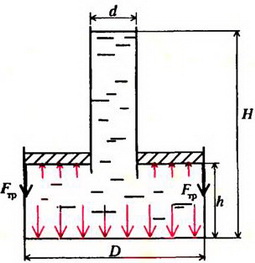
Рис. 2
Давление в жидкости на уровне поверхности поршня определяется расстоянием от этого уровня до свободной поверхности жидкости:
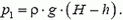
Поршень начнет двигаться, когда сила давления на него со стороны жидкости станет равной максимальной силе трения:
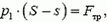
где 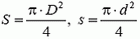 – плошали поперечных сечений сосуда и трубки соответственно. Подставляя сюда выражение для p1, находим
– плошали поперечных сечений сосуда и трубки соответственно. Подставляя сюда выражение для p1, находим
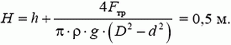
Давление на дно сосуда 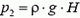 .
.
Сила давления 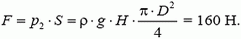
Задача 3. Длинная вертикальная труба с поршнем опущена одним концом в сосуд с водой. Вначале поршень находится у поверхности воды, затем его медленно поднимают. Как зависит сила, прикладываемая к поршню, от высоты h ее поднятия? Площадь поперечного сечения трубы S, атмосферное давление p0. Изменением уровня воды в сосуде, массой поршня и ею трением о стенки трубы пренебречь.
При поднятии поршня вода под действием атмосферного давления будет вначале заполнять трубу (рис 3, а). Давление в трубе на уровне жидкости в сосуде равно атмосферному давлению p0. Давление воды на поршень меньше атмосферного на величину веса столба жидкости высотой h и площадью основания, равной единице:
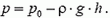
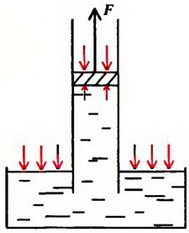
а
б
Рис. 3
Сверху на поршень по-прежнему действует атмосферное давление. Поэтому для удержания поршня на высоте h к нему надо приложить силу, равную
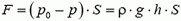
и направленную вверх.
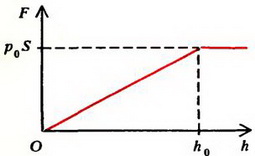
С увеличением h давление воды на поршень будет уменьшаться. На высоте
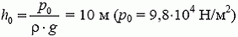
давление обратится в ноль. При дальнейшем поднятии поршня уровень воды в трубе изменяться не будет, тан как сила атмосферного давления, действующая на столб жидкости в трубе снизу, уравновесится силой тяжести. Для удержания поршня на высоте h > h0 к нему надо приложить силу 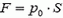 .
.
Зависимость прикладываемой к поршню силы F от высоты его поднятия h изображена графически на рисунке 3, б.
Высота столба воды в трубе 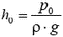 , очевидно, может служить для измерения атмосферного давлении p0. Однако обычно в барометрах используют ртуть, и нормальному атмосферному давлению тогда соответствует значительно меньшая высота столба ртути
, очевидно, может служить для измерения атмосферного давлении p0. Однако обычно в барометрах используют ртуть, и нормальному атмосферному давлению тогда соответствует значительно меньшая высота столба ртути 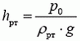 = 0,76 м (плотность ртути ρрт = 1,36×104 кг/м3).
= 0,76 м (плотность ртути ρрт = 1,36×104 кг/м3).
Примером другого гидростатического устройства, широко используемого в практике, являются сообщающиеся сосуды. Известен закон сообщающихся сосудов: если давление над жидкостью в сосудах одинаково, то уровни жидкости в них равны. Нетрудно доказать этот закон для случая цилиндрических сосудов (рис. 4). Так как жидкость в соединительной трубке находится в равновесии, то давления на нее с обеих сторон должны быть одинаковы. Поэтому равны и уровни жидкости в сосудах.
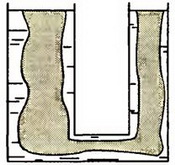
Рис. 4
В общем случае для доказательства закона сообщающихся сосудов можно воспользоваться принципом отвердевания, который часто используют в гидростатике. Суть этого принципа заключается в следующем: всегда можно представить себе, что часть жидкости отвердела – равновесие оставшейся части жидкости от этого не нарушится. Так, в цилиндрических сообщающихся сосудах мы можем мысленно выделить часть жидкости, которая заполняла бы сообщающиеся сосуды любой извилистой формы (см. рис. 4), и представить себе, что остальная часть жидкости отвердевает. Тогда равновесие выделенной нами части жидкости не нарушится, и, следовательно, уровни жидкости в извилистых сообщающихся сосудах будут такими же, какими были в цилиндрических сосудах, т.е. одинаковыми.
Закон сообщающихся сосудов справедлив только для однородной жидкости. Если в сосуды налиты жидкости разных плотностей, то уровни в сосудах могут быть разными.
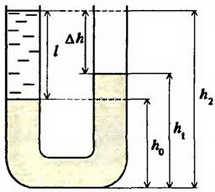
Задача 4. В U – образную трубку налита ртуть. Поверх ртути в одно из колен трубки налили воду (рис. 5, a). Высота столбика воды l = 0,1 м. Определите разность уровней жидкостей в коленах трубки. Нарисуйте график зависимости давления в обоих коленах трубки от высоты. Плотность ртути ρрт = 1,36×104 кг/м3, плотность воды ρрт = 103 кг/м3. Атмосферное давление не учитывайте.
а
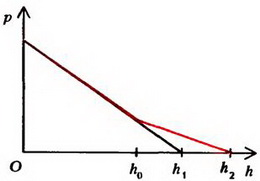
б
Рис. 5
Давления на ртуть на уровне ho соприкосновения воды и ртути в обоих коленах должны быть одинаковы (закон сообщающихся сосудов для однородной жидкости). Поэтому
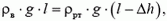
где разность уровней h2 – h1 обозначена через Δh. Отсюда
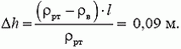
Давление в колене, содержащем только ртуть, меняется с высотой h по закону
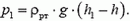
Эта формула справедлива и в изогнутой части трубки. (Представите себе, что изогнутое колено сообщается с прямым цилиндрическим сосудом, в котором тоже находится ртуть. Тогда давления на одинаковой высоте в обоих сосудах должны быть равны). В другом колене в области 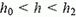 , где находится только вода, давление
, где находится только вода, давление
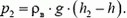
Ниже уровня h0 зависимость давления от высоты дается той же формулой, что и в первом колене:
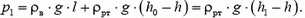
Зависимость давления в коленах трубки от высоты изображена графически на рисунке 5, б. Как видно, выше уровня h0 давления на одинаковой высоте разные.
Выталкивающая сила
На тело, погруженное в жидкость, как известно, действует выталкивающая сила. Эта сила является равнодействующей сил давления жидкости на тело. Найдем, например, выталкивающую силу, действующую на кубик с ребром a целиком погруженный в жидкость плотностью ρ. Сила давления со стороны жидкости на верхнюю грань кубика равна
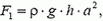
где h – расстояние от этой грани до поверхности жидкости (для простоты мы считаем, что плоскость верхней грани кубика параллельна поверхности жидкости). На нижнюю грань кубика действует сила
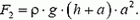
Силы давления на боковые грани кубика уравновешивают друг друга. Равнодействующая сил давлении, т.е. выталкивающая сила, равна
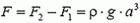
и направлена вертикально вверх. Мы получили закон Архимеда: выталкивающая сила равна силе тяжести, действующей на вытесненную телом жидкость.
В общем случае закон Архимеда можно доказать с помощью принципа отвердевания. Мысленно заменим погруженное тело жидкостью. Очевидно, что эта жидкость будет находиться в равновесии. Следовательно, сила тяжести, действующая на нее, уравновешена силами давления со стороны окружающей жидкости. Если теперь представить себе, что выделенная нами часть отвердела, то равновесие оставшейся части не нарушится, и поэтому не изменятся силы давления на отвердевшую жидкость. Равнодействующая этих сил будет по-прежнему равна силе тяжести.
При доказательстве мы считали, что тело целиком погружено в жидкость. Однако аналогичные рассуждения легко провести и в случае, когда только часть тела находится в жидкости (проделайте это сами). И мы опять получим, что выталкивающая сила равна силе тяжести, действующей на вытесненную телом жидкость:
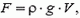
где ρ – плотность жидкости, V – объем погруженной в жидкость части тела, g –ускорение свободного падения.
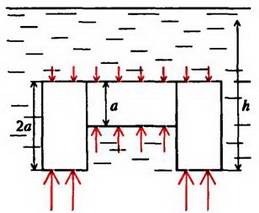
Задача 5. На дне водоема установлена П – образная конструкция из трех одинаковых балок, соединенных между собой (рис. 6). Как зависит сила давления этой конструкции на дно от уровня воды в водоеме? Рассмотрите два случая: 1) вода подтекает под опоры; 2) опоры плотно соприкасаются с дном. Балки имеют квадратное сечение со стороной a, длина балки l = 2a. Плотность материала балок ρ0. плотность воды ρ.
а
б
в
Рис. 6
Сила давления Fд на дно определяется разностью силы тяжести конструкции 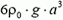 и выталкивающей силы F. В первом случае, когда вода подтекает под опоры (например, если дно водоема покрыто галькой – рисунок 6, а), справедлив закон Архимеда. Зависимость выталкивающей силы от высоты уровня воды h дается формулами:
и выталкивающей силы F. В первом случае, когда вода подтекает под опоры (например, если дно водоема покрыто галькой – рисунок 6, а), справедлив закон Архимеда. Зависимость выталкивающей силы от высоты уровня воды h дается формулами:
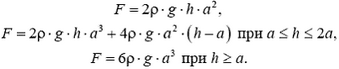
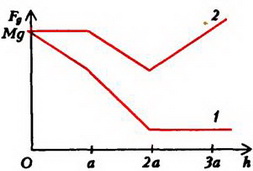
Соответствующий график для силы Fд изображен на рисунке 6, в – он обозначен цифрой 1.
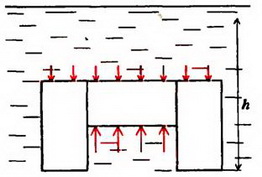
Во втором случае отсутствует давление воды на опоры снизу (рис.6, б), и пользоваться законом Архимеда уже нельзя. Для определения силы F необходимо найти равнодействующую сил давления:
F = 0 при h ≤ a,
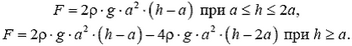
Последнее выражение обращается в нуль при 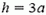 и при больших h становится отрицательным. Это означает, что при
и при больших h становится отрицательным. Это означает, что при 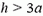 силы давления не выталкивают конструкцию из воды, а наоборот, прижимают ее ко дну. Зависимость силы давления на дно от высоты уровня воды показана на втором графике рисунка 6, в.
силы давления не выталкивают конструкцию из воды, а наоборот, прижимают ее ко дну. Зависимость силы давления на дно от высоты уровня воды показана на втором графике рисунка 6, в.
Задача 6. Пробковый кубик с ребром a = 0,1 м погрузили в воду на глубину h = 0,2 м с помощью тонкостенной трубки диаметром d = 0,05 м (рис. 7). Определите, какой груз надо положить в трубку, чтобы кубик от нее оторвался. Плотность пробки ρ0 = 200 кг/м3, плотность воды ρ = 103 кг/м3.
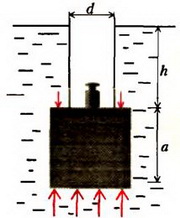
Рис. 7
Вес груза равен разности выталкивающей силы F действующей на кубик, и силы тяжести кубика 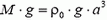 . Если бы кубик был окружен со всех сторон водой, то на него по закону Архимеда действовала бы выталкивающая сила
. Если бы кубик был окружен со всех сторон водой, то на него по закону Архимеда действовала бы выталкивающая сила 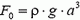 . В нашем случае выталкивающая сила будет большей, так как на часть поверхности верхней грани кубика, «заключенную» в трубку, не действует давление воды:
. В нашем случае выталкивающая сила будет большей, так как на часть поверхности верхней грани кубика, «заключенную» в трубку, не действует давление воды:
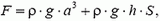
где 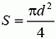 – площадь сечения трубки. Таким образом, сила тяжести грузика
– площадь сечения трубки. Таким образом, сила тяжести грузика
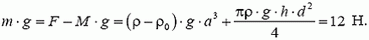
Масса грузика т = 1,2 кг.
Выталкивающую силу, действующую на кубик, можно найти и другим способом. Рассмотрим кубик с трубкой как единое тело, вытесняющее объем воды
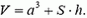
Тогда по закону Архимеда на кубик с трубкой действует выталкивающая сила
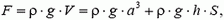
которая равна выталкивающей силе, действующей на кубик, так как равнодействующая сил давления воды на трубку равна нулю.
Жидкость в движущемся сосуде
Изучим теперь равновесие жидкости в сосуде, движущемся с ускорением. По второму закону Ньютона в этом случае векторная сумма всех сил, действующих на любой выделенный элемент жидкости, должна равняться 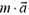 , где m – масса выделенной жидкости,
, где m – масса выделенной жидкости, 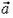 – ускорение сосуда. Но на выделенный элемент жидкости действуют сила тяжести и силы давления со стороны окружающей жидкости. Их равнодействующая и должна быть равна
– ускорение сосуда. Но на выделенный элемент жидкости действуют сила тяжести и силы давления со стороны окружающей жидкости. Их равнодействующая и должна быть равна 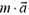 .
.
Задача 7. Сосуд с жидкостью плотностью ρ падает с ускорением a. Определите давление жидкости на глубине h и силу давления на дно сосуда. Высота уровня воды в сосуде H, площадь дна сосуда s.
Выделим столбик жидкости высотой h с площадью основания s. На него действуют сила тяжести 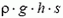 и сила давления
и сила давления 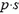 , направленная вверх. Равнодействующая этик сил создает ускорение столбика:
, направленная вверх. Равнодействующая этик сил создает ускорение столбика:
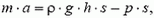
где 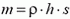 – масса столбика. Для давления p на глубине h отсюда находим
– масса столбика. Для давления p на глубине h отсюда находим
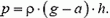
Сила давления на дно сосуда
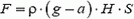
будет тем меньше, чем больше ускорение сосуда a. При 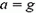 (свободное падение) сила давления жидкости обращается в ноль – наступает состояние невесомости. При
(свободное падение) сила давления жидкости обращается в ноль – наступает состояние невесомости. При 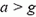 жидкость будет свободно падать с ускорением g, а сосуд – с большим ускорением, и вода вытечет из сосуда.
жидкость будет свободно падать с ускорением g, а сосуд – с большим ускорением, и вода вытечет из сосуда.
Задача 8. На дне сосуда с жидкостью лежит тело. Может ли тело всплыть, если сосуд начнет двигаться вверх с ускорением? Определите силу давления тела на дно сосуда, если ускорение сосуда a, плотность жидкости ρ0, плотность тела ρ, его объем V.
На тело, лежащее на дне сосуда, действуют сила тяжести mg сила реакции дна N и выталкивающая сила F (рис. 8). Если сосуд покоится, то сумма этих сил равняется нулю. При движении сосуда с ускорением a вверх по второму закону Ньютона имеем
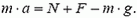
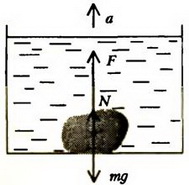
Рис. 8
Определим выталкивающую силу F. Аналогично решению предыдущей задачи, легко получить, что при ускоренном движении сосуда, вверх давление на глубине h дается формулой
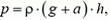
т.е. давление в 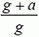 раз больше, чем в неподвижном сосуде. Соответственно будет большей и выталкивающая сила:
раз больше, чем в неподвижном сосуде. Соответственно будет большей и выталкивающая сила:
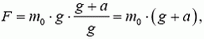
где 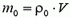 – масса вытесненной телом воды.
– масса вытесненной телом воды.
Подставляя это выражение в формулу второго закона Ньютона, для силы реакции дна получаем
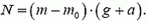
Легко видеть, что в сосуде, движущемся с ускорением вверх, сила реакции дна всегда больше, чем в неподвижном. Поэтому тело не только не всплывает, а наоборот, сильнее прижимается ко дну.
Задача 9. Сосуд с жидкостью движется горизонтально с ускорением a. Определите форму поверхности жидкости в сосуде.
Выделим горизонтальный столбик жидкости длиной l и площадью поперечного сечения S (рис. 9). По второму закону Ньютона
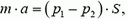
где 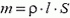 – масса столбика, p1 и p2 – давления на него слева и справа.
– масса столбика, p1 и p2 – давления на него слева и справа.
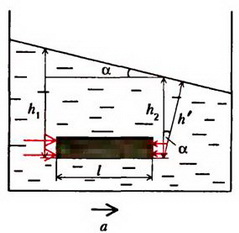
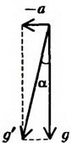
Рис. 9
Давление на глубине h определяется по обычной формуле 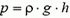 (по вертикали ускорения нет). Подставляя выражения для m и p в уравнение второго закона Ньютона, получаем
(по вертикали ускорения нет). Подставляя выражения для m и p в уравнение второго закона Ньютона, получаем
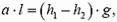
или
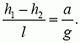
Но  – это разность высот точек поверхности жидкости. Мы получаем, что поверхность жидкости – плоскость, наклоненная к горизонту под углом α, причем
– это разность высот точек поверхности жидкости. Мы получаем, что поверхность жидкости – плоскость, наклоненная к горизонту под углом α, причем 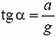 .
.
Заметим, что давление жидкости на данной высоте здесь не одно и то же. Линии равного давления параллельны поверхности жидкости. Если ввести расстояние h´ от точки до поверхности жидкости, то давление в этой точке
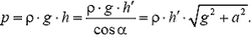
Поэтому можно сказать, что ускоренное движение сосуда эквивалентно замене ускорения свободного падения 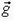 на величину
на величину 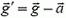 . Это утверждение в равной степени относится и к предыдущим двум задачам.
. Это утверждение в равной степени относится и к предыдущим двум задачам.
Упражнения
1. Три сосуда, имеющие формы цилиндра, усеченного конуса и перевернутого усеченного конус с одинаковыми площадями оснований и рапными объемами, доверху наполнены водой. Как соотносятся между собой силы давлении воды на дно сосудов?
2. Трубка ртутного барометра подвешена нити. Определите натяжение нити, если высота уровня ртути и трубке Н = 0,76 м, внешний диаметр трубки D = 0,02 м, внутренний d = 0,017 м. нижний конец трубки погружен в ртуть на глубину h = 0,1 м, масса трубки m = 0,3 кг, плотность ртути ρ = 1,36×104 кг/м4. Считайте, что торцы трубки плоские.
3. Длинная вертикальная трубка погружена одним концом в сосуд с ртутью. В трубку наливают m = 0,71 кг воды, которая не вытекает из трубки. Определите изменение уровня ртути и сосуде. Диаметр сосуда D = 0,06 м, плотность ртути ρ = 1,36×104 кг/м4. Толщиной стоим трубки пренебречь.
4. В сосуде с водой плавает кусок льда. Изменится ли уровень воды в сосуде, если лед растает? Что будет, если в лед вморожен а) кусочек свинца: б) кусочек пробки?
5. В цилиндрические сообщающиеся сосуды диаметрами D = 0,06 м и d = 0,02 м налита вода. Как изменятся уровни воды в сосудах, если в один из сосудов поместить тело массой т = 0,02 кг, которое будет плавать в воде? Плотность воды ρ = 103 кг/м3.
6. Сосуд с водой скользит без трения по наклонной плоскости с углом наклона α. Определите, как расположится поверхность воды и сосуде.
Ответы
1. Сила давления на дно наибольшая у сосуда, имеющего форму усеченного конуса, наименьшая – у перевернутого конуса.
2. 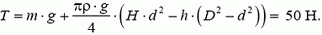
3. 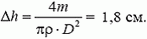
4. Если лед чистый или в него вморожен кусочек пробки, то уровень воды не изменится. Если же в лед вморожен кусочек свинца, уровень воды понизится.
5. 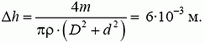
6. Поверхность параллельна наклонной плоскости.
Перейти к контенту
Условие задачи:
Какова сила давления на поршень насоса при высоте подачи воды 25 м, если площадь поршня 100 см2?
Задача №3.2.15 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(h=25) м, (S=100) см2, (P-?)
Решение задачи:
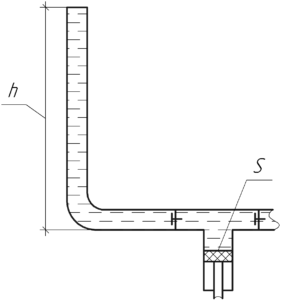 При подаче воды поршневым насосом на высоту (h) поршень насоса испытывает давление столба жидкости этой высоты, которое можно определить по формуле:
При подаче воды поршневым насосом на высоту (h) поршень насоса испытывает давление столба жидкости этой высоты, которое можно определить по формуле:
[p = rho gh]
Давление – это сила, приходящаяся на единицу площади, поэтому силу давления следует находить по следующей формуле:
[P = pS]
В итоге:
[P = rho ghS]
Плотность воды (rho) равна 1000 кг/м3. Переведем площадь в систему СИ и найдем численное значение силы давления на поршень (P).
[100;см^2 = 100 cdot {10^{ – 4}};м^2]
[P = 1000 cdot 10 cdot 25 cdot 100 cdot {10^{ – 4}} = 2500;Н]
Ответ: 2500 Н.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
3.2.14 В цилиндрическое ведро с площадью дна 0,02 м2 налита вода. Найдите массу воды
3.2.16 На какой глубине в пресной воде давление в 3 раза больше нормального
3.2.17 На какой глубине моря гидростатическое давление воды равно 4,9 МПа? Плотность
( 6 оценок, среднее 5 из 5 )
Содержание:
- § 1 Гидравлическая машина
- § 2 Гидравлический пресс
- § 3 Решение задач
- § 4 Важно запомнить
§ 1 Гидравлическая машина
В этом уроке мы изучим устройство и принцип действия гидравлических машин.
В жизни человеку очень часто приходится сталкиваться с такими ситуациями, где нужно поднять груз большой массы на высоту или сжать какое-либо тело. Например, автомобилисту нужно сменить проколотое колесо. Для этого нужно приподнять автомобиль. Поднять 5 кг, 10 кг взрослому человеку не так сложно. Но поднять автомобиль? Или нужно выжать масло из семян подсолнуха, спрессовать бумагу. И вот в таких случаях на помощь приходят разные механизмы, позволяющие получить большую силу, прилагая незначительные усилия.
Одним из таких механизмов является гидравлическая машина.
Гидравлическая машина (от греческого слова гидравликос – водяной) – это машина, действие которой основано на законах движения и равновесия жидкостей. Первая гидравлическая машина была создана Паскалем, который называл ее машиной для увеличения силы.
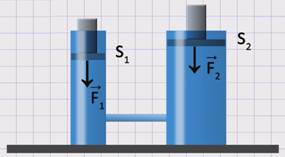
Гидравлическая машина представляет собой сообщающиеся сосуды – два соединенных друг с другом цилиндра разного диаметра, снабженных поршнями и заполненных жидкостью (водой или маслом).
Рассмотрим принцип действия гидравлической машины. Обозначим площадь поршня в малом цилиндре S1, площадь поршня в большом цилиндре – S2, F1 и F2 – силы, действующие на поршни.
Если на поршень S1 подействовать с силой F1, то давление в малом цилиндре будет определяться по формуле:
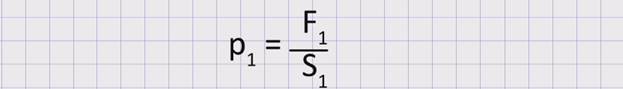
Давление в большом цилиндре:
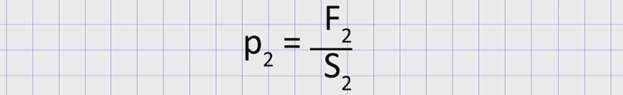
По закону Паскаля давление, производимое на жидкость или газ, передается в каждую точку по всем направлениям одинаково. Значит, давление в обоих цилиндрах будет одинаковым: p1 = p2 . Тогда можем приравнять правые части этих формул:

Читается эта формула так: сила F2, действующая на большой поршень, во столько раз больше силы F1, действующей на малый поршень, во сколько раз площадь большого поршня S2 больше площади малого поршняS1. Отношение F2 к F1показывается выигрышем в силе.
Итак, сделаем вывод. Приложив незначительное усилие F1 к малому поршню, мы можем получить во столько раз большую силу F2 на большом поршне, во сколько раз его площадь превышает площадь малого поршня.
Выигрыш в силе, полученный при помощи гидравлической машины, равен отношению площадей поршней.
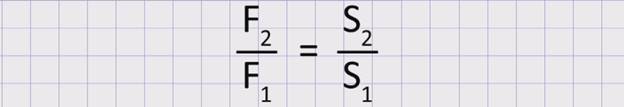
§ 2 Гидравлический пресс
Гидравлическая машина, служащая для прессования (сдавливания), называется гидравлическим прессом.
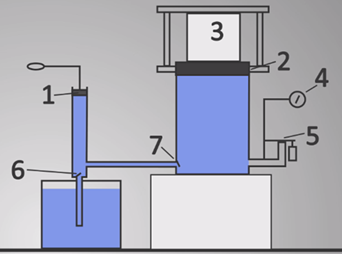
Принцип действия гидравлического пресса таков: на платформу большого поршня 2 кладется прессуемое тело 3. При помощи малого поршня 1 создается давление на жидкость, которое по закону Паскаля передается в каждую точку жидкости, заполняющей цилиндры. Так как площадь большого поршня во много раз больше площади малого, то и действующая на него сила окажется во столько же раз больше. Под действием этой силы большой поршень поднимается и сжимает тело. За значением давления, возникающего в жидкости, следят при помощи деформационного манометра 4, соединенного с предохранительным клапаном 5, который автоматически открывается при превышении допустимого значения давления. Клапаны 6 и 7 служат для перекачивания жидкости: при подъеме малого поршня 1 открывается клапан 6, и жидкость поступает в малый сосуд; при нажатии давление увеличивается, и этот клапан закрывается; открывается клапан 7, и жидкость переходит в большой сосуд.
Гидравлические прессы применяются для выжимания масла на маслобойных заводах, для прессования фанеры, картона, сена. В автомобилях используется гидравлический тормоз, в мастерских и в быту применяют гидравлический домкрат.
§ 3 Решение задач
Рассмотрим решение задачи на расчет выигрыша в силе в гидравлических машинах.

Запишем условие задачи. Нам известны масса m= 1500 кг, площадь малого поршня S1 = 10 см2 = 0, 001 м2, площадь большого поршня S2 = 0,1 м2. Найти F1.
Решение: Запишем формулу выигрыша в силе при помощи гидравлической машины:

Ответ: сила, приложенная к малому поршню,150 Н

Запишем условие задачи: F1= 200 Н, p = 400000 Па, S2 =0,04 м2. Найти показания динамометра, т.е. силу F2 = ? S1 =?

Ответ:F2 = 16 000 Н, S1 = 5 см2
§ 4 Важно запомнить
Гидравлическая машина – это машина, действие которой основано на законе Паскаля.
Гидравлическая машина представляет собой сообщающиеся сосуды – два соединенных друг с другом цилиндра разного диаметра, снабженных поршнями и заполненных жидкостью.
Выигрыш в силе, полученный при помощи гидравлической машины, равен отношению площадей поршней.
Гидравлическая машина, служащая для прессования (сдавливания), называется гидравлическим прессом.
Гидравлические прессы применяются для выжимания масла, для прессования фанеры, картона, сена. В автомашинах используется гидравлический тормоз, для подъема груза предназначен гидравлический домкрат.
Список использованной литературы:
- Волков В.А. Поурочные разработки по физике: 7 класс. – 3-е изд. – М.: ВАКО, 2009. – 368 с.
- Волков В.А. Тесты по физике: 7-9 классы. – М.: ВАКО, 2009. – 224 с. – (Мастерская учителя физики).
- Кирик Л.А. Физика -7. Разноуровневые самостоятельные и контрольные работы. – М.: Илекса, 2008. – 192 с.
- Контрольно-измерительные материалы. Физика: 7 класс / Сост. Зорин Н.И. – М.: ВАКО, 2012. – 80 с.
- Марон А.Е., Марон Е.А. Физика. 7 Дидактические материалы. – М.: Дрофа, 2010. – 128 с.
- Перышкин А.В. Физика. 7 класс – М.: Дрофа, 2011.
- Тихомирова С.А. Физика в пословицах и поговорках, стихах и прозе, сказках и анекдотах. Пособие для учителя. – М.: Новая школа, 2002. – 144 с.
- Я иду на урок физики: 7 класс. Часть III: Книга для учителя. – М.: Издательство «Первое сентября», 2002. – 272 с.
Использованные изображения:
Поршневой жидкостный насос. Гидравлический пресс.
«Хотя в мире нет предмета,
который был бы слабее и нежнее воды,
но она может разрушить самый твердый предмет»
Лао-Цзы
В данной теме речь пойдёт о принципах действия поршневого жидкостного насоса и гидравлического пресса.
В прошлых темах говорилось о сообщающихся сосудах — сосуды, которые имеют соединяющую их часть и заполненные покоящейся жидкостью. В открытых сообщающихся сосудах уровень поверхностей однородной жидкости устанавливается на одинаковом уровне (при условии, что давление воздуха над поверхностью жидкости одинаково) и не зависит от формы сосудов.
Также говорилось о законе Паскаля, согласно которому, жидкость или газ передает производимое на нее давление внешней силой по всем направлениям без изменений. Когда Блез Паскаль открыл свой закон, он задумался над тем, как его можно использовать. И придумал устройство гидравлической машиной. Слово «гидравлический» происходит от греческого «гидравликос» — водяной.
Таким образом, гидравлические машины — это машины, работа которых основана на законе Паскаля.
Давайте рассмотрим схему простейшей гидравлической машины.
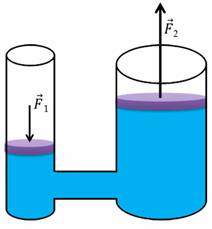
Как видно из рисунка, она состоит из двух сообщающихся сосудов с разными площадями поперечного сечения, заполненных практически несжимаемой жидкостью, обычно маслом, и закрытых подвижными поршнями. Как работает гидравлическая машина? Для этого подействуем на малый поршень небольшой силой. Эта сила будет создавать давление на жидкость, которое по закону Паскаля передается во все точки жидкости. Значит и на большой поршень подействует такое же давление. Тогда сила давления, действующая на большой поршень, будет направлена вверх и равна произведению давления и площади большого поршня. Сравним силы, действующие на малый и большой поршни.
p1 = p2
F1 = p1S1
F2 = p2S2 = p1S2
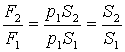
Таким образом, можно сделать вывод о том, что гидравлическая машина дает выигрыш в силе во столько раз, во сколько раз площадь поперечного сечения большого поршня больше площади поперечного сечения малого поршня. Это означает, что с помощью небольшой силы, приложенной к малому поршню гидравлической машины, можно уравновесить существенно большую силу, приложенную к большому поршню.
Гидравлическую машину, служащую для прессования, называют гидравлическим прессом. Он широко применяется в технике для обработки металлов, прессования фанеры, картона, древесностружечных плит. А в сельском хозяйстве гидравлический пресс используется для прессования сена, для выжимки масла из семян подсолнуха, кукурузы и т.д. Современные гидравлические прессы способны развивать силу в десятки и сотни миллионов Ньютонов. Прессуемое тело кладут на платформу, которая соединена с большим поршнем. С помощью малого поршня создается большое давление, которое, согласно закону Паскаля, передается в каждую точку жидкости, заполняющей цилиндры. Тогда и на большой поршень будет действовать такое же давление. Но так как площади поршней отличаются, то сила, действующая на большой поршень, будет больше силы, действующей на малый поршень. Под действием этой силы большой поршень будет подниматься. При его подъеме прессуемое тело упирается в неподвижную платформу и сжимается.
Из малого цилиндра в большой жидкость перекачивается с помощью поршневого жидкостного насоса. Рассмотрим схему и принцип действия такого насоса на примере колонки.
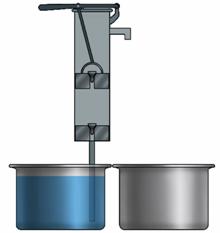
Поршневой жидкостный насос состоит из цилиндра, внутри которого находится плотно прилегающий к стенкам поршень. И в поршне, и в нижней части цилиндра располагаются клапаны, которые открываются только вверх. При движении поршня вверх жидкость под действием атмосферного давления поднимает нижний клапан и, двигаясь вслед за поршнем, входит в трубу. Когда поршень движется вниз, жидкость, находящаяся под поршнем, давит на нижний клапан, и он закрывается. В это же время, под давлением воды, открывается клапан в самом поршне, и жидкость переходит в пространство над поршнем. При следующем движении поршня вверх вместе с ним поднимается и находящаяся над ним жидкость, которая выливается в отводящую трубу. При этом за поршнем поднимается новая порция жидкости, которая при последующем опускании поршня, вновь окажется над ним.
Вернемся опять к гидравлическому прессу.
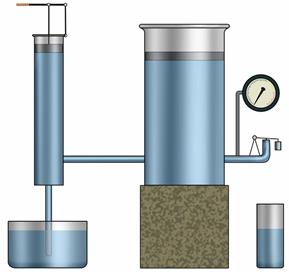
Обратим внимание, поршневой насос в гидравлическом прессе немного отличается от рассмотренного выше. Однако принцип его работы такой же. При подъеме малого поршня открывается клапан, и в пространство, находящееся под поршнем, засасывается жидкость. При опускании малого поршня под действием давления жидкости этот клапан закрывается и открывается клапан, связывающий большой и малый цилиндры, и жидкость переходит в большой сосуд.
Еще одной разновидностью гидравлических машин является гидравлический тормоз. Являющийся важной частью большинства автомобилей, именно он осуществляет быстрое и надежное торможение его колес. Работу гидравлического тормоза можно объяснить, используя упрощенную схему.
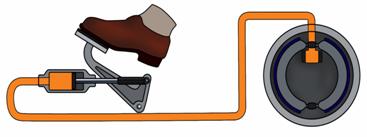
Нога водителя действует на тормозную педаль. Это действие передается на поршень цилиндра, в котором находится тормозная жидкость. Этот поршень создает давление на жидкость, которое согласно закону Паскаля передается в тормозные цилиндры всех колес автомобиля. В тормозном устройстве имеется цилиндр с двумя подвижными поршнями. Под давлением жидкости эти поршни расходятся и прижимают тормозные колодки к тормозным барабанам, что и останавливает вращение колес.
Еще одним эффективным гидравлическим механизмом является гидравлический домкрат, с помощью которого можно поднимать очень тяжелые машины. Принцип действия домкрата такой же, как и гидравлического пресса.

Упражнения.
Задача 1. На малый поршень гидравлического пресса действует сила 150 Н. Определите силу, действующую на большой поршень, если его площадь в 20 раз больше площади малого поршня.

Задача 2. Малый поршень гидравлического пресса за один ход опустился на расстояние 0,2 м, при этом большой поршень поднялся на высоту 0,01 м. С какой силой действует пресс на зажатое в нем тело, если на малый поршень 
Задача 3. Гидравлический пресс, заполненный водой, имеет поршни, площади которых 200 см2 и 20 см2. На большой поршень положили груз массой 60 кг. На какую высоту поднимается после этого малый поршень? Плотность воды примите равной 1000 кг/м3.



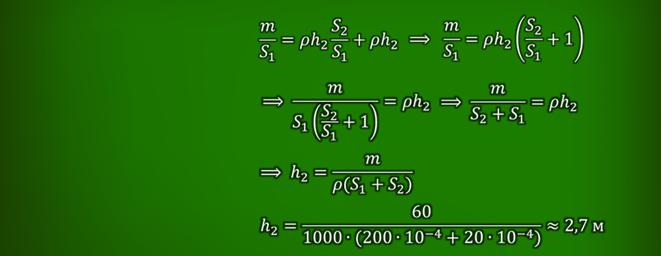
Основные выводы:
– Гидравлическая машина — машина, действие которой основано на законе Паскаля.
– Гидравлический пресс –это гидравлическая машина, служащая для прессования.
– Гидравлический пресс дает выигрыш в силе во столько раз, во сколько раз площадь большого поршня больше площади малого поршня.
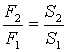
Пройдите тест
