Как найти давление при его сжатии

Формулы закона Бойля Мариотта

P1/P2=V2/V1

или

P1V1=P2V2

При пользовании этими формулами безразлично, в каких единицах вы будете измерять объем и давление, лишь бы оба объема и оба давления были измерены в одинаковых единицах. Например, если одно давление измерено в килограммах на квадратный сантиметр, то в тех же единицах должно быть измерено и другое давление. Если один объем измерен в кубических сантиметрах, то так же должен быть измерен и другой.

Применение закона Бойля Мариотта в быту

Пылесос состоит главным образом из вентилятора, приводимого в движение электромотором. Вентилятор выталкивает воздух своими лопастями и создает за ними разреженное пространство. Так как воздух, который из-за разности давлений внутри и снаружи устремляется по трубке в камеру вентилятора, проходит через ковер, то пыль уносится с ковра. В некоторых пылесосах применяется, кроме того, вращающаяся щетка, подметающая и выбивающая ковер. Воздух, прошедший вентилятор, поступает в мешок или другой отстойник для пыли и грязи, которые потом могут быть опорожнены различными способами в зависимости от типа пылесоса.

Водолазные колокола и водолазные костюмы. Когда водолазный колокол погружается в воду, воздух тоже сжимается, но при помощи компрессора, находящегося снаружи. Воздух нагнетается под колокол, поэтому вода совсем не входит в колокол. При этом необходимо все время накачивать в колокол свежий воздух в количестве, необходимом для работающих там людей. Излишек воздуха будет пузырями вырываться наружу. Важной частью водолазного костюма является шлем, который привинчивается к верхней части водонепроницаемого костюма. Обычно шлем снабжают воздухом таким же образом, как водолазный колокол. В некоторых типах костюмов водолаз имеет при себе собственный запас сжатого воздуха. 

Одно из своеобразных проявлений закона Бойля — наше дыхание. Когда мускулы, сокращаясь, тянут диафрагму вниз, объем пространства, где помещаются легкие, увеличивается, отчего давление внутри становится меньше наружного. В результате воздух из пространства с большим давлением поступает в легкие, где давление меньше. Обратное движение диафрагмы уменьшает объем легочного пространства и делает давление внутри легких большим наружного. Поэтому воздух и ненужные газы выходят из легких.

Содержание:

Давление:

Вы уже знаете, что тело, находящееся на горизонтальной опоре, действует на опору силой давления. Она приложена к опоре и направлена перпендикулярно к ней. Опора деформируется. А от чего зависит степень ее деформации?

Проделаем такой опыт. Поместим столик вверх ножками в ящик с песком, на столик поставим гирю (рис. 166, а). Столик с гирей лишь незначительно погрузится в песок. А теперь перевернем столик ножками вниз и поставим ту же гирю (рис. 166, б). Ножки погрузятся в песок. Результат действия одной и той же силы давления (веса столика с гирей) оказался разным. Почему? Потому, что сила давления действовала на разную площадь поверхности опоры. В первом случае ее действие распределилось на площадь поверхности песка под крышкой, во втором — на площадь поверхности песка под ножками столика. Ясно, что площадь под ножками значительно меньше площади под крышкой столика. А если убрать гирю, т. е. уменьшить силу давления, не меняя площади поверхности, на которую она действует (рис. 166, в)? Ножки погрузятся в песок, но не так сильно.

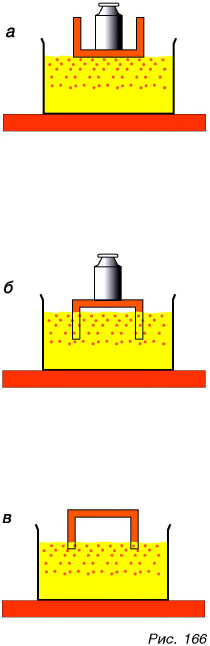
Результат действия силы давления на поверхность можно определить с помощью физической величины — давления. Обозначим давление буквой р. Из опыта следует, что давление тем больше, чем больше сила давления и чем меньше площадь поверхности, на которую она действует.

Что такое давление

Давление — это физическая величина, равная отношению силы давления, действующей перпендикулярно поверхности, к площади поверхности.

Математически это можно выразить так:

В СИ единицей давления является 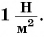 Ее называют паскалем (Па) в честь французского ученого Блеза Паскаля, изучавшего давление в жидкостях и газах.

1 паскаль — это давление на поверхность площадью 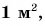производимое силой 1 Н, действующей перпендикулярно.

Применяют кратные единицы давления: гектопаскаль (гПа), килопаскаль (кПа) и мегапаскаль (МПа). Обратите внимание:

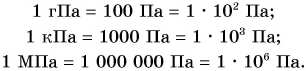
Позлее вы познакомитесь и с другими единицами давления.

Силой давления может быть не только вес тела, но и любая сила, перпендикулярная поверхности, на которую она действует.

Простой пример: вы загоняете канцелярскую кнопку в вертикальную доску (рис. 167). Силой давления на кнопку является сила действия руки, направленная горизонтально (перпендикулярно доске). Пружины дивана оказывают давление на сидящего на нем человека. Сила давления (сила упругости пружин) при этом направлена вертикально вверх.

Для практических целей иногда необходимо уменьшить давление, а в ряде случаев, наоборот, — увеличить. Как изменить давление?

Обратимся к формуле 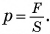 Совершенно ясно: чтобы уменьшить давление, нужно уменьшить силу давления или увеличить площадь поверхности.

Например, чтобы увеличить проходимость тяжелых машин (трактора, танка), их снабжают гусеницами (рис. 168). Площадь поверхности, на которую действует сила давления, увеличивается, а давление — уменьшается. Широкие шины у автомобилей, лыжи у человека (рис. 169), довольно большие по площади стопы у слона (рис. 170) играют ту же роль, что и гусеницы у трактора. Приведите сами подобные примеры.

А как увеличить давление? Из формулы давления следует: надо увеличить силу давления или уменьшить площадь поверхности, на которую действует сила. Затачивая лезвия ножей, ножниц (рис. 171), кос, острия игл, зубцы пил и др., мы стараемся уменьшить площадь поверхности. Тем самым, действуя малой силой, можно создать большое давление.

Животному миру природа сама обеспечила возможность создавать большое давление небольшим усилием, вооружив его представителей иглами, клювами и когтями (рис. 172), зубами, клыками, жалами и т. д.

Главные выводы:

1. Давление — это физическая величина, равная отношению силы давления к площади поверхности.
2. Чем больше действующая на поверхность сила давления, чем меньше площадь поверхности, на которую действует сила давления, тем больше давление.
3. В СИ единицей давления является 1 Па.

Для любознательных:

Человек при ходьбе создает давление до 300—400 кПа (определите давление, которое создаете вы, стоя на полу; сравните полу ценные результаты с приведенным значением и объясните причину расхождения этих значений). Гусеничный трактор создает давление на почву в 40—60 кПа, а колеса вагона поезда па рельсы — около 50 МПа.

Пример решения задачи:

Семиклассник массой m = 50 кг стоит на полу. Определите давление, которое он производит на пол, если площадь соприкосновения подошвы его ботинка с полом 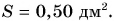Коэффициент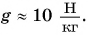 

Дано:

m = 50 кг

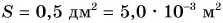
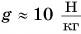
Решение:

Давление, которое производит семиклассник на пол:

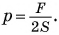
Сила давления F равна весу P семиклассника. Вес 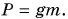 Тогда:

Ответ: p = 50 кПа.

Давление газа

Газы, как и твердые тела, тоже производят давление. Но твердые тела передают давление в том направлении, в котором действует сила давления. Кнопка (см. рис. 167) передает давление перпендикулярно доске, лопата (рис. 174) — в направлении силы давления ноги и т. д.

А вот газы передают давление во все стороны. Чем обусловлена такая особенность газов? От чего зависит давление газа?

Вам уже известно, что газы, как жидкости и твердые тела, состоят из частиц (атомов, молекул). Но расстояния между частицами у газов больше, чем у жидкостей и твердых тел. Поэтому силы взаимодействия между частицами у газов практически отсутствуют (кроме процессов столкновения). Двигаясь хаотически, они сталкиваются между собой и со стенками сосуда. Так как число частиц газа в сосуде чрезвычайно велико (например, в 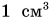их примерно 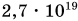), то стенка воспринимает удары частиц как действие вполне ощутимой силы давления.

В газах среднее число ударов хаотически движущихся частиц и средняя сила ударов на единицу площади поверхности стенки по всем направлениям одинаковы. Значит, и среднее давление по всем направлениям одинаково.

Подтвердим это опытом. Под стеклянный колокол поместим завязанную оболочку резинового шара, внутри которой находится газ (рис. 175). Будем откачивать воздух из-под колокола. Объем шара по мере откачки воздуха увеличивается. Это связано с тем, что давление газа под колоколом становится меньше, чем внутри шара.

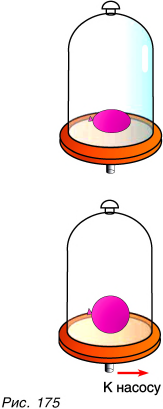
Форма оболочки в виде шара — доказательство того, что давление газа по всем направлениям одинаково.

Каким образом можно изменить давление газа? Поскольку давление обусловлено числом ударов частиц и силой удара каждой частицы о стенку, то есть два пути его изменения. Первый из них — изменить число частиц в единице объема.

Подтвердим сказанное опытом. В пробковом пистолете между пробкой и поршнем находится воздух (рис. 176, а), который оказывает давление по всем направлениям. Если будем поршнем сжимать газ, не меняя его температуры, то пробка вылетит из пистолета (рис. 176, б). Почему?

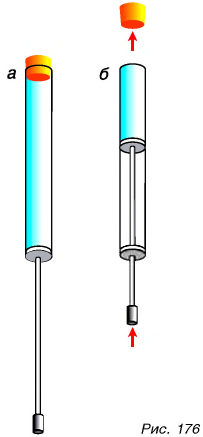
Уменьшая объем газа, мы увеличиваем число частиц в единице объема. Это приводит к увеличению числа ударов о стенки. Давление газа возрастает. А с увеличением давления растет сила давления газа на пробку, и она вылетает из пистолета. Если увеличивать объем газа при постоянной температуре, то давление будет уменьшаться.

Итак, при уменьшении объема (сжатии) газа при постоянной температуре его давление увеличивается, а при увеличении объема (расширении) газа давление уменьшается.

Второй путь изменить (например, увеличить) давление газа — это изменить силу удара частиц о стенки. Для этого газ нужно нагреть. Тогда скорость хаотического движения частиц увеличится, и, следовательно, увеличится и сила ударов их о стенки.

Зависимость давления от температуры можно подтвердить опытом. Если объем газа в пробковом пистолете (рис. 177, а) сохранять постоянным, но повышать температуру газа, подогревая его на спиртовке (рис. 177, б), то пробка вылетит вследствие увеличения давления. Значит, чем выше температура газа, тем больше его давление; чем ниже температура, тем меньше давление.

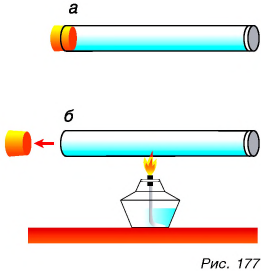
Главные выводы:

1. Давление газа есть результат ударов частиц о стенки сосуда, в котором он находится.
2. Давление газа можно увеличить, если уменьшать его объем при постоянной температуре или, сохраняя объем газа, увеличивать его температуру.
3. Давление газа можно уменьшить, если увеличивать (расширять) его объем при постоянной температуре или охлаждать газ, сохраняя его объем.

Для любознательных:

Возрастание давления газа при его нагревании вызвано не только увеличением силы отдельных ударов. В холодном и горячем газе будет неодинаковым и среднее число ударов частиц о стенки сосуда за единицу времени (т. е. частота ударов). Подумайте, как влияет этот фактор на давление газа.

На баллоне с лаком для волос написано: «Предохранять от воздействия прямых солнечных лучей и нагревания выше +50 °С!» Объясните необходимость таких мер предосторожности с точки зрения физики.

Передача давления газами и жидкостями. Закон Паскаля

Вы уже знаете, что частицы твердых тел (атомы, молекулы) жестко связаны между собой и могут совершать лишь хаотические колебательные движения около положений равновесия. У газов частицы движутся по всему объему хаотически поступательно. У жидкостей они совершают и хаотическое колебательное, и хаотическое поступательное движение. Значит, у газов и жидкостей подвижность частиц значительно выше, чем у твердых тел. Поэтому жидкости и газы не сохраняют своей формы, а принимают форму сосуда, в котором находятся (рис. 178).

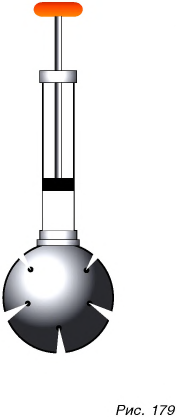
Кроме того, некоторые законы для жидкостей и газов одинаковы. Рассмотрим один из них. Проведем опыт. Шар с отверстиями заполним дымом и присоединим к трубке с поршнем. Дым с имеющимся в шаре воздухом займет весь объем шара. Будем перемещать поршень вниз. Мы заметим, что из всех отверстий начнут вытекать струйки дыма (рис. 179). Как объяснить это явление?

Подвижность частиц дыма и молекул воздуха приводит к тому, что они распределяются равномерно по всему объему. Сталкиваясь со стенками шара, молекулы и частицы дыма действуют на стенки, создавая давление. Сжимая газ (воздух с дымом), мы уменьшаем объем и тем самым увеличиваем вначале давление непосредственно под поршнем. Благодаря подвижности молекул давление передается газом во все точки шара, и газ вытекает из отверстий во всех направлениях. Такой же эффект достигается в случае, когда в шаре будет только воздух (без дыма). Дым лишь делает видимыми вытекающие струйки.

Аналогичный опыт можно провести с жидкостью, например с водой. При нажатии на поршень струйки воды через отверстия шара будут вытекать но всем направлениям.

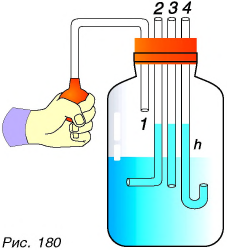
Проведем еще опыт. Через пробку в банку с водой вставим четыре трубки (рис. 180). Через трубку 1 будем накачивать в банку воздух, увеличивая там его давление. Увеличение внешнего давления (давления воздуха) на поверхность воды передается водой от слоя к слою по всем направлениям. В результате вода во всех трубках поднимается, причем на одну и ту же высоту. Значит, давление в воде сбоку (трубка 2), снизу (трубка 3), сверху (трубка 4) на одной глубине одинаково.

А вспомните, как с одинаковым напором вытекают струйки воды из всех дыр, появившихся в шланге для полива огорода (рис. 181). Давление, производимое внешней силой на жидкость (газ), находящуюся в сосуде, передается жидкостью (газом) во все точки жидкости (газа) без изменения. К такому выводу еще в XVII в. пришел французский ученый Блез Паскаль. Этот вывод называют законом Паскаля.

В твердых телах подвижность частиц ограничена, и эти тела не подчиняются закону Паскаля. Если вы поставите на стол тяжелый предмет, например гирю, то вес гири создаст давление лишь на площадь поверхности стола под гирей, т. е. только в направлении действия силы.

Главные выводы:

1. Частицы жидкости и газа обладают подвижностью.
2. Благодаря подвижности частиц жидкости и газы передают производимое на них давление во все точки без изменения.
3. Твердые тела передают давление только в направлении действия силы давления.

Давление жидкости, обусловленное ее весом

Благодаря подвижности частиц (атомов, молекул) жидкость принимает форму того сосуда, в который она налита. Если на жидкость действует внешняя сила давления, то жидкость передает созданное этой силой давление во все точки. Но жидкость создает давление и за счет своего веса, причем не только на дно сосуда, но и на стенки.

В том, что жидкость давит на стенки и дно сосуда, можно убедиться, используя эластичный полиэтиленовый пакет или трубку, нижний конец которой закрыт резиновой пленкой. Постепенно наливая подкрашенную воду в сосуд, мы обнаружим увеличивающийся прогиб пленки (рис. 182).

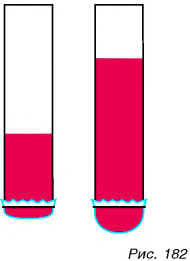
Причиной увеличения прогиба является рост давления воды на пленку. Притягиваясь к Земле, жидкость давит своим весом на пленку подобно тому, как давит на стол стопка книг. Давление неподвижной жидкости, обусловленное ее весом, называют гидростатическим (от лат. hydros — вода, station — неподвижный).

Гидростатическое давление можно рассчитать. Так, давление столба жидкости высотой h на дно сосуда с вертикальными стенками и площадью дна S (рис. 183) равно 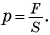Силой давления F является вес жидкости. Для неподвижной жидкости ее вес численно равен силе тяжести: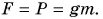 

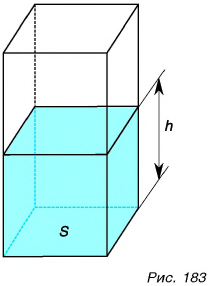
Запишем массу m жидкости через плотность 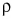 и объем V. Масса: 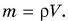Объем 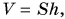 тогда 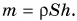 Подставим в формулу давления, получим: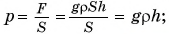

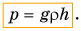
Итак, давление жидкости на дно сосуда зависит от ее плотности и высоты столба жидкости.

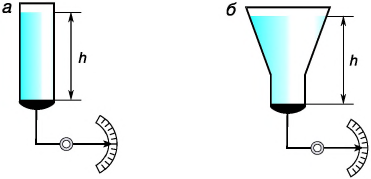
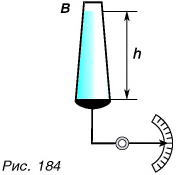
Выведенная формула справедлива для сосуда любой формы, даже если таким «сосудом» является пруд или океан. Чтобы подтвердить формулу, к сосуду с эластичным дном присоединим измерительную систему (рис. 184). При замене цилиндрического сосуда (а) на конические (б и в) (сосуды имеют одинаковую площадь дна и равные высоты столбов жидкости) прибор показывает равные силы давления. Значит, давления жидкости на дно всех сосудов равны, хотя масса жидкости в сосудах разная.

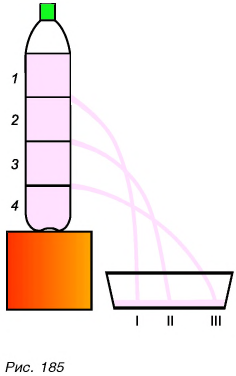
Формула 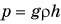позволяет найти давление не только на дно, но и на боковые стенки. Действительно, давление на стенку на данной глубине, как и на дно, зависит от высоты столба жидкости. Подтвердим это опытом. Нальем в пластиковую бутылку с проколотыми в стенке отверстиями подкрашенную воду (рис. 185). Наблюдения за вытекающими струями показывают, что гидростатическое давление действует и на стенку бутылки. Его величина возрастает по мере увеличения высоты столба воды в бутылке над отверстием, поэтому струя III падает дальше, чем струя I. Чтобы объяснить это явление, разделим мысленно жидкость на слои /, 2> 3, 4. На каждый нижний слой жидкости действует вес верхних ее слоев. Сила тяжести, действующая на слой /, прижимает его к слою 2. Слой 2 передает производимое на него давление слоя 1 по всем направлениям. На слой 3 действует вес слоев 2, 2. Следовательно, давление в слое 3 больше, чем в слое 2. Наибольшим оно будет на дно и стенку у дна сосуда.

Главные выводы:

1. Гидростатическое давление обусловлено весом покоящейся жидкости.
2. Гидростатическое давление на данной глубине зависит от плотности жидкости и высоты столба жидкости.
3. Гидростатическое давление на боковую стенку сосуда и на поверхность находящегося в жидкости тела на глубине h равно

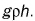
Для любознательных:

Гидростатическое давление — главное препятствие для проникновения людей в глубины Мирового океана. Уже на глубине 2,5 м нетренированный ныряльщик испытывает боль в ушах из-за давления воды на барабанные перепонки. Корпуса подводных лодок, изготовленные из прочнейших сталей, на глубине в несколько сотен метров находятся на грани превышения допустимой прочности. Тогда почему рыбы на большой глубине чувствуют себя комфортно? Оказывается, вода давит на рыб не только извне, но и изнутри, т. е. происходит компенсация сил давления.

Пример №1

Определите глубину водоема, на которой давление воды р = 100 кПа. Какая сила давления воды действует на ракушку с площадью поверхности 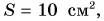лежащую на дне? Коэффициент  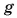примите равным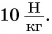

Дано:

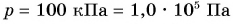
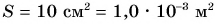
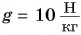
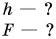
Давление воды на глубине h равно:

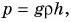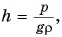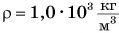 откуда  где  (плотность воды).

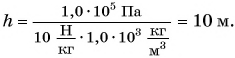
Сила давления:

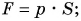
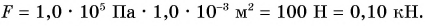
Ответ: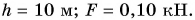 

Сообщающиеся сосуды

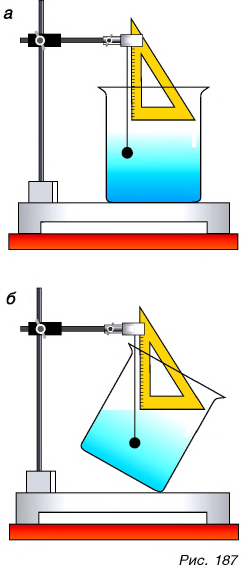
Действие на жидкость силы тяжести и подвижность ее молекул приводят к тому, что в широких сосудах поверхность жидкости устанавливается горизонтально. Это легко проверить с помощью прямоугольного треугольника (рис. 187). Горизонтальной будет поверхность жидкости и в сосудах, соединенных между собой, независимо от их формы.

Возьмем несколько соединенных между собой открытых сосудов. Их называют сообщающимися. Будем наливать в один из них воду. Вода перетечет в остальные сосуды и установится во всех сосудах на одном уровне (рис. 188) (если сосуды не очень узкие). Почему это происходит?

Рассмотрим самые простые сообщающиеся сосуды (рис. 189). Выделим внутри тонкий слой жидкости 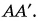 Как и вся жидкость, он неподвижен. Значит, слева и справа на него действуют силы с равными модулями, но противоположные по направлению. Это силы давления столбов жидкости 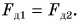Но чтобы модули этих сил были равны, необходимо, чтобы были одинаковыми давления, создаваемые левым и правым столбами жидкости, т. е.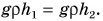

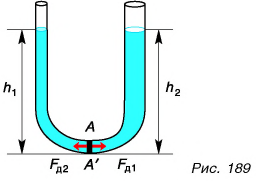
После сокращения получим: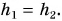

В открытых сообщающихся сосудах поверхности однородной жидкости устанавливаются на одинаковом уровне.

С сообщающимися сосудами вы встречаетесь постоянно: это чайники, лейки для полива (рис. 190, а), водомерные трубки в больших емкостях с водой или топливом (рис. 190, б). На принципе действия сообщающихся сосудов работает, к примеру, безнасосный фонтан (рис. 191).

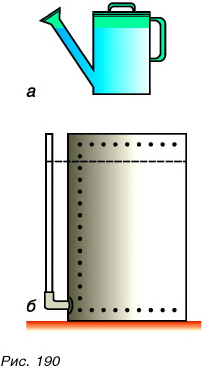
Сложную систему сообщающихся сосудов используют в дачных поселках и деревнях в башенном водопроводе. Схема простейшего водопровода представлена на рисунке 192. Вода из артезианского источника насосом (1) подается в бак водонапорной башни (2). От бака идут трубы с ответвлениями, вводимыми в дома на все этажи. Концы ответвлений труб закрываются кранами. Давление воды в кране определяется высотой столба воды в башне над уровнем крана. Поэтому чем выше этаж, тем давление воды в кране меньше. Чтобы вода смогла достигать всех этажей, башни строят высокими.

А если вам потребуется строго горизонтально установить поверхность стола или стиральной машины? Как в этом случае вам смогут помочь сообщающиеся сосуды? Приведите еще примеры использования сообщающихся сосудов.

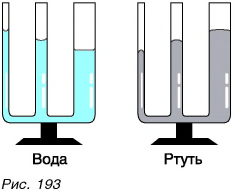
Все полученные в этом параграфе закономерности справедливы для широких сосудов, в которых поверхности жидкости плоские. В очень узких сосудах поверхности жидкости искривляются (рис. 193) и данные закономерности не выполняются.

Главные выводы:

1. В широких неподвижных сосудах поверхность жидкости всегда горизонтальна.
2. Уровень поверхностей однородной жидкости в открытых сообщающихся сосудах одинаков и не зависит от формы сосудов.

Для любознательных:

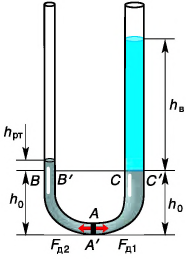
Что мы будем наблюдать, если в сообщающиеся сосуды налиты разные жидкости, например ртуть и вода (см. рис.)? В таком случае для равновесия тонкого слоя 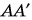 нужно, чтобы давление, создаваемое левым (ртутным) столбом высотой 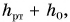было равно давлению правого столба воды и ртути высотой 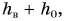, т. е.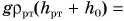 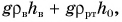откуда 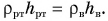Используя свойства пропорции, запишем окончательно:

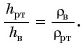
Посмотрите в таблицу плотностей жидкостей. Плотность ртути в 13,6 раза больше плотности воды. Значит, 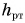 будет в 13,6 раза меньше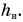

В открытых сообщающихся сосудах высоты столбов несмешивающихся жидкостей над уровнем их раздела обратно пропорциональны плотностям жидкостей.

Пример №2

Поверхность воды в водонапорной башне находится на h = 40 м выше кухонного водопроводного крана. Определите давление воды в кране. Коэффициент 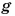 примите равным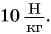 

Дано:

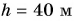
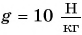
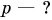
Решение:

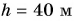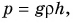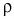Давление в кране создается столбом воды высотой ;  где  – плотность воды; 

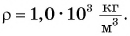
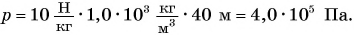
Ответ: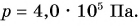 

Газы и их вес

То, что жидкость имеет вес, никого не удивляет. Каждый из вас ощущал вес, держа в руке ведро воды (рис. 197), бутылку растительного масла или напитка. Однако мы не чувствуем изменения веса футбольного мяча при его накачивании воздухом. Почему?

Посмотрите в таблицу плотностей и сравните плотность воздуха и воды. Плотность воздуха почти в 800 раз меньше плотности воды.

Расчеты показывают, что, например, в сильно накачанном мяче вес воздуха находится в пределах 0,1 Н, а его масса около 10 г.

Покажем на опыте наличие у воздуха массы, а следовательно, веса. Уравновесим на весах стеклянный сосуд, заполненный воздухом. Откачаем насосом воздух и взвесим сосуд повторно. Он стал легче (рис. 198). Добавляя на чашку с сосудом разновес, можно узнать массу откачанного воздуха и его вес.

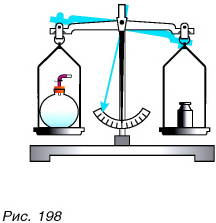
Воздушный слой, окружающий нашу Землю (земная атмосфера), тоже имеет вес. На каждую молекулу этого слоя действует Земля силой тяжести. Молекулы земной атмосферы, если бы на них не действовала сила тяжести, двигаясь хаотично, давно бы покинули нашу планету. Но тяготение Земли стремится расположить их у поверхности, что приводит к неоднородности атмосферы. Ее плотность заметно убывает с высотой. Так, на высоте 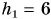км плотность воздуха уже в 2 раза меньше, чем у поверхности Земли. На высоте 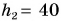км плотность  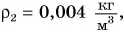а на высоте 400 км, где летают спутники, об атмосфере можно говорить лишь условно, так как ее плотность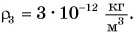 

Главные выводы:

1. Газы обладают массой и весом.
2. Земная атмосфера обладает весом вследствие действия на нее притяжения Земли.
3. Действие силы тяжести и хаотичное движение молекул приводят к неодинаковой плотности земной атмосферы.

Для любознательных:

Обратите внимание, что приведенные в таблице 3 плотности газов указаны при нормальных условиях, т. е. при строго определенной температуре и давлении. При сжатии газов (и обычного воздуха) их плотности могут возрастать во много раз. Такие сильно сжатые газы, во-первых, очень удобны при транспортировке, например в баллонах с кислородом для сварки или в баллонах аквалангистов. Во-вторых, сжатые до высокого давления газы удобно использовать при работе отбойного молотка и пневматических (от греч. pneuma — дуновение, дыхание) тормозов, которые устанавливаются на мощных автомобилях, в том числе на автомобилях МАЗ и БелАЗ. Устройства для сжатия различных газов называют компрессорами.

Атмосферное давление

Вы знаете, что атмосфера Земли — газовая оболочка, в состав которой входят азот, кислород, углекислый газ, водяные пары и другие газы (рис. 199).

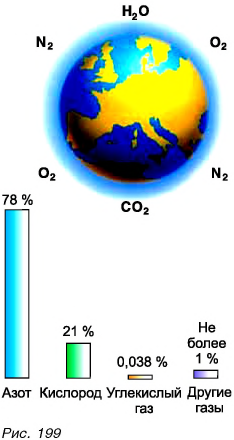
Всякий газ, если он находится в сосуде, производит давление на стенки сосуда, так как молекулы газа непрерывно бомбардируют эти стенки. А производит ли давление атмосфера Земли? Чем обусловлено это давление?

Атмосфера Земли удерживается силой тяжести, действующей со стороны Земли. В результате действия этой силы верхние слои атмосферы давят на нижние. Поэтому нижний слой оказывается наиболее сжатым. Давление одного слоя атмосферы на другой по закону Паскаля передается по всем направлениям и действует на любое тело: на здания, на растения, на людей. Это давление называют атмосферным. Атмосферное давление по мере удаления от поверхности Земли уменьшается. Уменьшается толщина слоя воздуха, создающего давление, и его плотность.

Атмосферное давление можно рассчитать. Результаты этих расчетов не могут не удивлять. Атмосферное давление равно примерно 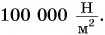 Значит, на каждый квадратный сантиметр нашего тела действует сила 10 Н, а на всю площадь поверхности тела (примем ее за 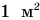) — сила 100 000 Н. Это равно весу десятитонного МАЗа! Как же мы живем под таким гигантским давлением?

Вспомним глубоководных рыб. Подобно им, мы просто не замечаем этой огромной сжимающей силы, так как она компенсируется равной расширяющей силой, создаваемой давлением воздуха внутри нас (он растворен даже в нашей крови).

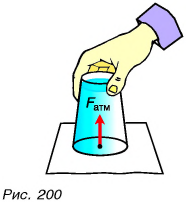
Так что же, атмосферное давление вообще нельзя обнаружить? Для ответа на этот вопрос обратимся к опыту. Возьмем стакан с водой, накроем его листом бумаги, перевернем, придерживая рукой лист, а затем уберем руку (см. рис. 200). Мы видим, что вода из стакана не выливается, лист не отрывается. Сила атмосферного давления, приложенная к листу бумаги, компенсирует действие веса налитой воды и разреженного воздуха в стакане.

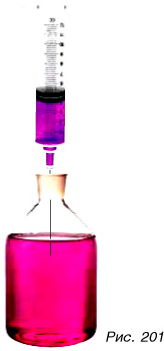
Опустите иглу шприца в подкрашенную воду и поднимайте поршень вверх. Вы увидите, что жидкость поднимается вслед за поршнем (рис. 201) противоположно направлению действия силы тяжести. Сила атмосферного давления заставляет сок подниматься вверх по трубочке (рис. 202). Опытов, в которых проявляется действие атмосферного давления, много.

Как измерить атмосферное давление? Рассмотрим наиболее важный из опытов, проведенный в 1643 г. по предложению итальянского физика и математика Эванджелисты Торричелли.

В этом опыте запаянная с одной стороны метровая стеклянная трубка (рис. 203, а) заполнялась ртутью. Верхний конец трубки закрывался, трубка переворачивалась и опускалась в широкий сосуд со ртутью, после чего отверстие открывалось. Часть ртути вытекала из трубки в сосуд. В трубке оставался столб ртути высотой Н около 76 см (760 мм) (рис. 203, б).

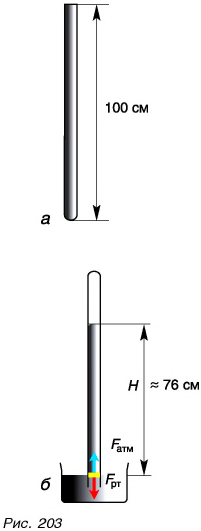
Что же удерживало от вытекания оставшуюся в трубке ртуть? Широкий сосуд и трубка — это, по сути, уже известные вам сообщающиеся сосуды. Над ртутью в трубке воздуха нет. На ртуть в широком сосуде действует атмосферное давление, которое жидкая ртуть передает по всем направлениям, в том числе вверх. Сила этого давления и поддерживает ртутный столб.

Рассмотрим условия равновесия тонкого слоя ртути (на рисунке 203, б он обозначен желтым цветом). Это условие требует, чтобы сила атмосферного давления снизу и сила гидростатического давления столба ртути сверху были равны. А это значит, что 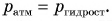Таким образом, измерив высоту столба ртути Н, мы можем рассчитать его давление по формуле 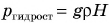и тем самым определить величину атмосферного давления.

Поскольку атмосферное давление определяется высотой столба ртути, то понятно, почему очень часто его измеряют не в международных единицах (паскалях), а в миллиметрах ртутного столба.

Выразим в паскалях внесистемную единицу давления 1 миллиметр ртутного столба (сокращенно 1 мм рт. ст.):

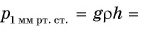
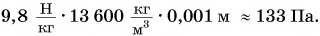
По договоренности атмосферное давление считают нормальным, если оно равно давлению столба ртути высотой h = 760 мм при температуре t = 20 °С. Такое давление называют одной нормальной, или физической, атмосферой (сокращенно 1 атм):

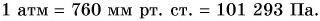
В большинстве случаев мы будем использовать округленное значение: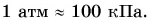 

Атмосферное давление играет важную роль во многих бытовых и технических устройствах. Оно не только позволяет пользоваться пипеткой или шприцом для набора лекарств, но и дает возможность простого, недорогого способа подъема воды. Знакомые многим резиновые присоски (рис. 204) используются как в быту, так и на заводах для переноса сложнейших узлов электроники, прикосновение к которым (даже в перчатках) совершенно недопустимо. 

Главные выводы:

1. Удерживаемая земным притяжением атмосфера Земли производит давление.
2. Человек не ощущает атмосферного давления, так как оно действует как снаружи, так и изнутри него.
3. За нормальное атмосферное давление принято давление столба ртути высотой 760 мм.

• Заказать решение задач по физике

Для любознательных:

В середине XVII в. в немецком городе Магдебурге ученым Отто фон Герике был проведен опыт-спектакль. Из пространства между двумя одинаковыми медными полушариями был выкачан воздух. Для разрыва полушарий, т. е. для преодоления сил атмосферного давления, потребовалось 8 пар самых сильных лошадей. Разрыв сопровождался сильным хлопком, подобным звуку выстрела.

Измерение атмосферного давления. Барометры и манометры

Ежедневно мы получаем информацию о величине атмосферного давления и его изменении. Почему оно не является постоянным? Почему на разных территориях Земли давление разное? Как давление зависит от высоты?

Атмосферное давление зависит от состава воздуха. Так, например, при поступлении влажного воздуха, насыщенного водяными парами, давление уменьшается, поскольку масса молекул воды заметно меньше массы других молекул атмосферы — азота и кислорода. Наиболее сжатыми, а значит, более плотными являются прилегающие к поверхности Земли слои атмосферы. Следовательно, значение атмосферного давления зависит от высоты места над уровнем моря. На вершине самой высокой (h = 8848 м) горы Эверест (рис. 208) давление почти в 3 раза меньше, чем у ее подножия.

Вода, как и другие жидкости, практически несжимаема. Поэтому давление жидкости от высоты столба зависит прямо пропорционально 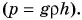Зависимость же атмосферного давления от высоты описывается гораздо более сложной формулой. Однако для расчетов, не требующих большой точности (при не очень больших высотах), можно считать, что при подъеме на каждые 12 м давление убывает на 1 мм рт. ст. Зависимость давления от высоты можно использовать для измерения высоты подъема (альпинистов, летательных аппаратов).

Так, если при подъеме давление уменьшилось на 20 мм рт. ст., то это значит, что высота подъема:

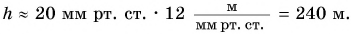
Приборы, измеряющие высоту по такому принципу, называют альтиметрами (от лат. altius — выше и metron — мера) (рис. 209).

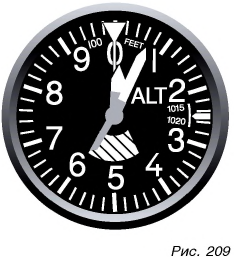
Атмосферное давление измеряют барометра ми (от греч. baros — тяжесть и metron — мера). Простейшим барометром является сосуд со ртутью и трубка, используемые в опыте Торричелли (см. рис. 203). Однако ртутные барометры не находят широкого применения, хотя имеют высокую точность. Пары ртути вредны для человека. На практике в основном пользуются металлическим барометром — анероидом. Хотя он менее точен, чем ртутный, но совершенно безопасен.

Внешний вид и внутреннее устройство барометра-анероида представлены на рисунке 210, а, б. Главной частью анероида является металлическая коробочка с волнистой (гофрированной) верхней и нижней поверхностями. Воздух из коробочки частично откачан.

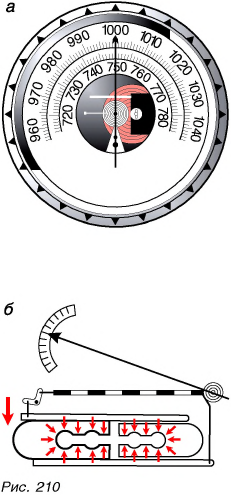
При увеличении атмосферного давления увеличивается сила давления на коробочку. Коробочка сжимается и растягивает пружину, прикрепленную к ней. Пружина связана со стрелкой, которая перемещается по шкале в сторону больших значений давления.

Если давление снижается, сила давления на коробочку уменьшается, силы упругости распрямляют коробочку, и стрелка перемешается по шкале в противоположную сторону.

Шкалу анероида предварительно градуируют, т. е. наносят деления по показаниям ртутного барометра. Значения давления на шкале выражены в миллиметрах ртутного столба и в гектопаскалях (гПа).

Для измерения разности давления в сосуде и атмосферного давления служат манометры. Простейший манометр — жидкостный. Он представляет собой рассмотренную нами ранее U-образную трубку с жидкостью (см. рис. 189). Одно колено трубки (рис. 211) присоединяется к сосуду, давление в котором необходимо измерить. Другое колено открыто. Если уровень поверхности жидкости в колене, соединенном с сосудом, ниже, чем в открытом, значит, давление газа 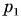 в сосуде больше атмосферного  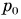на величину давления столба жидкости высотой h, т. е.

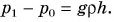
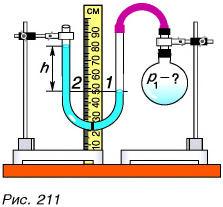
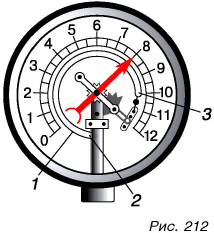
А если давление газа в несколько раз больше атмосферного? Для измерения высоких давлений применяют металлический манометр (рис. 212). Его основным элементом является полая тонкостенная металлическая трубка (/), согнутая в дугу. Один конец трубки (3) закрыт, другой (2) присоединяется к сосуду с газом. Закрытый конец (3) через зубчатый механизм соединен со стрелкой, движущейся относительно шкалы. Чем больше давление в трубке (а значит, в сосуде), тем больше распрямляется трубка и тем больше отклоняется стрелка. Нуль на шкале соответствует атмосферному давлению. Значит, если стрелка стоит на цифре «8», давление в сосуде в 9 раз больше атмосферного. Именно так устроен манометр для контроля давления в автомобильных шинах (рис. 213).

Главные выводы:

1. Атмосферное давление зависит от высоты местности и метеоусловий.
2. Зависимость атмосферного давления от высоты и метеоусловий можно использовать для измерения высоты и для прогноза погоды.
3. Атмосферное давление измеряют барометрами, а давление газов в сосудах — манометрами.

Для любознательных:

Жидкостными манометрами можно измерять давление, отличающееся от атмосферного лишь незначительно. Так, если в примере на с. 127—128 давление в сосуде будет в 2 раза больше атмосферного, т. е. 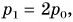то, согласно формуле 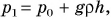имеем:

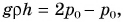
откуда

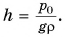
При использовании в манометре воды

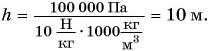
Только представьте размеры такого прибора! При использовании ртути размеры уменьшаются в 13,6 раза, но возникают новые проблемы — пары ртути ядовиты.

Пример №3

У подножия горы барометр показывает давление 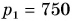мм рт. ст., а на ее вершине — 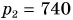мм рт. ст. Определите высоту данной горы.

Дано: 

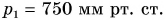
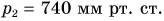
Решение:

Разность давлений у подножия горы и на ее вершине:

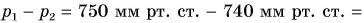
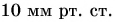
Учтем, что на 1 мм рт. ст. давление уменьшается при подъеме примерно на высоту 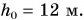Тогда высота горы:

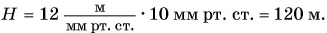
Ответ: H = 120 м.

Решебник по физике за 10, 11 класс (А.П. Рымкевич, 2001 год),
задача №511
к главе «25. Изопроцессы».

1 Если нет специальных оговорок, то при решении задач этого параграфа можно атмосферное давление принимать равным 100 кПа. В задачах 514—526 процесс считать изотермическим, в задачах 527—533 — изобарным и в задачах 534—540 — изохорным.

V₂ = 5 л, ΔP = 60 кПа. Найти: P.

Ответ

Проверено экспертом

Пусть газ находится в плотном сосуде, тогда его объем не меняется

раз объем не меняется (также допускаем, что масса тоже неизменна), то справедлив закон Шарля:

P0 / T0 = (P0 + 2*10^(4)) / T,

P0 T = T0 (P0 + 2*10^(4)).

дальше, в теории, можно выразить P0, но, как по мне, проще решить линейное уравнение:

Решение отдельных задач

Задача 1. При сжатии газа его объем уменьшился на 2 л, а давление увеличилось в 2 раза. Найти первоначальный объем газа V ₁ .

Обозначим Δ V изменение объема газа, P ₁ и P ₂ – давления газа до и после сжатия.

Решение. Судя по условию задачи, здесь процесс изотермический. Правда следовало бы добавить, что процесс сжатия происходит медленно, потому что, если бы он происходил быстро, то это был уже адиабатный процесс, при котором температура газа тоже меняется. Но, как правило, при условии задач на газовые процессы об этом упомянуть забывают, поэтому мы и обратили на этот момент внимание.

Произведем вычисления V ₁= 2·2л=4л

Задача 2. В узкой откачанной и запаянной с двух концов горизонтальной трубке посредине находится столбик ртути длиной 0,3 м. Если трубку поставить вертикально, столбик ртути сместится на 15 см. Определить давление в трубке до того как из нее откачали воздух, если ее длина 1м, а плотность ртути13,6·10 3 кг/м 3 .

Решение. По условию задачи температура газа остается постоянной, поэтому при решении задачи можно применить закон Бойля-Мариотта. Состояние воздуха в трубке в горизонтальном положении определялось параметрами: объемом V ₁ и давлением P . Выразим объем через поперечное сечение трубки S и высоту воздушного столбика , то есть

При вертикальном положении трубки состояние газа в верхней части трубки определялось параметрами: объемом и давлением P ₁. В нижней части трубки объем стал и давление P ₂= P ’+ P ₁. Столбик ртути находился в равновесии, когда давление воздуха в нижней части трубки равно сумме давления воздуха в верхней части трубки и давление столбика ртути P ’= ρgh .

Запишем закон Бойля-Мариотта для состояния газа в верхней части трубки

и для нижней части трубки

Выражение P ₁, полученное из (1), подставим в (2)

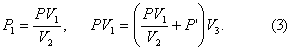
В равенство (3) подставим значения

Задача 3. Газ массой 12·10 -3 кг занимает объем 6·10 -3 м 3 при температуре 180 0 С. При какой температуре плотность этого газа будет равна 6 кг/м 3 .

Решение: Плотность газа при постоянном давлении и массе обратно пропорциональна объему, то есть

но при постоянном давлении объем прямо пропорционален абсолютной температуре 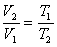тогда . Отсюда 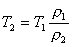, но , окончательно получим

Задача 4. Определить на сколько изменилась масса гелия, находящегося в баллоне объемом 0,25 м 3 под давлением 10 6 Па при температуре 20 0 С, если из баллона была выпущена часть массы газа, после чего давление понизилось до 10 5 Па, а температура уменьшилась до 10 0 С.

Решение. До того как часть газа была выпущена из баллона его состояние определялось такими параметрами: давление Р₁, объем V _, масса m ₁, температура Т₁. После того как часть газа была выпущена из баллона, состояние газа стало определяться параметрами: Р₂, V , m ₂, T ₂.Запишем уравнение Менделеева-Клапейрона для первого и второго состояния газа

где V – объем газа, который по условию задачи остается неизменным; μ – молекулярный вес гелия. Выразим из этих уравнений m ₁ и m ₂ и найдем их разность Δ m

Задача 5. Определить объем баллона со сжатым углекислым газом, находящимся под давлением в 100 атмосфер при температуре 27 0 С, если при нормальных условиях то же количество углекислого газа занимает объем 1,3 м 3 .

Решение. При нормальных условиях состояние газа определяется параметрами: Т, P , V . При данных условиях – параметрами Т, P , V . Так как масса газа не изменялась, то для решения задачи можно воспользоваться уравнением объединенного газового закона:

Задача 6. При какой температуре находилось 100 г водорода в баллоне объемом 10 л, если давление при этом было 2 . 10 4 Па?

m=100 г=0,1кг
μ=2 кг/кмоль
V =10л=10 -2 м 3
P =2·10 4 Па
R =8,3·10 3 Дж/кмоль·град

Решение. Из уравнения Менделеева-Клапейрона PV = m /_µ· RT находим температуру:

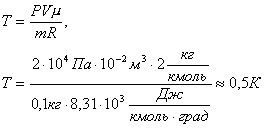
Задача 7. Определить плотность азота при температуре 27 0 С и давлении 760 мм рт. ст.

t =27 0 C
T =300К
P =760мм рт. ст. » 10 5 Па
μ=28 кг/кмоль
R =8,3·10 3 Дж/кмоль·град

Решение. Из уравнения Менделеева-Клапейрона найдем плотность азота PV = m /_µ· RT откуда

Задача 8. Определить по графику зависимость объема от температуры. Характер изменения давления, под которым находился газ во время нагревания, показан на рисунке (а).

Решение. Для решения задачи необходимо из начала координат провести изобары, на которых лежат точки 1 и 2 (см. рисунок (б)). Точка 1 лежит на изобаре, которая составляет с осью абсцисс меньший угол, чем изобара, проходящая через точку 2. Из уравнения газового состояния следует, что тангенс угла наклона изобары пропорционален 1/ P . Тогда из рисунка видим, что давление газа убывает при переходе из состояния 1 в состояние 2. Нагревание производилось при уменьшающемся давлении газа.

При изучении физики в восьмом классе мы говорили о том, что
изменить состояние термодинамической системы, то есть её внутреннюю энергию, можно
двумя способами: используя теплопередачу или совершая механическую работу.
Поговорим о последней более подробно.

Итак, когда мы изучали механику, мы с вами говорили о том,
что работа силы (то есть механическая работа) связана с превращением одного
вида энергии в другой, например, механической энергии во внутреннюю. При этом работу
силы мы рассматривали как меру изменения энергии физической системы.

А вот как определить работу в термодинамике, ведь при
рассмотрении термодинамических процессов механическое перемещение макротел в
целом не рассматривается?

Забавно, но работа в термодинамике определяется так же, как и
в механике, но она равна изменению не механической энергии тела, а изменению
его внутренней энергии.

Итак, давайте рассмотрим газ, находящийся в цилиндрическом
сосуде с площадью основания S, и закрытый
подвижным поршнем. Взаимодействие газа с поршнем, а также со стенками сосуда
можно характеризовать давлением, которое газ оказывает на них.

Начнём медленно нагревать газ так, чтобы его давление не
изменялось. Очевидно, что в этом случае газ будет изобарически расширяться, а
поршень начнёт перемещаться за счёт работы силы давления газа над внешними
телами.

Предположим, что поршень переместился на расстояние ∆l.
Так как в процессе расширения давление газа не изменялось, то и сила давления
газа на поршень оставалась неизменной:

F
= pS.

Поэтому работу этой силы мы можем найти как произведение
модуля силы на модуль перемещения и на косинус угла между направлением вектора
силы и вектора перемещения (в нашем примере правда, этот угол равен нулю):

Подставим в записанное уравнение выражение для силы давления:

А теперь давайте подумаем, что определяет произведение площади
основания сосуда (она же площадь основания поршня) и модуля перемещения поршня?..
Да, оно определяет приращение объёма:

Тогда работа газа при его изобарном расширении будет
определяться произведением давления газа на изменение его объёма:

Из этой формулы следует, что сила давления газа совершает
работу только в процессе изменения объёма газа.

А так как давление газа всегда величина положительная, то из
формулы также следует, что при расширении газ совершает положительную работу. При
сжатии же газа сила давления будет совершать отрицательную работу.

Процесс медленного изобарного сжатия газа можно
характеризовать и работой внешних сил над газом, которая отличается от работы
самого газа только знаком:

А теперь давайте запишем уравнение Клайперона — Менделеева
для двух состояний газа в цилиндре:

И вычтем из второго уравнение первое:

В левой части полученного равенства у нас стоит произведение
давления газа на изменение его объёма. А это, как мы с вами нашли ранее, есть не
что иное, как работа газа при изобарном процессе:

Теперь предположим, что в сосуде под поршнем находится один
моль идеального газа и в результате изобарного расширения его температура
изменилась на один кельвин. Тогда получим, что «А равно Эр»:

Отсюда вытекает физический смысл универсальной газовой
постоянной: она численно равна работе, совершаемой одним молем идеального
газа при его изобарном нагревании на один кельвин.

Работе газа при его изобарном расширении или сжатии можно
дать простое геометрическое токование. Для этого давайте построим график
зависимости давления газа от занимаемого им объёма. Очевидно, что графиком
является прямая линия, параллельная оси абсцисс.

А площадь прямоугольника, ограниченного графиком процесса,
осью V и прямыми, соответствующими значениям объёмов в начальном и
конечном состояниях газа, — это есть ничто иное, как работа газа.

Если процесс перехода газа из начального состояния в конечное
не является изобарным, то кривую зависимости давления газа от занимаемого им
объёма можно представить как ломаную, состоящую из большого числа изохор и
изобар. Работа на изохорных участках равна нулю, а суммарная работа на всех
изобарных участках будет равна площади заштрихованной фигуры.

А теперь для закрепления материала решим с вами несколько
классических задач. В первой задаче нам необходимо будет определить работу, совершаемую
силой давления идеального газа определённой массы при его изобарном нагревании от
290 К до 355 К, если давление газа и его начальный объём соответственно 200 кПа
и 0,1 м³.

Задача 2. Идеальный газ в количестве 3 молей находится
при температуре 350 К. После изохорного охлаждения, в результате которого
давление уменьшилось в два раза, газ испытывает изобарное расширение, причём в
конечном состоянии температура равна первоначальной. Изобразите графически эти
процессы в осях p, V и вычислите совершённую газом работу.

Содержание:

1. Свойства газов
2. Давление газов
3. Зависимость между объёмом и давлением газа. Закон Еойля — Мариотта
4. Зависимость между плотностью газа и его давлением
5. Зависимость объёма газа от температуры. Закон Гей-Люссака
6. Зависимость давления газа от температуры. Закон Шарля
7. Абсолютная шкала температур
8. Зависимость между объёмом, давлением и температурой газа
9. Физическая сущность понятия абсолютного нуля
10. Изменение температуры газа при быстром расширении и сжатии
11. Применение сжатых газов

Газ – это одно из трёх основных агрегатных состояний вещества, характеризующееся очень слабыми связями между составляющими его частицами (молекулами, атомами или ионами), а также их большой подвижностью. Частицы газа почти свободно и хаотически движутся в промежутках между столкновениями, во время которых происходит резкое изменение характера их движения.

На странице -> решение задач по физике собраны решения задач и заданий с решёнными примерами по всем темам физики.

Свойства газов

Главные свойства газов – это подвижность и хаотичное движение частиц, направление которых меняется при столкновении. Газ – одно из 4 агрегатных состояний веществ, которые на сегодняшний день известны науке.

Давление газов

Всякий газ производит давление на оболочку, внутри которой он находится.

Давление, производимое газом на стенки сосуда, объясняется ударами движущихся молекул.

При ударе о стенку молекулы газа отдают ей определённое количество движения; стенка испытывает при этом действие некоторой силы.

Удар каждой отдельной молекулы о стенку сосуда производит очень небольшое действие. Но молекул газа очень много, удары о стенки сосуда происходят беспрерывно, поэтому в результате получается значительное давление.

Хаотичность движения молекул приводит к тому, что давление газа одинаково во всех направлениях.

При нагревании давление газа увеличивается. Так как при этом число молекул газа не изменяется, то увеличение давления можно объяснить только тем, что удары молекул о стенки заключающего газ сосуда делаются при нагревании чаще и что каждый удар становится сильнее. Удары же могут стать чаще и сильнее, если увеличивается скорость движения молекул. Это подтверждается, как мы видели (гл. V), многочисленными опытами.

Зависимость между объёмом и давлением газа. Закон Еойля — Мариотта

Состояние газа определяется его объёмом, давлением и температурой. С изменением этих величин меняется и состояние газа. Мы будем рассматривать последовательно процессы, при которых одна из величин, характеризующих состояние газа, постоянна, а две другие меняются.

Изучим сначала такой процесс, при котором давление и объём газа изменяются, а температура остаётся постоянной. Такой процесс называется изотермическим ¹.

¹ От греч. слов: изос — равный, термос — тёплый.

Итак, рассмотрим, как изменяется давление данной массы газа при изменении его объёма, если температура газа не меняется.

Опыты, устанавливающие эту зависимость, можно произвести на приборе, три положения которого изображены на рисунке 134.

Рис. 134. Прибор для установления зависимости между объёмом и давлением газа (в трёх положениях).

В этом приборе стеклянная трубка А соединяется резиновой трубкой с другой стеклянной трубкой В. Трубка А вверху снабжена краном  обе трубки наполняются ртутью.

Откроем кран  и установим трубку В так, чтобы уровень ртути в трубке А был, например, на середине трубки (положение I). Давление над ртутью в обеих трубках атмосферное; допустим, что оно равно 76 см рт. ст. Закроем теперь кран, отделив этим массу воздуха в трубке А от атмосферного воздуха. Таким образом, в этой стадии опыта мы будем иметь в трубке А определённую массу воздуха, находящегося под давлением p₁ = 76 см рт. ст.

Поднимем теперь трубку В вверх на столько, чтобы объём воздуха в трубке А уменьшился вдвое (положение II). Уровень ртути в трубке В при этом значительно поднимется над уровнем в трубке А.

Рассмотрим теперь, чему будет равно давление воздуха в трубке А. Это давление уравновешивает атмосферное давление и давление всего столба ртути в трубке В, стоящего выше уровня n₁ высота этого столба n₁n оказывается равной 76 см. Таким образом, давление воздуха в трубке А уравновешивает не одну, как в первом случае, а две атмосферы (р₂ = 2 am).

Значит, с уменьшением объёма данной массы газа в два раза давление его увеличивается в два раза. Если уменьшить объём газа в 1,5; 2,5; 3 раза, то соответственно в 1,5; 2,5; 3 раза увеличится его давление.

Опустим теперь трубку В так, чтобы масса воздуха в трубке А заняла вдвое больший объём (положение III). Уровень ртути в трубке А при этом понизится. Атмосферное давление теперь уравновешивает давление воздуха в трубке А и давление столба ртути от уровня n в трубке А до уровня в трубке В. Измерения показывают, что высота этого столба ртути равна 38 см. Давление, производимое воздухом в трубке А, найдём, вычтя из атмосферного давления давление столба ртути: р₃ = 76 см—38 см = 38 см; следовательно, р₃ = 0,5 am.

Итак, при увеличении объёма газа в два раза его давление уменьшается в два раза.

Перемещая трубку В в различные положения и отсчитывая каждый раз объём и давление воздуха в трубке А, найдём, что при уменьшении объёма исследуемой массы воздуха в некоторое число раз давление его увеличивается во столько же раз. Температура воздуха при всех опытах остаётся постоянной.

Опыты, проведённые с другими газами, дали те же результаты.

Изучая на опыте зависимость давления газа от его объёма, английский учёный Бойль (1627—1691) и французский учёный Мариотт (1620—1684) независимо один от другого открыли следующий закон.

Давление данной массы газа при неизменной температуре обратно пропорционально объёму газа.

Этот закон называется законом Бойля — Мариотта.

Выразим закон Бойля — Мариотта математически. Пусть температура некоторой массы газа постоянная и пусть:

V₁ — объём газа при давлении р₁,

V2  » » » » р₂.

Согласно закону Бойля — Мариотта можно написать:

Из этой формулы следует, что:

Полученное равенство можно рассматривать как новое выражение закона Бойля — Мариотта.

Произведение объёма данной массы газа на его давление при неизменной температуре есть величина постоянная.

Изобразим графически изотермическое изменение состояния газа. Для этого по оси абсцисс будем откладывать значения объёмов газа, а по оси ординат соответствующие им значения давлений. Выберем масштаб так, чтобы начальные значения объёма и давления были равны 1. Тогда начальное состояние газа будет изображено точкой А (рис. 135). Если давление увеличится вдвое, объём уменьшится в два раза, состояние газа изобразится на графике точкой В. При уменьшении первоначального давления вдвое объём удвоится, получим точку С. Беря далее давления в три, четыре и т. д. раза больше или меньше начального, а объёмы соответственно в три, четыре и т. д. раза меньше или больше, получим ряд точек, изображающих различные состояния одной и той же массы газа при одинаковой температуре.

Рис. 135. График изотермического процесса.

Проведя через эти точки линию, получим кривую, которая называется изотермой.

Тщательными исследованиями установлено, что для реально существующих газов закон Бойля — Мариотта имеет лишь приближённое значение. Так, например, если произведение pV при 1 am равно единице, то при 2 am оно имеет следующие значения:

для воздуха ………………………0,99977

» водорода …………………….. 1,00026

» окиси углерода………………….. 0,99974

» двуокиси углерода………………… 0,99720

При очень больших давлениях (в сотни и тысячи атмосфер) закон Бойля — Мариотта становится совершенно неприменимым; в таких случаях зависимость между объёмом и давлением газа выражается более сложными уравнениями.

Зависимость между плотностью газа и его давлением

Плотность газа численно равна массе, заключённой в единице объёма.

Масса газа не меняется при его сжатии или расширении, но объём меняется; следовательно, меняется и плотность газа.

Пусть при постоянной температуре: D₁ — плотность газа при объёме V₁ и давлении p₁ , a D₂ —  плотность газа при объёме V₂ и давлении p₂.

Если масса газа равна m, то можно написать:

откуда:

Но  на основании закона Бойля — Мариотта; поэтому

При постоянной температуре плотность газа прямо пропорциональна его давлению.

Нетрудно понять справедливость этого вывода, исходя из молекулярно-кинетической теории. В самом деле, давление газа обусловлено ударами его молекул. Если объём газа уменьшится вдвое, то в новом объёме , плотность газа станет вдвое больше. Вдвое увеличится и число ударов молекул о стенки, т. е. давление газа возрастёт в два раза.

Зависимость объёма газа от температуры. Закон Гей-Люссака

Как и все тела, газы при нагревании расширяются, причём весьма заметно даже при незначительном нагревании. Это легко обнаружить на следующем простом опыте (рис. 136).

Рис. 136. Установка для наблюдения расширения газа при нагревании.

Колба А соединяется с расположенной горизонтально трубкой CD, которая укреплена вдоль шкалы. Внутри этой трубки находится небольшой столбик ртути. Достаточно к колбе прикоснуться рукой, как столбик ртути в трубке CD начнёт двигаться.

При охлаждении колбы столбик ртути перемещается влево, а при нагревании — вправо; следовательно, газ при охлаждении сжимается, а при нагревании расширяется. Зная объём колбы и диаметр трубки, можно измерить увеличение объёма газа.

Постепенно нагревая газ в колбе, можно установить, что при постоянном давлении изменение объёма данной массы газа пропорционально изменению температуры. Поэтому тепловое расширение газа, так же как и других тел, можно охарактеризовать при помощи коэффициента объёмного расширения.

Пусть при температуре 0°С объём газа равен V₀ , а при температуре t объём V_t. Увеличение объёма, приходящееся на каждую единицу объёма, взятого при 0°С, при нагревании на один градус будет равно:

откуда:  (1)

Величина входящая в писанные выше формулы, называется коэффициентом объёмного расширения газа.

Жозеф Луи Гей-Люссак (1778—1850)— один из выдающихся французских химиков и физиков. Он открыл ряд важных химических и физических законов, из которых в физике широко известен закон одинакового расширения газов и паров при одинаковом повышении температуры.

Французский учёный Гей-Люссак, исследуя на опыте тепловое расширение газов, открыл, что, коэффициент объёмного расширения у всех газов при постоянном давлении одинаков и численно равен

В этом отношении расширение газов при нагревании отличается от расширения твёрдых и жидких тел, где, как мы видели (см. § 81 и 82), коэффициент объёмного расширения зависит от химического состава тел.

Положим в формуле (1):

получим:  откуда следует, что при нагревании на 1° под постоянным давлением объём данной массы газа увеличивается на  того объёма, который газ занимал при 0°С.

Этот закон получил название закона Гей-Люссака. Процессы, подобные рассмотренному, протекающие при постоянном давлении, называются изобарными¹.

¹ От греч. слов: изос — равный, барос — тяжесть, вес.

Формула (1) показывает, что объём газа при температуре t° равен произведению его объёма, взятого при 0°С, на двучлен объёмного расширения

Пример. 1. Объём некоторой массы газа при 0°С равен 10 л. Найти объём его при t=273°С, если давление постоянно.

По условиям задачи нам известен объём газа при 0°С, т. е. V₀ = 10 л; подставляя числовые данные задачи в формулу найдем, что

Пример 2. При температуре 273°С объём некоторой массы газа равен 10 л. Чему будет равняться объём этого газа при температуре 546°С, если давление постоянно?

Нам известен объём газа при температуре 273°С; чтобы определить объём этого газа при t₂ = 546°С, надо предварительно найти его объём при 0°.

Этот объём найдётся из равенства:

откуда:

Найдём теперь объём газа при 546°:

Зависимость давления газа от температуры. Закон Шарля

Нагревая газ в закрытом цилиндре, например в папиновом котле (рис. 136а), можно по манометру заметить, что давление газа увеличивается. Следя по термометру за повышением температуры, легко установить, что при постоянном объёме давление газа возрастает пропорционально повышению температуры.

Рис. 136а. При нагревании газа в закрытом цилиндре давление его повышается.

Аналогично тому, как для характеристики теплового расширения газов мы ввели коэффициент объёмного расширения, введём величину, характеризующую изменение давления газа при изменении его температуры.

Обозначим буквой р₀ давление газа при 0°С, a p_t — давление при t°. Увеличение давления, приходящееся на каждую единицу начального давления при нагревании на 1°С, будет равно:

  (1)

Величина (греч. «гамма») называется термическим коэффициентом давления газа.

Измерения показывают, что величина термического коэффициента давления для всех

газов одинакова и равна

Определяя из формулы (1) величину p_t получим:

   (2)

Положим в формуле (2) тогда 

Отсюда следует, что давление данной массы газа при нагревании на 1° при постоянном объеме увеличивается на  того давления, которым обладал газ при 0°C. 

Этот закон называется законом Шарля, по имени французского учёного, открывшего его в 1787 г.

Из закона Шарля следует, что термический коэффициент давления газа равен коэффициенту объёмного расширения  Это равенство вытекает из закона Бойля — Мариотта. Докажем это.

Пусть некоторая масса газа заключена в цилиндре под поршнем (рис. 137, а) и пусть температура её в этом начальном состоянии равна 0°, объём V₀ и давление р₀. Закрепим поршень АВ и нагреем газ до температуры t° (рис. 137, б); тогда давление газа увеличится и станет равным р_t объём же его останется прежним.

По закону Шарля:

Будем теперь газ нагревать от 0 до t° (рис. 137, в), предоставив поршню свободно перемещаться. Давление газа останется таким же, каким было в начальном его состоянии, т. е. р₀ , объём же увеличится до V_t. По закону Гей-Люссака:

Рис. 137.

а)    начальное состояние газа: 0°, V₀, р₀;

б)    состояние газа, определяемое величинами: 

в)    состояние газа, определяемое величинами: 

Итак, имеем: при температуре t° объём данной массы газа V⁰ и давление при той же температуре: давление р₀ и объём По закону Бойля— Мариотта:

После упрощения этого выражения получаем равенство:

Выразим сначала в виде таблицы, а потом графически зависимость давления газа от температуры. Для этого воспользуемся уравнением:

Рис. 138. График изменения давления газа от температуры.

Отложим по оси абсцисс в некотором условном масштабе температуры газа, а по оси ординат соответствующие этим температурам давления, взятые из написанной выше таблицы.

Соединяя на графике отмеченные точки, получим прямую LM (рис. 138), представляющую собой график зависимости давления газа от температуры при постоянном объёме.

Процесс изменения состояния газа, происходящий при неизменном объёме газа, называется  изохорным ¹ процессом, а линия LM, изображающая изменение давления газа при постоянном объеме в зависимости от температуры, называется изохорой.

¹ От греч. слов: изос — разный, хорема — вместимость.

Пример 1. Давление газа при 0°С равно 780 мм рт. ст. Определить давление этого газа при температуре 273°С.

По формуле найдем, что

Пример 2. Чему будет равно давление газа при температуре 546°, если давление его при температуре 273° равно 780 мм рт. cm.?

В этой задаче прежде всего надо определить давление газа при 0°С. По формуле находим:

Теперь можно определить давление газа при t = 546°:

Законы Гей-Люссака и Шарля так же, как и закон Бойля — Мариотта, лишь приближённо отражают свойства газов. Это можно видеть хотя бы. из того факта, что для разных газов величины и несколько различаются между собой (см. таблицу).

      

Точные измерения показывают, что для каждого данного газа значения и получаются разные в зависимости от того, в каком температурном интервале и при каком давлении они определены. Однако эти различия очень незначительны, они учитываются лишь при весьма точных расчётах.

Абсолютная шкала температур

Вернёмся ещё раз к графику изменения давления газа с температурой (рис. 138).

Продолжим прямую LM на этом графике до пересечения её с горизонтальной осью, по которой откладываются температуры газа, она пересечёт эту ось в точке K. Отрезок ОК будет изображать на этом графике такую температуру газа, при которой давление его равно нулю. Чему равна эта температура?

Обратимся к уравнению Положим в этом уравнении p_t = 0, т. е. напишем следующее равенство:

Так как давление газа при 0°С не равно нулю то из написанного равенства следует, что:

откуда: или, так как

Итак, давление газа равняется нулю при температуре —273°С.

Вильям Томсон (Кельвин) (1824— 1907) — выдающийся английский физик. Ему принадлежат важные открытия в области теории электричества и теплоты и изобретения, из которых наиболее значительным было усовершенствование телеграфной связи. Он ввёл в физику понятие об абсолютной температуре. Его именем названы градусы шкалы абсолютных температур — градусы Кельвина.

Английский учёный Вильям Томсон (Кельвин) предложил такую шкалу температур, при которой за нуль градусов принята температура — 273°. Эта шкала получила название абсолютной шкалы температур, или шкалы Кельвина, а нуль градусов этой шкалы, равный — 273°, называется абсолютным нулём температур.

В шкале Кельвина величина градуса та же, что и в стоградусной шкале.

Будем обозначать температуру по шкале Кельвина буквой Т.

При нормальном атмосферном давлении температура таяния льда по шкале Кельвина Т₀ = 273°, температура же кипения воды T = 373°.

Всякая другая температура t° стоградусной шкалы связана с абсолютной температурой Т соотношениями:

Зависимость между объёмом, давлением и температурой газа

Объединённый закон газового состояния. Мы рассмотрели процессы, в которых одна из трёх величин, характеризующих состояние газа (объём, давление и температура), не меняется.

Вы видели, что если не меняется температура, то давление и объём газа связаны друг с другом законом Бойля —- Мариотта. При постоянном давлении объём газа изменяется с изменением температуры по закону Гей-Люссака, и, наконец, при постоянном объёме давление газа меняется с изменением температуры по закону Шарля.

Однако в природе часто имеют место процессы, когда одновременно меняются все три величины, характеризующие состояние газа. Установим теперь, какая связь существует между объёмом, давлением и температурой.

Пусть для двух каких-либо произвольных состояний некоторой массы газа эти величины будут:

Из этих состояний изменением величин р, V или t газ можно перевести в любые другие состояния. Будем, например, сохраняя постоянным давление, переводить газ из состояний 1) и 2) в состояния, при которых температура газа будет равна 0°С.

По закону Гей-Люссака объём газа V₁ после уменьшения температуры от до 0° будет равен объём V₂, после уменьшения температуры от t₂ до 0° будет 

Новые состояния газа выразятся так:

В обоих этих состояниях температура газа одинакова, поэтому на основании закона Бойля — Мариотта можно написать:

  (1)

Так как величины р, V, t, характеризующие состояние рассматриваемого газа и обозначенные индексами 1 и 2, выбраны были нами произвольно, то равенство (1) справедливо для любых состояний этого газа. Поэтому можно утверждать, что:

  (2)

Для данной массы газа произведение давления газа на его объём, делённое на двучлен объёмного расширения, есть величина постоянная.

Выведенная нами зависимость между объёмом, давлением и температурой газа называется объединённым законом газового состояния, а равенство (1) или (2) — уравнением состояния газа.

Уравнение состояния газа можно упростить, введя в него вместо температуры t по стоградусной шкале температуру Т по абсолютной шкале температур. Для этого преобразуем уравнение:

Введя в него значение получим:

что после сокращения на 273 даст:

Но и ; следовательно, можно написать:

Это означает, что для данной массы газа произведение давления на объём, делённое на абсолютную температуру, постоянно при всех температурах:

В частности, если при температуре Т = 273° объём газа равен V₀ и давление его р₀ , то можно написать:

Физическая сущность понятия абсолютного нуля

Мы уже отмечали, что реальные газы лишь приближённо следуют законам Гей-Люссака, Шарля и Бойля — Мариотта. Однако можно представить себе газ, для которого эти законы выполнялись бы в точности. Молекулы такого газа можно представить себе в виде упругих шариков исчезающе малого объёма, взаимодействие между которыми осуществляется только через их столкновения друг с другом. В физике такой газ принято называть идеальным газом.

Из уравнения следует, что при t = —273°, т. е. при абсолютном нуле, давление газа равно нулю. Но ведь давление газа есть результат ударов движущихся молекул о стенки сосуда. Следовательно, при температуре абсолютного нуля должно прекратиться тепловое движение молекул идеального газа.

Опыт показывает, что при малых давлениях свойства реальных газов очень близки к свойствам идеального газа. Следовательно, при приближении к температуре абсолютного нуля должно прекратиться тепловое движение молекул и реального газа. Этот вывод относится не только к газам, но и к твёрдым и жидким телам.

Физикой установлено, что такое состояние вещества недостижимо, но к нему можно подойти очень близко. В настоящее время достигнута температура, которая выше абсолютного нуля всего на несколько стотысячных долей градуса.

Изменение температуры газа при быстром расширении и сжатии

Опыты показывают, что при быстром сжатии температура газа повышается, а при быстром расширении понижается.

Увеличение температуры газа при сжатии можно показать на следующем простом опыте. Возьмём толстостенный цилиндрический стеклянный сосуд, внутри которого может двигаться поршень (рис. 139). При быстром сжатии воздух в сосуде сильно нагревается, и легко воспламеняющееся вещество (например, ватка, смоченная эфиром), положенное на дно сосуда, вспыхивает. Такого рода явление используется, например, в двигателях внутреннего сгорания —дизелях: при сжатии воздуха в цилиндре двигателя горючая смесь, введённая в цилиндр, нагревается до температуры воспламенения (работа двигателя описана в § 131).

Рис. 139. При быстром сжатии воздух в цилиндре сильно нагревается и легко воспламеняющееся вещество вспыхивает.

При быстром же расширении газа температура его понижается. Это можно наблюдать на следующем опыте. Будем накачивать воздух в прочную закрытую пробкой стеклянную банку, содержащую пары воды. При достижении определённого давления пробка выскочит; при этом воздух, расширяясь, совершит работу и охладится, вследствие чего водяной пар превратится в туман (рис. 140).

Рис. 140. Сжатый в сосуде воздух, выбрасывая пробку, расширяется. Совершая при этом работу, он охлаждается, вследствие чего водяной пар в сосуде превращается в туман.

Понижение температуры при быстром расширении газа используется для получения сжиженных газов; об этом будет рассказано в § 122.

Изменение температуры тела, как было установлено в § 71, связано с изменением внутренней энергии тела. Так как при быстром сжатии температура газа повышается, то внутренняя энергия его при этом увеличивается. Увеличение внутренней энергии газа происходит в результате работы, совершённой при его сжатии. Расширяясь же, газ совершает работу; при этом внутренняя энергия его уменьшается, и если расширение происходит быстро, то температура газа, как мы видели в наших опытах, понижается.

Процесс, происходящий в теле без теплообмена с окружающими его другими телами, называется адиабатным процессом.

Все быстро протекающие процессы практически могут считаться адиабатными.

Применение сжатых газов

Многие сжатые газы в настоящее время находят широкое применение в технике.

Сжатый воздух, например, применяется в работе различных пневматических инструментов: отбойных молотков, заклёпочных молотков, в разбрызгивателях краски и др.

На рисунке 141 показана схема устройства отбойного молотка. Сжатый воздух подаётся в молоток по шлангу М. Золотники Z, аналогичные применяемым в паровых машинах, направляют его поочерёдно то в заднюю, то в переднюю часть цилиндра. Поэтому воздух давит на поршень Р то с одной, то с другой стороны, что вызывает быстрое возвратно-поступательное движение поршня и пики молотка В. Последняя наносит быстро следующие друг за другом удары, внедряется в уголь и откалывает куски его от массива.

Рис. 141. Схема устройства отбойного молотка.

Существуют также пескоструйные аппараты, которые дают сильную струю воздуха, смешанную с песком. Эти аппараты применяются, например, для очистки стен. Сейчас нередко можно видеть работу специальных аппаратов, применяемых для окраски стен, где краска распыляется сжатым воздухом. Сжатым воздухом открываются двери вагонов метро и троллейбусов. Сжатый воздух используется в работе тормозов на транспорте. Схематическое устройство одного из видов пневматического тормоза железнодорожного вагона изображено на рисунке 142.

Компрессор подаёт воздух по магистрали в стальной резервуар А. Поршень В тормозного цилиндра оказывается под одинаковым давлением справа и слева; поэтому соединённая с ним тормозная колодка D отжата от колеса. Если открыть тормозной кран М, то находящийся в магистрали под давлением воздух устремится в атмосферу; клапан К захлопнется, и, таким образом, стальной резервуар изолируется от магистрали. Теперь давление на поршень В справа станет больше, чем давление слева, вследствие чего тормозная колодка прижмётся к ободу колеса. Если теперь кран М закрыть и снова подать в магистраль сжатый воздух, то восстановится первоначальное положение.

Рис. 142. Схема устройства железнодорожного пневматического тормоза.

В технике применяется не только сжатый воздух, но и некоторые другие газы, так, например, водород, ацетилен и кислород применяются при газовой сварке; аммиак используется в холодильном деле. Чтобы газы было удобно перевозить, их помещают в прочные стальные баллоны, накачивая до давления 60—200 am.

Рис. 142а. Внешний вид мощного компрессора.

Сжатие газов осуществляется с помощью мощных нагнетательных насосов — компрессоров.

На рисунке 143, а, б дана схема работы компрессора.

Компрессор состоит из цилиндра с поршнем и двумя клапанами; один из них входной, другой выходной. При движении поршня вниз (рис. 143, б) открывается входной клапан и в цилиндр поступает воздух из помещения; при движении поршня вверх (рис. 143, а) входной клапан закрывается, вошедший воздух сжимается поршнем и через выходной клапан поступает в стальной баллон для хранения сжатого газа.

Существуют так называемые многоступенчатые компрессоры, в которых газ последовательно  

сжимается в трёх или четырёх цилиндрах. Такие компрессоры позволяют получить газ, сжатый до давления в тысячи атмосфер. На рисунке 142а изображён внешний вид одного из типов многоступенчатых компрессоров.

Рис. 143, а, б. Схема работы компрессора.

Услуги по физике:

1. Заказать физику
2. Заказать контрольную работу по физике
3. Помощь по физике

Лекции по физике:

1. Физические величины и их измерение
2. Основные законы механики
3. Прямолинейное равномерное движение
4. Прямолинейное равнопеременное движение
5. Сила
6. Масса
7. Взаимодействия тел
8. Механическая энергия
9. Импульс
10. Вращение твердого тела
11. Криволинейное движение тел
12. Колебания
13. Колебания и волны
14. Механические колебания и волны
15. Бегущая волна
16. Стоячие волны
17. Акустика
18. Звук
19. Звук и ультразвук
20. Движение жидкости и газа
21. Молекулярно-кинетическая теория
22. Молекулярно-кинетическая теория строения вещества
23. Молекулярно – кинетическая теория газообразного состояния вещества
24. Теплота и работа
25. Температура и теплота
26. Термодинамические процессы
27. Идеальный газ
28. Уравнение состояния идеального газа
29. Изменение внутренней энергии
30. Переход вещества из жидкого состояния в газообразное и обратно
31. Кипение, свойства паров, критическое состояние вещества
32. Водяной пар в атмосфере
33. Плавление и кристаллизация
34. Тепловое расширение тел
35. Энтропия
36. Процессы перехода из одного агрегатного состояния в другое
37. Тепловое расширение твердых и жидких тел
38. Свойства жидкостей
39. Свойства твёрдых тел
40. Изменение агрегатного состояния вещества
41. Тепловые двигатели
42. Электрическое поле
43. Постоянный ток
44. Переменный ток
45. Магнитное поле
46. Электромагнитное поле
47. Электромагнитное излучение
48. Электрический заряд (Закон Кулона)
49. Электрический ток в металлах
50. Электрический ток в электролитах
51. Электрический ток в газах и в вакууме
52. Электрический ток в полупроводниках
53. Электромагнитная индукция
54. Работа, мощность и тепловое действие электрического тока
55. Термоэлектрические явления
56. Распространение электромагнитных волн
57. Интерференционные явления
58. Рассеяние
59. Дифракция рентгеновских лучей на кристалле
60. Двойное лучепреломление
61. Магнитное поле и электромагнитная индукция
62. Электромагнитные колебания и волны
63. Природа света
64. Распространение света
65. Отражение и преломление света
66. Оптические приборы и зрение
67. Волновые свойства света
68. Действия света
69. Линзы и получение изображений с помощью линз
70. Оптические приборы и глаз
71. Фотометрия
72. Излучение и спектры
73. Квантовые свойства излучения
74. Специальная теория относительности в физике
75. Теория относительности
76. Квантовая теория и природа поля
77. Строение и свойства вещества
78. Физика атомного ядра
79. Строение атома