Онлайн калькулятор поможет рассчитать какое будет конечное давления идеального газа от изменения температуры, при условии, что объем газа остается постоянным. Зависимость давления от температуры в этом случае описывается законом Гей-Люссака (законом Шарля).
Формула: P2 = P1×T2/T1
Где:
P1 – начальное давление;
P2 – конечное давление;
T1 – начальная температура (в Кельвинах);
T2 – конечная температура (в Кельвинах).
Например, данный калькулятор поможет приблизительно определить зависимость давления в шинах от температуры.
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

Смотрите также
Калькулятор ниже предназначен для решения задач на использование уравнения Клапейрона-Менделеева, или уравнение состояния идеального газа. Некоторая теория изложена под калькулятором, ну а чтобы было понятно, о чем идет речь — пара примеров задач:
Примеры задач на уравнение Менделеева-Клапейрона
-
В колбе объемом 2,6 литра находится кислород при давлении 2,3 атмосфер и температуре 26 градусов Цельсия .
Вопрос: сколько молей кислорода содержится в колбе? - Некоторое количество гелия при 78 градусах Цельсия и давлении 45,6 атмосфер занимает объем 16,5 литров.
Вопрос: Каков объем этого газа при нормальных условиях? (Напомню, что нормальными условиями для газов считается давление в 1 атмосферу и температура 0 градусов Цельсия)
В калькулятор вводим начальные условия, выбираем, что считать (число моль, новые объем, температуру или давление), заполняем при необходимости оставшиеся условия, и получаем результат.
![]()
Уравнение Клапейрона-Менделеева. Связь между числом молей газа, его температурой, объемом и давлением.
Точность вычисления
Знаков после запятой: 2
Теперь немного формул.
Уравнение Клапейрона-Менделеева
где
P — давление газа (например, в атмосферах)
V — объем газа (в литрах);
T — температура газа (в кельвинах);
R — газовая постоянная (0,0821 л·атм/моль·K).
Если используется СИ, то газовая постоянная равна 8,314 Дж/K·моль
Так как m-масса газа в (кг) и M-молярная масса газа кг/моль, то m/M — число молей газа, и уравнение можно записать также
где n — число молей газа
И как нетрудно заметить, соотношение
есть величина постоянная для одного и того же количества моль газа.
И эту закономерность опытным путем установили еще до вывода уравнения. Это так называемые газовые законы — законы Бойля-Мариотта, Гей-Люссака, Шарля.
Так, закон Бойля-Мариотта гласит (это два человека):
Для данной массы газа m при неизменной температуре Т произведение давления на объем есть величина постоянная.
Закон Гей-Люссака (а вот это один человек):
Для данной массы m при постоянном давлении P объем газа линейно зависит от температуры
Закон Шарля:
Для данной массы m при постоянном объеме V давление газа линейно зависит от температуры
Посмотрев на уравнение, нетрудно убедиться в справедливости этих законов.
Уравнение Менделеева-Клапейрона, также как и опытные законы Бойля-Мариотта, Гей-Люссака и Шарля справедливы для широкого интервала давлений, объемов и температур. То есть во многих случаях эти законы удобны для практического применения. Однако не стоит забывать, что когда давления превышают атмосферное в 300-400 раз, или температуры очень высоки, наблюдаются отклонения от этих законов.
Собственно, идеальный газ потому и называют идеальным, что по определению это и есть газ, для которого не существует отклонений от этих законов.
Как рассчитать давление насыщенного пара?
Анонимный вопрос
15 января 2019 · 5,6 K
Мои интересы: разнообразны, но можно выделить следующие: литература, история… · 28 янв 2019
Чтобы найти давление пара при данной температуре, воспользуйтесь уравнением Клапейрона-Клаузиуса: ln(P1/P2) = (ΔHvap/R)((1/T2) – (1/T1)), где:
- ΔHvap – энтальпия испарения жидкости. Ее, как правило, можно найти в таблице в учебниках по химии.
- R – газовая постоянная, равная 8,314 Дж/(K×моль)
- T1 – начальная температура (при которой давление пара известно).
- T2 – конечная температура (при которой давление пара неизвестно).
- P1 и P2 – давление пара при температуре T1 и T2, соответственно.
4,4 K
Комментировать ответ…Комментировать…
Как найти давление если знаешь температуру и массу.
Вы зашли на страницу вопроса Как найти давление если знаешь температуру и массу?, который относится к
категории Физика. По уровню сложности вопрос соответствует учебной
программе для учащихся 10 – 11 классов. В этой же категории вы найдете ответ
и на другие, похожие вопросы по теме, найти который можно с помощью
автоматической системы «умный поиск». Интересную информацию можно найти в
комментариях-ответах пользователей, с которыми есть обратная связь для
обсуждения темы. Если предложенные варианты ответов не удовлетворяют,
создайте свой вариант запроса в верхней строке.
Закон Бойля — Мариотта (Давление и объем газа)
Давление газа при постоянной температуре пропорционально числу молекул газа,
находящихся в данном объеме, т.е. массе газа.
Состояние газов описывается законом Бойля — Мариотта:
При постоянной температуре объем находящегося в замкнутом
сосуде газа обратно пропорционален давлению,
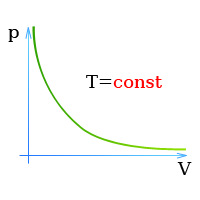
Закон Бойля — Мариотта (Давление и объем газа)
или
При постоянной температуре произведение давления газа, находящегося в замкнутом сосуде,
на его объем есть постоянная величина,
или
При постоянной температуре давление и плотность находящегося в замкнутом сосуде газа пропорциональны друг другу
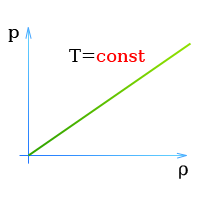
Закон Бойля — Мариотта (Давление и объем газа)
Если
| p1 | начальное давление газа, | Па |
|---|---|---|
| p2 | конечное давление газа, | Па |
| V1 | начальный объем газа, | м3 |
| V2 | конечный объем газа, | м3 |
то
[ frac{p_1}{p_2} = frac{V_2}{V_1} ]
или
[ pV = const ]
Закон Бойля – Мариотта (Давление и объем газа) |
стр. 507 |
|---|
