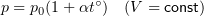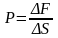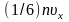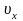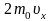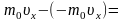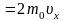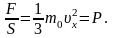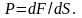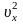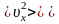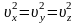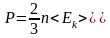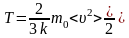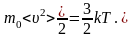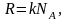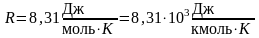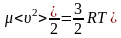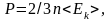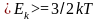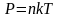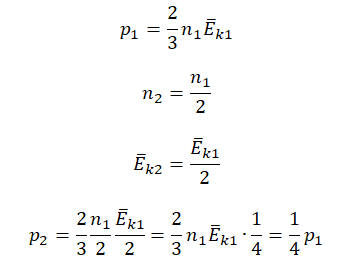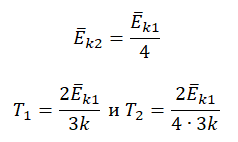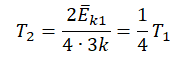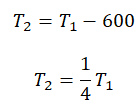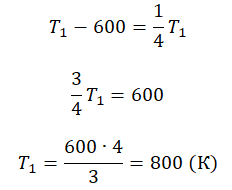Молекулярная физика Основные формулы
1. Основы молекулярно-кинетической теории. Газовые законы
1.1 Количество вещества
m — масса;
μ — молярная масса вещества;
N — число молекул;
NA = 6,02·1023 моль-1 — число Авогадро
1.2 Основное уравнение молекулярно-кинетической теории идеального газа
p — давление идеального газа;
m — масса одной молекулы;
n = N/V — концентрация молекул;
V — объем газа;
N — число молекул;

1.3 Средняя квадратичная скорость молекул идеального газа
k = 1,38·10-23 Дж/К — постоянная Больцмана;
R = kNA = 8,31 Дж/(моль·К) — универсальная газовая постоянная;
T = t+273 — абсолютная температура;
t — температура по шкале Цельсия.
1.4 Средняя кинетическая энергия молекулы одноатомного газа
1.5 Давление идеального газа
n — концентрация молекул;
k — постоянная Больцмана;
T — абсолютная температура.
1.6 Закон Бойля-Мариотта
p — давление;
V — объем газа.
1.7 Закон Шарля
p0 — давление газа при 0 °С;
α = 1/273 °C-1 — температурный коэффициент давления.
1.8 Закон Гей-Люссака
V0 — объем газа при 0 °С.
1.9 Уравнение Менделеева-Клапейрона
1.10 Объединенный закон газового состояния (уравнение Клапейрона)
1.11 Закон Дальтона
pi — парциальное давление i-й компоненты смеси газов.
2. Основы термодинамики
2.1 Внутренняя энергия идеального одноатомного газа
ν — количество вещества;
R = 8,31 Дж/(моль·К) — универсальная газовая постоянная;
T — абсолютная температура.
2.2 Элементарная работа, совершаемая газом,
при изменении объема на бесконечно малую величину dV
p — давление газа.
При изменении объема от V1 до V2
2.3 Первый закон термодинамики
ΔQ — количество подведенной теплоты;
ΔA — работа, совершаемая веществом;
ΔU — изменение внутренней энергии вещества.
2.4 Теплоемкость идеального газа
ΔQ — количество переданной системе теплоты на участке процесса;
ΔT — изменение температуры на этом участке процесса.
Давление идеального газа, теория и онлайн калькуляторы
Давление идеального газа
Определение давления идеального газа
Определение
Давление идеального газа – это один из самых важных макроскопических параметров, при помощи которого характеризуют состояние
системы в молекулярной физике.
Обозначают давление буквой $p$. Если для известной массы идеального газа определены давление и температура (или объем), то полагают, что состояние термодинамической системы в состоянии равновесия определяется однозначно, так как существующие законы и уравнения молекулярно кинетической теории (МКТ) позволяют все остальные параметры вычислить.
В общем случае давление определяют как:
[p={mathop{lim }_{Delta Sto 0} frac{Delta F_n}{Delta S} }left(1right),]
где $F_n$ проекция силы на нормаль к поверхности S данная сила оказывает воздействие, $Delta S$- площадь поверхности.
Идеальный газ оказывает давление на стенки сосуда, в котором он находится, за счет того, что молекулы этого газа движутся и ударяются о стенки сосуда. Давление идеального газа можно найти, применяя основные положение МКТ. При этом получают, что давление идеального газа равно:
[p=frac{1}{3}nm_0{leftlangle v_{kv}rightrangle }^2left(2right),]
где $m_0$ – масса одной молекулы газа; $n$- концентрация молекул газа; $leftlangle v_{kv}rightrangle =sqrt{frac{1}{N}sumlimits^N_{i=1}{v^2_i}}, N $- количество молекул в объеме газа равном $V$. Уравнение (2) называют основным уравнением МКТ. Его можно записать в другом виде, используя среднюю кинетическую энергию молекул ($leftlangle E_krightrangle $):
[p=frac{2}{3}nleftlangle E_krightrangle left(3right).]
С таким важным термодинамическим параметром как термодинамическая температура давление связывает формула:
[p=nkT left(4right),]
где $k$ – постоянная Больцмана. Уравнение (4) называют уравнением состояния идеального газа.
Если проводить изохорный процесс ($V=const$) с некоторой массой идеального газа, то давление его будет подчинено закону Шарля:
[p_2=p_1frac{T_2}{T_1}left(5right),]
где $p_1$- давление газа имеющего температуру $T_1$.
При проведении изотермического процесса ($T=const$) c постоянной массой некоторого газа поведение давления можно характеризовать, используя уравнение:
[p_1V_1=p_2V_2left(6right).]
В соответствии с законом Дальтона давление смеси газов можно найти как сумму давлений каждого газа:
[p=sumlimits^N_{i=1}{p_i} left(7right),]
где $p_i$ – давление каждого газа в отдельности.
Уравнения МКТ, содержащие давление идеального газа
Уравнение Менделеева – Клапейрона (еще один вариант уравнения состояния):
$pV=frac{m}{mu }RT$(8),
где $frac{m}{mu }=nu $ -количество вещества; $m$ – масса газа; $mu $- молярная масса газа; $R$ – универсальная газовая постоянная.textit{}
Определение работы газа в термодинамике:
[A=intlimits^{V_2}_{V_1}{pdV}left(9right).]
Соответственно, первое начало термодинамики для идеального газа в дифференциальном виде запишем как:
[delta Q=pdV+frac{i}{2}nu RdTleft(10right),]
где $i$ – число степеней свободы молекулы газа; $delta Q$ – элементарное количество теплоты, которое получает идеальный газ; $frac{i}{2}nu RdT=dU$ – изменение внутренней энергии термодинамической системы.textit{}
Примеры задач с решением
Пример 1
Задание. В идеальном газе проводят процесс, при котором $p=frac{AU}{V},$ где $U$ – внутренняя энергия газа; $A=const$ для определенного газа. Сравните коэффициенты пропорциональности $A$, если в первом случае газ одноатомный, во втором двух атомный. textit{}
Решение. Внутренняя энергия идеального газа для любого процесса равна:
[U=frac{i}{2}nu RT left(1.1right).]
Состояние идеального газа описывает уравнение Менделеева – Клайперона:
[pV=nu RT left(1.2right).]
Подставим правую часть уравнения, которое описывает заданный в условиях задачи процесс ($p=frac{AU}{V}$) вместо давления в (1.2), имеем:
[frac{AU}{V}V=nu RT left(1.3right).]
Получим из (1.3), что внутренняя энергия вычисляется как:
[U=frac{1}{A}nu RTleft(1.4right).]
Сравним выражения для внутренней энергии (1.1) и (1.4), имеем:
[frac{i}{2}=frac{1}{A}left(1.5right).]
Для одноатомного газа $i=3$; для двухатомного газа (без учета колебаний молекул) $i=5$.
[frac{3}{2}=frac{1}{A_1};; frac{5}{2}=frac{1}{A_2}to frac{A_2}{A_1}=frac{3}{2}cdot frac{2}{5}=frac{3}{5}.]
Ответ. $frac{A_2}{A_1}=frac{3}{5}$
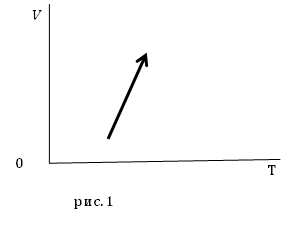
Пример 2
Задание. На рис.1 представлены процессы, проводимые с постоянной массой идеального газа, укажите, как изменяются давления в процессах?
Решение. Уравнение процесса можно аналитически описать уравнением:
[V(T)=AT-B left(2.1right),]
где $A$ и $B$ положительные постоянные величины.
Состояние газа определим при помощи уравнения Менделеева – Клапейрона:
[pV=nu RT left(2.2right).]
Вместо объема подставим уравнение процесса в (2.2):
[pleft(AT-Bright)=nu RTleft(2.3right).]
Раздели обе части (2.3) на температуру:
[frac{pleft(AT-Bright)}{T}=nu Rto pleft(A-frac{B}{T}right)=nu Rto p=frac{nu R}{A-frac{B}{T}} left(2.4right).]
Из уравнения (2.4) следует, что при увеличении температуры $frac{B}{T}$ уменьшается, следовательно, знаменатель дроби правой части выражения (2.4) увеличивается, значит, давление уменьшается.
Ответ. Давление в заданном процессе уменьшается.
Читать дальше: диэлектрический гистерезис.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Давление. Основное уравнение молекулярно-кинетической теории
находящиеся
под давлением газ или жидкость действуют
с некоторой силой на любую поверхность,
ограничивающую их объем. В этом случае
сила действует по нормали к ограничивающей
объем поверхности. Давление на поверхность
равно:
,
где
ΔF
– сила, действующая на поверхность
площадью ΔS.
Вычислим
давление, оказываемое газом на одну из
стенок сосуда (рис. 1.3).
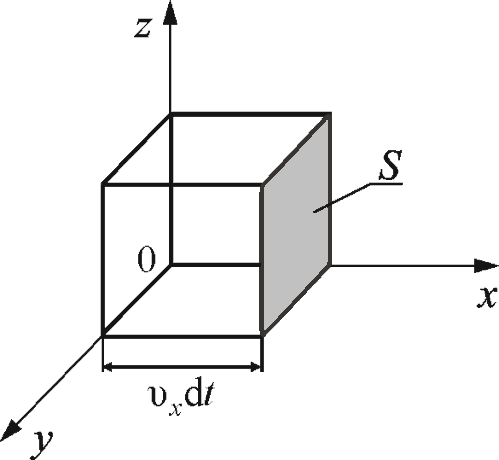
Рис.
1.3
Обозначим:
n
– концентрация молекул в сосуде; m0
– масса одной молекулы. Движение молекул
по всем осям равновероятно, поэтому к
одной из стенок сосуда площадью S,
подлетает в единицу времени
молекул, где
– проекция вектора скорости на
направление, перпендикулярное стенке.
Каждая
молекула обладает импульсом m0υx,
но стенка получает импульс
(при
абсолютно-упругом ударе
).
За время dt
о стенку площадью S
успеет удариться число молекул, которое
заключено в объёме V:
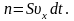
Общий
импульс, который получит стенка S:
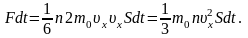
Разделив
обе части равенства на S
и dt,
получим выражение для давления:
(1.2.1)
Таким
образом, мы определили давление
как силу, действующую в единицу времени
на единицу площади:
(1.2.2)
Наивно
полагать, что все молекулы подлетают к
стенке S
с одной и той же скоростью
(рис. 1.3). На самом деле молекулы имеют
разные скорости, направленные в разные
стороны, то есть скорости газовых молекул
– случайные
величины.
Более
точно случайную
величину
характеризует среднеквадратичная
величина.
Поэтому под скоростью
понимаем среднеквадратичную
скорость
.
Вектор скорости, направленный произвольно
в пространстве, можно разделить на три
составляющих:
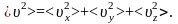
Ни
одной из этих проекций нельзя отдать
предпочтение из-за хаотичного
теплового движения
молекул,
то есть в среднем
.
Следовательно, на другие стенки будет
точно такое же давление. Тогда можно
записать в общем случае:
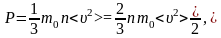
или
, (1.2.3)
где
– средняя
энергия одной молекулы. Это и есть
основное
уравнение
молекулярно-кинетической
теории газов.
Итак,
давление газов определяется средней
кинетической энергией поступательного
движения молекул.
Уравнение
(1.2.3) называют основным уравнением,
потому что давление Р
– макроскопический параметр системы
здесь связан с основными характеристиками
– массой и скоростью молекул.
Иногда
за основное уравнение принимают выражение
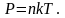
Из
опыта известно, что если привести в
соприкосновение два тела, горячее и
холодное, то через некоторое время их
температуры выравниваются. Что перешло
от одного тела к другому? Раньше, во
времена Ломоносова и Лавуазье, считали,
что носителем тепла является некоторая
жидкость – теплород.
На самом деле – ничто не переходит,
только изменяется средняя кинетическая
энергия – энергия движения молекул, из
которых состоят эти тела. Именно средняя
кинетическая энергия атомов и молекул
служит характеристикой системы в
состоянии равновесия.
Это
свойство позволяет определить параметр
состояния, выравнивающийся у всех тел,
контактирующих между собой, как величину,
пропорциональную средней кинетической
энергии частиц в сосуде. Чтобы связать
энергию с температурой, Больцман ввел
коэффициент пропорциональности k,
который впоследствии был назван его
именем:
, (1.3.1)
где
k
– постоянная
Больцмана,
k
= 1,38·1023
Дж·К1.
Величину
T
называют
абсолютной
температурой
и измеряют в градусах Кельвина
(К).
Она служит мерой
кинетической энергии теплового движения
частиц идеального газа.
Из
(1.3.1) получим:
(1.3.2)
Формула
(1.3.2) применима для расчетов средней
кинетической энергии на
одну молекулу
идеального газа.
Можно
записать:
.
Обозначим:
– универсальная
газовая постоянная,
.
Тогда,
с учетом обозначения получим:
, (1.3.3)
– это
формула для молярной
массы газа.
Так
как температура определяется средней
энергией движения молекул, то она, как
и давление, является статистической
величиной,
то есть параметром, проявляющимся в
результате совокупного действия
огромного числа молекул. Поэтому не
говорят: «температура одной молекулы»,
нужно сказать: «энергия одной молекулы,
но температура газа».
С
учетом вышесказанного о температуре,
основное
уравнение молекулярно-кинетической
теории
можно
записать по-другому. Так как из (1.2.3)
где
.
Отсюда
. (1.3.6)
В
таком виде основное
уравнение молекулярно-кинетической
теории употребляется
чаще.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Давление газа
Содержание:
- Давление газа — что это за параметр
- Причина возникновения давления в газах
- Формула давления идеального газа из молекулярно-кинетической теории
- Второй способ записи основного уравнения МКТ
Давление газа — что это за параметр
Определение
Давление в физике представляет собой один из трех ключевых термодинамических макроскопических характеристик для измерения любой газовой системы.
Определение
Газ — это одно из четырех, включая плазму, агрегатных состояний материи, характеризующееся очень слабыми связями между составляющими его частицами, а также их большой подвижностью.
В газообразной среде частицы в определенной концентрации расположены не упорядоченно и перемещаются в хаотичном порядке в разных направлениях с одинаковой вероятностью. Подобное строение не позволяет газам сохранять стабильность объема и формы даже при малом внешнем силовом воздействии. Для любого газа, включая одноатомный, значение средней кинетической энергии его частиц в виде атомов и молекул будет превышать энергию межмолекулярного взаимодействия между ними.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Кроме того, расстояние, на которое удалены частицы, значительно превышает их собственные размеры. В том случае, когда молекулярными взаимодействиями и габаритами частиц допускается пренебрегать, газ считают идеальным. Для такой формы материи характерен только один тип внутреннего взаимодействия в виде упругих столкновений. Так как размер частиц пренебрежимо мал по сравнению с расстоянием, на которое они удалены, вероятность столкновений частиц между собой будет низкой.
Примечание
По этой причине в идеальной газовой среде можно наблюдать лишь столкновения частиц со стенками сосуда. Какой-либо реальный газ с хорошей точностью можно отнести к идеальному, когда их температура выше, чем комнатная, а давление несущественно больше, чем атмосферное.
Причина возникновения давления в газах
Давление газа нельзя объяснить теми же причинами, что и давление твердого тела на опору. Расстояние, на которое удалены молекулы газообразной среды, существенно больше. В результате хаотичного движения они сталкиваются между собой и со стенками сосуда, который они занимают. Давление газа на стенки сосуда и вызвано ударами его молекул.
Данный параметр увеличивается по мере того, как нарастает сила ударов молекул о стенки. Газ характеризуется одинаковым давлением во всех направлениях, которое является следствием хаотичного движения огромного числа молекул.
Примечание
Важно отметить, что газ оказывает давление на дно и стенки сосуда, объем которого он занимает, во всех направления равномерно. В связи с этим, воздушный шарик сохраняет форму, несмотря на то, что его оболочка достаточно эластична.
Перед тем как транспортировать или отправить на хранение газообразные вещества, их сильно сжимают. В этом случае давление газа увеличивается. Его помещают в специальные баллоны из стали высокой прочности. Такие емкости необходимы для хранения сжатого воздуха на подводных лодках и кислорода, предназначенного для сварки металлов.
Свойства давления газа:
- Если объем уменьшается, то давление газа возрастает, а во время увеличения объема, давление будет снижаться при постоянных величинах массы и температуры вещества.
- Газ, находящийся в закрытом сосуде, характеризуется давлением, которое возрастает по мере увеличения температуры вещества при условии постоянства его массы и объема.
- В том случае, когда масса газа увеличивается, его давление также будет возрастать и наоборот.
Запись формул для определения давления газа начинают с выяснения причин, по которым оно возникает в рассматриваемой системе. Исходя из физического смысла, давление представляет собой величину, равную отношению силы, перпендикулярно воздействующей на некоторое основание, к площади этого основания:
(P=frac{F}{S})
Как было отмечено ранее, для идеальной газовой системы характерен лишь один тип взаимодействия — это абсолютно упругие столкновения. В процессе частицы передают количество движения Δp стенкам сосуда в течение времени соударения Δt. В данном случае применим второй закон Ньютона:
(F*Δt = Δp)
Таким образом, конкретно сила F является причиной формирования давления на стенки сосуда. Данная величина F, производимая одной частицей, незначительна. Однако, когда количество частиц огромно, они в совокупности создают ощутимый эффект, проявляемый в виде наличия давления в сосуде.
Формула давления идеального газа из молекулярно-кинетической теории
Объяснение концепции идеального газа построено на основных положениях молекулярно-кинетической теории, которая вытекает из принципов статистической механики. Наука получила активное развитие во второй половине XIX, благодаря таким ученым, как Джеймс Максвелл и Людвиг Больцман. Основы дисциплины были заложены еще Бернулли в первой половине XVIII века.
Исходя из статистики Максвелла-Больцмана, все частицы в системе обладают разными скоростями движения. При этом можно наблюдать небольшой процент частиц со скоростями, приближенными к нулю, и малую долю частиц, обладающих огромной скоростью. Средняя квадратичная скорость в этом случае будет соответствовать некоторой величине, не изменяющейся с течением времени.
Средняя квадратичная скорость частиц однозначно характеризует температуру газа. Используя приближения молекулярно-кинетической теории в виде невзаимодействующих безразмерных и хаотично движущихся частиц, получают формулу для расчета давления газа в сосуде:
(P=frac{N*m*v^{2}}{3*V})
где N является количеством частиц в системе; V обозначает объем; v представляет собой среднюю квадратичную скорость; m является массой одной частицы.
При наличии указанных в формуле параметров, выраженных в единицах СИ, можно вычислить давление газа в сосуде.
Второй способ записи основного уравнения МКТ
Определение
В середине 30-х годов XIX столетия французскому инженеру Эмилю Клапейрону удалось обобщить накопленный до этого времени экспериментальный опыт изучения поведения газов во время разнообразных изопроцессов и получить формулу, которую в будущем назвали универсальным уравнением состояния идеального газа:
(P*V = n*R*T )
n является количеством вещества в молях; T представляет собой температуру по абсолютной шкале и обозначается в кельвинах.
Величина R является универсальной газовой постоянной. Этот термин был введен в уравнение русским химиком Д.И. Менделеевым. Исходя из этого, запись уравнения называют законом Клапейрона-Менделеева.
Определение
С помощью данного выражения можно определить формулу для расчета давления газа:
(P=frac{n*R*T}{V})
Полученное уравнение объясняет линейный рост давления при увеличении температуры в условиях стабильности объема. Если объем уменьшается с сохранением температуры, то давление увеличивается по гиперболе. Данные закономерности явления отражены в законах Гей-Люссака и Бойля-Мариотта.
Сравнивая представленное выражение с записью формулы, которая вытекает из положений молекулярно-кинетической теории, можно установить связь кинетической энергии одной частицы, либо системы в общем, и абсолютной температуры.
Важно отметить, что при расчетах с использованием формулы для Р, вытекающей из уравнения Клапейрона, связь с химическим составом газа отсутствует. Если давление определяют с помощью выражения, согласно понятию молекулярно-кинетической теории, то данную связь следует учитывать в виде параметра m. В том случае, когда определяют давление смеси идеальных газов, применяют один из следующих методов:
- Расчет средней массы частиц m, либо среднего значения молярной массы М с учетом атомных процентов каждого газа в смеси.
- Применение закона Дальтона, согласно которому давление в системе равно сумме парциальных давлений всех ее компонентов.
Пример
Предположим, что молекулы кислорода движутся со средней скоростью в 500 м/с. Требуется рассчитать, каково давление в сосуде, объем которого равен 10 литров, содержащий 2 моль молекул.
Для того чтобы найти ответ, следует применить формулу для Р из молекулярно-кинетической теории:
(P=frac{N*m*v^{2}}{3*V})
Из-за неизвестных параметров m и N требуется выполнить некоторые преобразования формулы:
(m=frac{M}{NA})
(n=frac{N}{NA})
(m*N= M*n)
(P=frac{M*n*v^{2}}{3*V})
Таким образом, удельный объем сосуда в кубических метрах равен 0,01. Молярная масса молекулы кислорода М составляет 0,032 кг/моль. Данные параметры можно подставить в уравнение вместе со скоростью и количеством вещества. Тогда Р = 533333 Па, что представляет собой давление в 5,3 атмосферы.
Идеальный газ — газ, удовлетворяющий трем условиям:
- Молекулы — материальные точки.
- Потенциальная энергия взаимодействия молекул пренебрежительно мала.
- Столкновения между молекулами являются абсолютно упругими.
Реальный газ с малой плотностью можно считать идеальным газом.
Измерение температуры
Температуру можно измерять по шкале Цельсия и шкале Кельвина. По шкале Цельсия за нуль принимается температура, при которой происходит плавление льда. По шкале Кельвина за нуль принимается абсолютный нуль — температура, при котором давление идеального газа равно нулю, и его объем тоже равен нулю.
Обозначение температуры
- По шкале Цельсия — t. Единица измерения — 1 градус Цельсия (1 oC).
- По шкале Кельвина — T. Единица измерения — 1 Кельвин (1 К).
Цена деления обеих шкал составляет 1 градус. Поэтому изменение температуры в градусах Цельсия равно изменению температуры в Кельвинах:
∆t = ∆T
При решении задач в МКТ используют значения температуры по шкале Кельвина. Если в условиях задачи температура задается в градусах Цельсия, нужно их перевести в Кельвины. Это можно сделать по формуле:
T = t + 273
Если особо важна точность, следует использовать более точную формулу:
T = t + 273,15
Пример №1. Температура воды равна oC. Определить температуру воды в Кельвинах.
T = t + 273 = 2 + 273 = 275 (К)
Основное уравнение МКТ идеального газа
Давление идеального газа обусловлено беспорядочным движением молекул, которые сталкиваются друг с другом и со стенками сосуда. Основное уравнение МКТ идеального газа связывает давление и другие макропараметры (объем, температуру и массу) с микропараметрами (массой молекул, скоростью молекул и кинетической энергией).
Основное уравнение МКТ
Давление идеального газа пропорционально произведению концентрации молекул на среднюю кинетическую энергию поступательного движения молекулы.
p=23n−Ek
p — давление идеального газа, n — концентрация молекул газа, −Ek — средняя кинетическая энергия поступательного движения молекул.
Выражая физические величины друг через друга, можно получить следующие способы записи основного уравнения МКТ идеального газа:
|
p=13m0n−v2 |
m0— масса одной молекулы газа; n — концентрация молекул газа; −v2 — среднее значение квадрата скорости молекул газа. Среднее значение квадрата скорости не следует путать со среднеквадратичной скоростью v, которая равна корню из среднего значения квадрата скорости: v=√−v2 |
|
p=13ρ−v2 |
ρ — плотность газа |
|
p=nkT |
k — постоянная Больцмана (k = 1,38∙10–3 Дж/кг) T — температура газа по шкале Кельвина |
Пример №2. Во сколько раз уменьшится давление идеального одноатомного газа, если среднюю кинетическую энергию теплового движения молекул и концентрацию уменьшить в 2 раза?
Согласно основному уравнению МКТ идеального газа, давление прямо пропорционально произведению средней кинетической энергии теплового движения молекул и концентрации его молекул. Следовательно, если каждая из этих величин уменьшится в 2 раза, то давление уменьшится в 4 раза:
Следствия из основного уравнения МКТ идеального газа
Через основное уравнение МКТ идеального газа можно выразить скорость движения молекул (частиц газа):
v=√3kTm0=√3RTM
R — универсальная газовая постоянная, равная произведения постоянной Авогадро на постоянную Больцмана:
R=NAk=8,31 Дж/К·моль
Температура — мера кинетической энергии молекул идеального газа:
−Ek=32kT
T=2−Ek3k
Полная энергия поступательного движения молекул газа определяется формулой:
E=N−Ek
Пример №3. При уменьшении абсолютной температуры на 600 К средняя кинетическая энергия теплового движения молекул неона уменьшилась в 4 раза. Какова начальная температура газа?
Запишем формулу, связывающую температуру со средней кинетической энергией теплового движения молекул, для обоих случаев, с учетом что:
Следовательно:
Составим систему уравнений:
Отсюда:
Задание EF19012

Алгоритм решения
1.Указать, в каких координатах построен график.
2.На основании основного уравнения МКТ идеального газа и уравнения Менделеева — Клапейрона выяснить, как меняются указанные физические величины во время процессов 1–2 и 2–3.
Решение
График построен в координатах (V;Ek). Процесс 1–2 представляет собой прямую линию, исходящую из начала координат. Это значит, что при увеличении объема растет средняя кинетическая энергия молекул. Но из основного уравнения МКТ идеального газа следует, что мерой кинетической энергии молекул является температура:
T=2−Ek3
Следовательно, когда кинетическая энергия молекул растет, температура тоже растет.
Запишем уравнение Менделеева — Клапейрона:
pV=νRT
Так как количество вещества одинаковое для обоих состояния 1 и 2, запишем:
νR=p1V1T1=p2V2T2
Мы уже выяснили, что объем и температура увеличиваются пропорционально. Следовательно, давление в состояниях 1 и 2 равны. Поэтому процесс 1–2 является изобарным, давление во время него не меняется.
Процесс 2–3 имеет график в виде прямой линии, перпендикулярной кинетической энергии. Так как температуры прямо пропорциональна кинетической энергии, она остается постоянной вместе с этой энергией. Следовательно, процесс 2–3 является изотермическим, температура во время него не меняется. Мы видим, что объем при этом процессе уменьшается. Но так как объем и давление — обратно пропорциональные величины, то давление на участке 2–3 увеличивается.
Ответ:
• Участок 1–2 — изобарный процесс. Температура увеличивается, давление постоянно.
• Участок 2–3 — изотермический процесс. Температура постоянно, давление увеличивается.
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17560
Первоначальное давление газа в сосуде равнялось р1. Увеличив объём сосуда, концентрацию молекул газа уменьшили в 3 раза, и одновременно в 2 раза увеличили среднюю энергию хаотичного движения молекул газа. В результате этого давление р2 газа в сосуде стало равным
Ответ:
а) 13p1
б) 2p1
в) 23p1
г) 43p1
Алгоритм решения
1.Записать исходные данные.
2.Записать основное уравнение МКТ идеального газа.
3.Составить уравнения для состояний 1 и 2.
4.Выразить искомую величину.
Решение
Исходные данные:
• Начальное давление: p0.
• Начальная концентрация молекул: n1 = 3n.
• Конечная концентрация молекул: n2 = n.
• Начальная средняя энергия хаотичного движения молекул: Ek1 = Ek.
• Конечная средняя энергия хаотичного движения молекул: Ek2 = 2Ek.
Основное уравнение МКТ:
p=23n−Ek
Составим уравнения для начального и конечного состояний:
p1=23n1−Ek1=233n−Ek=2n−Ek
p2=23n2−Ek2=23n2−Ek=43n−Ek
Отсюда:
n−Ek=p12=3p24
p2=4p16=23p1
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18416
Цилиндрический сосуд разделён неподвижной теплоизолирующей перегородкой. В одной части сосуда находится кислород, в другой – водород, концентрации газов одинаковы. Давление кислорода в 2 раза больше давления водорода. Чему равно отношение средней кинетической энергии молекул кислорода к средней кинетической энергии молекул водорода?
Алгоритм решения
1.Записать исходные данные.
2.Записать основное уравнение МКТ идеального газа.
3.Составить уравнения для обоих газов.
4.Найти отношение средней кинетической энергии молекул кислорода к средней кинетической энергии молекул водорода.
Решение
Анализируя условия задачи, можно выделить следующие данные:
• Концентрации кислорода и водорода в сосуде равны. Следовательно, n1 = n2 = n.
• Давление кислорода вдвое выше давления водорода. Следовательно, p1 = 2p, а p2 = p.
Запишем основное уравнение идеального газа:
p=23n−Ek
Применим его для обоих газов и получим:
p1=23n1−Ek1 или 2p=23n−Ek1
p2=23n2−Ek2 или p=23n−Ek2
Выразим среднюю кинетическую энергию молекул газа из каждого уравнения:
−Ek1=3pn
−Ek2=3p2n
Поделим уравнения друг на друга и получим:
−Ek1−Ek2=3pn·2n3p=2
Ответ: 2
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18824
В одном сосуде находится аргон, а в другом – неон. Средние кинетические энергии теплового движения молекул газов одинаковы. Давление аргона в 2 раза больше давления неона. Чему равно отношение концентрации молекул аргона к концентрации молекул неона?
Алгоритм решения
1.Записать исходные данные.
2.Записать основное уравнение МКТ идеального газа.
3.Составить уравнения для обоих газов.
4.Найти отношение концентрации молекул аргона к концентрации молекул неона.
Решение
Анализируя условия задачи, можно выделить следующие данные:
• Средние кинетические энергии теплового движения молекул газов одинаковы. Следовательно, −Ek1=−Ek2=−Ek.
• Давление аргона в 2 раза больше давления неона. Следовательно, p1 = 2p, а p2 = p.
Запишем основное уравнение идеального газа:
p=23n−Ek
Применим его для обоих газов и получим:
p1=23n1−Ek1 или 2p=23n1−Ek
p2=23n2−Ek2 или p=23n2−Ek
Выразим концентрации молекул газа из каждого уравнения:
n1=3p−Ek
n2=3p2−Ek
Поделим уравнения друг на друга и получим:
n1n2=3p−Ek·2−Ek3p=2
Ответ: 2
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 10.7k