Как найти давление в промежуточном шарнире

Задание
С-3. Определение реакций опор составной
конструкции.

Вариант
№ 1.

Найти реакции опор и
давление в промежуточном шарнире
составной конструкции. Схема конструкции
представлена на рис. 1 (размеры – в м),
нагрузка указана в таблице 1.

Рис.
1

Таблица
1.

P1, кН	М, кНм	q, кН/м
6,0	25,0	0,8

Лист

С-3.
Определение реакций опор составной
конструкции.

Решение.
Рассмотрим
систему уравновешивающихся сил,
приложенных
ко всей конструкции (рис. 2).

y

P_1y P₁

90

P_1x C

Q
M

R_Ay R_By

R_Ax R_Bx x

A

B

Рис.
2.

Разложим
силу P
на
составляющие P_x
и P_y.

P_1y
P₁



P_1x 



6

Рис.
3.

P_1x
= P₁sin(),

P_1y
= P₁cos().


= arctg(1,5/6) = arctg(0,25) = 14.

P_1x
= P₁sin()
= P₁sin(14)
= 60,24
= 1,44 (кН),

P_1y
= P₁cos()
= P₁cos(14)
= 60,97
= 5,82 (кН).

Q
= q3,5
=
0,83,5
=
2,8
(кН).

Лист

С-3.
Определение реакций опор составной
конструкции.

Запишем
уравнения равновесия:

(1)

(2)

(3)

Данная
система из 3 уравнений содержит 4
неизвестных, для их нахождения рассмотрим
отдельно правую и левую части конструкции.

Рассмотрим
систему уравновешивающихся сил,
приложенных к левой части конструкции
(рис.4):

y

P_1y P₁

90

P_1x C

R_Cx

Q
R_Cy

R_Ay

R_Ax x

A

Рис.
4.

Запишем уравнения
равновесия:

(4)

(5)

Лист

С-3.
Определение реакций опор составной
конструкции.

(6)

Рассмотрим систему
уравновешивающихся сил, приложенных к
правой части конструкции (рис.5):

y

R`_Cy

R`_Cx

C

M

R_By

R_Bx x

B

Рис.5.

Запишем уравнения
равновесия:

(7)

(8)

(9)

где
R_Cx
= R`<sub>Cx</sub>,
R<sub>Cy</sub>
= R`_Cy.

Таким
образом, имеем систему 4 уравнений (1),
(2), (6) и (9) с 4 неизвестными.

Из
уравнения (9)

Из уравнения (1)

Лист

С-3.
Определение реакций опор составной
конструкции.

Из
уравнения (6)

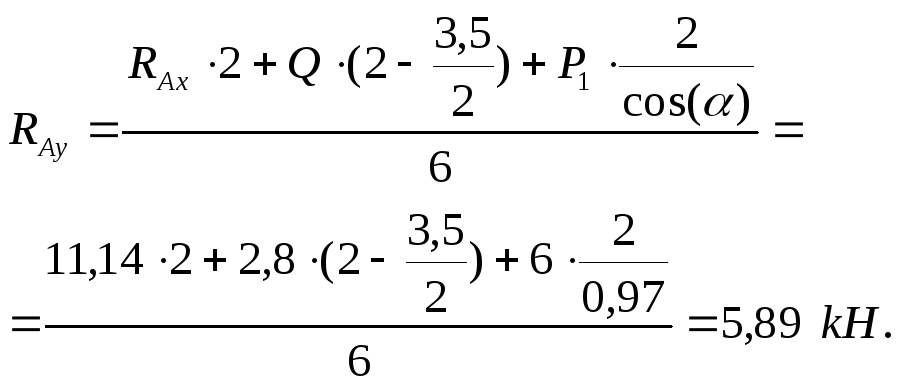
Из уравнения (2)

Найдем реакции
шарнира С:

R_Cx
= -R_Bx
= 12,5 кН,

R_Cy
= -R_By
= 0,07 кН.

Отрицательные
значения R_Bx
и R_By
говорят о
том, что действительное направление
R_Bx
и R_By
противоположно
указанному на рис.4.

Итак,

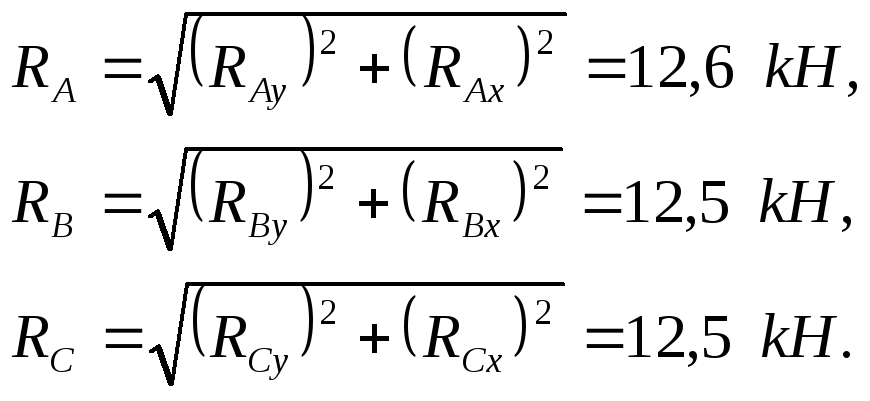
Лист

С-3.
Определение реакций опор составной
конструкции.

Соседние файлы в папке Задача С3-1

• #
• #

Найти реакции опор и давление в промежуточном шарнире составной конструкции. Схема конструкции представлена на рисунке (размеры – в м), нагрузка указана в таблице.

Решение	Формат	Размер	Наличие
Вариант 1	doc / pdf	363 КБ / 187 КБ	Готово
Вариант 2	doc / pdf	316 КБ / 182 КБ	Готово
Вариант 3	doc / pdf	334 КБ / 183 КБ	Готово
Вариант 4	doc / pdf	331 КБ / 179 КБ	Готово
Вариант 5	doc / pdf	348 КБ / 259 КБ	Готово
Вариант 6	doc / pdf	368 КБ / 260 КБ	Готово
Вариант 7	doc / pdf	391 КБ / 183 КБ	Готово
Вариант 8	doc / pdf	380 КБ / 181 КБ	Готово
Вариант 9	doc / pdf	326 КБ / 184 КБ	Готово
Вариант 10	doc / pdf	342 КБ / 180 КБ	Готово
Вариант 11	doc / pdf	393 КБ / 185 КБ	Готово
Вариант 12	doc / pdf	375 КБ / 183 КБ	Готово
Вариант 13	doc / pdf	419 КБ / 184 КБ	Готово
Вариант 14	doc / pdf	333 КБ / 185 КБ	Готово
Вариант 15	doc / pdf	378 КБ / 264 КБ	Готово
Вариант 16	doc / pdf	344 КБ / 267 КБ	Готово
Вариант 17	doc / pdf	363 КБ / 181 КБ	Готово
Вариант 18	doc / pdf	374 КБ / 261 КБ	Готово
Вариант 19	doc / pdf	337 КБ / 260 КБ	Готово
Вариант 20	doc / pdf	405 КБ / 190 КБ	Готово
Вариант 21	doc / pdf	373 КБ / 182 КБ	Готово
Вариант 22	doc / pdf	394 КБ / 184 КБ	Готово
Вариант 23	doc / pdf	344 КБ / 183 КБ	Готово
Вариант 24	doc / pdf	368 КБ / 189 КБ	Готово
Вариант 25	doc / pdf	377 КБ / 185 КБ	Готово
Вариант 26	doc / pdf	388 КБ / 185 КБ	Готово
Вариант 27	doc / pdf	409 КБ / 265 КБ	Готово
Вариант 28	doc / pdf	350 КБ / 259 КБ	Готово
Вариант 29	doc / pdf	327 КБ / 260 КБ	Готово
Вариант 30	doc / pdf	334 КБ / 261 КБ	Готово

Вариант № 1.

Найти реакции опор и давление в промежуточном шарнире составной конструкции. Схема конструкции представлена на рис. 1 (размеры – в м), нагрузка указана в таблице 1.

Рис. 1

Таблица 1.

P1, кН	М, кНм	q, кН/м
6,0	25,0	0,8

С-3. Определение реакций опор составной конструкции

Решение. Рассмотрим систему уравновешивающихся сил, приложенных ко всей конструкции (рис. 2).

y

P_1y P₁

90

P_1x C

Q M

R_Ay R_By

R_Ax R_Bx x

A B

Рис. 2.

Разложим силу P на составляющие Px и Py.

P_1y P₁

P_1x

6

Рис. 3.

P1x = P1sin(),

P1y = P1cos().

= arctg(1,5/6) = arctg(0,25) = 14.

P1x = P1sin() = P1sin(14) = 60,24 = 1,44 (кН),

P1y = P1cos() = P1cos(14) = 60,97 = 5,82 (кН).

Q = q3,5 = 0,83,5 = 2,8 (кН).

С-3. Определение реакций опор составной конструкции.

Запишем уравнения равновесия:

(1)

(2)

(3)

Данная система из 3 уравнений содержит 4 неизвестных, для их нахождения рассмотрим отдельно правую и левую части конструкции.

Рассмотрим систему уравновешивающихся сил, приложенных к левой части конструкции (рис.4):

y

P_1y P₁

90

P_1x C

R_Cx

Q R_Cy

R_Ay

R_Ax x

A

Рис. 4.

Запишем уравнения равновесия:

(4)

(5)

С-3. Определение реакций опор составной конструкции

(6)

Рассмотрим систему уравновешивающихся сил, приложенных к правой части конструкции (рис.5):

y

R`_Cy

R`_Cx

C

M

R_By

R_Bx x

B

Рис.5.

Запишем уравнения равновесия:

(7)

(8)

(9)

где RCx = R`Cx, RCy = R`Cy.

Таким образом, имеем систему 4 уравнений (1), (2), (6) и (9) с 4 неизвестными.

Из уравнения (9)

Из уравнения (1)

С-3. Определение реакций опор составной конструкции

Из уравнения (6)

Из уравнения (2)

Найдем реакции шарнира С:

RCx = -RBx = 12,5 кН,

RCy = -RBy = 0,07 кН.

Отрицательные значения RBx и RBy говорят о том, что действительное направление RBx и RBy противоположно указанному на рис.4.

Итак,

С-3. Определение реакций опор составной конструкции

Найти реакции опор конструкции изображенной на рис.1.

Дано: Q = 2, G = 20, a = 20, b = 30, c = 10 R =15, r =5. Решение: Разложим реакции в опорах А и Б на их составляющие по осям коардинат, при этом RAy=RBy=RDy=0

Составим уравнения сумм моментов относительно всех осей:

Р*15-q*5=0, где , отсюда Р=(q*5)/15

-qx*20+P*60-RBx*80, отсюда RBx=(qx*20-P*60)/80

-qx*20-G*(20+30)+RBz*(20+30+30) отсюда RBz= (qx*20+G*50)/80

-Raz*80+qz*60+G*30=0 отсюда Raz= (qz*60+G*30)/80

Rax*80+ qx*60-P*30=0 отсюда Rax=-( qx*60-P*30)/80

qx=Q*cos45; qz=Q*sin45

Ra= RB=

Результаты работы

Raz	Rax	Ra	RBz	RBx	RB

Применение теоремы об изменении кинетической энергии к изучению движения механической системы.

Вариант № 1.

Механическая система под действием сил тяжести приходит в движение из состояния покоя; начальное положение системы показано на рис. 1. Учитывая трение скольжения тела 1, пренебрегая другими силами сопротивления и массами нитей, предполагаемых нерастяжимыми, определить скорость тела 1 в тот момент, когда пройденный им путь станет равным s.

В задании приняты следующие обозначения: m1, m2, m3, m4 – массы тел 1, 2, 3, 4; – угол наклона плоскости к горизонту; f – коэффициент трения скольжения.

Необходимые для решения данные приведены в таблице 1. Блоки и катки считать сплошными однородными цилиндрами. Наклонные участки нитей параллельны соответствующим наклонным плоскостям.

Рис. 1

Таблица 1.

m1, кг	m2, кг	m3, кг	m4, кг	, град	f	s, м
m	4m	0,2m	4m/3	60	0,10	2

Решение.

Применим теорему об изменении кинетической энергии системы:

(1)

где T0 и T – кинетическая энергия системы в начальном и конечном положениях; – сумма работ внешних сил, приложенных к системе; – сумма работ внутренних сил системы.

Для рассматриваемых систем, состоящих из абсолютно твердых тел, соединенных нерастяжимыми нитями,

Так как в начальном положении система находится в покое, то Т0=0.

Следовательно, уравнение (1) принимает вид:

(2)

Кинетическая энергия рассматриваемой системы Т в конечном ее положении (рис.2) равна сумме кинетических энергий тел 1, 2, 3 и 4:

Т = Т1 + Т2 + Т3 + Т4. (3)

2

1

₂

V_A

V₃

3 V₁

A C₃ C_V

₃

V₄

4

Рис. 2.

Д-10

Кинетическая энергия груза 1, движущегося поступательно,

(4)

Кинетическая энергия барабана 2, совершающего вращательное движение,

, (5)

где J2x – момент инерции барабана 2 относительно центральной продольной оси:

, (6)

2 – угловая скорость барабана 2:

. (7)

После подстановки (6) и (7) в (5) выражение кинетической энергии барабана 2 принимает вид:

. (8)

Кинетическая энергия барабана 3, совершающего плоское движение:

, (9)

где VC3 – скорость центра тяжести С3 барабана 3, J3x – момент инерции барабана 3 относительно центральной продольной оси:

, (10)

3 – угловая скорость барабана 3.

Так как двигается по нити без скольжения, то мгновенный центр скоростей находится в точке СV. Поэтому

, (11)

. (12)

Подставляя (10), (11) и (12) в (9), получим:

. (13)

Кинетическая энергия груза 4, движущегося поступательно,

, (14)

где V4 = VC3 = V1/2:

. (15)

Кинетическая энергия всей механической системы определяется по формуле (3) с учетом (4), (8), (13), (15):

Подставляя и заданные значения масс в (3), имеем:

или

. (16)

Найдем сумму работ всех внешних сил, приложенных к системе, на заданном ее перемещении (рис. 3).

2

1

N₁

F_TP

3

C₃

P₃ P₁

4

P₄

Рис. 2.

Работа силы тяжести :

(17)

Работа силы трения скольжения :

Так как

то

(18)

Работа силы тяжести , препятствующей движению тела 1:

(19)

Работа силы тяжести , препятствующей движению тела 1:

(20)

Сумма работ внешних сил определится сложением работ, вычисляемых по формулам (17) – (20):

.

Подставляя заданные значения масс, получаем:

или

. (21)

Согласно теореме (2) приравняем значения Т и , определяемые по формулам (16) и (21):

,

откуда

м/с.

Д-10

Сочлененные системы:

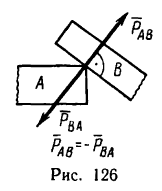
Сочлененной называется система нескольких тел, соединенных друг с другом при помощи внутренних связей: простого опирания, стержней или нитей (цепей), шарниров.

При решении некоторых задач с сочлененными системами равновесие каждого тела системы рассматривают отдельно. При этом в месте сочленения тел возникают две силы, одна из которых приложена к одному телу, а другая — ко второму телу. Эти силы равны по модулю, направлены вдоль одной прямой, но в противоположные стороны (закон равенства действия и противодействия).

На рис. 126 показаны силы взаимодействия, возникающие между телами A и В:

На рис. 127 показаны силы, возникающие при взаимодействии тел A и В не непосредственно друг с другом, а через стержень. Если допустить, что тело A действует на В через стержень силой 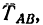, то тогда со стороны тела В возникнет сила В задачах, как правило, рассматривают только эти две силы, приложенные к телам A и В (рис. 127, а).

На рис. 127,6 показаны силы, приложенные только к стержню, т. е. показаны действия на стержень тел A и В.
Если два тела А и В связаны друг с другом при помощи так называемого внутреннего шарнира (рис. 128), то направление сил взаимодействия заранее неизвестно. Поэтому каждая из сил взаимодействия между телами (силы — предполoжительно

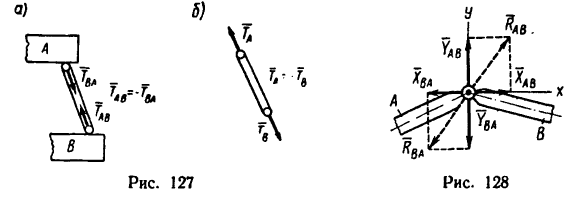
показаны на рис. 128 штриховыми векторами) заменяются составляющими 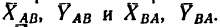Причем 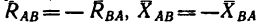и

Задача №1

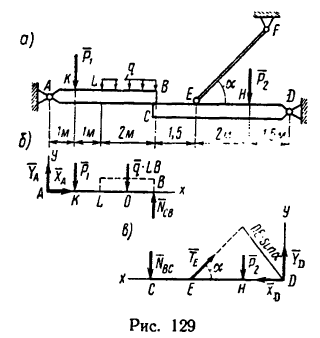
Балка АВ, имея в точке А шарнирное крепление, опирается в точке В на балку CD (рис. 129, а), которая удерживается в равновесии стержнем EF (в точках Е и F — шарнирные соединения) и шарниром D. Размеры и расположение нагрузок показаны на рисунке.

Определить реакции шарниров A, D и стержня EF. 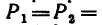20 кн,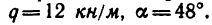

Решение.

1.    Рассмотрим равновесие каждой балки. Для этого изобразим балки АВ и CD раздельно. На рис. 129, б изображена балка АВ с двумя нагрузками 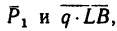составляющими реакции шарнира 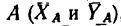и реакцией опоры в точке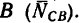

На рис. 129, в изображена балка CD, имеющая заданную нагрузку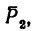 нагрузку 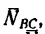которая неизвестна, составляющие реакции шарнира 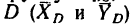и реакцию 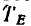стержня EF.

2.    Рассмотрим равновесие балки АВ и составим уравнения (начинать решение задачи с рассмотрения равновесия балки CD пока не имеет смысла, так как в три уравнения равновесия, которые можно составить для плоской системы сил, войдут четыре неизвестные силы ):

Из уравнения (1)
Из уравнения (2)

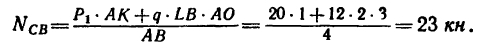
Из уравнения (3)

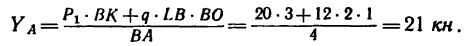
3.    Теперь можно рассмотреть равновесие балки CD. Реакция балки CD, иными словами ее противодействие давлению балки АВ, уже известна: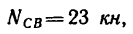
а значит известна и сила давления 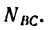Таким образом,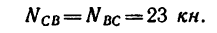
Учитывая это, составим уравнения равновесия для балки CD и решим их:

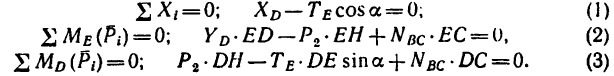
Из уравнения (3)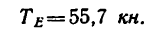
Из уравнения (1)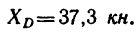

Из уравнения (2)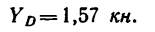
Реакция шарнира А определена выше: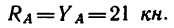

Проверку решения можно произвести при помощи любого из трех уравнений равновесия, составленного для всей сочлененной системы. В данном случае для проверки можно, например, использовать уравнение моментов относительно точки опоры одной балки на другую (точка В или С):

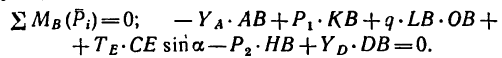
Подставив в уравнение значения величин, убедимся в том, что уравнение обратится в тождество. Значит, задача решена правильно.

Задача №2

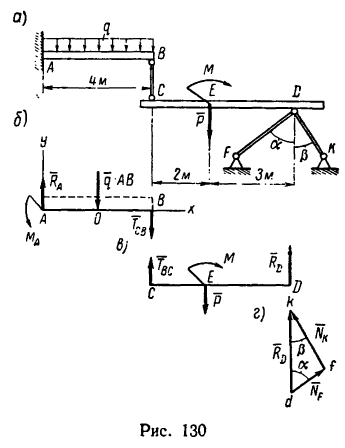
Балка АВ жестко заделана у точки А и нагружена по всей длине равномерно распределенной нагрузкой интенсивностью q = 8 кн/м (рис. 130, а). В точке В к балке шарнирно прикреплен стержень, ко второму концу которого также шарнирно прикреплена вторая балка CD, опирающаяся кроме того, в точке D на стержни DF и DK (соединения в точках D, F и К — шарнирные). Балка CD нагружена силой P = 10 кн и моментом М = 50 кн * м.

Определить реакции в заделке и усилия во всех трех стержнях, если стержень ВС вертикален и углы а=52°, 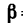= 38°.

Решение.

1.    Рассмотрим равновесие каждой балки отдельно.

К балке АВ приложены две нагрузки – по всей длине равномерно распределена нагрузка 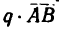и в точке В сила 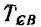— переданное стержнем действие балки CD (рис. 130, б). Обе эти нагрузки уравновешиваются вертйкальной реакцией 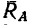и реактивным моментом 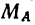заделки (реакция 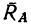заделки не отклонена от вертикали, так как в данном случае нет усилий, стремящихся сместить балку АВ в горизонтальном направлении).

К балке CD приложены сосредоточенная сила Р и момент М. Обе нагрузки уравновешиваются реакциями,возникшими в стержнях ВС, DF и DK. Но так как соединительный стержень ВС расположен перпендикулярно к балке, а нагрузки не смещают ее в горизонтальном направлении, то равнодействующая реакций стержней DF и DK, приложенная в точке D, направлена перпендикулярно к балке (реакция 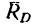(рис. 130, в).

2.    Составим уравнения равновесия для балки CD

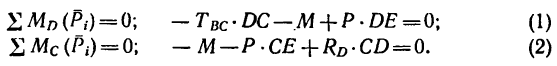
Из уравнения (1)

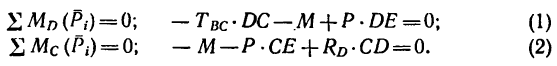
Знак минус показывает, что реакция 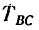направлена не вверх, как показано на рис. 130, в, а вниз. Таким образом, стержень ВС не растянут, как предполагалось, а сжат. Значит и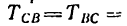

= – 4 кн, т. е. нагрузка 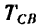на балку АВ действует вверх, а Не вниз, как показано на рис. 130, б.

Из уравнения (2)

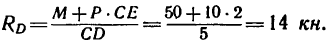
3.    Реакция 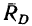является равнодействующей реакций 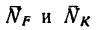стержней DF и DK- Найдем эти реакции из рассмотрения треугольника dkf (рис. 130, г), построенного на силе 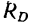(см. задачу 87-14, решение 2).

Треугольник dkf прямоугольный, так как 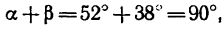следовательно,

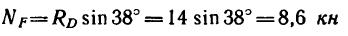
(стержень ED сжат, так как реакция направлена от стержня к шарниру D):

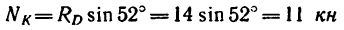(стержень KD также сжат).

Таким образом, усилия во всех стержнях найдены и все стержни сжаты.

4.    Для определения реакций в заделке нужно составить уравнения равновесия для балки АВ (см. рис. 130, б):

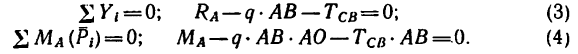
Из уравнения (3) находим RA (учитывая, что):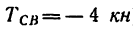

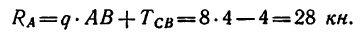
Из уравнения (4)

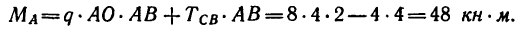
Проверку решения рекомендуется выполнить самостоятельно.

При решении задач, в которых сочленение тел произведено при помощи промежуточного шарнира, целесообразно сначала составить уравнения равновесия для всей системы, а затем добавить к ним уравнение моментов сил относительно промежуточного шарнира для одного из тел сочлененной системы.

Покажем это на примере следующей задачи.

Задача №3

Балки 1 и 2, шарниром С соединенные между собой, шарнирно прикреплены к неподвижным опорам в точках А и В (рис. 131, а). Длина балок одинакова: АС=ВС=4 м. Балка 1 в точке D Нагружена вертикальной силой 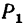=100 кГ, а в точке £ —горизонтальной силой 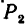=80 кГ. Балка 2 в точке F нагружена перпендикулярной к ней силой 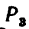=200 кГ. Угол а=50°. Определить реакции шарниров А и В.

Решение.

1. Освободим балки от связей в точках А и В. Действие шарниров А и В заменим их реакциями, разложив каждую реакцию

на две составляющие по осям х и у (рис. 131, 6).

При рассмотрении равновесия обеих балок силы взаимодействия, возникающие в промежуточном шарнире С (составляющие этих сил показаны на рис. 131,6 штриховой линией), друг друга уравновешивают и поэтому могут не учитываться при составлении уравнений равновесия.

Таким образом, на систему балок 1 и 2 действуют всего семь внешних сил, расположенных в одной плоскости: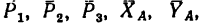 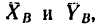из них четыре последние силы неизвестны.

2.    Для определения четырех неизвестных сил необходимо составить четыре уравнения.

Из условия равновесия системы балок составим три уравнения равновесия, приняв для третьего уравнения за центр моментов точку В:

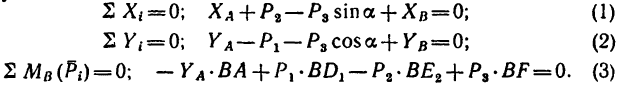
Четвертое уравнение составим исходя из равновесия балки 2 (на нее действует меньше сил, чем на балку 1):

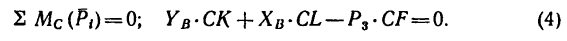
3.    Определяем плечи сил, входящие в уравнения (3) и (4) (рис. 131, б):

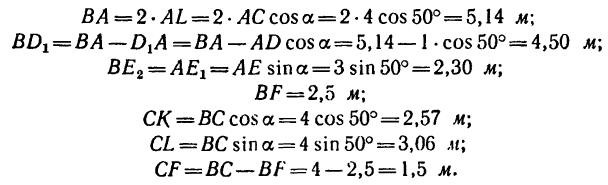
4 Теперь из уравнения (3) находим

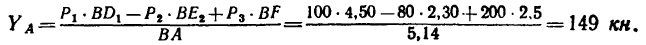
Из уравнения (2)

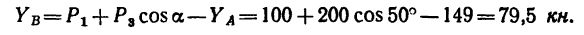
Из уравнения (4)

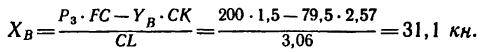
Из уравнения (I)

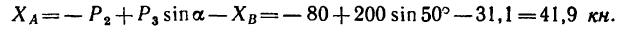Проверку решения рекомендуется сделать самостоятельно при помощи уравнения моментов относительно точки С, составленного для всей системы.

Если в соответствии с условием задачи требуется определить силу взаимодействия между балками в шарнире С, то теперь ее легко найти, рассмотрев равновесие одной из балок.

В следующей задаче рассмотрим равновесие сочлененной системы при наличии сил трения.

Задача №4

На наклонных плоскостях АС и ВС помещены два тела 1 и 2, связанные нитью, которая перекинута через блок D (рис. 132, а),

—коэффициент трения при взаимодействии тела 1 с плоскостью 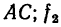— коэффициент трения при взаимодействии тела 2 с плоскостью ВС. Вес первого тела G. При каком весе Q второго тела будет соблюдаться равновесие?

Решение.

1.    Допустим, что тела 1 и 2, связанные нитью, поставлены на наклонные плоскости и находятся в равновесии.

2.    Если вес тела 2 постепенно увеличивать, то при некотором значении- веса 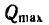равновесие нарушится и оба тела начнут скользить вправо (тело 2— вниз по СВ, а тело 1 — вверх по АС).

Изобразим оба тела с действующими на них силами в предельном состоянии (рис. 132, б) равновесия, т. е. в момент перед началом движения. На каждое тело действуют их веса 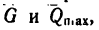нормальные реакции наклонных плоскостей 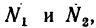реакции нитей 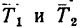и силы трения 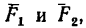направленные в стороны, противоположные движению тел.

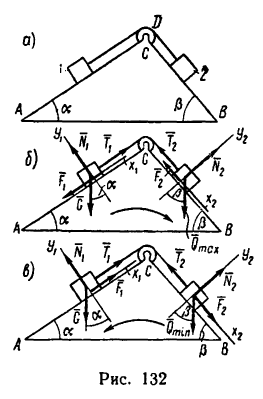
3.    Рассмотрим равновесие каждого из тел в отдельности, пренебрегая их размерами, т. е. считая, что на тела действуют системы сходящихся сил.

Для сил, действующих на тело 1, получим такие уравнения равновесия:

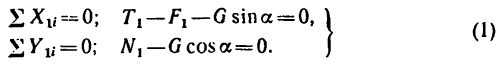
Для сил, действующих на тело 2, получим такие уравнения:

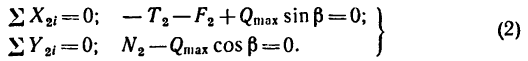
Из системы уравнений (1)

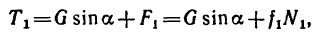
а так как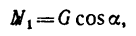 
то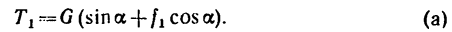

Из системы уравнений (2)

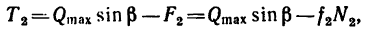
а так как

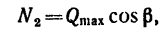
TO

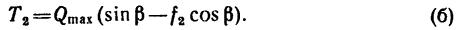
Натяжение нити, перекинутой через блок, по всей длине одинаково, поэтому

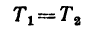
и, следовательно, правые части равенств (а) и (б) также равны между собой, т. с.

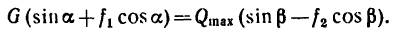
Отсюда определяем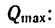

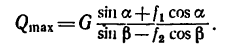
4.    Теперь представим себе, что вес тела 2 постепенно уменьшается. При некотором значении веса 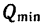равновесие снова нарушится, но теперь оба тела начнут скользить влево (тело 1 — вниз по С А, а тело 2 —вверх но ВС).

Изобразим на рис. 132, в оба тела с действующими на них силами в момент перед началом движения.

В этом случае но сравнению с предыдущим обе силы трения 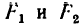изменяют свое направление, так как изменяется направление скольжения тел.

Рассматривая равновесия каждого из тел в отдельности, получаем следующие системы уравнений равновесия:
для тела 1

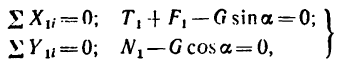
для тела 2

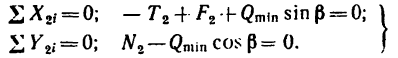
Решая эти системы уравнений так же, как и в предыдущем случае, находим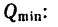

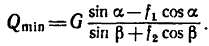
5.    Таким образом, тела 1 и 2 находятся в равновесии при соблюдении условия

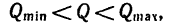
причем значения 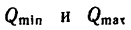зависят от веса первого тела, от коэффициентов трения и от углов подъема наклонных плоскостей. Так, например, при 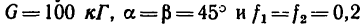имеем:

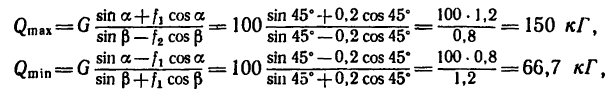
т. е. вес Q удовлетворяет условию

Определение реакций опор составной конструкции

Работа добавлена на сайт samzan.net: 2016-06-09

Задание С-10. Определение реакций опор составной конструкции

Найти реакции опор и давление в промежуточном шарнире составной конструкции. Схема конструкции представлена на рис. 1 (размеры – в м), нагрузка указана в таблице 1.

Рис. 1

Таблица 1

P1, кН	М, кНЧм	q, кН/м
6,0	25,0	0,8

Решение.

опора конструкция шарнир

1) Выберем объект равновесия: тело АDСВ;

) В точках А и В связь шарнирно-неподвижная;

) Рассмотрим систему уравновешивающихся сил, приложенных ко всей конструкции (рис. 2).

  y

 D        P1y  P1

         90°

           P1x   C

    Q          M

YA        YB

    XA               XB  x

A

        B

Рис. 2.

= qЧ3,5 = 0,8Ч3,5 = 2,8 (кН)-равномерно распределенная сила.

Запишем уравнения равновесия для всей системы:

XB +XA- P1x+Q =0   (1)

YA+ YB- P1y =0  (2)

M- (x+2)*P1x -4*P1y +AB*YB-Q*AD/2M=0.  (3)

4) Разложим силу P на составляющие Px и Py (Рис. 3):

P1x = P1Чsin(a),y = P1Чcos(a).

a = arctg(1,5/6) = arctg(0,25) = 14°.

x = P1Чsin(a) = P1Чsin(14°) = 6Ч0,24 = 1,44 (кН),y = P1Чcos(a) = P1Чcos(14°) = 6Ч0,97 = 5,82 (кН).

      P1y  P1

       a

1,5

    P1x a x   a

      6

Рис. 3.

Из треугольника: x/2=tg 14°, x=0,5 (м).

Решаем уравнении 3 относительно YB получим :

M+ (x+2)*P1x -4*P1y +AB*YB-Q*AD/2M=0.

25+2,5*1,44-4*5,82+6 *YB -2,8*3,5/2=0;

YB =-0,07 (кН);

Из уравнения (2) находим:

YA= P1y-YB =5,82+0,07=5,89(кН)

)Рассмотрим систему уравновешивающихся сил, приложенных к правой части конструкции (рис.4):

     y

    YC

      XC

            C

         M

         YB

      XB  x

           B

        

Рис.4.

Запишем уравнения равновесия для правой части конструкции:

XB + Xc=0   (4)

YB + Yc=0   (5)

2* XB +M=0   (6)

Из уравнения (6) находим: XB=-25/2=-12,5 (kH)

Из уравнения (4) находим:: XB =-Xc  , Xc=12,5 (kH)

Из уравнения (5) находим:: YB + Yc=0, Yc=0,07 (кН);

Из уравнения (1) находим::

XB +XA- P1x+Q =0; XA= -2,8+1,44-(-12,5)=11,5 (kH).

Ответ:

YB (kH)	YA (kH)	XB (kH)	XC (kH)	YC (kH)	XA (kH)
0,07	5,89	-12,5	12,5	0,07	11,15