-
Давление жидкости на дно и стенки сосуда
В соответствии с законом Паскаля
гидростатическое давление на уровне
горизонтального дна сосуда при высоте
жидкости в сосуде, равной Н,
![]() (1.7)
(1.7)
Отсюда следует, что абсолютное давление
рна горизонтальное дно не зависит
от формы сосуда и объема жидкости в нем.
При данной плотности жидкости оно
определяется лишь высотой столба
жидкостиНи внешним давлениемр0.
Сила давления жидкости Ржна
дно сосуда зависит от его площадиF:
![]() (1.8)
(1.8)
Общая сила давления на дно сосуда
![]() (1.9)
(1.9)
Внешнее давление р0передается
жидкостью каждому элементу поверхности
стенки одинаково, поэтому равнодействующая
внешнего давления приложена в точке
центра тяжести поверхности стенки.
Давление веса жидкости на стенку не
одинаково по высоте: чем глубже расположен
элемент стенки, тем большее давление
веса жидкости он испытывает. Поэтому
центр давления жидкости на вертикальную
стенку расположен всегда ниже центра
тяжести смоченной поверхности стенки.
Сила полного гидростатического давления
на плоскую стенку равна произведению
гидростатического давления в центре
тяжести этой стенки и ее площади:
![]() (1.10)
(1.10)
где
![]() – расстояние от верхнего уровня жидкости
– расстояние от верхнего уровня жидкости
до центра тяжести смоченной поверхности
стенки; оно зависит от геометрической
формы стенки.
Сила избыточного давления (собственно
жидкости) Ризбна стенку![]()
Точка приложения сил РиРизбносит название центра давленияhди может быть определена в соответствии
с законами теоретической механики через
момент инерции смоченной поверхности
стенки
![]() (1.11)
(1.11)
где Jx– момент инерции
стенки относительно осиox.
Для прямоугольной стенки при уровне
жидкости в сосуде, равном Н, и ширине
стенкиВ
![]()
Следовательно,
![]()
-
Практическое использование законов гидростатики
Применив закон Паскаля к сообщающимся
сосудам, можно прийти к следующим
выводам.
Если сосуды (рис. 1.4 а) заполнены
однородной жидкостью (одинаковой
плотности), то при равновесии давление
в точке 0 может быть выражено:
![]() либо
либо![]() ,
,
т.е. в сообщающихся сосудах заполняющая
их однородная жидкость располагается
на одинаковом уровне.
При заполнении сосудов жидкостями с
различной плотностью (рис 1.4 б) в
условиях равновесия давление в точке
О будет
![]() либо
либо![]() .
.

Рисунок 1.4
– Сообщающиеся сосуды, заполненные
жидкостью:
а– одной плотности;б– разной плотности
Следовательно
![]() ,
,
т.е.
![]() . (1.12)
. (1.12)
Соотношение (1.12) указывает на то, что
высоты уровней жидкости, отсчитываемые
от поверхности раздела, обратно
пропорциональны плотностям жидкостей.
Этот принцип используется для измерения
уровня жидкости в закрытых аппаратах
с помощью водомерных стёкол, в жидкостных
манометрах.
Если сообщающиеся сосуды заполнены
одной и той же жидкостью, но давление
над уровнем жидкости в них разное – р1ир2, то при равновесии
![]() ,
,
![]() ,
,
откуда
![]() . (1.13)
. (1.13)
Последнее выражение используется при
измерении давления или разности давлений
между различными точками с помощью
дифференциальных U-образных
манометров.

Рисунок 1.5.
– К определению высоты гидравлического
затвора
Этот же принцип используется для
определения высоты гидравлического
затвора в аппаратах, заполненных
жидкостью (рис. 1.5).
На рисунке представлен сосуд, заполненный
двумя жидкостями с плотностями 1и2; уровень
их раздела на глубинеz1необходимо поддерживать в процессе
работы постоянным с помощью гидрозатвора,
представляющего собойU-образную
трубку, подсоединённую снизу (на выходе
жидкости из аппарата).
В соответствии с уравнением (1.12) высота
гидравлического затвора в случае
одинакового давления над жидкостью
внутри аппарата и на выходе из затвора
![]() . (1.14)
. (1.14)
На использовании данного уравнения
гидростатики основана работа таких
простейших гидравлических машин, как
гидравлический пресс, мультипликатор
(для повышения давления), домкрат,
подъемник и др.
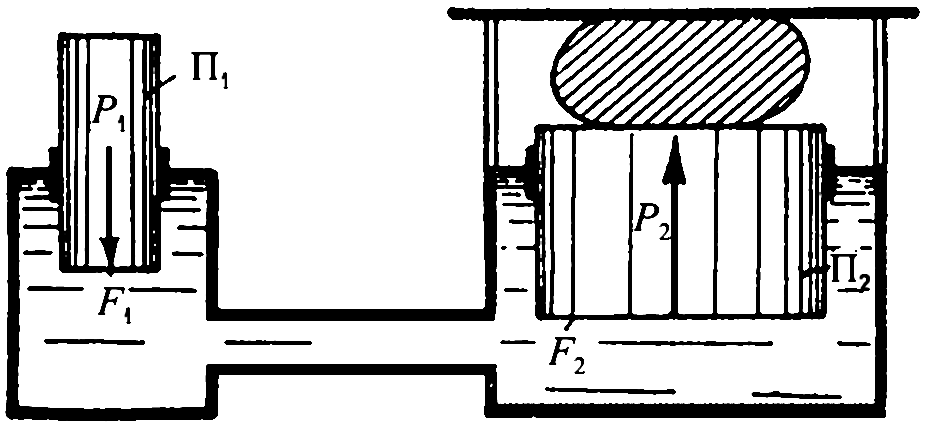
Рисунок 1.6
– Схема гидравлического пресса
На рис. 1.6 показана схема
гидравлического пресса. Если к поршню
П1, имеюшему площадьF1,
приложена силаР1, то эта сила
будет передаваться на жидкость; жидкость
же будет давить на поршень П2,
имеющий площадьF2, с силойР2
![]() (1.15)
(1.15)
так как гидростатические давления в
точках площади F1и площадиF2практически равны между собой:
![]() (1.16)
(1.16)
Из уравнения (1.16) следует, что при помощи
пресса сила Р1увеличивается
во столько раз, во сколько площадьF2больше площадиF1.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Закон Паскаля: давление, производимое на жидкость или газ, передается жидкостью или газом во все стороны одинаково.
Такая особенность передача давления жидкостями и газами связана с подвижностью молекул в жидком и газообразном состояниях.
Давление столба жидкости определяется формулой:
p = ρжgh
p — давление столба жидкости (Па), ρж — плотность жидкости (кг/м3), g — ускорение свободного падения (≈10 м/с2), h — высота столба жидкости, или ее глубина (м).
Важно! Высоту h нужно определять от поверхности жидкости.
Сила давления жидкости
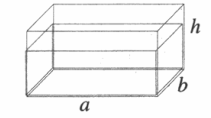
Сила давления жидкости на дно сосуда — это произведение давления, оказываемого жидкостью на дно сосуда, на площадь этого дна:
F = pS = ρжghab
Сила давления жидкости на боковую грань сосуда — это произведение половины давления, оказываемого жидкостью на дно сосуда, на площадь грани:
F=ρжgh2hb
Подсказки к задачам:
- Плотность пресной воды равна 1000 кг/м3.
- Плотность соленой воды равна 1030 кг/м3.
Пример №1. Чему равно давление, созданное водой, на глубине 2 м?
Давление в жидкостях определяется формулой:
p = ρжgh.
Давление, созданное пресной водой, равно:
p = 1000∙10∙2 = 20000 (Па) = 20 (кПа)
Давление, созданное соленой водой, равно:
p = 1030∙10∙2 = 20600 (Па) = 20,6 (кПа)
Гидростатический парадокс
Из закона Паскаля следует, что давление на дно сосуда определяется только плотностью жидкости и высотой ее столба. Поэтому, если в разные сосуды налить одинаковую жидкость одинаковой высоты, давление, оказываемое ею на дно каждого из сосудов, будет одинаковым.
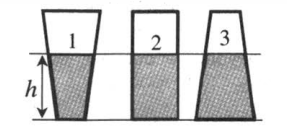
p1 = p2 = p3
Сила давления при этом будет разная, так как она прямо пропорционально зависит от площади дна. Так как площадь дна первого сосуда минимальна, а третьего максимальна, силы давления, оказываемые жидкостью на дно сосудов, будут такими:
F1 < F2 < F3
Пример №2. На рисунке изображены три сосуда с разными жидкостями. Площади дна сосудов равны. В первом сосуде находится вода (ρ1 = 1 г/см3), во втором — керосин (ρ2 = 0,8 г/см3), в третьем — спирт (ρ3 = 0,8 г/см3). В каком сосуде оказывается максимальное давление на дно?
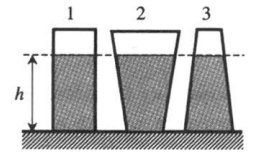
Давление зависит только от плотности жидкости и от ее столба: площадь сосудов никакой роли не играет. Так как столбы жидкостей во всех сосудах одинаково, остается сравнивать плотности. Плотность воды больше плотности керосина и плотности спирта. Поэтому в сосуде 1 давление на дно сосуда будет максимальным.
Задание EF18645
В сосуд высотой 20 см налита вода, уровень которой ниже края сосуда на 2 см. Чему равна сила давления воды на дно сосуда, если площадь дна 0,01м2? Атмосферное давление не учитывать.
Алгоритм решения
- Записать исходные данные и перевести единицы измерения величин в СИ.
- Записать формулу для вычисления силы давления.
- Выполнить решение задачи в общем виде.
- Вычислить искомую величину, подставив известные данные.
Решение
Запишем исходные данные:
- Высота сосуда H = 20 см.
- Разница между высотой сосуда и уровнем налитой в него воды: b = 2 см.
- Площадь дна сосуда: S = 0,01 м2.
20 см = 0,2 м
2 см = 0,02 м
Сила давления равна произведению давления на площадь, на которую это давление оказывается:
F = pS
Давление равно произведению высоты столба жидкости на ускорение свободного падения и на плотность самой жидкости. А высота столба воды в данном случае равна разности высоту стакана и разнице между высотой сосуда и уровнем воды. Поэтому:
F = pS = ρжghS = ρжg(H – b)S = 1000∙10∙(0,2 – 0,02)∙0,01 = 18 (Н)
Ответ: 18
pазбирался: Алиса Никитина | обсудить разбор
Задание EF22709
Какова сила давления керосина, заполняющего цистерну, на заплату в её стене, находящуюся на глубине 2 м? Площадь заплаты 10 см2. Атмосферное давление не учитывать.
Алгоритм решения
- Записать исходные данные и перевести единицы измерения величин в СИ.
- Записать формулу для вычисления силы давления.
- Выполнить решение задачи в общем виде.
- Вычислить искомую величину, подставив известные данные.
Решение
Запишем исходные данные:
- Глубина заплаты в цистерне h = 2 м.
- Площадь заплаты: S = 10 см2.
10 см2 = 0,001 м2
Сила давления равна произведению давления на площадь, на которую это давление оказывается:
F = pS
Давление равно произведению высоты столба жидкости на ускорение свободного падения и на плотность самой жидкости. Поэтому:
F = pS = ρкghS = 800∙10∙2∙0,001 = 16 (Н)
Ответ: 16
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18804
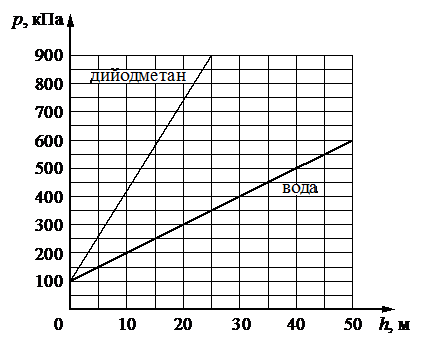
На рисунке представлены графики зависимости давления p от глубины погружения h для двух покоящихся жидкостей: воды и тяжёлой жидкости дийодметана, при постоянной температуре.
Выберите два верных утверждения, согласующихся с приведёнными графиками.
Ответ:
а) В воде на глубине 25 м давление p в 2,5 раза больше атмосферного.
б) С ростом глубины погружения давление в дийодметане возрастает быстрее, чем в воде.
в) Плотность керосина 0,82 г/см3, аналогичный график зависимости давления от глубины для керосина окажется между графиками для воды и дийодметана.
г) Если внутри пустотелого шарика давление равно атмосферному, то в воде на глубине 10 м давления на его поверхность извне и изнутри будут равны друг другу.
д) Плотность оливкового масла 0,92 г/см3, аналогичный график зависимости давления от глубины для масла окажется между графиком для воды и осью абсцисс (горизонтальной осью).
Алгоритм решения
1.Проверить все утверждения на истинность.
2.Записать буквы, соответствующие верным утверждениям, последовательно без пробелов.
Решение
Проверим истинность первого утверждения (а). Для этого определим по графику давление воды на глубине 25 м. Если пустить перпендикуляр к графику зависимости давления воды от глубины погружения через h = 25 м, то он пересечет график в точке, которой соответствует давление p = 350 кН. Атмосферное давление равно 100 кН. Следовательно, давление воды на этой глубине в 3,5 раза превышает атмосферное давление. Утверждение неверно.
Проверим второе утверждение (б). Согласно ему, с ростом глубины погружения давление в дийодметане возрастает быстрее, чем в воде. Это действительно так, потому что угол наклона графика зависимости давления дийодметана от глубины погружения к оси абсцисс больше того же графика для воды. Это можно подтвердить и математически: давление в более плотной жидкости с глубиной растет быстрее, так как давление имеет прямо пропорциональную зависимость с глубиной. Утверждение верно.
Проверим третье утверждение (в). Согласно ему, если на этом же рисунке построить график зависимости давления керосина от глубины погружения, то он окажется между двумя уже существующими графиками. Но этого не может быть, потому что давление в воде растет медленнее, чем давление в дийодметане, так как вода менее плотная. По этой же причине давление в керосине будет расти медленнее, чем в воде, так как керосин менее плотный по сравнению с водой. Третий график в этом случае займет положение между графиком зависимости давления воды от глубины погружения и осью абсцисс. Утверждение неверно.
Проверим четвертое утверждение (г). Согласно графику, давление воды на глубине 10 м равно 200 кПа. Поэтому давление на поверхность шарика снаружи, погруженного на такую глубину, будет вдвое больше, чем давление, оказываемое на его стенки изнутри (при условии, что давление внутри равно 1 атм.). Утверждение неверно.
Проверим последнее утверждение (д). Согласно ему, если на этом же рисунке построить график зависимости давления оливкового масла от глубины погружения, то он окажется между графиком для воды и осью абсцисс. Это действительно так, потому что плотность оливкового масла меньше плотности воды. Утверждение верно.
Верный ответ: бд.
Ответ: бд
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 8.4k
Как вы уже знаете, согласно закону Паскаля, давление в жидкостях распространяется одинаково во всех направлениях. Что же необходимо знать, чтобы рассчитать это давление? От чего зависит давление жидкости?
Взгляните на рисунок 1.
Как вы думаете, в каком сосуде больше жидкости? А будет ли одинаково давление, оказываемое на дно сосудов? С этими вопросами нам и предстоит разобраться.
Вывод формулы
Выведем формулу для расчета давления жидкости на дно сосуда, имеющего форму прямоугольного параллелепипеда (рисунок 2).
Давление жидкости $p$ рассчитывается по формуле: $p = frac{F}{S}$, где $F$ — это сила, действующая на дно сосуда, а $S$ — это площадь дна сосуда.
- Сила $F$ в данном случае равна весу $P$ жидкости, которая находится в сосуде;
- Как узнать вес жидкости? Необходимо знать массу $m$ жидкости;
- Массу $m$ мы можем вычислить по известной нам формуле:
$m = rho V$;
- Так как нам известна жидкость, находящаяся в сосуде, мы знаем ее плотность . Остается вычислить объем $V$ жидкости. Обозначим высоту столба жидкости буквой $h$, площадь дна сосуда — $S$. Тогда объем можно вычислить по формуле:
$V = Sh$;
- Итак, подставляем наши данные в формулу для вычисления массы и получаем:
$m = rho Sh$;
- Таким образом, возвращаемся к весу жидкости и получаем, что:
$P = mg$, где $g$ — ускорение свободного падения, или $P = g rho Sh$.
С другой стороны, мы знаем, что вес столба жидкости равен силе, с которой жидкость давит на дно сосуда. Поэтому если мы разделим вес $P$ на площадь $S$, то получим искомое давление жидкости:
$p = frac{P}{S}$,
или $p =frac{g rho Sh}{S}$,
То есть:
$p = rho gh$.
Рассмотрим измерительные величины, которые мы будем использовать в данной формуле: плотность мы будем выражать в килограммах на кубический метр ($frac{кг}{м^3}$), $g = 9.8 frac{H}{кг}$, высоту столба жидкости — в метрах ($м$). Тогда давление $p$ будет выражено в паскалях ($Па$).
Выводы
Так мы с вами вывели формулу для расчета давления жидкости на дно сосуда. Какие выводы мы можем сделать?
От каких величин зависит давление жидкости на дно сосуда?
Давление жидкости не зависит от формы сосуда, оно зависит только от плотности жидкости и высоты ее столба.
Обратите внимание, что во многих случаях, когда говорят о высоте столба жидкости, говорят о глубине.
По какой формуле рассчитывают давление жидкости на стенки сосуда, давление внутри жидкости?
По формуле $p = rho gh$ можно вычислить давление на стенки сосуда или внутри жидкости, так как на одной глубине давление в жидкости будет одинаково во всех направлениях.
Вопросы и пример задачи
Вопрос №1
Как вы думаете, изменится ли давление на дно цилиндрического сосуда, частично заполненного водой, если в него опустить деревянный брусок (рисунок 3)?
Посмотреть ответ
Скрыть
Ответ:
В данном случае уровень воды поднимется и высота столба станет больше, значит и давление увеличится.
Вопрос №2
Какая вода: пресная или соленая оказывает большее давление на дно сосуда при одинаковом объеме?
Посмотреть ответ
Скрыть ответ
Ответ:
Здесь достаточно вспомнить, что в соленой воде нам намного проще плавать и держаться на поверхности, что о говорит о ее большей плотности. А давление прямо пропорционально плотности. Соответственно, большее давление оказывает соленая вода.
Задача
Определите давление керосина на дно цистерны, если высота столба керосина $8 space м$, а его плотность $800 frac{кг}{м^3}$.
Дано:
$rho = 800 frac{кг}{м^3}$
$h = 8 space м$
$p — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Давление рассчитывается по формуле:
$p= rho gh$.
Подставим все величины и рассчитаем его:
$p = 800 frac{кг}{м^3} cdot 9.8 frac{Н}{кг} cdot 8 space м = 62 720 space Па approx 63 space кПа$.
Ответ: $p approx 63 space кПа$.
Упражнения
Упражнение №1
Определите давление на глубине $0.6 space м$ в воде, керосине, ртути.
Дано:
$h = 0.6 space м$
$rho_1 = 1000 frac{кг}{м^3}$
$rho_2 = 800 frac{кг}{м^3}$
$rho_3 = 13600 frac{кг}{м^3}$
$g = 9.8 frac{Н}{кг}$
$p_1 — ?$
$p_2 — ?$
$p_3 — ?$
Показать решение и ответ
Скрыть
Решение:
Для расчета давления на заданной глубине будем использовать формулу $p = rho gh$.
Давление в воде:
$p_1 = rho_1 gh$,
$p_1 = 1000 frac{кг}{м^3} cdot 9.8 frac{Н}{кг} cdot 0.6 space м = 5880 space Па approx 5.9 space кПа$.
Давление в керосине:
$p_2 = rho_2 gh$,
$p_2 = 800 frac{кг}{м^3} cdot 9.8 frac{Н}{кг} cdot 0.6 space м = 4704 space Па approx 4.7 space кПа$.
Давление в ртути:
$p_3 = rho_3 gh$,
$p_3 = 13600 frac{кг}{м^3} cdot 9.8 frac{Н}{кг} cdot 0.6 space м = 79 space 968 space Па approx 80 space кПа$.
Ответ: $p_1 approx 5.9 space кПа$, $p_2 approx 4.7 space кПа$, $p_3 approx 80 space кПа$.
Упражнение №2
Вычислите давление воды на дно одной из глубочайших морских впадин — Марианской, глубина которой приблизительно равна $10 space 900 space м$. Плотность морской воды равна $1030 frac{кг}{м^3}$.
Дано:
$h = 10 space 900 space м$
$rho = 1030 frac{кг}{м^3}$
$g = 9.8 frac{Н}{кг}$
$p — ?$
Показать решение и ответ
Скрыть
Решение:
Рассчитаем давление на дне Марианской впадины по формуле:
$p = rho gh$,
$p = 1030 frac{кг}{м^3} cdot 9.8 frac{Н}{кг} cdot 10 space 900 space м = 110 space 024 space 600 space Па approx 110 space МПа$.
Ответ: $p approx 110 space МПа$.
Упражнение №3
На рисунке 3 изображена футбольная камера, соединенная с вертикально расположенной стеклянной трубкой. В камере и трубке находится вода. На камеру положена дощечка, а на нее — гиря массой $5 space кг$. Высота столба воды в трубке равна $1 space м$. Определите площадь соприкосновения дощечки с камерой.
Дано:
$m = 5 space кг$
$h = 1 space м$
$rho = 1000 frac{кг}{м^3}$
$g = 9.8 frac{Н}{кг}$
$S — ?$
Показать решение и ответ
Скрыть
Решение:
Гиря оказывает давление на футбольную камеру:
$p_1 = frac{F}{S}$.
Сила $F$, с которой она давит, будет определяться ее весом:
$F = P = F_{тяж} = mg$.
Тогда формула для давления примет следующий вид:
$p_1 = frac{mg}{S}$.
В то же время вода в трубке и камере давит на нее изнутри снизу вверх:
$p_2 = rho gh$.
Так как гиря и камера находятся в равновесии:
$p_1 = p_2$,
$frac{mg}{S} = rho gh$,
$S = frac{m}{rho h}$.
Рассчитаем эту площадь:
$S = frac{5 space кг}{1000 frac{кг}{м^3} cdot 1 space м} = 0.005 space м^2 = 50 space см^2$.
Ответ: $S = 50 space см^2$.
Задания
Задание №1
Возьмите высокий сосуд. В боковой поверхности его на разной высоте от дна сделайте три небольших отверстия. Закройте отверстия спичками и наполните сосуд водой. Откройте отверстия и проследите за струйками вытекающей воды (рисунок 4). Почему вода вытекает из отверстий? Из чего следует, что давление увеличивается с глубиной?
Показать ответ
Скрыть
Ответ:
Вода вытекает из отверстий по действием давления самой жидкости. Мы видим, что из самого нижнего отверстия бьет струйка воды с самым сильным напором, а из верхнего отверстия — с самым слабым. Этот момент объясняется тем, что с увеличением глубины давление увеличивается.
Задание №2
Налейте в стеклянный сосуд (стакан или банку) произвольное количество воды. Сделайте необходимые измерения и рассчитайте давление воды на дно сосуда.
Дано:
$h = 0.086 space м$
$rho = 1000 frac{кг}{м^3}$
$g = 9.8 frac{Н}{кг}$
$p — ?$
Показать решение и овет
Скрыть
Решение:
Рассчитаем давление воды на дно нашего стакана по формуле:
$p = rho gh$,
$p = 1000 frac{кг}{м^3} cdot 9.8 frac{Н}{кг} cdot 0.086 space м = 842.8 space Па approx 843 space Па$.
Ответ: $p approx 843 space Па$.
Главная страница
Содержание
Введение
Основы гидростатики
Основы гидродинамики
Гидравлические сопротивления
Истечние жидкости из отверстий, насадков и из-под затворов
Гидравлический расчет простых трубопроводов
Гидравлические машины
Лекция 2. ОСНОВЫ ГИДРОСТАТИКИ
Гидравлика делится на два раздела: гидростатика и гидродинамика. Гидродинамика является более обширным
разделом и будет рассмотрена в последующих лекциях. В этой лекции будет рассмотрена гидростатика.
Гидростатикой называется раздел гидравлики, в котором рассматриваются законы равновесия жидкости
и их практическое применение.
В покоящейся жидкости всегда присутствует сила давления, которая называется гидростатическим давлением.
Жидкость оказывает силовое воздействие на дно и стенки сосуда. Частицы жидкости, расположенные в верхних
слоях водоема, испытывают меньшие силы сжатия, чем частицы жидкости, находящиеся у дна.
Рассмотрим резервуар с плоскими вертикальными стенками, наполненный жидкостью (рис.2.1, а). На дно
резервуара действует сила P равная весу налитой жидкости G = γ V, т.е. P = G.
Если эту силу P разделить на площадь дна Sabcd, то мы получим среднее гидростатическое
давление, действующее на дно резервуара.
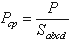
Гидростатическое давление обладает свойствами.
Свойство 1. В любой точке жидкости гидростатическое давление перпендикулярно площадке
касательной к выделенному объему и действует внутрь рассматриваемого объема жидкости.
Для доказательства этого утверждения вернемся к рис.2.1, а. Выделим на боковой стенке резервуара
площадку Sбок (заштриховано). Гидростатическое давление действует на эту площадку в виде
распределенной силы, которую можно заменить одной равнодействующей, которую обозначим P. Предположим,
что равнодействующая гидростатического давления P, действующая на эту площадку, приложена в точке
А и направлена к ней под углом φ (на рис. 2.1 обозначена штриховым отрезком со
стрелкой). Тогда сила реакции стенки R на жидкость будет иметь ту же самую величину, но
противоположное направление (сплошной отрезок со стрелкой). Указанный вектор R можно разложить на
два составляющих вектора: нормальный Rn (перпендикулярный к заштрихованной площадке) и
касательный Rτ к стенке.
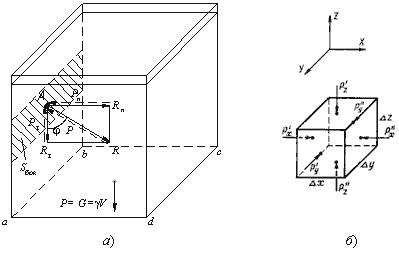
Рис. 2.1. Схема, иллюстрирующая свойства гидростатического давления
а – первое свойство; б – второе свойство
Сила нормального давления Rn вызывает в жидкости напряжения сжатия. Этим напряжениям
жидкость легко противостоит. Сила Rτ действующая на жидкость вдоль
стенки, должна была бы вызвать в жидкости касательные напряжения вдоль стенки и частицы должны были бы
перемещаться вниз. Но так как жидкость в резервуаре находится в состоянии покоя, то составляющая
Rτ отсутствует. Отсюда можно сделать вывод первого свойства
гидростатического давления.
Свойство 2. Гидростатическое давление неизменно во всех направлениях.
В жидкости, заполняющей какой-то резервуар, выделим элементарный кубик с очень малыми сторонами
Δx, Δy, Δz (рис.2.1, б). На каждую из боковых поверхностей будет
давить сила гидростатического давления, равная произведению соответствующего давления Px,
Py , Pz на элементарные площади. Обозначим вектора давлений,
действующие в положительном направлении (согласно указанным координатам) как P’x,
P’y, P’z, а вектора давлений, действующие в обратном направлении
соответственно P”x, P”y, P”z. Поскольку кубик
находится в равновесии, то можно записать равенства
P’xΔyΔz=P”xΔyΔz
P’yΔxΔz = P”yΔxΔz
P’zΔxΔy + γΔx, Δy, Δz = P”zΔxΔy
где γ – удельный вес жидкости;
Δx, Δy, Δz – объем кубика.
Сократив полученные равенства, найдем, что
P’x = P”x; P’y = P”y; P’z + γΔz = P”z
Членом третьего уравнения γΔz, как бесконечно малым по сравнению с P’z
и P”z, можно пренебречь и тогда окончательно
P’x = P”x; P’y = P”y; P’z=P”z
Вследствие того, что кубик не деформируется (не вытягивается вдоль одной из осей), надо полагать, что
давления по различным осям одинаковы, т.е.
P’x = P”x = P’y = P”y = P’z=P”z
Это доказывает второй свойство гидростатического давления.
Свойство 3. Гидростатическое давление в точке зависит от ее координат в пространстве.
Это положение не требует специального доказательства, так как ясно, что по мере увеличения погружения точки
давление в ней будет возрастать, а по мере уменьшения погружения уменьшаться. Третье свойство гидростатического
давления может быть записано в виде
P=f(x, y, z)
Рассмотрим распространенный случай равновесия жидкости, когда на нее действует только одна массовая сила –
сила тяжести, и получим уравнение, позволяющее находить гидростатическое давление в любой точке
рассматриваемого объема жидкости. Это уравнение называется основным уравнением гидростатики.
Пусть жидкость содержится в сосуде (рис.2.2) и на ее свободную поверхность действует давление P0
. Найдем гидростатическое давление P в произвольно взятой точке М, расположенной на
глубине h. Выделим около точки М элементарную горизонтальную площадку dS и построим на
ней вертикальный цилиндрический объем жидкости высотой h. Рассмотрим условие равновесия указанного
объема жидкости, выделенного из общей массы жидкости. Давление жидкости на нижнее основание цилиндра теперь
будет внешним и направлено по нормали внутрь объема, т.е. вверх.
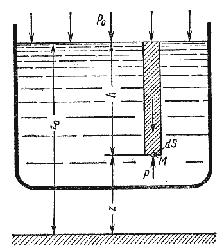
Рис. 2.2. Схема для вывода основного уравнения гидростатики
Запишем сумму сил, действующих на рассматриваемый объем в проекции на вертикальную ось:
PdS – P0 dS – ρghdS = 0
Последний член уравнения представляет собой вес жидкости, заключенный в рассматриваемом вертикальном цилиндре
объемом hdS. Силы давления по боковой поверхности цилиндра в уравнение не входят, т.к. они
перпендикулярны к этой поверхности и их проекции на вертикальную ось равны нулю. Сократив выражение на
dS и перегруппировав члены, найдем
P = P0 + ρgh = P0 + hγ
Полученное уравнение называют основным уравнением гидростатики. По нему можно посчитать давление в любой
точке покоящейся жидкости. Это давление, как видно из уравнения, складывается из двух величин: давления
P0 на внешней поверхности жидкости и давления, обусловленного весом вышележащих слоев
жидкости.
Из основного уравнения гидростатики видно, что какую бы точку в объеме всего сосуда мы не взяли, на нее
всегда будет действовать давление, приложенное к внешней поверхности P0. Другими словами
давление, приложенное к внешней поверхности жидкости, передается всем точкам этой жидкости по всем
направлениям одинаково. Это положение известно под названием закона Паскаля.
Поверхность, во всех точках которой давление одинаково, называется поверхностью уровня (подробно рассмотрим
в п.2.6). В обычных условиях поверхности уровня представляют собой горизонтальные плоскости.
Пусть мы имеем резервуар с наклонной правой стенкой, заполненный жидкостью с удельным весом γ. Ширина
стенки в направлении, перпендикулярном плоскости чертежа (от читателя), равна b
(рис.2.3). Стенка условно показана развернутой относительно оси АВ и заштрихована на рисунке. Построим
график изменения избыточного гидростатического давления на стенку АВ.
Так как избыточное гидростатическое давление изменяется по линейному закон P=γgh,
то для построения графика, называемого эпюрой давления, достаточно найти давление в двух точках, например
А и B.
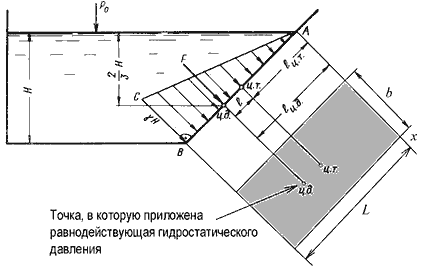
Рис. 2.3. Схема к определению равнодействующей гидростатического давления на плоскую
поверхность
Избыточное гидростатическое давление в точке А будет равно
PA = γh = γ·0 = 0
Соответственно давление в точке В:
PB = γh = γH
где H – глубина жидкости в резервуаре.
Согласно первому свойству гидростатического давления, оно всегда направлено по нормали к ограждающей
поверхности. Следовательно, гидростатическое давление в точке В, величина которого равна γH,
надо направлять перпендикулярно к стенке АВ. Соединив точку А с концом
отрезка γH, получим треугольную эпюру распределения давления АВС с прямым
углом в точке В. Среднее значение давления будет равно
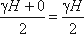
Если площадь наклонной стенки S=bL, то равнодействующая гидростатического давления равна
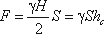
где hc = Н/2 – глубина погружения центра тяжести плоской поверхности под уровень жидкости.
Однако точка приложения равнодействующей гидростатического давления ц.д. не всегда будет совпадать
с центром тяжести плоской поверхности. Эта точка находится на расстоянии l от центра тяжести и равна
отношению момента инерции площадки относительно центральной оси к статическому моменту этой же площадки.
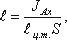
где JАx – момент инерции площади S относительно центральной оси, параллельной
Аx.
В частном случае, когда стенка имеет форму прямоугольника размерами bL и одна из его сторон лежит
на свободной поверхности с атмосферным давлением, центр давления ц.д. находится на расстоянии b/3
от нижней стороны.
Пусть жидкость заполняет резервуар, правая стенка которого представляет собой цилиндрическую криволинейную
поверхность АВС (рис.2.4), простирающуюся в направлении читателя на ширину b. Восстановим из
точки А перпендикуляр АО к свободной поверхности жидкости. Объем жидкости в отсеке АОСВ
находится в равновесии. Это значит, что силы, действующие на поверхности выделенного объема V, и
силы веса взаимно уравновешиваются.
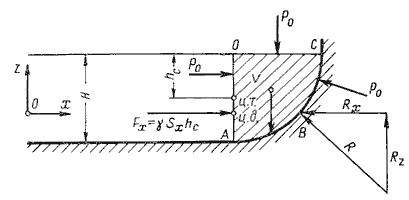
Рис. 2.4. Схема к определению равнодействующей гидростатического давления на
цилиндрическую поверхность
Представим, что выделенный объем V представляет собой твердое тело того же удельного веса, что и
жидкость (этот объем на рис.2.4 заштрихован). Левая поверхность этого объема (на чертеже вертикальная
стенка АО) имеет площадь Sx = bH, являющуюся проекцией криволинейной поверхности АВС на
плоскость yOz.
Cила гидростатического давления на площадь Sx равна Fx = γ
Sxhc.
С правой стороны на отсек будет действовать реакция R цилиндрической поверхности. Пусть точка
приложения и направление этой реакции будут таковы, как показано на рис.2.4. Реакцию R разложим на
две составляющие Rx и Rz.
Из действующих поверхностных сил осталось учесть только давление на свободной поверхности
Р0. Если резервуар открыт, то естественно, что давление Р0 одинаково
со всех сторон и поэтому взаимно уравновешивается.
На отсек АВСО будет действовать сила собственного веса G = γV, направленная вниз.
Спроецируем все силы на ось Ох:
Fx – Rx = 0 откуда Fx = Rx = γSxhc
Теперь спроецируем все силы на ось Оz:
Rx – G = 0 откуда Rx = G = γV
Составляющая силы гидростатического давления по оси Oy обращается в нуль, значит Ry = Fy = 0.
Таким образом, реакция цилиндрической поверхности в общем случае равна
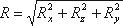
а поскольку реакция цилиндрической поверхности равна равнодействующей гидростатического давления R=F,
то делаем вывод, что
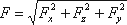
Тело, погруженное (полностью или частично) в жидкость, испытывает со стороны жидкости суммарное давление,
направленное снизу вверх и равное весу жидкости в объеме погруженной части тела.
Pвыт = ρжgVпогр
Для однородного тела плавающего на поверхности справедливо соотношение
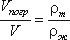
где: V – объем плавающего тела;
ρm – плотность тела.
Существующая теория плавающего тела довольно обширна, поэтому мы ограничимся рассмотрением лишь
гидравлической сущности этой теории.
Способность плавающего тела, выведенного из состояния равновесия, вновь возвращаться в это состояние
называется устойчивостью. Вес жидкости, взятой в объеме погруженной части судна называют
водоизмещением, а точку приложения равнодействующей давления (т.е. центр давления) – центром
водоизмещения. При нормальном положении судна центр тяжести С и центр водоизмещения d лежат
на одной вертикальной прямой O’-O”, представляющей ось симметрии судна и называемой осью плавания
(рис.2.5).
Пусть под влиянием внешних сил судно наклонилось на некоторый угол α, часть судна
KLM вышла из жидкости, а часть K’L’M’, наоборот, погрузилось в нее. При этом получили новое
положении центра водоизмещения d’. Приложим к точке d’ подъемную силу R и линию ее
действия продолжим до пересечения с осью симметрии O’-O”. Полученная точка m называется
метацентром, а отрезок mC = h называется метацентрической высотой. Будем считать h
положительным, если точка m лежит выше точки C, и отрицательным – в противном случае.
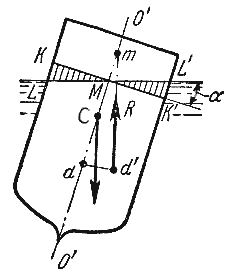
Рис. 2.5. Поперечный профиль судна
Теперь рассмотрим условия равновесия судна:
1) если h > 0, то судно возвращается в первоначальное положение;
2) если h = 0, то это случай безразличного равновесия;
3) если h<0, то это случай неостойчивого равновесия, при котором продолжается дальнейшее
опрокидывание судна.
Следовательно, чем ниже расположен центр тяжести и, чем больше метацентрическая высота, тем больше
будет остойчивость судна.
Как уже отмечалось выше, поверхность, во всех точках которой давление одинаково, называется поверхностью
уровня или поверхностью равного давления. При неравномерном или непрямолинейном движении на частицы
жидкости кроме силы тяжести действуют еще и силы инерции, причем если они постоянны по времени, то жидкость
принимает новое положение равновесия. Такое равновесие жидкости называется относительным покоем.
Рассмотрим два примера такого относительного покоя.
В первом примере определим поверхности уровня в жидкости, находящейся в цистерне, в то время как цистерна
движется по горизонтальному пути с постоянным ускорением a (рис.2.6).
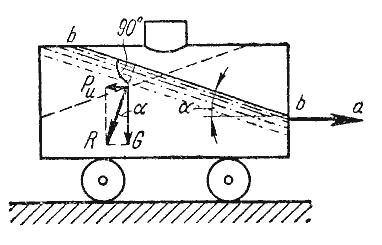
Рис. 2.6. Движение цистерны с ускорением
К каждой частице жидкости массы m должны быть в этом случае приложены ее вес G = mg и сила
инерции Pu, равная по величине ma. Равнодействующая 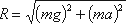
этих сил направлена к вертикали под углом α, тангенс которого равен
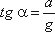
Так как свободная поверхность, как поверхность равного давления, должна быть нормальна к указанной
равнодействующей, то она в данном случае представит собой уже не горизонтальную плоскость, а наклонную,
составляющую угол α с горизонтом. Учитывая, что величина этого угла зависит только от
ускорений, приходим к выводу, что положение свободной поверхности не будет зависеть от рода находящейся в
цистерне жидкости. Любая другая поверхность уровня в жидкости также будет плоскостью, наклоненной к горизонту
под углом α. Если бы движение цистерны было не равноускоренным, а равнозамедленным,
направление ускорения изменилось бы на обратное, и наклон свободной поверхности обратился бы в другую сторону
(см. рис.2.6, пунктир).
В качестве второго примера рассмотрим часто встречающийся в практике случай относительного покоя жидкости
во вращающихся сосудах (например, в сепараторах и центрифугах, применяемых для разделения жидкостей). В этом
случае (рис.2.7) на любую частицу жидкости при ее относительном равновесии действуют массовые силы: сила
тяжести G = mg и центробежная сила Pu = mω2r, где r
– расстояние частицы от оси вращения, а ω – угловая скорость вращения сосуда.
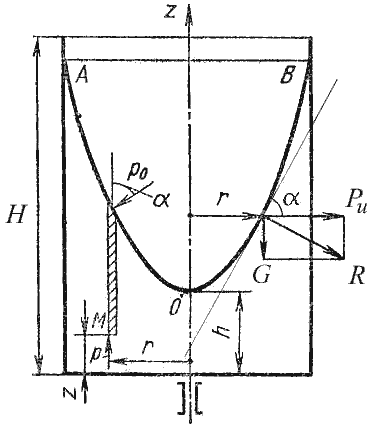
Рис. 2.7. Вращение сосуда с жидкостью
Поверхность жидкости также должна быть нормальна в каждой точке к равнодействующей этих сил R и
представит собой параболоид вращения. Из чертежа находим
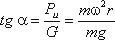
С другой стороны:
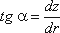
где z – координата рассматриваемой точки. Таким образом, получаем:
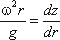
откуда
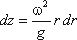
или после интегрирования
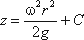
В точке пересечения кривой АОВ с осью вращения r = 0, z = h = C, поэтому окончательно будем
иметь
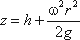
т.е. кривая АОВ является параболой, а свободная поверхность жидкости параболоидом. Такую же форму
имеют и другие поверхности уровня.
Для определения закона изменения давления во вращающейся жидкости в функции радиуса и высоты выделим
вертикальный цилиндрический объем жидкости с основанием в виде элементарной горизонтальной площадки dS
(точка М) на произвольном радиусе r и высоте z и запишем условие его равновесия в
вертикальном направлении. С учетом уравнения (2.11) будем иметь
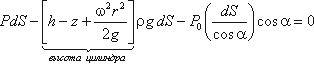
После сокращений получим
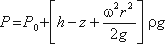
Это значит, что давление возрастает пропорционально радиусу r и уменьшается пропорционально
высоте z.
Проверить себя ( Тест )
Наверх страницы
