Давление. Единицы давления.

По рыхлому снегу человек идёт с большим трудом, глубоко проваливаясь при каждом шаге. Но, надев лыжи, он может идти, почти не проваливаясь в него. Почему? На лыжах или без лыж человек действует на снег с одной и той же силой, равной своему весу. Однако действие этой силы в обоих случаях различно, потому что различна площадь поверхности, на которую давит человек, с лыжами и без лыж. Площадь поверхности лыж почти в 20 раз больше площади подошвы. Поэтому, стоя на лыжах, человек действует на каждый квадратный сантиметр площади поверхности снега с силой, в 20 раз меньшей, чем стоя на снегу без лыж.
Ученик, прикалывая кнопками газету к доске, действует на каждую кнопку с одинаковой силой. Однако кнопка, имеющая более острый конец, легче входит в дерево.
Значит, результат действия силы зависит не только от её модуля, направления и точки приложения, но и от площади той поверхности, к которой она приложена (перпендикулярно которой она действует).
Этот вывод подтверждают физические опыты.

По углам небольшой доски надо вбить гвозди. Сначала гвозди, вбитые в доску, установим на песке остриями вверх и положим на доску гирю. В этом случае шляпки гвоздей лишь незначительно вдавливаются в песок. Затем доску перевернем и поставим гвозди на острие. В этом случае площадь опоры меньше, и под действием той же силы гвозди значительно углубляются в песок.

От того, какая сила действует на каждую единицу площади поверхности, зависит результат действия этой силы.
В рассмотренных примерах силы действовали перпендикулярно поверхности тела. Вес человека был перпендикулярен поверхности снега; сила, действовавшая на кнопку, перпендикулярна поверхности доски.
Величина, равная отношению силы, действующей перпендикулярно поверхности, к площади этой поверхности, называется давлением.
Чтобы определить давление, надо силу, действующую перпендикулярно поверхности, разделить на площадь поверхности:
давление = сила / площадь.
Обозначим величины, входящие в это выражение: давление – p, сила, действующая на поверхность, – F и площадь поверхности – S.
Тогда получим формулу:
p = F/S
Понятно, что бóльшая по значению сила, действующую на ту же площадь, будет производить большее давление.
За единицу давления принимается такое давление, которое производит сила в 1 Н, действующая на поверхность площадью 1 м2 перпендикулярно этой поверхности.
Единица давления – ньютон на квадратный метр ( 1 Н / м2 ). В честь французского ученого Блеза Паскаля она называется паскалем (Па). Таким образом,
1 Па = 1 Н / м2 .
Используется также другие единицы давления: гектопаскаль (гПа) и килопаскаль (кПа).
1 кПа = 1000 Па;
1 гПа = 100 Па;
1 Па = 0,001 кПа;
1 Па = 0,01 гПа.
Пример. Рассчитать давление, производимое на пол мальчиком, масса которого 45 кг, а площадь подошв его ботинок, соприкасающихся с полом, равна 300 см2.
Запишем условие задачи и решим её.
Дано: m = 45 кг, S = 300 см2; p = ?
В единицах СИ: S = 0,03 м2
Решение:
p = F/S,
F = P,
P = g·m,
P = 9,8 Н · 45 кг ≈ 450 Н,
p = 450/0,03 Н / м2 = 15000 Па = 15 кПа
‘Ответ’: p = 15000 Па = 15 кПа
Способы уменьшения и увеличения давления.
Тяжелый гусеничный трактор производит на почву давление равное 40 – 50 кПа, т. е. всего в 2 – 3 раза больше, чем давление мальчика массой 45 кг. Это объясняется тем, что вес трактора распределяется на бóльшую площадь за счёт гусеничной передачи. А мы установили, что чем больше площадь опоры, тем меньше давление, производимое одной и той же силой на эту опору.
В зависимости от того, нужно ли получить малое или большое давление, площадь опоры увеличивается или уменьшается. Например, для того, чтобы грунт мог выдержать давление возводимого здания, увеличивают площадь нижней части фундамента.
Шины грузовых автомобилей и шасси самолетов делают значительно шире, чем легковых. Особенно широкими делают шины у автомобилей, предназначенных для передвижения в пустынях.
Тяжелые машины, как трактор, танк или болотоход, имея большую опорную площадь гусениц, проходят по болотистой местности, по которой не пройдет человек.
С другой стороны, при малой площади поверхности можно небольшой силой произвести большое давление. Например, вдавливая кнопку в доску, мы действуем на нее с силой около 50 Н. Так как площадь острия кнопки примерно 1 мм2, то давление, производимое ею, равно:
p = 50 Н/ 0, 000 001 м2 = 50 000 000 Па = 50 000 кПа.
Для сравнения, это давление в 1000 раз больше давления, производимого гусеничным трактором на почву. Можно найти еще много таких примеров.
Лезвие режущих и острие колющих инструментов (ножей, ножниц, резцов, пил, игл и др.) специально остро оттачивается. Заточенный край острого лезвия имеет маленькую площадь, поэтому при помощи даже малой силы создается большое давление, и таким инструментом легко работать.
Режущие и колющие приспособления встречаются и в живой природе: это зубы, когти, клювы, шипы и др. – все они из твердого материала, гладкие и очень острые.
Давление


Мы уже знаем, что газы, в отличие от твердых тел и жидкостей, заполняют весь сосуд, в котором находятся. Например, стальной баллон для хранения газов, камера автомобильной шины или волейбольный мяч. При этом газ оказывает давление на стенки, дно и крышку баллона, камеры или любого другого тела, в котором он находится. Давление газа обусловлено иными причинами, чем давление твердого тела на опору.
Известно, что молекулы газа беспорядочно движутся. При своем движении они сталкиваются друг с другом, а также со стенками сосуда, в котором находится газ. Молекул в газе много, поэтому и число их ударов очень велико. Например, число ударов молекул воздуха, находящегося в комнате, о поверхность площадью 1 см2 за 1 с выражается двадцатитрехзначным числом. Хотя сила удара отдельной молекулы мала, но действие всех молекул на стенки сосуда значительно, — оно и создает давление газа.
Итак, давление газа на стенки сосуда (и на помещенное в газ тело) вызывается ударами молекул газа.
Рассмотрим следующий опыт. Под колокол воздушного насоса поместим резиновый шарик. Он содержит небольшое количество воздуха и имеет неправильную форму. Затем насосом откачиваем воздух из-под колокола. Оболочка шарика, вокруг которой воздух становится все более разреженным, постепенно раздувается и принимает форму правильного шара.
Как объяснить этот опыт?

В нашем опыте движущиеся молекулы газа непрерывно ударяют о стенки шарика внутри и снаружи. При откачивании воздуха число молекул в колоколе вокруг оболочки шарика уменьшается. Но внутри шарика их число не изменяется. Поэтому число ударов молекул о внешние стенки оболочки становится меньше, чем число ударов о внутренние стенки. Шарик раздувается до тех пор, пока сила упругости его резиновой оболочки не станет равной силе давления газа. Оболочка шарика принимает форму шара. Это показывает, что газ давит на ее стенки по всем направлениям одинаково. Иначе говоря, число ударов молекул, приходящихся на каждый квадратный сантиметр площади поверхности, по всем направлениям одинаково. Одинаковое давление по всем направлениям характерно для газа и является следствием беспорядочного движения огромного числа молекул.
Попытаемся уменьшить объем газа, но так, чтобы масса его осталась неизменной. Это значит, что в каждом кубическом сантиметре газа молекул станет больше, плотность газа увеличится. Тогда число ударов молекул о стенки увеличится, т. е. возрастет давление газа. Это можно подтвердить опытом.
На рисунке а изображена стеклянная трубка, один конец которой закрыт тонкой резиновой пленкой. В трубку вставлен поршень. При вдвигании поршня объем воздуха в трубке уменьшается, т. е. газ сжимается. Резиновая пленка при этом выгибается наружу, указывая на то, что давление воздуха в трубке увеличилось.
Наоборот, при увеличении объема этой же массы газа, число молекул в каждом кубическом сантиметре уменьшается. От этого уменьшится число ударов о стенки сосуда – давление газа станет меньше. Действительно, при вытягивании поршня из трубки объем воздуха увеличивается, пленка прогибается внутрь сосуда. Это указывает на уменьшение давления воздуха в трубке. Такие же явления наблюдались бы, если бы вместо воздуха в трубке находился бы любой другой газ.
Итак, при уменьшении объема газа его давление увеличивается, а при увеличении объема давление уменьшается при условии, что масса и температура газа остаются неизменными.
А как изменится давление газа, если нагреть его при постоянном объеме? Известно, что скорость движения молекул газа при нагревании увеличивается. Двигаясь быстрее, молекулы будут ударять о стенки сосуда чаще. Кроме того, каждый удар молекулы о стенку будет сильнее. Вследствие этого, стенки сосуда будут испытывать большее давление.
Следовательно, давление газа в закрытом сосуде тем больше, чем выше температура газа, при условии, что масса газа и объем не изменяются.
Из этих опытов можно сделать общий вывод, что давление газа тем больше, чем чаще и сильнее молекулы ударяют о стенки сосуда.
Для хранения и перевозки газов их сильно сжимают. При этом давление их возрастает, газы необходимо заключать в специальные, очень прочные баллоны. В таких баллонах, например, содержат сжатый воздух в подводных лодках, кислород, используемый при сварке металлов. Конечно же, мы должны навсегда запомнить, что газовые баллоны нельзя нагревать, тем более, когда они заполнены газом. Потому что, как мы уже понимаем, может произойти взрыв с очень неприятными последствиями.
Закон Паскаля.



В отличие от твердых тел отдельные слои и мелкие частицы жидкости и газа могут свободно перемещаться относительно друг друга по всем направлениям. Достаточно, например, слегка подуть на поверхность воды в стакане, чтобы вызвать движение воды. На реке или озере при малейшем ветерке появляется рябь.
Подвижностью частиц газа и жидкости объясняется, что давление, производимое на них, передается не только в направлении действия силы, а в каждую точку. Рассмотрим это явление подробнее.
На рисунке, а изображен сосуд, в котором содержится газ (или жидкость). Частицы равномерно распределены по всему сосуду. Сосуд закрыт поршнем, который может перемещаться вверх и вниз.
Прилагая некоторую силу, заставим поршень немного переместиться внутрь и сжать газ (жидкость), находящийся непосредственно под ним. Тогда частицы (молекулы) расположатся в этом месте более плотно, чем прежде(рис, б). Благодаря подвижности частицы газа будут перемещаться по всем направлениям. Вследствие этого их расположение опять станет равномерным, но более плотным, чем раньше (рис, в). Поэтому давление газа всюду возрастет. Значит, добавочное давление передается всем частицам газа или жидкости. Так, если давление на газ (жидкость) около самого поршня увеличится на 1 Па, то во всех точках внутри газа или жидкости давление станет больше прежнего на столько же. На 1 Па увеличится давление и на стенки сосуда, и на дно, и на поршень.
Давление, производимое на жидкость или газ, передается на любую точку одинаково во всех направлениях.
Это утверждение называется законом Паскаля.
На основе закона Паскаля легко объяснить следующие опыты.
На рисунке изображен полый шар, имеющий в различных местах небольшие отверстия. К шару присоединена трубка, в которую вставлен поршень. Если набрать воды в шар и вдвинуть в трубку поршень, то вода польется из всех отверстий шара. В этом опыте поршень давит на поверхность воды в трубке. Частицы воды, находящиеся под поршнем, уплотняясь, передают его давление другим слоям, лежащим глубже. Таким образом, давление поршня передается в каждую точку жидкости, заполняющей шар. В результате часть воды выталкивается из шара в виде одинаковых струек, вытекающих из всех отверстий.
Если шар заполнить дымом, то при вдвигании поршня в трубку из всех отверстий шара начнут выходить одинаковые струйки дыма. Это подтверждает, что и газы передают производимое на них давление во все стороны одинаково.
Давление в жидкости и газе.

На жидкости, как и на все тела на Земле, действует сила тяжести. Поэтому, каждый слой жидкости, налитой в сосуд, своим весом создает давление, которое по закону Паскаля передается по всем направлениям. Следовательно, внутри жидкости существует давление. В этом можно убедиться на опыте.
В стеклянную трубку, нижнее отверстие которой закрыто тонкой резиновой пленкой, нальем воду. Под действием веса жидкости дно трубки прогнется.
Опыт показывает, что, чем выше столб воды над резиновой пленкой, тем больше она прогибается. Но всякий раз после того, как резиновое дно прогнулось, вода в трубке приходит в равновесие (останавливается), так как, кроме силы тяжести, на воду действует сила упругости растянутой резиновой пленки.


Опустим трубку с резиновым дном, в которую налита вода, в другой, более широкий сосуд с водой. Мы увидим, что по мере опускания трубки резиновая пленка постепенно выпрямляется. Полное выпрямление пленки показывает, что силы, действующие на нее сверху и снизу, равны. Наступает полное выпрямление пленки тогда, когда уровни воды в трубке и сосуде совпадают.
Такой же опыт можно провести с трубкой, в которой резиновая пленка закрывает боковое отверстие, как это показано на рисунке, а. Погрузим эту трубку с водой в другой сосуд с водой, как это изображено на рисунке, б. Мы заметим, что пленка снова выпрямится, как только уровни воды в трубке и сосуде сравняются. Это означает, что силы, действующие на резиновую пленку, одинаковы со всех сторон.
Возьмем сосуд, дно которого может отпадать. Опустим его в банку с водой. Дно при этом окажется плотно прижатым к краю сосуда и не отпадет. Его прижимает сила давления воды, направленная снизу вверх.
Будем осторожно наливать воду в сосуд и следить за его дном. Как только уровень воды в сосуде совпадет с уровнем воды в банке, оно отпадет от сосуда.
В момент отрыва на дно давит сверху вниз столб жидкости в сосуде, а снизу вверх на дно передается давление такого же по высоте столба жидкости, но находящейся в банке. Оба эти давления одинаковы, дно же отходит от цилиндра вследствие действия на него собственной силы тяжести.
Выше были описаны опыты с водой, но если взять вместо воды любую другую жидкость, результаты опыта будут те же.
Итак, опыты показывают, что внутри жидкости существует давление, и на одном и том же уровне оно одинаково по всем направлениям. С глубиной давление увеличивается.
Газы в этом отношении не отличаются от жидкостей, ведь они тоже имеют вес. Но надо помнить, что плотность газа в сотни раз меньше плотности жидкости. Вес газа, находящегося в сосуде, мал, и его “весовое” давление во многих случаях можно не учитывать.
Расчет давления жидкости на дно и стенки сосуда.

Рассмотрим, как можно рассчитывать давление жидкости на дно и стенки сосуда. Решим сначала задачу для сосуда, имеющего форму прямоугольного параллелепипеда.
Сила F, с которой жидкость, налитая в этот сосуд, давит на его дно, равна весу P жидкости, находящейся в сосуде. Вес жидкости можно определить, зная ее массу m. Массу, как известно, можно вычислить по формуле: m = ρ·V. Объем жидкости, налитой в выбранный нами сосуд, легко рассчитать. Если высоту столба жидкости, находящейся в сосуде, обозначить буквой h, а площадь дна сосуда S, то V = S·h.
Масса жидкости m = ρ·V, или m = ρ·S·h .
Вес этой жидкости P = g·m, или P = g·ρ·S·h.
Так как вес столба жидкости равен силе, с которой жидкость давит на дно сосуда, то, разделив вес P на площадь S, получим давление жидкости p:
p = P/S , или p = g·ρ·S·h/S,
то есть
p = g·ρ·h.
Мы получили формулу для расчета давления жидкости на дно сосуда. Из этой формулы видно, что давление жидкости на дно сосуда зависит только от плотности и высоты столба жидкости.
Следовательно, по выведенной формуле можно рассчитывать давление жидкости, налитой в сосуд любой формы (строго говоря, наш расчет годится только для сосудов, имеющих форму прямой призмы и цилиндра. В курсах физики для института доказано, что формула верна и для сосуда произвольной формы). Кроме того, по ней можно вычислить и давление на стенки сосуда. Давление внутри жидкости, в том числе давление снизу вверх, также рассчитывается по этой формуле, так как давление на одной и той же глубине одинаково по всем направлениям.
При расчете давления по формуле p = gρh надо плотность ρ выражать в килограммах на кубический метр (кг/м3), а высоту столба жидкости h – в метрах (м), g = 9,8 Н/кг, тогда давление будет выражено в паскалях (Па).
Пример. Определите давление нефти на дно цистерны, если высота столба нефти 10 м, а плотность ее 800 кг/м3 .
Запишем условие задачи и запишем ее.
Дано:
h = 10 м
ρ = 800 кг/м3
P = ?
Решение:
p = gρh,
p = 9.8 Н/кг · 800 кг/м3 · 10 м ≈ 80 000 Па ≈ 80 кПа.
Ответ: p ≈ 80 кПа.
Сообщающиеся сосуды.

На рисунке изображены два сосуда, соединённые между собой резиновой трубкой. Такие сосуды называются сообщающимися. Лейка, чайник, кофейник – примеры сообщающихся сосудов. Из опыта мы знаем, что вода, налитая, например, в лейку, стоит всегда на одном уровне в носике и внутри.
С сообщающимися сосудами можно проделать следующий простой опыт. В начале опыта резиновую трубку зажимаем в середине, и в одну из трубок наливаем воду. Затем зажим открываем, и вода вмиг перетекает в другую трубку, пока поверхности воды в обеих трубках не установятся на одном уровне. Можно закрепить одну из трубок в штативе, а другую поднимать, опускать или наклонять в разные стороны. И в этом случае, как только жидкость успокоится, ее уровни в обеих трубках уравняются.
В сообщающихся сосудах любой формы и сечения поверхности однородной жидкости устанавливаются на одном уровне (при условии, что давление воздуха над жидкостью одинаково) (рис. 109).
Это можно обосновать следующим образом. Жидкость покоится, не перемещаясь из одного сосуда в другой. Значит, давления в обоих сосудах на любом уровне одинаковы. Жидкость в обоих сосудах одна и та же, т. е. имеет одинаковую плотность. Следовательно, должны быть одинаковы и ее высоты. Когда мы поднимаем один сосуд или доливаем в него жидкость, давление в нем увеличивается и жидкость перемещается в другой сосуд до тех пор, пока давления не уравновесятся.
Если в один из сообщающихся сосудов налить жидкость одной плотности, а во второй – другой плотности, то при равновесии уровни этих жидкостей не будут одинаковыми. И это понятно. Мы ведь знаем, что давление жидкости на дно сосуда прямо пропорционально высоте столба и плотности жидкости. А в этом случае плотности жидкостей будут различны.
При равенстве давлений высота столба жидкости с большей плотностью будет меньше высоты столба жидкости с меньшей плотностью (рис.).

Вес воздуха. Атмосферное давление.


На воздух, как и на всякое тело, находящееся на Земле, действует сила тяжести, и, значит, воздух обладает весом. Вес воздуха легко вычислить, зная его массу.
На опыте покажем, как вычислить массу воздуха. Для этого нужно взять прочный стеклянный шар с пробкой и резиновой трубкой с зажимом. Выкачаем из него насосом воздух, зажмем трубку зажимом и уравновесим на весах. Затем, открыв зажим на резиновой трубке, впустим в него воздух. Равновесие весов при этом нарушится. Для его восстановления на другую чашку весов придется положить гири, масса которых будет равна массе воздуха в объеме шара.
Опытами установлено, что при температуре 0 °С и нормальном атмосферном давлении масса воздуха объемом 1 м3 равна 1,29 кг. Вес этого воздуха легко вычислить:
P = g·m, P = 9,8 Н/кг · 1,29 кг ≈ 13 Н.
Воздушная оболочка, окружающая Землю, называется атмосфера (от греч. атмос – пар, воздух, и сфера – шар).
Атмосфера, как показали наблюдения за полетом искусственных спутников Земли, простирается на высоту нескольких тысяч километров.
Вследствие действия силы тяжести верхние слои атмосферы, подобно воде океана, сжимают нижние слои. Воздушный слой, прилегающий непосредственно к Земле, сжат больше всего и, согласно закону Паскаля, передает производимое на него давление по всем направлениям.
В результате этого земная поверхность и телá, находящиеся на ней, испытывают давление всей толщи воздуха, или, как обычно говорится в таких случаях, испытывают атмосферное давление.
Существованием атмосферного давления могут быть объяснены многие явления, с которыми мы встречаемся в жизни. Рассмотрим некоторые из них.
На рисунке изображена стеклянная трубка, внутри которой находится поршень, плотно прилегающий к стенкам трубки. Конец трубки опущен воду. Если поднимать поршень, то за ним будет подниматься и вода.
Это явление используется в водяных насосах и некоторых других устройствах.
На рисунке показан цилиндрический сосуд. Он закрыт пробкой, в которую вставлена трубка с краном. Из сосуда насосом откачивается воздух. Затем конец трубки помещается в воду. Если теперь открыть кран, то вода фонтаном брызнет в внутрь сосуда. Вода поступает в сосуд потому, что атмосферное давление больше давления разреженного воздуха в сосуде.
Почему существует воздушная оболочка Земли.
Как и все тела, молекулы газов, входящих в состав воздушной оболочки Земли, притягиваются к Земле.
Но почему же тогда все они не упадут на поверхность Земли? Каким образом сохраняется воздушная оболочка Земли, ее атмосфера? Чтобы понять это, надо учесть, что молекулы газов находятся в непрерывном и беспорядочном движении. Но тогда возникает другой вопрос: почему эти молекулы не улетают в мировое пространство, то есть в космос.
Для того, чтобы совсем покинуть Землю, молекула, как и космический корабль или ракета, должна иметь очень большую скорость (не меньше 11,2 км/с). Это так называемая вторая космическая скорость. Скорость большинства молекул воздушной оболочки Земли значительно меньше этой космической скорости. Поэтому большинство их привязано к Земле силой тяжести, лишь ничтожно малое количество молекул улетает за пределы Земли в космос.
Беспорядочное движение молекул и действие на них силы тяжести приводят в результате к тому, что молекулы газов “парят” в пространстве около Земли, образуя воздушную оболочку, или известную нам атмосферу.
Измерения показывают, что плотность воздуха быстро уменьшается с высотой. Так, на высоте 5,5 км над Землей плотность воздуха в 2 раза меньше его плотность у поверхности Земли, на высоте 11 км – в 4 раза меньше, и т. д. Чем выше, тем воздух разреженнее. И наконец, в самых верхних слоях (сотни и тысячи километров над Землей) атмосфера постепенно переходит в безвоздушное пространство. Четкой границы воздушная оболочка Земли не имеет.
Строго говоря, вследствие действия силы тяжести плотность газа в любом закрытом сосуде неодинакова по всему объему сосуда. Внизу сосуда плотность газа больше, чем в верхних его частях, поэтому и давление в сосуде неодинаково. На дне сосуда оно больше, чем вверху.
Однако для газа, содержащегося в сосуде, это различие в плотности и давлении столь мало, что его можно во многих случаях совсем не учитывать, просто знать об этом. Но для атмосферы, простирающейся на несколько тысяч километров, различие это существенно.
Измерение атмосферного давления. Опыт Торричелли.
Рассчитать атмосферное давление по формуле для вычисления давления столба жидкости (§ 38) нельзя. Для такого расчета надо знать высоту атмосферы и плотность воздуха. Но определенной границы у атмосферы нет, а плотность воздуха на разной высоте различна. Однако измерить атмосферное давление можно с помощью опыта, предложенного в 17 веке итальянским ученым Эванджелиста Торричелли, учеником Галилея.
Опыт Торричелли состоит в следующем: стеклянную трубку длиной около 1 м, запаянную с одного конца, наполняют ртутью. Затем, плотно закрыв второй конец трубки, ее переворачивают и опускают в чашку с ртутью, где под уровнем ртути открывают этот конец трубки. Как и в любом опыте с жидкостью, часть ртути при этом выливается в чашку, а часть ее остается в трубке. Высота столба ртути, оставшейся в трубке, равна примерно 760 мм. Над ртутью внутри трубки воздуха нет, там безвоздушное пространство, поэтому никакой газ не оказывает давления сверху на столб ртути внутри этой трубки и не влияет на измерения.

Торричелли, предложивший описанный выше опыт, дал и его объяснение. Атмосфера давит на поверхность ртути в чашке. Ртуть находится в равновесии. Значит, давление в трубке на уровне аа1 (см. рис) равно атмосферному давлению. При изменении атмосферного давления меняется и высота столба ртути в трубке. При увеличении давления столбик удлиняется. При уменьшении давления — столб ртути уменьшает свою высоту.
Давление в трубке на уровне аа1 создается весом столба ртути в трубке, так как в верхней части трубки над ртутью воздуха нет. Отсюда следует, что атмосферное давление равно давлению столба ртути в трубке, т. е.
pатм = pртути .
Измерив высоту столба ртути, можно рассчитать давление, которое производит ртуть. Оно и будет равно атмосферному давлению. Если атмосферное давление уменьшится, то столб ртути в трубке Торричелли понизится.
Чем больше атмосферное давление, тем выше столб ртути в опыте Торричелли. Поэтому на практике атмосферное давление можно измерить высотой ртутного столба (в миллиметрах или сантиметрах). Если, например, атмосферное давление равно 780 мм рт. ст. (говорят “миллиметров ртутного столба”), то это значит, что воздух производит такое же давление, какое производит вертикальный столб ртути высотой 780 мм.
Следовательно, в этом случае за единицу измерения атмосферного давления принимается 1 миллиметр ртутного столба (1 мм рт. ст.). Найдем соотношение между этой единицей и известной нам единицей – паскалем (Па).
Давление столба ртути ρртути высотой 1 мм равно:
p = g·ρ·h, p = 9,8 Н/кг · 13 600 кг/ м3 · 0,001 м ≈ 133,3 Па.
Итак, 1 мм рт. ст. = 133,3 Па.
В настоящее время атмосферное давление принято измерять в гектопаскалях ( 1 гПа = 100 Па). Например, в сводках погоды может быть объявлено, что давление равно 1013 гПа, это то же самое, что 760 мм рт. ст.
Наблюдая ежедневно за высотой ртутного столба в трубке, Торричелли обнаружил, что эта высота меняется, т. е. атмосферное давление непостоянно, оно может увеличиваться и уменьшаться. Торричелли заметил также, что атмосферное давление связано с изменением погоды.
Если к трубке с ртутью, использовавшейся в опыте Торричелли, прикрепить вертикальную шкалу, то получится простейший прибор – ртутный барометр (от греч. барос – тяжесть, метрео – измеряю). Он служит для измерения атмосферного давления.
Барометр – анероид.


В практике для измерения атмосферного давления используют металлический барометр, называемый анероидом (в переводе с греческого – безжидкостный). Так барометр называют потому, что в нем нет ртути.
Внешний вид анероида изображен на рисунке. Главная часть его – металлическая коробочка 1 с волнистой (гофрированной) поверхностью (см. др. рис.). Из этой коробочки выкачан воздух, а чтобы атмосферное давление не раздавило коробочку, ее крышка 2 пружиной оттягивается вверх. При увеличении атмосферного давления крышка прогибается вниз и натягивает пружину. При уменьшении давления пружина выпрямляет крышку. К пружине с помощью передаточного механизма 3 прикреплена стрелка-указатель 4, которая продвигается вправо или влево при изменении давления. Под стрелкой укреплена шкала, деления которой нанесены по показаниям ртутного барометра. Так, число 750, против которого стоит стрелка анероида (см. рис.), показывает, что в данный момент в ртутном барометре высота ртутного столба 750 мм.
Следовательно, атмосферное давление равно 750 мм рт. ст. или ≈ 1000 гПа.
Значение атмосферного давления весьма важно для предвидения погоды на ближайшие дни, так как изменение атмосферного давления связано с изменением погоды. Барометр – необходимый прибор для метеорологических наблюдений.
Атмосферное давление на различных высотах.
В жидкости давление, как мы знаем, зависит от плотности жидкости и высоты ее столба. Вследствие малой сжимаемости плотность жидкости на различных глубинах почти одинакова. Поэтому, вычисляя давление, мы считаем ее плотность постоянной и учитываем только изменение высоты.
Сложнее дело обстоит с газами. Газы сильно сжимаемы. А чем сильнее газ сжат, тем больше его плотность, и тем большее давление он производит. Ведь давление газа создается ударами его молекул о поверхность тела.
Слои воздуха у поверхности Земли сжаты всеми вышележащими слоями воздуха, находящимися над ними. Но чем выше от поверхности слой воздуха, тем слабее он сжат, тем меньше его плотность. Следовательно, тем меньшее давление он производит. Если, например, воздушный шар поднимается над поверхностью Земли, то давление воздуха на шар становиться меньше. Это происходит не только потому, что высота столба воздуха над ним уменьшается, но еще и потому, что уменьшается плотность воздуха. Вверху она меньше, чем внизу. Поэтому зависимость давления воздуха от высоты сложнее, чем жидкости.
Наблюдения показывают, что атмосферное давление в местностях, лежащих на уровне моря, в среднем равно 760 мм рт. ст.
Атмосферное давление, равное давлению столба ртути высотой 760 мм при температуре 0 °С, называется нормальным атмосферным давлением.
Нормальное атмосферное давление равно 101 300 Па = 1013 гПа.
Чем больше высота над уровнем моря, тем давление меньше.
При небольших подъемах, в среднем, на каждые 12 м подъема давление уменьшается на 1 мм рт. ст. (или на 1,33 гПа).
Зная зависимость давления от высоты, можно по изменению показаний барометра определить высоту над уровнем моря. Анероиды, имеющие шкалу, по которой непосредственно можно измерить высоту над уровнем моря, называются высотомерами. Их применяют в авиации и при подъеме на горы.
Манометры.

Мы уже знаем, что для измерения атмосферного давления применяют барометры. Для измерения давлений, бóльших или меньших атмосферного, используется манометры (от греч. манос – редкий, неплотный, метрео – измеряю). Манометры бывают жидкостные и металлические.
Рассмотрим сначала устройство и действие открытого жидкостного манометра. Он состоит из двухколенной стеклянной трубки, в которую наливается какая-нибудь жидкость. Жидкость устанавливается в обоих коленах на одном уровне, так как на ее поверхность в коленах сосуда действует только атмосферное давление.


Чтобы понять, как работает такой манометр, его можно соединить резиновой трубкой с круглой плоской коробкой, одна сторона которой затянута резиновой пленкой. Если надавить пальцем на пленку, то уровень жидкости в колене манометра, соединенном в коробкой, понизится, а в другом колене повысится. Чем это объясняется?
При надавливании на пленку увеличивается давление воздуха в коробке. По закону Паскаля это увеличение давления передается и жидкости в том колене манометра, которое присоединено к коробке. Поэтому давление на жидкость в этом колене будет больше, чем в другом, где на жидкость действует только атмосферное давление. Под действием силы этого избыточного давления жидкость начнет перемещаться. В колене со сжатым воздухом жидкость опустится, в другом – поднимется. Жидкость придет в равновесие (остановится), когда избыточное давление сжатого воздуха уравновесится давлением, которое производит избыточный столб жидкости в другом колене манометра.
Чем сильнее давить на пленку, тем выше избыточный столб жидкости, тем больше его давление. Следовательно, об изменении давления можно судить по высоте этого избыточного столба.
На рисунке показано, как таким манометром можно измерять давление внутри жидкости. Чем глубже погружается в жидкость трубочка, тем больше становится разность высот столбов жидкости в коленах манометра, тем, следовательно, и большее давление производит жидкость.
Если установить коробочку прибора на какой-нибудь глубине внутри жидкости и поворачивать ее пленкой вверх, вбок и вниз, то показания манометра при этом не будут меняется. Так и должно быть, ведь на одном и том же уровне внутри жидкости давление одинаково по всем направлениям.

На рисунке изображен металлический манометр. Основная часть такого манометра – согнутая в трубу металлическая трубка 1, один конец которой закрыт. Другой конец трубки с помощью крана 4 сообщается с сосудом, в котором измеряют давление. При увеличении давления трубка разгибается. Движение её закрытого конца при помощи рычага 5 и зубчатки 3 передается стрелке 2, движущейся около шкалы прибора. При уменьшении давления трубка, благодаря своей упругости, возвращается в прежнее положение, а стрелка – к нулевому делению шкалы.
Поршневой жидкостный насос.
В опыте, рассмотренном нами ранее (§ 40), было установлено, что вода в стеклянной трубке под действием атмосферного давления поднималась вверх за поршнем. На этом основано действие поршневых насосов.
Насос схематически изображен на рисунке. Он состоит из цилиндра, внутри которого ходит вверх и вниз, плотно прилегая к стенкам сосуда, поршень 1. В нижней части цилиндра и в самом поршне установлены клапаны 2, открывающиеся только вверх. При движении поршня вверх вода под действием атмосферного давления входит в трубу, поднимает нижний клапан и движется за поршнем.
При движении поршня вниз вода, находящаяся под поршнем, давит на нижний клапан, и он закрывается. Одновременно под давлением воды открывается клапан внутри поршня, и вода переходит в пространство над поршнем. При следующем движении поршня вверх в месте с ним поднимается и находящаяся над ним вода, которая и выливается в отводящую трубу. Одновременно за поршнем поднимается и новая порция воды, которая при последующем опускании поршня окажется над ним, и вся эта процедура повторяется вновь и вновь, пока работает насос.
Гидравлический пресс.

Закон Паскаля позволяет объяснить действие гидравлической машины (от греч. гидравликос – водяной). Это машины, действие которых основано на законах движения и равновесия жидкостей.
Основной частью гидравлической машины служат два цилиндра разного диаметра, снабженные поршнями и соединительной трубкой. Пространство под поршнями и трубку заполняют жидкостью (обычно минеральным маслом). Высоты столбов жидкости в обоих цилиндрах одинаковы, пока на поршни не действуют силы.
Допустим теперь, что силы F1 и F2 – силы, действующие на поршни, S1 и S2 – площади поршней. Давление под первым (малым) поршнем равно p1 = F1 / S1, а под вторым (большим) p2 = F2 / S2 . По закону Паскаля давление покоящейся жидкостью во все стороны передается одинаково, т. е. p1 = p2 или F1 / S1 = F2 / S2 , откуда:
F2 / F1 = S2 / S1 .
Следовательно, сила F2 во столько раз больше силы F1 , во сколько раз площадь большого поршня больше площади малого поршня. Например, если площадь большого поршня 500 см2, а малого 5 см2, и на малый поршень действует сила 100 Н, то на больший поршень будет действовать сила, в 100 раз бóльшая, то есть 10 000 Н.
Таким образом, с помощью гидравлической машины можно малой силой уравновесить бóльшую силу.
Отношение F1 / F2 показывает выигрыш в силе. Например, в приведенном примере выигрыш в силе равен 10 000 Н / 100 Н = 100.
Гидравлическая машина, служащая для прессования (сдавливания), называется гидравлическим прессом.

Гидравлические прессы применяются там, где требуется большая сила. Например, для выжимания масла из семян на маслобойных заводах, для прессования фанеры, картона, сена. На металлургических заводах гидравлические прессы используют для изготовления стальных валов машин, железнодорожных колес и многих других изделий. Современные гидравлические прессы могут развивать силу в десятки и сотни миллионов ньютонов.
Устройство гидравлического пресса схематически показано на рисунке. Прессуемое тело 1 (A) кладут на платформу, соединенную с большим поршнем 2 (B). При помощи малого поршня 3 (D) создается большое давление на жидкость. Это давление передается в каждую точку жидкости, заполняющей цилиндры. Поэтому такое же давление действует и на второй, большой поршень. Но так как площадь 2-го (большого) поршня больше площади малого, то и сила, действующая на него, будет больше силы, действующей на поршень 3 (D). Под действием этой силы поршень 2 (B) будет подниматься. При подъеме поршня 2 (B) тело (A) упирается в неподвижную верхнюю платформу и сжимается. При помощи манометра 4 (M) измеряется давление жидкости. Предохранительный клапан 5 (P) автоматически открывается, когда давление жидкости превышает допустимое значение.
Из малого цилиндра в большой жидкость перекачивается повторными движениями малого поршня 3 (D). Это осуществляется следующим образом. При подъеме малого поршня (D) клапан 6 (K) открывается, и в пространство, находящееся под поршнем, засасывается жидкость. При опускании малого поршня под действием давления жидкости клапан 6 (K) закрывается, а клапан 7 (K’) открывается, и жидкость переходит в большой сосуд.
Действие воды и газа на погруженное в них тело.

Под водой мы легко можем поднять камень, который с трудом поднимается в воздухе. Если погрузить пробку под воду и выпустить ее из рук, то она всплывет. Как можно объяснить эти явления?
Мы знаем (§ 38), что жидкость давит на дно и стенки сосуда. И если внутрь жидкости поместить какое-нибудь твердое тело, то оно также будет подвергаться давлению, как и стенки сосуда.
Рассмотрим силы, которые действуют со стороны жидкости на погруженное в нее тело. Чтобы легче было рассуждать, выберем тело, которое имеет форму параллелепипеда с основаниями, параллельными поверхности жидкости (рис.). Силы, действующие на боковые грани тела, попарно равны и уравновешивают друг друга. Под действием этих сил тело сжимается. А вот силы, действующие на верхнюю и нижнюю грани тела, неодинаковы. На верхнюю грань давит сверху силой F1 столб жидкости высотой h1 . На уровне нижней грани давление производит столб жидкости высотой h2. Это давление, как мы знаем (§ 37), передается внутри жидкости во все стороны. Следовательно, на нижнюю грань тела снизу вверх с силой F2 давит столб жидкости высотой h2. Но h2 больше h1, следовательно, и модуль силы F2 больше модуля силы F1. Поэтому тело выталкивается из жидкости с силой Fвыт, равной разности сил F2 – F1 , т. е.
Fвыт = F2– F1
Рассчитаем эту выталкивающую силу. Силы F1 и F2 , действующие на верхнюю и нижнюю грани параллелепипеда, можно вычислить, зная площади этих граней (S1 и S2) и давление жидкости на уровнях этих граней (p1 и p2):
F1 = p1·S1, а F2 = p2·S2, так как p1 = ρж·g·h1 , p2 = ρж·g·h2 , а S1 = S2 = S, где S – площадь грани параллелепипеда (все грани равны).
Тогда, Fвыт = F2 – F1 = ρ·g·h2·S – ρ·g·h1·S = ρ·g·S·(h2 – h1) = ρ·g·S·h, где h – высота параллелепипеда (h = h2 – h1).
Но S·h = V, где V – объем параллелепипеда, а ρж·V = mж – масса жидкости в объеме параллелепипеда. Следовательно,
Fвыт = g·mж = Pж ,
т. е. выталкивающая сила равна весу жидкости в объеме погруженного в нее тела (выталкивающая сила равна весу жидкости такого же объёма, как и объём погруженного в нее тела).
Существование силы, выталкивающей тело из жидкости, легко обнаружить на опыте.
На рисунке а изображено тело, подвешенное к пружине со стрелкой-указателем на конце. Стрелка отмечает на штативе растяжение пружины. При отпускании тела в воду пружина сокращается (рис., б). Такое же сокращение пружины получится, если действовать на тело снизу вверх с некоторой силой, например, нажать рукой (приподнять).
Следовательно, опыт подтверждает, что на тело, находящееся в жидкости, действует сила, выталкивающая это тело из жидкости.
К газам, как мы знаем, также применим закон Паскаля. Поэтому на тела, находящиеся в газе, действует сила, выталкивающая их из газа. Под действием этой силы воздушные шары поднимаются вверх. Существование силы, выталкивающей тело из газа, можно также наблюдать на опыте.
К укороченной чашке весов подвесим стеклянный шар или большую колбу, закрытую пробкой. Весы уравновешиваются. Затем под колбу (или шар) ставят широкий сосуд так, чтобы он окружал всю колбу. Сосуд наполняется углекислым газом, плотность которого больше плотности воздуха (поэтому углекислый газ опускается вниз и заполняет сосуд, вытесняя из него воздух). При этом равновесие весов нарушается. Чашка с подвешенной колбой поднимается вверх (рис.). На колбу, погруженную в углекислый газ, действует бóльшая выталкивающая сила, по сравнению с той, которая действует на нее в воздухе.
Сила, выталкивающая тело из жидкости или газа, направлена противоположно силе тяжести, приложенной к этому телу.
Поэтому пролкосмосе). Именно этим объясняется, что в воде мы иногда легко поднимаем тела, которые с трудом удерживаем в воздухе.
Архимедова сила.

Силу, с которой тело, находящееся в жидкости, выталкивается ею, можно рассчитать (как это сделано в § 48). А можно определить ее значение на опыте, используя для этого прибор, изображенный на рисунке.

К пружине подвешивается небольшое ведерко и тело цилиндрической формы (рис., а). Стрелка на штативе отмечает растяжение пружины. Она показывает вес тела в воздухе. Приподняв тело, под него подставляется отливной сосуд, наполненный жидкостью до уровня отливной трубки. После чего тело погружается целиком в жидкость (рис., б). При этом часть жидкости, объем которой равен объему тела, выливается из отливного сосуда в стакан. Пружина сокращается, и указатель пружины поднимается вверх, показывая уменьшение веса тела в жидкости. В данном случае на тело, кроме силы тяжести, действует еще одна сила, выталкивающая его из жидкости. Если в верхнее ведерко вылить жидкость из стакана (т. е. ту, которую вытеснило тело), то указатель пружины возвратится к своему начальному положению (рис., в).

На основании этого опыта можно заключить, что сила, выталкивающая целиком погруженное в жидкость тело, равна весу жидкости в объеме этого тела. Такой же вывод мы получили и в § 48.
Если подобный опыт проделать с телом, погруженным в какой-либо газ, то он показал бы, что сила, выталкивающая тело из газа, также равна весу газа, взятого в объеме тела.
Сила, выталкивающая тело из жидкости или газа, называется архимедовой силой, в честь ученого Архимеда, который впервые указал на ее существование и рассчитал ее значение.
Итак, опыт подтвердил, что архимедова (или выталкивающая) сила равна весу жидкости в объеме тела, т. е. FА = Pж = g·mж. Массу жидкости mж, вытесняемую телом, можно выразить через ее плотность ρж и объем тела Vт, погруженного в жидкость (так как Vж – объем вытесненной телом жидкости равен Vт – объему тела, погруженного в жидкость), т. е. mж = ρж·Vт. Тогда получим:
FA = g·ρж·Vт
Следовательно, архимедова сила зависит от плотности жидкости, в которую погружено тело, и от объема этого тела. Но она не зависит, например, от плотности вещества тела, погружаемого в жидкость, так как эта величина не входит в полученную формулу.
Определим теперь вес тела, погруженного в жидкость (или в газ). Так как две силы, действующие на тело в этом случае, направлены в противоположные стороны (сила тяжести вниз, а архимедова сила вверх), то вес тела в жидкости P1 будет меньше веса тела в вакууме P = g·m на архимедову силу FА = g·mж (где mж – масса жидкости или газа, вытесненной телом).
Таким образом, если тело погружено в жидкость или газ, то оно теряет в своем весе столько, сколько весит вытесненная им жидкость или газ.
Пример. Определить выталкивающую силу, действующую на камень объемом 1,6 м3 в морской воде.
Запишем условие задачи и решим ее.
Дано:
Vт =1,6 м3
ρж = 1030 кг/м3
g = 9,8 Н/кг
FА – ?
Решение:
FА = g·ρж·Vт,
FА = 9.8 Н/кг · 1030 кг/м3 · 1,6 м3 = 16 480 Н ≈ 16,5 кН.
Ответ: FА = 16,5 кН.
Плавание тел.

На тело, находящееся внутри жидкости, действуют две силы: сила тяжести, направленная вертикально вниз, и архимедова сила, направленная вертикально вверх. Рассмотрим, что будет происходить с телом под действием этих сил, если в начале оно было неподвижно. При этом возможны три случая:
1) если сила тяжести Fтяж больше архимедовой силы FА, то тело будет опускаться на дно, тонуть, т. е. если
Fтяж > FА, то тело тонет;
2) если сила тяжести равна архимедовой силе, то тело может находиться в равновесии в любом месте жидкости, т. е. если
Fтяж = FА, то тело плавает;
3) если сила тяжести меньше архимедовой силы, то тело будет подниматься из жидкости, всплывать, т. е. если
Fтяж < FА, то тело всплывает.
Рассмотрим последний случай подробнее.

Когда всплывающее тело достигнет поверхности жидкости, то при дальнейшем его движении вверх архимедова сила будет уменьшаться. Почему? А потому, что будет уменьшаться объем части тела, погруженной в жидкость, а архимедова сила равна весу жидкости в объеме погруженной в нее части тела.
Когда архимедова сила станет равной силе тяжести, тело остановится и будет плавать на поверхности жидкости, частично погрузившись в нее.
Полученный вывод легко проверить на опыте.
В отливной сосуд нальем воду до уровня отливной трубки. После этого погрузим в сосуд плавающее тело, предварительно взвесив его в воздухе. Опустившись в воду, тело вытесняет объем воды, равный объему погруженной в нее части тела. Взвесив эту воду, находим, что ее вес (архимедова сила) равен силе тяжести, действующей на плавающее тело, или весу этого тела в воздухе.
Проделав такие же опыты с любыми другими телами, плавающими в разных жидкостях – в воде, спирте, растворе соли, можно убедиться, что если тело плавает в жидкости, то вес вытесненной им жидкости равен весу этого тела в воздухе.
Легко доказать, что если плотность сплошного твердого тела больше плотности жидкости, то тело в такой жидкости тонет. Тело с меньшей плотностью всплывает в этой жидкости. Кусок железа, например, тонет в воде, но всплывает в ртути. Тело же, плотность которого равна плотности жидкости, остается в равновесии внутри жидкости.
Плавает на поверхности воды лед, так как его плотность меньше плотности воды.
Чем меньше плотность тела по сравнению с плотностью жидкости, тем меньшая часть тела погружена в жидкость.
При равных плотностях тела и жидкости тело плавает внутри жидкости на любой глубине.
Две несмешивающиеся жидкости, например вода и керосин, располагаются в сосуде в соответствии со своими плотностями: в нижней части сосуда – более плотная вода (ρ = 1000 кг/м3), сверху – более легкий керосин (ρ = 800 кг/м3).
Средняя плотность живых организмов, населяющих водную среду, мало отличается от плотности воды, поэтому их вес почти полностью уравновешивается архимедовой силой. Благодаря этому водные животные не нуждаются в столь прочных и массивных скелетах, как наземные. По этой же причине эластичны стволы водных растений.
Плавательный пузырь рыбы легко меняет свой объем. Когда рыба с помощью мышц опускается на большую глубину, и давление воды на нее увеличивается, пузырь сжимается, объем тела рыбы уменьшается, и она не выталкивается вверх, а плавает в глубине. Таким образом, рыба может в определенных пределах регулировать глубину своего погружения. Киты регулируют глубину своего погружения за счет уменьшения и увеличения объема легких.
Плавание судов.
Суда, плавающие по рекам, озерам, морям и океанам, построены из разных материалов с различной плотностью. Корпус судов обычно делается из стальных листов. Все внутренние крепления, придающие судам прочность, также изготовляют из металлов. Для постройки судов используют различные материалы, имеющие по сравнению с водой как бóльшие, так и меньшие плотности.
Благодаря чему суда держатся на воде, принимают на борт и перевозят большие грузы?
Опыт с плавающим телом (§ 50) показал, что тело вытесняет своей подводной частью столько воды, что по весу эта вода равна весу тела в воздухе. Это также справедливо и для любого судна.
Вес воды, вытесняемой подводной частью судна, равен весу судна с грузом в воздухе или силе тяжести, действующей на судно с грузом.
Глубина, на которую судно погружается в воду, называется осадкой. Наибольшая допускаемая осадка отмечена на корпусе судна красной линией, называемой ватерлинией (от голланд. ватер – вода).
Вес воды, вытесняемой судном при погружении до ватерлинии, равный силе тяжести, действующей на судно с грузом, называется водоизмещением судна.
В настоящее время для перевозки нефти строятся суда водоизмещением 5 000 000 кН (5 · 106 кН) и больше, т. е. имеющие вместе с грузом массу 500 000 т (5 · 105 т) и более.
Если из водоизмещения вычесть вес самого судна, то мы получим грузоподъемность этого судна. Грузоподъемность показывает вес груза, перевозимого судном.
Судостроение существовало еще в Древнем Египте, в Финикии (считается, что Финикийцы были одними из лучших судостроителей), Древнем Китае.
В России судостроение зародилось на рубеже 17-18 вв. Сооружались главным образом военные корабли, но именно в России были построены первый ледокол, суда с двигателем внутреннего сгорания, атомный ледокол “Арктика”.
Воздухоплавание.

С давних времен люди мечтали о возможности летать над облаками, плавать в воздушном океане, как они плавали по морю. Для воздухоплавания
вначале использовали воздушные шары, которые наполняли или нагретым воздухом, или водородом либо гелием.
Для того, чтобы воздушный шар поднялся в воздух, необходимо, чтобы архимедова сила (выталкивающая) FА, действующая на шар, была больше силы тяжести Fтяж, т. е. FА > Fтяж.
По мере поднятия шара вверх архимедова сила, действующая на него, уменьшается (FА = gρV), так как плотность верхних слоев атмосферы меньше, чем у поверхности Земли. Чтобы подняться выше, с шара сбрасывается специальный балласт (груз) и этим облегчает шар. В конце концов шар достигает своей своей предельной высоты подъема. Для спуска шара из его оболочки при помощи специального клапана выпускается часть газа.
В горизонтальном направлении воздушный шар перемещается только под действием ветра, поэтому он называется аэростатом (от греч аэр – воздух, стато – стоящий). Для исследования верхних слоев атмосферы, стратосферы еще не так давно применялись огромные воздушные шары – стратостаты.
До того как научились строить большие самолеты для перевозки по воздуху пассажиров и грузов, применялись управляемые аэростаты – дирижабли. Они имеют удлиненную форму, под корпусом подвешивается гондола с двигателем, который приводит в движение пропеллер.
Воздушный шар не только сам поднимается вверх, но может поднять и некоторый груз: кабину, людей, приборы. Поэтому для того, чтобы узнать, какой груз может поднять воздушный шар, необходимо определить его подъемную силу.
Пусть, например, в воздух запущен шар объемом 40 м3, наполненный гелием. Масса гелия, заполняющая оболочку шара, будет равна:
mГе = ρГе·V = 0,1890 кг/м3 · 40 м3 = 7,2 кг,
а его вес равен:
PГе = g·mГе ; PГе = 9,8 Н/кг · 7,2 кг = 71 Н.
Выталкивающая же сила (архимедова), действующая на этот шар в воздухе, равна весу воздуха объемом 40 м3, т. е.
FА = g·ρвоздV; FА = 9,8 Н/кг · 1,3 кг/м3 · 40 м3 = 520 Н.
Значит, этот шар может поднять груз весом 520 Н – 71 Н = 449 Н. Это и есть его подъемная сила.
Шар такого же объема, но наполненный водородом, может поднять груз 479 Н. Значит, подъемная сила его больше, чем шара, наполненного гелием. Но все же чаще используют гелий, так как он не горит и поэтому безопаснее. Водород же горючий газ.
Гораздо проще осуществить подъем и спуск шара, наполненного горячим воздухом. Для этого под отверстием, находящимся в нижней части шара, располагается горелка. При помощи газовой горелки можно регулировать температуру воздуха внутри шара, а значит, его плотность и выталкивающую силу. Чтобы шар поднялся выше, достаточно сильнее нагреть воздух в нем, увеличив пламя горелки. При уменьшении пламени горелки температура воздуха в шаре уменьшается, и шар опускается вниз.
Можно подобрать такую температуру шара, при которой вес шара и кабины будет равен выталкивающей силе. Тогда шар повиснет в воздухе, и с него будет легко проводить наблюдения.
По мере развития науки происходили и существенные изменения в воздухоплавательной технике. Появилась возможность использования новых оболочек для аэростатов, которые стали прочными, морозоустойчивыми и легкими.
Достижения в области радиотехники, электроники, автоматики позволили сконструировать беспилотные аэростаты. Эти аэростаты используются для изучения воздушных течений, для географических и медико-биологических исследований в нижних слоях атмосферы.
Ссылки
- Уроки по физике за 7 класс по школьной программе
Содержание:
- Определение и формула давления
- Среднее давление
- Давление идеального газа
- Гидростатическое давление
- Единицы измерения давления
- Примеры решения задач
Определение и формула давления
Определение
Давление – это физическая величина,характеризующая состояние сплошной среды. Оно равно пределу отношения нормальной составляющей силы,
которая действует на участок поверхности тела площади
$Delta S$ к размеру данной площади при
$Delta S rightarrow 0$ . Обозначается давление буквой p. Тогда математической
записью определения давления станет формула:
$$p=lim _{Delta S rightarrow 0} frac{Delta F_{n}}{Delta S}=frac{d F_{n}}{d S}$$
Выражение (1) определяет давление в точке.
Среднее давление
Средним давлением на поверхность называют величину:
$$langle prangle=frac{F_{n}}{S}(2)$$
где Fn – нормальная составляющая силы, которая действует на рассматриваемую поверхность, S – площадь этой поверхности.
Давление идеального газа
Давление идеального газа вычисляют, используя основное уравнение молекулярно – кинетической теории:
$$p=n k T(3)$$
где $n=frac{N}{V}$– концентрация молекул газа
(N – число частиц), k=1,38•10-23 Дж/К – постоянная Больцмана, T – абсолютная температура газа.
Гидростатическое давление
Гидростатическое давление – давление внутри столба жидкости или газа, находится по формуле:
$$p=p_{0}+rho g h(4)$$
где $rho$ – плотность вещества, g=9,8 м/с2 –
ускорение свободного падения, h- высота столба вещества. p0 – внешнее давление на газ или жидкость.
Искривление поверхностного слоя жидкости ведет к возникновению дополнительного давления на жидкость, тогда давление под искривленной
жидкостью определяется как:
$$p=p_{0}^{*}+2 sigma H(5)$$
где $mathrm{P}_{0}^{*}$ –поверхностное натяжение жидкости,p0* – давление под не искривлённым слоем жидкости,
H – средняя кривизна поверхности жидкости, вычисляемая по закону Лапласа:
$$H=frac{1}{2}left(frac{1}{R_{1}}+frac{1}{R_{2}}right)$$
R1, R2 – главные радиусы кривизны.
Единицы измерения давления
Основной единицей измерения давления в системе СИ является: [p]=Па (паскаль)
Внесистемные единицы давления: [p]=мм рт.ст.(миллиметр ртутного столба),мм в.ст (мм водяного столба),атмосфера,бар.
Па= Н/м2 и 1 бар=105 Па.
Техническая атмосфера ~1 бар. Физическая атмосфера 1,01 бар=760 мм рт.ст.. 1 мм рт.ст.=133 Па.
Примеры решения задач
Пример
Задание. Каково давление в море на глубине h=8,5 м, если атмосферное давление равно
p0=105 Па, плотность морской воды равна
$rho$=1,03•103 кг/м3
Решение. Основой для решения задачи служит выражение:
$$p=p_{0}+rho g h(1.1)$$
Все данные в задаче указаны в системе СИ, поэтому можно провести вычисления:
$p=10^{5}+1,03 cdot 10^{3} cdot 9,8 cdot 8,5=1,88 cdot 10^{5}$ (Па).
Ответ. $p=1,88 cdot 10^{5}$ (Па)

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Каково давление струи на неподвижную плоскость, если струя воды ударяет ее под углом
$alpha$ к нормали
плоскости, и упруго отскакивает от нее без изменения скорости? Скорость струи v.
Решение. Сделаем рисунок.
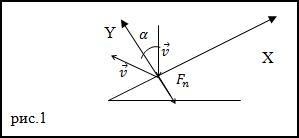
За время $Delta t$ о стенку ударяется масса воды равная:
$$m=l S rho=v Delta t S rho$$
где S – поперечное сечение струи, $rho$ – плотность воды. В соответствии с законом сохранения импульса имеем:
$$F Delta t=m Delta v rightarrow F=frac{m Delta v}{Delta t}(2.2)$$
где F – сила, с которой вода действует на стенку.
Примем за положительное направление нормали внешней к опоре и учитывая, что струя отскакивает от стены без потери скорости, получаем:
$$Delta v=v_{2} cos alpha-left(-v_{1} cos alpharight)=v_{2} cos alpha+v_{1} cos alpha=2 v cos alpha(2.3)$$
Подставим $Delta v$ из (2.3) в выражение (2.2), учтем выражение (2.1) имеем:
$$F=frac{m 2 v cos alpha}{Delta t}=frac{v Delta t S rho 2 v cos alpha}{Delta t}=2 operatorname{Sov}^{2} cos alpha(2.4)$$
В таком случае искомое давление струи на стенку будет равно:
$$p=frac{F_{n}}{S}=2 rho v^{2}$$
Ответ. $p=2 rho v^{2}$
Читать дальше: Формула закона Ома.
Содержание:
Сила давления и единицы давления:
Вы уже знаете, что действие одного тела на другое характеризуют приложенной к нему силой. От чего зависит результат действия этой силы на тело?
Наблюдение 1. Из собственного опыта вы знаете, что очень тяжело идти по глубокому рыхлому снегу, поскольку ноги глубоко проваливаются в нём, а на лыжах передвигаться намного легче, так как проседание снеговой поверхности в этому случае значительно меньше. В обоих случаях вы действуете на снег с одинаковой силой, но площадь поверхности, на которую она распределяется в случае лыж значительно больше, чем в случае обуви, поэтому и деформация снега оказывается разной. Стоя на лыжах, выдавите на каждую единицу площади поверхности снега с силой, меньшей во столько раз, во сколько раз площадь поверхности лыж больше площади подошв обуви.
Наблюдение 2. Легковой автомобиль, в отличие от гусеничного трактора или болотохода, не может проехать по болотистой местности, хотя его вес намного меньше веса трактора. Рассмотрев колёса легкового автомобиля и гусеницы трактора, вы убеждаетесь в том, что площадь поверхности гусениц намного больше, чем колес.
Результат действия силы на поверхность зависит не , только от её значения, но и от площади той поверхности, перпендикулярно к которой она действует.
Убедимся в этом с помощью опытов.
Опыт 1. Заполним стеклянный сосуд песком. На песок поставим столик ножками вверх и на него — гирю массой 2 кг. Результат: столик почти не погрузился в песок (рис. 93, а). Поставим столик ножками на песок и на него — снова гирю массой 2 кг. Результат: ножки стола увязли в песке (рис. 93, б). Возьмём столик с острыми ножками. Поставим его ножками на песок, положив сверху ту же гирю массой 2 кг. Результат: заострённые ножки полностью погрузились в песок (рис. 93, в).

Опыт свидетельствует, что чем меньше площадь опоры столика, тем глубже он погружается в песок под действием одинаковой силы.
Опыт 2. Возьмём два столика. Площадь поверхности ножек одного столика вдвое больше, чем второго. Положим на столики груз, причем на столик с большей площадью поверхности ножек положим вдвое больший груз. Результат действия силы будет одинаковый.
В рассмотренных примерах имела значение сила, действующая перпендикулярно к поверхности тела. Такую силу называют силой давления.
Величину, которая определяется отношением значения силы давления к площади поверхности, на которую она действует, называют давлением.
Давление обозначают малой латинской буквой р. Итак, чтобы определить давление р, нужно силу F , действующую перпендикулярно к поверхности, поделить на площадь этой поверхности S, т. е.
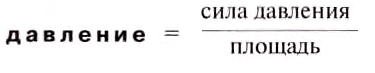
Единицей давления является один паскаль (1 Па), она названа в честь французского учёного Блеза Паскаля. Давление 1 Па создаёт сила давления 1 Н, действующая на поверхность площадью 1 м2, то есть 1 Па = 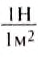 = 1
= 1 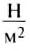 .
.
На практике ещё используют кратные единицы давления: гектопаскаль (гПа), килопаскаль (кПа): 
Зная давление, можно определить силу давления, действующую на поверхность тела. Давление показывает, какая сила давления действует на единицу площади, поэтому эта сила давления равна произведению давления и площади поверхности: .
.
Всем хорошо известно, что во время шитья иглой швеи пользуются напёрстком. Иглу делают очень острой, чтобы умеренной силой пальцев создавать большое давление на ткань и прокалывать её. Но во время нажима пальца на иглу она с такой же силой давит на палец. Конец иглы со стороны ушка делают притуплённым, но во время работы давление на кожу пальца может быть очень большим, достаточным, чтобы ее поранить. Прочный металлический наперсток надежно защищает палец.
Почему подушка мягкая? Почему удобно лежать на перине или на надувном матрасе, а лежать на досках или твёрдой поверхности неудобно ? Оказывается, ощущение мягкости или твёрдости зависит не от свойства материала, а от значения давления на поверхность тела. Сделаем небольшие расчеты.
Будем считать, что масса взрослого человека составляет 60 кг, что равно весу приблизительно 600 Н, а поверхность тела — приблизительно 2 м2. Если человек лежит в кровати на перине, которая прогибается и будто охватывает тело, с ней соприкасается приблизительно четверть всей поверхности его тела, т. е. 0,5 м2 Расчёты по таким данным дают давление 1200 Па. А если человек ляжет на твердую поверхность, то площадь соприкосновения будет составлять около 0,01 м2. Это соответствует давлению 60 000 Па, т. е. давление тела на твёрдую поверхность увеличится в 50 раз, отсюда и неудобства.
В разных областях современной техники приходится решать задачи получения высоких давлений, снижения давления или сохранения его в заданных границах. Проблема давления играет важную роль в транспорте. Дороги и железнодорожные пути должны надежно выдерживать давление разных транспортных средств. Этого достигают, уменьшая вес транспортных средств и увеличивая их площадь опоры. Колеса легкового автомобиля производят на дорогую давление около 300 кПа. Чтобы уменьшить давление на дорогу грузовых автомобилей, их делают многоосными, с колёсами большого диаметра, используют гусеницы. Так, давление, производимое трактором Т-130, вес которого — сотни тысяч ньютонов, равен 27 кПа. Это в 1,5 раза больше давления, которое оказывает на дорогу человек весом 600 Н.
С помощью чрезвычайно тонкого инструмента – жала — оса создаёт давление, соизмеримое с давлением во время взрыва (33 000 000 000 Па).
Кстати:
В Арктике и Антарктике на научных станциях пользуются такими транспортными средствами, как снегоходы «Пингвин» и «Харьковчанка». Снегоход «Харьковчанка» имеет дизельный двигатель мощностью 736 кВт и запас горючего на 1500 км. При массе 35 т он имеет гусеницы шириной 1 м, что даёт ему возможность преодолевать снежную целину, ледовые торосы, крутые склоны. Снегоход имеет утеплённую кабину площадью 25 м2 с мощной отопительной системой, специальной герметичной обшивкой, позволяющей работать даже при морозах ниже – 70 0С. В кабине есть спальные места, радиорубка, рабочая комната, кухня, сушилка, гардероб, санузел. Размеры снегохода: длина – 8,5 м, ширина – 3,5 м, высота – 4,2 м.
Пример №1
С какой целью под головку болта и гайку подкладывают широкие металлические кольца — шайбы, особенно когда скрепляют деревянные детали (рис. 94)?

Ответ: во избежание повреждений деталей уменьшают на них давление за счёт увеличения площади контактной поверхности.
Пример №2
Взрослый человек, у которого площадь подошв обуви равна 450 см2, давит на пол с силой 700 Н. Определите давление человека на пол.
Дано:
F = 700 Н
S = 450 см2 = 0,0450 м2
р — ?
Решение:
Определим давление человека на пол по формуле:
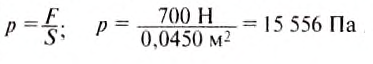
Ответ: давление человека на пол равно 15 556 Па.
Давление жидкостей и газов и закон Паскаля
Опыт 1. Возьмём три цилиндрических сосуда: в один положим деревянный брусок, в другой насыпем какой-либо крупы или песку, а в третий нальём воды (рис. 96).

Деревянный брусок вследствие действия на него силы тяжести будет давить лишь на дно сосуда. Горох будет давить не только на дно, а и на стенки сосуда во всех точках касания горошин. Каждая горошина внутри сжата со всех сторон соседними горошинами и вследствие действия сил упругости сама будет давить во все стороны на горошины. Эти силы давления будут тем больше, чем глубже лежит горошина, т. е. чем больший слой гороха давит на неё сверху.
Вода, налитая в сосуд, вследствие большой подвижности молекул будет давить на дно и стенки сосуда. Каждая частица внутри воды будет сжата со всех сторон соседними частицами и вследствие упругости будет с такой же силой давить на соседние частицы. Эти силы будут тем больше, чем глубже будет находиться частица.
На рис. 97, а изображён прибор, который называют шаром Паскаля. Он имеет в разных местах поверхности маленькие отверстия. К нему присоединена трубка-цилиндр, в которую вставлен поршень. Если набрать в шар воды и нажать на поршень, то увидим, что струйки воды сквозь отверстия бьют во все стороны с одинаковой силой. Это объясняется тем, что поршень давит на поверхность жидкости в трубке. Частицы воды передают давление поршня другим частицам, которые лежат глубже. Таким способом давление поршня передаётся на все частицы воды в шаре. Вследствие этого часть воды выталкивается из шара в виде струек, бьющих изо всех отверстий.
Если шар заполнить дымом, то из всех отверстий шара начнут выходить струи дыма (рис. 97, б).
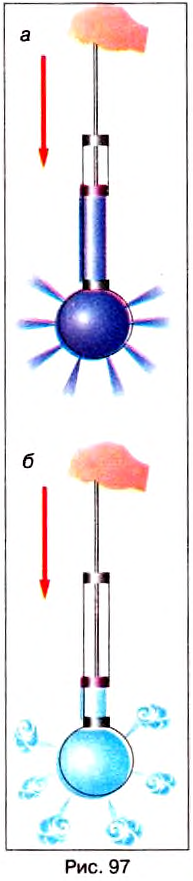
Это подтверждает, что и газы передают давление, оказываемое на них, во все стороны одинаково.
Давление, оказываемое на жидкость или газ внешними силами, передаётся жидкостью или газом одинаково во всех направлениях.
Это утверждение называют законом Паскаля.
На законе Паскаля основывается действие шприца: давление пальца врача на поршень шприца передаётся без изменений жидкости, содержащейся в нём, и лекарство выходят через иглу шприца.
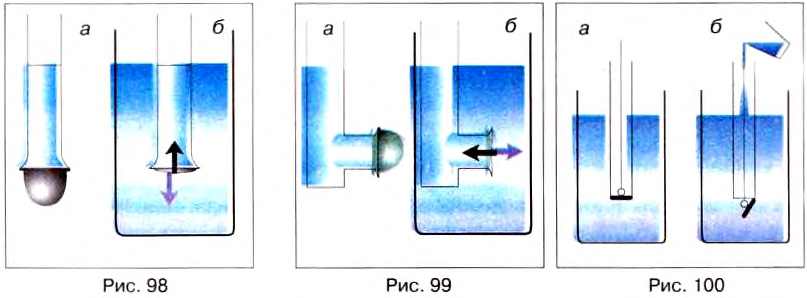
Опыт 2. В стеклянную трубку, нижнее отверстие которой закрыто тонкой резиновой плёнкой, нальём воду (рис. 98, а). Дно трубки прогнётся. Значит, на дно действует сила давления воды. Чем больше наливаем воды, тем более прогибается плёнка. Но каждый раз после того, как резиновое дно прогнулось, вода в трубке находится в равновесии, так как кроме силы тяжести на воду действует сила упругости резиновой плёнки.
Опустим трубку с резиновым дном, в которую налита вода, в более широкий сосуд с водой. Видим, что по мере опускания трубки вниз резиновая плёнка постепенно распрямляется (рис. 98, б). Полное распрямление плёнки показывает, что давление на неё сверху и снизу одинаковое. Значит, в жидкости существует давление, направленное снизу вверх, и на этой глубине оно равно давлению, направленному сверху вниз.
Если выполнить опыт с трубкой, в которой резиновая плёнка закрывает боковое отверстие (рис. 99, а, б), то мы убедимся, что боковое давление жидкости на резиновую плёнку также будет одинаковым с обеих сторон.
Опыт 3. Сосуд, дно которого может отпадать, опускаем в банку с водой (рис. 100, а). Дно при этом плотно прижимается к краям сосуда давлением воды снизу вверх. Потом в сосуд осторожно нальём воды. Когда уровень воды в ней совпадёт с уровнем воды в банке, дно оторвётся от сосуда (рис. 100, б). В момент отрывания на дно давит сверху столб жидкости в сосуде, а снизу – столб воды, находящейся в банке. Эти давления одинаковы по значениям, однако дно отрывается от сосуда под действием силы тяжести.
Согласно закону Паскаля давление внутри жидкости на одном уровне одинаково во всех направлениях. Давление увеличивается с глубиной.
Давление жидкостей, обусловленное силой тяжести, называют гидростатическим.
А как рассчитать давление жидкости на дно и стенки сосуда ?
Чтобы ответить на этот вопрос припомним, что для того, чтобы определить плотность вещества р, нужно массу тела m разделить на его объём V, т. е.: 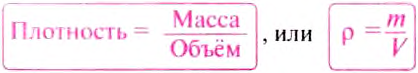
Единицей плотности в СИ является один килограмм на кубический метр 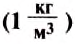 .
.
Из формулы для плотности можно определить массу тела. Для этого нужно плотность вещества р умножить на объем тела V, т. е.: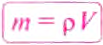
Теперь возвратимся к рис. 98 в опыте 2. Рассчитаем давление, которое создаёт столбик жидкости высотой h на дно цилиндрического сосуда. Мы уже знаем, что давление р равно отношению силы давления F к площади поверхности S, на которую она действует: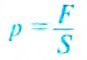
В нашей задаче сила давления равно весу жидкости Р : 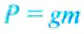
где m – масса жидкости, которую можем определить через плотность жидкости 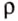 и объём жидкости V :
и объём жидкости V : 
Объём цилиндрического столба жидкости V равен произведению площади дна сосуда S и высоты уровня жидкости над дном h: 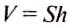 .
.
С учётом этих соотношений формула для давления приобретёт окончательный вид:

Видим, что гидростатическое давление на любой глубине внутри жидкости зависит только от ее плотности 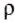 и высоты уровня h: оно равно произведению этих величин и постоянной
и высоты уровня h: оно равно произведению этих величин и постоянной 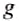 .
.
Гидростатическое давление жидкости не зависит ни от формы сосуда, ни от массы жидкости в сосуде, ни от площади его дна. Согласно закону Паскаля это давление на одном уровне жидкости одинаково действует и на дно, и на стенки сосуда.
Кстати:
В 1648 г. Блез Паскаль провёл интересный опыт. Он вставил в закрытую деревянную бочку, наполненную водой, тонкую трубку и, поднявшись на балкон второго этажа, влил в эту трубку кварту
(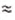 0,9 дм3) воды. Из-за малой толщины трубки вода в ней поднялась на значительную высоту, и давление в бочке увеличилось настолько, что крепления бочки не выдержали, и она треснула.
0,9 дм3) воды. Из-за малой толщины трубки вода в ней поднялась на значительную высоту, и давление в бочке увеличилось настолько, что крепления бочки не выдержали, и она треснула.
Пример №3
Чем объяснить, что вёдра в форме срезанного конуса очень распространены (рис. 101), хотя они менее устойчивы, и из них больше расплёскивается вода по сравнению с ведрами цилиндрической формы и такой же высоты? Кроме того, конусообразные ведра неудобно нести, так как приходится широко расставлять руки.

Ответ: оказывается, в большинстве случаев вёдра выходят из строя из-за того, что у них выпадает дно. Следовательно, прочность дна определяет долговечность ведра. В ведре конической формы площадь дна меньше, чем в ведре цилиндрической формы такой же вместимости, а потому сила давления на дно меньше. Это единственное преимущество конических ведер оправдывает все другие их недостатки.
Пример №4
Наибольшая глубина, на которой учёные с корабля «Витязь» выловили рыбу, составляет 7200 м. Какое давление создаёт вода на этой глубине?
Дано:
h = 7200м
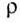 = 1030
= 1030 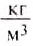
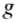 = 9,81
= 9,81 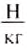
p = ?
Решение:
Давление создаваемое морской водой на глубине, определим по формуле: 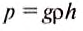 .
.
Подставив значения величин, получим: 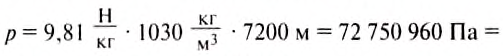
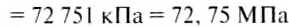 .
.
Ответ:  = 72, 75 МПа.
= 72, 75 МПа.
Давление и закон Архимеда
Почему жители севера для передвижения по снегу используют лыжи? Почему женщина, обутая летом в обувь на шпильках, оставляет на мягком асфальте заметные и глубокие следы? Зачем лезвия ножей время от времени натачивают? для чего у гвоздя есть острие? Попытаемся выяснить ответы на эти вопросы.
Давление твердых тел на поверхность и сила давления
Наблюдаем последствия действия силы: Одно из последствий действия силы — деформация тел, при этом чем большая сила действует на тело, тем больше будет деформация. Деформация зависит и от других факторов, в частности от площади поверхности, по которой распределяется действие силы.
В большинстве случаев чем больше площадь поверхности, на которую действует данная сила, тем меньше будет деформация. Проиллюстрируем это утверждение с помощью простого опыта: поставим деревянный брусок на снег сначала гранью меньшей площади, а затем — гранью большей площади (рис. 22.1).
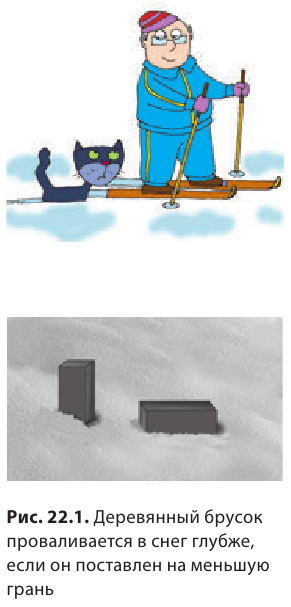
В первом случае снег деформируется сильнее (брусок глубже провалится в снег), хотя в обоих случаях сила, действующая на снег со стороны бруска (то есть вес бруска), одинакова. Можно провести еще один опыт: нажмите с одинаковой небольшой силой на поверхность песка сначала раскрытой ладонью, а затем пальцем — и вы увидите, в каком случае глубина следа будет больше (рис. 22.2).

Определение давления
Для характеристики зависимости результата действия силы от площади поверхности, на которую действует эта сила, используют такое понятие, как давление.
Давление — это физическая величина, которая характеризует результат действия силы и равна отношению силы, действующей перпендикулярно поверхности, к площади этой поверхности: 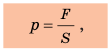 где p — давление; F — сила давления — сила, действующая на поверхность перпендикулярно этой поверхности; S — площадь поверхности. Единица давления в СИ — паскаль (Па); названа в честь французского ученого Блеза Паскаля (рис. 22.3): [p]=Па. 1 Па — это давление, которое создает сила 1 Н, действуя перпендикулярно поверхности площадью
где p — давление; F — сила давления — сила, действующая на поверхность перпендикулярно этой поверхности; S — площадь поверхности. Единица давления в СИ — паскаль (Па); названа в честь французского ученого Блеза Паскаля (рис. 22.3): [p]=Па. 1 Па — это давление, которое создает сила 1 Н, действуя перпендикулярно поверхности площадью 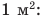
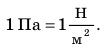 1 Па — небольшое давление (примерно такое давление оказывает на стол альбомный лист для рисования), поэтому чаще используют кратные единицы давления: гектопаскаль (1 гПа = 100 Па), килопаскаль (1 кПа = 1000 Па), мегапаскаль (1 МПа = 1 000 000 Па). Рассмотрите таблицу и подумайте, почему, например, гусеницы трактора оказывают на грунт намного меньшее давление, чем колеса легкового автомобиля.
1 Па — небольшое давление (примерно такое давление оказывает на стол альбомный лист для рисования), поэтому чаще используют кратные единицы давления: гектопаскаль (1 гПа = 100 Па), килопаскаль (1 кПа = 1000 Па), мегапаскаль (1 МПа = 1 000 000 Па). Рассмотрите таблицу и подумайте, почему, например, гусеницы трактора оказывают на грунт намного меньшее давление, чем колеса легкового автомобиля.

Как можно увеличить или уменьшить давление
Из определения давления 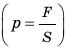 следует, что давление твердых тел можно изменить двумя способами. Первый способ: изменить силу, действующую на поверхность данной площади. С увеличением силы давление увеличивается; с уменьшением силы давление уменьшается. Второй способ: изменить площадь поверхности, на которую действует данная сила давления. Для увеличения давления площадь нужно уменьшить (именно поэтому натачивают инструменты — ножницы, ножи, шила и т. п.) (рис. 22.4). Для уменьшения давления площадь поверхности нужно увеличить. Рассмотрите рис. 22.5 и объясните, почему человек оказывает на снег большее давление, чем тяжелый вездеход.
следует, что давление твердых тел можно изменить двумя способами. Первый способ: изменить силу, действующую на поверхность данной площади. С увеличением силы давление увеличивается; с уменьшением силы давление уменьшается. Второй способ: изменить площадь поверхности, на которую действует данная сила давления. Для увеличения давления площадь нужно уменьшить (именно поэтому натачивают инструменты — ножницы, ножи, шила и т. п.) (рис. 22.4). Для уменьшения давления площадь поверхности нужно увеличить. Рассмотрите рис. 22.5 и объясните, почему человек оказывает на снег большее давление, чем тяжелый вездеход.


Пример №5
Сравните давления, которые оказывают на поверхность снега юные спортсмены — турист и лыжник. Масса каждого из них вместе со снаряжением равна 63 кг. Площадь подошвы ботинка туриста — приблизительно 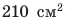 , площадь лыжи — приблизительно
, площадь лыжи — приблизительно 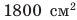 . Анализ физической проблемы. Давление, которое оказывает каждый спортсмен, определяется силой давления и площадью, на которую он опирается. В обоих случаях сила давления —это вес спортсмена; он распределяется на две подошвы или две лыжи. Будем считать, что на обе подошвы (лыжи) нагрузка распределяется равномерно. Задачу будем решать в единицах СИ.
. Анализ физической проблемы. Давление, которое оказывает каждый спортсмен, определяется силой давления и площадью, на которую он опирается. В обоих случаях сила давления —это вес спортсмена; он распределяется на две подошвы или две лыжи. Будем считать, что на обе подошвы (лыжи) нагрузка распределяется равномерно. Задачу будем решать в единицах СИ.
Дано:
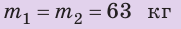 ,
,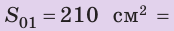
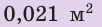 ,
,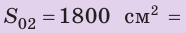
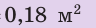 ,
,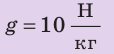
Найти:
 ,
,
Решение:
По определению давления: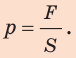
Здесь 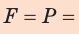
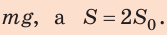 Подставив выражения для F и S в формулу давления, имеем:
Подставив выражения для F и S в формулу давления, имеем: 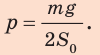 Проверим единицу, найдем значения искомых величин:
Проверим единицу, найдем значения искомых величин: 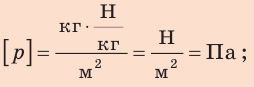 для туриста:
для туриста: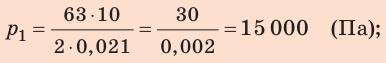
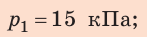
для лыжника:
Анализ результатов. Давление, создаваемое туристом, приблизительно в 8,6 раза больше давления, создаваемого лыжником. Это реальный результат, ведь при равных силах большее давление создает та сила, которая действует на меньшую площадь.
Ответ: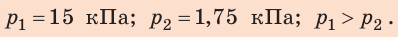
Итоги:
Давление p — это физическая величина, которая характеризует результат действия силы и равна отношению силы, действующей перпендикулярно поверхности, к площади этой поверхности: 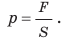 . Единица давления в СИ — паскаль
. Единица давления в СИ — паскаль 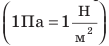 . Для увеличения давления следует уменьшить площадь поверхности, на которую действует сила давления, или увеличить силу давления. Для уменьшения давления нужно увеличить площадь поверхности, на которую действует сила давления, или уменьшить силу давления.
. Для увеличения давления следует уменьшить площадь поверхности, на которую действует сила давления, или увеличить силу давления. Для уменьшения давления нужно увеличить площадь поверхности, на которую действует сила давления, или уменьшить силу давления.
Давление газов и жидкостей. Закон паскаля
Почему при надувании резинового воздушного шарика увеличивается его объем? ответ понятен: в шарике становится больше воздуха. а можно ли увеличить объем шарика без того, чтобы его надувать? Почему налитая в сосуд жидкость создает давление не только на дно сосуда, но и на его боковые поверхности? Почему водитель, нажимая на тормоз, может остановить тяжелый автомобиль? Попробуем «разгадать» эти загадки.

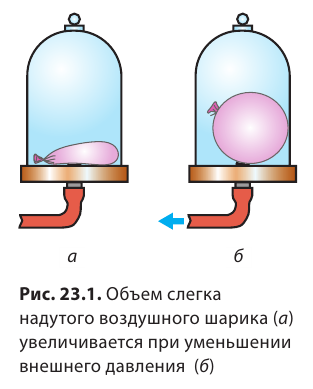
Почему газы создают давление
Положим слегка надутый завязанный воздушный шарик под колокол воздушного насоса (рис. 23.1, а). Если из под колокола откачивать воздух, объем шарика будет увеличиваться (рис. 23.1, б). Почему это происходит?
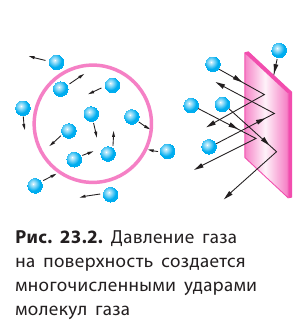
И снаружи шарика, и внутри него находится воздух (газ). Газ состоит из частиц (атомов и молекул), которые непрерывно движутся во всех направлениях и «бомбардируют» резиновую пленку, создавая на нее давление (рис. 23.2). Понятно, что сила удара одной частицы очень мала. Однако частиц в газе очень много — всего за 1 секунду количество их ударов по поверхности пленки таково, что для его записи требуется число с 23 нулями!
Поэтому общая сила, с которой ударяет такое огромное количество частиц, является значительной. Воздух внутри и снаружи шарика оказывает давление соответственно на внутреннюю и внешнюю поверхности резиновой пленки.
Если эти давления одинаковы, резиновая пленка не растягивается. А вот если давление внутри шарика становится больше внешнего давления, то шарик увеличивает свой объем. Надеемся, теперь вы сможете объяснить, почему воздушный шарик раздувается и тогда, когда мы его надуваем, и тогда, когда откачиваем воздух снаружи шарика.
- Заказать решение задач по физике
От чего зависит давление газов
Давление газа создается ударами его частиц, поэтому увеличение как количества ударов, так и силы ударов приводит к увеличению давления газа. Следовательно, давление газов можно увеличить двумя способами. Первый способ — увеличить плотность газа 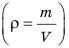 . Для этого можно добавить газ в сосуд (увеличить массу m газа), а можно уменьшить объем V самого сосуда (рис. 23.3)
. Для этого можно добавить газ в сосуд (увеличить массу m газа), а можно уменьшить объем V самого сосуда (рис. 23.3)
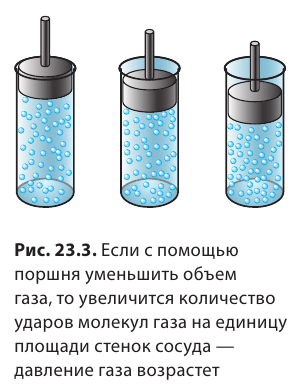
Второй способ — увеличить температуру газа. Чем выше температура газа, тем быстрее движутся его частицы. Удары частиц о стенки сосуда становятся чаще, сила их ударов возрастает, и в результате давление газа в сосуде увеличивается. Соответственно уменьшение давления газа будет происходить при уменьшении плотности или температуры газа.
Исследование давления жидкостей
В отличие от твердых тел жидкости легко изменяют свою форму — они приобретают форму того сосуда, в котором находятся, другими словами, жидкости текучи. Именно поэтому жидкости оказывают давление и на дно, и на боковые стенки сосуда, в котором находятся (в отличие от твердых тел, которые оказывают давление только на ту часть поверхности, на которую опираются). Если в боковой стенке сосуда, заполненного жидкостью, сделать отверстия, то жидкость польется через них (рис. 23.4).

Следствием текучести жидкостей является также то, что на любое погруженное в жидкость тело жидкость давит со всех сторон.
Закон Паскаля
Благодаря своей текучести жидкость способна передавать давление по всему объему сосуда, в котором находится. Сделав иглой небольшие отверстия в полиэтиленовом пакете, наберем в пакет воду и завяжем. Нажмем на пакет — вода будет выливаться из всех отверстий (рис. 23.5).

Аналогичный эксперимент можно провести с воздухом или другим газом (рис. 23.6). Опираясь на подобные опыты, французский физик Б. Паскаль открыл закон, который сейчас называется закон Паскаля: давление, оказываемое на неподвижную жидкость, передается жидкостью одинаково во всех направлениях. То же самое можно сказать о газах.
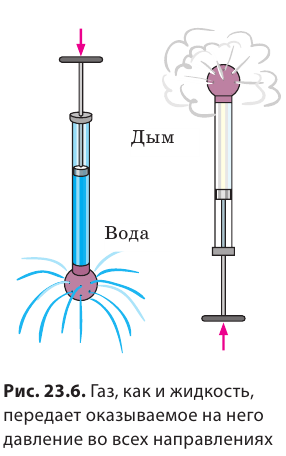
Применяем закон Паскаля:
Свойство жидкостей и газов передавать давление во всех направлениях мы наблюдаем в повседневной жизни; это свойство широко используют в технике. Благодаря ему мы имеем возможность слышать, ведь воздух передает звук; работает наша сердечнососудистая система, ведь несмотря на то, что кровеносные сосуды имеют большое количество изгибов, давление, создаваемое сердцем, передается во все части тела. На законе Паскаля основана система торможения многих транспортных средств, действие домкратов, насосов и других гидравлических машин. Рассмотрим принцип действия гидравлических машин на примере гидравлического пресса, который применяют для прессования фанеры и картона, отжима растительных масел, изготовления деталей машин и механизмов и т. п.
Гидравлический пресс — это простейшая гидравлическая машина, которую используют для создания больших сил давления. Гидравлический пресс состоит из двух соединенных между собой цилиндров разного диаметра, заполненных рабочей жидкостью (чаще машинным маслом) и закрытых подвижными поршнями (см. рис. 23.7). Если к поршню меньшего цилиндра приложить силу 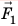 (см. рис. 23.7, б), то эта сила создаст на поверхность жидкости некоторое дополнительное давление p:
(см. рис. 23.7, б), то эта сила создаст на поверхность жидкости некоторое дополнительное давление p: 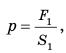 где
где 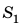 — площадь меньшего поршня. Согласно закону Паскаля это дополнительное давление будет передаваться во все точки жидкости, заполняющей сообщающиеся цилиндры. Следовательно, жидкость начнет давить на поршень большего цилиндра с некоторой силой
— площадь меньшего поршня. Согласно закону Паскаля это дополнительное давление будет передаваться во все точки жидкости, заполняющей сообщающиеся цилиндры. Следовательно, жидкость начнет давить на поршень большего цилиндра с некоторой силой 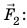
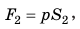 где
где 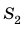 — площадь большего поршня; р — дополнительное давление.
— площадь большего поршня; р — дополнительное давление.
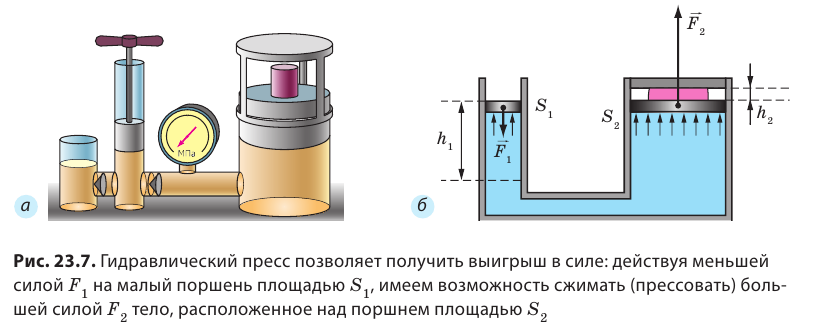
Поскольку 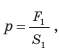 имеем:
имеем: 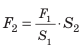 , то есть
, то есть 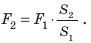 сила давления, которая действует со стороны жидкости на большой поршень, больше силы, которая действует на малый поршень, во столько раз, во сколько раз площадь большого поршня больше площади малого:
сила давления, которая действует со стороны жидкости на большой поршень, больше силы, которая действует на малый поршень, во столько раз, во сколько раз площадь большого поршня больше площади малого: 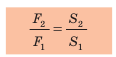 Отношение
Отношение 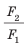 — это выигрыш в силе. Гидравлический пресс позволяет получить значительный выигрыш в силе: чем больше будут различаться между собой площади поршней, тем большим будет выигрыш в силе (рис. 23.7). По такому принципу работают и другие гидравлические инструменты и устройства. Так, гидравлический подъемник позволяет, приложив небольшую силу, поднять тяжелый автомобиль (рис. 23.8), гидравлический тормоз позволяет остановить автомобиль, приложив незначительную силу давления ноги, и т. д. Опираясь на рис. 23.8, попробуйте разобраться, как работает гидравлический подъемник.
— это выигрыш в силе. Гидравлический пресс позволяет получить значительный выигрыш в силе: чем больше будут различаться между собой площади поршней, тем большим будет выигрыш в силе (рис. 23.7). По такому принципу работают и другие гидравлические инструменты и устройства. Так, гидравлический подъемник позволяет, приложив небольшую силу, поднять тяжелый автомобиль (рис. 23.8), гидравлический тормоз позволяет остановить автомобиль, приложив незначительную силу давления ноги, и т. д. Опираясь на рис. 23.8, попробуйте разобраться, как работает гидравлический подъемник.
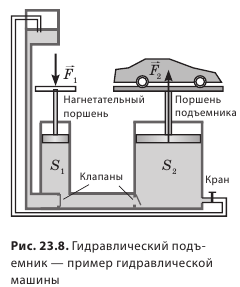
Итоги:
Газ оказывает давление на поверхность в результате многочисленных ударов об эту поверхность частиц газа. Давление газа возрастает при увеличении плотности или температуры газа и уменьшается при уменьшении плотности или температуры газа. Вследствие своей текучести жидкость оказывает давление на дно и боковые стенки сосуда, а также на любое тело, погруженное в данную жидкость. Давление, оказываемое на неподвижную жидкость, передается этой жидкостью одинаково во всех направлениях (закон Паскаля). Свойство жидкостей передавать давление одинаково во всех направлениях положено в основу действия гидравлических машин. Сила, действующая со стороны жидкости на большой поршень гидравлической машины, больше силы, действующей на малый поршень, во столько раз, во сколько раз площадь большого поршня больше площади малого: 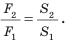
Гидростатическое давление
На рис. 24.1 изображен современник Блеза Паскаля, стоящий на кожаной подушке, заполненной водой. с подушкой соединена открытая сверху трубка — ее исследователь держит в руках. Почему доска, на которой стоит человек, не сжимает подушку полностью и не вытесняет через трубку всю воду наружу?
Получаем формулу для расчета:
Гидростатического давления Вы уже знаете, что в результате притяжения к Земле и благодаря собственной текучести жидкость оказывает давление как на дно, так и на стенки сосуда, в котором содержится. Жидкость оказывает давление и на любое погруженное в нее тело. Давление неподвижной жидкости называют гидростатическим давлением.

Определим гидростатическое давление на дно сосуда. Чтобы упростить расчеты, возьмем цилиндрический сосуд с площадью дна S. Пусть в сосуд налита жидкость плотностью ρ, а высота столба жидкости в сосуде — h (рис. 24.2).
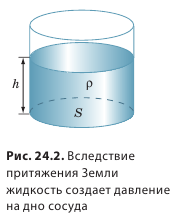
Чтобы вычислить давление, которое создает жидкость на дно сосуда, следует силу F, действующую на дно, разделить на площадь S дна: 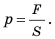 В данном случае сила F, создающая давление на дно сосуда, — это вес P жидкости. Поскольку жидкость в сосуде неподвижна, вес жидкости равен произведению массы m жидкости на ускорение свободного падения g:
В данном случае сила F, создающая давление на дно сосуда, — это вес P жидкости. Поскольку жидкость в сосуде неподвижна, вес жидкости равен произведению массы m жидкости на ускорение свободного падения g: 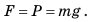 Массу жидкости найдем через объем и плотность жидкости: m=ρ ;V объем налитой в сосуд жидкости — через высоту h столба жидкости и площадь S дна сосуда: V= Sh. Следовательно, массу жидкости можно найти по формуле:
Массу жидкости найдем через объем и плотность жидкости: m=ρ ;V объем налитой в сосуд жидкости — через высоту h столба жидкости и площадь S дна сосуда: V= Sh. Следовательно, массу жидкости можно найти по формуле: 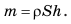 Подставив последовательно выражения для F и m в формулу давления, получим:
Подставив последовательно выражения для F и m в формулу давления, получим:  Итак, имеем формулу для расчета гидростатического давления — давления, которое создает неподвижная жидкость:
Итак, имеем формулу для расчета гидростатического давления — давления, которое создает неподвижная жидкость: 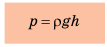 Как видим, гидростатическое давление зависит только от плотности жидкости и высоты столба жидкости в сосуде.
Как видим, гидростатическое давление зависит только от плотности жидкости и высоты столба жидкости в сосуде.
Проводим исследования и делаем выводы:
Зависимость гидростатического давления от высоты столба жидкости впервые продемонстрировал Блез Паскаль. Взяв бочку, до краев заполненную водой, исследователь герметично закрыл ее крышкой со вставленной длинной тонкой трубкой. Поднявшись на балкон второго этажа жилого дома, Паскаль вылил в трубку всего один стакан воды. Вода заполнила всю трубку и создала на стенки и дно бочки такое огромное давление, что в боковых стенках бочки появились щели (рис. 24.3).

Обратите внимание! Согласно закону Паскаля давление жидкости передается во всех направлениях, а значит, по формуле 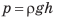 можно также определить давление, которое создает слой жидкости высотой h на любое тело, погруженное в эту жидкость на данную глубину, а также давление на стенки сосуда. Из закона Паскаля и формулы гидростатического давления также следует, что давление внутри неподвижной однородной жидкости на одном уровне* одинаково. Рассмотрите рис. 24.4. Казалось бы, давление воды на дне подводной пещеры меньше, чем на дне открытого моря. Однако, если бы это действительно было так, вследствие большего давления вода из моря хлынула бы в пещеру. Но этого не происходит.
можно также определить давление, которое создает слой жидкости высотой h на любое тело, погруженное в эту жидкость на данную глубину, а также давление на стенки сосуда. Из закона Паскаля и формулы гидростатического давления также следует, что давление внутри неподвижной однородной жидкости на одном уровне* одинаково. Рассмотрите рис. 24.4. Казалось бы, давление воды на дне подводной пещеры меньше, чем на дне открытого моря. Однако, если бы это действительно было так, вследствие большего давления вода из моря хлынула бы в пещеру. Но этого не происходит.

Пример №6
На дне бассейна расположено круглое отверстие, закрытое пробкой радиусом 5 см. Какую силу нужно приложить к пробке, чтобы вынуть ее из отверстия, если высота воды в бассейне 2 м? Массой пробки и силой трения между пробкой и отверстием пренебречь. Анализ физической проблемы. Вынуть пробку мешает сила давления воды в бассейне. Массу пробки и силу трения учитывать не нужно, поэтому сила, необходимая для того, чтобы вынуть пробку из отверстия, по значению должна быть не меньше, чем сила гидростатического давления воды на пробку: 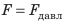 (см. рисунок).
(см. рисунок).
Уровнем называют любую горизонтальную поверхность.
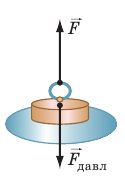
Дано:
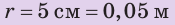 ,
,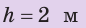 ,
,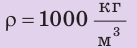 ,
,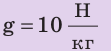
найти:

Решение:
По определению давления:
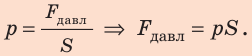
Здесь 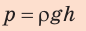 — гидростатическое давление;
— гидростатическое давление; 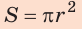 — площадь круга. Подставив выражения для p и S в формулу для
— площадь круга. Подставив выражения для p и S в формулу для 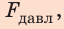 получим:
получим:
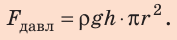
Так как 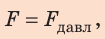 окончательно имеем:
окончательно имеем: 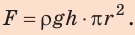 Проверим единицу, найдем значение искомой величины:
Проверим единицу, найдем значение искомой величины:
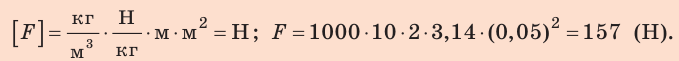
Ответ: следует приложить силу не менее чем 157 Н.
Итоги:
В результате притяжения к Земле жидкости создают давление на дно и стенки сосудов, а также на любое погруженное в них тело. Давление p неподвижной жидкости называют гидростатическим давлением — оно зависит только от плотности ρ жидкости и высоты h столба жидкости. Гидростатическое давление вычисляют по формуле 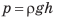 . Давление внутри неподвижной однородной жидкости на одном уровне одинаково.
. Давление внутри неподвижной однородной жидкости на одном уровне одинаково.
Атмосферное давление и его измерение. Барометры
Когда мы делаем глоток чая, то вряд ли размышляем над физикой этого процесса. При этом глотание, как и многие другие процессы, происходит благодаря давлению воздуха вокруг нас — атмосферному давлению. откроем для себя некоторые важные свойства атмосферного давления и научимся его измерять.
Что такое атмосфера
Вы хорошо знаете, что наша планета Земля окружена воздушной оболочкой, которую называют атмосферой (в переводе с греческого — «пар» и «сфера») (рис. 25.1). Почему же существует воздушная оболочка Земли? Воздух состоит из молекул и атомов. Молекулы и атомы имеют массу, поэтому они притягиваются к Земле благодаря действию силы тяжести. Все огромное количество молекул газов, составляющих атмосферу, находится в непрерывном хаотическом движении — они все время сталкиваются, отскакивают друг от друга, изменяют значение и направление скорости своего движения… Именно поэтому они не «падают» на Землю, а находятся в пространстве вблизи нее.

По подсчетам, атмосфера Земли имеет массу около  . Под действием силы тяжести верхние слои атмосферы давят на нижние, поэтому воздушный слой непосредственно у поверхности Земли сжат больше и, согласно закону Паскаля, создает давление на поверхность Земли и на все тела вблизи нее. Это и есть атмосферное давление p(атм .) Атмосферное давление обусловливает существование всасывания — поднятия жидкости за поршнем (в насосах, шприцах и т. п.) (рис. 25.2). Если поднимать поршень, то атмосферное давление, действуя на свободную поверхность жидкости в сосуде, будет нагнетать жидкость вверх, в пустоту под поршнем. Со стороны все выглядит так, будто жидкость поднимается за поршнем сама по себе.
. Под действием силы тяжести верхние слои атмосферы давят на нижние, поэтому воздушный слой непосредственно у поверхности Земли сжат больше и, согласно закону Паскаля, создает давление на поверхность Земли и на все тела вблизи нее. Это и есть атмосферное давление p(атм .) Атмосферное давление обусловливает существование всасывания — поднятия жидкости за поршнем (в насосах, шприцах и т. п.) (рис. 25.2). Если поднимать поршень, то атмосферное давление, действуя на свободную поверхность жидкости в сосуде, будет нагнетать жидкость вверх, в пустоту под поршнем. Со стороны все выглядит так, будто жидкость поднимается за поршнем сама по себе.
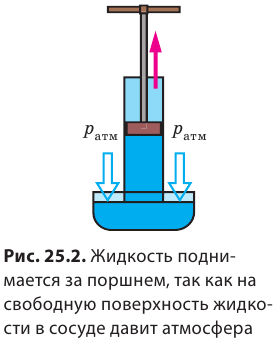
Кстати, долгое время поднятие жидкости за поршнем, движущимся вверх, приводилось как одно из доказательств известного принципа Аристотеля «Природа боится пустоты». Однако в середине XVII в. при строительстве фонтанов во Флоренции столкнулись с непонятным явлением: оказалось, что вода, которая всасывается насосами, не поднимается выше 10,3 м (рис. 25.3). Галилео Галилей предложил разобраться в этом своим ученикам — Эванджелисте Торричелли (1608–1647) и Винченцо Вивиани (1622–1703). Разбираясь с данной проблемой, Э. Торричелли впервые доказал существование атмосферного давления.
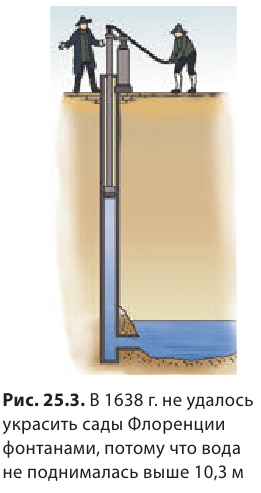
Измерение атмосферное давления
Для удобства проведения опытов Э. Торричелли догадался заменить воду жидкостью с намного большей плотностью. Стеклянную трубку длиной около метра, запаянную с одного конца, ученый доверху наполнил ртутью. Затем, плотно закрыв отверстие, он перевернул трубку, опустил ее в чашу с ртутью и открыл отверстие — часть жидкости из трубки вылилась в чашу. В трубке остался столб ртути высотой приблизительно 760 мм, а над ртутью образовалась пустота (рис. 25.4). Проведя множество опытов, Торричелли установил: высота столба ртути, остающейся в трубке (760 мм), не зависит ни от длины трубки, ни от ее диаметра, — эта высота немного изменяется только в зависимости от погоды.
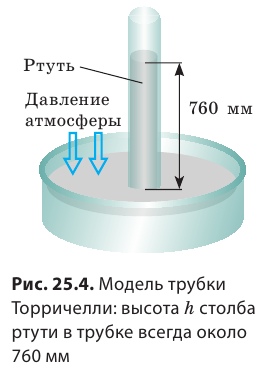
Торричелли сумел также объяснить, почему высота столба ртути имеет именно такую высоту. Однородная жидкость в трубке и чаше неподвижна. Значит, согласно закону Паскаля давление на поверхность ртути со стороны атмосферы и гидростатическое давление столба ртути в трубке одинаковы. То есть давление столба ртути высотой 760 мм равно атмосферному давлению.давление, которое создает столб ртути высотой 760 мм, называют нормальным атмосферным давлением: 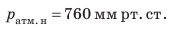 В данном случае в качестве единицы атмосферного давления взят один миллиметр ртутного столба (1 мм рт. ст.). Выразим нормальное атмосферное давление в единицах СИ — паскалях. Из материала 4 вы знаете, что гидростатическое давление вычисляют по формуле: p=ρ hg. Учитывая, что плотность ртути
В данном случае в качестве единицы атмосферного давления взят один миллиметр ртутного столба (1 мм рт. ст.). Выразим нормальное атмосферное давление в единицах СИ — паскалях. Из материала 4 вы знаете, что гидростатическое давление вычисляют по формуле: p=ρ hg. Учитывая, что плотность ртути 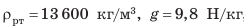 , а высота столба ртути h = 0,76 м, имеем:
, а высота столба ртути h = 0,76 м, имеем: 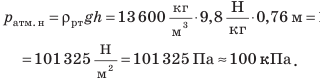 Обратите внимание: выражая атмосферное давление в паскалях, для расчетов следует брать
Обратите внимание: выражая атмосферное давление в паскалях, для расчетов следует брать  В физике и технике также используют внесистемную единицу атмосферного давления — физическую атмосферу (1 атм). Одна физическая атмосфера равна нормальному атмосферному давлению: 1атм ≈100кПа.
В физике и технике также используют внесистемную единицу атмосферного давления — физическую атмосферу (1 атм). Одна физическая атмосфера равна нормальному атмосферному давлению: 1атм ≈100кПа.
Конструкция барометра-анероида
Если к трубке Торричелли присоединить вертикальную шкалу (линейку), то получим простейший барометр — прибор для измерения атмосферного давления. Действие такого барометра основано на том, что столб жидкости прекращает подниматься (опускаться) как только гидростатическое давление столба жидкости становится равным атмосферному давлению. Барометр Торричелли — достаточно точный прибор, однако большой размер, ядовитые пары ртути и стеклянная трубка делают его неудобным для повседневного использования. Сейчас широко применяют барометры анероиды — приборы для измерения атмосферного давления, работающие без помощи жидкости (рис. 25.5). Главная часть барометраанероида — легкая и упругая пустая металлическая коробочка 1 с гофрированной (ребристой) поверхностью. Воздух в коробочке находится при сниженном давлении. К стенке коробочки прикреплена стрелка 2, насаженная на ось 3. Конец стрелки передвигается по шкале 4, размеченной в миллиметрах ртутного столба или паскалях. Все детали барометра размещены в корпусе, передняя часть которого закрыта стеклом. Изменение атмосферного давления вызывает изменение силы, сжимающей стенки коробочки. Соответственно изменяется изгиб стенок коробочки. Изгиб стенок передается стрелке и вызывает ее движение.
Барометры анероиды более удобны в использовании, чем ртутные приборы: они легкие, компактные и безопасные.
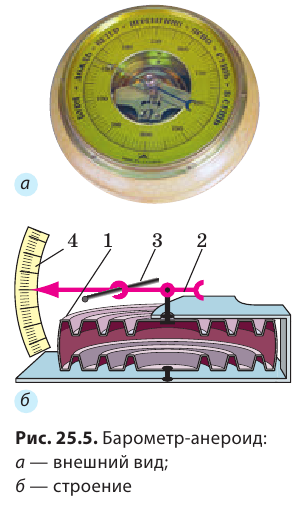
Определение зависимости атмосферного давления от погоды и высоты
Наблюдая за барометром, можно легко прогнозировать изменение погоды. Например, перед ненастьем атмосферное давление обычно падает. Показания барометра зависят не только от погоды, а и от высоты над уровнем моря. Чем выше место наблюдения над уровнем моря, тем меньше атмосферное давление. Вблизи поверхности Земли через каждые 11 м высоты атмосферное давление уменьшается приблизительно на 1 мм рт. ст. Поскольку атмосферное давление зависит от высоты, барометр можно проградуировать таким образом, чтобы по давлению воздуха определять высоту. Так был изобретен альтиметр — прибор для измерения высоты (рис. 25.6).

Итоги:
Воздух имеет массу. Из-за притяжения Земли верхние слои атмосферы (воздушной оболочки Земли) давят на нижние. Давление воздуха на поверхность Земли и на все тела вблизи нее называют атмосферным давлением. Точное измерение атмосферного давления обеспечивает ртутный барометр (барометр Торричелли). Давление столба ртути высотой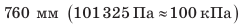 — это нормальное атмосферное давление. На практике используют барометры анероиды благодаря их удобству, небольшим размерам и безопасности. С помощью барометров можно прогнозировать изменение погоды и определять высоту: атмосферное давление уменьшается перед ненастьем, а также с высотой.
— это нормальное атмосферное давление. На практике используют барометры анероиды благодаря их удобству, небольшим размерам и безопасности. С помощью барометров можно прогнозировать изменение погоды и определять высоту: атмосферное давление уменьшается перед ненастьем, а также с высотой.
- Механическое давление в физике
- Столкновения в физике
- Рычаг в физике
- Блоки в физике
- Вес тела в физике
- Закон всемирного тяготения
- Свободное падение тела
- Равнодействующая сила и движение тела под действием нескольких сил
| давление | |
|---|---|
 |
|
| Размерность | L−1MT−2 |
| Единицы измерения | |
| СИ | Па |
| СГС | дин·см-2 |
| Примечания | |
| скалярная величина |
Давле́ние на поверхность — интенсивная физическая величина, численно равная силе, действующей на единицу площади поверхности перпендикулярно этой поверхности. В данной точке давление определяется как отношение нормальной составляющей силы 

Среднее давление по всей поверхности есть отношение нормальной составляющей силы 

Давле́ние сплошной среды — скалярная интенсивная физическая величина; характеризует состояние среды и является диагональной компонентой тензора напряжений. В простейшем случае изотропной равновесной неподвижной среды не зависит от ориентации. Для обозначения давления обычно используется символ 
В соответствии с рекомендациями ИЮПАК давление в классической механике рекомендуется обозначать как 

Давление идеального газа (вообще говоря, системы пренебрежимо мало взаимодействующих частиц) на стенку ищется как

где 


где 


Единицы измерения[править | править код]
В Международной системе единиц (СИ) измеряется в паскалях (русское обозначение: Па; международное: Pa). Паскаль равен давлению, вызываемому силой, равной одному ньютону, равномерно распределённой по нормальной к ней поверхности площадью один квадратный метр.
Наряду с паскалем в Российской Федерации допущены к использованию в качестве внесистемных единиц измерения давления следующие единицы[3]:
- бар;
- килограмм-сила на квадратный сантиметр;
- миллиметр водяного столба;
- метр водяного столба;
- атмосфера техническая;
- миллиметр ртутного столба.
При этом наименования и обозначения данных единиц с дольными и кратными приставками СИ не применяются. Существовавшее ранее ограничение срока действия допуска указанных единиц в августе 2015 году было отменено[4].
Кроме того, на практике используются также единицы торр и физическая атмосфера.
| Паскаль (Pa, Па) |
Бар (bar, бар) |
Техническая атмосфера (at, ат) |
Физическая атмосфера (atm, атм) |
Миллиметр ртутного столба (мм рт. ст., mm Hg, Torr, торр) |
Миллиметр водяного столба (мм вод. ст., mm H2O) |
Фунт-сила на квадратный дюйм (psi) |
|
|---|---|---|---|---|---|---|---|
| 1 Па | 1 | 10−5 | 1,01972⋅10−5 | 9,8692⋅10−6 | 7,5006⋅10−3 | 0,101972 | 1,4504⋅10−4 |
| 1 бар | 105 | 1 | 1,01972 | 0,98692 | 750,06 | 10197,2 | 14,504 |
| 1 ат | 98066,5 | 0,980665 | 1 | 0,96784 | 735,56 | 104 | 14,223 |
| 1 атм | 101325 | 1,01325 | 1,03323 | 1 | 760 | 10332,3 | 14,696 |
| 1 мм рт. ст. | 133,322 | 1,3332⋅10−3 | 1,3595⋅10−3 | 1,3158⋅10−3 | 1 | 13,595 | 0,019337 |
| 1 мм вод. ст. | 9,80665 | 9,80665⋅10−5 | 10-4 | 9,6784⋅10-5 | 0,073556 | 1 | 1,4223⋅10-3 |
| 1 psi | 6894,76 | 0,068948 | 0,070307 | 0,068046 | 51,715 | 703,07 | 1 |
Измерение давления газов и жидкостей выполняется с помощью манометров, дифманометров, вакуумметров, датчиков давления, атмосферного давления — барометрами, артериального давления — сфигмоманометрами.
Примечания[править | править код]
- ↑ ДАВЛЕ́НИЕ : [арх. 25 февраля 2017] / В. Н. Кузнецов // Григорьев — Динамика. — М. : Большая российская энциклопедия, 2007. — С. 217. — (Большая российская энциклопедия : [в 35 т.] / гл. ред. Ю. С. Осипов ; 2004—2017, т. 8). — ISBN 978-5-85270-338-5.
- ↑ англ. E. R. Cohen et al, «Quantities, Units and Symbols in Physical Chemistry», IUPAC Green Book, 3rd Edition, 2nd Printing, IUPAC & RSC Publishing, Cambridge (2008). — p. 14.
- ↑ Положение о единицах величин, допускаемых к применению в Российской Федерации. Архивировано 2 ноября 2013 года. Утверждено Постановлением Правительства РФ от 31 октября 2009 г. N 879.
- ↑ Постановление Правительства РФ от 15.08.2015 № 847 «О внесении изменений в приложение № 3 к Положению о единицах величин, допускаемых к применению в Российской Федерации». Архивировано 4 марта 2016 года.

Никому не нравится быть под давлением. И не важно, под каким. Об этом спела еще группа Queen вместе с Дэвидом Боуи в своем знаменитом сингле “Under pressure”. Что такое давление? Как понять давление? В чем оно измеряется, какими приборами и методами, куда направлено и на что давит. Ответы на эти и другие вопросы – в нашей статье про давление в физике и не только.
Давление в физике
Если преподаватель давит на вас, задавая каверзные задачки, мы сделаем так, чтобы вы смогли верно на них ответить. Ведь понимание самой сути вещей – ключ к успеху! Итак, что такое давление в физике?
По определению:
Давление – скалярная физическая величина, равная силе, действующей на единицу площади поверхности.
В международной системе СИ измеряется в Паскалях и обозначается буквой p. Единица измерения давления – 1 Паскаль. Русское обозначение – Па, международное – Pa.
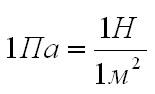
Согласно определению, чтобы найти давление, нужно силу разделить на площадь.
Любая жидкость или газ, помещенный в сосуд, оказывает на стенки сосуда давление. Например, борщ в кастрюле действует на ее дно и стены с некоторым давлением. Формула определения давления жидкости:
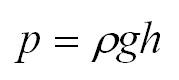
где g – ускорение свободного падения в гравитационном поле земли, h – высота столба борща в кастрюле, греческая буква «ро» – плотность борща.
Одно из важнейших свойств жидкостей – изотропность. Это значит, что по закону Паскаля во всех направлениях жидкости производимое ею давление передается одинаково. Кстати, подробнее о жидкостях, их свойствах и движении читайте в нашем материале про уравнение Бернулли.
Наиболее распространенный в быту прибор для определения давления – барометр. Но в чем измеряют давление? Кроме паскаля существуют и другие внесистемные единицы измерения:
- атмосфера;
- миллиметр ртутного столба;
- миллиметр водяного столба;
- метр водяного столба;
- килограмм-сила.
В зависимости от контекста применяются разные внесистемные единицы.
Например, когда вы слушаете или читаете прогноз погоды, там и речи не идет о паскалях. Говорят о миллиметрах ртутного столба. Один миллиметр ртутного столба – это 133 Паскаля. Если вы ездите за рулем, то наверное знаете, что нормальное давление в колесах легкового автомобиля – около двух атмосфер.

Атмосферное давление
Атмосфера – это газ, точнее, смесь газов, которая удерживается у Земли благодаря гравитации. Атмосфера переходит в межпланетное пространство постепенно, а ее высота – примерно 100 километров.
Как понимать выражение «атмосферное давление»? Над каждым квадратным метром земной поверхности находится стокилометровый столб газа. Конечно, воздух прозрачен и приятен, но у него есть масса, которая давит на поверхность земли. Это и есть атмосферное давление.
Нормальное атмосферное давление принято считать равным 101325 Па. Это давление на уровне мирового океана при температуре 0 градусов Цельсия. Такое же давление при этой же температуре оказывает на свое основание столб ртути высотой 766 миллиметров.
Чем больше высота над уровнем моря, тем ниже атмосферное давление. Например, на вершине горы Джомолунгма оно составляет всего одну четвертую от нормального атмосферного давления.

Артериальное давление
Еще один пример, где мы сталкиваемся с давлением в повседневной жизни – это измерение кровяного давления.
Артериальное давление – это кровяное давление, т.е. давление, которое кровь оказывает на стенки сосудов, в данном случае – артерий.
Если вы измерили артериальное давление и оно у вас 120 на 80, то все хорошо. Если 90 на 50 или 240 на 180, то вам уже точно будет неинтересно разбираться, в чем это давление измеряется и что это вообще значит.
Тем не менее, возникает вопрос: 120 на 80 чего именно? Паскалей, миллиметров ртутного столба, атмосфер или еще каких-то единиц измерения?
Артериальное давление измеряется в миллиметрах ртутного столба. Оно определяет превышение давления жидкости в кровеносной системе над атмосферным давлением.
Кровь оказывает давление на сосуды и тем самым компенсирует действие атмосферного давления. Будь иначе, нас бы просто раздавило огромной массой воздуха над нами.
Но почему в измерении артериального давления две цифры?
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Дело в том, что кровь движется в сосудах не равномерно, а толчками. Первая цифра (120) называется систолическим давлением. Это давление на стенки сосудов в момент сокращения сердечной мышцы, его величина – наибольшая. Вторая цифра (80) определяет наименьшее значение и называется диастолическим давлением.
При измерении фиксируются значения систолического и диастолического давлений. Например, для здорового человека типичное значение артериального давления составляет 120 на 80 миллиметров ртутного столба. Это означает, что систолическое давление равно 120 мм. рт. ст., а диастолическое – 80 мм рт. ст. Разница между систолическим и диастолическим давлениями называется пульсовым давлением.
Физический вакуум
Вакуум – это отсутствие давления. Точнее, практически полное его отсутствие. Абсолютный вакуум является приближением, как идеальный газ в термодинамике и материальная точка в механике.
В зависимости от концентрации вещества различают низкий, средний и высокий вакуум. Наилучшее приближение к физическому вакууму – космическое пространство, в котором концентрация молекул и давление минимальны.

Давление – основной термодинамический параметр состояния системы. Определить давление воздуха или другого газа можно не только по приборам, но и пользуясь уравнениями, формулами и законами термодинамики. А если у вас нет времени разбираться, студенческий сервис поможет решить любую задачу на определение давления.


