Как найти давление водяного пара
Вода может находиться в трех основных агрегатных состояниях: жидком, твердом и газообразном. Пар, в свою очередь, бывает ненасыщенным и насыщенным – имеющим одинаковую температуру и давление с кипящей водой. Если же температура водяного пара при повышении давления превысила 100 градусов Цельсия, то такой пар называют перегретым. Часто при изучении школьного курса физики или при проведении технологического процесса возникает задача: определить давление водяного пара при каких-то конкретных условиях.

Инструкция
Допустим, вам дана следующая задача: в некий металлический сосуд залили воду в количестве, которое равно четверти его объема. После этого сосуд герметически закрыли и нагрели до температуры, равной 500оС. Если представить, что вся вода, находившаяся в сосуде, превратилась в пар, каково будет давление этого пара? Сначала в сосуде содержалась одна вода (ее количество, перешедшее в газообразное состояние ничтожно мало, поэтому им можно пренебречь). Обозначьте ее массу как m, а объем как V1. Следовательно, плотность воды будет вычисляться по формуле: ρ1 = m/V1.
После нагрева в сосуде находился один водяной пар той же массы m, но занимавший вчетверо больший объем V2. Следовательно, плотность водяного пара равна: ρ2 = ρ1/4.
Теперь переведите температуру из градусов Цельсия в градусы Кельвина. 500 градусов Цельсия приблизительно равны 773 градусам Кельвина (273 + Тц).
Напишите универсальное уравнение Менделеева-Клапейрона. Конечно, сильно нагретый водяной пар никоим образом не может считаться идеальным газом, состояние которого оно описывает, но погрешность в расчетах будет сравнительно небольшой. Р2V2 = mRT/µ или, преобразуя его с учетом того, что V2 в четыре раза больше, чем V1: 4Р2V1 = mRT/µ. Где Р2 – то самое давление водяного пара, которое вам необходимо найти; R – универсальная газовая постоянная, примерно равная 8,31; Т – температура в градусах Кельвина (773); а µ – молярная масса воды (или водяного пара), равная 18 грамм/моль (0,018 кг/моль).
Таким образом, у вас получается формула: Р2 = mRT/4V1 µ. Однако поскольку первоначальный объем V1 = m/ρ1, то итоговый вид уравнения таков:P2 = ρ1RT/4µ. Подставив в формулу известные величины, и зная, чему равна плотность воды, вычислите искомую величину давления водяного пара.
Источники:
- водяной пар формула
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Насыщенный пар
-
Темы кодификатора ЕГЭ: насыщенные и ненасыщенные пары, влажность воздуха.
-
Испарение и конденсация
-
Динамическое равновесие
-
Свойства насыщенного пара
-
Влажность воздуха
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: насыщенные и ненасыщенные пары, влажность воздуха.
Если открытый стакан с водой оставить на долгое время, то в конце концов вода полностью улетучится. Точнее — испарится. Что такое испарение и почему оно происходит?
Испарение и конденсация
При данной температуре молекулы жидкости обладают разными скоростями. Скорости большинства молекул находятся вблизи некоторого среднего значения (характерного для этой температуры). Но попадаются молекулы, скорости которых значительно отличаются от средней как в меньшую, так и большую сторону.
На рис. 1 изображён примерный график распределения молекул жидкости по скоростям. Голубым фоном показано то самое большинство молекул, скорости которых группируются около среднего значения. Красный «хвост» графика — это небольшое число «быстрых» молекул, скорости которых существенно превышают среднюю скорость основной массы молекул жидкости.
Рис. 1. Распределение молекул по скоростям
Когда такая весьма быстрая молекула окажется на свободной поверхности жидкости (т.е. на границе раздела жидкости и воздуха), кинетической энергии этой молекулы может хватить на то, чтобы преодолеть силы притяжения остальных молекул и вылететь из жидкости. Данный процесс и есть испарение, а молекулы, покинувшие жидкость, образуют пар.
Итак, испарение — это процесс превращения жидкости в пар, происходящий на свободной поверхности жидкости (при особых условиях превращение жидкости в пар может происходить по всему объёму жидкости. Данный процесс вам хорошо известен — это кипение).
Может случиться, что через некоторое время молекула пара вернётся обратно в жидкость.
Процесс перехода молекул пара в жидкость называется конденсацией. Конденсация пара — процесс, обратный испарению жидкости.
к оглавлению ▴
Динамическое равновесие
А что будет, если сосуд с жидкостью герметично закрыть? Плотность пара над поверхностью жидкости начнёт увеличиваться; частицы пара будут всё сильнее мешать другим молекулам жидкости вылетать наружу, и скорость испарения станет уменьшаться. Одновременно начнёт увеличиваться скорость конденсации, так как с возрастанием концентрации пара число молекул, возвращающихся в жидкость, будет становиться всё больше.
Наконец, в какой-то момент скорость конденсации окажется равна скорости испарения. Наступит динамическое равновесие между жидкостью и паром: за единицу времени из жидкости будет вылетать столько же молекул, сколько возвращается в неё из пара. Начиная с этого момента количество жидкости перестанет убывать, а количество пара — увеличиваться; пар достигнет «насыщения».
Насыщенный пар — это пар, который находится в состоянии динамического равновесия со своей жидкостью. Пар, не достигший состояния динамического равновесия с жидкостью, называется ненасыщенным.
Давление и плотность насыщенного пара обозначаются и
. Очевидно,
и
— это максимальные давление и плотность, которые может иметь пар при данной температуре. Иными словами, давление и плотность насыщенного пара всегда превышают давление и плотность ненасыщенного пара.
к оглавлению ▴
Свойства насыщенного пара
Оказывается, что состояние насыщенного пара (а ненасыщенного — тем более) можно приближённо описывать уравнением состояния идеального газа (уравнением Менделеева — Клапейрона). В частности, имеем приближённое соотношение между давлением насыщенного пара и его плотностью:
(1)
Это весьма удивительный факт, подтверждаемый экспериментом. Ведь по своим свойствам насыщенный пар существенно отличается от идеального газа. Перечислим важнейшие из этих отличий.
1. При неизменной температуре плотность насыщенного пара не зависит от его объёма.
Если, например, насыщенный пар изотермически сжимать, то его плотность в первый момент возрастёт, скорость конденсации превысит скорость испарения, и часть пара конденсируется в жидкость — до тех пор, пока вновь не наступит динамическое равновесие, в котором плотность пара вернётся к своему прежнему значению.
Аналогично, при изотермическом расширении насыщенного пара его плотность в первый момент уменьшится (пар станет ненасыщенным), скорость испарения превысит скорость конденсации, и жидкость будет дополнительно испаряться до тех пор, пока опять не установится динамическое равновесие — т.е. пока пар снова не станет насыщенным с прежним значением плотности.
2. Давление насыщенного пара не зависит от его объёма.
Это следует из того, что плотность насыщенного пара не зависит от объёма, а давление однозначно связано с плотностью уравнением (1).
Как видим, закон Бойля — Мариотта, справедливый для идеальных газов, для насыщенного пара не выполняется. Это и не удивительно — ведь он получен из уравнения Менделеева — Клапейрона в предположении, что масса газа остаётся постоянной.
3. При неизменном объёме плотность насыщенного пара растёт с повышением температуры и уменьшается с понижением температуры.
Действительно, при увеличении температуры возрастает скорость испарения жидкости.
Динамическое равновесие в первый момент нарушается, и происходит дополнительное испарение некоторой части жидкости. Пара будет прибавляться до тех пор, пока динамическое равновесие вновь не восстановится.
Точно так же при понижении температуры скорость испарения жидкости становится меньше, и часть пара конденсируется до тех пор, пока не восстановится динамическое равновесие — но уже с меньшим количеством пара.
Таким образом, при изохорном нагревании или охлаждении насыщенного пара его масса меняется, поэтому закон Шарля в данном случае не работает. Зависимость давления насыщенного пара от температуры уже не будет линейной функцией.
4. Давление насыщенного пара растёт с температурой быстрее, чем по линейному закону.
В самом деле, с увеличением температуры возрастает плотность насыщенного пара, а согласно уравнению (1) давление пропорционально произведению плотности на температуру.
Зависимость давления насыщенного пара от температуры является экспоненциальной (рис. 2). Она представлена участком 1–2 графика. Эту зависимость нельзя вывести из законов идеального газа.
Рис. 2. Зависимость давления пара от температуры
В точке 2 вся жидкость испаряется; при дальнейшем повышении температуры пар становится ненасыщенным, и его давление растёт линейно по закону Шарля (участок 2–3).
Вспомним, что линейный рост давления идеального газа вызван увеличением интенсивности ударов молекул о стенки сосуда. В случае нагревания насыщенного пара молекулы начинают бить не только сильнее, но и чаще — ведь пара становится больше. Одновременным действием этих двух факторов и вызван экспоненциальный рост давления насыщенного пара.
к оглавлению ▴
Влажность воздуха
Воздух, содержащий водяной пар, называется влажным.Чем больше пара находится в воздухе, тем выше влажность воздуха.
Абсолютная влажность — это парциальное давление водяного пара, находящегося в воздухе (т. е. давление, которое водяной пар оказывал бы сам по себе, в отсутствие других газов). Иногда абсолютной влажностью называют также плотность водяного пара в воздухе.
Относительная влажность воздуха — это отношение парциального давления водяного пара в нём к давлению насыщенного водяного пара при той же температуре. Как правило, это отношение выражают в процентах:
Из уравнения Менделеева-Клапейрона (1) следует, что отношение давлений пара равно отношению плотностей. Так как само уравнение (1), напомним, описывает насыщенный пар лишь приближённо, мы имеем приближённое соотношение:
Одним из приборов, измеряющих влажность воздуха, является психрометр. Он включает в себя два термометра, резервуар одного из которых завёрнут в мокрую ткань. Чем ниже влажность, тем интенсивнее идёт испарение воды из ткани, тем сильнее охлаждается резервуар «мокрого» термометра, и тем больше разность его показаний и показаний сухого термометра. По этой разности с помощью специальной психрометрической таблицы определяют влажность воздуха.
Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Насыщенный пар» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
08.05.2023
Это пар, находящийся в термодинамическом равновесии с жидкой (или твёрдой) фазой одного и того же вещества.
Одним из параметров, характеризующим насыщенный пар, является его давление.
Давление насыщенного пара зависит от температуры и не зависит от объема.
Разберемся подробнее, почему так происходит.
Почему давление насыщенного пара не зависит от объема?
Рассмотрим этот вопрос на примере дистиллированной воды.
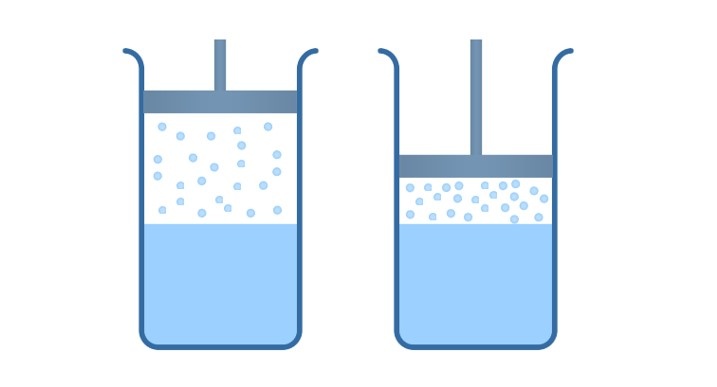
Возьмем цилиндр с поршнем, в полости которого находится дистиллят в термодинамическом равновесии с паром. Начинаем двигать поршень вниз, объем цилиндра начинает уменьшаться, происходит сжатие насыщенного пара, при этом мы поддерживаем постоянную температуру.
Система начнёт выходить из равновесия, плотность пара будет увеличиваться, и из газообразной фазы в жидкую будет переходить молекул больше, чем из жидкой в газообразную.
Другими словами, мы будем наблюдать процесс превращения насыщенного пара обратно в жидкость, этот процесс называется конденсация.
Если мы начнем поднимать поршень, объем полости увеличится, концентрация водяных паров над жидкостью начнет уменьшаться, вследствие чего, вода в сосуде начнет испаряться до тех пор, пока давление и концентрация насыщенного пара над жидкостью не придет в исходное состояние, то есть пока не наступит термодинамическое равновесие.
Из выше сказанного мы делаем вывод, что концентрация молекул насыщенного пара над жидкостью при постоянной температуре не зависит от его объема.
P=nkT,P=nkT,
где PP – давление пара (Па), nn – концентрация молекул пара (м-3), kk – постоянная Больцмана (равна 1,380649 Дж/К), ТТ – температура (К).
Из приведенной формулы мы видим, что давление насыщенного пара прямо пропорционально концентрации молекул и температуре паров над жидкостью (или твердым веществом) и, следовательно, не зависит от занимаемого им объема.
Как давление насыщенного пара зависит от температуры?
Из формулы, приведенной выше, мы наблюдаем, что давление насыщенного пара прямо пропорционально температуре термодинамической системы.
Несмотря на это, экспериментальная зависимость отличается от описанной уравнением, и давление пара увеличивается с большей скоростью с повышением температуры, нежели по линейному закону. Почему так происходит?
Всё дело в том, что во время увеличения подведенной температуры растёт и скорость испарения жидкости (или сублимации твёрдого вещества), вследствие этих факторов, увеличивается и концентрация испарённых (или сублимированных) молекул в газообразном состоянии над жидкой (или твёрдой) фазой. Поэтому и давление насыщенных паров изменяется быстрее. Плотность пара будет возрастать до тех пор, пока термодинамическое равновесие для данной температуры вновь не восстановится.
На участке 1-2 мы как раз видим влияние двух факторов – увеличение температуры и концентрации паров. В точке 2 вся жидкость испаряется (или твердое вещество сублимируется) и пар становится ненасыщенным, тогда давление начинает расти по линейному закону, что видно на участке 2-3.
Значения давления насыщенного пара для воды и других веществ при различных температурах получены эмпирическим методом. Эти данные можно найти в справочных материалах.
Тест по теме «Давление насыщенного пара»
Содержание
- Что это за параметр, в чем измеряется?
- От чего зависит?
- Абсолютное и относительное
- Как называется значение, при котором наступает конденсация пара?
- В чем разница в давлении пара?
- Высокого и низкого
- Насыщенного и ненасыщенного
- Чистой и загрязненной воды
- Как меняется от изменения температуры?
- Таблица зависимости
- Как определить?
- Формула и правила расчета
- Несколько примеров
- Где используют знания в жизни?
- Видео по теме статьи
- Заключение
Что это за параметр, в чем измеряется?
Давлением пара является физическая величина, которая показывает величину нагрузки, оказываемой паром, находящимся в замкнутом состоянии. При этом давление оказывается на стенки предмета, в котором пар находится.
Для расчета берется показатель, при котором пар находится в термодинамическом равновесии с жидкостью. Также учитывается температура кипения жидкости на единицу времени.
Единицей измерения этой величины является Паскаль (Па). Его часто сопоставляют с атмосферным: 760 мм.рт.ст = 101 кПа=1,01 Бар=1 атм. В расчетных формулах и документации давление пара обозначается буквой «P».
От чего зависит?
На величину давления влияют следующие факторы:
-
Температура кипения. Чем выше температура кипения, тем выше давление пара.
Также учитывается интенсивность испарения, которая различна для всех жидкостей и твердых тел.
-
Интенсивность. Чем быстрее вода или иная жидкость испаряется, тем быстрее растет давление.
Это применимо только при испарении в закрытых сосудах. На открытом воздухе интенсивность испарения не влияет на величину давления.
- Высота. На большой высоте давление пара всегда меньше, так как на него не оказывает влияние атмосферное давление. Также стоит учитывать, что атмосферное давление влияет на температуру кипения жидкости. Она значительно ниже на высоте, а, значит, процесс испарения происходит быстрее.
- Площадь. Чем меньше площадь, тем выше давление. В емкостях этот параметр всегда выше, чем на открытой местности.
- Насыщение. Давление насыщенного пара выше, так как в нем содержится больше воды. Но этот параметр может быстро измениться с началом конденсации. Также существует зависимость давления от типа пара. Давление ненасыщенного или перегретого пара всегда ниже.
Все эти параметры влияют на давление пара. Для различных химических или твердых элементов степень воздействия может быть разной.
Абсолютное и относительное
Существует 2 основных типа величины давления, которые применимы для расчета пара:
-
Абсолютное. Этой величиной является любое давление, которое выше эталонной точки отсчета от абсолютного нулевого вакуума. Согласно этому, даже давление небольшого испарения с поверхности естественного источника может быть рассчитано как абсолютное.
Данный параметр обозначается как «ABS». Если пар находится в закрытом сосуде, то абсолютное давление рассчитывается из суммы атмосферного и избыточного давления, с учетом чтобы результат был больше величины атмосферного.
- Относительное или избыточное давление является величиной, которая отличается от актуального атмосферного давления. Например, атмосферное давление 0,75 мм. рт. ст=100 Па.
Абсолютное и относительное давление используется для контроля работы паровых установок различного типа.
Как называется значение, при котором наступает конденсация пара?
Конденсация — это процесс возврата молекул жидкости из пара обратно в воду. Данный процесс характерен для насыщенного пара. Давление, при котором наступает процесс конденсации воды, является давлением насыщенного пара.
Этот параметр характеризуется образованием термодинамического равновесия между водой и паром. Иными словами, это давление одинаковой температуры пара и жидкости.
Этот тип давления используется в паровых установках, имеющих датчики конденсата и его слив. Таким образом контролируется образование конденсата и время его обратного испарения. Для паров ненасыщенного или перегретого типа эта характеристика не применима.
В чем разница в давлении пара?
Давление может быть различным при одинаковой температуре. Все зависит от качества исходной жидкости и типа самого пара.
Высокого и низкого
Пар низкого давления образуется при температуре кипения от 100 до 140 градуса. Его давление варьируется в пределах 2-3 атмосфер. Его часто применяют в теплоносителях.
Пар высокого давления является перегретым. В его структуре нет молекул воды. Он образуется при температуре от 180 градусов. Точка отсчета давления такого пара начинается от 10 атм. Такой пар используют в качестве энергии движения или для нагрева вязких жидкостей.
Насыщенного и ненасыщенного
Давление насыщенного пара не имеет прямой зависимости от его объема. При температуре кипения 100 градусов, при сохранении нормальных значений атмосферного давления, давление насыщенного пара приблизительно равняется 100 кПа.
Между насыщенным и ненасыщенным паром всегда есть разница в давлении. Давление ненасыщенного всегда на порядок меньше.
Это связано с тем, что при одинаковой температуре кипения, ненасыщенный пар не входит в термодинамическое равновесие и испаряется. Это приводит к потере давления и повторному парообразованию.
Чистой и загрязненной воды

Связано это с процессом кипения. Чистая вода закипает быстрее, так как на нее затрачивается меньше энергии.
Грязная вода прогревается значительно дольше, по причине затраты энергии на выпаривание загрязнений. Также большую роль играет испарение загрязнений (характерно для химических веществ).
Чужеродные химические элементы нарушают термодинамическое равновесие, что приводит к испарению и потере давления.
Также стоит учитывать свойства некоторых растворителей к выпариванию без осадка. Это значит, что пар насыщается долей инородных веществ, значительно увеличивающих плотность пара.
Как меняется от изменения температуры?
При повышении температуры давление пара увеличивается. Это происходит по причине перенасыщения молекулами воды. Из-за этого плотность пара возрастает, и начинается процесс конденсации.
При продолжительном росте температуры нарушается термодинамическое равновесие, повышается температура самого пара. Это приводит к выпариванию молекул воды и образованию перегретого пара.
При снижении температуры нагревания заметно снижается давление пара. Это происходит по причине снижения плотности пара. Образованный конденсат больше не меняет свое агрегатное состояние, а, значит, не происходит образование нового пара. При этом падает плотность.
Таблица зависимости
Пар отличается от идеальных газов. Его давление зависит от температуры и чем быстрее температура растет, тем сильнее давление. Это можно проследить по графику насыщенного водяного пара:
| T — °С | p-кПа |
| 5 | 0,88 |
| 10 | 1,23 |
| при 14 | 1,6 |
| 15 | 1,71 |
| 20 | 2,33 |
| при 22 градусах | 2,56 |
| 25 | 3,17 |
| при 27 | 3,4 |
| 30 | 4,6 |
| 35 | 5,62 |
| 40 | 7,38 |
| 45 | 9,5 |
| 50 | 12,3 |
| 75 | 38,2 |
| 100 | 101,3 |
Из таблицы хорошо видно, что с ростом температуры происходит увеличение давления, вследствие увеличения скорости парообразования. Значения, выше описанных в таблице, могут способствовать снижению давления по причине выпаривания и перегрева пара.
Как определить?
Рассмотрим, как произвести расчеты.
Формула и правила расчета

- «n» — величина концентрации пара.
- «k» — постоянная Больцмана.
- «t» — температура среды.
При расчете учитываются свойства: давление зависит от температуры и не зависит от объема.
Несколько примеров
Простой расчет давления пара над растворителем делается по формуле P=P0*N. Выражение состоит:
- P0 – давление пара раствора.
- N – доля растворителя (моль).
Также стоит учесть долю уже растворенной части растворителя. Например:
- Масса электролита 28,5 г.
- Объем воды 785 г.
- Понижение давления пара 52,37 Па.
- Температура 40 градусов.
Это уравнение имеет зависимость от табличных величин молекулярных масс растворов.
Для жидкости и пара, находящихся в емкости, расчет делается так:
- Объем емкости 0,5 м3.
- Масса воды 0,5 кг.
- Температура 147 градусов.
- Давление пара неизвестно.
0,5*0,5*147=367,5 кПа.
Где используют знания в жизни?
Самым известным измерительным устройством контроля давления является манометр. Давление пара используется во многих сферах:
- Отопление. Паровые котельные применяют пар для обогрева помещений. При этом контроль давления помогает поддерживать работоспособность всей системы. Данная характеристика указывает на переизбыток или недостаток давления, что приводит к нарушению подачи пара или разгерметизации.
- Пар применяется в установках в качестве движущей силы. Например, в паровозах. Тут контроль давления помогает рассчитать не только расход воды и энергии, но и поддерживать стабильность хода.
- Давление пара используется также синоптиками. Эта характеристика указывает влажность воздуха или уровень его сухости.
Давление пара несет множество полезных функций. Но недостаточный его контроль может быть губительным как для человека, так и для промышленного оборудования.
Видео по теме статьи
О давлении водяного пара расскажет видео:
Заключение
В статье была раскрыта тема давления пара. Эта величина является основной, как при расчетах, так и при регулировке температуры теплоносителей. Этот параметр помогает людям контролировать работу оборудования, работающего на энергии пара.
Download Article
Download Article
Have you ever left a bottle of water out in the hot sun for a few hours and heard a slight “hissing” noise when you opened it? This is caused by a principle called vapor pressure. In chemistry, vapor pressure is the pressure that is exerted on the walls of a sealed container when a substance in it evaporates (converts to a gas).[1]
To find the vapor pressure at a given temperature, use the Clausius-Clapeyron equation: ln(P1/P2) = (ΔHvap/R)((1/T2) – (1/T1)). You could also use Raoult’s Law to find the vapor pressure: Psolution=PsolventXsolvent.
-
1
Write the Clausius-Clapeyron equation. The formula used for calculating vapor pressure given a change in the vapor pressure over time is known as the Clausius-Clapeyron equation (named for physicists Rudolf Clausius and Benoît Paul Émile Clapeyron).[2]
This is the formula you’ll use to solve the most common sorts of vapor pressure problems you’ll find in physics and chemistry classes. The formula looks like this: ln(P1/P2) = (ΔHvap/R)((1/T2) – (1/T1)). In this formula, the variables refer to:- ΔHvap: The enthalpy of vaporization of the liquid. This can usually be found in a table at the back of chemistry textbooks.
- R: The real gas constant, or 8.314 J/(K × Mol).
- T1: The temperature at which the vapor pressure is known (or the starting temperature.)
- T2: The temperature at which the vapor pressure is to be found (or the final temperature.)
- P1 and P2: The vapor pressures at the temperatures T1 and T2, respectively.
-
2
Plug in the variables you know. The Clausius-Clapeyron equation looks tricky because it has so many different variables, but it’s actually not very difficult when you have the right information. The most basic vapor pressure problems will give you two temperature values and a pressure value or two pressure values and a temperature value — once you have these, solving is a piece of cake.
- For example, let’s say that we’re told that we have a container full of liquid at 295 K whose vapor pressure is 1 atmosphere (atm). Our question is: What is the vapor pressure at 393 K? We have two temperature values and a pressure, so we can solve for the other pressure value with the Clausius-Clapeyron equation. Plugging in our variables, we get ln(1/P2) = (ΔHvap/R)((1/393) – (1/295)).
- Note that, for Clausius-Clapeyron equations, you must always use Kelvin temperature values. You can use any pressure values as long as they are the same for both P1 and P2.
Advertisement
-
3
Plug in your constants. The Clausius-Clapeyron equation contains two constants: R and ΔHvap. R is always equal to 8.314 J/(K × Mol). ΔHvap (the enthalpy of vaporization), however, depends on the substance whose vapor pressure you are examining. As noted above, you can usually find the ΔHvap values for a huge variety of substances in the back of chemistry or physics textbooks, or else online.
- In our example, let’s say that our liquid is pure liquid water. If we look in a table of ΔHvap values, we can find that the ΔHvap is roughly 40.65 kJ/mol. Since our H value uses joules, rather than kilojoules, we can convert this to 40,650 J/mol.
- Plugging our constants in to our equation, we get ln(1/P2) = (40,650/8.314)((1/393) – (1/295)).
-
4
Solve the equation. Once you have all of your variables in the equation plugged in except for the one you are solving for, proceed to solve the equation according to the rules of ordinary algebra.[3]
- The only difficult part of solving our equation (ln(1/P2) = (40,650/8.314)((1/393) – (1/295))) is dealing with the natural log (ln). To cancel out a natural log, simply use both sides of the equation as the exponent for the mathematical constant e. In other words, ln(x) = 2 → eln(x) = e2 → x = e2.
- Now, let’s solve our equation:
- ln(1/P2) = (40,650/8.314)((1/393) – (1/295))
- ln(1/P2) = (4,889.34)(-0.00084)
- (1/P2) = e(-4.107)
- 1/P2 = 0.0165
- P2 = 0.0165-1 = 60.76 atm. This makes sense — in a sealed container, increasing the temperature by almost 100 degrees (to almost 20 degrees over the boiling point of water) will create lots of vapor, increasing the pressure greatly
Advertisement
-
1
Write Raoult’s Law. In real life, it’s rare to work with a single pure liquid — usually, we deal with liquids that are mixtures of several different component substances. Some of the most common of these mixtures are created by dissolving a small amount of a certain chemical called a solute in a large amount of a chemical called a solvent to create a solution. In these cases, it’s useful to know an equation called Raoult’s Law (named for physicist François-Marie Raoult),[4]
which looks like this: Psolution=PsolventXsolvent. In this formula, the variables refer to;- Psolution: The vapor pressure of the entire solution (all of the component parts combined)
- Psolvent: The vapor pressure of the solvent
- Xsolvent: The mole fraction of the solvent.
- Don’t worry if you don’t know terms like “mole fraction” — we’ll explain these in the next few steps.
-
2
Identify the solvent and solute in your solution. Before you calculate the vapor pressure of a mixed liquid, you need to identify the substances with which you are working. As a reminder, a solution is formed when a solute is dissolved in a solvent — the chemical that dissolves is always the solute and the chemical that does the dissolving is always the solvent.
- Let’s work through a simple example in this section to illustrate the concepts we’re discussing. For our example, let’s say that we want to find the vapor pressure of simple syrup. Traditionally, simple syrup is one part sugar dissolved in one part water, so we’ll say that sugar is our solute and water is our solvent.
- Note that the chemical formula for sucrose (table sugar) is C12H22O11. This will be important soon.
-
3
Find the temperature of the solution. As we saw in the Clausius-Clapeyron section above, a liquid’s temperature will affect its vapor pressure. In general, the higher the temperature, the greater the vapor pressure — as the temperature increases, more of the liquid will evaporate and form vapor, increasing the pressure in the container.[5]
- In our example, let’s say that the simple syrup’s current temperature is 298 K ( about 25 C).
-
4
Find the solvent’s vapor pressure. Chemical reference materials usually have vapor pressure values for many common substances and compounds, but these pressure values are usually only for when the substance is at 25 C/298 K or at its boiling point. If your solution is at one of these temperatures, you can use the reference value, but if not, you’ll need to find the vapor pressure at its current temperature.[6]
- The Clausius-Clapeyron can help here — use the reference vapor pressure and 298 K (25 C) for P1 and T1 respectively.
- In our example, our mixture is at 25 C, so we can use our easy reference tables. We find that water at 25 C has a vapor pressure of 23.8 mm HG [7]
-
5
Find the mole fraction of your solvent. The last thing we need to do before we can solve is to find the mole fraction of our solvent. Finding mole fractions is easy: just convert your components to moles, then find what percentage of the total number of moles in the substance each component occupies. In other words, each component’s mole fraction equals (moles of component)/(total number of moles in the substance.)[8]
- Let’s say that our recipe for simple syrup uses 1 liter (L) of water and 1 liter of sucrose (sugar.) In this case, we’ll need to find the number of moles in each. To do this, we’ll find the mass of each, then use the substance’s molar masses to convert to moles.
- Mass (1 L of water): 1,000 grams (g)
- Mass (1 L of raw sugar): Approx. 1,056.7 g[9]
- Moles (water): 1,000 grams × 1 mol/18.015 g = 55.51 moles
- Moles (sucrose): 1,056.7 grams × 1 mol/342.2965 g = 3.08 moles (note that you can find sucrose’s molar mass from its chemical formula, C12H22O11.)
- Total moles: 55.51 + 3.08 = 58.59 moles
- Mole fraction of water: 55.51/58.59 = 0.947
-
6
Solve. Finally, we have everything we need to solve our Raoult’s Law equation. This part is surprisingly easy: just plug your values in for the variables in the simplified Raoult’s Law equation at the beginning of this section (Psolution = PsolventXsolvent).[10]
- Substituting our values, we get:
- Psolution = (23.8 mm Hg)(0.947)
- Psolution = 22.54 mm Hg. This makes sense — in mole terms, there’s only a little sugar dissolved in a lot of water (even though in real-world terms the two ingredients have the same volume), so the vapor pressure will only decrease slightly.
Advertisement
-
1
Be aware of Standard Temperature and Pressure conditions. Scientists frequently use a set of temperature and pressure values as a sort of convenient “default”. These values are called Standard Temperature and Pressure (or STP for short). Vapor pressure problems frequently make reference to STP conditions, so it’s handy to have these values memorized. STP values are defined as:[11]
- Temperature: 273.15 K / 0 C / 32 F
- Pressure: 760 mm Hg / 1 atm / 101.325 kilopascals
-
2
Rearrange the Clausius-Clapeyron equation to find other variables. In our example in Section 1, we saw that the Clausius-Clapeyron equation is very useful for finding the vapor pressures of pure substances. However, not every question will ask you to find P1 or P2 — many will ask you to find a temperature value or even sometimes an ΔHvap value. Luckily, in these cases, getting the right answer is simply a matter of rearranging the equation so that the variable you’re solving for is alone on one side of the equals sign.[12]
- For instance, let’s say that we have an unknown liquid with a vapor pressure of 25 torr at 273 K and 150 torr at 325 K and we want to find this liquid’s enthalpy of vaporization (ΔHvap). We could solve like this:
- ln(P1/P2) = (ΔHvap/R)((1/T2) – (1/T1))
- (ln(P1/P2))/((1/T2) – (1/T1)) = (ΔHvap/R)
- R × (ln(P1/P2))/((1/T2) – (1/T1)) = ΔHvap Now, we plug in our values:
- 8.314 J/(K × Mol) × (-1.79)/(-0.00059) = ΔHvap
- 8.314 J/(K × Mol) × 3,033.90 = ΔHvap = 25,223.83 J/mol
-
3
Account for the vapor pressure of the solute when it produces vapor. In our Raoult’s Law example above, our solute, sugar, doesn’t produce any vapor on its own at normal temperatures (think — when was the last time you saw a bowl of sugar evaporate on your counter top?) However, when your solute does evaporate, this will affect your vapor pressure.[13]
We account for this by using a modified version of the Raoult’s Law equation: Psolution = Σ(PcomponentXcomponent) The sigma (Σ) symbol means that we just need to add up all of the different components’ vapor pressures to find our answers.- For example, let’s say that we have a solution made from two chemicals: benzene and toluene. The total volume of the solution is 120 milliliters (mL); 60 mL of benzene and 60 of toluene. The temperature of the solution is 25 C and the vapor pressures of each of these chemicals at 25 C is 95.1 mm Hg for benzene 28.4 mm Hg for toluene. Given these values, find the vapor pressure of the solution. We can do this as follows, using standard density, molar mass, and vapor pressure values for our two chemicals:
- Mass (benzene): 60 mL = .060 L × 876.50 kg/1,000 L = 0.053 kg = 53 g
- Mass (toluene): .060 L × 866.90 kg/1,000 L = 0.052 kg = 52 g
- Moles (benzene): 53 g × 1 mol/78.11 g = 0.679 mol
- Moles (toluene): 52 g × 1 mol/92.14 g = 0.564 mol
- Total moles: 0.679 + 0.564 = 1.243
- Mole fraction (benzene): 0.679/1.243 = 0.546
- Mole fraction (toluene): 0.564/1.243 = 0.454
- Solve: Psolution = PbenzeneXbenzene + PtolueneXtoluene
- Psolution = (95.1 mm Hg)(0.546) + (28.4 mm Hg)(0.454)
- Psolution = 51.92 mm Hg + 12.89 mm Hg = 64.81 mm Hg
Advertisement
Add New Question
-
Question
How is vapor pressure affected by temperature?
As the temperature of a liquid or solid increases, its vapor pressure also increases. Conversely, vapor pressure decreases as the temperature decreases.
-
Question
How can I solve this problem? “The vapor pressure of pure water is 760mm at 25 degree Celsius. The vapor pressure of a solution containing 1 m of solution of glucose will be what?”
I suggest you study colligative properties. The pressure lowering of the water is PX’ as P stands for the pressure of pure solvent and X’ is the molar fraction of the solute. 1L of water has 1000g of water, so there are 1000/18 mols of water ~ 55.6 mols. So, there’s 56.6 mols of molecules for every 1L of solution (one comes from glucose and 55.6 from water as calculated). So, the solute molar fraction is 1/56.6 ~ 1.768.10^-2. So the pressure lowering is 760mmHg times 1.768.10^-2, which is ~ 13.44 mmHg. Finally, the vapor pressure of the solution is 760mmHg-13.44mmHg = 746.56mmHg.
-
Question
At an ambient temperature, what would be the vapor pressure of water?
You can use the Antoine’s equation to calculate the vapor pressure of any substance and any temperature. At an ambient pressure of 25 degrees Celsius, the vapor pressure of water is 23.8 torr.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
-
To use the Clausius Clapeyron equation above, temperature must be measured in Kelvin (denoted as K). If you have the temperature in Centigrade, then you need to convert it with the following formula: Tk = 273 + Tc
-
The methods above work because energy is directly proportional to the amount of heat supplied. The temperature of the liquid is the only environmental factor upon which the vapor pressure depends.
Advertisement
References
About This Article
Article SummaryX
To calculate vapor pressure, use the Clausius-Clapeyron equation, which includes the variables for the enthalpy of the liquid, the real gas constant, the starting and final temperatures, and the starting and final vapor pressures. Plug all of the known variables and constants into the equation, and isolate the unknown variable, which will be the pressure. Solve the equation for the pressure by following the order of operations. Be sure to label your final answer in atmospheres! For information on how to find the vapor pressure of dissolved solutions, read on!
Did this summary help you?
Thanks to all authors for creating a page that has been read 577,888 times.
Reader Success Stories
-
Noah Franklin
Dec 6, 2018
“I was helping my friend with a chemistry problem about vapor pressure and mole fractions. I couldn’t figure it…” more


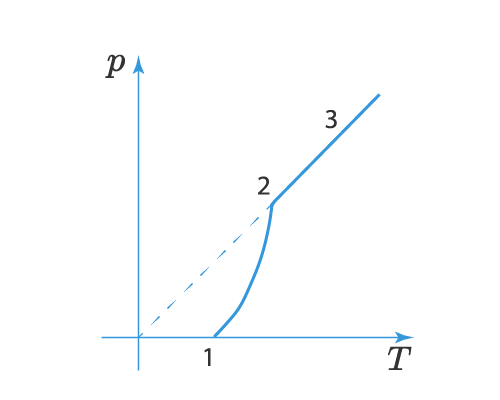
 Температура кипения. Чем выше температура кипения, тем выше давление пара.
Температура кипения. Чем выше температура кипения, тем выше давление пара.















