Как найти давление воздуха в трубке

Давление. Единицы давления.

По рыхлому снегу человек идёт с большим трудом, глубоко проваливаясь при каждом шаге. Но, надев лыжи, он может идти, почти не проваливаясь в него. Почему? На лыжах или без лыж человек действует на снег с одной и той же силой, равной своему весу. Однако действие этой силы в обоих случаях различно, потому что различна площадь поверхности, на которую давит человек, с лыжами и без лыж. Площадь поверхности лыж почти в 20 раз больше площади подошвы. Поэтому, стоя на лыжах, человек действует на каждый квадратный сантиметр площади поверхности снега с силой, в 20 раз меньшей, чем стоя на снегу без лыж.

Ученик, прикалывая кнопками газету к доске, действует на каждую кнопку с одинаковой силой. Однако кнопка, имеющая более острый конец, легче входит в дерево.

Значит, результат действия силы зависит не только от её модуля, направления и точки приложения, но и от площади той поверхности, к которой она приложена (перпендикулярно которой она действует).

Этот вывод подтверждают физические опыты.

По углам небольшой доски надо вбить гвозди. Сначала гвозди, вбитые в доску, установим на песке остриями вверх и положим на доску гирю. В этом случае шляпки гвоздей лишь незначительно вдавливаются в песок. Затем доску перевернем и поставим гвозди на острие. В этом случае площадь опоры меньше, и под действием той же силы гвозди значительно углубляются в песок.

От того, какая сила действует на каждую единицу площади поверхности, зависит результат действия этой силы.

В рассмотренных примерах силы действовали перпендикулярно поверхности тела. Вес человека был перпендикулярен поверхности снега; сила, действовавшая на кнопку, перпендикулярна поверхности доски.

Величина, равная отношению силы, действующей перпендикулярно поверхности, к площади этой поверхности, называется давлением.

Чтобы определить давление, надо силу, действующую перпендикулярно поверхности, разделить на площадь поверхности:

давление = сила / площадь.

Обозначим величины, входящие в это выражение: давление – p, сила, действующая на поверхность, – F и площадь поверхности – S.

Тогда получим формулу:

p = F/S

Понятно, что бóльшая по значению сила, действующую на ту же площадь, будет производить большее давление.

За единицу давления принимается такое давление, которое производит сила в 1 Н, действующая на поверхность площадью 1 м² перпендикулярно этой поверхности.

Единица давления – ньютон на квадратный метр ( 1 Н / м² ). В честь французского ученого Блеза Паскаля она называется паскалем (Па). Таким образом,

1 Па = 1 Н / м² .

Используется также другие единицы давления: гектопаскаль (гПа) и килопаскаль (кПа).

1 кПа = 1000 Па;

1 гПа = 100 Па;

1 Па = 0,001 кПа;

1 Па = 0,01 гПа.

Пример. Рассчитать давление, производимое на пол мальчиком, масса которого 45 кг, а площадь подошв его ботинок, соприкасающихся с полом, равна 300 см².

Запишем условие задачи и решим её.

Дано: m = 45 кг, S = 300 см²; p = ?

В единицах СИ: S = 0,03 м²

Решение:

p = F/S,

F = P,

P = g·m,

P = 9,8 Н · 45 кг ≈ 450 Н,

p = 450/0,03 Н / м² = 15000 Па = 15 кПа

‘Ответ’: p = 15000 Па = 15 кПа

Способы уменьшения и увеличения давления.

Тяжелый гусеничный трактор производит на почву давление равное 40 – 50 кПа, т. е. всего в 2 – 3 раза больше, чем давление мальчика массой 45 кг. Это объясняется тем, что вес трактора распределяется на бóльшую площадь за счёт гусеничной передачи. А мы установили, что чем больше площадь опоры, тем меньше давление, производимое одной и той же силой на эту опору.

В зависимости от того, нужно ли получить малое или большое давление, площадь опоры увеличивается или уменьшается. Например, для того, чтобы грунт мог выдержать давление возводимого здания, увеличивают площадь нижней части фундамента.

Шины грузовых автомобилей и шасси самолетов делают значительно шире, чем легковых. Особенно широкими делают шины у автомобилей, предназначенных для передвижения в пустынях.

Тяжелые машины, как трактор, танк или болотоход, имея большую опорную площадь гусениц, проходят по болотистой местности, по которой не пройдет человек.

С другой стороны, при малой площади поверхности можно небольшой силой произвести большое давление. Например, вдавливая кнопку в доску, мы действуем на нее с силой около 50 Н. Так как площадь острия кнопки примерно 1 мм², то давление, производимое ею, равно:

p = 50 Н/ 0, 000 001 м² = 50 000 000 Па = 50 000 кПа.

Для сравнения, это давление в 1000 раз больше давления, производимого гусеничным трактором на почву. Можно найти еще много таких примеров.

Лезвие режущих и острие колющих инструментов (ножей, ножниц, резцов, пил, игл и др.) специально остро оттачивается. Заточенный край острого лезвия имеет маленькую площадь, поэтому при помощи даже малой силы создается большое давление, и таким инструментом легко работать.

Режущие и колющие приспособления встречаются и в живой природе: это зубы, когти, клювы, шипы и др. – все они из твердого материала, гладкие и очень острые.

Давление

Мы уже знаем, что газы, в отличие от твердых тел и жидкостей, заполняют весь сосуд, в котором находятся. Например, стальной баллон для хранения газов, камера автомобильной шины или волейбольный мяч. При этом газ оказывает давление на стенки, дно и крышку баллона, камеры или любого другого тела, в котором он находится. Давление газа обусловлено иными причинами, чем давление твердого тела на опору.

Известно, что молекулы газа беспорядочно движутся. При своем движении они сталкиваются друг с другом, а также со стенками сосуда, в котором находится газ. Молекул в газе много, поэтому и число их ударов очень велико. Например, число ударов молекул воздуха, находящегося в комнате, о поверхность площадью 1 см² за 1 с выражается двадцатитрехзначным числом. Хотя сила удара отдельной молекулы мала, но действие всех молекул на стенки сосуда значительно, — оно и создает давление газа.

Итак, давление газа на стенки сосуда (и на помещенное в газ тело) вызывается ударами молекул газа.

Рассмотрим следующий опыт. Под колокол воздушного насоса поместим резиновый шарик. Он содержит небольшое количество воздуха и имеет неправильную форму. Затем насосом откачиваем воздух из-под колокола. Оболочка шарика, вокруг которой воздух становится все более разреженным, постепенно раздувается и принимает форму правильного шара.

Как объяснить этот опыт?

В нашем опыте движущиеся молекулы газа непрерывно ударяют о стенки шарика внутри и снаружи. При откачивании воздуха число молекул в колоколе вокруг оболочки шарика уменьшается. Но внутри шарика их число не изменяется. Поэтому число ударов молекул о внешние стенки оболочки становится меньше, чем число ударов о внутренние стенки. Шарик раздувается до тех пор, пока сила упругости его резиновой оболочки не станет равной силе давления газа. Оболочка шарика принимает форму шара. Это показывает, что газ давит на ее стенки по всем направлениям одинаково. Иначе говоря, число ударов молекул, приходящихся на каждый квадратный сантиметр площади поверхности, по всем направлениям одинаково. Одинаковое давление по всем направлениям характерно для газа и является следствием беспорядочного движения огромного числа молекул.

Попытаемся уменьшить объем газа, но так, чтобы масса его осталась неизменной. Это значит, что в каждом кубическом сантиметре газа молекул станет больше, плотность газа увеличится. Тогда число ударов молекул о стенки увеличится, т. е. возрастет давление газа. Это можно подтвердить опытом.

На рисунке а изображена стеклянная трубка, один конец которой закрыт тонкой резиновой пленкой. В трубку вставлен поршень. При вдвигании поршня объем воздуха в трубке уменьшается, т. е. газ сжимается. Резиновая пленка при этом выгибается наружу, указывая на то, что давление воздуха в трубке увеличилось.

Наоборот, при увеличении объема этой же массы газа, число молекул в каждом кубическом сантиметре уменьшается. От этого уменьшится число ударов о стенки сосуда – давление газа станет меньше. Действительно, при вытягивании поршня из трубки объем воздуха увеличивается, пленка прогибается внутрь сосуда. Это указывает на уменьшение давления воздуха в трубке. Такие же явления наблюдались бы, если бы вместо воздуха в трубке находился бы любой другой газ.

Итак, при уменьшении объема газа его давление увеличивается, а при увеличении объема давление уменьшается при условии, что масса и температура газа остаются неизменными.

А как изменится давление газа, если нагреть его при постоянном объеме? Известно, что скорость движения молекул газа при нагревании увеличивается. Двигаясь быстрее, молекулы будут ударять о стенки сосуда чаще. Кроме того, каждый удар молекулы о стенку будет сильнее. Вследствие этого, стенки сосуда будут испытывать большее давление.

Следовательно, давление газа в закрытом сосуде тем больше, чем выше температура газа, при условии, что масса газа и объем не изменяются.

Из этих опытов можно сделать общий вывод, что давление газа тем больше, чем чаще и сильнее молекулы ударяют о стенки сосуда.

Для хранения и перевозки газов их сильно сжимают. При этом давление их возрастает, газы необходимо заключать в специальные, очень прочные баллоны. В таких баллонах, например, содержат сжатый воздух в подводных лодках, кислород, используемый при сварке металлов. Конечно же, мы должны навсегда запомнить, что газовые баллоны нельзя нагревать, тем более, когда они заполнены газом. Потому что, как мы уже понимаем, может произойти взрыв с очень неприятными последствиями.

Закон Паскаля.

В отличие от твердых тел отдельные слои и мелкие частицы жидкости и газа могут свободно перемещаться относительно друг друга по всем направлениям. Достаточно, например, слегка подуть на поверхность воды в стакане, чтобы вызвать движение воды. На реке или озере при малейшем ветерке появляется рябь.

Подвижностью частиц газа и жидкости объясняется, что давление, производимое на них, передается не только в направлении действия силы, а в каждую точку. Рассмотрим это явление подробнее.

На рисунке, а изображен сосуд, в котором содержится газ (или жидкость). Частицы равномерно распределены по всему сосуду. Сосуд закрыт поршнем, который может перемещаться вверх и вниз.

Прилагая некоторую силу, заставим поршень немного переместиться внутрь и сжать газ (жидкость), находящийся непосредственно под ним. Тогда частицы (молекулы) расположатся в этом месте более плотно, чем прежде(рис, б). Благодаря подвижности частицы газа будут перемещаться по всем направлениям. Вследствие этого их расположение опять станет равномерным, но более плотным, чем раньше (рис, в). Поэтому давление газа всюду возрастет. Значит, добавочное давление передается всем частицам газа или жидкости. Так, если давление на газ (жидкость) около самого поршня увеличится на 1 Па, то во всех точках внутри газа или жидкости давление станет больше прежнего на столько же. На 1 Па увеличится давление и на стенки сосуда, и на дно, и на поршень.

Давление, производимое на жидкость или газ, передается на любую точку одинаково во всех направлениях.

Это утверждение называется законом Паскаля.

На основе закона Паскаля легко объяснить следующие опыты.

На рисунке изображен полый шар, имеющий в различных местах небольшие отверстия. К шару присоединена трубка, в которую вставлен поршень. Если набрать воды в шар и вдвинуть в трубку поршень, то вода польется из всех отверстий шара. В этом опыте поршень давит на поверхность воды в трубке. Частицы воды, находящиеся под поршнем, уплотняясь, передают его давление другим слоям, лежащим глубже. Таким образом, давление поршня передается в каждую точку жидкости, заполняющей шар. В результате часть воды выталкивается из шара в виде одинаковых струек, вытекающих из всех отверстий.

Если шар заполнить дымом, то при вдвигании поршня в трубку из всех отверстий шара начнут выходить одинаковые струйки дыма. Это подтверждает, что и газы передают производимое на них давление во все стороны одинаково.

Давление в жидкости и газе.

На жидкости, как и на все тела на Земле, действует сила тяжести. Поэтому, каждый слой жидкости, налитой в сосуд, своим весом создает давление, которое по закону Паскаля передается по всем направлениям. Следовательно, внутри жидкости существует давление. В этом можно убедиться на опыте.

В стеклянную трубку, нижнее отверстие которой закрыто тонкой резиновой пленкой, нальем воду. Под действием веса жидкости дно трубки прогнется.

Опыт показывает, что, чем выше столб воды над резиновой пленкой, тем больше она прогибается. Но всякий раз после того, как резиновое дно прогнулось, вода в трубке приходит в равновесие (останавливается), так как, кроме силы тяжести, на воду действует сила упругости растянутой резиновой пленки.

Опустим трубку с резиновым дном, в которую налита вода, в другой, более широкий сосуд с водой. Мы увидим, что по мере опускания трубки резиновая пленка постепенно выпрямляется. Полное выпрямление пленки показывает, что силы, действующие на нее сверху и снизу, равны. Наступает полное выпрямление пленки тогда, когда уровни воды в трубке и сосуде совпадают.

Такой же опыт можно провести с трубкой, в которой резиновая пленка закрывает боковое отверстие, как это показано на рисунке, а. Погрузим эту трубку с водой в другой сосуд с водой, как это изображено на рисунке, б. Мы заметим, что пленка снова выпрямится, как только уровни воды в трубке и сосуде сравняются. Это означает, что силы, действующие на резиновую пленку, одинаковы со всех сторон.

Возьмем сосуд, дно которого может отпадать. Опустим его в банку с водой. Дно при этом окажется плотно прижатым к краю сосуда и не отпадет. Его прижимает сила давления воды, направленная снизу вверх.

Будем осторожно наливать воду в сосуд и следить за его дном. Как только уровень воды в сосуде совпадет с уровнем воды в банке, оно отпадет от сосуда.

В момент отрыва на дно давит сверху вниз столб жидкости в сосуде, а снизу вверх на дно передается давление такого же по высоте столба жидкости, но находящейся в банке. Оба эти давления одинаковы, дно же отходит от цилиндра вследствие действия на него собственной силы тяжести.

Выше были описаны опыты с водой, но если взять вместо воды любую другую жидкость, результаты опыта будут те же.

Итак, опыты показывают, что внутри жидкости существует давление, и на одном и том же уровне оно одинаково по всем направлениям. С глубиной давление увеличивается.

Газы в этом отношении не отличаются от жидкостей, ведь они тоже имеют вес. Но надо помнить, что плотность газа в сотни раз меньше плотности жидкости. Вес газа, находящегося в сосуде, мал, и его “весовое” давление во многих случаях можно не учитывать.

Расчет давления жидкости на дно и стенки сосуда.

Рассмотрим, как можно рассчитывать давление жидкости на дно и стенки сосуда. Решим сначала задачу для сосуда, имеющего форму прямоугольного параллелепипеда.

Сила F, с которой жидкость, налитая в этот сосуд, давит на его дно, равна весу P жидкости, находящейся в сосуде. Вес жидкости можно определить, зная ее массу m. Массу, как известно, можно вычислить по формуле: m = ρ·V. Объем жидкости, налитой в выбранный нами сосуд, легко рассчитать. Если высоту столба жидкости, находящейся в сосуде, обозначить буквой h, а площадь дна сосуда S, то V = S·h.

Масса жидкости m = ρ·V, или m = ρ·S·h .

Вес этой жидкости P = g·m, или P = g·ρ·S·h.

Так как вес столба жидкости равен силе, с которой жидкость давит на дно сосуда, то, разделив вес P на площадь S, получим давление жидкости p:

p = P/S , или p = g·ρ·S·h/S,

то есть

p = g·ρ·h.

Мы получили формулу для расчета давления жидкости на дно сосуда. Из этой формулы видно, что давление жидкости на дно сосуда зависит только от плотности и высоты столба жидкости.

Следовательно, по выведенной формуле можно рассчитывать давление жидкости, налитой в сосуд любой формы (строго говоря, наш расчет годится только для сосудов, имеющих форму прямой призмы и цилиндра. В курсах физики для института доказано, что формула верна и для сосуда произвольной формы). Кроме того, по ней можно вычислить и давление на стенки сосуда. Давление внутри жидкости, в том числе давление снизу вверх, также рассчитывается по этой формуле, так как давление на одной и той же глубине одинаково по всем направлениям.

При расчете давления по формуле p = gρh надо плотность ρ выражать в килограммах на кубический метр (кг/м³), а высоту столба жидкости h – в метрах (м), g = 9,8 Н/кг, тогда давление будет выражено в паскалях (Па).

Пример. Определите давление нефти на дно цистерны, если высота столба нефти 10 м, а плотность ее 800 кг/м³ .

Запишем условие задачи и запишем ее.

Дано:

h = 10 м

ρ = 800 кг/м³

P = ?

Решение:

p = gρh,

p = 9.8 Н/кг · 800 кг/м³ · 10 м ≈ 80 000 Па ≈ 80 кПа.

Ответ: p ≈ 80 кПа.

Сообщающиеся сосуды.

На рисунке изображены два сосуда, соединённые между собой резиновой трубкой. Такие сосуды называются сообщающимися. Лейка, чайник, кофейник – примеры сообщающихся сосудов. Из опыта мы знаем, что вода, налитая, например, в лейку, стоит всегда на одном уровне в носике и внутри.

С сообщающимися сосудами можно проделать следующий простой опыт. В начале опыта резиновую трубку зажимаем в середине, и в одну из трубок наливаем воду. Затем зажим открываем, и вода вмиг перетекает в другую трубку, пока поверхности воды в обеих трубках не установятся на одном уровне. Можно закрепить одну из трубок в штативе, а другую поднимать, опускать или наклонять в разные стороны. И в этом случае, как только жидкость успокоится, ее уровни в обеих трубках уравняются.

В сообщающихся сосудах любой формы и сечения поверхности однородной жидкости устанавливаются на одном уровне (при условии, что давление воздуха над жидкостью одинаково) (рис. 109).

Это можно обосновать следующим образом. Жидкость покоится, не перемещаясь из одного сосуда в другой. Значит, давления в обоих сосудах на любом уровне одинаковы. Жидкость в обоих сосудах одна и та же, т. е. имеет одинаковую плотность. Следовательно, должны быть одинаковы и ее высоты. Когда мы поднимаем один сосуд или доливаем в него жидкость, давление в нем увеличивается и жидкость перемещается в другой сосуд до тех пор, пока давления не уравновесятся.

Если в один из сообщающихся сосудов налить жидкость одной плотности, а во второй – другой плотности, то при равновесии уровни этих жидкостей не будут одинаковыми. И это понятно. Мы ведь знаем, что давление жидкости на дно сосуда прямо пропорционально высоте столба и плотности жидкости. А в этом случае плотности жидкостей будут различны.

При равенстве давлений высота столба жидкости с большей плотностью будет меньше высоты столба жидкости с меньшей плотностью (рис.).

Вес воздуха. Атмосферное давление.

На воздух, как и на всякое тело, находящееся на Земле, действует сила тяжести, и, значит, воздух обладает весом. Вес воздуха легко вычислить, зная его массу.

На опыте покажем, как вычислить массу воздуха. Для этого нужно взять прочный стеклянный шар с пробкой и резиновой трубкой с зажимом. Выкачаем из него насосом воздух, зажмем трубку зажимом и уравновесим на весах. Затем, открыв зажим на резиновой трубке, впустим в него воздух. Равновесие весов при этом нарушится. Для его восстановления на другую чашку весов придется положить гири, масса которых будет равна массе воздуха в объеме шара.

Опытами установлено, что при температуре 0 °С и нормальном атмосферном давлении масса воздуха объемом 1 м³ равна 1,29 кг. Вес этого воздуха легко вычислить:

P = g·m, P = 9,8 Н/кг · 1,29 кг ≈ 13 Н.

Воздушная оболочка, окружающая Землю, называется атмосфера (от греч. атмос – пар, воздух, и сфера – шар).

Атмосфера, как показали наблюдения за полетом искусственных спутников Земли, простирается на высоту нескольких тысяч километров.

Вследствие действия силы тяжести верхние слои атмосферы, подобно воде океана, сжимают нижние слои. Воздушный слой, прилегающий непосредственно к Земле, сжат больше всего и, согласно закону Паскаля, передает производимое на него давление по всем направлениям.

В результате этого земная поверхность и телá, находящиеся на ней, испытывают давление всей толщи воздуха, или, как обычно говорится в таких случаях, испытывают атмосферное давление.

Существованием атмосферного давления могут быть объяснены многие явления, с которыми мы встречаемся в жизни. Рассмотрим некоторые из них.

На рисунке изображена стеклянная трубка, внутри которой находится поршень, плотно прилегающий к стенкам трубки. Конец трубки опущен воду. Если поднимать поршень, то за ним будет подниматься и вода.

Это явление используется в водяных насосах и некоторых других устройствах.

На рисунке показан цилиндрический сосуд. Он закрыт пробкой, в которую вставлена трубка с краном. Из сосуда насосом откачивается воздух. Затем конец трубки помещается в воду. Если теперь открыть кран, то вода фонтаном брызнет в внутрь сосуда. Вода поступает в сосуд потому, что атмосферное давление больше давления разреженного воздуха в сосуде.

Почему существует воздушная оболочка Земли.

Как и все тела, молекулы газов, входящих в состав воздушной оболочки Земли, притягиваются к Земле.

Но почему же тогда все они не упадут на поверхность Земли? Каким образом сохраняется воздушная оболочка Земли, ее атмосфера? Чтобы понять это, надо учесть, что молекулы газов находятся в непрерывном и беспорядочном движении. Но тогда возникает другой вопрос: почему эти молекулы не улетают в мировое пространство, то есть в космос.

Для того, чтобы совсем покинуть Землю, молекула, как и космический корабль или ракета, должна иметь очень большую скорость (не меньше 11,2 км/с). Это так называемая вторая космическая скорость. Скорость большинства молекул воздушной оболочки Земли значительно меньше этой космической скорости. Поэтому большинство их привязано к Земле силой тяжести, лишь ничтожно малое количество молекул улетает за пределы Земли в космос.

Беспорядочное движение молекул и действие на них силы тяжести приводят в результате к тому, что молекулы газов “парят” в пространстве около Земли, образуя воздушную оболочку, или известную нам атмосферу.

Измерения показывают, что плотность воздуха быстро уменьшается с высотой. Так, на высоте 5,5 км над Землей плотность воздуха в 2 раза меньше его плотность у поверхности Земли, на высоте 11 км – в 4 раза меньше, и т. д. Чем выше, тем воздух разреженнее. И наконец, в самых верхних слоях (сотни и тысячи километров над Землей) атмосфера постепенно переходит в безвоздушное пространство. Четкой границы воздушная оболочка Земли не имеет.

Строго говоря, вследствие действия силы тяжести плотность газа в любом закрытом сосуде неодинакова по всему объему сосуда. Внизу сосуда плотность газа больше, чем в верхних его частях, поэтому и давление в сосуде неодинаково. На дне сосуда оно больше, чем вверху.
Однако для газа, содержащегося в сосуде, это различие в плотности и давлении столь мало, что его можно во многих случаях совсем не учитывать, просто знать об этом. Но для атмосферы, простирающейся на несколько тысяч километров, различие это существенно.

Измерение атмосферного давления. Опыт Торричелли.

Рассчитать атмосферное давление по формуле для вычисления давления столба жидкости (§ 38) нельзя. Для такого расчета надо знать высоту атмосферы и плотность воздуха. Но определенной границы у атмосферы нет, а плотность воздуха на разной высоте различна. Однако измерить атмосферное давление можно с помощью опыта, предложенного в 17 веке итальянским ученым Эванджелиста Торричелли, учеником Галилея.

Опыт Торричелли состоит в следующем: стеклянную трубку длиной около 1 м, запаянную с одного конца, наполняют ртутью. Затем, плотно закрыв второй конец трубки, ее переворачивают и опускают в чашку с ртутью, где под уровнем ртути открывают этот конец трубки. Как и в любом опыте с жидкостью, часть ртути при этом выливается в чашку, а часть ее остается в трубке. Высота столба ртути, оставшейся в трубке, равна примерно 760 мм. Над ртутью внутри трубки воздуха нет, там безвоздушное пространство, поэтому никакой газ не оказывает давления сверху на столб ртути внутри этой трубки и не влияет на измерения.

Торричелли, предложивший описанный выше опыт, дал и его объяснение. Атмосфера давит на поверхность ртути в чашке. Ртуть находится в равновесии. Значит, давление в трубке на уровне аа1 (см. рис) равно атмосферному давлению. При изменении атмосферного давления меняется и высота столба ртути в трубке. При увеличении давления столбик удлиняется. При уменьшении давления — столб ртути уменьшает свою высоту.

Давление в трубке на уровне аа1 создается весом столба ртути в трубке, так как в верхней части трубки над ртутью воздуха нет. Отсюда следует, что атмосферное давление равно давлению столба ртути в трубке, т. е.

p_атм = p_ртути .

Измерив высоту столба ртути, можно рассчитать давление, которое производит ртуть. Оно и будет равно атмосферному давлению. Если атмосферное давление уменьшится, то столб ртути в трубке Торричелли понизится.

Чем больше атмосферное давление, тем выше столб ртути в опыте Торричелли. Поэтому на практике атмосферное давление можно измерить высотой ртутного столба (в миллиметрах или сантиметрах). Если, например, атмосферное давление равно 780 мм рт. ст. (говорят “миллиметров ртутного столба”), то это значит, что воздух производит такое же давление, какое производит вертикальный столб ртути высотой 780 мм.

Следовательно, в этом случае за единицу измерения атмосферного давления принимается 1 миллиметр ртутного столба (1 мм рт. ст.). Найдем соотношение между этой единицей и известной нам единицей – паскалем (Па).

Давление столба ртути ρ_ртути высотой 1 мм равно:

p = g·ρ·h, p = 9,8 Н/кг · 13 600 кг/ м³ · 0,001 м ≈ 133,3 Па.

Итак, 1 мм рт. ст. = 133,3 Па.

В настоящее время атмосферное давление принято измерять в гектопаскалях ( 1 гПа = 100 Па). Например, в сводках погоды может быть объявлено, что давление равно 1013 гПа, это то же самое, что 760 мм рт. ст.

Наблюдая ежедневно за высотой ртутного столба в трубке, Торричелли обнаружил, что эта высота меняется, т. е. атмосферное давление непостоянно, оно может увеличиваться и уменьшаться. Торричелли заметил также, что атмосферное давление связано с изменением погоды.

Если к трубке с ртутью, использовавшейся в опыте Торричелли, прикрепить вертикальную шкалу, то получится простейший прибор – ртутный барометр (от греч. барос – тяжесть, метрео – измеряю). Он служит для измерения атмосферного давления.

Барометр – анероид.

В практике для измерения атмосферного давления используют металлический барометр, называемый анероидом (в переводе с греческого – безжидкостный). Так барометр называют потому, что в нем нет ртути.

Внешний вид анероида изображен на рисунке. Главная часть его – металлическая коробочка 1 с волнистой (гофрированной) поверхностью (см. др. рис.). Из этой коробочки выкачан воздух, а чтобы атмосферное давление не раздавило коробочку, ее крышка 2 пружиной оттягивается вверх. При увеличении атмосферного давления крышка прогибается вниз и натягивает пружину. При уменьшении давления пружина выпрямляет крышку. К пружине с помощью передаточного механизма 3 прикреплена стрелка-указатель 4, которая продвигается вправо или влево при изменении давления. Под стрелкой укреплена шкала, деления которой нанесены по показаниям ртутного барометра. Так, число 750, против которого стоит стрелка анероида (см. рис.), показывает, что в данный момент в ртутном барометре высота ртутного столба 750 мм.

Следовательно, атмосферное давление равно 750 мм рт. ст. или ≈ 1000 гПа.

Значение атмосферного давления весьма важно для предвидения погоды на ближайшие дни, так как изменение атмосферного давления связано с изменением погоды. Барометр – необходимый прибор для метеорологических наблюдений.

Атмосферное давление на различных высотах.

В жидкости давление, как мы знаем, зависит от плотности жидкости и высоты ее столба. Вследствие малой сжимаемости плотность жидкости на различных глубинах почти одинакова. Поэтому, вычисляя давление, мы считаем ее плотность постоянной и учитываем только изменение высоты.

Сложнее дело обстоит с газами. Газы сильно сжимаемы. А чем сильнее газ сжат, тем больше его плотность, и тем большее давление он производит. Ведь давление газа создается ударами его молекул о поверхность тела.

Слои воздуха у поверхности Земли сжаты всеми вышележащими слоями воздуха, находящимися над ними. Но чем выше от поверхности слой воздуха, тем слабее он сжат, тем меньше его плотность. Следовательно, тем меньшее давление он производит. Если, например, воздушный шар поднимается над поверхностью Земли, то давление воздуха на шар становиться меньше. Это происходит не только потому, что высота столба воздуха над ним уменьшается, но еще и потому, что уменьшается плотность воздуха. Вверху она меньше, чем внизу. Поэтому зависимость давления воздуха от высоты сложнее, чем жидкости.

Наблюдения показывают, что атмосферное давление в местностях, лежащих на уровне моря, в среднем равно 760 мм рт. ст.

Атмосферное давление, равное давлению столба ртути высотой 760 мм при температуре 0 °С, называется нормальным атмосферным давлением.

Нормальное атмосферное давление равно 101 300 Па = 1013 гПа.

Чем больше высота над уровнем моря, тем давление меньше.

При небольших подъемах, в среднем, на каждые 12 м подъема давление уменьшается на 1 мм рт. ст. (или на 1,33 гПа).

Зная зависимость давления от высоты, можно по изменению показаний барометра определить высоту над уровнем моря. Анероиды, имеющие шкалу, по которой непосредственно можно измерить высоту над уровнем моря, называются высотомерами. Их применяют в авиации и при подъеме на горы.

Манометры.

Мы уже знаем, что для измерения атмосферного давления применяют барометры. Для измерения давлений, бóльших или меньших атмосферного, используется манометры (от греч. манос – редкий, неплотный, метрео – измеряю). Манометры бывают жидкостные и металлические.

Рассмотрим сначала устройство и действие открытого жидкостного манометра. Он состоит из двухколенной стеклянной трубки, в которую наливается какая-нибудь жидкость. Жидкость устанавливается в обоих коленах на одном уровне, так как на ее поверхность в коленах сосуда действует только атмосферное давление.

Чтобы понять, как работает такой манометр, его можно соединить резиновой трубкой с круглой плоской коробкой, одна сторона которой затянута резиновой пленкой. Если надавить пальцем на пленку, то уровень жидкости в колене манометра, соединенном в коробкой, понизится, а в другом колене повысится. Чем это объясняется?

При надавливании на пленку увеличивается давление воздуха в коробке. По закону Паскаля это увеличение давления передается и жидкости в том колене манометра, которое присоединено к коробке. Поэтому давление на жидкость в этом колене будет больше, чем в другом, где на жидкость действует только атмосферное давление. Под действием силы этого избыточного давления жидкость начнет перемещаться. В колене со сжатым воздухом жидкость опустится, в другом – поднимется. Жидкость придет в равновесие (остановится), когда избыточное давление сжатого воздуха уравновесится давлением, которое производит избыточный столб жидкости в другом колене манометра.

Чем сильнее давить на пленку, тем выше избыточный столб жидкости, тем больше его давление. Следовательно, об изменении давления можно судить по высоте этого избыточного столба.

На рисунке показано, как таким манометром можно измерять давление внутри жидкости. Чем глубже погружается в жидкость трубочка, тем больше становится разность высот столбов жидкости в коленах манометра, тем, следовательно, и большее давление производит жидкость.

Если установить коробочку прибора на какой-нибудь глубине внутри жидкости и поворачивать ее пленкой вверх, вбок и вниз, то показания манометра при этом не будут меняется. Так и должно быть, ведь на одном и том же уровне внутри жидкости давление одинаково по всем направлениям.

На рисунке изображен металлический манометр. Основная часть такого манометра – согнутая в трубу металлическая трубка 1, один конец которой закрыт. Другой конец трубки с помощью крана 4 сообщается с сосудом, в котором измеряют давление. При увеличении давления трубка разгибается. Движение её закрытого конца при помощи рычага 5 и зубчатки 3 передается стрелке 2, движущейся около шкалы прибора. При уменьшении давления трубка, благодаря своей упругости, возвращается в прежнее положение, а стрелка – к нулевому делению шкалы.

Поршневой жидкостный насос.

В опыте, рассмотренном нами ранее (§ 40), было установлено, что вода в стеклянной трубке под действием атмосферного давления поднималась вверх за поршнем. На этом основано действие поршневых насосов.

Насос схематически изображен на рисунке. Он состоит из цилиндра, внутри которого ходит вверх и вниз, плотно прилегая к стенкам сосуда, поршень 1. В нижней части цилиндра и в самом поршне установлены клапаны 2, открывающиеся только вверх. При движении поршня вверх вода под действием атмосферного давления входит в трубу, поднимает нижний клапан и движется за поршнем.

При движении поршня вниз вода, находящаяся под поршнем, давит на нижний клапан, и он закрывается. Одновременно под давлением воды открывается клапан внутри поршня, и вода переходит в пространство над поршнем. При следующем движении поршня вверх в месте с ним поднимается и находящаяся над ним вода, которая и выливается в отводящую трубу. Одновременно за поршнем поднимается и новая порция воды, которая при последующем опускании поршня окажется над ним, и вся эта процедура повторяется вновь и вновь, пока работает насос.

Гидравлический пресс.

Закон Паскаля позволяет объяснить действие гидравлической машины (от греч. гидравликос – водяной). Это машины, действие которых основано на законах движения и равновесия жидкостей.

Основной частью гидравлической машины служат два цилиндра разного диаметра, снабженные поршнями и соединительной трубкой. Пространство под поршнями и трубку заполняют жидкостью (обычно минеральным маслом). Высоты столбов жидкости в обоих цилиндрах одинаковы, пока на поршни не действуют силы.

Допустим теперь, что силы F₁ и F₂ – силы, действующие на поршни, S₁ и S₂ – площади поршней. Давление под первым (малым) поршнем равно p₁ = F₁ / S₁, а под вторым (большим) p₂ = F₂ / S₂ . По закону Паскаля давление покоящейся жидкостью во все стороны передается одинаково, т. е. p₁ = p₂ или F₁ / S₁ = F₂ / S₂ , откуда:

F₂ / F₁ = S₂ / S₁ .

Следовательно, сила F₂ во столько раз больше силы F₁ , во сколько раз площадь большого поршня больше площади малого поршня. Например, если площадь большого поршня 500 см², а малого 5 см², и на малый поршень действует сила 100 Н, то на больший поршень будет действовать сила, в 100 раз бóльшая, то есть 10 000 Н.

Таким образом, с помощью гидравлической машины можно малой силой уравновесить бóльшую силу.

Отношение F₁ / F₂ показывает выигрыш в силе. Например, в приведенном примере выигрыш в силе равен 10 000 Н / 100 Н = 100.

Гидравлическая машина, служащая для прессования (сдавливания), называется гидравлическим прессом.

Гидравлические прессы применяются там, где требуется большая сила. Например, для выжимания масла из семян на маслобойных заводах, для прессования фанеры, картона, сена. На металлургических заводах гидравлические прессы используют для изготовления стальных валов машин, железнодорожных колес и многих других изделий. Современные гидравлические прессы могут развивать силу в десятки и сотни миллионов ньютонов.

Устройство гидравлического пресса схематически показано на рисунке. Прессуемое тело 1 (A) кладут на платформу, соединенную с большим поршнем 2 (B). При помощи малого поршня 3 (D) создается большое давление на жидкость. Это давление передается в каждую точку жидкости, заполняющей цилиндры. Поэтому такое же давление действует и на второй, большой поршень. Но так как площадь 2-го (большого) поршня больше площади малого, то и сила, действующая на него, будет больше силы, действующей на поршень 3 (D). Под действием этой силы поршень 2 (B) будет подниматься. При подъеме поршня 2 (B) тело (A) упирается в неподвижную верхнюю платформу и сжимается. При помощи манометра 4 (M) измеряется давление жидкости. Предохранительный клапан 5 (P) автоматически открывается, когда давление жидкости превышает допустимое значение.

Из малого цилиндра в большой жидкость перекачивается повторными движениями малого поршня 3 (D). Это осуществляется следующим образом. При подъеме малого поршня (D) клапан 6 (K) открывается, и в пространство, находящееся под поршнем, засасывается жидкость. При опускании малого поршня под действием давления жидкости клапан 6 (K) закрывается, а клапан 7 (K’) открывается, и жидкость переходит в большой сосуд.

Действие воды и газа на погруженное в них тело.

Под водой мы легко можем поднять камень, который с трудом поднимается в воздухе. Если погрузить пробку под воду и выпустить ее из рук, то она всплывет. Как можно объяснить эти явления?

Мы знаем (§ 38), что жидкость давит на дно и стенки сосуда. И если внутрь жидкости поместить какое-нибудь твердое тело, то оно также будет подвергаться давлению, как и стенки сосуда.

Рассмотрим силы, которые действуют со стороны жидкости на погруженное в нее тело. Чтобы легче было рассуждать, выберем тело, которое имеет форму параллелепипеда с основаниями, параллельными поверхности жидкости (рис.). Силы, действующие на боковые грани тела, попарно равны и уравновешивают друг друга. Под действием этих сил тело сжимается. А вот силы, действующие на верхнюю и нижнюю грани тела, неодинаковы. На верхнюю грань давит сверху силой F₁ столб жидкости высотой h₁ . На уровне нижней грани давление производит столб жидкости высотой h₂. Это давление, как мы знаем (§ 37), передается внутри жидкости во все стороны. Следовательно, на нижнюю грань тела снизу вверх с силой F₂ давит столб жидкости высотой h₂. Но h₂ больше h₁, следовательно, и модуль силы F₂ больше модуля силы F₁. Поэтому тело выталкивается из жидкости с силой F_выт, равной разности сил F₂ – F₁ , т. е.

F_выт = F₂– F₁

Рассчитаем эту выталкивающую силу. Силы F₁ и F₂ , действующие на верхнюю и нижнюю грани параллелепипеда, можно вычислить, зная площади этих граней (S₁ и S₂) и давление жидкости на уровнях этих граней (p₁ и p₂):

F₁ = p₁·S₁, а F₂ = p₂·S₂, так как p₁ = ρ_ж·g·h₁ , p₂ = ρ_ж·g·h₂ , а S₁ = S₂ = S, где S – площадь грани параллелепипеда (все грани равны).

Тогда, F_выт = F₂ – F₁ = ρ·g·h₂·S – ρ·g·h₁·S = ρ·g·S·(h₂ – h₁) = ρ·g·S·h, где h – высота параллелепипеда (h = h₂ – h₁).

Но S·h = V, где V – объем параллелепипеда, а ρ_ж·V = m_ж – масса жидкости в объеме параллелепипеда. Следовательно,

F_выт = g·m_ж = P_ж ,

т. е. выталкивающая сила равна весу жидкости в объеме погруженного в нее тела (выталкивающая сила равна весу жидкости такого же объёма, как и объём погруженного в нее тела).

Существование силы, выталкивающей тело из жидкости, легко обнаружить на опыте.

На рисунке а изображено тело, подвешенное к пружине со стрелкой-указателем на конце. Стрелка отмечает на штативе растяжение пружины. При отпускании тела в воду пружина сокращается (рис., б). Такое же сокращение пружины получится, если действовать на тело снизу вверх с некоторой силой, например, нажать рукой (приподнять).

Следовательно, опыт подтверждает, что на тело, находящееся в жидкости, действует сила, выталкивающая это тело из жидкости.

К газам, как мы знаем, также применим закон Паскаля. Поэтому на тела, находящиеся в газе, действует сила, выталкивающая их из газа. Под действием этой силы воздушные шары поднимаются вверх. Существование силы, выталкивающей тело из газа, можно также наблюдать на опыте.

К укороченной чашке весов подвесим стеклянный шар или большую колбу, закрытую пробкой. Весы уравновешиваются. Затем под колбу (или шар) ставят широкий сосуд так, чтобы он окружал всю колбу. Сосуд наполняется углекислым газом, плотность которого больше плотности воздуха (поэтому углекислый газ опускается вниз и заполняет сосуд, вытесняя из него воздух). При этом равновесие весов нарушается. Чашка с подвешенной колбой поднимается вверх (рис.). На колбу, погруженную в углекислый газ, действует бóльшая выталкивающая сила, по сравнению с той, которая действует на нее в воздухе.

Сила, выталкивающая тело из жидкости или газа, направлена противоположно силе тяжести, приложенной к этому телу.

Поэтому пролкосмосе). Именно этим объясняется, что в воде мы иногда легко поднимаем тела, которые с трудом удерживаем в воздухе.

Архимедова сила.

Силу, с которой тело, находящееся в жидкости, выталкивается ею, можно рассчитать (как это сделано в § 48). А можно определить ее значение на опыте, используя для этого прибор, изображенный на рисунке.

К пружине подвешивается небольшое ведерко и тело цилиндрической формы (рис., а). Стрелка на штативе отмечает растяжение пружины. Она показывает вес тела в воздухе. Приподняв тело, под него подставляется отливной сосуд, наполненный жидкостью до уровня отливной трубки. После чего тело погружается целиком в жидкость (рис., б). При этом часть жидкости, объем которой равен объему тела, выливается из отливного сосуда в стакан. Пружина сокращается, и указатель пружины поднимается вверх, показывая уменьшение веса тела в жидкости. В данном случае на тело, кроме силы тяжести, действует еще одна сила, выталкивающая его из жидкости. Если в верхнее ведерко вылить жидкость из стакана (т. е. ту, которую вытеснило тело), то указатель пружины возвратится к своему начальному положению (рис., в).

На основании этого опыта можно заключить, что сила, выталкивающая целиком погруженное в жидкость тело, равна весу жидкости в объеме этого тела. Такой же вывод мы получили и в § 48.

Если подобный опыт проделать с телом, погруженным в какой-либо газ, то он показал бы, что сила, выталкивающая тело из газа, также равна весу газа, взятого в объеме тела.

Сила, выталкивающая тело из жидкости или газа, называется архимедовой силой, в честь ученого Архимеда, который впервые указал на ее существование и рассчитал ее значение.

Итак, опыт подтвердил, что архимедова (или выталкивающая) сила равна весу жидкости в объеме тела, т. е. F_А = P_ж = g·m_ж. Массу жидкости m_ж, вытесняемую телом, можно выразить через ее плотность ρ_ж и объем тела V_т, погруженного в жидкость (так как V_ж – объем вытесненной телом жидкости равен V_т – объему тела, погруженного в жидкость), т. е. m_ж = ρ_ж·V_т. Тогда получим:

F_A = g·ρ_ж·V_т

Следовательно, архимедова сила зависит от плотности жидкости, в которую погружено тело, и от объема этого тела. Но она не зависит, например, от плотности вещества тела, погружаемого в жидкость, так как эта величина не входит в полученную формулу.

Определим теперь вес тела, погруженного в жидкость (или в газ). Так как две силы, действующие на тело в этом случае, направлены в противоположные стороны (сила тяжести вниз, а архимедова сила вверх), то вес тела в жидкости P₁ будет меньше веса тела в вакууме P = g·m на архимедову силу F_А = g·m_ж (где m_ж – масса жидкости или газа, вытесненной телом).

Таким образом, если тело погружено в жидкость или газ, то оно теряет в своем весе столько, сколько весит вытесненная им жидкость или газ.

Пример. Определить выталкивающую силу, действующую на камень объемом 1,6 м³ в морской воде.

Запишем условие задачи и решим ее.

Дано:

V_т =1,6 м³

ρ_ж = 1030 кг/м³

g = 9,8 Н/кг

F_А – ?

Решение:

F_А = g·ρ_ж·V_т,

F_А = 9.8 Н/кг · 1030 кг/м³ · 1,6 м³ = 16 480 Н ≈ 16,5 кН.

Ответ: F_А = 16,5 кН.

Плавание тел.

На тело, находящееся внутри жидкости, действуют две силы: сила тяжести, направленная вертикально вниз, и архимедова сила, направленная вертикально вверх. Рассмотрим, что будет происходить с телом под действием этих сил, если в начале оно было неподвижно. При этом возможны три случая:

1) если сила тяжести F_тяж больше архимедовой силы F_А, то тело будет опускаться на дно, тонуть, т. е. если

F_тяж > F_А, то тело тонет;

2) если сила тяжести равна архимедовой силе, то тело может находиться в равновесии в любом месте жидкости, т. е. если

F_тяж = F_А, то тело плавает;

3) если сила тяжести меньше архимедовой силы, то тело будет подниматься из жидкости, всплывать, т. е. если

F_тяж < F_А, то тело всплывает.

Рассмотрим последний случай подробнее.

Когда всплывающее тело достигнет поверхности жидкости, то при дальнейшем его движении вверх архимедова сила будет уменьшаться. Почему? А потому, что будет уменьшаться объем части тела, погруженной в жидкость, а архимедова сила равна весу жидкости в объеме погруженной в нее части тела.

Когда архимедова сила станет равной силе тяжести, тело остановится и будет плавать на поверхности жидкости, частично погрузившись в нее.

Полученный вывод легко проверить на опыте.

В отливной сосуд нальем воду до уровня отливной трубки. После этого погрузим в сосуд плавающее тело, предварительно взвесив его в воздухе. Опустившись в воду, тело вытесняет объем воды, равный объему погруженной в нее части тела. Взвесив эту воду, находим, что ее вес (архимедова сила) равен силе тяжести, действующей на плавающее тело, или весу этого тела в воздухе.

Проделав такие же опыты с любыми другими телами, плавающими в разных жидкостях – в воде, спирте, растворе соли, можно убедиться, что если тело плавает в жидкости, то вес вытесненной им жидкости равен весу этого тела в воздухе.

Легко доказать, что если плотность сплошного твердого тела больше плотности жидкости, то тело в такой жидкости тонет. Тело с меньшей плотностью всплывает в этой жидкости. Кусок железа, например, тонет в воде, но всплывает в ртути. Тело же, плотность которого равна плотности жидкости, остается в равновесии внутри жидкости.

Плавает на поверхности воды лед, так как его плотность меньше плотности воды.

Чем меньше плотность тела по сравнению с плотностью жидкости, тем меньшая часть тела погружена в жидкость.

При равных плотностях тела и жидкости тело плавает внутри жидкости на любой глубине.

Две несмешивающиеся жидкости, например вода и керосин, располагаются в сосуде в соответствии со своими плотностями: в нижней части сосуда – более плотная вода (ρ = 1000 кг/м³), сверху – более легкий керосин (ρ = 800 кг/м³).

Средняя плотность живых организмов, населяющих водную среду, мало отличается от плотности воды, поэтому их вес почти полностью уравновешивается архимедовой силой. Благодаря этому водные животные не нуждаются в столь прочных и массивных скелетах, как наземные. По этой же причине эластичны стволы водных растений.

Плавательный пузырь рыбы легко меняет свой объем. Когда рыба с помощью мышц опускается на большую глубину, и давление воды на нее увеличивается, пузырь сжимается, объем тела рыбы уменьшается, и она не выталкивается вверх, а плавает в глубине. Таким образом, рыба может в определенных пределах регулировать глубину своего погружения. Киты регулируют глубину своего погружения за счет уменьшения и увеличения объема легких.

Плавание судов.

Суда, плавающие по рекам, озерам, морям и океанам, построены из разных материалов с различной плотностью. Корпус судов обычно делается из стальных листов. Все внутренние крепления, придающие судам прочность, также изготовляют из металлов. Для постройки судов используют различные материалы, имеющие по сравнению с водой как бóльшие, так и меньшие плотности.

Благодаря чему суда держатся на воде, принимают на борт и перевозят большие грузы?

Опыт с плавающим телом (§ 50) показал, что тело вытесняет своей подводной частью столько воды, что по весу эта вода равна весу тела в воздухе. Это также справедливо и для любого судна.

Вес воды, вытесняемой подводной частью судна, равен весу судна с грузом в воздухе или силе тяжести, действующей на судно с грузом.

Глубина, на которую судно погружается в воду, называется осадкой. Наибольшая допускаемая осадка отмечена на корпусе судна красной линией, называемой ватерлинией (от голланд. ватер – вода).

Вес воды, вытесняемой судном при погружении до ватерлинии, равный силе тяжести, действующей на судно с грузом, называется водоизмещением судна.

В настоящее время для перевозки нефти строятся суда водоизмещением 5 000 000 кН (5 · 10⁶ кН) и больше, т. е. имеющие вместе с грузом массу 500 000 т (5 · 10⁵ т) и более.

Если из водоизмещения вычесть вес самого судна, то мы получим грузоподъемность этого судна. Грузоподъемность показывает вес груза, перевозимого судном.

Судостроение существовало еще в Древнем Египте, в Финикии (считается, что Финикийцы были одними из лучших судостроителей), Древнем Китае.

В России судостроение зародилось на рубеже 17-18 вв. Сооружались главным образом военные корабли, но именно в России были построены первый ледокол, суда с двигателем внутреннего сгорания, атомный ледокол “Арктика”.

Воздухоплавание.

С давних времен люди мечтали о возможности летать над облаками, плавать в воздушном океане, как они плавали по морю. Для воздухоплавания

вначале использовали воздушные шары, которые наполняли или нагретым воздухом, или водородом либо гелием.

Для того, чтобы воздушный шар поднялся в воздух, необходимо, чтобы архимедова сила (выталкивающая) F_А, действующая на шар, была больше силы тяжести F_тяж, т. е. F_А > F_тяж.

По мере поднятия шара вверх архимедова сила, действующая на него, уменьшается (F_А = gρV), так как плотность верхних слоев атмосферы меньше, чем у поверхности Земли. Чтобы подняться выше, с шара сбрасывается специальный балласт (груз) и этим облегчает шар. В конце концов шар достигает своей своей предельной высоты подъема. Для спуска шара из его оболочки при помощи специального клапана выпускается часть газа.

В горизонтальном направлении воздушный шар перемещается только под действием ветра, поэтому он называется аэростатом (от греч аэр – воздух, стато – стоящий). Для исследования верхних слоев атмосферы, стратосферы еще не так давно применялись огромные воздушные шары – стратостаты.

До того как научились строить большие самолеты для перевозки по воздуху пассажиров и грузов, применялись управляемые аэростаты – дирижабли. Они имеют удлиненную форму, под корпусом подвешивается гондола с двигателем, который приводит в движение пропеллер.

Воздушный шар не только сам поднимается вверх, но может поднять и некоторый груз: кабину, людей, приборы. Поэтому для того, чтобы узнать, какой груз может поднять воздушный шар, необходимо определить его подъемную силу.

Пусть, например, в воздух запущен шар объемом 40 м³, наполненный гелием. Масса гелия, заполняющая оболочку шара, будет равна:
m_Ге = ρ_Ге·V = 0,1890 кг/м³ · 40 м³ = 7,2 кг,
а его вес равен:
P_Ге = g·m_Ге ; P_Ге = 9,8 Н/кг · 7,2 кг = 71 Н.
Выталкивающая же сила (архимедова), действующая на этот шар в воздухе, равна весу воздуха объемом 40 м³, т. е.
F_А = g·ρ_воздV; F_А = 9,8 Н/кг · 1,3 кг/м³ · 40 м³ = 520 Н.

Значит, этот шар может поднять груз весом 520 Н – 71 Н = 449 Н. Это и есть его подъемная сила.

Шар такого же объема, но наполненный водородом, может поднять груз 479 Н. Значит, подъемная сила его больше, чем шара, наполненного гелием. Но все же чаще используют гелий, так как он не горит и поэтому безопаснее. Водород же горючий газ.

Гораздо проще осуществить подъем и спуск шара, наполненного горячим воздухом. Для этого под отверстием, находящимся в нижней части шара, располагается горелка. При помощи газовой горелки можно регулировать температуру воздуха внутри шара, а значит, его плотность и выталкивающую силу. Чтобы шар поднялся выше, достаточно сильнее нагреть воздух в нем, увеличив пламя горелки. При уменьшении пламени горелки температура воздуха в шаре уменьшается, и шар опускается вниз.

Можно подобрать такую температуру шара, при которой вес шара и кабины будет равен выталкивающей силе. Тогда шар повиснет в воздухе, и с него будет легко проводить наблюдения.

По мере развития науки происходили и существенные изменения в воздухоплавательной технике. Появилась возможность использования новых оболочек для аэростатов, которые стали прочными, морозоустойчивыми и легкими.

Достижения в области радиотехники, электроники, автоматики позволили сконструировать беспилотные аэростаты. Эти аэростаты используются для изучения воздушных течений, для географических и медико-биологических исследований в нижних слоях атмосферы.

Ссылки

• Уроки по физике за 7 класс по школьной программе

На предыдущих уроках мы рассчитывали давление жидкости на дно и стенки сосуда по формуле $p=rho gh$. Но атмосферное давление так рассчитать не получится.

Почему нельзя рассчитывать давление воздуха так же, как рассчитывают давление жидкости на дно или стенки сосуда?
Для этого нам нужно будет знать высоту атмосферы и плотность воздуха. Но определенной границы у атмосферы нет, а плотность воздуха меняется в зависимости от высоты: в нижних слоях атмосферы она больше, чем в верхних (рисунок 1).

На данном уроке мы рассмотрим известный опыт, который позволяет рассчитать величину атмосферного давления и познакомимся с новой единицей измерения давления — миллиметрами ртутного столба.

Опыт Торричелли

В XVII веке во Флоренции герцог Тосканский готовился к балу в своем замке и приготовил для своих гостей необычный сюрприз. Это был фонтан, струи которого должны были зрелищно окружить террасу своими струями.

Однако, несмотря на работу ручных насосов, вода поднималась только на высоту около 10 метров. Недоумевающие строители обратились за помощью к Галилею, который предложил разобраться в этом своему ученику Торричелли.

Эванджелиста Торричелли (рисунок 2) смог не только объяснить «упрямство фонтана» действием атмосферного давления, но пошел дальше и рассчитал это атмосферное давление.

Рассмотрим известнейший опыт Торричелли. На рисунке 3 показана стеклянная трубка длиной $1 space м$, один конец которой запаян. Трубку наполняют ртутью (рисунок 3, а). Затем плотно закрывают ее открытый конец (рисунок 3, б). Далее трубку переворачивают и опускают в чашу с ртутью (рисунок 3, в). После этого трубку открывают (рисунок 3, г).

Мы видим, что часть ртути при этом вылилась в чашу, а другая ее часть осталась в трубке. Высота столба ртути, оставшейся в трубке, равна примерно 760 мм. Заметим, что в трубке над ртутью воздуха нет, там безвоздушное пространство.

Объяснение опыта Торричелли

Теперь давайте рассмотрим объяснение данного опыта. Поверхность ртути в чаше испытывает атмосферное давление. Ртуть в чаше находится в равновесии, то есть давление в трубке на уровне AB (рисунок 4) равно атмосферному давлению $p_{атм}$. Если бы это было не так и давление в трубке было бы больше атмосферного, то ртуть выливалась бы в чашу. А если меньше — то ртуть поднималась бы в трубке вверх.

Так как в верхней части трубки воздуха нет, то давление создается только весом столба ртути. Из этого следует, что атмосферное давление равно давлению столба ртути в трубке, то есть:

$p_{атм}=p_{ртути}$.

Соответственно, чтобы посчитать величину атмосферного давления, достаточно измерить высоту столба ртути. Из формулы $p=rho gh$ мы видим, что величина атмосферного давления будет прямо пропорциональна высоте столба ртути в трубке. При уменьшении атмосферного давления мы увидим, что столб ртути понизился, а при увеличении атмосферного давления столб ртути в опыте Торричелли станет выше.

Единицы измерения атмосферного давления

Что означает запись: «Атмосферное давление равно 760 мм рт. ст.»?
На практике атмосферное давление часто измеряется высотой ртутного столба. Если, например, атмосферное давление 760 мм рт. ст., то это значит, что воздух производит такое же давление, что и вертикальный столб ртути высотой 760 мм. Каждый из вас слышал прогноз погоды от гидрометцентра. В сводках погоды атмосферное давление также передают в мм рт. ст.

А в каких единицах мы обычно рассчитываем давление на занятиях, решая задачи? Давайте найдем соотношения между этими единицами и выясним, чему равен 1 мм рт. ст. в паскалях (Па).

Давление столба ртути высотой 1 мм равно:
$p = rho gh$,
$p = 13600 frac{кг}{м^3} cdot 9.8frac{Н}{кг} cdot 0.001 space м approx 133.3 space Па$.

$1 space мм space рт. space ст. = 133.3 space Па$.

Скольким гектопаскалям равно давление ртутного столба высотой 1 мм?
$1 space мм space рт. space ст. = 133.3 space Па = 1.333 space гПа approx 1.3 space гПа$.

Среднее значение атмосферного давления равно 760 мм рт. ст. Выразим это значение в паскалях и в гектопаскалях (также довольно широко используемая величина измерения):
$760 space мм space рт. space ст. approx 101 space 300 space Па approx 1013 space гПа$.

Ртутный барометр

Если к трубке с ртутью, использовавшейся в опыте Торричелли, прикрепить вертикальную шкалу, то получится измерительный прибор — ртутный барометр (рисунок 5).

Ртутный барометр — это прибор для измерения атмосферного давления.

После ежедневного наблюдения за высотой столба ртути в трубке, Торричелли сделал вывод, что периодически атмосферное давление меняется и его изменения связаны с погодными условиями.

Другие опыты

В конце 1646 года семья Паскалей жила во французском городе Руане. Блез Паскаль повторил известный опыт, экспериментируя не только с ртутью, как Торричелли, но и с водой, маслом, красным вином.

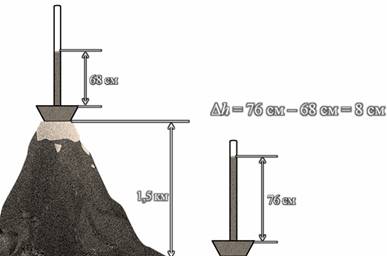
Интересный эксперимент был проведен 19 сентября 1648 года. Блез Паскаль и его зять Флорен Перье проделали опыт, доказавший существование атмосферного давления. При помощи стеклянной трубки и чаши с ртутью предстояло измерить, на какую высоту поднимается в ней ртуть у подножия и на вершине горы Пюи-де-Дом высотой 1647 метров в Клермоне. На вершине столбик ртути остановился на более низкой отметке. Причина — земная атмосфера на вершине на 1647 метров меньше. Разница уровней ртути составила почти 8 см (рисунок 7).

Интересный факт: самый большой водяной барометр был сконструирован в 1985 году Бертом Болле. Он был хранителем музея барометров в Маартенсдейке (Нидерланды), а высота барометра была более 12,5 метров. Барометр был установлен в этом музее и пробыл там вплоть до его закрытия (рисунок 8).

Упражнения

$h — ?$

Посмотреть решение и ответ

Скрыть

$F — ?$

Посмотреть решение и ответ

Скрыть

Посмотреть ответ

Скрыть

Посмотреть ответ

Скрыть

Посмотреть ответ

Скрыть

Задания

Посмотреть ответ

Скрыть

Посмотреть ответ

Скрыть

Посмотреть ответ

Скрыть

Измерение атмосферного давления

“Мы живем на дне сказочно красивого океана.

Он велик и безбрежен”

Э. Торричелли

В рамках данной темы речь пойдёт о том, каким же способом можно измерить атмосферное давление.

Ранее говорилось о том, что подобно твердым телам и жидкостям, газы также обладают массой и, соответственно, весом. Планету Земля окружает невидимая газовая оболочка, которая называется атмосферой. Земная атмосфера также обладает весом вследствие действия на нее притяжения Земли, а, следовательно, производит давление, которое называется атмосферным давлением.

Каким способом можно рассчитать атмосферное давление? Формулой для вычисления гидростатического давления здесь пользоваться нельзя, так как для такого расчета требуется знать высоту атмосферы и ее плотность. Действие силы тяжести и хаотичное движение молекул воздуха приводит к тому, что плотность земной атмосферы неодинакова и сильно зависит от высоты.

Измерить атмосферное давление можно. Рассмотрим насос – это прибор с помощью которого в дачных поселках добывают из-под земли воду. С древних времен и почти до середины 17 века многими учеными считалось непререкаемым утверждение древнегреческого учёного Аристотеля о том, что подъем воды в насосе вслед за поршнем происходит из-за того, что «природа боится пустоты».

В 1638 году герцог Тосканский решил украсить сады Флоренции великолепными фонтанами, что и было поручено сделать итальянским инженерам. При помощи всасывающих насосов им предстояло поднимать воду на достаточно большие высоты. Однако сделать им этого не удалось. Оказалось, что вода, засасываемая насосами, отказывалась подниматься выше 18 итальянских локтей (что примерно составляет 10,3 м). После многочисленных попыток как-то все исправить, недоумевающие инженеры обратились за помощью к престарелому Галилео Галилею. Великий ученый не смог объяснить этого явления и лишь пошутил: «вероятно, природа действительно не любит пустоты, но лишь до определенного предела».

После смерти Галилея этим вопросом занялись два его ученика — Торричелли и Вивиани.

Рассмотрим наиболее важный из опытов, проведенный в 1643 году Эванджелиста Торричелли. Для опыта он предложил использовать метровую трубку, запаянную с одного конца, наполненную ртутью. Верхний конец трубки закрывался. Трубка переворачивалась и опускалась в широкий сосуд с ртутью, после чего пробка убиралась. При этом часть ртути вытекала из трубки в сосуд, а в трубке оставался столбик ртути высотой около 760 миллиметров.

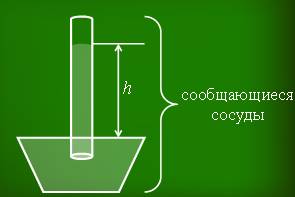
Но что же удерживало от вытекания оставшуюся в трубке ртуть? Торричелли рассуждал так. Широкий сосуд и трубка — это сообщающиеся сосуды. Над ртутью в трубке нет воздуха. А на ртуть в широком сосуде действует атмосферное давление, которое жидкая ртуть передает по всем направлениям, в том числе и вверх. Сила этого давления и поддерживает ртутный столбик.

Рассмотрим условие равновесия тонкого слоя ртути. Это условие требует, чтобы сила атмосферного давления снизу и сила гидростатического давления столба ртути сверху были равны.

p_атм = p_гидр

Это значит, что атмосферное давление равно гидростатическому давлению столба ртути в трубке. Поэтому, измерив высоту столба ртути, можно рассчитать его давление по формуле и тем самым определить величину атмосферного давления. Таким образом, Торричелли делает важный вывод о том, что «истинной причиной поднятия воды в трубке является давление воздуха, а не «боязнь пустоты».

В конце 1646 года до французского городка Руана, где в то время жил Блез Паскаль, докатилась молва об удивительных итальянских опытах с пустотой. Паскаль повторяет опыты Торричелли не только с ртутью, но и с водой, маслом, и даже красным вином, для чего ему потребовались трубки длиной около 15 метров. Причем все свои опыты Паскаль проводил прямо на улицах Руаны, тем самым радуя его жителей. Но для полного доказательства существования атмосферного давления этого Паскалю было не достаточно. Он считал, что для полного доказательства опыт следует повторить, причем два раза — один раз у подножия какой-нибудь горы, а второй раз — на ее вершине.

«Вы понимаете, если бы высота столба ртути на вершине горы оказалась бы ниже, чем у подножия, то следовало бы, что единственная причина этого — вес воздуха, а не «боязнь природой пустоты». Ясно, что внизу горы воздух должен быть плотнее, чем наверху, между тем нет никаких оснований предполагать, что природа испытывала большую боязнь высоты внизу, чем вверху». В 1648 году по поручению ученого такой эксперимент был проделан его учеником. Он полностью подтвердил предположение Паскаля о том, что атмосферное давление зависит от высоты. Так, при высоте горы в 1,5 км разница уровней ртути составила более 8 см. Таким образом, опыты Паскаля окончательно опровергли теорию Аристотеля о «боязни природой пустоты» и подтвердили существование атмосферного давления.

Так как в рассмотренных опытах Торричелли и Паскаля давление определялось высотой столба ртути, то понятно, почему его очень часто измеряют не в международных единицах — паскалях, а в миллиметрах ртутного столба.

Выразим в паскалях внесистемную единицу давления 1 миллиметр ртутного столба.

p = rgh

p_{1 мм рт. ст.} = 13 600×9,81×0,001

p_{1 мм рт. ст.} ≈ 133,3 Па

В настоящее время, по договоренности атмосферное давление считают нормальным, если оно равно давлению столба ртути высотой 760 мм при температуре воздуха 20 ºС. Такое давление часто называют 1 нормальной, или физической атмосферой. В международных единицах измерения оно составляет 101 325 Па.

Упражнения.

Задача 1. Определите высоту столба ртути, который уравновешивается атмосферным давлением 90 кПа.

Задача 2. Рассчитайте силу, сжимающую полушария, если их диаметры составляют 14 дюймов, а атмосферное давление в тот день было нормальным. Площадь сферы можно рассчитать по формуле S = 4pR², а 1 дюйм ≈ 2,54 см.

Основные выводы:

– Атмосфера нашей планеты оказывает давление на все тела, расположенные на Земле.

– Нормальное атмосферное давление принято давление столба ртути высотой 760 миллиметров при температуре воздуха 20ºС. Такое давление часто называют 1 нормальной, или физической, атмосферой.

– Давление, создаваемое 1 мм рт. ст., приблизительно составляет 133,3 Па.

Пройдите тест

Домашнее задание

Стр. 123 — 125 читать

Атмосферное давление и его измерение