Ответы Mail.ru
Образование
ВУЗы, Колледжи
Детские сады
Школы
Дополнительное образование
Образование за рубежом
Прочее образование
Вопросы – лидеры.
Найти вероятность данной задачи
1 ставка
Лидеры категории
Лена-пена
Искусственный Интеллект
М.И.
Искусственный Интеллект
Y.Nine
Искусственный Интеллект
•••
Лёха Спирин
Знаток
(302),
закрыт
11 лет назад
Лучший ответ
Продолжаем жить дальше!
Искусственный Интеллект
(170772)
11 лет назад
Нужно плотность воды умножить на 9,8 Н/кг умножить на глубину. Получится давление жидкости на такой глубине.
Остальные ответы
Владимир Соколов
Искусственный Интеллект
(212258)
11 лет назад
Формула: P=pж*g*h=1000*10*2=20000 Па.
Похожие вопросы
Давление жидкости .
(h) это глубина.
(rho) это плотность жидкости

1. Определить давление воды на глубине 7 м.Плотность воды: (rho=1000dfrac{кг}{м^3}).Атмосферное давление не учитывать.
Показать ответ
Показать решение
Видеорешение
2. Найти давление на дно цистерны с нефтью, если ее глубина (h=5м), а плотность нефти (rho=800dfrac{кг}{м^3}).Атмосферное давление не учитывать.
Показать ответ
Показать решение
Видеорешение
3. На какой глубине давление воды (p= 250 кПа) ? Плотность воды (rho=1000dfrac{кг}{м^3}).Атмосферное давление не учитывать.
Показать ответ
Показать решение
Видеорешение
4. Определить глубину озера, если давление воды на дне (p=900 кПа). Плотность воды (rho=1000dfrac{кг}{м^3}).Атмосферное давление не учитывать.
Показать ответ
Показать решение
Видеорешение
5. Давление жидкости на глубине (h=2м) равно 16 кПа. Найти плотность этой жидкости. Атмосферное давление не учитывать.
Показать ответ
Показать решение
Видеорешение
6. Определить силу, действующую снаружи на иллюминатор подводной лодки, если она находится на глубине (h=) 20 м, а его площадь (s=500 см^2) .Плотность воды (rho=1000dfrac{кг}{м^3}). Атмосферное давление не учитывать.
Показать ответ
Показать решение
Видеорешение
7. Определить силу, действующую на дно аквариума, если его глубина (h=40 см ) , а площадь дна (S= 3600 см^2) . Плотность воды (rho=1000dfrac{кг}{м^3}). Атмосферное давление не учитывать.
Показать ответ
Показать решение
Видеорешение
2016-11-22
Калькулятор доступен на полной версии сайта, с помощью него вы можете узнать давление жидкости на глубине 1, 5, 10, 20, 50, 100, 500, 1000 метров.
Вычисления осуществляются по избыточной шкале давления, в которой за 0 принято давление атмосферы.
Результат расчета давления на глубине
Вычислить давление на другой глубине
Расчет давления на глубине
Расчетная схема показана на рисунке:
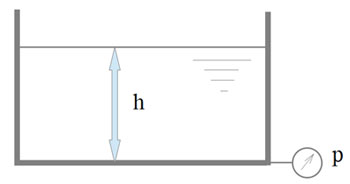
Для расчета используется формула:
P=ρ × g × h
- ρ – плотность жидкость
- h – глубина погружения
- g – ускорение свободного падения
- P – величина давления на глубине h
Пример расчета давления воды на глубине 10 метров
Для расчета давления воды на глубине 10 м, введите в графу глубина (h) – 10, выберите жидкость – вода, нажмите кнопку рассчитать.
Каждые 10 метров воды создают давление в 1 атмосферу
Полученное значение давления воды на 10 метрах равно 98,1 кПа, что примерно равно атмосферному давлению 101 кПа. Поэтому в приблизительных расчетах принимают давление в воде на глубине 10 метров равным 1 атмосфере про избыточной шкале.
Администрация сайта за результаты онлайн вычислений ответственности не несет.
Читайте также:

Все новости
Как вы уже знаете, согласно закону Паскаля, давление в жидкостях распространяется одинаково во всех направлениях. Что же необходимо знать, чтобы рассчитать это давление? От чего зависит давление жидкости?
Взгляните на рисунок 1.
Как вы думаете, в каком сосуде больше жидкости? А будет ли одинаково давление, оказываемое на дно сосудов? С этими вопросами нам и предстоит разобраться.
Вывод формулы
Выведем формулу для расчета давления жидкости на дно сосуда, имеющего форму прямоугольного параллелепипеда (рисунок 2).
Давление жидкости $p$ рассчитывается по формуле: $p = frac{F}{S}$, где $F$ — это сила, действующая на дно сосуда, а $S$ — это площадь дна сосуда.
- Сила $F$ в данном случае равна весу $P$ жидкости, которая находится в сосуде;
- Как узнать вес жидкости? Необходимо знать массу $m$ жидкости;
- Массу $m$ мы можем вычислить по известной нам формуле:
$m = rho V$;
- Так как нам известна жидкость, находящаяся в сосуде, мы знаем ее плотность . Остается вычислить объем $V$ жидкости. Обозначим высоту столба жидкости буквой $h$, площадь дна сосуда — $S$. Тогда объем можно вычислить по формуле:
$V = Sh$;
- Итак, подставляем наши данные в формулу для вычисления массы и получаем:
$m = rho Sh$;
- Таким образом, возвращаемся к весу жидкости и получаем, что:
$P = mg$, где $g$ — ускорение свободного падения, или $P = g rho Sh$.
С другой стороны, мы знаем, что вес столба жидкости равен силе, с которой жидкость давит на дно сосуда. Поэтому если мы разделим вес $P$ на площадь $S$, то получим искомое давление жидкости:
$p = frac{P}{S}$,
или $p =frac{g rho Sh}{S}$,
То есть:
$p = rho gh$.
Рассмотрим измерительные величины, которые мы будем использовать в данной формуле: плотность мы будем выражать в килограммах на кубический метр ($frac{кг}{м^3}$), $g = 9.8 frac{H}{кг}$, высоту столба жидкости — в метрах ($м$). Тогда давление $p$ будет выражено в паскалях ($Па$).
Выводы
Так мы с вами вывели формулу для расчета давления жидкости на дно сосуда. Какие выводы мы можем сделать?
От каких величин зависит давление жидкости на дно сосуда?
Давление жидкости не зависит от формы сосуда, оно зависит только от плотности жидкости и высоты ее столба.
Обратите внимание, что во многих случаях, когда говорят о высоте столба жидкости, говорят о глубине.
По какой формуле рассчитывают давление жидкости на стенки сосуда, давление внутри жидкости?
По формуле $p = rho gh$ можно вычислить давление на стенки сосуда или внутри жидкости, так как на одной глубине давление в жидкости будет одинаково во всех направлениях.
Вопросы и пример задачи
Вопрос №1
Как вы думаете, изменится ли давление на дно цилиндрического сосуда, частично заполненного водой, если в него опустить деревянный брусок (рисунок 3)?
Посмотреть ответ
Скрыть
Ответ:
В данном случае уровень воды поднимется и высота столба станет больше, значит и давление увеличится.
Вопрос №2
Какая вода: пресная или соленая оказывает большее давление на дно сосуда при одинаковом объеме?
Посмотреть ответ
Скрыть ответ
Ответ:
Здесь достаточно вспомнить, что в соленой воде нам намного проще плавать и держаться на поверхности, что о говорит о ее большей плотности. А давление прямо пропорционально плотности. Соответственно, большее давление оказывает соленая вода.
Задача
Определите давление керосина на дно цистерны, если высота столба керосина $8 space м$, а его плотность $800 frac{кг}{м^3}$.
Дано:
$rho = 800 frac{кг}{м^3}$
$h = 8 space м$
$p — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Давление рассчитывается по формуле:
$p= rho gh$.
Подставим все величины и рассчитаем его:
$p = 800 frac{кг}{м^3} cdot 9.8 frac{Н}{кг} cdot 8 space м = 62 720 space Па approx 63 space кПа$.
Ответ: $p approx 63 space кПа$.
Упражнения
Упражнение №1
Определите давление на глубине $0.6 space м$ в воде, керосине, ртути.
Дано:
$h = 0.6 space м$
$rho_1 = 1000 frac{кг}{м^3}$
$rho_2 = 800 frac{кг}{м^3}$
$rho_3 = 13600 frac{кг}{м^3}$
$g = 9.8 frac{Н}{кг}$
$p_1 — ?$
$p_2 — ?$
$p_3 — ?$
Показать решение и ответ
Скрыть
Решение:
Для расчета давления на заданной глубине будем использовать формулу $p = rho gh$.
Давление в воде:
$p_1 = rho_1 gh$,
$p_1 = 1000 frac{кг}{м^3} cdot 9.8 frac{Н}{кг} cdot 0.6 space м = 5880 space Па approx 5.9 space кПа$.
Давление в керосине:
$p_2 = rho_2 gh$,
$p_2 = 800 frac{кг}{м^3} cdot 9.8 frac{Н}{кг} cdot 0.6 space м = 4704 space Па approx 4.7 space кПа$.
Давление в ртути:
$p_3 = rho_3 gh$,
$p_3 = 13600 frac{кг}{м^3} cdot 9.8 frac{Н}{кг} cdot 0.6 space м = 79 space 968 space Па approx 80 space кПа$.
Ответ: $p_1 approx 5.9 space кПа$, $p_2 approx 4.7 space кПа$, $p_3 approx 80 space кПа$.
Упражнение №2
Вычислите давление воды на дно одной из глубочайших морских впадин — Марианской, глубина которой приблизительно равна $10 space 900 space м$. Плотность морской воды равна $1030 frac{кг}{м^3}$.
Дано:
$h = 10 space 900 space м$
$rho = 1030 frac{кг}{м^3}$
$g = 9.8 frac{Н}{кг}$
$p — ?$
Показать решение и ответ
Скрыть
Решение:
Рассчитаем давление на дне Марианской впадины по формуле:
$p = rho gh$,
$p = 1030 frac{кг}{м^3} cdot 9.8 frac{Н}{кг} cdot 10 space 900 space м = 110 space 024 space 600 space Па approx 110 space МПа$.
Ответ: $p approx 110 space МПа$.
Упражнение №3
На рисунке 3 изображена футбольная камера, соединенная с вертикально расположенной стеклянной трубкой. В камере и трубке находится вода. На камеру положена дощечка, а на нее — гиря массой $5 space кг$. Высота столба воды в трубке равна $1 space м$. Определите площадь соприкосновения дощечки с камерой.
Дано:
$m = 5 space кг$
$h = 1 space м$
$rho = 1000 frac{кг}{м^3}$
$g = 9.8 frac{Н}{кг}$
$S — ?$
Показать решение и ответ
Скрыть
Решение:
Гиря оказывает давление на футбольную камеру:
$p_1 = frac{F}{S}$.
Сила $F$, с которой она давит, будет определяться ее весом:
$F = P = F_{тяж} = mg$.
Тогда формула для давления примет следующий вид:
$p_1 = frac{mg}{S}$.
В то же время вода в трубке и камере давит на нее изнутри снизу вверх:
$p_2 = rho gh$.
Так как гиря и камера находятся в равновесии:
$p_1 = p_2$,
$frac{mg}{S} = rho gh$,
$S = frac{m}{rho h}$.
Рассчитаем эту площадь:
$S = frac{5 space кг}{1000 frac{кг}{м^3} cdot 1 space м} = 0.005 space м^2 = 50 space см^2$.
Ответ: $S = 50 space см^2$.
Задания
Задание №1
Возьмите высокий сосуд. В боковой поверхности его на разной высоте от дна сделайте три небольших отверстия. Закройте отверстия спичками и наполните сосуд водой. Откройте отверстия и проследите за струйками вытекающей воды (рисунок 4). Почему вода вытекает из отверстий? Из чего следует, что давление увеличивается с глубиной?
Показать ответ
Скрыть
Ответ:
Вода вытекает из отверстий по действием давления самой жидкости. Мы видим, что из самого нижнего отверстия бьет струйка воды с самым сильным напором, а из верхнего отверстия — с самым слабым. Этот момент объясняется тем, что с увеличением глубины давление увеличивается.
Задание №2
Налейте в стеклянный сосуд (стакан или банку) произвольное количество воды. Сделайте необходимые измерения и рассчитайте давление воды на дно сосуда.
Дано:
$h = 0.086 space м$
$rho = 1000 frac{кг}{м^3}$
$g = 9.8 frac{Н}{кг}$
$p — ?$
Показать решение и овет
Скрыть
Решение:
Рассчитаем давление воды на дно нашего стакана по формуле:
$p = rho gh$,
$p = 1000 frac{кг}{м^3} cdot 9.8 frac{Н}{кг} cdot 0.086 space м = 842.8 space Па approx 843 space Па$.
Ответ: $p approx 843 space Па$.
 Главная
Главная  Учёба
Учёба  Калькулятор давления жидкости
Калькулятор давления жидкости
Калькулятор давления жидкости
Давление жидкости это давление, оказываемое покоящейся жидкостью, на любой глубине в не зависимости от формы сосуда, в котором находится жидкость.
Найти давление жидкости в зависимости от глубины (высоты столба)
Формула расчёта давления жидкости в зависимости от глубины (высоты столба): P=h * y. Высоту (h) умножаем на удельный вес жидкости.
| Высота столба жидкости (см) | |
| Удельный вес жидкости (г/см3) |
Найти давление жидкости в зависимости от глубины (высоты столба)
Формула расчёта давления жидкости в зависимости от глубины (высоты столба): P=F/S. Вес жидкости (сила) делим на площадь поверхности.
| Вес жидкости | |
| Площадь поверхности |
Понравилась страница? Поделитесь ссылкой в социальных сетях. Поддержите проект!
Нет комментариев.
