Давление электромагнитного излучения, давление света — давление, которое оказывает световое (и вообще электромагнитное) излучение, падающее на поверхность тела.
История[править | править код]
Схематическое изображение опыта Лебедева
Впервые гипотеза о существовании светового давления была высказана И. Кеплером в XVII веке для объяснения поведения хвостов комет при пролёте их вблизи Солнца. В 1873 г. Максвелл дал теорию давления света в рамках своей классической электродинамики. Экспериментально световое давление впервые исследовал П. Н. Лебедев в 1899 г. В его опытах в вакуумированном сосуде на тонкой серебряной нити подвешивались крутильные весы, к коромыслам которых были прикреплены тонкие диски из слюды и различных металлов. Главной сложностью было выделить световое давление на фоне радиометрических и конвективных сил (сил, обусловленных разностью температуры окружающего газа с освещённой и неосвещённой стороны). Кроме того, поскольку в то время не были разработаны вакуумные насосы, отличные от простых механических, Лебедев не имел возможности проводить свои опыты в условиях даже среднего, по современной классификации, вакуума.
Путём попеременного облучения разных сторон крылышек Лебедев нивелировал радиометрические силы и получил удовлетворительное (±20 %) совпадение с теорией Максвелла. Позднее, в 1907—1910 гг., Лебедев провёл более точные опыты по изучению давления света в газах и также получил приемлемое согласие с теорией[1].
Вычисление[править | править код]
В отсутствие рассеяния[править | править код]
Для вычисления давления света при нормальном падении излучения и отсутствии рассеяния можно воспользоваться следующей формулой:
,
где 
— интенсивность падающего излучения; 
— скорость света, 
— коэффициент пропускания, 
— коэффициент отражения.
Давление солнечного света на перпендикулярную свету зеркальную поверхность, находящуюся в космосе в районе Земли, легко рассчитать через плотность потока солнечной (электромагнитной) энергии на расстоянии одной астрономической единицы от Солнца (солнечная постоянная). Оно составляет около 9 мкН/м²=9 микропаскалей, или 9⋅10−11 атм[2].
Если свет падает под углом θ к нормали, то давление можно выразить формулой:
- ,
где 
— объёмная плотность энергии излучения, — коэффициент пропускания, — коэффициент отражения, 
— единичный вектор в направлении падающего пучка, 
— единичный вектор в направлении отражённого пучка.
Например, тангенциальная составляющая силы давления света на единичную площадку будет равна
- .
Нормальная составляющая силы давления света на единичную площадку будет равна
- .
Отношение нормальной и тангенциальной составляющих равно
- .
При рассеянии[править | править код]
Если рассеяние света поверхностью и при пропускании, и при отражении подчиняется закону Ламберта, то при нормальном падении давление будет равно:
где — интенсивность падающего излучения, 
— коэффициент диффузного пропускания, 
— альбедо.
Вывод[править | править код]
Найдём импульс, уносимый электромагнитной волной от ламбертова источника. Полная светимость ламбертова источника, как известно, равна
- ,
где 
— сила света в направлении нормали.
Отсюда сила света под произвольным углом 
к нормали, по закону Ламберта, равна
- .
Энергия, излучаемая в элемент телесного угла, имеющий вид сферического кольца, равна
- .
Для определения импульса, уносимого излучением, нужно учитывать только его нормальную составляющую, так как в силу поворотной симметрии все тангенциальные составляющие взаимно компенсируются:
- .
Отсюда
- .
Для рассеянного обратно излучения 
и 
.
Для излучения, прошедшего сквозь пластинку, 
и 
(минус возникает из-за того, что это излучение направлено вперёд).
Складывая давление, создаваемое падающим и обоими видами рассеянного излучения, получаем искомое выражение.
В случае, когда отражённое и пропущенное излучение является частично направленным и частично рассеянным, справедлива формула:
где I — интенсивность падающего излучения, k — коэффициент направленного пропускания, K — коэффициент диффузного пропускания, ρ — коэффициент направленного отражения, A — альбедо рассеяния.
Давление фотонного газа[править | править код]
Изотропный фотонный газ, имеющий плотность энергии u, оказывает давление:
В частности, если фотонный газ является равновесным (излучение абсолютно чёрного тела) с температурой T, то его давление равно:
где σ — постоянная Стефана — Больцмана.
Физический смысл[править | править код]
Давление электромагнитного излучения является следствием того, что оно, как и любой материальный объект, обладающий энергией E и движущийся со скоростью v, также обладает импульсом p = Ev/c². А поскольку для электромагнитного излучения v = c, то p = E/c.
В электродинамике давление электромагнитного излучения описывается тензором энергии-импульса электромагнитного поля.
Корпускулярное описание[править | править код]
Если рассматривать свет как поток фотонов, то, согласно принципам классической механики, частицы при ударе о тело должны передавать ему импульс, другими словами — оказывать давление.
Волновое описание[править | править код]
С точки зрения волновой теории света электромагнитная волна представляет собой изменяющиеся и взаимосвязанные во времени и пространстве колебания электрического и магнитного полей. При падении волны на отражающую поверхность электрическое поле возбуждает токи в приповерхностном слое, на которые действует магнитная составляющая волны. Таким образом, световое давление есть результат сложения многих сил Лоренца, действующих на частицы тела.
| Расстояние от Солнца, а. е. |
Давление, мкПа (мкН/м²) |
|---|---|
| 0.20 | 227 |
| 0.39 (Меркурий) | 60.6 |
| 0.72 (Венера) | 17.4 |
| 1.00 (Земля) | 9.08 |
| 1.52 (Марс) | 3.91 |
| 3.00 (пояс астероидов) | 1.01 |
| 5.20 (Юпитер) | 0.34 |
Применение[править | править код]
Космические двигатели[править | править код]
Возможными областями применения являются солнечный парус и разделение газов[1], а в более отдалённом будущем — фотонный двигатель.
Ядерная физика[править | править код]
В настоящее время[когда?] широко обсуждается возможность ускорения световым давлением, создаваемым сверхсильными лазерными импульсами, тонких (толщиной от 5 до 10 нм) металлических плёнок с целью получения высокоэнергичных протонов[5].
См. также[править | править код]
- Давление звукового излучения
- Радиометр Крукса
- Пондеромоторная сила
Примечания[править | править код]
- ↑ 1 2 Давление света // Физическая энциклопедия. — М., «Советская энциклопедия», 1988. — Т. 1. — С. 553—554. Архивировано 23 октября 2008 года.
- ↑ A. Bolonkin. High Speed AB-Solar Sail (англ.). — 2007. — arXiv:physics/0701073.
- ↑ Georgevic, R. M. (1973) «The Solar Radiation Pressure Forces and Torques Model», The Journal of the Astronautical Sciences, Vol. 27, No. 1, Jan-Feb. First known publication describing how solar radiation pressure creates forces and torques that affect spacecraft.
- ↑ Wright, Jerome L. (1992), Space Sailing, Gordon and Breach Science Publishers
- ↑
T. Esirkepov, M. Borghesi, S. V. Bulanov, G. Mourou, and T. Tajima. Highly Efficient Relativistic-Ion Generation in the Laser-Piston Regime (англ.) // Phys. Rev. Lett.. — 2004. — Vol. 92. — P. 175003.
Литература[править | править код]
- Lebedew P., Untersuchungen liber die Dnickkräfte des Lichtes, «Annalen der Physik», 1901, fasc. 4, Bd 6, S. 433—458. DOI: https://dx.doi.org/10.1002/andp.19013111102;
- Лебедев П. Н., Избр. соч., М. — Л., 1949
- Ландсберг Г. С., Оптика, 4 изд., М., 1957;
- Свет, вещество, электромагнитное поле, гравитация [1]
Давление света можно объяснить с помощью электромагнитной теории Максвелла. Свет — это электромагнитная волна. Электрическое поле разгоняет электроны вещества. Из-за присутствия магнитного поля на движущиеся электроны действует сила Лоренца, которая направлена внутрь вещества.
В (1873) году с помощью своей теории Максвелл доказал, что давление света вычисляется по формуле:
(P=frac{2W}{c}). ((1))
Давление света можно объяснить и с точки зрения квантовой теории, то есть рассматривая свет как поток частиц с энергией (E=hnu) и импульсом (p=hnu/c). Если энергетическая освещённость поверхности (W), то можно определить число фотонов, падающих на поверхность площадью (S) за время (Delta t):
(boxed{n=frac{W}{SDelta t hnu}}). ((2))
Коэффициент отражения (R) показывает отношение количества отражённых фотонов к количеству падающих, поэтому в среднем фотон передаёт импульс:
(Delta p=p-R(-p)=(1+R)p=(1+R)frac{h}{c}.) ((3))
Используя закон изменения импульса, можно записать, что:
(F=n frac{Delta p}{Delta t}). ((4))
Если поверхность чёрная ((R=0)), то давление света выразится как:
(boxed{P_{черн}=frac{W}{SDelta t hnu} cdot frac{h}{c Delta t}=frac{W}{c}}). ((5))
Зеркало можно представить как поверхность с коэффициентом отражения (R=1). В этом случае давление света определяется как:
(boxed{P_{зерк}=frac{W}{SDelta t hnu} cdot frac{2 h}{c Delta t}=frac{W}{c} =frac{2W}{c}}). ((6))
Формула для подсчёта давления света в теории Максвелла ((1)) является частным случаем формулы ((6)) корпускулярной (квантовой) теории. Результаты, предсказанные формулами ((5)) и ((6)), с высокой точностью (погрешность (2) (%)) подтверждаются экспериментальными данными.
Давление света — Поток фотонов (свет), который при соударении с поверхностью оказывает давление.
Поток фотонов, падающие на поглощающую поверхность 
:
Поток фотонов, падающие на зеркальную поверхность 
:
Поток фотонов, падающие на поверхность 
:
Физический смысл Давления света:
Свет — это поток фотонов, то, согласно принципам классической механики, частицы при ударе о тело должны передавать ему импульс, другими словами — оказывать давление
Прибор, измерения давления света, представлял собой очень чувствительный крутильный динамометр (крутильные весы). Создал данный прибор Лебедев. Его подвижной частью являлась подвешенная на тонкой кварневой нити легкая рамка с укрепленными на ней крылышками — светлыми и черными дисками толщиной до 0,01 мм. Крылышки делали из металлической фольги. Рамка была подвешена внутри сосуда, из которого откачали воздух. Свет, падая на крылышки, оказывал на светлые и черные диски разное давление. В результате на рамку действовал вращающий момент, который закручивал нить подвеса. По углу закручивания нити и определяли давление света.
В Формуле мы использовали :
— Давление света
— Сила, с которой давит фотон
— Площадь поверхности, на которую происходит давление света
— Импульс одного фотона
— Постоянная Планка
— Скорость света
— Плотность потока энергии
— Интенсивность света
— Промежуток времени
Содержание
- Что значит давление света
- Кто первый измерил силу давления света
- Формула для расчета
- Опыты Лебедева
- Вывод
Писатели-фантасты в своих произведениях описывают космические путешествия на кораблях, приводимых в движение солнечным ветром. На самом деле, это не такая уж и фантастика. Свет действительно способен оказывать давление на предметы, на которые он падает.
Что значит давление света
Если на лист бумаги направить струю воздуха, легко увидеть, что поток газа оказывает давление на поверхность. Если на бумагу или любую другую поверхность направить световой поток, то и в этом случае будет оказываться давление, хотя и намного меньшее.
Объяснить это можно с точки зрения двух теорий.
В современной физике считается, что частицы света – фотоны – имеют дуальные свойства:
- Свойства электромагнитной волны (волновая теория света).
- Свойства материальной частицы (корпускулярная теория).
Согласно первой теории, электромагнитные волны, попадая на поверхность предметов (или в толщу газов), возбуждает в ней токи. Эти токи взаимодействуют с магнитной составляющей волны. Возникающие при этом силы Лоренца складываются, создавая воздействие на облучаемый предмет.
Согласно корпускулярной теории, фотоны бомбардируют поверхность, подобно летящим мячам. Частицы передают свой импульс облучаемому предмету. Таким образом создается давление.
Кто первый измерил силу давления света
Считается, что давление света открыл русский физик Петр Николаевич Лебедев. На самом деле, это явление предсказал еще в 17 веке Иоганн Кеплер по результатам своих астрономических наблюдений. Создатель классической электродинамики Максвелл теоретически обосновал, что световой поток может оказывать давление, и объяснил это с точки зрения волновой теории света.
Величайшая заслуга Лебедева перед мировой физикой в том, что он экспериментальным путем доказал, что давление света существует, а также смог измерить величину этого давления. До этого ученый мир был разделен на две группы:
- одни считали, что подобное явление существует, но с помощью технических средств того времени доказать это было невозможно;
- другие (включая авторитетнейшего Уильяма Томсона) считали, что свет давления не производит.
И у той, и у другой стороны были весомые на то время аргументы. Разрешить спор мог только удачный эксперимент, результаты которого признали бы все.
Формула для расчета
В 1873 году Максвелл в своем «Трактате по электричеству и магнетизму» вывел теоретическую формулу давления света:
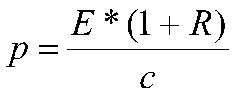
, где:
- E – энергия светового потока за единицу времени, отнесенная к площади поверхности;
- R – коэффициент отражения;
- с – скорость света в вакууме.
Задачей экспериментаторов стало измерить величины, входящие в эту формулу и подтвердить или опровергнуть выводы Максвелла.
Опыты Лебедева
Попытки провести опыты, доказывающие правоту той или иной стороны, заканчивались неудачей, хотя идея была проста. На легкое крылышко, подвешенное в вакууме, надо было направить световой поток, а по углу отклонения крылышка вычислить искомую величину.
При облучении светом поверхностей возникали иные силы, искажавшие результаты экспериментов. Например, часть излучения поглощалась, что вызывало нагрев освещаемого предмета. Этот нагрев практически всегда носил неравномерный характер, поэтому окружающий газ также нагревался неравномерно. Возникающие при этом конвекционные явления вызывали дополнительное воздействие, превышающее силу светового потока. Для этого приходилось помещать облучаемый предмет в прозрачный сосуд, из которого откачивался воздух. При этом возникала еще одна проблема – неравномерный нагрев стенок сосуда, вызывавший дополнительные конвекционные явления, ведь создавать глубокий вакуум при существовавшем тогда уровне техники было крайне сложно.
Лебедев смог решить все проблемы, хотя для этого понадобилось 4 года напряженной работы. Сначала он научился эффективно, для того времени, удалять воздух из сосуда. Чтобы снизить конвекцию, он применил сосуды большого объема, что привело к практическому устранению влияния движения разреженного воздуха. Нагрев сосуда удалось нивелировать, благодаря применению светофильтров, «вырезающих» часть светового спектра, наиболее поглощаемую стеклянными стенками. Удалось побороть и другие факторы, влияющие на точность измерения.
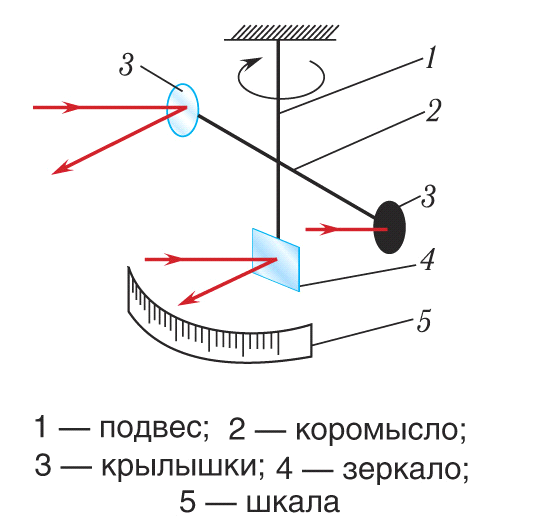
Лебедев облучал видимым светом «вертушку» из крылышек из платиновой фольги различной толщины. Часть поверхностей была отполирована до зеркального состояния, часть – зачернена. Посредством этого приема можно было проверить гипотезу о том, что при отражении свет оказывает большее давление, чем при поглощении.
«Вертушки» подвешивались внутри сосуда на нити. По углу закручивания этой нити можно было определить силу светового давления. Для измерения этого угла использовалось зеркальце со шкалой.
На тот момент доминирующей являлась электромагнитная теория света, давление объяснялось с максвелловской точки зрения. Из этой теории следует, что сила давления пропорциональна энергии светового пучка. Чтобы измерить эту энергию физик применил калориметр, который временно помещался на место вертушки. Опыты Лебедева доказали верность Максвелловских взглядов, и результаты экспериментов совпали с расчетными данными в пределах 20%. На тот момент это был прорыв.
Через несколько месяцев русский ученый усовершенствовал экспериментальную установку, получив расхождение с теорией менее 1%.
Через короткое время в мире физики получила распространение и подтверждение теория и корпускулярной (наряду с электромагнитной) природы света. Опыты Лебедева ей не противоречили, и во многом ее подтверждали.
Для наглядности видео.
Вывод
Существование давления света, как физического явления, давно никем не оспаривается. При точных расчетах траекторий спутников, например, учитывается величина давления солнечного света.
Практическое же применение этого эффекта достаточно ограничено. Хотя мечты фантастов о космических путешествиях под солнечным парусом, приводимым в движение давлением солнечного света, остаются пока мечтами, экспериментальный исследовательский объект к Венере, движущийся по подобному принципу, уже запущен. Для дальнейшего развития таких движителей придется подождать появления легких, но прочных материалов.
Еще это физическое явление применяется в ядерной физике для разгона мельчайший объектов до подсветовых скоростей. Перспективным, но не очень широко применимым, выглядит и изобретение «светового пинцета» для микроскопических объектов. Но ведь и электричество, и телевидение, и многое другое, что прочно вошло в жизнь современного человека, тоже сначала выглядело бесполезными игрушками. Подождем развития технологий.
Интенсивность света I в выбранной точке – это модуль средней по времени величины плотности потока энергии, которую световая волна переносит.
Определение плотности потока электромагнитной энергии возможно при помощи вектора Умова-Пойнтинга P→. Отсюда следует, что математический вид определения интенсивности света записывается в виде формулы:
I=P→=E→×H→.
По выражению усреднение проводится за период времени t, причем больший по сравнению с периодом колебания волны T t≫T. Интенсивность света записывается как:
It=1T∫tt+TP→(t)dt.
В системе СИ единицей измерения является Втм2.
Модули амплитуд (Em и Hm) векторов напряженностей электрического E→ и магнитного H→ полей в электромагнитной волн записываются в виде отношения:
Имеем, что μ≈1. Необходимо выразить амплитуду Hm:
где n=εμ=ε при μ≈1 является показателем преломления вещества, в котором распространяется свет.
Модуль среднего значения вектора Умова-Пойнтинга пропорционален произведению амплитуд Em·Hm.
Интенсивность света не может быть измерена в связи с тем, что поле изменяется с высокой частотой ν=1015 Гц, соответственно период колебаний составляет T=10-15 с, а приемники колебаний обладают временем инерции существенно больше, чем 10-15 c.
Отсюда следует, что среднее значение интенсивности можно регистрировать. Также возможно измерение средней интенсивности, но не фазы поля.
Давление света
По закону сохранения при поглощении и отражении света телом ему сообщается импульс, равняющийся разности импульсов пучка света до и после этих процессов. Отсюда следует, что на тело действует сила, свет производит соответствующее давление на тело. Еще Кеплер выдвинул свое предположение о существовании давления света, которое было принято при рассмотрении отклонений хвостов комет от Солнца.
Последователи волновой теории отрицали давление света, отсутствие доказательств опытами о существовании светового давления служило аргументом против корпускулярной. То есть существование светового давления считалось следствием электромагнитной теории.
Если световая волна падает перпендикулярно плоскости поверхности тела и полностью поглощает свет, то определение давления p производится по формуле.
Где G считается плотностью импульса световой волны, P – модулем вектора Умова-Пойнтинга, с – скоростью света в вакууме.
Если происходит полное отражение света при помощи поверхности тела, то импульс, который при помощи него передается, имеет значение в 2 раза больше, также как и значение давления.
При падении световой волны на поверхность под углом относительно нормали, производя расчеты давления, применяют только перпендикулярную составляющую плотности потока энергии. Если имеются обычные условия, то давление крайне малое, то есть в 1010 раз меньше атмосферного.
П.Н. Лебедев в 1899 году смог измерить световое давление. Для этого он применил крутильные весы, находящиеся в вакууме. Позже его опыты определения существования давления света подтвердили электромагнитную теорию света Максвелла.
Давление электромагнитных волн считается результатом воздействия электрического поля волны частицы вещества, которые обладают электрическим зарядом, движутся упорядоченно, на них действуют силы Лоренца.
Примеры
Определить давление, оказываемое плоской световой волной, падающей перпендикулярно относительно поверхности тела и поглощаемой телом. Значение амплитуды напряженности электрического поля равняется 2 Вм.
Решение
Будем использовать формулу:
p=Pc (1.1).
Где P принимается за среднее значение модуля вектора Умова-Пойнтинга, c=3·108 мс – за скорость света в вакууме.
Для нахождения среднего значения модуля вектора Умова-Пойнтинга необходимо использовать:
P=E·H (1.2).
В условии имеем плоскую волну, тогда уравнение ее колебаний зафиксируем как:
E=Emcos ωt-kx, H=Hmcos ωt-kx (1.3).
Для нахождения значения амплитуды напряжения магнитного поля следует применить:
εε0Em=μμ0Hm (1.4).
Когда для вакуума ε=1, μ=1, можно выразить из (1.4) Hm. Получим:
Hm=ε0μ0Em (1.5),
где μ0=4π·10-7 Гнм, ε0=14π·9·109Фм. Это говорит о том, что средним значением модуля вектора Умова-Пойнтинга будет:
P=Emcos ωt-kx·ε0μ0Emcosωt-kx=ε0μ0Em2cosωt-kx==12ε0μ0Em2 (1.6).
Далее производим подстановку правой части выражения (1.6) в (1.1) вместо P, тогда искомое давление света:
p=12ε0μ0Em2c.
Заменим числовые значения и получим:
p=12·3·10814π·10-7·4π·9·109·4=4120π·6·108=1,77·1011 (Па)
Ответ: 17,7 пПа.
Определить интенсивность I плоской световой волны, распространяющейся вдоль Ох. Значение напряженности электрического поля волны равняется EmВм.
Решение
Из определения выявим интенсивность световой волны:
I=P (2.1).
Запись модуля вектора Умова-Пойтинга для плоской световой волны обозначится как:
P=EH=EmHmcos2ωt-kx (2.2).
Среднее значение P:
P=12EmHm 2.3, так как cos2ωt-kx=12.
Сравнивая с примером 1, можно произвести выражение амплитуды напряженности магнитного поля:
εε0Em=μμ0Hm→Hm=εε0μμ0Em (2.4).
Из (2.1), (2.3), (2.4) получим:
I=12εε0μμ0Em2.
Ответ: I=12εε0μμ0Em2.
