Как определить длину волны де Бройля для электрона
Содержание:
- Волна де Бройля или волна амплитуды вероятности
- Природа волн де Бройля, фазовая и групповая скорость
- Какой формулой определяется длина волны
- Как определить длину волны де Бройля для электрона
Волна де Бройля или волна амплитуды вероятности
Волна де Бройля является волной вероятности или волной амплитуды вероятности, которая определяет плотность вероятности обнаружения объекта в конкретной точке конфигурационного пространства.
Согласно определения волн де Бройля, можно сделать вывод об их взаимодействии с какими-либо частицами и их волновой природе. Формулировка волн материи была введена в науку в 1924 году французским физиком-теоретиком Луи де Бройлем. Благодаря теории, свойство корпускулярно-волнового дуализма (или двойственности) было распространено на любые проявления материи, включая излучение и какие-либо частицы вещества.
В современной квантовой теории «волна материи» понимается несколько иначе. Однако название данного физического феномена, связанного с частицами вещества, включая водород, сформулировано в честь автора гипотезы.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
В 1913 году Н. Бор предложил полуклассическую модель атома, в основе которой было два постулата:
- Момент импульса электрона в атоме строго определен. Величина в любом случае пропорциональна nh/2π, где n – какое-либо целое число, начиная с 1, а h – постоянная Планка, присутствие которой в формуле ясно свидетельствует о том, что момент импульса частицы квантован. Таким образом, атом включает комплекс разрешенных орбит, по которым только и может перемещаться электрон. Когда электрон расположен на этих орбитах, излучение (то есть потеря энергии) отсутствует.
- Атомный электрон излучает или поглощает энергию в процессе перехода с одной орбиты на другую в количестве, определяемом, как разность энергий на этих орбитах. В связи с тем, что промежуточные состояния между разрешенными орбитами отсутствуют, излучение строго квантуется. Показатель его частоты составляет (E1 – E2)/h, что является выводом из формулы Планка для энергии E = hν.
Таким образом, боровская модель атома не предусматривает излучение электрона на орбите, его нахождение между орбитами. Однако согласно простой рассматриваемой модели, движение электрона рассматривают с классической точки зрения, как вращение планеты вокруг Солнца.
В процессе поиска ответа на вопрос о поведении электрона Де Бройль предположил, что электрону в любом случае должна соответствовать определенная волна. Благодаря ей, частица «выбирает» исключительно такие орбиты, на которых данная волна укладывается целое число раз. В этом и заключался смысл целочисленного коэффициента в постулированной Бором формуле.
Гипотеза приводит к выводу, что электронная волна де Бройля не является электромагнитной, а волновые параметры должны быть характерны для любых материальных частиц, а не только для электронов в атоме. Ученому удалось получить важное соотношение, с помощью которого можно определить тип этих рассматриваемых волновых свойств. Формула расчета волны де Бройля:
(λ = h/p)
где λ – является длиной волны, p – определяет импульс частицы в уравнении.
Де Бройль объединил в одном соотношении корпускулярную и волновую характеристики материи: такие, как импульс и длина волны. Данные параметры связывает постоянная Планка, величина которой примерно составляет (6,626*10^{-27} эрг∙с) или (6,626*10^{-34} Дж∙с), задающая масштаб проявления волновых свойств вещества.
Природа волн де Бройля, фазовая и групповая скорость
Следует отметить, что волны де Бройля, называемые электронными волнами, не являются электромагнитными. В 1927 году американским физикам Дэвиссону и Джермеру удалось подтвердить гипотезу де Бройля. Ученые обнаружили дифракцию электронов на кристалле никеля. В процессе получилось определить дифракционные максимумы, которые соответствуют формуле Вульфа-Брэггов:
(2dsinj = nl)
Расчет брэгговской длины волны подтвердил ее соответствие формуле:
В дальнейшем гипотеза де Бройля была подтверждена опытным путем Л.С. Тартаковским и Г. Томсоном. Ученым удалось зафиксировать дифракционную картину, когда пучок быстрых электронов при Е≈ 50 кэВ проходит сквозь фольгу из разных металлов.
Чуть позже получилось обнаружить дифракцию нейтронов, протонов, атомных пучков и молекулярных пучков. В дальнейшем были изобретены инновационные методики исследования вещества, включая нейтронографию и электронографию, сформировалось направление электронной оптики.
Макротела должны характеризоваться аналогичными свойствами. В случае, если m = 1кг, (l = 6,62*10^{-31} м) – невозможно обнаружить современными методами – поэтому макротела рассматриваются только в качестве корпускул.
В том случае, когда частица с массой m перемещается со скоростью v, фазовая скорость волн де Бройля будет определяться по формуле:
Исходя из того, что c > v, фазовая скорость волн де Бройля превышает скорость света в вакууме. Можно отметить, что фазовая скорость Vф может быть больше и может быть меньше с, в отличие от групповой скорости. Формула групповой скорости:
Таким образом, групповая скорость волн де Бройля соответствует скорости движения частицы. В случае фотона она будет равна:
В результате, значение групповой скорости равно скорости света.
Волны де Бройля подвержены дисперсии. Если подставить выражение:
в формулу:
получим следующее равенство:
(Vф= f(λ))
Примечание
Так как присутствует дисперсия, волны де Бройля невозможно представить, как волновой пакет. В противном случае, он мгновенно «расплывется», то есть исчезнет, в течение 10-26 с.
Какой формулой определяется длина волны
Количественные соотношения, которые связывают корпускулярные и волновые способности частиц, аналогичны свойствам фотонов:
Гипотеза де Бройля основана на универсальном характере данного равенства, что справедливо в условиях любых волновых процессов. Какой-либо частице, которая обладает импульсом р, соответствует волна. Ее длину можно определить с помощью формулы де Бройля:
p =mv– является импульсом частицы, h – определяется, как постоянная Планка.
Как определить длину волны де Бройля для электрона
Рассчитать длину волны де Бройля для электрона можно на конкретном примере. Предположим, то требуется определить длину волны де Бройля λ для электрона, кинетическая энергия которого составляет:
- W1 = 10 кэВ;
- W2 = 1 МэВ.
В первую очередь стоит записать исходные данные:
(m_{e}=9,1*10^{-31} кг)
(W1 = 10 кэВ = 10*10^{3}*1,6*10^{-19} = 1,6*10^{-15}Дж)
(W2 = 1 МэВ = 10*10^{6}*1,6*10^{-19}= 1,6*10^{-13} Дж)
Требуется найти λ.
Решение:
Формула волны де Бройля:
Так как известна кинетическая энергия электронов, можно рассчитать их скорость:
Далее можно определить длину волны де Бройля:
В том случае, когда скорость v частиц соизмерима со скоростью света с, длину волны де Бройля можно рассчитать по формуле:

3.1.Гипотеза де Бройля
3.2.Дифракция частиц
3.3.Корпускулярно-волновой дуализм микрочастиц вещества
3.1. Гипотеза де Бройля
Недостатки теории Бора указывали на необходимость пересмотра основ квантовой теории и представлений о природе микрочастиц (электронов, протонов и т.п.). Возник вопрос о том, насколько исчерпывающим является представление электрона в виде малой механической частицы, характеризующейся определенными координатами и определенной скоростью.
Мы уже знаем, что в оптических явлениях наблюдается своеобразный дуализм. Наряду с явлениями дифракции, интерференции (волновыми явлениями) наблюдаются и явления, характеризующие корпускулярную природу света (фотоэффект, эффект Комптона).
В 1924 г. Луи де Бройль выдвинул гипотезу, что дуализм не явля-
ется особенностью только оптических явлений, а имеет универ-
сальный характер. Частицы вещества также обладают волновыми свойствами.
Луи де Бройль (1892–1987), французский физик, удостоенный Нобелевской премии (1929 г). по физике за открытие волновой природы электрона. В 1923 г., развив идею А. Эйнштейна о двойственной природе, предположил, что поток материальных частиц должен обладать и волновыми свойствами, связанными с их массой и энергией (волны де Бройля). Экспериментальное подтверждение этой идеи было получено в 1927 г. в опытах по дифракции электронов в кристаллах, а позже она получила практическое применение при разработке магнитных линз для
электронного микроскопа. Концепцию Луи де Бройля о корпускулярно-волновом дуализме использовал Э. Шредингер при создании волновой механики.
«В оптике, – писал Луи де Бройль, – в течение столетия слишком пренебрегали корпускулярным способом рассмотрения по сравнению с волновым; не делалась ли в теории вещества обратная ошибка?» Допуская, что частицы вещества наряду с корпускулярными свойствами имеют также и волновые, де Бройль перенес на случай частиц вещества те же правила перехода от одной картины к другой, какие справедливы в случае света.
33

Если фотон обладает энергией E = hν и импульсом p = h / λ, то и
частица (например электрон), движущаяся с некоторой скоростью, обладает волновыми свойствами, т.е. движение частицы можно рас-
сматривать как движение волны.
Согласно квантовой механике, свободное движение частицы с массой m и импульсом p = mυ (где υ – скорость частицы) можно предста-
вить как плоскую монохроматическую волну Ψ0 (волну де Бройля) с длиной волны
|
λ = |
h |
, |
(3.1.1) |
|
|
p |
||||
распространяющуюся в том же направлении (например в направлении оси х), в котором движется частица (рис. 3.1).
Рис. 3.1
Зависимость волновой функции Ψ0 от координаты х даётся формулой
|
Ψ0 ~ cos(k0 x) , |
(3.1.2) |
|
|
где k0 – волновое число, а волновой вектор k0 |
направлен в сторону |
|
|
распространения волны или вдоль движения частицы: |
||
|
r |
2π r |
(3.1.3) |
|
k0 = |
h |
p . |
Таким образом, волновой вектор монохроматической волны, свя-
занной со свободно движущейся микрочастицей, пропорционален её им-
пульсу или обратно пропорционален длине волны.
Поскольку кинетическая энергия сравнительно медленно движу-
щейся частицы К = mυ2 / 2 , то длину волны можно выразить и через энергию:
|
λ = |
h |
. |
(3.1.4) |
|
2mК |
При взаимодействии частицы с некоторым объектом – с кристаллом, молекулой и т.п. – её энергия меняется: к ней добавляется потенциальная энергия этого взаимодействия, что приводит к изменению движения
34
частицы. Соответственно, меняется характер распространения связанной с частицей волны, причём это происходит согласно принципам, общим для всех волновых явлений. Поэтому основные геометрические закономерности дифракции частиц ничем не отличаются от закономерно-
стей дифракции любых волн. Общим условием дифракции волн любой природы является соизмеримость длины падающей волны λ с расстоянием d между рассеивающими центрами: λ ≤ d .
Гипотеза Луи де Бройля была революционной, даже для того революционного в науке времени. Однако, она вскоре была подтверждена многими экспериментами.
3.2. Дифракция частиц
Дифракция частиц – рассеяние микрочастиц (электронов, нейтронов, атомов и т.п.) кристаллами или молекулами жидкостей и газов, при котором из начального пучка частиц данного типа возникают дополнительно отклонённые пучки этих частиц. Направление и интен-
сивность таких отклонённых пучков зависят от строения рассеивающего объекта.
Дифракция частиц может быть понята лишь на основе квантовой теории. Дифракция – явление волновое, оно наблюдается при распространении волн различной природы: дифракция света, звуковых волн, волн на поверхности жидкости и т.д. Дифракция при рассеянии частиц, с точки зрения классической физики, невозможна.
Квантовая механика устранила абсолютную грань между волной и частицей. Основным положением квантовой механики, описывающей поведение микрообъектов, является корпускулярно-волновой дуализм,
т.е. двойственная природа микрочастиц. Так, поведение электронов в одних явлениях, например при наблюдении их движения в камере Вильсона или при измерении электрического заряда в фотоэффекте, может быть описано на основе представлений о частицах. В других же, особенно в явлениях дифракции, – только на основе представления о волнах. Идея «волн материи», высказанная французским физиком Л. де Бройлем, получила блестящее подтверждение в опытах по дифракции частиц.
Опыты по дифракции частиц и их квантово-механическая интерпретация
Первым опытом по дифракции частиц, блестяще подтвердившим исходную идею квантовой механики – корпускулярно-волновой дуализм, явился опыт американских физиков К. Дэвиссона и Л. Джермера, проведенный в 1927 году по дифракции электронов на монокристаллах
35

никеля. На рис. 3.2 изображена схема опыта (А – электронная пушка, В – детектор излучения) и на рис. 3.3 – динамика дифракционного отражения электронов при изменении ускоряющей разности потенциалов.
Рис. 3.2 Рис. 3.3
Если ускорять электроны электрическим полем с напряжением U, то они приобретут кинетическую энергию К = eU (е – заряд электрона), что после подстановки в равенство (3.1.4) числовых значений даёт
|
λ = |
12,26 |
. |
(3.2.1) |
|
U |
Здесь U выражено в В, а λ – в Å (1 Å = 10–10 м).
При напряжениях U порядка 100 В, которые использовались в этих опытах, получаются так называемые «медленные» электроны с λ порядка 1 Å. Эта величина близка к межатомным расстояниям d в кристаллах, которые составляют несколько Å и менее, и соотношение λ ≤ d , необходимое для возникновения дифракции, выполняется.
Кристаллы обладают высокой степенью упорядоченности. Атомы в них располагаются в трёхмерно-периодической кристаллической решётке, т.е. образуют пространственную дифракционную решётку для соответствующих длин волн. Дифракция волн на такой решётке происходит в результате рассеяния на системах параллельных кристаллографических плоскостей, на которых в строгом порядке расположены рассеивающие центры. Условием наблюдения дифракционного максимума
|
при отражении от кристалла является условие Вульфа–Брэггов: |
|
|
2d sin θ = nλ, |
(3.2.2) |
здесь θ – угол, под которым падает пучок электронов на данную кристаллографическую плоскость (угол скольжения), а d – расстояние между соответствующими кристаллографическими плоскостями.
36

Вопыте Дэвиссона и Джермера при «отражении» электронов от поверхности кристалла никеля при определённых углах отражения возникали максимумы. Как видно из рис. 3.3, экспериментальная кривая зависимости интенсивности от ускоряющего напряжения имеет несколько максимумов, равностоящих друг от друга.
Эти максимумы отражённых пучков электронов соответствовали формуле (3.2.2), и их появление не могло быть объяснено никаким другим путём, кроме как на основе представлений о волнах и их дифракции. Таким образом, волновые свойства частиц – электронов – были доказаны экспериментом.
При более высоких ускоряющих электрических напряжениях (десятках кВ) электроны приобретают достаточную кинетическую энер-
гию, чтобы проникать сквозь тонкие плёнки вещества (толщиной порядка 10–5 см, т. е. тысячи Å). Тогда возникает так называемая дифракция быстрых электронов на прохождение, которую на поликристаллических плёнках алюминия и золота впервые в 1927 г. исследовали английский учёный Дж. Дж. Томсон и, независимо от него, советский физик П. С. Тартаковский.
В1949 г. советские ученые Л.М. Биберман, Н.Г. Сушкин, В.А. Фабрикант поставили такой же опыт, но интенсивность электронного пучка была настолько слабой, что электроны проходили через прибор практически поодиночке. Однако картина после длительной экспозиции была точно такой же. Т.е. было доказано, что волновыми
свойствами обладает каждый отдельный электрон.
Вскоре после этого удалось наблюдать и явления дифракции атомов и молекул. Атомам с массой М, находящимся в газообразном состоянии в сосуде при абсолютной температуре Т, соответствует, по формуле (3.1.4), длина волны
|
λ = |
h |
, |
(3.2.3) |
|
|
3MkT |
||||
т.к. средняя кинетическая энергия атома К = 2 / 3kT .
Для лёгких атомов и молекул (Н, H2, Не), и температур в сотни градусов Кельвина, длина волны λ составляет около 1 Å. Дифрагирующие атомы или молекулы практически не проникают в глубь кристалла.
Сформированный с помощью диафрагм молекулярный или атомный пучок направляют на кристалл и тем или иным способом фиксируют «отражённые» дифракционные пучки. Таким путём немецкие учёные О. Штерн и И. Эстерман, а также другие исследователи на рубеже 30-х гг. наблюдали дифракцию атомных и молекулярных пучков
(рис. 3.4).
37

Рис. 3.4 Рис. 3.5
Позже наблюдалась дифракция протонов, а также дифракция нейтронов (рис. 3.5), получившая широкое распространение как один из методов исследования структуры вещества.
Так, было доказано экспериментально, что волновые свойства присущи всем без исключения микрочастицам.
Дифракция частиц, сыгравшая в своё время столь большую роль в установлении двойственной природы материи – корпускулярноволнового дуализма (и тем самым послужившая экспериментальным обоснованием квантовой механики), давно уже стала одним из главных рабочих методов для изучения строения вещества. На дифракции частиц основаны два важных современных метода анализа атомной структуры вещества – электронография и нейтронография.
3.3. Корпускулярно-волновой дуализм микрочастиц вещества
Итак, микрочастицы обладают необычайными свойствами. Микро-
частицы – это элементарные частицы (электроны, протоны, нейтроны и т.д.), а также сложные частицы, образованные из небольшого числа элементарных (пока неделимых) частиц (атомы, молекулы, ядра атомов). Называя эти микрочастицы частицами, мы подчеркиваем только одну сторону, правильнее было бы назвать «частица-волна».
Микрочастицы не способны непосредственно воздействовать на наши органы чувств – ни видеть, ни осязать их нельзя. Мы знаем, что будет с большим предметом; но именно так микрочастицы не поступают! Поэтому, изучая их, приходится прибегать к различного рода абстракциям, напрягать воображение и не пытаться связывать их с нашим непосредственным опытом.
38

В доквантовой физике понять – значить составить себе наглядный образ объекта или процесса. В квантовой физике так рассуждать нельзя. Всякая наглядная модель будет действовать по классическим законам, и поэтому не пригодна для представления квантовых процессов. Например, вращение электрона по орбите вокруг атома – такое представление. Это дань классической физике и не соответствует истинному положению вещей, не соответствует квантовым законам.
Рассмотренные нами волны Луи де Бройля не являются электромагнитными, это волны особой природы.
Вычислим дебройлевскую длину волны мячика массой 0,20 кг, движущегося со скоростью 15 м/с.
|
λ = |
h |
= |
6,67 10−34 Дж с |
= 2,2 10 |
−34 |
м. |
(3.3.1) |
|
mυ |
0,2 15 |
||||||
|
Это чрезвычайно малая длина волны. Даже при крайне низких ско- |
|||||||
|
ростях, скажем 10−4 м/с, дебройлевская |
длина волны |
составляла бы |
примерно 10−29 м. Дебройлевская длина волны обычного тела слишком мала, чтобы ее можно было обнаружить и измерить. Дело в том, что типичные волновые свойства – интерференция и дифракция – проявляются только тогда, когда размеры предметов или щелей сравнимы по своей величине с длиной волны. Но нам не известны предметы и щели, на ко-
торых могли бы дифрагировать волны с длиной волны 10−30 м, поэтому
волновые свойства обычных тел обнаружить не удается.
Другое дело, если речь идет об элементарных частицах типа электронов. Т.к. масса входит в знаменатель формулы 3.3.1, определяющей дебройлевскую длину волны, очень малой массе соответствует большая длина волны.
Определим дебройлевскую длину волны электрона, ускоренного разностью потенциалов 100 В.
|
1 mυ2 |
= eU |
υ = |
2eU |
= 5,9 106 |
м/с, |
||||||
|
2 |
m |
||||||||||
|
откуда |
λ = |
h |
= |
6,6 10−34 |
=1,2 10 |
−10 |
м. |
||||
|
mυ |
10−31 5,9 106 |
||||||||||
|
9,1 |
Из приведенного примера видно, что электрон может соответствовать длине волны порядка 10−10 м. Хотя это очень короткие волны, их можно обнаружить экспериментально: межатомные расстояния в кристалле того же порядка величины (10−10 м) и регулярно расположенные
атомы кристалла можно использовать в качестве дифракционной решетки, как в случае рентгеновского излучения. Итак, если гипотеза Луи
39

де Бройля справедлива, то, как указал Эйнштейн, для электронов долж-
но наблюдаться явление дифракции.
Отвлечемся на время и поставим мысленный эксперимент. Направим на преграду с двумя узкими щелями параллельный пучок моноэнергетических (т.е. обладающих одинаковой кинетической энергией) электронов (рис. 3.6), за преградой поставим фотопластину (Фп).
Сначала закроем вторую щель и произведем экспонирование в течение времени t. Почернение на обработанной Фп будет характеризоваться кривой 1, рис. 3.6, б. Затем закроем первую щель и произведем экспонирование второй фотопластины. Характер почернения передается в этом случае кривой 2 (рис. 3.6, б). Наконец, откроем обе щели и подвергнем экспонированию в течение времени t третью пластину. Картина почернения, получающаяся в последнем случае, изображена на рис. 3.6, в. Эта картина отнюдь не эквивалентна положению первых двух. Каким образом открывание второй щели может повлиять на те электроны, которые, казалось бы, прошли через другую щель? Полученная картина (рис. 3.6, в) оказывается аналогичной картине, получающейся при интерференции двух когерентных световых волн. Характер картины свидетельствует о том, что на движение каждого электрона оказывают влияние оба отверстия. Такой вывод несовместим с представлением о траекториях. Если бы электрон находился в каждый момент в определенной точке пространства и двигался по траектории, он проходил бы через определенное отверстие – первое или второе. Явление же дифракции доказывает, что в прохождении каждого электрона участвуют оба отверстия – и первое, и второе.
Таким образом, дифракция электронов и других микрочастиц
доказывает справедливость гипотезы Луи де Бройля и подтверждает корпускулярно-волновой дуализм микрочастиц вещества.
40
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
 Готовое решение: Заказ №8389
Готовое решение: Заказ №8389
 Тип работы: Задача
Тип работы: Задача
 Статус: Выполнен (Зачтена преподавателем ВУЗа)
Статус: Выполнен (Зачтена преподавателем ВУЗа)
 Предмет: Физика
Предмет: Физика
 Дата выполнения: 28.09.2020
Дата выполнения: 28.09.2020
 Цена: 227 руб.
Цена: 227 руб.
Чтобы получить решение, напишите мне в WhatsApp, оплатите, и я Вам вышлю файлы.
Кстати, если эта работа не по вашей теме или не по вашим данным, не расстраивайтесь, напишите мне в WhatsApp и закажите у меня новую работу, я смогу выполнить её в срок 1-3 дня!
Описание и исходные данные задания, 50% решения + фотография:
№1-2 629. Определите дебройлевскую длину волны л электрона, кинетическая энергия которого T = 1,02 МэВ.
Решение.
Длина волны де Бройля частицы равна: , где Дж∙с – постоянная Планка; – импульс частицы. Импульс частицы связан с её кинетической энергией : – в нерелятивистском случае, – в релятивистском случае, где – масса покоя частицы; – энергия покоя частицы;

- Кинетическая энергия нерелятивистского протона в два раза больше кинети-ческой энергии нейтрона. Чему равно отношение длины волны де Бройля протона к длине волны де Бройля нейтрона?
- Две одинаковые нерелятивистские частицы движутся перпендикулярно друг к другу с дебройлевскими длинами волн л1 и л2. Найти дебройлевскую длину волны каждой частицы в системе их центра инерции.
- Найти длину волны де Бройля для электрона, движущегося по первой боровской орбите атома водорода.
- Кинетическая энергия электрона равна 0,6 МэВ. Определите длину волны де Бройля.
Цели урока:
- Ознакомить учащихся с корпускулярно-волновой
природой материи. - Сформировать представление о том, что поведение
микрочастицы может существенным образом
отличаться от поведения макроскопических тел. - Выработать у учащихся убеждение, что критерием
истинности любой физической гипотезы является
эксперимент. - Привить учащимся культуру оформления решения
задач на расчёт длины волны де Бройля для
релявистских и нерелятивистских частиц. - Показать учащимся практическое применение
волновых свойств микрочастиц. - Сформировать у учащихся представление.
Волновые свойства микрочастиц. Волны де Бройля.
Французский физик Луи де Бройль – потомок
королей и будущий Нобелевский лауреат, родился в
1892 году.
Как и многие во время I Мировой войны воевал, а
после войны стал работать в лаборатории своего
старшего брата Мориса. Его занимал всё тот же
вопрос: “Почему атомы устойчивы? Почему на
стационарных орбитах электроны не излучают?”
Третий постулат Бора выделял эти орбиты из
набора всех мыслимых орбит правилом квантования:
Де Бройль хотел найти разумные основания для
этого условия, то есть пытался понять физический
смысл правила квантования.
В 1923 году де Бройль выдвинул гипотезу: не только
свет, но и все тела в природе должны обладать и
волновыми, и корпускулярными свойствами
одновременно.
Чтобы понять это, нужно иметь непредвзятый ум.
Природа не создала зримых образов, которые
помогли бы наглядно представить это.
Длина волны ![]() , присущая
, присущая
частицам вещества, получила название длины волны
де Бройля, а сами такие волны – волны де Бройля.
Волны де Бройля для электрона.
Движение электрона вокруг ядра в атоме будет
устойчивым тогда, когда на длине орбиты
укладывается целое число n длин волн электрона.
![]() , откуда
, откуда ![]() . Домножим на h,
. Домножим на h,
имеем
![]() ,
, ![]() ;
;
![]() .
.
Получили третий постулат Бора.
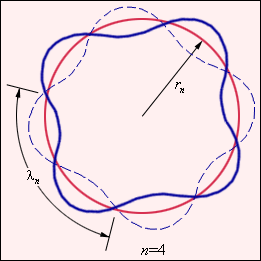
Рис. 1 Иллюстрация теории де Бройля
Новое понятие стационарной орбиты: это
такая орбита, на которой укладывается целое
число длин волн электрона.
Определим длину волны электрона.
![]() ; (*)
; (*)
Выразим n из третьего постулата и подставим в (*).
Получим:
![]() ;
; ![]()
![]()
![]() – “длина волны” электрона на n орбите.
– “длина волны” электрона на n орбите.
Пример: электрон в атоме движется со
средней скоростью v=106 м/с, тогда длина
волны электрона в атоме ![]() .
.
Волны де Бройля для частиц вещества.
I. Если частица релятивистская 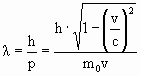 .
.
II. Если частица нерелятивистская, то есть v <<
c, имеем ![]() .
.
Пример. Для тела массой m=1 кг
при v=1 м/с имеем ![]() .
.
Волновые эффекты такой малости обнаружить
невозможно.
Задача.
Условие:
Определить длину волны де Бройля для протона ![]() 1, который разогнали в
1, который разогнали в
электрическом поле при напряжении 3,0 МВ и
дебройлевскую длину волны электрона ![]() 2, прошедшего ту же разность
2, прошедшего ту же разность
потенциалов.
Решение:
Экспериментальное подтверждение волновых
свойств микрочастиц.
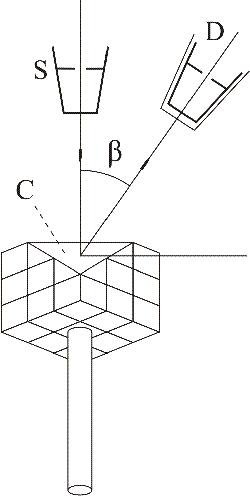
Рис. 2 Схема опыта Дэвиссона и
Джермера
После высказывания де Бройлем столь
фантастической гипотезы – каждое тело
одновременно есть и частица и волна – встал
вопрос об её экспериментальном подтверждении.
Важным доказательством существования волновых
свойств у частиц вещества является наличие
явлений дифракции и интерференции для потока
таких частиц. Первые экспериментальные
исследования были выполнены американскими
учёными К. Девиссоном и Л. Джермером
в 1927 году. Они исследовали дифракцию
электронов на монокристалле никеля,
кристаллическая структура которого была
известна из опытов по дифракции рентгеновского
излучения.
Схема опыта:
Электроны от электронной пушки S, прошедшие
ускоряющую разность потенциалов U, падали
нормально на сошлифованную поверхность
кристалла никеля C. С помощью детектора D
исследовалось число электронов , отраженных от
кристалла под углом ![]() при различных значениях U.
при различных значениях U.
Кристаллическая решетка в опыте Дэвиссона и
Джермера играла роль объёмной отражательной
дифракционной решетки.
Результаты экспериментальных исследований:
Максимальное отражение электронов наблюдалось
при ускоряющей разности потенциалов U=54 В, что
соответствует дебройлевской длине волны
![]() =
=
0,167 нм.
Расчетное значение длины волны:
Теоретический анализ дифракции электронов на
кристаллах аналогичен анализу дифракции
рентгеновского излучения. При значении угла ?,
удовлетворяющем условию Брега-Вульфа
![]() ,
,
возникает интенсивный дифракционный максимум
отраженной волны. Здесь d – расстояние между
отражающими плоскостями (постоянная решетки
кристалла). Для никеля d=2,15?10-10 м. ![]() – брегговский
– брегговский
угол, то есть угол скольжения, под которым
электроны падают на поверхность кристалла. Тогда
![]() . Расчетное
. Расчетное
значение длины волны равнялось ![]() =0,165 нм.
=0,165 нм.
Это совпадение экспериментальных и расчетных
значений ![]() служит
служит
прекрасным подтверждением гипотезы де Бройля о
наличии у частиц волновых свойств.
Применение микрочастиц для исследования
структуры вещества.
В настоящее время опыты по дифракции
электронов и нейтронов и основанные на них
приборы получили широкое распространение в
науке и технике. Дифракция электронов
применяется при исследовании структуры
поверхности. Например, при изучении коррозии, при
адсорбции газов на поверхностях.
Метод исследования структуры вещества,
основанный на дифракции электронов, получил
название электронография. Наличие у
электронов заряда вызывает сильное
взаимодействие с веществом, благодаря чему
проникающая способность электронов намного
меньше, чем у рентгеновских лучей. Это
обстоятельство делает электронографию особенно
ценной при исследовании структур поверхностей.
Она позволяет изучать перестройку
кристаллической структуры на поверхности и
самые начальные стадии кристаллизации твёрдых
тел.
Метод исследования структуры вещества,
основанный на дифракции электронов, называется нейтронографией.
Нейтрон не имеет электрического заряда и
поэтому, в отличие от электрона, обладает высокой
проникающей способностью, что позволяет
исследовать свойства вещества во всём объёме.
Поскольку дебройлевская длина волны ? тепловых
нейтронов имеет тот же порядок, что и расстояния
между атомами в конденсированных средах,
дифракция нейтронов даёт возможность изучать
взаимное расположение атомов, то есть структуру
вещества.
Открытие волновых свойств электронов вызвало
появление новой отрасли науки, получившей
название электронной оптики, и нового
прибора – электронного микроскопа.
Разрешающая способность любого микроскопа
определяется длинной волны применяемого
излучения. Использование вместо световых лучей
пучков электронов позволяет существенно, в
тысячи раз, повысить разрешающую способность
микроскопа благодаря чрезвычайно малому
значению дебройлевской длины волны электрона.
Действительно, для электронов, прошедших
ускоряющую разность потенциалов U=10 кВ, длина
волны де Бройля составляет ![]() =0,0122 нм, что на порядок меньше характерных
=0,0122 нм, что на порядок меньше характерных
размеров атомов.
С помощью ускорителей заряженных частиц
оказывается возможным получать пучки электронов
и протонов очень высоких энергий. В современных
ускорителях энергия заряженных частиц может
достигать порядка 103 ГэВ. Дебройлевская
длина волны таких частиц очень мала. Электроны,
ускоренные до таких энергий, использовались в
экспериментах по изучению размеров и структуры
атомных ядер, а также образующих ядра нуклонов –
протонов и нейтронов.
В каких случаях волновые свойства играют
решающую роль в поведении частицы, а в каких
случаях они оказываются несущественными и их
можно не учитывать?
Волновые свойства частиц будут наиболее ярко
проявляться в тех случаях, когда дебройлевская
длина волны частицы сравнима с характерными
размерами области движения частицы L. Тоесть, ![]() . Например, при
. Например, при
взаимодействии электрона с атомами, а так же при
их движении в твёрдых телах, волновые свойства
электронов будут проявляться максимальным
образом, так как дебройлевская длина волны
электрона и размеры атома, а также расстояние
между атомами в кристалле имеют один и тот же
порядок. В тех же случаях, когда длина волны ![]() << L, волновые
<< L, волновые
свойства частицы становятся несущественными, и
для описания движения таких объектов необходимо
пользоваться законами классической механики.
