Запросы «Дб» и «Бел» перенаправляются сюда; см. также другие значения терминов Дб и Бел.
Децибе́л (русское обозначение: дБ; международное: dB) — дольная единица, равная одной десятой единицы бел[⇨]. В основе единицы лежит десятичный логарифм. Единица названа в честь американского учёного Александра Белла.
Отношение 

Отсюда следует, что увеличение энергетической величины на 1 дБ означает её увеличение в 100,1 ≈ 1,259 раза.
Энергетические величины пропорциональны квадратам силовых величин (или величин поля, как принято в международных документах[1][2]), таких как звуковое давление, электрическое напряжение, сила электрического тока и т. п., поэтому отношение 

Отсюда следует, что увеличение силовой величины на 1 дБ означает её увеличение в 100,05 ≈ 1,122 раза.
Децибел относится к единицам, не входящим в Международную систему единиц (СИ), но в соответствии с решением Международного комитета мер и весов допускается к применению без ограничений совместно с единицами СИ[3]. В основном применяется в электросвязи, акустике, радиотехнике, в теории систем автоматического управления[4][5][6].
История[править | править код]
Распространение децибела берёт начало от методов, используемых для количественной оценки потери (ослабления) сигнала в телеграфных и телефонных линиях. Единицей потерь изначально была миля стандартного кабеля (англ. mile of standard cable — m.s.c.). 1 m.s.c. соответствовала потерям мощности сигнала с частотой 800 Гц в кабеле длиной в 1 милю (примерно 1,6 км), имеющем распределённое сопротивление 88 Ом (на петлю) и распределённую ёмкость 0,054 мкФ[7] (диаметр жил витой пары около 0,9 мм). Такая величина потерь была близка к наименьшей различимой средним слушателем разнице двух сигналов по громкости. Однако миля стандартного кабеля была частотно-зависимой, и она не могла быть полноценной единицей отношения мощностей[8].
В 1924 году компания «Белл телефон» получила положительный ответ на новое определение единицы среди членов Международного телеграфного союза в Европе: вместо m.s.c. — единица передачи (transmission unit, TU). Единица передачи определялась так, что численное выражение в этих единицах соответствовало десяти десятичным логарифмам отношения измеренной мощности к исходной мощности[9]. Удобство такого определения было в приблизительном соответствии старой и новой единиц (1 m.s.c. — это примерно 0,95 TU). В 1928 году компания «Белл телефон» переименовала единицу передачи TU в децибел[10], который стал одной десятой вновь определённой единицы логарифмического отношения мощностей, получившей наименование бел в честь американского учёного Александра Белла[11].
Единица бел используется редко, в то время как децибел получил широкое распространение[12].
Изначальное определение децибела в Ежегоднике стандартов Национального института стандартов и технологий в США от 1931 года[13]:
Децибел может быть определён таким утверждением, что две величины мощности отличаются на 1 децибел, когда они находятся в соотношении 100,1, и любые две величины мощности отличаются на N децибел, когда они находятся в соотношении 10N(0,1). Количество единиц передачи (децибелов), выражающее отношение любых двух мощностей, в десять раз превышает десятичный логарифм этого отношения.
The decibel may be defined by the statement that two amounts of power differ by 1 decibel when they are in the ratio of 100.1 and any two amounts of power differ by N decibels when they are in the ratio of 10N(0.1). The number of transmission units expressing the ratio of any two powers is therefore ten times the common logarithm of that ratio.
В апреле 2003 года Международный комитет мер и весов (МКМВ) рассматривал рекомендацию о включении децибела в Международную систему единиц (СИ), но отказался от этого предложения[14]. Однако децибел признан другими международными организациями, такими как Международная электротехническая комиссия (МЭК) и Международная организация по стандартизации (ИСО)[15]. МЭК позволяет использовать децибел и с силовыми, и с энергетическими величинам, и этой рекомендации следуют многие национальные организации по стандартизации.
Определение[править | править код]
Децибелы принято использовать для измерения или выражения отношения одноимённых энергетических величин, таких как мощность, энергия, интенсивность, плотность потока мощности, спектральная плотность мощности и т. п., а также силовых величин, таких как напряжение, сила тока, напряженность поля, звуковое давление и т. п. Часто в качестве одной из величин отношения (в знаменателе) выступает общепринятая исходная (или опорная) величина. Тогда отношение, выраженное в децибелах, принято называть уровнем соответствующей физической величины (например, уровень мощности, уровень напряжения и т. д.)[1][2].
Энергетические величины[править | править код]
 |
 |

|
|---|---|---|
| 40 dB | 10000 | 100 |
| 20 dB | 100 | 10 |
| 10 dB | 10 | ≈ 3,16 |
| 6 dB | ≈ 4 | ≈ 2 |
| 3 dB | ≈ 2 | ≈ 1,41 |
| 1 dB | ≈ 1,26 | ≈ 1,12 |
| 0 dB | 1 | 1 |
| −1 dB | ≈ 0,79 | ≈ 0,89 |
| −3 dB | ≈ 0,5 | ≈ 0,71 |
| −6 dB | ≈ 0,25 | ≈ 0,5 |
| −10 dB | 0,1 | ≈ 0,32 |
| −20 dB | 0,01 | 0,1 |
| −40 dB | 0,0001 | 0,01 |
Отношение 


Отсюда:
00или00
Силовые величины[править | править код]
Энергетические величины пропорциональны квадратам силовых величин. Например, в электрической цепи мощность 


Отсюда отношение двух величин:
Логарифмическое отношение в частном случае, при 
Таким образом, сохранение численных значений в децибелах при переходе от отношения мощностей к отношению напряжений при одинаковых нагрузках требует, чтобы выполнялось следующее соотношение:
00где0
Отсюда:
00или00
Определение единицы бел[править | править код]
Бел (русское обозначение: Б; международное: ) выражает отношение двух мощностей как десятичный логарифм этого отношения[2].
Согласно ГОСТ 8.417—2002[16], бел — единица логарифмического отношения физической величины к одноимённой физической величине, принимаемой за исходную. Для энергетических величин (P): 1 Б = lg(P2/P1) при P2 = 10P1; для силовых величин (F): 1 Б = 2·lg(F2/F1) при F2 = 100,5 F1.
Таким образом, бел соответствует отношению 10 для энергетических величин или отношению 100,5 ≈ 3,162 для силовых величин.
Бел редко применяется как без приставки, так и с какими-либо другими приставками СИ, кроме деци. Например, вместо тысячной доли бела предпочтительным является использование сотой доли децибела (общепринятой будет запись не 5 мБ, а 0,05 дБ)[17].
Сравнение логарифмических единиц[править | править код]
| Единица | Обозначение | Изменение энергетической величины в … раз |
Изменение силовой величины в … раз |
Пересчёт в … | ||
|---|---|---|---|---|---|---|
| дБ | Б | Нп | ||||
| децибел | дБ, dB | ![sqrt[10]{10}](https://wikimedia.org/api/rest_v1/media/math/render/svg/640a47a05663578069ba03cd5ebb8ec412d4131e) ≈ 1,259 ≈ 1,259 |
![{displaystyle {sqrt[{20}]{10}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3cba419e91dd4b2131d31468bd0b1353a869cfb4) ≈ 1,122 ≈ 1,122 |
1 | 0,1 | ≈0,1151 |
| бел | Б, B | 10 |  ≈ 3,162 ≈ 3,162 |
10 | 1 | ≈1,151 |
| непер | Нп, Np | e2 ≈ 7,389 | e ≈ 2,718 | ≈8,686 | ≈0,8686 | 1 |
Применение[править | править код]
Децибелы широко применяются в областях техники, где требуется измерение или представление величин, меняющихся в широком диапазоне: в радиотехнике, антенной технике, в системах передачи информации, автоматического регулирования и управления, в оптике, акустике (в децибелах измеряется уровень громкости звука) и др. Так, в децибелах принято измерять или указывать динамический диапазон (например, диапазон громкости звучания музыкального инструмента), затухание волны при распространении в поглощающей среде, коэффициент затухания радиочастотного кабеля, коэффициент усиления и коэффициент шума усилителя.
Акустика[править | править код]
Звуковое давление — силовая величина, а интенсивность звука, пропорциональная квадрату звукового давления, — энергетическая величина. Например, если громкость звука (субъективно определяемая его интенсивностью) возросла на 10 дБ, то это значит, что интенсивность звука возросла в 10 раз, а звуковое давление — приблизительно в 3,16 раза.
Использование децибелов при указании громкости звука обусловлено человеческой способностью воспринимать звук в очень большом диапазоне изменений его интенсивности. Применение линейной шкалы оказывается практически неудобным. Кроме того, на основании закона Вебера — Фехнера, ощущение громкости звука пропорционально логарифму его интенсивности. Отсюда удобство логарифмической шкалы. Диапазон величин звукового давления от минимального порога слышимости звука человеком (20 мкПа) до максимального, вызывающего болевые ощущения, составляет примерно 120 дБ. Например, утверждение «громкость звука составляет 30 дБ» означает, что интенсивность звука в 1000 раз превышает порог слышимости звука человеком.
Для выражения громкости звука также используют единицы фон и сон, учитывающие частотную и субъективную восприимчивость звука человеком.
Удобства применения децибелов[править | править код]
Прежде всего следует отметить удобство децибела по сравнению с единицей бел. Для практических применений бел оказался слишком крупной единицей, часто предполагающей дробную запись значения логарифмической величины. Перечисленные ниже удобства так или иначе связаны с применением не только децибелов, а логарифмической шкалы и логарифмических величин вообще.
- Характер отображения в органах чувств человека и животных изменений течения многих физических и биологических процессов пропорционален логарифму интенсивности раздражителя (см. Закон Вебера — Фехнера). Эта особенность делает применение логарифмических шкал, логарифмических величин и их единиц вполне естественным. Например, одной из таких шкал является музыкальная равномерно темперированная шкала частот.
- Логарифмическая шкала даёт наглядное графическое представление и упрощение анализа величины, изменяющейся в очень широких пределах (примеры — диаграмма направленности антенны, амплитудно-частотная характеристика (АЧХ) системы автоматического регулирования). Это же относится к передаточным частотным характеристикам электрических фильтров (см. Логарифмическая амплитудно-фазовая частотная характеристика). При этом форма кривой упрощается и возможно применение кусочно-линейной аппроксимации, при которой скорость убывания частотной характеристики имеет размерность дБ/декада или дБ/октава[6]. Упрощается анализ частотной характеристики фильтров, составленных из последовательно включенных звеньев с независимыми друг от друга частотными характеристиками. Следует заметить, что построение графиков в логарифмическом масштабе требует определённого навыка (см. Логарифмическая бумага).
- Логарифмическое представление некоторых относительных величин в ряде случаев упрощает математические операции с ними, в частности, умножение и деление заменяются сложением и вычитанием. Например, если собственные коэффициенты усиления последовательно включённых усилителей выражены в децибелах, то общий коэффициент усиления находится как сумма собственных коэффициентов.
Опорные величины и обозначения уровней[править | править код]
Если в качестве одной из величин отношения (в знаменателе) выступает общепринятая исходная (или опорная) величина Xref, то отношение, выраженное в децибелах, называют уровнем (иногда называют абсолютным уровнем) соответствующей физической величины X и обозначают LX (от англ. level).
В соответствии с действующими стандартами[16][15] при необходимости указать исходную величину её значение помещают в скобках после обозначения логарифмической величины. Например, уровень LP звукового давления P можно записать: LP (исх. 20 мкПа) = 20 дБ, а с использованием международных обозначений — LP (re 20 µPa) = 20 dB (re — сокращение от англ. referred to, «отнесённое к»). Допускается указывать значение исходной величины после значения уровня, в скобках после обязательного пробела, например: 20 дБ (исх. 20 мкПа). Также используется краткая форма, например, уровень LW мощности W можно записать: LW/1 мВт = 30 дБ, или LW = 30 дБ (1 мВт). Для сокращения записи широко используются специальные обозначения, например: LW = 30 дБм. Запись означает, что уровень мощности составляет +30 дБ относительно 1 мВт, то есть мощность равна 1 Вт.
Специальные обозначения[править | править код]
Приведены некоторые специальные обозначения, которые в предельно краткой форме указывают на значение исходной (опорной) величины, по отношению к которой определён соответствующий уровень, выраженный в децибелах[1][2]. Для указанных ниже опорных величин под электрическим напряжением понимается его среднеквадратичное (эффективное) значение.
- dBW (русское дБВт) — опорная мощность 1 Вт. Например, уровень мощности +30 дБВт соответствует мощности 1 кВт.
- dBm (русское дБм) — опорная мощность 1 мВт.
- dBm0 (русское дБм0) — опорная мощность 1 мВт. Обозначение применяется в электросвязи для указания абсолютного уровня мощности, приведённого к так называемой точке нулевого относительного уровня[en].
- dBV (русское дБВ) — опорное напряжение 1 В.
- dBuV или dBμV (русское дБмкВ) — опорное напряжение 1 мкВ.

Схематическое представление соотношения между дБн (источник напряжения) и дБм (мощность, рассеиваемая в тепло на резисторе 600 Ом)
- dBu (русское дБн) — опорное напряжение
≈ 0,775 В, соответствующее мощности 1 мВт на нагрузке 600 Ом.
- dBrn — опорное напряжение соответствует мощности теплового шума идеального резистора с сопротивлением
, равным 50 Ом, при комнатной температуре в полосе частот 1 Гц:
. Это значение соответствует уровню напряжения −61 dBμV или уровню мощности −168 dBm.
- dBFS (от англ. full scale — «полная шкала») — опорный сигнал (мощность, напряжение) соответствует полной шкале аналого-цифрового преобразователя.
- dB SPL (от англ. sound pressure level — «уровень звукового давления») — опорное значение амплитуды звукового давления составляет 20 мкПа и соответствует порогу слышимости гармонического звукового колебания с частотой 1 кГц.
- dB(A), dB(B), dB(C) — эти символы применяются для обозначения взвешенного уровня звукового давления относительно 20 мкПа, когда при измерениях используются фильтры с соответствующими стандартными частотными характеристиками.
- dBc (русское дБн) — опорная величина соответствует мощности излучения на частоте несущего сигнала (англ. carrier).
- dBi (русское дБи) — изотропный децибел. Обозначение применяется для описания характеристик антенны (коэффициент направленного действия, коэффициент усиления) по сравнению с гипотетической изотропной антенной, которая равномерно излучает энергию по всем направлениям.
- dBd (русское дБд) — децибел относительно полуволнового вибратора (диполя). Обозначение применяется для описания характеристик антенны по сравнению с полуволновым вибратором (0 dBd = 2,15 dBi).
- dBsm (от англ. square meter, русское дБкв.м или дБ(м²)) — децибел относительно одного квадратного метра. Характеризует эффективную поверхность рассеяния рассеивателя в радиолокации.
- dBZ[en] — используется в радарной технике (в основном в метеорадарах); опорным уровнем является коэффициент отражения капли дождя диаметром 1 мм; значения свыше 20 dBZ обычно указывают на выпадение осадков[18].
По аналогии образуются составные единицы[1][2], например уровня спектральной плотности мощности: дБВт/Гц — «децибельный» аналог единицы Вт/Гц (мощность на номинальной нагрузке в полосе частот 1 Гц с центром на заданной частоте) — здесь опорный уровень равен 1 Вт/Гц.
См. также[править | править код]
- Аттенюатор
- Отношение сигнал/шум
- Децилог
Примечания[править | править код]
- ↑ 1 2 3 4 Recommendation ITU-R V.574-3. Use of the decibel and the neper in Telecommunications (1978-1982-1986-1990). Дата обращения: 19 марта 2015. Архивировано 2 апреля 2015 года.
- ↑ 1 2 3 4 5 Рекомендация МСЭ-R V.574-4. Использование децибела и непера в электросвязи (1978-1982-1986-1990-2000). Дата обращения: 15 февраля 2017. Архивировано 3 февраля 2017 года.
- ↑ Non-SI units accepted for use with the SI, and units based on fundamental constants (contd.) (англ.). SI Brochure: The International System of Units (SI). BIPM. Дата обращения: 12 октября 2015. Архивировано 20 октября 2014 года.
- ↑ Ерофеев А. А. Теория автоматического управления. — СПб., 2003. — С. 265—270
- ↑ Бесекерский В. А., Попов Е. П. Теория систем автоматического регулирования. — М. : Наука, 1972. — 768 с. — С. 65
- ↑ 1 2 Поляков К. Ю. Теория автоматического управления для «чайников». — СПб., 2008. — С. 32—33. Дата обращения: 19 сентября 2018. Архивировано 27 января 2018 года.
- ↑ Johnson, Kenneth Simonds. Transmission Circuits for Telephonic Communication: Methods of Analysis and Design (англ.). — New York: D. Van Nostrand Co., 1944. — P. 10.
- ↑ mile of standard cable (англ.). sizes.com. Дата обращения: 26 января 2017. Архивировано 24 июня 2016 года.
- ↑ Don Davis and Carolyn Davis. Sound system engineering (неопр.). — 2nd. — Focal Press (англ.) (рус., 1997. — С. 35. — ISBN 978-0-240-80305-0.
- ↑ R. V. L. Hartley. [[1] в «Книгах Google» ‘TU’ becomes ‘Decibel’] (неопр.) // Bell Laboratories Record. — AT&T, 1928. — December (т. 7, № 4). — С. 137—139.
- ↑ Martin, W. H. DeciBel—The New Name for the Transmission Unit (англ.) // Bell System Technical Journal (англ.) (рус. : journal. — 1929. — January (vol. 8, no. 1).
- ↑ Robert J. Chapuis, Amos E. Joel 100 Years of Telephone Switching в «Книгах Google», 2003
- ↑ Standards for Transmission of Speech (англ.) // Standards Yearbook. — National Bureau of Standards, U. S. Govt. Printing Office, 1931. — Vol. 119.
- ↑ Consultative Committee for Units, Meeting minutes Архивная копия от 29 декабря 2016 на Wayback Machine, Section 3
- ↑ 1 2 ГОСТ Р МЭК 60027-3-2016 Государственная система обеспечения единства измерений (ГСИ). Обозначения буквенные, применяемые в электротехнике. Часть 3. Логарифмические и относительные величины и единицы измерений, ГОСТ Р от 28 декабря 2016 года №МЭК 60027-3-2016. docs.cntd.ru. Дата обращения: 12 июня 2019. Архивировано 28 мая 2019 года.
- ↑ 1 2 ГОСТ 8.417-2002 Государственная система обеспечения единства измерений (ГСИ). Единицы величин, ГОСТ от 04 февраля 2003 года №8.417-2002. docs.cntd.ru. Дата обращения: 26 августа 2018. Архивировано 16 июня 2019 года.
- ↑ Fedor Mitschke, Fiber Optics: Physics and Technology, Springer, 2010 ISBN 3-642-03703-8.
- ↑ RIDGE Radar Frequently Asked Questions. Дата обращения: 8 августа 2019. Архивировано 31 марта 2019 года.
Литература[править | править код]
- Гинкин Г. Г. Логарифмы, децибелы, децилоги. — М.-Л., 1962.
- Сена Л. А. Единицы физических величин и их размерности. — М.: Наука, 1977. — 336 с.
Ссылки[править | править код]
- Что такое децибел?
Очень часто новички сталкивается с таким понятием, как децибел. Многие из них интуитивно догадываются, что это такое, но у большинства до сих пор возникают вопросы.
Что такое децибел?
Относительные логарифмические единицы Белы (децибелы) широко используются при количественных оценках параметров различных аудио, видео, измерительных устройств. Физическая природа сравниваемых мощностей может быть любой — электрической, электромагнитной, акустической, механической, — важно лишь, чтобы обе величины были выражены в одинаковых единицах — ваттах, милливаттах и т. п. Бел выражает отношение двух значений энергетической величины десятичным логарифмом этого отношения, причем под энергетическими величинами понимаются: мощность, энергия.
Кстати, эта единица получила свое название в честь Александра Белл (1847 — 1922) — американского ученого шотландского происхождения, основоположника телефонии, основателя всемирно известных компаний AT&T и «Bell Laboratories». Еще интересно напомнить, что во многих современных мобильных телефонах (смартфонах) обязательно есть выбираемый звук звонка (оповещения), так и называемый «bell». Впрочем, Бел относится к единицам, не входящим в Международную систему единиц (СИ), но в соответствии с решением Международного комитета мер и весов допускается к применению без ограничений совместно с единицами СИ. В основном применяется в электросвязи, акустике, радиотехнике.
Формулы для вычисления децибелов
Бел (Б) = lg (P2/P1)

где
P1 — мощность до усиления, Вт
P2 — мощность после усиления или ослабления, Вт
На практике, оказалось, что удобнее пользоваться уменьшенным в 10 раз значением Бел, т.е. децибел, поэтому:
дециБел (дБ) = 10 * lg(P2/P1)
Усиление или ослабление мощности в децибелах выражается формулой:

где
NдБ — усиление, либо ослабление мощности в децибелах
P1 — мощность до усиления, Вт
P2 — мощность после усиления или ослабления, Вт
Значения Бел, децибел могут быть со знаком «плюс», если P2 > P1 (усиление сигнала) и со знаком «минус», если P2 < P1 (ослабление сигнала)
Во многих случаях, сравнение сигналов путем измерения мощностей может быть неудобным или невозможным — проще измерить напряжение или ток.
В этом случае, если мы сравниваем напряжения или токи, формула примет уже другой вид:

где
NдБ — усиление, либо ослабление мощности в децибелах
U1 — это напряжение до усиления, В
U2 — напряжение после усиления, В
I1 — сила тока до усиления, А
I2 — сила тока после усиления, А
Вот небольшая табличка, в которой приведены основные отношения напряжений и соответствующее число децибел:

Дело в том, что операции умножения и деления над числами в обычном базисе, заменяются операциями сложения и вычитания в логарифмическом базисе. Например, у нас есть два каскадно-включенных усилителя с коэффициентами усиления K1 = 963 и K2 = 48. Какой общий коэффициент усиления? Правильно — он равен произведению K = K1 * K2. Вы можете в уме быстро вычислить 963*48? Я — нет. Я могу прикинуть K = 1000*50 = 50 тыс., не более. А, если нам известно, что K1 = 59 дБ и K2 = 33 дБ, то К = 59+33 = 92 дБ — сложить было не трудно, надеюсь.
Впрочем, актуальность таких вычислений было велика в эпоху, когда ввели понятие Бел и когда не было не то, что айфонов, но и электронных калькуляторов. Сейчас же достаточно открыть калькулятор на ваших гаджетах и быстренько посчитать , что есть что. Ну и чтобы не париться каждый раз при переводе дБ в разы, удобнее всего найти в интернете онлайн-калькулятор. Да хотя бы вот.
Закон Вебера-Фехнера
Почему именно децибелы? Все исходит от закона Вебера-Фехнера, который говорит нам, что интенсивность ощущения человеческих чувств прямо-пропорциональна логарифму интенсивности какого-либо раздражителя.

Так светильник, в котором восемь лампочек, кажется нам настолько же ярче светильника из четырёх лампочек, насколько светильник из четырёх лампочек ярче светильника из двух лампочек. То есть количество лампочек должно увеличиваться каждый раз вдвое, чтобы нам казалось, что прирост яркости постоянен. То есть если добавить к нашим 32 лампочкам на графике еще одну лампочку, то мы даже и не заметим разницы. Для того, чтобы для нашего глаза была заметна разница, мы должны к 32 лампочкам добавить еще 32 лампочки, и т.д. Или иными словами, для того, чтобы нам казалось, что наш светильник плавно набирает яркость, нам надо зажигать вдвое больше лампочек каждый раз, чем было предыдущее значение.
Поэтому децибел действительно удобнее в некоторых случаях, так как сравнивать две величины намного проще в маленьких цифрах, чем в миллионах и миллиардах. А так как электроника — это чисто физическое явление, то и децибелы не обошли ее стороной.
Небольшое отклонение от статьи)) Читайте — последовательное и параллельное соединение проводников.
Децибелы и АЧХ усилителя
Как вы помните в прошлом примере с ОУ, у нас неинвертирующий усилитель усиливал сигнал в 10 раз. Если посмотреть в нашу табличку, то это получается 20 дБ относительно входного сигнала. Ну да, так оно и есть:

Также в дБ на некоторых графиках АЧХ обозначают наклон характеристики АЧХ. Это может выглядеть примерно вот так:

На графике мы видим АЧХ полосового фильтра. Изменение сигнала +20 дБ на декаду (дБ/дек, dB/dec) говорит нам о том, что при каждом увеличении частоты в 10 раз, амплитуда сигнала возрастает на 20 дБ. То же самое можно сказать и про спад сигнала -20 дБ на декаду. При каждом увеличении частоты в 10 раз, у нас амплитуда сигнала будет уменьшаться на -20 дБ. Есть также похожая характеристика дБ на октаву (дБ/окт, dB/oct). Здесь почти все то же самое, только изменение сигнала происходит при каждом увеличении частоты в 2 раза.
Давайте рассмотрим пример. Имеем фильтр высоких частот (ФВЧ) первого порядка, собранного на RC-цепи.

Его АЧХ будет выглядеть следующим образом (кликните для полного открытия)

Нас сейчас интересует наклонная прямая линия АЧХ. Так как у нее наклон примерно одинаковый до частоты среза в -3дБ, то можно найти ее крутизну, то есть узнать, во сколько раз увеличивается сигнал при каждом увеличении частоты в 10 раз.
Итак возьмем первую точку на частоте в 10 Герц. На частоте в 10 Герц амплитуда сигнала уменьшилась на 44 дБ, это видно в правом нижнем углу (out:-44)

Умножаем частоту на 10 (декада) и получаем вторую точку в 100 Герц. На частоте в 100 Герц наш сигнал уменьшился приблизительно на 24 дБ

То есть получается за одну декаду у нас сигнал увеличился с -44 до -24 дБ на декаду. То есть наклон характеристики составил +20 дБ/декаду. Если +20 дБ/декаду перевести в дБ на октаву, то получится 6 дБ/октаву.
Достаточно часто, дискретные аттенюаторы (делители) выходного сигнала на измерительных приборах (особенно на генераторах) проградуированы в децибелах:
0, -3, -6, -10, -20, -30, -40 дБ. Это позволяет быстро ориентироваться в относительном уровне выходного сигнала.

Что еще измеряют в децибелах?
Также очень часто в дБ выражают отношение сигнал-шум (signal-to-noise ratio, сокр. SNR)

где
Uc — это эффективное значение напряжения сигнала, В
Uш — эффективное значение напряжения шума, В
Чем выше значение сигнал/шум, тем более чистый звук обеспечивается аудиосистемой. Для музыкальной аппаратуры желательно, чтобы это отношение было не менее 75 дБ, а для Hi-Fi аппаратуры не менее 90 дБ. Не имеет значение физическая природа сигнала, важно, чтобы единицы были в одинаковых измерениях.
В качестве единицы логарифмического отношения двух одноимённых физических величин применяется также непер (Нп) — 1 Нп ~ 0,8686 Б. В основе лежит не десятичный (lg), а натуральный (ln) логарифм отношений. В настоящее время используется редко.
Во многих случаях, удобно сравнивать между собой не произвольные величины, а одну величину относительно другой, названной условно опорной (нулевой, базовой).
В электротехнике, в качестве такой опорной или нулевой величины выбрано значение мощности равное 1 мВт выделяемое на резисторе сопротивлением 600 Ом.
В этом случае, базовыми значениями при сравнении напряжений или токов станут величины 0.775 В или 1.29 мА.
Для звуковой мощности такой базовой величиной является 20 микроПаскаль (0 дБ), а порог +130 дБ считается болевым для человека:

Более подробно об этом написано в Википедии по этой ссылке.
Для случаев когда в качестве базовых значений используются те или иные конкретные величины, придуманы даже специальные обозначения единиц измерений:
dbW (дБВт) — здесь отсчет идет относительно 1 Ватта (Вт). Например, пусть уровень мощности составил +20 дБВт. Это значит что мощность увеличилась в 100 раз, то есть на 100 Вт.
dBm (дБм) — здесь у нас отсчет уже идет относительно 1 милливатта (мВт). Например, уровень мощности в +30дБм будет соответственно равен 1 Вт. Не забываем, что это у нас энергетические децибелы, поэтому для них будет справедлива формула

Следующие характеристики — это уже амплитудные децибелы. Для них будет справедлива формула

dBV (дБВ) — как вы догадались, опорное напряжение 1 Вольт. Например, +20дБВ даст — это 10 Вольт
От дБВ также вытекают другие виды децибелов с разными приставками:
dBmV (дБмВ) — опорный уровень 1 милливольт.
dBuV (дБмкВ) — опорное напряжение 1 микровольт.
Здесь я привел наиболее употребимые специальные виды децибелов в электронике.
Децибелы используются и в других отраслях, где они также показывают отношение каких-либо двух измеряемых величин в логарифмическом масштабе.
Также на YouTube есть интересное видео о децибелах.
У нас есть интересная статья — сопротивление проводника.
The decibel (symbol: dB) is a relative unit of measurement equal to one tenth of a bel (B). It expresses the ratio of two values of a power or root-power quantity on a logarithmic scale. Two signals whose levels differ by one decibel have a power ratio of 101/10 (approximately 1.26) or root-power ratio of 101⁄20 (approximately 1.12).[1][2]
The unit expresses a relative change or an absolute value. In the latter case, the numeric value expresses the ratio of a value to a fixed reference value; when used in this way, the unit symbol is often suffixed with letter codes that indicate the reference value. For example, for the reference value of 1 volt, a common suffix is “V” (e.g., “20 dBV”).[3][4]
Two principal types of scaling of the decibel are in common use. When expressing a power ratio, it is defined as ten times the logarithm in base 10.[5] That is, a change in power by a factor of 10 corresponds to a 10 dB change in level. When expressing root-power quantities, a change in amplitude by a factor of 10 corresponds to a 20 dB change in level. The decibel scales differ by a factor of two, so that the related power and root-power levels change by the same value in linear systems, where power is proportional to the square of amplitude.
The definition of the decibel originated in the measurement of transmission loss and power in telephony of the early 20th century in the Bell System in the United States. The bel was named in honor of Alexander Graham Bell, but the bel is seldom used. Instead, the decibel is used for a wide variety of measurements in science and engineering, most prominently in acoustics, electronics, and control theory. In electronics, the gains of amplifiers, attenuation of signals, and signal-to-noise ratios are often expressed in decibels.
| dB | Power ratio | Amplitude ratio | ||
|---|---|---|---|---|
| 100 | 10000000000 | 100000 | ||
| 90 | 1000000000 | 31623 | ||
| 80 | 100000000 | 10000 | ||
| 70 | 10000000 | 3162 | ||
| 60 | 1000000 | 1000 | ||
| 50 | 100000 | 316 | .2 | |
| 40 | 10000 | 100 | ||
| 30 | 1000 | 31 | .62 | |
| 20 | 100 | 10 | ||
| 10 | 10 | 3 | .162 | |
| 6 | 3 | .981 ≈ 4 | 1 | .995 ≈ 2 |
| 3 | 1 | .995 ≈ 2 | 1 | .413 ≈ √2 |
| 1 | 1 | .259 | 1 | .122 |
| 0 | 1 | 1 | ||
| −1 | 0 | .794 | 0 | .891 |
| −3 | 0 | .501 ≈ 1⁄2 | 0 | .708 ≈ √1⁄2 |
| −6 | 0 | .251 ≈ 1⁄4 | 0 | .501 ≈ 1⁄2 |
| −10 | 0 | .1 | 0 | .3162 |
| −20 | 0 | .01 | 0 | .1 |
| −30 | 0 | .001 | 0 | .03162 |
| −40 | 0 | .0001 | 0 | .01 |
| −50 | 0 | .00001 | 0 | .003162 |
| −60 | 0 | .000001 | 0 | .001 |
| −70 | 0 | .0000001 | 0 | .0003162 |
| −80 | 0 | .00000001 | 0 | .0001 |
| −90 | 0 | .000000001 | 0 | .00003162 |
| −100 | 0 | .0000000001 | 0 | .00001 |
| An example scale showing power ratios x, amplitude ratios √x, and dB equivalents 10 log10 x. |
History[edit]
The decibel originates from methods used to quantify signal loss in telegraph and telephone circuits. Until the mid-1920s, the unit for loss was Miles of Standard Cable (MSC). 1 MSC corresponded to the loss of power over one mile (approximately 1.6 km) of standard telephone cable at a frequency of 5000 radians per second (795.8 Hz), and matched closely the smallest attenuation detectable to a listener. A standard telephone cable was “a cable having uniformly distributed resistance of 88 ohms per loop-mile and uniformly distributed shunt capacitance of 0.054 microfarads per mile” (approximately corresponding to 19 gauge wire).[6]
In 1924, Bell Telephone Laboratories received favorable response to a new unit definition among members of the International Advisory Committee on Long Distance Telephony in Europe and replaced the MSC with the Transmission Unit (TU). 1 TU was defined such that the number of TUs was ten times the base-10 logarithm of the ratio of measured power to a reference power.[7]
The definition was conveniently chosen such that 1 TU approximated 1 MSC; specifically, 1 MSC was 1.056 TU. In 1928, the Bell system renamed the TU into the decibel,[8] being one tenth of a newly defined unit for the base-10 logarithm of the power ratio. It was named the bel, in honor of the telecommunications pioneer Alexander Graham Bell.[9]
The bel is seldom used, as the decibel was the proposed working unit.[10]
The naming and early definition of the decibel is described in the NBS Standard’s Yearbook of 1931:[11]
Since the earliest days of the telephone, the need for a unit in which to measure the transmission efficiency of telephone facilities has been recognized. The introduction of cable in 1896 afforded a stable basis for a convenient unit and the “mile of standard” cable came into general use shortly thereafter. This unit was employed up to 1923 when a new unit was adopted as being more suitable for modern telephone work. The new transmission unit is widely used among the foreign telephone organizations and recently it was termed the “decibel” at the suggestion of the International Advisory Committee on Long Distance Telephony.
The decibel may be defined by the statement that two amounts of power differ by 1 decibel when they are in the ratio of 100.1 and any two amounts of power differ by N decibels when they are in the ratio of 10N(0.1). The number of transmission units expressing the ratio of any two powers is therefore ten times the common logarithm of that ratio. This method of designating the gain or loss of power in telephone circuits permits direct addition or subtraction of the units expressing the efficiency of different parts of the circuit …
In 1954, J. W. Horton argued that the use of the decibel as a unit for quantities other than transmission loss led to confusion, and suggested the name logit for “standard magnitudes which combine by multiplication”, to contrast with the name unit for “standard magnitudes which combine by addition”.[12][clarification needed]
In April 2003, the International Committee for Weights and Measures (CIPM) considered a recommendation for the inclusion of the decibel in the International System of Units (SI), but decided against the proposal.[13] However, the decibel is recognized by other international bodies such as the International Electrotechnical Commission (IEC) and International Organization for Standardization (ISO).[14] The IEC permits the use of the decibel with root-power quantities as well as power and this recommendation is followed by many national standards bodies, such as NIST, which justifies the use of the decibel for voltage ratios.[15] In spite of their widespread use, suffixes (such as in dBA or dBV) are not recognized by the IEC or ISO.
Definition[edit]
ISO 80000-3 describes definitions for quantities and units of space and time.
The IEC Standard 60027-3:2002 defines the following quantities. The decibel (dB) is one-tenth of a bel: 1 dB = 0.1 B. The bel (B) is 1⁄2 ln(10) nepers: 1 B = 1⁄2 ln(10) Np. The neper is the change in the level of a root-power quantity when the root-power quantity changes by a factor of e, that is 1 Np = ln(e) = 1, thereby relating all of the units as nondimensional natural log of root-power-quantity ratios, 1 dB = 0.115 13… Np = 0.115 13…. Finally, the level of a quantity is the logarithm of the ratio of the value of that quantity to a reference value of the same kind of quantity.
Therefore, the bel represents the logarithm of a ratio between two power quantities of 10:1, or the logarithm of a ratio between two root-power quantities of √10:1.[16]
Two signals whose levels differ by one decibel have a power ratio of 101/10, which is approximately 1.25893, and an amplitude (root-power quantity) ratio of 101⁄20 (1.12202).[17][18]
The bel is rarely used either without a prefix or with SI unit prefixes other than deci; it is preferred, for example, to use hundredths of a decibel rather than millibels. Thus, five one-thousandths of a bel would normally be written 0.05 dB, and not 5 mB.[19]
The method of expressing a ratio as a level in decibels depends on whether the measured property is a power quantity or a root-power quantity; see Power, root-power, and field quantities for details.
Power quantities[edit]
When referring to measurements of power quantities, a ratio can be expressed as a level in decibels by evaluating ten times the base-10 logarithm of the ratio of the measured quantity to reference value. Thus, the ratio of P (measured power) to P0 (reference power) is represented by LP, that ratio expressed in decibels,[20] which is calculated using the formula:[21]
The base-10 logarithm of the ratio of the two power quantities is the number of bels. The number of decibels is ten times the number of bels (equivalently, a decibel is one-tenth of a bel). P and P0 must measure the same type of quantity, and have the same units before calculating the ratio. If P = P0 in the above equation, then LP = 0. If P is greater than P0 then LP is positive; if P is less than P0 then LP is negative.
Rearranging the above equation gives the following formula for P in terms of P0 and LP:
Root-power (field) quantities[edit]
When referring to measurements of root-power quantities, it is usual to consider the ratio of the squares of F (measured) and F0 (reference). This is because the definitions were originally formulated to give the same value for relative ratios for both power and root-power quantities. Thus, the following definition is used:
The formula may be rearranged to give
Similarly, in electrical circuits, dissipated power is typically proportional to the square of voltage or current when the impedance is constant. Taking voltage as an example, this leads to the equation for power gain level LG:
where Vout is the root-mean-square (rms) output voltage, Vin is the rms input voltage. A similar formula holds for current.
The term root-power quantity is introduced by ISO Standard 80000-1:2009 as a substitute of field quantity. The term field quantity is deprecated by that standard and root-power is used throughout this article.
Relationship between power and root-power levels[edit]
Although power and root-power quantities are different quantities, their respective levels are historically measured in the same units, typically decibels. A factor of 2 is introduced to make changes in the respective levels match under restricted conditions such as when the medium is linear and the same waveform is under consideration with changes in amplitude, or the medium impedance is linear and independent of both frequency and time. This relies on the relationship
holding.[22] In a nonlinear system, this relationship does not hold by the definition of linearity. However, even in a linear system in which the power quantity is the product of two linearly related quantities (e.g. voltage and current), if the impedance is frequency- or time-dependent, this relationship does not hold in general, for example if the energy spectrum of the waveform changes.
For differences in level, the required relationship is relaxed from that above to one of proportionality (i.e., the reference quantities P0 and F0 need not be related), or equivalently,
must hold to allow the power level difference to be equal to the root-power level difference from power P1 and F1 to P2 and F2. An example might be an amplifier with unity voltage gain independent of load and frequency driving a load with a frequency-dependent impedance: the relative voltage gain of the amplifier is always 0 dB, but the power gain depends on the changing spectral composition of the waveform being amplified. Frequency-dependent impedances may be analyzed by considering the quantities power spectral density and the associated root-power quantities via the Fourier transform, which allows elimination of the frequency dependence in the analysis by analyzing the system at each frequency independently.
Conversions[edit]
Since logarithm differences measured in these units often represent power ratios and root-power ratios, values for both are shown below. The bel is traditionally used as a unit of logarithmic power ratio, while the neper is used for logarithmic root-power (amplitude) ratio.
| Unit | In decibels | In bels | In nepers | Power ratio | Root-power ratio |
|---|---|---|---|---|---|
| 1 dB | 1 dB | 0.1 B | 0.11513 Np | 101⁄10 ≈ 1.25893 | 101⁄20 ≈ 1.12202 |
| 1 Np | 8.68589 dB | 0.868589 B | 1 Np | e2 ≈ 7.38906 | e ≈ 2.71828 |
| 1 B | 10 dB | 1 B | 1.151 3 Np | 10 | 101⁄2 ≈ 3.162 28 |
Examples[edit]
The unit dBW is often used to denote a ratio for which the reference is 1 W, and similarly dBm for a 1 mW reference point.
- Calculating the ratio in decibels of 1 kW (one kilowatt, or 1000 watts) to 1 W yields:
- The ratio in decibels of √1000 V ≈ 31.62 V to 1 V is
(31.62 V / 1 V)2 ≈ 1 kW / 1 W, illustrating the consequence from the definitions above that LG has the same value, 30 dB, regardless of whether it is obtained from powers or from amplitudes, provided that in the specific system being considered power ratios are equal to amplitude ratios squared.
- The ratio in decibels of 10 W to 1 mW (one milliwatt) is obtained with the formula
- The power ratio corresponding to a 3 dB change in level is given by
A change in power ratio by a factor of 10 corresponds to a change in level of 10 dB. A change in power ratio by a factor of 2 or 1⁄2 is approximately a change of 3 dB. More precisely, the change is ±3.0103 dB, but this is almost universally rounded to 3 dB in technical writing. This implies an increase in voltage by a factor of √2 ≈ 1.4142. Likewise, a doubling or halving of the voltage, and quadrupling or quartering of the power, is commonly described as 6 dB rather than ±6.0206 dB.
Should it be necessary to make the distinction, the number of decibels is written with additional significant figures. 3.000 dB corresponds to a power ratio of 103⁄10, or 1.9953, about 0.24% different from exactly 2, and a voltage ratio of 1.4125, 0.12% different from exactly √2. Similarly, an increase of 6.000 dB corresponds to the power ratio is 106⁄10 ≈ 3.9811, about 0.5% different from 4.
Properties[edit]
The decibel is useful for representing large ratios and for simplifying representation of multiplicative effects, such as attenuation from multiple sources along a signal chain. Its application in systems with additive effects is less intuitive, such as in the combined sound pressure level of two machines operating together. Care is also necessary with decibels directly in fractions and with the units of multiplicative operations.
Reporting large ratios[edit]
The logarithmic scale nature of the decibel means that a very large range of ratios can be represented by a convenient number, in a manner similar to scientific notation. This allows one to clearly visualize huge changes of some quantity. See Bode plot and Semi-log plot. For example, 120 dB SPL may be clearer than “a trillion times more intense than the threshold of hearing”.[citation needed]
Representation of multiplication operations[edit]
Level values in decibels can be added instead of multiplying the underlying power values, which means that the overall gain of a multi-component system, such as a series of amplifier stages, can be calculated by summing the gains in decibels of the individual components, rather than multiply the amplification factors; that is, log(A × B × C) = log(A) + log(B) + log(C). Practically, this means that, armed only with the knowledge that 1 dB is a power gain of approximately 26%, 3 dB is approximately 2× power gain, and 10 dB is 10× power gain, it is possible to determine the power ratio of a system from the gain in dB with only simple addition and multiplication. For example:
- A system consists of 3 amplifiers in series, with gains (ratio of power out to in) of 10 dB, 8 dB, and 7 dB respectively, for a total gain of 25 dB. Broken into combinations of 10, 3, and 1 dB, this is:
25 dB = 10 dB + 10 dB + 3 dB + 1 dB + 1 dB
With an input of 1 watt, the output is approximately
1 W × 10 × 10 × 2 × 1.26 × 1.26 ≈ 317.5 W
Calculated precisely, the output is 1 W × 1025⁄10 ≈ 316.2 W. The approximate value has an error of only +0.4% with respect to the actual value, which is negligible given the precision of the values supplied and the accuracy of most measurement instrumentation.
However, according to its critics, the decibel creates confusion, obscures reasoning, is more related to the era of slide rules than to modern digital processing, and is cumbersome and difficult to interpret.[23][24]
Quantities in decibels are not necessarily additive,[25][26] thus being “of unacceptable form for use in dimensional analysis”.[27]
Thus, units require special care in decibel operations. Take, for example, carrier-to-noise-density ratio C/N0 (in hertz), involving carrier power C (in watts) and noise power spectral density N0 (in W/Hz). Expressed in decibels, this ratio would be a subtraction (C/N0)dB = CdB − N0dB. However, the linear-scale units still simplify in the implied fraction, so that the results would be expressed in dB-Hz.
Representation of addition operations[edit]
According to Mitschke,[28] “The advantage of using a logarithmic measure is that in a transmission chain, there are many elements concatenated, and each has its own gain or attenuation. To obtain the total, addition of decibel values is much more convenient than multiplication of the individual factors.” However, for the same reason that humans excel at additive operation over multiplication, decibels are awkward in inherently additive operations:[29]
if two machines each individually produce a sound pressure level of, say, 90 dB at a certain point, then when both are operating together we should expect the combined sound pressure level to increase to 93 dB, but certainly not to 180 dB!; suppose that the noise from a machine is measured (including the contribution of background noise) and found to be 87 dBA but when the machine is switched off the background noise alone is measured as 83 dBA. […] the machine noise [level (alone)] may be obtained by ‘subtracting’ the 83 dBA background noise from the combined level of 87 dBA; i.e., 84.8 dBA.; in order to find a representative value of the sound level in a room a number of measurements are taken at different positions within the room, and an average value is calculated. […] Compare the logarithmic and arithmetic averages of […] 70 dB and 90 dB: logarithmic average = 87 dB; arithmetic average = 80 dB.
Addition on a logarithmic scale is called logarithmic addition, and can be defined by taking exponentials to convert to a linear scale, adding there, and then taking logarithms to return. For example, where operations on decibels are logarithmic addition/subtraction and logarithmic multiplication/division, while operations on the linear scale are the usual operations:
The logarithmic mean is obtained from the logarithmic sum by subtracting 
Fractions[edit]
Attenuation constants, in topics such as optical fiber communication and radio propagation path loss, are often expressed as a fraction or ratio to distance of transmission. In this case, dB/m represents decibel per meter, dB/mi represents decibel per mile, for example. These quantities are to be manipulated obeying the rules of dimensional analysis, e.g., a 100-meter run with a 3.5 dB/km fiber yields a loss of 0.35 dB = 3.5 dB/km × 0.1 km.
Uses[edit]
Perception[edit]
The human perception of the intensity of sound and light more nearly approximates the logarithm of intensity rather than a linear relationship (see Weber–Fechner law), making the dB scale a useful measure.[30][31][32][33][34][35]
Acoustics[edit]

Examples of sound levels in decibels from various sound sources and activities, taken from the “How loud is too loud” screen of the NIOSH Sound Level Meter app
The decibel is commonly used in acoustics as a unit of sound pressure level. The reference pressure for sound in air is set at the typical threshold of perception of an average human and there are common comparisons used to illustrate different levels of sound pressure. As sound pressure is a root-power quantity, the appropriate version of the unit definition is used:
where prms is the root mean square of the measured sound pressure and pref is the standard reference sound pressure of 20 micropascals in air or 1 micropascal in water.[36]
Use of the decibel in underwater acoustics leads to confusion, in part because of this difference in reference value.[37]
Sound intensity is proportional to the square of sound pressure. Therefore the sound intensity level can also be defined as:
The human ear has a large dynamic range in sound reception. The ratio of the sound intensity that causes permanent damage during short exposure to that of the quietest sound that the ear can hear is equal to or greater than 1 trillion (1012).[38] Such large measurement ranges are conveniently expressed in logarithmic scale: the base-10 logarithm of 1012 is 12, which is expressed as a sound intensity level of 120 dB re 1 pW/m2. The reference values of I and p in air have been chosen such that this also corresponds to a sound pressure level of 120 dB re 20 μPa.
Since the human ear is not equally sensitive to all sound frequencies, the acoustic power spectrum is modified by frequency weighting (A-weighting being the most common standard) to get the weighted acoustic power before converting to a sound level or noise level in decibels.[39]
Telephony[edit]
The decibel is used in telephony and audio. Similarly to the use in acoustics, a frequency weighted power is often used. For audio noise measurements in electrical circuits, the weightings are called psophometric weightings.[40]
Electronics[edit]
In electronics, the decibel is often used to express power or amplitude ratios (as for gains) in preference to arithmetic ratios or percentages. One advantage is that the total decibel gain of a series of components (such as amplifiers and attenuators) can be calculated simply by summing the decibel gains of the individual components. Similarly, in telecommunications, decibels denote signal gain or loss from a transmitter to a receiver through some medium (free space, waveguide, coaxial cable, fiber optics, etc.) using a link budget.
The decibel unit can also be combined with a reference level, often indicated via a suffix, to create an absolute unit of electric power. For example, it can be combined with “m” for “milliwatt” to produce the “dBm”. A power level of 0 dBm corresponds to one milliwatt, and 1 dBm is one decibel greater (about 1.259 mW).
In professional audio specifications, a popular unit is the dBu. This is relative to the root mean square voltage which delivers 1 mW (0 dBm) into a 600-ohm resistor, or √1 mW×600 Ω ≈ 0.775 VRMS. When used in a 600-ohm circuit (historically, the standard reference impedance in telephone circuits), dBu and dBm are identical.
Optics[edit]
In an optical link, if a known amount of optical power, in dBm (referenced to 1 mW), is launched into a fiber, and the losses, in dB (decibels), of each component (e.g., connectors, splices, and lengths of fiber) are known, the overall link loss may be quickly calculated by addition and subtraction of decibel quantities.[41]
In spectrometry and optics, the blocking unit used to measure optical density is equivalent to −1 B.
Video and digital imaging[edit]
In connection with video and digital image sensors, decibels generally represent ratios of video voltages or digitized light intensities, using 20 log of the ratio, even when the represented intensity (optical power) is directly proportional to the voltage generated by the sensor, not to its square, as in a CCD imager where response voltage is linear in intensity.[42]
Thus, a camera signal-to-noise ratio or dynamic range quoted as 40 dB represents a ratio of 100:1 between optical signal intensity and optical-equivalent dark-noise intensity, not a 10,000:1 intensity (power) ratio as 40 dB might suggest.[43]
Sometimes the 20 log ratio definition is applied to electron counts or photon counts directly, which are proportional to sensor signal amplitude without the need to consider whether the voltage response to intensity is linear.[44]
However, as mentioned above, the 10 log intensity convention prevails more generally in physical optics, including fiber optics, so the terminology can become murky between the conventions of digital photographic technology and physics. Most commonly, quantities called “dynamic range” or “signal-to-noise” (of the camera) would be specified in 20 log dB, but in related contexts (e.g. attenuation, gain, intensifier SNR, or rejection ratio) the term should be interpreted cautiously, as confusion of the two units can result in very large misunderstandings of the value.
Photographers typically use an alternative base-2 log unit, the stop, to describe light intensity ratios or dynamic range.
Suffixes and reference values[edit]
Suffixes are commonly attached to the basic dB unit in order to indicate the reference value by which the ratio is calculated. For example, dBm indicates power measurement relative to 1 milliwatt.
In cases where the unit value of the reference is stated, the decibel value is known as “absolute”. If the unit value of the reference is not explicitly stated, as in the dB gain of an amplifier, then the decibel value is considered relative.
This form of attaching suffixes to dB is widespread in practice, albeit being against the rules promulgated by standards bodies (ISO and IEC),[15] given the “unacceptability of attaching information to units”[a] and the “unacceptability of mixing information with units”[b]. The IEC 60027-3 standard recommends the following format:[14] Lx (re xref) or as Lx/xref, where x is the quantity symbol and xref is the value of the reference quantity, e.g., LE (re 1 μV/m) = 20 dB or LE/(1 μV/m)= 20 dB for the electric field strength E relative to 1 μV/m reference value.
If the measurement result 20 dB is presented separately, it can be specified using the information in parentheses, which is then part of the surrounding text and not a part of the unit: 20 dB (re: 1 μV/m) or 20 dB (1 μV/m).
Outside of documents adhering to SI units, the practice is very common as illustrated by the following examples. There is no general rule, with various discipline-specific practices. Sometimes the suffix is a unit symbol (“W”,”K”,”m”), sometimes it is a transliteration of a unit symbol (“uV” instead of μV for microvolt), sometimes it is an acronym for the unit’s name (“sm” for square meter, “m” for milliwatt), other times it is a mnemonic for the type of quantity being calculated (“i” for antenna gain with respect to an isotropic antenna, “λ” for anything normalized by the EM wavelength), or otherwise a general attribute or identifier about the nature of the quantity (“A” for A-weighted sound pressure level). The suffix is often connected with a hyphen, as in “dB‑Hz”, or with a space, as in “dB HL”, or enclosed in parentheses, as in “dB(sm)”, or with no intervening character, as in “dBm” (which is non-compliant with international standards).
List of suffixes[edit]
Voltage[edit]
Since the decibel is defined with respect to power, not amplitude, conversions of voltage ratios to decibels must square the amplitude, or use the factor of 20 instead of 10, as discussed above.

- dBV
- dB(VRMS) – voltage relative to 1 volt, regardless of impedance.[3] This is used to measure microphone sensitivity, and also to specify the consumer line-level of −10 dBV, in order to reduce manufacturing costs relative to equipment using a +4 dBu line-level signal.[45]
- dBu or dBv
- RMS voltage relative to
(i.e. the voltage that would dissipate 1 mW into a 600 Ω load). An RMS voltage of 1 V therefore corresponds to
[3] Originally dBv, it was changed to dBu to avoid confusion with dBV.[46] The v comes from volt, while u comes from the volume unit used in the VU meter.[47]dBu can be used as a measure of voltage, regardless of impedance, but is derived from a 600 Ω load dissipating 0 dBm (1 mW). The reference voltage comes from the computation
where
is the resistance and
is the power. In professional audio, equipment may be calibrated to indicate a “0” on the VU meters some finite time after a signal has been applied at an amplitude of +4 dBu. Consumer equipment typically uses a lower “nominal” signal level of −10 dBV.[48] Therefore, many devices offer dual voltage operation (with different gain or “trim” settings) for interoperability reasons. A switch or adjustment that covers at least the range between +4 dBu and −10 dBV is common in professional equipment.
- dBm0s
- Defined by Recommendation ITU-R V.574.; dBmV: dB(mVRMS) – voltage relative to 1 millivolt across 75 Ω.[49] Widely used in cable television networks, where the nominal strength of a single TV signal at the receiver terminals is about 0 dBmV. Cable TV uses 75 Ω coaxial cable, so 0 dBmV corresponds to −78.75 dBW (−48.75 dBm) or approximately 13 nW.
- dBμV or dBuV
- dB(μVRMS) – voltage relative to 1 microvolt. Widely used in television and aerial amplifier specifications. 60 dBμV = 0 dBmV.
Acoustics[edit]
Probably the most common usage of “decibels” in reference to sound level is dB SPL, sound pressure level referenced to the nominal threshold of human hearing:[50] The measures of pressure (a root-power quantity) use the factor of 20, and the measures of power (e.g. dB SIL and dB SWL) use the factor of 10.
- dB SPL
- dB SPL (sound pressure level) – for sound in air and other gases, relative to 20 micropascals (μPa), or 2×10−5 Pa, approximately the quietest sound a human can hear. For sound in water and other liquids, a reference pressure of 1 μPa is used.[51] An RMS sound pressure of one pascal corresponds to a level of 94 dB SPL.
- dB SIL
- dB sound intensity level – relative to 10−12 W/m2, which is roughly the threshold of human hearing in air.
- dB SWL
- dB sound power level – relative to 10−12 W.
- dBA, dBB, and dBC
- These symbols are often used to denote the use of different weighting filters, used to approximate the human ear’s response to sound, although the measurement is still in dB (SPL). These measurements usually refer to noise and its effects on humans and other animals, and they are widely used in industry while discussing noise control issues, regulations and environmental standards. Other variations that may be seen are dBA or dB(A). According to standards from the International Electro-technical Committee (IEC 61672-2013)[52] and the American National Standards Institute, ANSI S1.4,[53] the preferred usage is to write LA = x dB. Nevertheless, the units dBA and dB(A) are still commonly used as a shorthand for A‑weighted measurements. Compare dBc, used in telecommunications.
- dB HL
- dB hearing level is used in audiograms as a measure of hearing loss. The reference level varies with frequency according to a minimum audibility curve as defined in ANSI and other standards, such that the resulting audiogram shows deviation from what is regarded as ‘normal’ hearing.[citation needed]
- dB Q
- sometimes used to denote weighted noise level, commonly using the ITU-R 468 noise weighting[citation needed]
- dBpp
- relative to the peak to peak sound pressure.[54]
- dBG
- G‑weighted spectrum[55]
Audio electronics[edit]
See also dBV and dBu above.
- dBm
- dB(mW) – power relative to 1 milliwatt. In audio and telephony, dBm is typically referenced relative to a 600 Ω impedance,[56] which corresponds to a voltage level of 0.775 volts or 775 millivolts.
- dBm0
- Power in dBm (described above) measured at a zero transmission level point.
- dBFS
- dB(full scale) – the amplitude of a signal compared with the maximum which a device can handle before clipping occurs. Full-scale may be defined as the power level of a full-scale sinusoid or alternatively a full-scale square wave. A signal measured with reference to a full-scale sine-wave appears 3 dB weaker when referenced to a full-scale square wave, thus: 0 dBFS(fullscale sine wave) = −3 dBFS(fullscale square wave).
- dBVU
- dB volume unit[57]
- dBTP
- dB(true peak) – peak amplitude of a signal compared with the maximum which a device can handle before clipping occurs.[58] In digital systems, 0 dBTP would equal the highest level (number) the processor is capable of representing. Measured values are always negative or zero, since they are less than or equal to full-scale.
Radar[edit]
- dBZ
- dB(Z) – decibel relative to Z = 1 mm6⋅m−3:[59] energy of reflectivity (weather radar), related to the amount of transmitted power returned to the radar receiver. Values above 20 dBZ usually indicate falling precipitation.[60]
- dBsm
- dB(m2) – decibel relative to one square meter: measure of the radar cross section (RCS) of a target. The power reflected by the target is proportional to its RCS. “Stealth” aircraft and insects have negative RCS measured in dBsm, large flat plates or non-stealthy aircraft have positive values.[61]
Radio power, energy, and field strength[edit]
- dBc
- relative to carrier – in telecommunications, this indicates the relative levels of noise or sideband power, compared with the carrier power. Compare dBC, used in acoustics.
- dBpp
- relative to the maximum value of the peak power.
- dBJ
- energy relative to 1 joule. 1 joule = 1 watt second = 1 watt per hertz, so power spectral density can be expressed in dBJ.
- dBm
- dB(mW) – power relative to 1 milliwatt. In the radio field, dBm is usually referenced to a 50 Ω load, with the resultant voltage being 0.224 volts.[62]
- dBμV/m, dBuV/m, or dBμ
- [63] dB(μV/m) – electric field strength relative to 1 microvolt per meter. The unit is often used to specify the signal strength of a television broadcast at a receiving site (the signal measured at the antenna output is reported in dBμV).
- dBf
- dB(fW) – power relative to 1 femtowatt.
- dBW
- dB(W) – power relative to 1 watt.
- dBk
- dB(kW) – power relative to 1 kilowatt.
- dBe
- dB electrical.
- dBo
- dB optical. A change of 1 dBo in optical power can result in a change of up to 2 dBe in electrical signal power in a system that is thermal noise limited.[64]
Antenna measurements[edit]
- dBi
- dB(isotropic) – the gain of an antenna compared with the gain of a theoretical isotropic antenna, which uniformly distributes energy in all directions. Linear polarization of the EM field is assumed unless noted otherwise.
- dBd
- dB(dipole) – the gain of an antenna compared with the gain a half-wave dipole antenna. 0 dBd = 2.15 dBi
- dBiC
- dB(isotropic circular) – the gain of an antenna compared to the gain of a theoretical circularly polarized isotropic antenna. There is no fixed conversion rule between dBiC and dBi, as it depends on the receiving antenna and the field polarization.
- dBq
- dB(quarterwave) – the gain of an antenna compared to the gain of a quarter wavelength whip. Rarely used, except in some marketing material. 0 dBq = −0.85 dBi
- dBsm
- dB(m2) – decibel relative to one square meter: measure of the antenna effective area.[65]
- dBm−1
- dB(m−1) – decibel relative to reciprocal of meter: measure of the antenna factor.
Other measurements[edit]
- dB‑Hz
- dB(Hz) – bandwidth relative to one hertz. E.g., 20 dB‑Hz corresponds to a bandwidth of 100 Hz. Commonly used in link budget calculations. Also used in carrier-to-noise-density ratio (not to be confused with carrier-to-noise ratio, in dB).
- dBov or dBO
- dB(overload) – the amplitude of a signal (usually audio) compared with the maximum which a device can handle before clipping occurs. Similar to dBFS, but also applicable to analog systems. According to ITU-T Rec. G.100.1 the level in dBov of a digital system is defined as:
,
- with the maximum signal power
, for a rectangular signal with the maximum amplitude
. The level of a tone with a digital amplitude (peak value) of
is therefore
.[66]
- dBr
- dB(relative) – simply a relative difference from something else, which is made apparent in context. The difference of a filter’s response to nominal levels, for instance.
- dBrn
- dB above reference noise. See also dBrnC
- dBrnC
- dBrnC represents an audio level measurement, typically in a telephone circuit, relative to a -90 dBm reference level, with the measurement of this level frequency-weighted by a standard C-message weighting filter. The C-message weighting filter was chiefly used in North America. The Psophometric filter is used for this purpose on international circuits. See Psophometric weighting to see a comparison of frequency response curves for the C-message weighting and Psophometric weighting filters.[67]
- dBK
- dB(K) – decibels relative to 1 K; used to express noise temperature.[68]
- dB/K
- dB(K−1) – decibels relative to 1 K−1.[69] — not decibels per kelvin: Used for the G/T factor, a figure of merit utilized in satellite communications, relating the antenna gain G to the receiver system noise equivalent temperature T.[70][71]
List of suffixes in alphabetical order[edit]
Unpunctuated suffixes[edit]
- dBA
- see dB(A).
- dBa
- see dBrn adjusted.
- dBB
- see dB(B).
- dBc
- relative to carrier – in telecommunications, this indicates the relative levels of noise or sideband power, compared with the carrier power.
- dBC
- see dB(C).
- dBD
- see dB(D).
- dBd
- dB(dipole) – the forward gain of an antenna compared with a half-wave dipole antenna. 0 dBd = 2.15 dBi
- dBe
- dB electrical.
- dBf
- dB(fW) – power relative to 1 femtowatt.
- dBFS
- dB(full scale) – the amplitude of a signal compared with the maximum which a device can handle before clipping occurs. Full-scale may be defined as the power level of a full-scale sinusoid or alternatively a full-scale square wave. A signal measured with reference to a full-scale sine-wave appears 3 dB weaker when referenced to a full-scale square wave, thus: 0 dBFS(fullscale sine wave) = −3 dBFS(fullscale square wave).
- dBG
- G-weighted spectrum
- dBi
- dB(isotropic) – the forward gain of an antenna compared with the hypothetical isotropic antenna, which uniformly distributes energy in all directions. Linear polarization of the EM field is assumed unless noted otherwise.
- dBiC
- dB(isotropic circular) – the forward gain of an antenna compared to a circularly polarized isotropic antenna. There is no fixed conversion rule between dBiC and dBi, as it depends on the receiving antenna and the field polarization.
- dBJ
- energy relative to 1 joule. 1 joule = 1 watt second = 1 watt per hertz, so power spectral density can be expressed in dBJ.
- dBk
- dB(kW) – power relative to 1 kilowatt.
- dBK
- dB(K) – decibels relative to kelvin: Used to express noise temperature.
- dBm
- dB(mW) – power relative to 1 milliwatt.
- dBm0
- Power in dBm measured at a zero transmission level point.
- dBm0s
- Defined by Recommendation ITU-R V.574.
- dBmV
- dB(mVRMS) – voltage relative to 1 millivolt across 75 Ω.
- dBo
- dB optical. A change of 1 dBo in optical power can result in a change of up to 2 dBe in electrical signal power in system that is thermal noise limited.
- dBO
- see dBov
- dBov or dBO
- dB(overload) – the amplitude of a signal (usually audio) compared with the maximum which a device can handle before clipping occurs.
- dBpp
- relative to the peak to peak sound pressure.
- dBpp
- relative to the maximum value of the peak power.
- dBq
- dB(quarterwave) – the forward gain of an antenna compared to a quarter wavelength whip. Rarely used, except in some marketing material. 0 dBq = −0.85 dBi
- dBr
- dB(relative) – simply a relative difference from something else, which is made apparent in context. The difference of a filter’s response to nominal levels, for instance.
- dBrn
- dB above reference noise. See also dBrnC
- dBrnC
- dBrnC represents an audio level measurement, typically in a telephone circuit, relative to the circuit noise level, with the measurement of this level frequency-weighted by a standard C-message weighting filter. The C-message weighting filter was chiefly used in North America.
- dBsm
- dB(m2) – decibel relative to one square meter
- dBTP
- dB(true peak) – peak amplitude of a signal compared with the maximum which a device can handle before clipping occurs.
- dBu or dBv
- RMS voltage relative to
.
- dBu0s
- Defined by Recommendation ITU-R V.574.
- dBuV
- see dBμV
- dBuV/m
- see dBμV/m
- dBv
- see dBu
- dBV
- dB(VRMS) – voltage relative to 1 volt, regardless of impedance.
- dBVU
- dB volume unit
- dBW
- dB(W) – power relative to 1 watt.
- dBW·m−2·Hz−1
- spectral density relative to 1 W·m−2·Hz−1[72]
- dBZ
- dB(Z) – decibel relative to Z = 1 mm6⋅m−3
- dBμ
- see dBμV/m
- dBμV or dBuV
- dB(μVRMS) – voltage relative to 1 microvolt.
- dBμV/m, dBuV/m, or dBμ
- dB(μV/m) – electric field strength relative to 1 microvolt per meter.
Suffixes preceded by a space[edit]
- dB HL
- dB hearing level is used in audiograms as a measure of hearing loss.
- dB Q
- sometimes used to denote weighted noise level
- dB SIL
- dB sound intensity level – relative to 10−12 W/m2
- dB SPL
- dB SPL (sound pressure level) – for sound in air and other gases, relative to 20 μPa in air or 1 μPa in water
- dB SWL
- dB sound power level – relative to 10−12 W.
Suffixes within parentheses[edit]
- dB(A), dB(B), dB(C), dB(D), dB(G), and dB(Z)
- These symbols are often used to denote the use of different weighting filters, used to approximate the human ear’s response to sound, although the measurement is still in dB (SPL). These measurements usually refer to noise and its effects on humans and other animals, and they are widely used in industry while discussing noise control issues, regulations and environmental standards. Other variations that may be seen are dBA or dBA.
Other suffixes[edit]
- dB-Hz
- dB(Hz) – bandwidth relative to one hertz.
- dB/K
- dB(K−1) – decibels relative to reciprocal of kelvin
- dBm−1
- dB(m−1) – decibel relative to reciprocal of meter: measure of the antenna factor.
- mBm
- mB(mW) – power relative to 1 milliwatt, in millibels (one hundredth of a decibel). 100 mBm = 1 dBm. This unit is in the Wi-Fi drivers of the Linux kernel[73] and the regulatory domain sections.[74]
See also[edit]
- Apparent magnitude
- Cent (music)
- Day–evening–night noise level (Lden) and day-night average sound level (Ldl), European and American standards for expressing noise level over an entire day
- dB drag racing
- Decade (log scale)
- Loudness
- One-third octave § Base 10
- pH
- Phon
- Richter magnitude scale
- Sone
Notes[edit]
- ^ “When one gives the value of a quantity, it is incorrect to attach letters or other symbols to the unit in order to provide information about the quantity or its conditions of measurement. Instead, the letters or other symbols should be attached to the quantity.”[15]: 16
- ^ “When one gives the value of a quantity, any information concerning the quantity or its conditions of measurement must be presented in such a way as not to be associated with the unit. This means that quantities must be defined so that they can be expressed solely in acceptable units…”[15]: 17
References[edit]
- ^ Mark, James E. (2007). Physical Properties of Polymers Handbook. Springer. p. 1025. Bibcode:2007ppph.book…..M.
[…] the decibel represents a reduction in power of 1.258 times […]
- ^ Yost, William (1985). Fundamentals of Hearing: An Introduction (Second ed.). Holt, Rinehart and Winston. p. 206. ISBN 978-0-12-772690-8.
[…] a pressure ratio of 1.122 equals + 1.0 dB […]
- ^ a b c Utilities : VRMS / dBm / dBu / dBV calculator, Analog Devices, retrieved 16 September 2016
- ^ Thompson and Taylor 2008, Guide for the Use of the International System of Units (SI), NIST Special Publication SP811 Archived 2016-06-03 at the Wayback Machine.
- ^ IEEE Standard 100: a dictionary of IEEE standards and terms (7th ed.). New York: The Institute of Electrical and Electronics Engineering. 2000. p. 288. ISBN 978-0-7381-2601-2.
- ^ Johnson, Kenneth Simonds (1944). Transmission Circuits for Telephonic Communication: Methods of analysis and design. New York: D. Van Nostrand Co. p. 10.
- ^ Davis, Don; Davis, Carolyn (1997). Sound system engineering (2nd ed.). Focal Press. p. 35. ISBN 978-0-240-80305-0.
- ^ Hartley, R. V. L. (December 1928). “‘TU’ becomes ‘Decibel’“. Bell Laboratories Record. AT&T. 7 (4): 137–139.
- ^ Martin, W. H. (January 1929). “DeciBel—The New Name for the Transmission Unit”. Bell System Technical Journal. 8 (1).
- ^ 100 Years of Telephone Switching, p. 276, at Google Books, Robert J. Chapuis, Amos E. Joel, 2003
- ^ Harrison, William H. (1931). “Standards for Transmission of Speech”. Standards Yearbook. National Bureau of Standards, U. S. Govt. Printing Office. 119.
- ^ Horton, J. W. (1954). “The bewildering decibel”. Electrical Engineering. 73 (6): 550–555. doi:10.1109/EE.1954.6438830. S2CID 51654766.
- ^ “Meeting minutes” (PDF). Consultative Committee for Units. Section 3. Archived (PDF) from the original on 6 October 2014.
- ^ a b “Letter symbols to be used in electrical technology”. International Electrotechnical Commission. 19 July 2002. Part 3: Logarithmic and related quantities, and their units. IEC 60027-3, Ed. 3.0.
- ^ a b c d Thompson, A. and Taylor, B. N. sec 8.7, “Logarithmic quantities and units: level, neper, bel”, Guide for the Use of the International System of Units (SI) 2008 Edition, NIST Special Publication 811, 2nd printing (November 2008), SP811 PDF
- ^ “Letter symbols to be used in electrical technology”. International Standard CEI-IEC 27-3. International Electrotechnical Commission. Part 3: Logarithmic quantities and units.
- ^ Mark, James E. (2007). Physical Properties of Polymers Handbook. Springer. p. 1025. Bibcode:2007ppph.book…..M.
[…] the decibel represents a reduction in power of 1.258 times […]
- ^ Yost, William (1985). Fundamentals of Hearing: An Introduction (Second ed.). Holt, Rinehart and Winston. p. 206. ISBN 978-0-12-772690-8.
[…] a pressure ratio of 1.122 equals + 1.0 dB […]
- ^ Fedor Mitschke, Fiber Optics: Physics and Technology, Springer, 2010 ISBN 3642037038.
- ^ Pozar, David M. (2005). Microwave Engineering (3rd ed.). Wiley. p. 63. ISBN 978-0-471-44878-5.
- ^ IEC 60027-3:2002
- ^ I M Mills; B N Taylor; A J Thor (2001), “Definitions of the units radian, neper, bel and decibel”, Metrologia, 38 (4): 353, Bibcode:2001Metro..38..353M, doi:10.1088/0026-1394/38/4/8, S2CID 250827251
- ^ R. Hickling (1999), Noise Control and SI Units, J Acoust Soc Am 106, 3048
- ^ Hickling, R. (2006). Decibels and octaves, who needs them?. Journal of sound and vibration, 291(3-5), 1202-1207.
- ^ Nicholas P. Cheremisinoff (1996) Noise Control in Industry: A Practical Guide, Elsevier, 203 pp, p. 7
- ^ Andrew Clennel Palmer (2008), Dimensional Analysis and Intelligent Experimentation, World Scientific, 154 pp, p.13
- ^ J. C. Gibbings, Dimensional Analysis, p.37, Springer, 2011 ISBN 1849963177.
- ^ Fiber Optics. Springer. 2010.
- ^ R. J. Peters, Acoustics and Noise Control, Routledge, 12 November 2013, 400 pages, p. 13
- ^ Sensation and Perception, p. 268, at Google Books
- ^ Introduction to Understandable Physics, Volume 2, p. SA19-PA9, at Google Books
- ^ Visual Perception: Physiology, Psychology, and Ecology, p. 356, at Google Books
- ^ Exercise Psychology, p. 407, at Google Books
- ^ Foundations of Perception, p. 83, at Google Books
- ^ Fitting The Task To The Human, p. 304, at Google Books
- ^ ISO 1683:2015
- ^ C. S. Clay (1999), Underwater sound transmission and SI units, J Acoust Soc Am 106, 3047
- ^ “Loud Noise Can Cause Hearing Loss”. cdc.gov. Centers for Disease Control and Prevention. 7 October 2019. Retrieved 30 July 2020.
- ^ Richard L. St. Pierre, Jr. and Daniel J. Maguire (July 2004), The Impact of A-weighting Sound Pressure Level Measurements during the Evaluation of Noise Exposure (PDF), archived (PDF) from the original on 22 December 2015, retrieved 13 September 2011
- ^ Reeve, William D. (1992). Subscriber Loop Signaling and Transmission Handbook – Analog (1st ed.). IEEE Press. ISBN 0-87942-274-2.
- ^
Chomycz, Bob (2000). Fiber optic installer’s field manual. McGraw-Hill Professional. pp. 123–126. ISBN 978-0-07-135604-6. - ^
Stephen J. Sangwine and Robin E. N. Horne (1998). The Colour Image Processing Handbook. Springer. pp. 127–130. ISBN 978-0-412-80620-9. - ^
Francis T. S. Yu and Xiangyang Yang (1997). Introduction to optical engineering. Cambridge University Press. pp. 102–103. ISBN 978-0-521-57493-8. - ^
Junichi Nakamura (2006). “Basics of Image Sensors”. In Junichi Nakamura (ed.). Image sensors and signal processing for digital still cameras. CRC Press. pp. 79–83. ISBN 978-0-8493-3545-7. - ^ Winer, Ethan (2013). The Audio Expert: Everything You Need to Know About Audio. Focal Press. p. 107. ISBN 978-0-240-82100-9.
- ^ Stas Bekman. “3.3 – What is the difference between dBv, dBu, dBV, dBm, dB SPL, and plain old dB? Why not just use regular voltage and power measurements?”. stason.org.
- ^ Rupert Neve, Creation of the dBu standard level reference, archived from the original on 30 October 2021
- ^ deltamedia.com. “DB or Not DB”. Deltamedia.com. Retrieved 16 September 2013.
- ^ The IEEE Standard Dictionary of Electrical and Electronics terms (6th ed.). IEEE. 1996 [1941]. ISBN 978-1-55937-833-8.
- ^ Jay Rose (2002). Audio postproduction for digital video. Focal Press. p. 25. ISBN 978-1-57820-116-7.
- ^ Morfey, C. L. (2001). Dictionary of Acoustics. Academic Press, San Diego.
- ^ IEC 61672-1:2013 Electroacoustics – Sound Level meters – Part 1: Specifications. Geneva: International Electrotechnical Committee. 2013.
- ^ ANSI S1.4-19823 Specification for Sound Level Meters, 2.3 Sound Level, p. 2–3.
- ^ Zimmer, Walter MX, Mark P. Johnson, Peter T. Madsen, and Peter L. Tyack. “Echolocation clicks of free-ranging Cuvier’s beaked whales (Ziphius cavirostris).” The Journal of the Acoustical Society of America 117, no. 6 (2005): 3919–3927.
- ^ “Turbine Sound Measurements”. Archived from the original on 12 December 2010.
- ^ Bigelow, Stephen (2001). Understanding Telephone Electronics. Newnes. p. 16. ISBN 978-0750671750.
- ^ Tharr, D. (1998). Case Studies: Transient Sounds Through Communication Headsets. Applied Occupational and Environmental Hygiene, 13(10), 691–697.
- ^ ITU-R BS.1770
- ^ “Glossary: D’s”. National Weather Service. Archived from the original on 8 August 2019. Retrieved 25 April 2013.
- ^ “RIDGE Radar Frequently Asked Questions”. Archived from the original on 31 March 2019. Retrieved 8 August 2019.
- ^ “Definition at Everything2”. Archived from the original on 10 June 2019. Retrieved 8 August 2019.
- ^ Carr, Joseph (2002). RF Components and Circuits. Newnes. pp. 45–46. ISBN 978-0750648448.
- ^ “The dBµ vs. dBu Mystery: Signal Strength vs. Field Strength?”. radio-timetraveller.blogspot.com. 24 February 2015. Retrieved 13 October 2016.
- ^ Chand, N., Magill, P. D., Swaminathan, S. V., & Daugherty, T. H. (1999). Delivery of digital video and other multimedia services (> 1 Gb/s bandwidth) in passband above the 155 Mb/s baseband services on a FTTx full service access network. Journal of lightwave technology, 17(12), 2449–2460.
- ^ David Adamy. EW 102: A Second Course in Electronic Warfare. Retrieved 16 September 2013.
- ^ ITU-T Rec. G.100.1 The use of the decibel and of relative levels in speechband telecommunications https://www.itu.int/rec/dologin_pub.asp?lang=e&id=T-REC-G.100.1-201506-I!!PDF-E&type=items
- ^ dBrnC is defined on page 230 in “Engineering and Operations in the Bell System,” (2ed), R.F. Rey (technical editor), copyright 1983, AT&T Bell Laboratories, Murray Hill, NJ, ISBN 0-932764-04-5
- ^ K. N. Raja Rao (31 January 2013). Satellite Communication: Concepts And Applications. Retrieved 16 September 2013.
- ^ Ali Akbar Arabi. Comprehensive Glossary of Telecom Abbreviations and Acronyms. Retrieved 16 September 2013.
- ^ Mark E. Long. The Digital Satellite TV Handbook. Retrieved 16 September 2013.
- ^ Mac E. Van Valkenburg (19 October 2001). Reference Data for Engineers: Radio, Electronics, Computers and Communications. Retrieved 16 September 2013.
- ^ “Archived copy”. Archived from the original on 3 March 2016. Retrieved 24 August 2013.
{{cite web}}: CS1 maint: archived copy as title (link) - ^ “en:users:documentation:iw [Linux Wireless]”. wireless.kernel.org.
- ^ “Is your WiFi AP Missing Channels 12 & 13?”. wordpress.com. 16 May 2013.
Further reading[edit]
- Tuffentsammer, Karl (1956). “Das Dezilog, eine Brücke zwischen Logarithmen, Dezibel, Neper und Normzahlen” [The decilog, a bridge between logarithms, decibel, neper and preferred numbers]. VDI-Zeitschrift (in German). 98: 267–274.
- Paulin, Eugen (1 September 2007). Logarithmen, Normzahlen, Dezibel, Neper, Phon – natürlich verwandt! [Logarithms, preferred numbers, decibel, neper, phon – naturally related!] (PDF) (in German). Archived (PDF) from the original on 18 December 2016. Retrieved 18 December 2016.
External links[edit]
- What is a decibel? With sound files and animations
- Conversion of sound level units: dBSPL or dBA to sound pressure p and sound intensity J
- OSHA Regulations on Occupational Noise Exposure
- Working with Decibels (RF signal and field strengths)
Мы часто встречаем уровни звука, указанные в децибелах — дБ или dBu и привыкли считать что это единица измерения шума, звука. А вот и нет. Это совсем не так. Децибел — это не единица измерения вообще. Это относительная характеристика, которая может отражать напряжение, мощность, силу тока и т.д. Что-то типа процентов, долей, но в логарифмической зависимости. Сначала понять, что такое децибел, непросто, но затем оказывается, что это очень удобно.
Содержание статьи
- 1 Понятие децибела
- 1.1 Что значит бел и децибел
- 1.2 Почему используют децибелы, а не прямые величины
- 1.3 Что такое dBm, dBv, dBA (дБм, дБв, дБА)
- 2 Как считают децибелы
- 3 Децибелы в акустике
- 3.1 Таблица уровней шумов
- 4 Перевод децибелов в разы
Понятие децибела
Мы хорошо воспринимаем измерение каких-либо параметров в прямых величинах. Например, напряжение измеряется в вольтах, сила тока — в амперах, сопротивление — в омах и т.д. Когда говорим об этом, все ясно и понятно. Когда говорим об увеличении или снижении в этих прямых единицах измерения тоже все понятно. Например, напряжение с 220 вольт снизилось до 150 вольт. Все понятно. Выражение «мощность возросла на 50 ватт» тоже вопросов не вызывает.

Как понять что такое децибел и что он означает
Но иногда говорят об увеличении или уменьшении того же напряжения или мощности на 2 децибела. Как это понять? Что измеряется в децибелах? Ведь мощность меряем в ваттах? Как соотнести децибелы с ваттами или вольтами, амперами и другими величинами. Ведь так описывают многие параметры. Тут надо разбираться. Не очень просто сначала понять, но потом все становится очевидным.
Что значит бел и децибел
Сразу стоит уяснить, что бел и децибел — это не единицы измерения чего-либо. Это не результат измерений. Децибел — это величина, которая показывает насколько/во сколько раз изменился тот или иной параметр. То есть бел или децибел — это относительная величина, которая высчитывается при сравнении двух измерений одного и того же параметра.
Например, на рисунке дан график, который построили по результатам измерения напряжение на выходе прибора при изменении подаваемой на вход частоты (АЧХ). Сняты были характеристики при уровне сигнала 1 V (график 1) и 100 мV (график 2). Если смотреть на графики прямых измерений, понять что-то сложно. На втором рисунке график построен в децибелах. На этом графике очевидно, что реакция прибора одинаковая, изменился только уровень сигнала на выходе, что и понятно.

Два графика измерений. Левый — прямая зависимость (напряжения от частоты), правый — изменение напряжения в дБ при изменении частоты
Первоначально стали использовать единицу Бел. Международное обозначение бела — B, российское — Б (например, 10Б или 10B). Но более удобным оказалось применение одной ее десятой доли — децибела или дБ в российском обозначении и dBu в международном. То есть один децибел — это 0,1 Бела.
Дальше, к сожалению, без математики не обойтись. Придется вспомнить что такое десятичный логарифм. Десятичный логарифм показывает, в какую степень надо возвести число 10 чтобы получить требуемую цифру. На рисунке вы видите соотношение, возможно будет понятнее в таком виде.

Несколько значений десятичных логарифмов
Теперь, собственно о Белах и децибелах. Если говорить об определениях, то Бел — это десятичный логарифм отношения двух величин. Любых двух величин. Мощностей, напряжения, силы звука, частоты и т.д. Давайте на примере. Надо понять, что выдает прибор на выходе при изменении параметров на входе. Выбирают какую-то точку отсчета — базу. Затем изменяют параметр, проводят измерение результата, делят его на «базу» и берут десятичный логарифм. Получают результат измерения в децибелах. Так измеряют параметры, пересчитывают в децибелы и строят зависимости.

Формула, которая поясняет что такое дБ (децибел) и как их считают
На рисунке даны две формулы — для вычисления энергетических величин (по мощности) и амплитудных (по напряжению). Как видите, они отличаются только коэффициентом. U1 тут — это результат измерений, а Uo — базовая величина, с который сравнивают измерений.
Почему используют децибелы, а не прямые величины
Использование логарифмических зависимостей часто более понятно и несет больше информации, чем прямые измерения. Это видно на примере построения графиков амплитудно-частотной характеристики. И такой случай не единичный, многие зависимости более информативны в логарифмической зависимости.
Кроме того, децибелы используют в тех областях, где параметры изменяются в очень широком диапазоне. Более понятна нам ситуация со звуками. Человек в состоянии воспринимать частоты от 20 Гц до 20 000 Гц. Ничего себе разброс! В тысячу раз.

Интенсивность звука и его соответствие в дБА
С уровнем звука еще круче. Нижний предел восприятия — 10-12 Вт/м, а уровень, при котором возникает боль — 10 Вт/м. То есть, диапазон измерения значений — 13 порядков. Это 10 000 000 000 000 раз. Оперировать такими цифрами, как минимум неудобно. С использованием относительных величин — децибел — цифры получаются значительно меньше, работать, воспринимать и запоминать их легче. Несколько примеров:
- Если показатель увеличился в 10 раз, говорят, что он увеличился на 1 Бел.
- Если тот же показатель увеличился в 100 раз, то говорят об увеличении на 2 Бела.
- Увеличение в 100 000 тысяч раз — всего на 5 Бел.
Заметили разницу? Показатель увеличился в 100 раз, а в белах увеличился на 2 Б. Это удобнее. Согласитесь, проще оперировать единицами, чем сотнями тысяч. Важно просто понимать смысл сказанного. При возрастании прямых величин их надо умножать на то число, на которое параметр увеличился. При оперировании децибелами их складывают. Согласитесь, это проще.
Что такое dBm, dBv, dBA (дБм, дБв, дБА)
Как вы уже поняли, децибел — это относительная величина и отражать она может что угодно. Надо только выбрать точку отсчета, базу, эталон, с которым сравнивают все последующие изменения. База для сравнения может быть взята произвольно. Но тогда непонятно как соотносить разные измерения. В таком случае, обычно, указывают относительно чего считался логарифм. То есть, что подставляли в знаменатель (в формуле выше это Uo).
Для электротехники и мощностей были выбраны базовые точки отсчета — две величины напряжения, с которыми сравнивают большую часть измерений электрических величин.
- Основная база — это мощность в один милливатт (1 мВт) при нагрузке 600 Ом. Если пересчитать, то напряжение получаем 0,775 Вольта. Именно эти значения и являются той базой, относительно которой высчитывают логарифмы. Это принято и в международных измерениях, и в отечественных. Именно при использовании такой базы ставят обозначение dBu или дБ в русском варианте. Реже встречается обозначение dBm. Это тоже, что dBu.
- Иногда выходное напряжение сравнивают с 1 В. В этом случае результат подписывают как dBv или дБв.
На что влияет точка отсчета? Просто на уровень, на котором строится зависимость. Если же по данным построить график, он будет иметь ту же форму.
При описании звуков и шумов употребляют дБА (dBA) или акустические децибелы. При таком исчислении за точку отсчета берут нижний порог слышимости или частоты, которую различает человеческое ухо. Это 2·10-5 Па и относительно нее вычисляют отношение.
Как считают децибелы
Больше в ходу не Белы, а их десятая часть — децибелы (обозначение dB или дБ). Ведь чаще увеличение не в сотни и тысячи раз, а чуть поскромнее. Так что обычно говорят об увеличении того или иного показания или характеристики на 5 дБ или на 10 дБ.

Пример соответствия децибел и «раз»
Но важно помнить, что описанная выше прямая зависимость характерна только для энергетических величин (это если мощность возросла в 10 раз, то она увеличилась на 10 дБ). Для других зависимость тоже логарифмическая, но вычисляется по другой формуле. И это надо помнить.
| Децибелы | Соотношение мощностей | Соотношение амплитуд |
|---|---|---|
| -3 | 0,5 | 0,7 |
| -6 | 0,25 | 0,5 |
| -10 | 0,1 | 0,3 |
| -20 | 1,01 | 0,1 |
| -25 | 0,03 | 0,05 |
| -40 | 0,01 | 0,0001 |
| -60 | 0,001 | 0,000001 |
Возможно, поможет понять что такое децибел следующие сравнение. Представим, что мощность изменяется литрами. Соотношение между 0,5 литра и 1 литром такое же как и между 1 литром и 2 литрами. Это 0,5 и равно оно 6 дБ. Но если сравнивать 0,5 и 0,75 литра, то они относятся как 0,66(6) что в децибелах около 3,6 дБ. Примерно так.
Децибелы в акустике
Вы, возможно, удивитесь, но для акустики децибелы подходят просто идеально. Собственно, Александр Белл ввел понятие Бел при исследовании порога слышимости. Он определил, что «громкость» мы воспринимаем не по реальной мощности сигнала, а по десятичному логарифму от этой мощности. Как так? Давайте рассмотрим пример.
Имеется усилитель, который выдает сигнал мощностью 1 Вт. Чтобы увеличить его в 1,1 раза, добавить надо только 0,1 Вт. А если на выходе у нас 100 Вт, то чтобы увеличить мощность в 1,1 раза надо поднять мощность на 10 Вт. Увеличение громкости в обоих случаях будет «для уха» одинаковым, а увеличение мощности имеет явно нелинейный характер.

Мы воспринимаем не реальный уровень сигнала, а логарифмическую зависимость
На основании вот этого явления Белл и вывел то самое логарифмическое отношение. В его честь и названа эта относительная единица измерений. Что еще это нам дает? А вот такие факты:
- 1 дБ — это минимальный уровень слышимости сигнала. Звуки с более низкой мощностью (о дБ и ниже) большинство людей не замечают и определяют как «абсолютную тишину».
- Если говорят о том, что мощность сигнала/звука возросла на 3 дБ, то значит она возросла в два раза. Не путайте с громкостью.
- При увеличении мощности звука на 10 дБ, громкость увеличивается в 2 раза.
- Увеличение напряжения в два раза — это 6 дБ.
Принять децибелы не так легко. Но наверное, вы уже поняли, что в децибелах громкость звука/шума не измеряется. Эта цифра показывает насколько изменился сигнал относительно «нулевой» точки восприятия. Примерно так можно это сформулировать.
Таблица уровней шумов
Ну, а чтобы было понятнее, приведем таблицу сравнений привычных, знакомых звуков и их среднего уровня.
| дБ | С чем можно сравнить | дБ | С чем можно сравнить |
|---|---|---|---|
| 0 дБ | Полная тишина | 90 дБ | Звук работающего фена, мотоцикла, поезда |
| 1 дБ | Самый нижний порог слышимости | 100-105 дБ | Ремонт и рок-концерт |
| 10-24 дБ | Шелест листвы | 110 дБ | Музыка в ночном клубе |
| 20 дБ | Шепот | 120 дБ | Автомобильный гудок |
| 40 дБ | Так звучит дождь | 130-135 дБ | Звук работающей дрели |
| 45 дБ | Тихий разговор | 140 дБ | Шум турбин самолета |
| 60 дБ | Громкий разговор | 160 дБ | Звук выстрела возле уха |
| 80-90 дБ | Шоссе с интенсивным движением | 200 дБ | Смертельный уровень шума |

Каждый шум или звук имеет определенный уровень мощности, но проще его описывать в децибелах
Факты, которые позволят оценить важность акустики и децибелов:
- Комфортным уровнем шума считается 50-55 дБ. Как видите, эту величину можно сравнить с разговором обычной «громкости». Именно этот уровень по СНиПу определен как приемлемый для дневного времени.
- Уровень 70-90 дБ относится к «терпимым», но длительное воздействие может привести к заболеваниям нервной системы.
- Длительное воздействие шума в 100 дБ приводит к снижению слуха и глухоте.
- Звуки мощностью 130 дБ вызывают болевые ощущения.
- Мощность звука в 200 дБ может быть смертельной.
Вообще, постоянное нахождение в шумном помещении сильно снижает способность воспринимать звуки. Мало того, оно приводит к расстройствам психики, сна, что негативно сказывается и на общем самочувствии. Поэтому шумные производства — зона риска. Чтобы хорошо себя чувствовать, просто необходимо время от времени находится если не при полной тишине, то при низком уровне шума.
Перевод децибелов в разы
Давайте попробуем сформулировать что такое децибел по-другому. Децибел — это логарифм соотношения двух величин. Эта относительная величина, которая показывает во сколько одно значение больше или меньше другого (базового). «Во сколько раз» это нам понятно. Поэтому часто приходится переводить децибелы в разы и наоборот. Можно, конечно, посчитать, но проще пользоваться таблицей.
| дБ | Увеличение напряжения (силы тока) в разы | Увеличение мощности (энергетической составляющей) в разы | дБ | Увеличение напряжения (силы тока) в разы | Увеличение мощности (энергетической составляющей) в разы |
|---|---|---|---|---|---|
| 0 | 1 | 1 | 28 | 25,12 | 631 |
| 1 | 1,12 | 1,26 | 29 | 28,17 | 794 |
| 2 | 1,26 | 1,59 | 30 | 31,64 | 1000 |
| 3 | 1,41 | 2 | 31 | 35,46 | 1257 |
| 4 | 1,59 | 2,51 | 32 | 39,84 | 1587 |
| 5 | 1,78 | 3,16 | 33 | 44,64 | 1993 |
| 6 | 2 | 2,98 | 34 | 48,08 | 2312 |
| 7 | 2,24 | 5,01 | 35 | 56,82 | 3165 |
| 8 | 2,51 | 6,31 | 36 | 63,29 | 4006 |
| 9 | 2,82 | 7,94 | 37 | 70,92 | 5030 |
| 10 | 3,16 | 10 | 38 | 79,36 | 6298 |
| 11 | 3,55 | 12,59 | 39 | 89,29 | 7973 |
| 12 | 3,98 | 15,85 | 40 | 100 | 10000 |
| 13 | 4,47 | 19,96 | 41 | 112,23 | 12596 |
| 14 | 5,01 | 25,12 | 42 | 125,94 | 15861 |
| 15 | 5,62 | 31,65 | 43 | 141,24 | 19949 |
| 16 | 6,31 | 39,84 | 44 | 158,48 | 25116 |
| 17 | 7,08 | 48,08 | 45 | 177,94 | 31663 |
| 18 | 7,94 | 63,59 | 46 | 199,60 | 39840 |
| 19 | 8,91 | 79,36 | 47 | 223,71 | 50046 |
| 20 | 10 | 100 | 48 | 251,26 | 63132 |
| 21 | 11,22 | 125,94 | 49 | 281,69 | 79349 |
| 22 | 12,59 | 158,48 | 50 | 316,5 | 100 000 |
| 23 | 14,12 | 199,60 | 60 | 1 000 | 1 000 000 |
| 24 | 15,85 | 251,26 | 70 | 3165 | 10 000 000 |
| 25 | 17,79 | 316,50 | 80 | 10 000 | 100 000 000 |
| 26 | 19,96 | 398,4 | 90 | 31650 | 1 000 000 000 |
| 27 | 22,37 | 500,42 | 100 | 100 000 | 10 000 000 000 |
Как видите, чтобы напряжение увеличилось в три раза, мощность необходимо поднять в 10 раз. Впечатляющая разница. Эта таблица позволяет точно понять связь между этими величинами.
Но сигналы и величины не только увеличиваются, они могут и снижаться. Следующая таблица дана для падения значений относительно эталона.
| дБ | Снижение напряжения (силы тока) в разы | Снижение мощности (энергетической составляющей) в разы | дБ | Снижение напряжения (силы тока) в разы | Снижение мощности (энергетической составляющей) в разы |
|---|---|---|---|---|---|
| 0 | 1 | 1 | -8,0 | 0,398 | 0,159 |
| -0,1 | 0,989 | 0,977 | -9,0 | 0,355 | 0,126 |
| -0,2 | 0,977 | 0,955 | -10 | 0,316 | 0,1 |
| -0,3 | 0,966 | 0,933 | -11 | 0,282 | 0,0794 |
| -0,4 | 0,955 | 0,912 | -12 | 0,251 | 0,0631 |
| -0,5 | 0,944 | 0,891 | -13 | 0,224 | 0,0501 |
| -0,6 | 0,933 | 0,871 | -14 | 0,2 | 0,0398 |
| -0,8 | 0,912 | 0,832 | -15 | 0,178 | 0,0316 |
| -1,0 | 0,891 | 0,794 | -16 | 0,159 | 0,0251 |
| -1,5 | 0,841 | 0,708 | -18 | 0,126 | 0,0159 |
| -2,0 | 0,794 | 0,631 | -20 | 0,1 | 0,01 |
| -2,5 | 0,750 | 0,562 | -30 | 0,0316 | 0,001 |
| -3,0 | 0,668 | 0,501 | -40 | 0,01 | 0,0001 |
| -3,5 | 0,631 | 0,447 | -50 | 0,00316 | 0,00001 |
| -4,0 | 0,596 | 0,398 | -60 | 0,001 | 0,000001 |
| -4,5 | 0,562 | 0,355 | -70 | 0,000316 | 0,0000001 |
| -5,0 | 0,501 | 0,316 | -80 | 0,0001 | 0,00000001 |
| -6,0 | 0,501 | 0,251 | -90 | 0,0000316 | 0,000000001 |
| -7,0 | 0,447 | 0,2 | -100 | 0,00001 | 0,0000000001 |
Ослабление того или иного сигнала проще описывать в децибелах. Простые цифры легче запоминаются. Но иногда надо знать и реальный уровень мощности. Для этого используют таблицы (перевод дБ в мкВ)

Перевод ослабления сигнала в дБ в микровольты мкВ
ПРИМЕНЕНИЕ ДЕЦИБЕЛ В РАДИОЭЛЕКТРОНИКЕ И ЭЛЕКТРОАКУСТИКЕ
ЧТО ТАКОЕ ДЕЦИБЕЛЫ?
Универсальные логарифмические единицы децибелы широко используются при количественных оценках параметров различных аудио и видео устройств в нашей стране и за рубежом. В радиоэлектронике, в частности, в проводной связи, технике записи и воспроизведения информации децибелы являются универсальной мерой.
Децибел — не физическая величина, а математическое понятие
В электроакустике децибел служит по существу единственной единицей для характеристики различных уровней — интенсивности звука, звукового давления, громкости, а также для оценки эффективности средств борьбы с шумами.
Децибел — специфическая единица измерений, не схожая ни с одной из тех, с которыми приходится встречаться в повседневной практике. Децибел не является официальной единицей в системе единиц СИ, хотя, по решению Генеральной конференции по мерам и весам, допускается его применение без ограничений совместно с СИ, а Международная палата мер и весов рекомендовала включить его в эту систему.
Децибел — не физическая величина, а математическое понятие.
В этом отношении у децибел есть некоторое сходство с процентами. Как и проценты, децибелы безразмерны и служат для сравнения двух одноименных величин, в принципе самых различных, независимо от их природы. Следует отметить, что термин «децибел» всегда связывают только с энергетическими величинами, чаще всего с мощностью и, с некоторыми оговорками, с напряжением и током.
Децибел (русское обозначение — дБ, международное — dB) составляет десятую часть более крупной единицы — бела1.
Бел — это десятичный логарифм отношения двух мощностей. Если известны две мощности Р1 и Р2, то их отношение, выраженное в белах, определяется формулой:
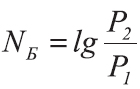
Физическая природа сравниваемых мощностей может быть любой — электрической, электромагнитной, акустической, механической, — важно лишь, чтобы обе величины были выражены в одинаковых единицах — ваттах, милливаттах и т. п.
Напомним вкратце, что такое логарифм. Любое положительное2 число, как целое, так и дробное, можно представить другим числом в определенной степени.
Так, например, если 102 = 100, то 10 называют основанием логарифма, а число 2 — логарифмом числа 100 и обозначают log10 100=2 или lg 100 = 2 (читается так: «логарифм ста при основании десять равен двум»).
Логарифмы с основанием 10 называются десятичными логарифмами и применяются чаще всего. Для чисел, кратных 10, этот логарифм численно равен количеству нулей за единицей, а для остальных чисел вычисляется на калькуляторе или находится по таблицам логарифмов.
Логарифмы с основанием е = 2,718… называются натуральными. В вычислительной технике обычно применяются логарифмы с основанием 2.
Основные свойства логарифмов:
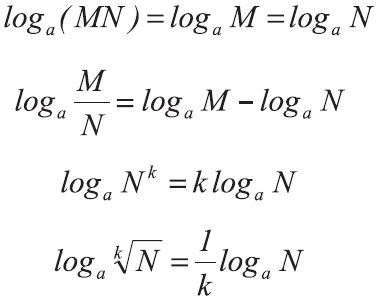
Разумеется, эти свойства справедливы и для десятичных и натуральных логарифмов. Логарифмический способ представления чисел часто оказывается очень удобным, так как позволяет подменять умножение — сложением, деление — вычитанием, возведение в степень умножением, а извлечение корня — делением.
На практике бел оказался слишком крупной величиной, например, любые отношения мощностей в границах от 100 до 1000 укладываются в пределах одного бела — от 2 Б до 3 Б. Поэтому для большей наглядности решили число, показывающее количество бел, умножать на 10 и полученное произведение считать показателем в децибелах, т. е., например, 2 Б = 20 дБ, 4,62 Б = 46,2 дБ и т. д.
Обычно отношение мощностей выражают сразу в децибелах по формуле:
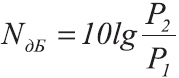
Действия с децибелами не отличаются от операций с логарифмами.
Нетрудно посчитать, что 1 дБ соответствует отношению мощностей примерно равному 1,259 или 26%.
2 дБ = 1 дБ + 1 дБ → 1,259 * 1,259 = 1,585;
3 дБ → 1,2593 = 1,995;
4 дБ → 2,512;
5 дБ → 3,161;
6 дБ → 3,981;
7 дБ → 5,012;
8 дБ → 6,310;
9 дБ → 7,943;
10 дБ → 10,00.
Знак → означает «соответствует».
Подобным образом можно составить таблицу и для отрицательных значений децибел. Минус 1 дБ характеризует убывание мощности в 1/0,794 = 1,259 раза, т. е. тоже примерно на 26%.
Запомните, что:
⇒ Если Р2=Р1 т. е. P2 /P1=1, то NдБ = 0, так как lg 1=0.
⇒ Если P2 > Pl, то число децибел положительно.
⇒ Если Р2 < P1, то децибелы выражаются отрицательными числами.
Положительные децибелы часто называют децибелами усиления. Отрицательные децибелы, как правило, характеризуют потери энергии (в фильтрах, делителях, длинных линиях) и называются децибелами затухания или потерь.
Между децибелами усиления и затухания существует простая зависимость: одинаковому числу децибел с разными знаками соответствуют обратные числа отношений. Если, например, отношению Р2/Р1 = 2 → 3 дБ, то –3 дБ → 1/2, т. е. 1 / Р2/Р1 = Р1/Р2
⇒ Если Р2/Р1 представляет степень десяти, т. е. Р2/Р1 = 10k, где k — любое целое число (положительное или отрицательное), то NдБ = 10k, так как lg 10k = k.
⇒ Если Р2 или Р1 равно нулю, то выражение для NдБ теряет смысл.
И еще одна особенность: кривая, определяющая значения децибел в зависимости от отношений мощностей, вначале быстро растет, затем ее рост замедляется.
Зная число децибел, соответствующих одному отношению мощностей, можно произвести пересчет для другого — близкого или кратного отношения. В частности, для отношений мощностей, различающихся в 10 раз, число децибел отличается на 10 дБ. Эту особенность децибел следует хорошо понять и твердо запомнить — она является одной из основ всей системы
К достоинствам системы децибел относят:
⇒ универсальность, т. е. возможность использования при оценке различных параметров и явлений;
⇒ огромные перепады преобразуемых чисел — от единиц и до миллионов — отображаются в децибелах числами первой сотни;
⇒ натуральные числа, представляющие степени десяти, выражаются в децибелах числами, кратными десяти;
⇒ взаимообратные числа выражаются в децибелах равными числами, но с разными знаками;
⇒ в децибелах могут быть выражены как отвлеченные, так и именованные числа.
К недостаткам системы децибел относят:
⇒ малую наглядность: для преобразования децибел в отношения двух чисел или выполнения обратных действий требуется проведение расчетов;
⇒ отношения мощностей и отношения напряжений (или токов) пересчитываются в децибелы по разным формулам, что иногда ведет к ошибкам и путанице;
⇒ децибелы могут отсчитываться только относительно не равного нулю уровня; абсолютный нуль, например 0 Вт, 0 В, децибелами не выражается.
Зная число децибел, соответствующих одному отношению мощностей, можно произвести пересчет для другого — близкого или кратного отношения. В частности, для отношений мощностей, различающихся в 10 раз, число децибел отличается на 10 дБ. Эту особенность децибел следует хорошо понять и твердо запомнить — она является одной из основ всей системы.
Сравнение двух сигналов путем сопоставления их мощностей не всегда бывает удобным, так как для непосредственного измерения электрической мощности в диапазоне звуковых и радиочастот требуются дорогие и сложные приборы. На практике при работе с аппаратурой гораздо проще измерять не мощность, которая выделяется на нагрузке, а падение напряжения на ней, а в некоторых случаях — протекающий ток.
Зная напряжение или ток и сопротивление нагрузки, легко определить мощность. Если измерения проводятся на одном и том же резисторе, то:
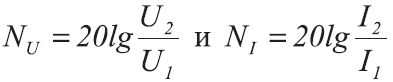
Этими формулами очень часто пользуются практике, но обратите внимание, что если напряжения или токи измеряются на разных нагрузках, эти формулы не работают и следует использовать другие, более сложные зависимости.
Пользуясь приемом, который был использован при составлении таблицы децибел мощности, можно аналогично определить, чему равен 1 дБ отношения напряжений и токов. Положительный децибел будет равен 1,122, а отрицательный децибел будет равен 0,8913, т.е. 1 дБ напряжения или тока характеризует возрастание или убывание этого параметра примерно на 12% по отношению к первоначальному значению.
Формулы выводились в предположении, что сопротивления нагрузок имеют активный характер и между напряжениями или токами нет фазового сдвига. Строго говоря, следовало бы рассматривать общий случай и учитывать для напряжений (токов) наличие угла сдвига по фазе, а для нагрузок не только активное, но полное сопротивление, включая и реактивные составляющие, однако это существенно только на высоких частотах.
Полезно запомнить некоторые часто встречающиеся на практике значения децибел и характеризующие их отношения мощностей и напряжений (токов), приведенные в табл. 1.
Таблица 1. Часто встречающиеся значения децибел мощности и напряжения
| ± дБ | 1 | 3 | 10 | 20 | 30 | |
| Р2/Р1 |
1,26 (0,79) |
2 (0,5) |
10 (0,1) |
100 (0,01) |
1000 (0,001) |
|
| ± дБ | 1 | 3 | 6 | 10 | 20 | 40 |
|
U2/U1 или I2/I1 |
1,12 (0,9) |
1,41 (0,707) |
2 (0,5) |
3,16 (0,316) |
10 (0,1) |
100 (0,01) |
Пользуясь этой таблицей и свойствами логарифмов легко подсчитать, чему соответствуют произвольные значения логарифм. Например, 36 дБ мощности можно представить как 30+3+3, что соответствует 1000*2*2 = 4000. Тот же самый результат мы получим, представив 36 как 10+10+10+3+3 → 10*10*10*2*2 = 4000.
СОПОСТАВЛЕНИЕ ДЕЦИБЕЛ С ПРОЦЕНТАМИ
Ранее отмечалось, что понятие децибел имеет некоторое сходство с процентами. Действительно, так как в процентах выражается отношение какого-то числа к другому, условно принятому за сто процентов, отношение этих чисел также можно представить в децибелах при условии, что оба числа характеризуют мощность, напряжение или ток. Для отношения мощностей:
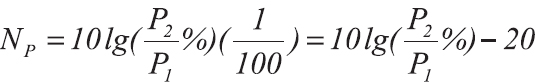
Для отношения напряжений или токов:
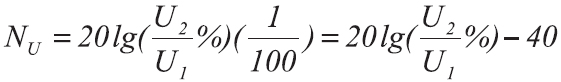
Можно также вывести формулы для пересчета децибел в проценты отношения:
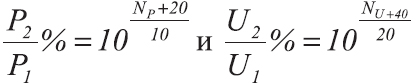
В табл. 2 дан перевод некоторых, наиболее часто встречающихся значений децибел в проценты отношений. Различные промежуточные значения можно найти по номограмме на рис. 1.
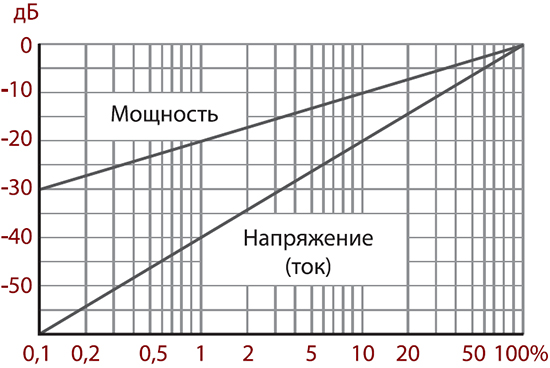
Рис. 1. Перевод децибел в проценты отношений по номограмме
Таблица 2. Перевод децибел в проценты отношений
| % | 100 | 50 | 10 | 1 | 0,1 |
| NU или NI | 0 | -6 | -20 | -40 | -60 |
| NP | 0 | -3 | -10 | -20 | -30 |
Рассмотрим два практических примера, поясняющих перевод процентного отношения в децибелы.
Пример 1. Какому уровню гармоник в децибелах по отношению к уровню сигнала основной частоты соответствует коэффициент нелинейных искажений в 3%?
Воспользуемся рис. 1. Через точку пересечения вертикальной линии 3% с графиком «напряжение» проведем горизонтальную линию до пересечения с вертикальной осью и получим ответ: –31 дБ.
Пример 2. Какому ослаблению напряжения в процентах соответствует его изменение на –6 дБ?
Ответ. На 50% первоначальной величины.
В практических расчетах дробную часть численного значения децибел часто округляют до целого числа, однако при этом в результаты расчетов вносится дополнительная погрешность.
ДЕЦИБЕЛЫ В РАДИОЭЛЕКТРОНИКЕ
Рассмотрим несколько примеров, поясняющих методику использования децибел в радиоэлектронике.
Затухание в кабеле
Потери энергии в линиях и кабелях на единицу длины характеризуются коэффициентом затухания α, который при равном входном и выходном сопротивлениях линии определяется в децибелах:
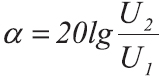
где U1 — напряжение в произвольном сечении линии; U2 — напряжение в другом сечении, отстоящем от первого на единицу длины: 1 м, 1 км и т. д. Например, высокочастотный кабель типа РК-75-4-14 имеет на частоте 100 МГц коэффициент затухания α, = –0,13 дБ/м, кабель витой пары категории 5 на той же частоте имеет затухание порядка –0,2 дБ/м, а у кабеля категории 6 несколько меньше. График затухания сигнала в неэкранированном кабеле витой пары показан на рис. 2.
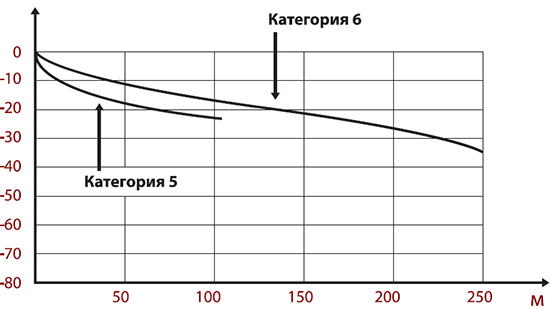
Рис. 2. График затухания сигнала в неэкранированном кабеле витой пары
Оптоволоконные кабели имеют существенно более низкие величины затухания в диапазоне от 0,2 до 3 дБ при длине кабеля в 1000 м. Все оптические волокна имеют сложную зависимость затухания от длины волны, которая имеет три «окна прозрачности» 850 нм, 1300 нм и 1550 нм. «Окно прозрачности» означает наименьшие потери при максимальной дальности передачи сигнала. График затухания сигнала в оптоволоконных кабелях показан на рис. 3.
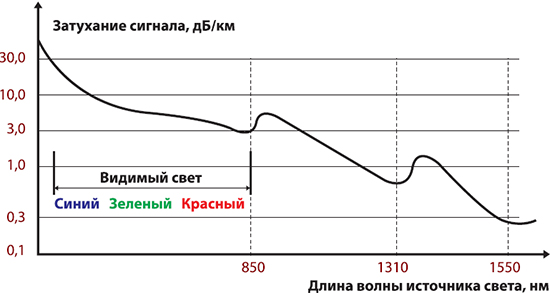
Рис. 3. График затухания сигнала в оптоволоконных кабелях
Пример 3. Найти, каким будет напряжение на выходе отрезка кабеля РК-75-4-14 длиной l = 50 м, если ко входу его приложено напряжение 8 В частоты 100 МГц. Сопротивление нагрузки и волновое сопротивление кабеля равны, или, как говорят, согласованы между собой.
Очевидно, что затухание, вносимое отрезком кабеля, составляет K = –0,13 дБ/м * 50 м = –6,5 дБ. Это значение децибел примерно соответствует отношению напряжений 0,47. Значит, напряжение на выходном конце кабеля U2 = 8 В * 0,47 = 3,76 В.
Этот пример иллюстрирует очень важное положение: потери в линии или кабеле с ростом их длины возрастают чрезвычайно быстро. Для отрезка кабеля длиной в 1 км затухание составит уже –130 дБ, т. е. сигнал будет ослаблен более чем в триста тысяч раз!
Затухание в значительной мере зависит от частоты сигналов — в диапазоне звуковых частот оно будет гораздо меньше, чем в видео диапазоне, но логарифмический закон затухания будет тот же, и при большой длине линии ослабление будет существенным.
Усилители звуковой частоты
В усилители звуковой частоты с целью повышения их качественных показателей обычно вводится отрицательная обратная связь. Если коэффициент усиления устройства по напряжению без обратной связи равен К, а с обратной связью КОС то число, показывающее, во сколько раз изменяется коэффициент усиления под действием обратной связи, называют глубиной обратной связи. Ее обычно выражают в децибелах. В работающем усилителе коэффициенты К и КОС определяются экспериментально, если только усилитель не возбуждается при разомкнутой петле обратной связи. При проектировании усилителя сначала вычисляют К, а затем определяют значение КОС следующим образом:
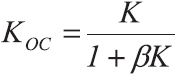
где β — коэффициент передачи цепи обратной связи, т. е. отношение напряжения на выходе цепи обратной связи к напряжению на ее входе.
Глубина обратной связи в децибелах может быть рассчитана по формуле:
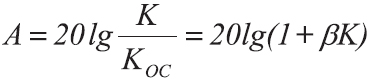
Стереофонические устройства по сравнению с монофоническими должны удовлетворять дополнительным требованиям. Эффект объемного звучания обеспечивается только при хорошем разделении каналов, т. е. при отсутствии проникновения сигналов из одного канала в другой. В практических условиях это требование полностью удовлетворить не удается, и взаимное просачивание сигналов имеет место, главным образом, через узлы, общие для обоих каналов. Качество разделения по каналам характеризуется так называемым переходным затуханием аПЗ Мерой переходного затухания в децибелах служит отношение выходных мощностей обоих каналов, когда входной сигнал подается только на один канал:
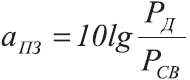
где РД — максимальная выходная мощность действующего канала; РСВ — выходная мощность свободного канала.
Хорошему разделению каналов соответствует переходное затухание 60—70 дБ, отличному –90—100 дБ.
Шум и фон
На выходе любого приемно-усилительного устройства даже при отсутствии полезного входного сигнала можно обнаружить переменное напряжение, которое вызвано собственными шумами устройства. Причины, вызывающие собственные шумы, могут быть как внешними — за счет наводок, плохой фильтрации напряжения питания, так и внутренними, обусловленными собственными шумами радиокомпонентов. Сильнее всего сказываются шумы и, помехи, возникающие во входных цепях и в первом усилительном каскаде, так как они усиливаются всеми последующими каскадами. Собственные шумы ухудшают реальную чувствительность приемника или усилителя.
Количественная оценка шумов осуществляется несколькими способами.
Простейший состоит в том, что все шумы, независимо от причины и места их возникновения, пересчитываются ко входу, т. е. напряжение шумов на выходе (при отсутствии входного сигнала) делится на коэффициент усиления:
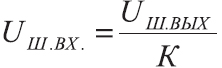
Это напряжение, выраженное в микровольтах, и служит мерой собственных шумов. Однако для оценки устройства с точки зрения помех важно не абсолютное значение шумов, а отношение между полезным сигналом и этим шумом (отношение сигнал/шум), так как полезный сигнал должен надежно выделяться на фоне помех. Отношение сигнал/шум обычно выражают в децибелах:
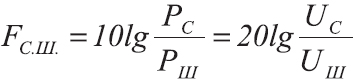
где Рс — заданная или номинальная выходная мощность полезного сигнала вместе с шумом; Рш — выходная мощность шумов при выключенном источнике полезного сигнала; Uc — напряжение сигнала и шумов на нагрузочном резисторе; UШ — напряжение шумов на том же резисторе. Так получается т.н. «невзвешенное» («unweighted») отношение сигнал/шум.
Часто в параметрах аудиоаппаратуры приводится отношение сигнал/шум, измеренное со взвешивающим фильтром («weighted»). Фильтр позволяет учесть разную чувствительность слуха человека к шуму на разных частотах. Чаще всего используется фильтр типа А, в этом случае в обозначении обычно указывается единица измерения «дБА» («dBA»). Использование фильтра дает обычно лучшие количественные результаты, чем для невзвешенного шума (обычно отношение сигнал/шум получается на 6—9 дБ больше), поэтому (из маркетинговых соображений) производители аппаратуры чаще указывают именно «взвешенное» значение. Подробнее о взвешивающих фильтрах см. ниже в разделе «Шумомеры».
Очевидно, что для успешной эксплуатации устройства отношение сигнал/шум должно быть выше какого-то минимально допустимого значения, которое зависит от назначения и требований, предъявляемых к устройству. Для аппаратуры класса Hi-Fi этот параметр должен быть не менее 75 дБ, для аппаратуры Hi-End — не менее 90 дБ.
Иногда на практике пользуются обратным отношением, характеризуя им уровень шумов относительно полезного сигнала. Уровень шумов выражается тем же числом децибел, что и отношение сигнал/шум, но с отрицательным знаком.
В описаниях приемно-усилительной аппаратуры иногда фигурирует термин уровень фона, который характеризует в децибелах отношение составляющих напряжения фона к напряжению, соответствующему заданной номинальной мощности. Составляющие фона кратны частоте питающей сети (50, 100, 150 и 200 Гц) и при измерении выделяются из общего напряжения помех при помощи полосовых фильтров.
Отношение сигнал/шум не позволяет, однако, судить о том, какая часть шумов обусловлена непосредственно элементами схемы, а какая внесена в результате несовершенства конструкции (наводки, фон). Для оценки шумовых свойств радиокомпонентов вводится понятие коэффициента (фактора) шума. Коэффициент шума оценивается по мощности и также выражается в децибелах. Характеризовать этот параметр можно следующим образом. Если на входе устройства (приемника, усилителя) одновременно действуют полезный сигнал мощностью Рс и шумы мощностью Рш, то отношение сигнал/шум на входе будет (Рс/Рш)вх После усиления отношение (Рс/Рш)вых окажется меньше, так как к входным шумам добавятся и усиленные собственные шумы усилительных каскадов.
Коэффициентом шума называют выраженное в децибелах отношение:
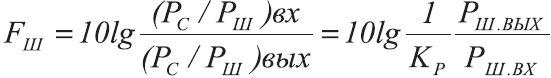
где Кр — коэффициент усиления по мощности.
Следовательно, коэффициент шума представляет отношение мощности шумов на выходе к усиленной мощности шумов, действующих на входе.
Значение Рш.вх определяется расчетным путем; Рш.вых измеряется, а Кр обычно . известно из расчета или после измерения. Идеальный с точки зрения шумов усилитель должен усиливать только полезные сигналы и не должен вносить дополнительные шумы. Как следует из уравнения, для подобного усилителя коэффициент шума FШ = 0 дБ.
Для транзисторов и ИС, предназначенных для работы в первых каскадах усилительных устройств, коэффициент шума регламентируется и приводится в справочниках.
Напряжение собственных шумов определяет и другой важный параметр многих усилительных устройств — динамический диапазон.
Динамический диапазон и регулировки
Динамическим диапазоном называется выраженное в децибелах отношение максимальной неискаженной выходной мощности к ее минимальному значению, при котором, еще обеспечивается допустимое отношение сигнал/шум:
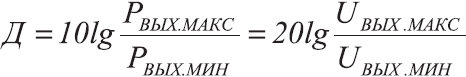
Чем меньше уровень собственных шумов и чем выше неискаженная выходная мощность, тем шире динамический диапазон.
Аналогичным образом определяется и динамический диапазон источников звука — оркестра, голоса, только здесь минимальная мощность звука определяется шумовым фоном. Чтобы устройство могло передать без искажений как минимальную, так и максимальную амплитуды входного сигнала, его динамический диапазон должен быть не меньше динамического диапазона сигнала. В случаях, когда динамический диапазон входного сигнала превышает динамический диапазон устройства, его искусственно сжимают. Так поступают, например, при звукозаписи.
Эффективность действия ручного регулятора громкости проверяется при двух крайних положениях регулятора. Сначала при регуляторе в положении максимальной громкости на вход усилителя звуковой частоты подается напряжение частотой 1 кГц такой величины, чтобы на выходе усилителя установилось напряжение, соответствующее некоторой заданной мощности. Затем ручку регулятора громкости переводят на минимальную громкость, а напряжение на входе усилителя поднимают до тех пор, пока напряжение на выходе снова не станет равным первоначальному. Отношение входного напряжения при регуляторе в положении минимальной громкости к входному напряжению при максимальной громкости, выраженное в децибелах, является показателем работы регулятора громкости.
Приведенными примерами далеко не исчерпываются практические случаи приложения децибел к оценке параметров радиоэлектронных устройств. Зная общие правила, применения этих единиц, можно понять, как они используются в других, не рассмотренных здесь условиях. Встретившись с незнакомым термином, определенным в децибелах, следует отчетливо представить, отношению каких двух величин он соответствует. В одних случаях это понятно из самого определения, в других случаях связь между составляющими сложнее, и, когда нет четкой ясности, следует обратиться к описанию методики измерения во избежание серьезных ошибок.
Оперируя с децибелами, следует всегда обращать внимание на то, отношению каких единиц — мощности или напряжения — соответствует каждый конкретный случай, т. е. какой коэффициент — 10 или 20 — должен стоять перед знаком логарифма.
ЛОГАРИФМИЧЕСКИЙ МАСШТАБ
Логарифмическая система, в том числе и децибелы, часто применяется при построении амплитудно-частотных характеристик (АЧХ) — кривых, изображающих зависимость коэффициента передачи различных устройств (усилителей, делителей, фильтров) от частоты внешнего воздействия. Для построения частотной характеристики расчетным или опытным путем определяется ряд точек, характеризующих выходное напряжение или мощность при неизменном входном напряжении на разных частотах. Плавная кривая, соединяющая эти точки, характеризует частотные свойства устройства или системы.
Если по оси частот численные значения откладывать в линейном масштабе, т. е. пропорционально их фактическим значениям, то такая частотная характеристика окажется неудобной для пользования и не будет наглядной: в области низших частот она сжата, а высших — растянута.
Частотные характеристики строятся обычно в так называемом логарифмическом масштабе. По оси частот в удобном для работы масштабе откладываются величины, пропорциональные не самой частоте f, а логарифму lgf/fo, где fо — частота, соответствующая началу отсчета. Против отметок на оси надписываются значения f. Для построения логарифмических АЧХ используют специальную логарифмическую миллиметровую бумагу.
При проведении теоретических расчетов обычно пользуются не просто частотой f, а величиной ω = 2πf которую называют круговой частотой.
Частота fо, соответствующая началу отсчета, может быть сколь угодно малой, но не может быть равной нулю.
По вертикальной оси откладываются в децибелах либо в относительных числах отношения коэффициентов передачи при различных частотах к его максимальному либо среднему значению.
Логарифмический масштаб позволяет на небольшом отрезке оси отобразить широкий диапазон частот. На такой оси одинаковым отношениям двух частот соответствуют равные по длине участки. Интервал, характеризующий рост частоты в десять раз, называют декадой; двукратному отношению частот соответствует октава (этот термин заимствован из теории музыки).
Частотный диапазон с граничными частотами fH и fВ занимает в декадах полосу fB/fH= 10m, где m — число декад, а в октавах 2n, где n — число октав.
Если полоса в одну октаву слишком широка, то можно применять интервалы с меньшим отношением частот в пол-октавы или трети октавы.
Средняя частота октавы (полуоктава) не равна среднему арифметическому от нижней и верхней частот октавы, а равна 0,707 fВ.
Частоты, найденные подобным образом, называют среднеквадратичными.
Для двух соседних октав средние частоты также образуют октавы. Пользуясь этим свойством, можно по желанию один и тот же логарифмический ряд частот считать либо границами октав, либо их средними частотами.
На бланках с логарифмической сеткой средняя частота делит октавный ряд пополам.
На оси частот в логарифмическом масштабе на каждую треть октавы приходятся равные отрезки оси, каждый длиной в одну треть октавы.
При испытаниях электроакустической аппаратуры и проведении акустических измерений рекомендуется применять ряд предпочтительных частот. Частоты этого ряда являются членами геометрической прогрессии со знаменателем 1,122. Для удобства значения некоторых частот округлены в пределах ±1%.
Интервал между рекомендованными частотами составляет одну шестую октавы. Сделано это не случайно: ряд содержит достаточно большой набор частот для разных видов измерений и вбирает ряды частот с интервалами в 1/3, 1/2 и целую октаву.
И еще одно важное свойство ряда предпочтительных частот. В некоторых случаях в качестве основного интервала частот используется не октава, а декада. Так вот, предпочтительный ряд частот в равной мере можно рассматривать и как двоичный (октавный), и как десятичный (декадный).
Знаменатель прогрессии, на основе которой построен предпочтительный ряд частот, численно равен 1дБ напряжения, или 1/2 дБ мощности.
ПРЕДСТАВЛЕНИЕ ИМЕНОВАННЫХ ЧИСЕЛ В ДЕЦИБЕЛАХ
До сих пор мы полагали, что и делимое и делитель под знаком логарифма имеют произвольную величину и для выполнения децибельного пересчета важно знать только их отношение независимо от абсолютных значений.
В децибелах можно выражать также конкретные значения мощностей, а также напряжений и токов. Когда величина одного из членов, стоящих под знаком логарифма в рассмотренных ранее формулах задана, второй член отношения и числа децибел будут однозначно определять друг друга. Следовательно, если задаться какой-либо эталонной мощностью (напряжением, током) в качестве условного уровня сравнения, то другой мощности (напряжению, току), сопоставляемой с ней, будет соответствовать строго определенное число децибел. Нулю децибел в этом случае отвечает мощность, равная мощности условного уровня сравнения, так как при NP= 0 Р2=Р1 поэтому этот уровень обычно называют нулевым. Очевидно, что при разных нулевых уровнях одна и та же конкретная мощность (напряжение, ток) будут выражаться разными числами децибел.
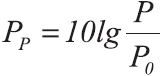
где Р — мощность, подлежащая преобразованию в децибелы, а Р0 — нулевой уровень мощности. Величина Р0 ставится в знаменателе, при этом положительными децибелами выражаются мощности Р > Р0.
Условный уровень мощности, с которым производится сравнение, в принципе может быть любым, однако не каждый был бы удобен для практического использования. Чаще всего за нулевой уровень выбирается мощность в 1 мВт, рассеиваемая на резисторе сопротивлением 600 Ом. Выбор этих параметров произошел исторически: первоначально децибел как единица измерения появился в технике телефонной связи. Волновое сопротивление воздушных двухпроводных линий из меди близко к 600 Ом, а мощность в 1 мВт развивает без усиления высококачественный угольный телефонный микрофон на согласованном сопротивлении нагрузки.
Для случая, когда Р0 = 1 мВт=10–3 Вт: Pр = 10 lg P + 30
Тот факт, что децибелы представляемого параметра отчитываются относительно определенного уровня, подчеркивают термином «уровень»: уровень помех, уровень мощности, уровень громкости
Пользуясь этой формулой, легко найти, что относительно нулевого уровня 1 мВт мощность 1 Вт определяется как 30 дБ, 1 кВт как 60 дБ, а 1 МВт — это 90 дБ, т. е. практически все мощности, с которыми приходится встречаться, укладываются в пределах первой сотни децибел. Мощности, меньшие 1 мВт, будут выражаться отрицательными числами децибел.
Децибелы, определенные относительно уровня 1 мВт, называют децибел-милливаттом и обозначают дБм или dBm. Наиболее распространенные значения нулевых уровней сведены в таблицу 3.
Аналогичным образом можно представить формулы для выражения в децибелах напряжений и токов:
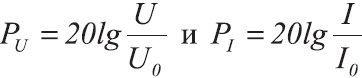
- Главная
- Статьи
-
Измерения. Единицы измерения. Децибелы – универсальная мера























