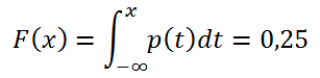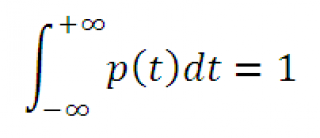17 авг. 2022 г.
читать 2 мин
В статистике децили — это числа, которые разбивают набор данных на десять групп с одинаковой частотой.
Первый дециль — это точка, ниже которой лежат 10% всех значений данных. Второй дециль — это точка, ниже которой лежат 20% всех значений данных, и так далее.
Мы можем использовать следующую функцию для вычисления децилей для набора данных в Excel:
=PERCENTILE( CELL RANGE , PERCENTILE )
В следующем примере показано, как использовать эту функцию на практике.
Пример: расчет децилей в Excel
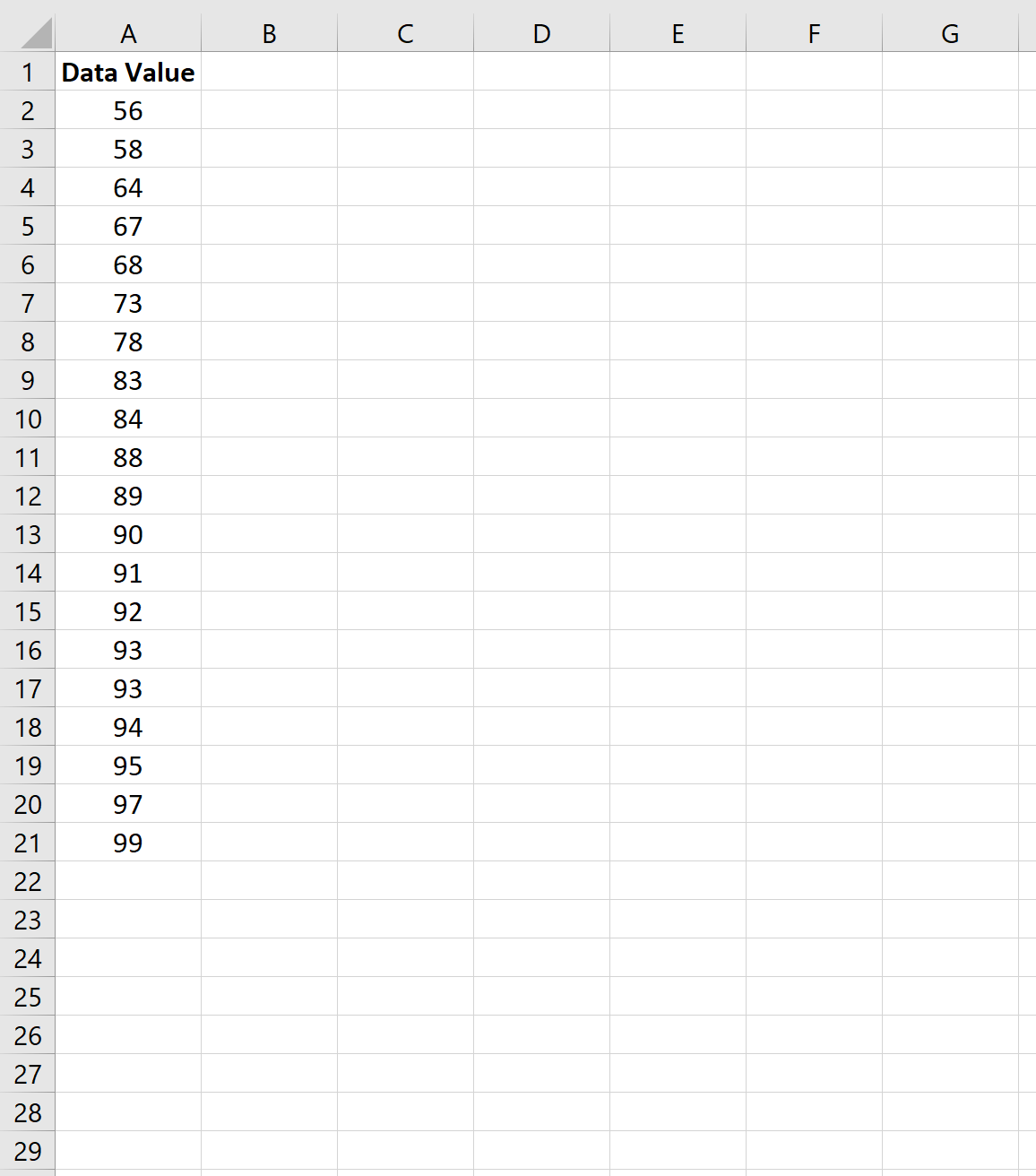
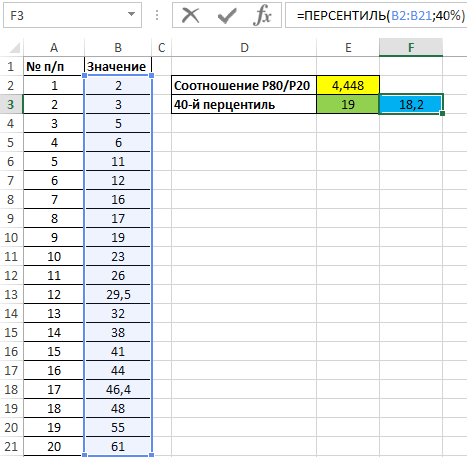
Предположим, у нас есть следующий набор данных с 20 значениями:
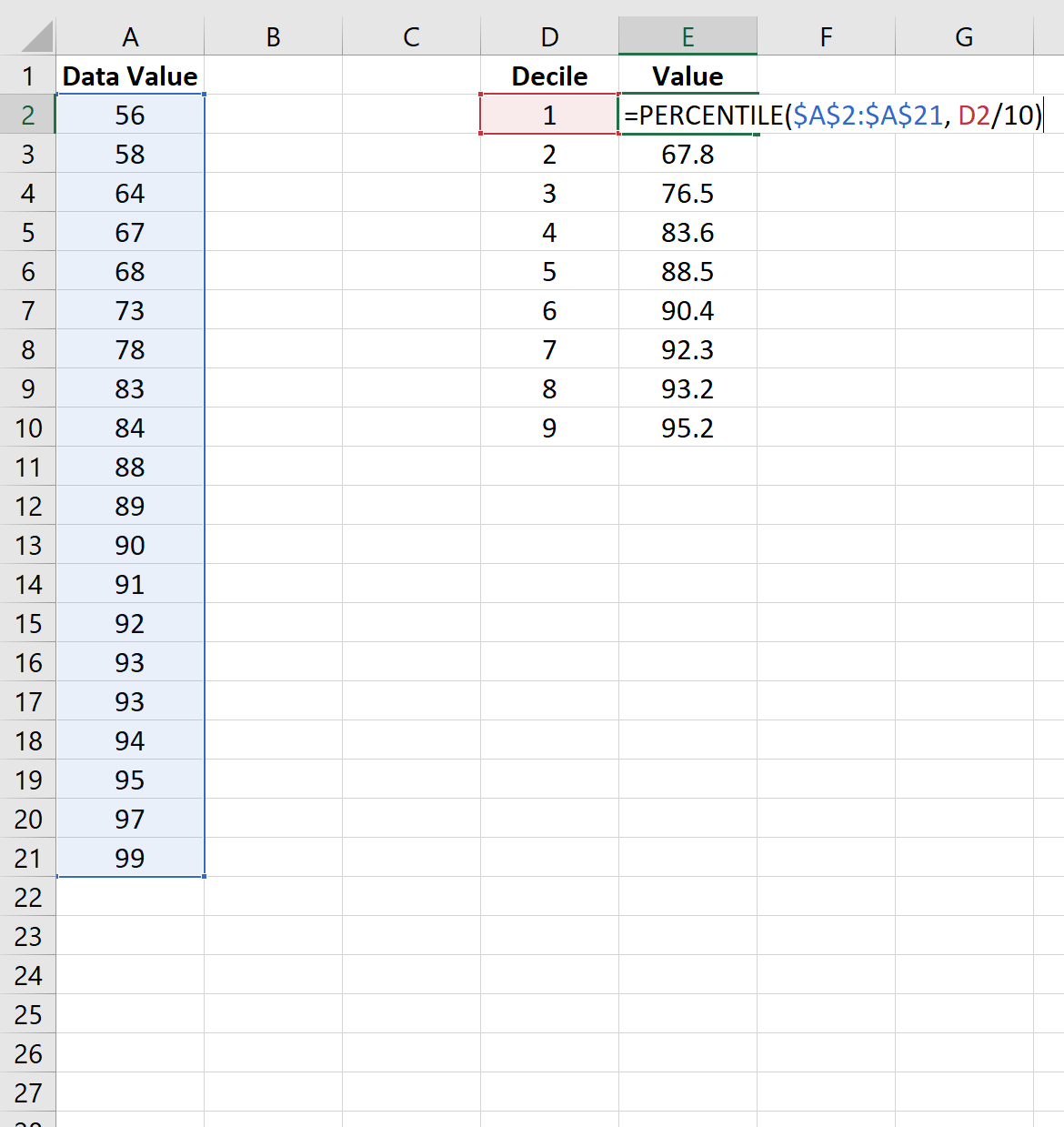
На следующем изображении показано, как рассчитать децили для набора данных:
Способ интерпретации децилей следующий:
- 20% всех значений данных лежат ниже 67,8 .
- 30% всех значений данных лежат ниже 76,5 .
- 40% всех значений данных лежат ниже 83,6 .
И так далее.
Чтобы поместить каждое значение данных в дециль, мы можем использовать функцию ПРОЦЕНТРАНГ.ИСКЛ() , которая использует следующий синтаксис:
=PERCENTRANK.EXC( CELL RANGE , DATA VALUE , SIGNIFICANCE )
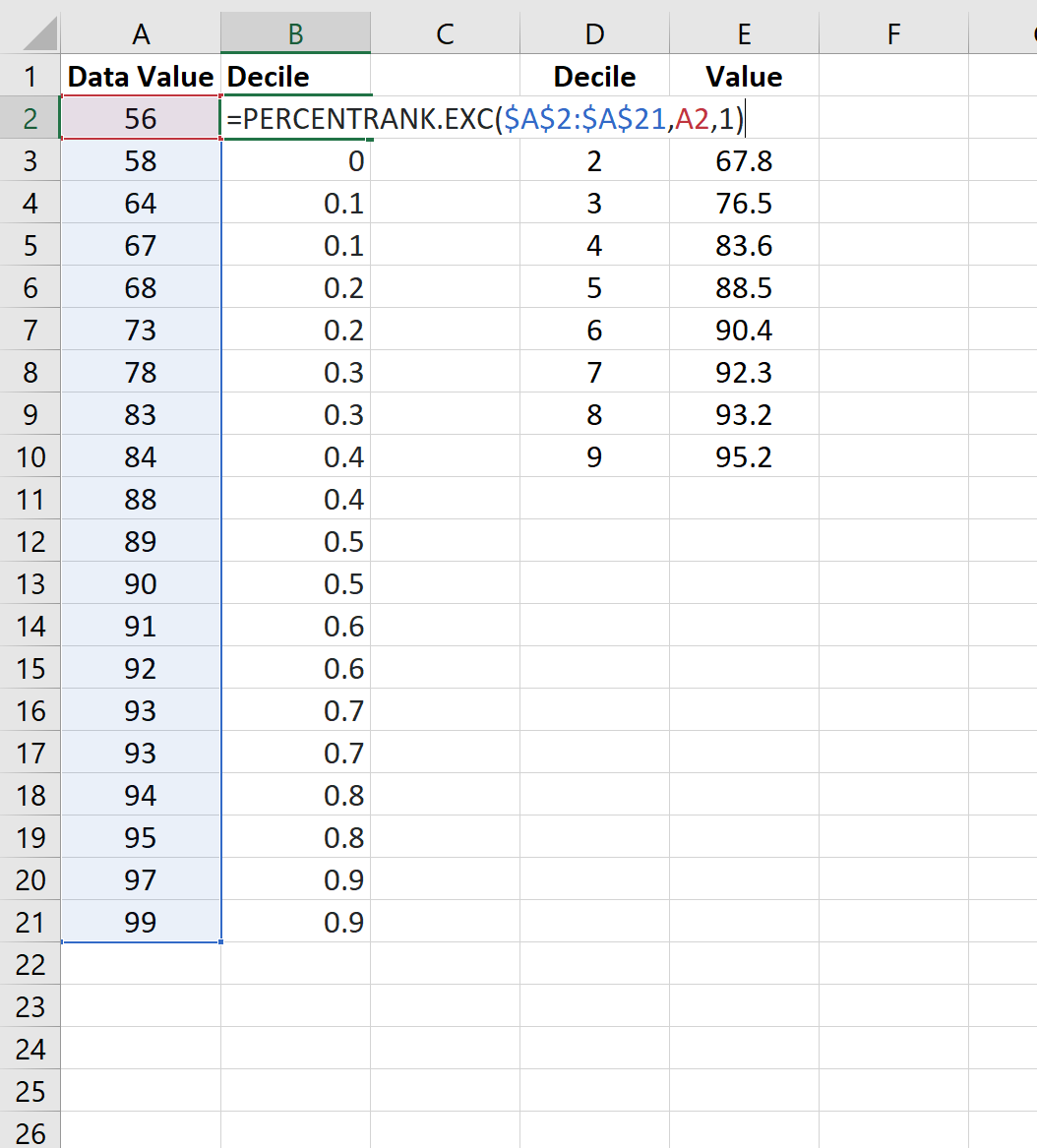
На следующем изображении показано, как использовать эту функцию для нашего набора данных:
Обратите внимание, что эта функция находит относительный ранг значения в наборе данных в процентах и округляет до одной цифры, что эквивалентно нахождению дециля, в который попадает значение.
Способ интерпретации вывода следующий:
- Значение данных 58 находится между процентилем от 0 до 0,1, таким образом, оно попадает в первый дециль.
- Значение данных 64 находится между процентилями 0,1 и 0,2, таким образом, оно попадает во второй дециль.
- Значение данных 67 находится между процентилями 0,1 и 0,2, таким образом, оно попадает во второй дециль.
- Значение данных 68 находится между процентилями 0,2 и 0,3, таким образом, оно попадает в третий дециль.
И так далее.
Дополнительные ресурсы
Как рассчитать сводку из пяти чисел в Excel
Как нормализовать данные в Excel
Как легко найти выбросы в Excel
Написано

Замечательно! Вы успешно подписались.
Добро пожаловать обратно! Вы успешно вошли
Вы успешно подписались на кодкамп.
Срок действия вашей ссылки истек.
Ура! Проверьте свою электронную почту на наличие волшебной ссылки для входа.
Успех! Ваша платежная информация обновлена.
Ваша платежная информация не была обновлена.
Примеры функции ПЕРСЕНТИЛЬ для расчета перцентиля в Excel
Функция ПЕРСЕНТИЛЬ в Excel предназначена для определения k-й доли перцентили для числовых значений исследуемого интервала и возвращает соответствующий результат.
Метод перцентилей в Excel по функции ПЕРСЕНТИЛЬ с примерами
Предположим, имеется вариационный ряд данных с минимальным и максимальным значениями, обозначаемых P0 и P100 соответственно. K-й перцентиль – это некоторое значение X из данного ряда, которое делит все имеющиеся в нем значения на две группы: K% значений, которые меньше X, и оставшиеся значения (то есть 1-K%), которые превышают X.
Для определения перцентилей необходимо:
- Отсортировать значения в исследуемом ряде данных в порядке возрастания.
- Найти некоторое значение в отсортированном ряде, для которого K% значений будут меньшими данного значения. При ручном расчете можно использовать формулу n*K%-1, где n – число элементов в исследуемом ряде значений.
- Определенное выше значение является K-й перцентилю по определению.
Функция ПЕРСЕНТИЛЬ считается устаревшей после выхода MS Office версии 2010 года, в которую были включены функции ПРОЦЕНТИЛЬ.ИСКЛ и ПРОЦЕНТИЛЬ.ВКЛ, которые в совокупности предлагают расширенный функционал для расчетов. Рассматриваемая функция была оставлена для совместимости с более старыми версиями табличного редактора.
Пример расчета перцентиля с использованием функции ПЕРСЕНТИЛЬ в Excel
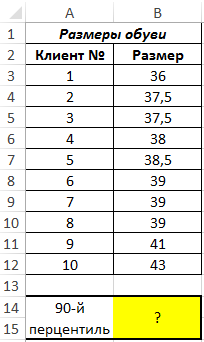
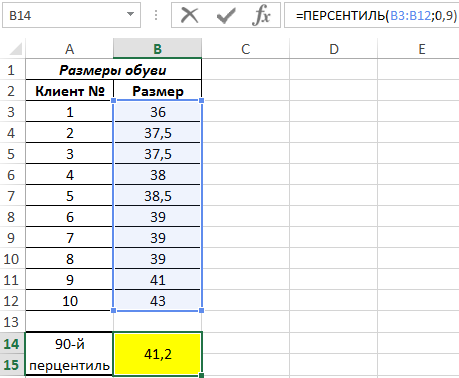
Пример 1. В магазин будет завезена новая партия обуви. Ранее в рамках маркетингового исследования были записаны размеры ног 10 случайных клиентов. На основании имеющихся данных определить размер обуви, являющийся пороговым значением для 90% клиентов.
Вид таблицы данных:
Для расчета используем функцию:
- B3:B12 – исследуемый ряд значений;
- 0,9 – число, указывающее, что необходим поиск 90-й перцентили (0,9=90%).
В результате вычислений формулы получен 90 перцентиль. Найденное значение не соответствует ни одному из рассматриваемого ряда, поскольку функция ПЕРСЕНТИЛЬ выполнила интерполяцию данных. 90% клиентов покупают обувь до 41 размера включительно.
Как рассчитать перцентиль в Excel с помощью функции ПЕРСЕНТИЛЬ
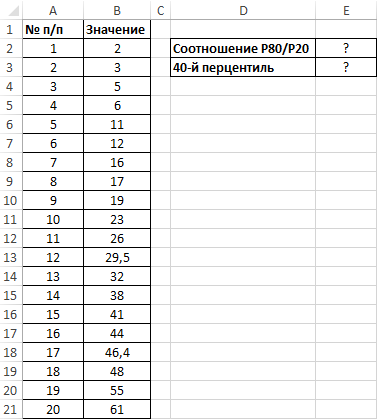
Пример 2. В таблице введен ряд некоторых значений. Необходимо:
- Определить, во сколько раз 80-й перцентиль превышает 20-й перцентиль.
- Рассчитать 40-й перцентиль без использования рассматриваемой функции.
Вид таблицы данных:
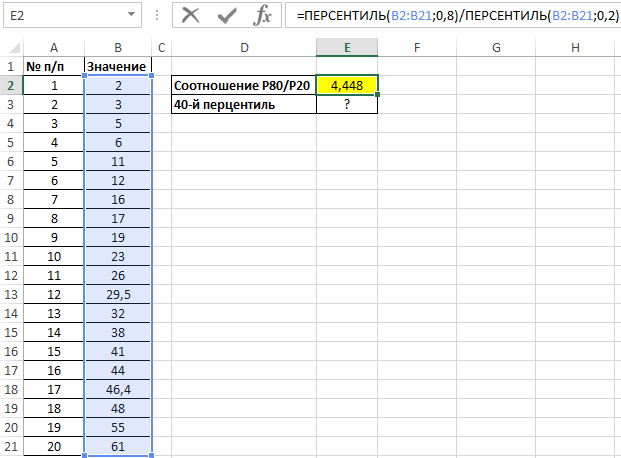
Для поиска значения соотношения используем следующую запись:
То есть, для исследуемого ряда значений 80-й перцентиль превышает 20-й почти в 4,5 раз.
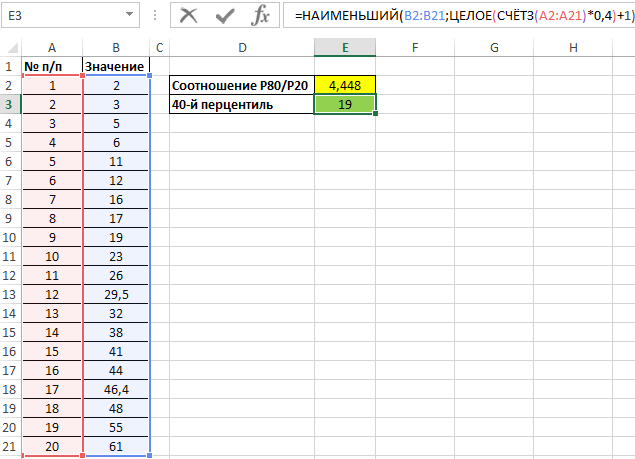
Альтернативный способ нахождения перцентиля – следующая формула:
Данная запись соответствует формуле, указанной в определении понятия перцентиль. Результат вычислений:
Рядом (справа) указано значение, полученное с использованием функции ПЕРСЕНТИЛЬ:
Значения отличаются, поскольку рассматриваемая функция выполняет интерполяцию данных.
Что такое функция ПЕРСЕНТИЛЬ и как с ней работать в Excel
Функция имеет следующий синтаксис:
- массив – обязательный для заполнения, принимает статический массив числовых данных или ссылку на диапазон ячеек с числами, для которых требуется вычислить значение k-го перцентиля;
- k – обязательный для заполнения, принимает числовые значения из диапазона от 0 до 1 (оба включительно), характеризующие номер перцентили для расчета (например, 0,25 – 25-я перцентиль, 0,5 – 50-я перцентиль).
- Перцентиль удобен для установления критериев отбора каких-либо данных. Например, на вступительных экзаменах почти все студенты не смогли преодолеть проходной порог (минимальное количество баллов для поступления в ВУЗ). Чтобы избежать недобора, можно ввести другой критерий – перцентиль, который поможет отобрать лучших абитуриентов на основании имеющихся данных о баллах за экзамены, а не установленных ранее критериев (проходного балла).
- Если исследуемый ряд (указан в виде аргумента массив) содержит нечисловые данные (текст, логические ИСТИНА или ЛОЖЬ, имена), функция исключает их из расчетов. Например, =ПЕРСЕНТИЛЬ(<1;4;5;7;11>;0,5) вернет значение 5, а =ПЕРСЕНТИЛЬ(<1;4;”е”;7;11>;0,5) – 5,5.
- Функция возвращает код ошибки #ЗНАЧ!, если аргумент k указан в виде нечисловых данных (имя или текст, не преобразуемые в число). Нечисловые данные, преобразуемые к числам, являются допустимыми вариантами указания аргумента k . Например, =ПЕРСЕНТИЛЬ(<1;4;5;7;11>;”0,5”) вернет значение 5, =ПЕРСЕНТИЛЬ(<1;4;5;7;11>;ИСТИНА) – 11.
- Рассматриваемая функция генерирует код ошибки #ЧИСЛО!, если аргумент k задан в виде числа не из диапазона допустимых значений, то есть >1 или k , не кратных 1/(n-1), функция интерполирует данные для расчетов (n – число элементов массива).
Расчет децилей для интервального ряда
1. Определяем номер дециля по формуле: ,
2. Определяем децильный интервал. Это первый интервал, для которого накопленная частота будет больше или равна номеру дециля.
3. Рассчитываем дециль по формуле:
где – значение j-го дециля,
— нижняя граница децильного интервала;
— ширина децильного интервала;
– сумма всех частот,
-накопленная частота интервала, предшествующего децильному;
— частота децильного интервала.
Пример. Найти 9-ый дециль D9
1) Определяем номер 9-го дециля
для первой бригады ;
2) Номер дециля — нецелое число. Для определения дециля нужны значения двух элементов – х68 и х69. Значение дециля находится между ними.
Определяем их значение с помощью самой первой накопленной частоты большей или равной порядковым номерам элементов (68 и 69). Х68= 20, х69= 20.
Теперь определяем значение 9-го дециля:
D7 = x68+ (х69 – х68)×0,4=20 + (20 – 20)×0,2 =20тыс.руб.
Это значит, что заработная плата90% рабочих бригады не превышает 18 тыс.руб.
Пример. Найти седьмой дециль D7 для интервального ряда.
| Возрастные группы | Число студентовf | Накопленная частота S |
| До 20 лет | ||
| 20 — 25 | ||
| 25 — 30 | ||
| 30 — 35 | ||
| 35 — 40 | ||
| 40 — 45 | ||
| 45 лет и более | ||
| Итого |
1. Определяем номер седьмого дециля по формуле 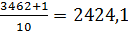
2. Седьмой дециль находится в возрастной группе 30-35 лет, так как это первый интервал, для которого накопленная частота больше (или равна) номера дециля (2272 2424,1).
3. Определяем седьмой дециль по формуле
4.
Это значит, что 70% студентов младше 30,97 лет.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Для студентов недели бывают четные, нечетные и зачетные. 9955 — 
или читать все.
Определение коэффициента эластичности
1. Задача по статистике – Коэффициент эластичности.
Для данного товара коэффициент эластичности k эл = -0,5.
Как изменится потребление этого товара, если цены на него возрастут на 10%?
Коэффициент эластичности – это отношение процентного изменения спроса к процентному изменению цены.
Следовательно процентное изменение спроса = k эл*процентное изменение цены=
=-0,5*10=5%. То есть потребление снизится на 5%.
Найти децильный коэффициен, моду и медианну по следующим данным.
Средний доход, руб. / (чел. мес)
Количество человек, млн. чел
Накопленная частота, млн. чел
Мода рассчитывается по формуле:
,
Где – нижняя граница модального интервала.
– модальный интервал.
– частота модального интервала.
– частота интервала, предшествующего модальному.
– частота интервала, следующего за модальным.
Модальный интервал определяется по наибольшей частоте. Наибольшая частота в данной задаче 31,3, что соответствует интервалу от 4000 до 6000 рублей.
=
=4000+2000*(31,3-30,6) / (( 31,3-30,6)-( 31,3-25,3))=4209 рублей.
Таким образом самый частый доход 4209 рублей.
Медианна рассчитывается по формуле:
,
Где – нижняя граница медианного интервала.
– медианный интервал.
– f частота.
– частота медианного интервала.
– накопленная частота интервала, предшествующего медианному.
Медианный интервал определяется по накопленной частоте. Суммируются f частоты до тех пор, пока очередная накопленная частота не превысит середину совокупности. В данной задаче совокупность состоит из 147,5 млн человек. Поэтому суммируем f частоты пока не превысим 147,5 /2=7 3,75 млн человек. Это произойдет в интервале от 6000 до 8000 руб, поскольку накопленная частота данного интервала равна 87.2, т.е. больше половины совокупности.
Следовательно интервал от 6000 до 8000 руб является медианным интервалом. Накопленная частота интервала, предшествующего медианному, равна 61,9.
=
=6000+2000*(0,5*147,5-61,9) /2 5,3 = 6937 руб. / мес.
Значит половина людей в совокупности имеет доход менее 6937 рублей, а половина более 6937 рублей.
Расчет децильного коэффициента
Рассчитаем дециль №1 (10% совокупности).
=0.1*1 47,5 =14. 75 млн чел.(14,75 млн чел соответствует 1-му интервалу).
Таким образом, дециль №1 входит в 1-й интервал с доходом до 4000.
Дециль рассчитывается по формуле:
,
Где – нижняя граница децильного интервала (интервала, содержащего дециль).
– децильный интервал.
– f частота.
– частота децильного интервала.
– накопленная частота интервала, предшествующего децильному.
– коэффициент дециля (для дециля №1 10%, т.е. 0,1).
Рассчитаем первый дециль
=
=0+4000*(14,75-0) / 30,6 = 1928 рублей.
Рассчитаем дециль №9 (90% совокупности).
=0. 9 *14 7,5 = 132,75 млн чел.(соответствует интервалу 16000-20000, а накопленная частота, предшествующая интервалу, содержащему дециль, равно 132,6)
Рассчитаем девятый дециль
=
=16000+4000*(132,75-132,6) /7= 16086 рублей.
Децильный коэффициент рассчитывается по формуле
.
=16086 / 1928=8,34.
Таким образом, минимальный доход 10% самого богатого населения в 8,4 раза выше, чем максимальный доход 10% самого бедного населения.
Квартили и интерквартильный интервал (IQR) в EXCEL
Для вычисления квартилей в MS EXCEL существует специальная функция КВАРТИЛЬ() . В этой статье дадим определение квартилей и научимся их вычислять для выборки и для непрерывного распределения. Также вычислим интерквартильный интервал.
Квартили (Quartiles) — значения, которые делят выборку (набор значений) на четыре части, содержащие приблизительно равное количество наблюдений (по 25%).
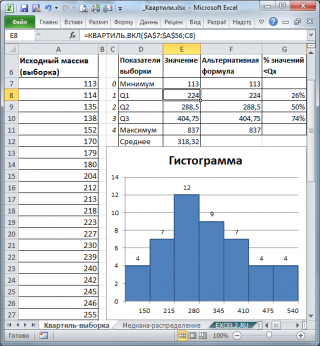
Поясним определение квартиля на примере. Пусть имеется выборка , состоящая из 50 значений в ячейках А7:А56 (см. файл примера , лист Квартиль-выборка). Для наглядности отсортируем значения по возрастанию и построим гистограмму .
Чтобы разделить выборку на 4 части достаточно 3-х квартилей .
Первый квартиль (или нижний квартиль , Q1) делит выборку , на 2 части: примерно 25% значений в выборке меньше Q1, остальные 75% — больше. Для вычисления 1-го квартиля используйте формулу =КВАРТИЛЬ.ВКЛ(A7:A56;1) . Для нашей выборки формула вернет значение 224. Значения 224 нет в выборке , формула произвела интерполяцию на основе 2-х соседних значений 223 и 227.
Примечание : Функция КВАРТИЛЬ.ВКЛ() появилась в MS EXCEL 2010. В более ранних версиях использовалась аналогичная ей функция КВАРТИЛЬ() .
Чтобы убедиться, что примерно 25% значений меньше, чем 224, используем формулу =СЧЁТЕСЛИ(A7:A56;» . В результате получим, что 26% меньше, чем 1-й квартиль .
Чем в выборке больше значений и меньше повторов , тем точнее деление выборки квартилями на четверти.
Примечание : Первый квартиль — это то же самое, что и 25-я процентиль . Подробнее см. статью про процентили .
Второй квартиль (или медиана , Q2) также делит выборку , на 2 равные части: половина чисел множества больше, чем медиана , а половина чисел меньше, чем медиана . Для вычисления 2-го квартиля используйте формулу =КВАРТИЛЬ.ВКЛ(A7:A56;2) или =МЕДИАНА(A7:A56)
Третий квартиль (или верхний квартиль , Q3) делит выборку , на 2 части: примерно 75% значений в выборке меньше Q3, остальные 25% — больше. Для вычисления 3-го квартиля используйте формулу =КВАРТИЛЬ.ВКЛ(A7:A56;3) или =ПРОЦЕНТИЛЬ.ВКЛ(A7:A56;0,75)
Примечание : Третий квартиль — это то же самое, что и 75-я процентиль .
Второй аргумент функции КВАРТИЛЬ.ВКЛ() может также принимать значения 0 и 4. В первом случае функция вернет минимальное значение , во втором – максимальное .
Интерквартильный размах
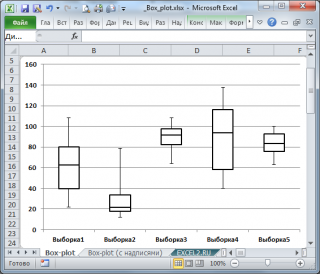
Интерквартильным размахом или интерквартильным интервалом (InterQuartile range, IQR) называется разность между третьим и первым квартилями (Q3 — Q1). Интерквартильный размах является характеристикой разброса значений в выборке .
Примечание : Характеристикой разброса значений в выборке является также дисперсия и стандартное отклонение .
Интерквартильный размах , а также квартили используются при построении Блочной диаграммы , которая полезна для оценки разброса значений (variation) в небольших выборках или для сравнения нескольких выборок имеющих сходные распределения.
Подробнее о построении Блочной диаграммы см. статью Блочная диаграмма в MS EXCEL .
Квартили непрерывного распределения
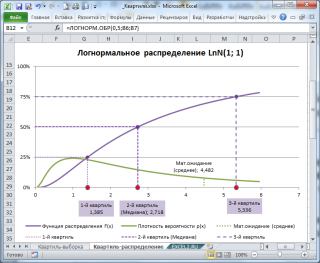
Если функция распределения F (х) случайной величины х непрерывна, то 1-й квартиль является решением уравнения F(х) =0,25, второй — F(х) =0,5, а третий F(х) =0,75.
Если известна функция плотности вероятности p (х) , то 1-й квартиль можно найти из уравнения:
Например, решив аналитическим способом это уравнение для Логнормального распределения lnN(μ; σ 2 ), получим, что медиана (2-й квартиль ) вычисляется по формуле e μ или в MS EXCEL =EXP(μ). При μ=1, медиана равна 2,718.
Обратите внимание на точку Функции распределения , для которой F(х)=0,5 (см. картинку выше или файл примера , лист Квартиль-распределение) . Абсцисса этой точки равна 2,718. Это и есть значение 2-го квартиля ( медианы ), что естественно совпадает с ранее вычисленным значением по формуле e μ .
Примечание : Напомним, что интеграл от функции плотности вероятности по всей области задания случайной величины равен единице:
Поэтому, линии квартилей ( х=квартиль ) делят площадь под графиком функции плотности вероятности на 4 равные части.
Квартили в MS EXCEL
Чтобы вычислить в MS EXCEL квартили заданного распределения необходимо использовать соответствующую обратную функцию распределения .
При вычислении квартилей в MS EXCEL используются обратные функции распределения : НОРМ.СТ.ОБР() , ЛОГНОРМ.ОБР() , ХИ2.ОБР() , ГАММА.ОБР() и т.д. Подробнее о распределениях, представленных в MS EXCEL, можно прочитать в статье Распределения случайной величины в MS EXCEL .
Например, в MS EXCEL 1-й квартиль для логнормального распределения LnN(1;1) можно вычислить по формуле =ЛОГНОРМ.ОБР(0,25;1;1) , а 3-й квартиль для стандартного нормального распределения по формуле =НОРМ.СТ.ОБР(0,75) .
In statistics, deciles are numbers that split a dataset into ten groups of equal frequency.
The first decile is the point where 10% of all data values lie below it. The second decile is the point where 20% of all data values lie below it, and so forth.
We can use the following function to calculate the deciles for a dataset in Excel:
=PERCENTILE(CELL RANGE, PERCENTILE)
The following example shows how to use this function in practice.
Example: Calculate Deciles in Excel
Suppose we have the following dataset with 20 values:
The following image shows how to calculate the deciles for the dataset:
The way to interpret the deciles is as follows:
- 20% of all data values lie below 67.8.
- 30% of all data values lie below 76.5.
- 40% of all data values lie below 83.6.
And so on.
To place each data value into a decile, we can use the PERCENTRANK.EXC() function, which uses the following syntax:
=PERCENTRANK.EXC(CELL RANGE, DATA VALUE, SIGNIFICANCE)
The following image shows how to use this function for our dataset:
Note that this function finds the relative rank of a value in a dataset as a percentage and rounds to one digit, which is equivalent to finding the decile that the value falls in.
The way to interpret the output is as follows:
- The data value 58 falls between the percentile 0 and 0.1, thus it falls in the first decile.
- The data value 64 falls between the percentile 0.1 and 0.2, thus it falls in the second decile.
- The data value 67 falls between the percentile 0.1 and 0.2, thus it falls in the second decile.
- The data value 68 falls between the percentile 0.2 and 0.3, thus it falls in the third decile.
And so on.
Additional Resources
How to Calculate a Five Number Summary in Excel
How to Normalize Data in Excel
How to Easily Find Outliers in Excel
- Что такое децильная формула?
Формула дециля (Содержание)
- формула
- Примеры
Что такое децильная формула?
Дециль, как звучит его название, является статистическим термином, который делит данные на десять определенных интервалов. Он в основном делит точки данных на набор данных в 10 равных частях в числовой строке. Этот тип ранжирования данных используется во многих областях, таких как финансы, экономика и т. Д. Мы должны помнить одну вещь: точки данных могут быть случайными, и мы должны поместить эти числа в строку сначала в числовой строке в порядке возрастания, а затем разделите их в децилях. Как только мы разделим данные, ранжирование по децилям может быть дано:
Как и другие инструменты квартиль и процентиль, дециль также является методом, который делит данные на более мелкие части, которые легче измерять, анализировать и понимать.
Формула для дециля:
Допустим, у нас есть набор данных с N точками данных:
X – (X1, X2, X3 ……… .. XN)
Формула для децилей дается:
D i = (N + 1) * i / 10
D1 = (N + 1) * 1/10
D2 = (N + 1) * 2/10
И так до
D9 = (N + 1) * 9/10
Из приведенной выше формулы видно, что D5 = (N + 1) * 5/10 = (N + 1) / 2, что является медианой. Таким образом, 5- й дециль представляет собой медиану.
Для сгруппированных данных:
Di = L + (h / f) * (i * (N / 10) – C)
Где:
я = 1, 2, 3, 4, 5…, 9
- L – нижняя граница группы
- h – ширина
- f – частота
- N – общее количество точек данных
- C – накопленная частота, предшествующая этому классу
Примеры формул дециля (с шаблоном Excel)
Давайте рассмотрим пример, чтобы лучше понять расчет децилей.
Вы можете скачать этот шаблон Excel с формулой дециля здесь – Шаблон Excel с формулой дециля
Децильная формула – пример № 1
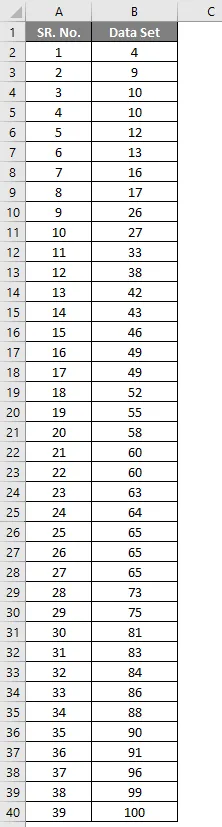
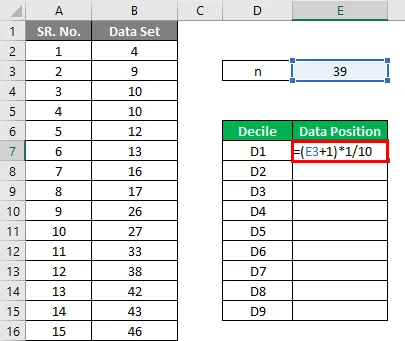
Допустим, у нас есть наборы данных, которые содержат 39 точек данных. Рассчитайте децили.
Набор данных:
Решение:
Прежде всего, мы должны расположить это в порядке возрастания, т.е. от низшего к высшему.
Дециль рассчитывается по формуле, приведенной ниже
D i = (N + 1) * i / 10
Результат будет таким, как указано ниже.
Аналогичным образом рассчитайте для всех точек.
Сейчас
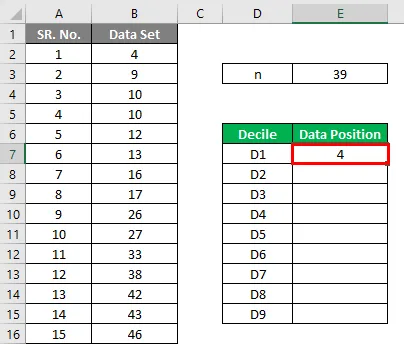
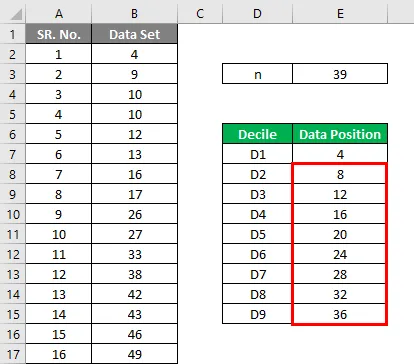
- D1 = (39 + 1) * 1/10 = 40/10 = 4- я точка данных = 10
- D2 = (39 + 1) * 2/10 = 80/10 = 8- я точка данных = 17
- D3 = (39 + 1) * 3/10 = 120/10 = 12- я точка данных = 38
- D4 = (39 + 1) * 4/10 = 160/10 = 16- я точка данных = 49
- D5 = (39 + 1) * 5/10 = 200/10 = 20- я точка данных = 58
- D6 = (39 + 1) * 6/10 = 240/10 = 24- я точка данных = 64
- D7 = (39 + 1) * 7/10 = 280/10 = 28- я точка данных = 73
- D8 = (39 + 1) * 8/10 = 320/10 = 32- я точка данных = 84
- D9 = (39 + 1) * 9/10 = 360/10 = 36- я точка данных = 91
Если вы видите набор данных, медиана этого набора: (n + 1) / 2 = 40/2 = 20- е значение, т.е. 58, это то же самое, что и D5.
Децильная формула – пример № 2
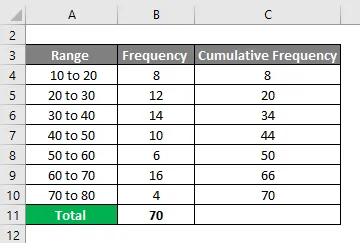
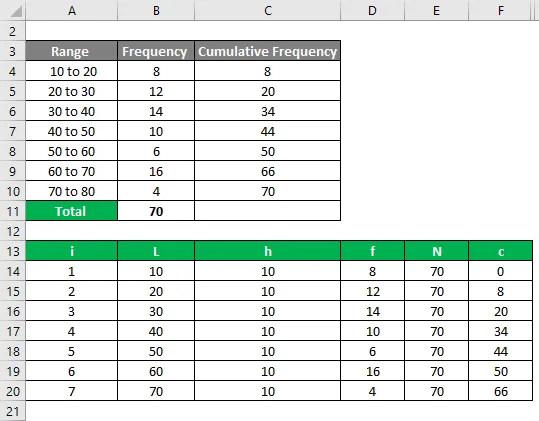
Предположим, ниже приведена таблица частот, которая у вас есть, для которой вам нужно рассчитать децили.
Из приведенного выше изображения, мы дали следующую информацию.
Дециль рассчитывается по формуле, приведенной ниже
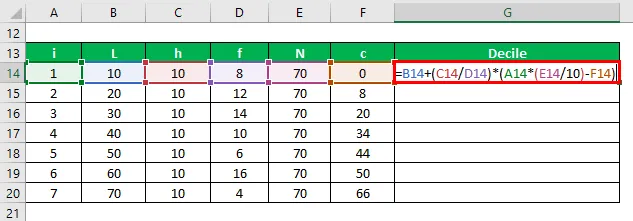
Di = L + (h / f) * (I * (N / 10) – C)
Результат будет как указано ниже
Аналогичным образом рассчитайте для других значений
Di = L + (h / f) * (i * (N / 10) – C)
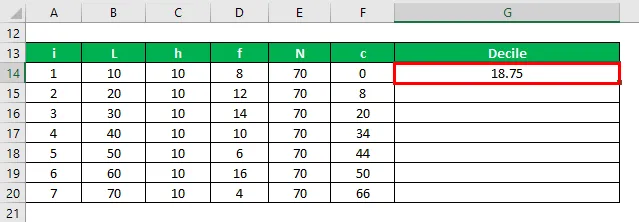
- D1 = 10 + (10/8) * (1 * (70/10) – 0) = 18, 75
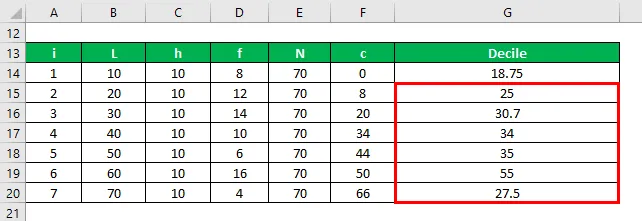
- D2 = 20 + (10/12) * (2 * (70/10) – 8) = 25
- D3 = 30 + (10/14) * (3 * (70/10) – 20) = 30, 7
- D4 = 40 + (10/10) * (4 * (70/10) – 34) = 34
- D5 = 50 + (10/6) * (5 * (70/10) – 44) = 35
- D6 = 60 + (10/16) * (6 * (70/10) – 50) = 55
- D7 = 70 + (10/4) * (7 * (70/10) – 66) = 27, 5
объяснение
Мы знаем, что квартили делят данные на четыре равные группы, дециль делит данные на десять равных частей. Дециль, как обсуждалось выше, ранжирует набор данных от самого низкого до самого высокого. Это делается по шкале от 1 до 10, где каждое число в основном указывает на увеличение на 10 процентных пунктов. Таким образом, 1-й дециль имеет 10% точек данных под ним, D2 имеет 20% точек данных под ним и так далее. Таким образом, ранжирование по децилям является еще одним методом классификации данных, таких как квартиль или процентиль.
Актуальность и использование формулы дециля
Как обсуждалось выше, Decile помогает нам очень быстро разделить данные на десять частей и, в конечном итоге, облегчает понимание данных в этих частях. В финансах децили используются для анализа эффективности различных фондов путем их ранжирования и измерения производительности одного фонда по сравнению с аналогичными фондами. Например, вы являетесь аналитиком и оцениваете набор взаимных фондов, поэтому любой фонд, который занимает 6 место по шкале децилей, означает, что он входит в верхние 60% фондов. Таким образом, в основном мы можем использовать децили и разделять эти средства на наиболее эффективные и худшие за определенный период.
Рекомендуемые статьи
Это руководство по формуле децилей. Здесь мы обсудим, как рассчитать децили, а также практические примеры и загружаемый шаблон Excel. Вы также можете посмотреть следующие статьи, чтобы узнать больше –
- Калькулятор формулы Quartile Deviation
- ВВП на душу населения с примерами
- Как рассчитать процент прибыли с помощью формулы?
- Расчет чистого операционного дохода с помощью шаблона Excel
События,
характеризующие данные, могут носить
случайный характер и появляться с разной
вероятностью.
Вероятность
события p
есть отношение числа благоприятных
исходов m
к числу всех возможных исходов n
этого
события:
p=m/n.
Например, вероятность появления туза
в наугад выбранной карте из колоды в 52
карты равна 4/52=0.0769, так как m=4,
а n=52.
Если
известно соответствие между появлениями
(величинами) x1,
x2,
…, xn
случайного события (переменной)
X
и
соответствующими вероятностями их
реализации p1,
p2,
…, pn,
то говорят, что известен закон
распределения случайной величины
F(x).
Большинство встречающихся на практике
распределений вероятностей реализовано
в Excel.
Распределения
вероятностей имеют числовые характеристики.
Функции
Excel
для вычисления числовых характеристик
распределения вероятностей. Они входят
в группу Статистические.
При вычислении функций в качестве
случайных величин используйте следующие
значения:
Математическое
ожидание
случайной величины (среднее арифметическое),
характеризующее центр распределения
вероятностей, вычисляется функцией
СРЗНАЧ. СРЗНАЧ(A1:A7)
= 9.
Дисперсия,
характеризует разброс случайной величины
относительно центра распределения
вероятностей и вычисляется функцией
ДИСПР. ДИСПР(A1:A7)
= 4.857.
Среднеквадратичное
отклонение
есть квадратный корень из дисперсии,
характеризует разброс случайной величины
в единицах случайной величины и
вычисляется функцией СТАНДОТКЛОНП.
СТАНДОТКЛОНП(A1:A7) = 2.203893.
Квантиль
случайной величины с законом распределения
F(x)
есть значение случайной величины x
при заданной вероятности p.,
т.е. есть решение уравнения F(x)=p.
Медиана
есть квантиль с вероятностью p=0.5.
Excel,
вместо квантилей содержит функции
вычисления х
для определенных уровней р:
квартили
(кварта – четверть), децили
(дециль
– десятая часть),
персентили
(персент – процент). Различают нижний
квартиль с вероятностью p=0.25
и верхний квартиль с вероятностью
p=0.75.
Децили это квантили с вероятностью 0.1,
0.2, …, 0.9.
Функцию
КВАРТИЛЬ используют, чтобы разбить
данные на группы. В качестве второго
аргумента указывают уровень (четверть),
для которого нужно вернуть решение: 0 –
минимальное значение распределения, 1
– первый, нижний квартиль, 2 – медиана,
3 – третий, верхний квартиль, 4 –
максимальное значение. Например,
КВАРТИЛЬ(A1:A7;3)
= 10, т.е. 75% всех значений меньше 10,
КВАРТИЛЬ(A1:A7;2) = 9.
Функция
ПЕРСЕНТИЛЬ вычисляет квантиль указанного
уровня вероятности и используется для
определения порога приемлемости
значений. В качестве второго аргумента
указывают уровень 0.1, 0.2, …, 0.9.
ПЕРСЕНТИЛЬ(A1:A7;0,9) = 11.8, т.е. 90% всех значений
меньше 11.8.
Excel
содержит инструмент Ранг
и персентиль,
который на основе набора данных формирует
выходную таблицу, содержащую порядковый
и процентный ранги для каждого значения
в наборе данных. См. справку по F1.
Ниже приведен пример установки надстройки
Пактет
анализа
Распределения
вероятностей, реализованные в Excel.
Каждый
закон распределения описывает процессы
разной вероятностной природы и
характеризуется специфическими
параметрами:
-
равномерное
распределение
– n
случайных чисел выпадает с одной и той
же вероятностью p=1/n;
характеризуется нижней и верхней
границей; примером является появление
чисел 1, 2, …, 6 при бросании игральной
кости (p=1/6); -
биномиальное
распределение
моделирует взаимосвязь числа успешных
испытаний m
и вероятностей успеха каждого испытания
p
при общем количестве испытаний n
– функции БИНОМРАСП и КРИТБИНОМ; -
нормальное
(гауссово) распределение
описывает процессы, в которых на
результат воздействует большое число
независимых случайных факторов, среди
которых нет сильно выделяющихся –
функции НОРМРАСП, НОРМСТРАСП, НОРМОБР,
НОРМСТОБР и НОРМАЛИЗАЦИЯ; -
распределение
Пуассона, предсказывает
число случайных событий на определенном
отрезке времени или на определенном
пространстве, позволяет аппроксимировать
биномиальное распределение – функция
ПУАССОН; -
экспоненциальное
(показательное) распределение,
моделирует временные задержки между
событиями, описывает процессы в задачах
массового обслуживания и в задачах с
«временем жизни» – ЭКСПРАСП; -
распределение
хи-квадрат,
связано с нормальным, возвращает
одностороннюю вероятность распределения
и используется для сравнения предполагаемых
и наблюдаемых значений – функция
ХИ2РАСП; -
распределение
Стьюдента,
связано с нормальным, возвращает
вероятность для t-распределения Стьюдента
и используется для проверки гипотез
при малом объеме выборки – функция
СТЬЮДРАСП; -
F-распределение
(Фишера), связано с нормальным и может
быть использовано в F-тесте, который
сравнивает степени разброса двух
множеств данных – fраспобр; -
гамма-распределение
используется для изучения случайных
величин, имеющих асимметричное
распределение, в теории очередей –
функция ГАММАРАСП; -
а
также другие распределения – функции
БЕТАРАСП, ВЕЙБУЛЛ, ОТРБИНОМРАСП,
ГИПЕРГЕОМЕТ, ЛОГНОРМРАСП и др.
Биномиальное
распределение
характеризуется
числом успешных испытаний m,
вероятностью успеха каждого испытания
p
и общим количеством испытаний n.
Классическим примером использования
биномиального распределения является
выборочный контроль качества больших
партий товара, изделий в торговле, на
производстве, когда сплошная проверка
невозможна. Из партии выбирают n
образцов и регистрируют число бракованных
m.
Бракованными могут быть 1, 2, … , n
образцов, но вероятности реального
числа бракованных будут различными.
Если контрольная вероятность брака
ниже допустимой вероятности, то можно
гарантировать достаточное качество
всей партии.
В
Excel
функция БИНОМРАСП вычисляет вероятность
отдельного значения распределения по
заданным m,
n
и р,
а функция КРИТБИНОМ – случайное число
по заданной вероятности. Обычно функция
КРИТБИНОМ используется для определения
наибольшего допустимого числа брака.
В
качестве примера построим график
плотности вероятности биномиального
распределения для n=10
(1, 2, …, 10) и p=0.2.
Введите исходные данные, как показано
на рисунке:
Далее
в ячейку В4 введите статистическую
функцию БИНОМРАСП и заполните ее
параметры как показано на рисунке:
Здесь
параметр Число_s
есть число успешных испытаний m,
Испытания
– число независимых испытаний n,
Вероятность_s
–
вероятность успеха каждого испытания
p.
Параметр Интегральный
равен 0, если требуется получить плотность
распределения (вероятность для значения
m),
и равен 1, если требуется получить
вероятность с накоплением (вероятность
того, что число успешных испытаний не
меньше значения аргумента Число_s).
Формулу
из В4 размножьте в ячейки В5:В13. Ниже
показан результат:
В
колонке В вычислены вероятности успешных
испытаний m=1,
2, …, 10. Теперь по диапазону В4:В13 постройте
график или гистограмму биномиальной
функции плотности распределения –
результат на рисунке. Поэкспериментируйте,
изменяя значение вероятности в ячейке
В1: 0.3, 0.4, 0.8, проследите за изменениями
формы графика.
Для
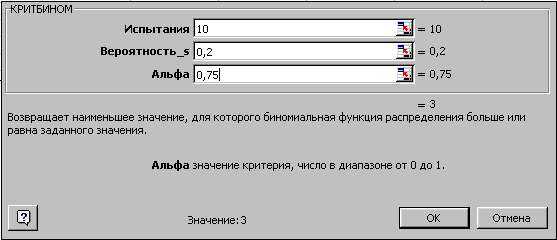
иллюстрации функции КРИТБИНОМ используем
предыдущий пример – необходимо найти
число m,
для которого вероятность интегрального
распределения больше или равна 0.75.
Вызовите функцию КРИТБИНОМ и заполните
параметры. Вы должны получить значение
3. Это означает, что при вероятности
интегрального распределения >= 0.75
будет не менее трех (m>=3)
успешных испытаний.
Нормальное
распределение
характеризуется
средним арифметическим (математическим
ожиданием) m
и стандартным (среднеквадратичным)
отклонением r.
Дисперсия равна r2.
Краткое обозначение распределения
N(m,r2).
График нормального распределения
симметричен относительно центра
распределения (точки m),
чем меньше r,
тем больше вероятность появления
случайной величины. В пределы [m–r,m+r]
нормально распределенная случайная
величина попадает с вероятностью 0,683 в
пределы [m-2r,m+2r]
– с вероятностью 0,955 и т.д.
При
m=0
и r=1
нормальное распределение называется
стандартным
или нормированным – N(0,1).
Нормальное
распределение имеет очень широкий круг
приложений. В качестве примера построим
график плотности вероятностей нормального
распределения при m=15
и r=1,5
в диапазоне [m-3r,m+3r]
c
шагом 0,5. Результат показан на рисунке.
Выполните
следующие действия:
-
в
ячейку А4 введите формулу =B1-3*B2, в ячейку
А5 формулу =A4+B$3 и размножьте ее по ячейку
А22; -
в
ячейку В4 введите функцию НОРМРАСП из
группы Статистические
– параметры заполните как на рисунке; -
размножьте
формулу из ячейки В4 по ячейку В22 и по
диапазону В4:В22 постройте график; на
2-ом шаге мастера диаграмм в закладке
Ряд
введите подписи к оси х
из диапазона А4:А22.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #