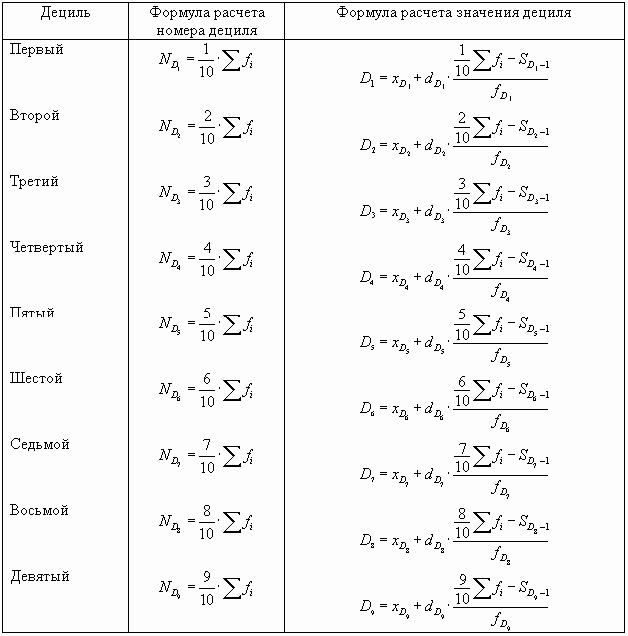Расчет квартилей для интервального ряда:
Для
расчета квартилей для интервального
ряда
-
Определяем номер квартиля по тем же
формулам, что и для дискретного ряда, -
Определяем квартильный интервал по
накопленной частоте. Это
первый интервал, для которого накопленная
частота будет больше или равна номеру
квартиля. -
Рассчитываем квартиль по формуле:

Где:
J
– номер квартиля,
 –
–
нижняя граница интервала, содержащего
квартиль. Интервал определяется по
накопленной частоте интервалов,
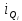 –
–
ширина интервала, содержащего квартиль,
 –
–
накопленная частота интервала,
предшествующего интервалу, содержащему
квартиль,
 –
–
частота интервала, содержащего квартиль.


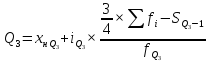
Пример.
Найти первый квартиль для интервального
ряда.
|
Возрастные |
Число |
Накопленная |
|
До |
346 |
346 |
|
20 |
872 |
1218 |
|
25 |
1054 |
2272 |
|
30 |
781 |
3053 |
|
35 |
212 |
3265 |
|
40 |
121 |
3386 |
|
45 |
76 |
3462 |
|
Итого |
3462 |
Решение:
-
Определяем номер первого квартиля по
формуле

-
Первый квартиль находится в возрастной
группе 20-25 лет, так как это первый
интервал, для которого накопленная
частота больше (или равна) номера
квартиля (346<865,75; 1218>865,75). -
Определяем первый квартиль по формуле
-

Это значит, что четверть студентов
младше 22,98 лет.
-
Децили
Децили –
значения признака, делящие ранжированный
ряд на десять равных частей.
Первый
дециль отсекает 1/10 часть совокупности,
а девятый дециль отсекает 9/10 частей.
Таким образом, различают 9 децилей.
Рассчитываются
децили аналогично квартилям.
Расчет децилей для дискретного ряда
-
Определяем номер
дециля по формуле:
 ,
, -
Если номер дециля
– целое число,
то значение дециля будет равно величине
элемента ряда, которое обладает
накопленной частотой равной номеру
дециля. Например, если номер дециля
равен 20, его значение будет равно
значению признака с S =20 (накопленной
частотой равной 20).
Если номер дециля
– нецелое число,
то дециль попадает между двумя
наблюдениями. Значением дециля будет
сумма, состоящая из значения элемента,
для которого накопленная частота равна
целому значению номера дециля, и указанной
части (нецелая часть номера дециля)
разности между значением этого элемента
и значением следующего элемента.
Например, если номер
дециля равна 20,25, дециль попадает между
20-м и 21-м наблюдениями, и его значение
будет равно значению 20-го наблюдения
плюс 1/4 разности между значением 20-го и
21-го наблюдений.
Расчет децилей для интервального ряда
-
Определяем номер
дециля по формуле:
 ,
, -
Определяем децильный
интервал. Это первый интервал, для
которого накопленная частота будет
больше или равна номеру дециля. -
Рассчитываем дециль
по формуле:

где
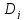 – значение j-го дециля,
– значение j-го дециля,

– нижняя граница децильного интервала;

– ширина децильного интервала;

 –
–
сумма всех частот,

 -накопленная
-накопленная
частота интервала, предшествующего
децильному;

 –
–
частота децильного интервала.
Пример.
Найти 9-ый дециль D9
|
Заработная
|
бригада |
|
|
число |
накопленная частота |
|
|
15 |
20 |
20 |
|
18 |
37 |
57 |
|
20 |
14 |
71 |
|
25 |
4 |
75 |
|
Итого: |
75 |
-
Определяем номер 9-го дециля
для первой бригады
 ;
;
-
Номер дециля – нецелое число. Для
определения дециля нужны значения двух
элементов – х68и х69. Значение
дециля находится между ними.
Определяем
их значение с помощью самой первой
накопленной частоты большей или равной
порядковым номерам элементов (68 и 69).
Х68= 20, х69= 20.
Теперь
определяем значение 9-го дециля:D7=x68+ (х69–
х68)×0,4=20 + (20 – 20)×0,2 =20тыс.руб.
Это значит, что заработная плата90%
рабочих бригады не превышает 18 тыс.руб.
Пример.
Найти седьмой дециль D7
для интервального ряда.
|
Возрастные |
Число |
Накопленная |
|
До |
346 |
346 |
|
20 |
872 |
1218 |
|
25 |
1054 |
2272 |
|
30 |
781 |
3053 |
|
35 |
212 |
3265 |
|
40 |
121 |
3386 |
|
45 |
76 |
3462 |
|
Итого |
3462 |
Решение:
-
Определяем номер седьмого дециля по
формуле
 7×
7×
-
Седьмой дециль находится в возрастной
группе 30-35 лет, так как это первый
интервал, для которого накопленная
частота больше (или равна) номера дециля
(2272<2424,1; 3053>2424,1). -
Определяем седьмой дециль по формуле
-

Это значит, что 70% студентов младше 30,97
лет.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
8.2. Медиана, квартили, децили
Медиана – это значение признака, которое делит статистическую совокупность на две равные части: половина единиц совокупности имеет значения признака не меньше медианы, другая половина – значения признака не больше медианы.
Значения изучаемого признака всех единиц статистической совокупности можно расположить в порядке возрастания (или убывания). В этом случае мы получим ранжированный ряд. Если число единиц совокупности нечетное, то значение признака, находящееся в середине ранжированного ряда, будет являться медианой. Если число единиц совокупности четное, то медианой будет средняя величина из двух значений признака, находящихся в середине ряда.
Пример 8.5. Имеются следующие данные о результатах сдачи экзамена по статистике в студенческой группе:
| Номер студента | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Оценка по статистике | 3 | 4 | 2 | 3 | 4 | 4 | 4 | 3 | 4 | 5 | 5 |
Представим их в виде ранжированного ряда:
| Номер студента | 3 | 1 | 4 | 8 | 2 | 5 | 6 | 7 | 9 | 10 | 11 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Оценка по статистике | 2 | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 4 | 5 | 5 |
Как видим, в ранжированном ряду оценки расположились следующим образом: сначала записана одна неудовлетворительная оценка (ее получил студент, имеющий в ведомости номер 3), затем три оценки “удовлетворительно”, пять оценок “хорошо” и две оценки “отлично”. В середине ранжированного ряда, имеющего нечетное число членов, стоит оценка “4”, которую получил студент, записанный в ведомости под номером 5. Следовательно, оценка “4 (хорошо)” является медианой для данного ряда распределения. Пять студентов получили оценки 4 и ниже (2, 3, 3, 3, 4), другие пять студентов – 4 и выше (4, 4, 4, 5, 5).
Пример 8.6. Имеются данные о цене антоновских яблок в шести магазинах города. Представим их сразу в виде ранжированного ряда:
| Название магазина | “Огонек” | “Маяк” | “Заря” | “Татьяна” | “Ночной” | “Любимый” |
|---|---|---|---|---|---|---|
| Цена яблок, руб. за кг | 40 | 41 | 42 | 44 | 44 | 45 |
В середине ранжированного ряда находятся цены двух магазинов, причем они разные. Медиана определяется как средняя величина из этих значений признака. Она равна 43 руб. [(42 + 44) : 2 = 43].
Таким образом, в 50% магазинов города яблоки продаются по цене не выше 43 руб. за килограмм, а в других 50% магазинов – по цене не ниже 43 руб.
Квартили (Q) делят ранжированный ряд на четыре равные части: первый квартиль (Q1) включает значения признака, не превышающие 25% единиц совокупности, второй квартиль (Q2) – совпадает с медианой (Ме), третий квартиль (Q3) – значения признака, не превышающие 75% единиц совокупности (рис. 8.3).
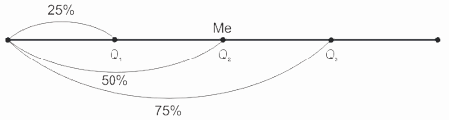
Рис.
8.3.
Деление ранжированного ряда на четыре равные части
Децили (D) делят ранжированный ряд на десять равных частей: первым децилем (D1) является значение признака, которое не превышает 10% единиц совокупности, вторым (D2) – 20%, третьим (D3) – 30% и т.д. При этом пятый дециль (D5) совпадает с медианой и вторым квартилем (Q2) (рис. 8.4).

Рис.
8.4.
Деление ранжированного ряда на десять равных частей
Медиана, квартили и децили относятся к группе квантилей. Квантили – это показатели, которые делят вариационные ряды на определенное количество равных частей. Среди них, помимо названных, также имеются квантили, которые делят ряд на пять равных частей, перцентили – на сто и т.д.
Структурные показатели не зависят от того, имеются ли в статистической совокупности аномальные (резко выделяющиеся) наблюдения. И если средняя величина при их наличии теряет свою практическую значимость, то информативность медианы наоборот усиливается – она начинает выполнять функции средней, т.д. характеризовать центр совокупности.
Способы расчета рассматриваемых структурных показателей зависят от вида вариационного ряда. Рассмотрим их подробнее.
8.2.1. Определение структурных средних в дискретных вариационных рядах
Для определения медианы в дискретных вариационных рядах:
- находят ее порядковый номер по формуле
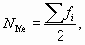
- строят ряд накопленных частот;
- находят накопленную частоту, которая равна порядковому номеру медианы или его превышает;
- варианта, соответствующая данной накопленной частоте, является медианой.
Пример 8.7. Определим медианный стаж сотрудников страховой компании на основе следующих данных:
| Время работы, лет, xi | Число сотрудников, чел., fi | Накопленная частота, Si |
|---|---|---|
| 1 | 5 | 5 |
| 2 | 7 | 12 |
| 3 | 4 | 16 |
| 4 | 9 | 25 |
| 5 | 13 | 38 |
| 6 | 10 | 48 |
| 7 | 16 | 64 |
| 8 | 13 | 77 |
| Итого | 77 | – |
Номер медианы равен
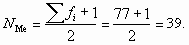
Для того чтобы найти значение варианты, стоящей на 39 месте, рассчитаем накопленные частоты. Для пятой группы накопленная частота равна 38. Это означает, что 38 работников имеют стаж работы 5 лет и меньше. Для шестой группы накопленная частота – 48 (она первая превышает порядковый номер медианы), следовательно, в эту группу входят сотрудники с порядковыми номерами от 39 до 48, в том числе и искомый 39-й сотрудник. Стаж работы сотрудников в шестой группе – 6 лет. Значит, Ме = 6. Итак, 50% сотрудников работают в данной страховой компании не более шести лет.
Квартили и децили определяют аналогично медиане: сначала находят их номер, затем среди накопленных частот ищут такую, которая первая равна или превышает порядковый номер показателя, ей соответствует варианта, которая является искомым показателем. Номера квартилей рассчитываются по формулам:
- первый (нижний) квартиль имеет номер:

- третий (верхний) квартиль:

Порядковые номера децилей исчисляются следующим образом:
- для первого дециля:

- для второго дециля:
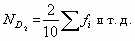
Определим квартили по данным примера 8.7. Их номера равны:
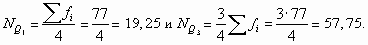
Первая накопленная частота, превышающая 19,25, равна 25. Ей соответствует варианта 4, являющаяся первым квартилем. Первая накопленная частота, которая превышает 57,75 – это 64; ей соответствует варианта, равная 7. Это третий квартиль. Итак, 25% сотрудников работают в данной компании не более четырех лет, а 75% – не более семи лет.
Аналогично определяются децили. Например, восьмой дециль вычисляется следующим образом:

Накопленная частота 64 – первая, превышающая ND8, ей соответствует значение признака – 7 лет, т.д. у 80% сотрудников стаж работы в данной компании не превышает семи лет.
8.2.2. Определение структурных средних в интервальном вариационном ряду
В интервальных рядах сначала определяют медианный интервал. Для этого так же, как и в дискретных рядах, рассчитывают порядковый номер медианы

Накопленной частоте, которая равна номеру медианы или первая его превышает, в интервальном вариационном ряду соответствует медианный интервал. Обозначим эту накопленную частоту SМе. Непосредственно расчет медианы проводят по формуле:

где хМе – нижняя граница медианного интервала;
dMe – величина медианного интервала;
SMe – 1 – накопленная частота интервала, предшествующего медианному;
fMe – частота медианного интервала.
Пример 8.8. По следующим данным определим медианное значение суммы выданных банками кредитов:
| Сумма выданных кредитов, млн ден. ед. | Количество банков, fi | Накопленная частота, Si. |
|---|---|---|
| 20-40 | 8 | 8 |
| 40-60 | 15 | 23 |
| 60-80 | 21 | 44 |
| 80-100 | 12 | 56 |
| 100-120 | 9 | 65 |
| 120-140 | 7 | 72 |
| 140-160 | 4 | 76 |
| Итого | 76 | – |
Проведем расчет:
- определим порядковый номер медианы
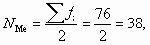
- определим накопленную частоту медианного интервала: SМе > NМе; SМе = 44;
- определим соответствующий ей медианный интервал “60-80”;
- рассчитаем значение медианы по формуле

т.е. у 50% банков сумма выданных кредитов не превышает 74,286 млн ден. ед.
Далее произведем расчет квартилей и децилей в интервальном вариационном ряду.
Для приведенного интервального ряда необходимо определить:
- номер первого (нижнего) квартиля:

тогда ей соответствует интервал “40-60”, в котором находится первый квартиль;
- номер третьего (верхнего) квартиля:

тогда ей соответствует интервал “100-120”, в котором находится третий квартиль;
- первый (нижний) квартиль рассчитаем по формуле:

т.е. у 25% банков сумма выданных кредитов не превышает 54,7 млн ден. ед.;
- третий (верхний) квартиль рассчитаем по формуле:

т.е. у 75% банков сумма выданных кредитов не превышает 102,2 млн ден. ед.
Аналогично квартилям определяем децили. Формулы, используемые в ходе расчетов, поместим в таблицу.
|
|
|
Здесь хD – нижняя граница децильного интервала; dD – величина децильного интервала; SD – 1 – сумма накопленных частот интервала, предшествующего децильному; fD – частота децильного интервала. |
Номер шестого дециля равен: следовательно SQ6 = 56, этой накопленной частоте соответствует интервал “80-100”, в котором находится шестой дециль. Величина децильного значения равна:
следовательно SQ6 = 56, этой накопленной частоте соответствует интервал “80-100”, в котором находится шестой дециль. Величина децильного значения равна:  (млн ден. ед.), т.д. у 60% банков сумма выданных кредитов не превышает 82,7 млн ден. ед.
(млн ден. ед.), т.д. у 60% банков сумма выданных кредитов не превышает 82,7 млн ден. ед.
В статистике для характеристики степени неоднородности совокупности часто используют коэффициенты дифференциации (квартильные и децильные). Децильный коэффициент дифференциации представляет собой отношение девятого дециля к первому:

Данный коэффициент показывает, во сколько раз варианта, выше которой находятся 10% единиц совокупности, имеющих самые большие значения признака, больше варианты, ниже которой находятся 10% единиц совокупности с самыми маленькими значениями признака. Аналогично квартильный коэффициент дифференциации определяется как отношение третьего квартиля к первому.
В заключение отметим, что приблизительное равенство средней арифметической, моды и медианы, рассчитанных по отношению к одному и тому же ряду, говорит о том, что значения признака в изучаемой совокупности имеют нормальный закон распределения (или приближаются к нему).
Медиана может быть определена графически по кумуляте. Для этих целей на оси ординат, где отмечаются накопленные частоты, находится точка, соответствующая полусумме всех частот (т.е. порядковому номеру медианы). Из нее проводится прямая параллельно оси абсцисс до пересечения с графиком (кумулятой распределения). Абсцисса точки пересечения соответствует медиане данного ряда распределения.
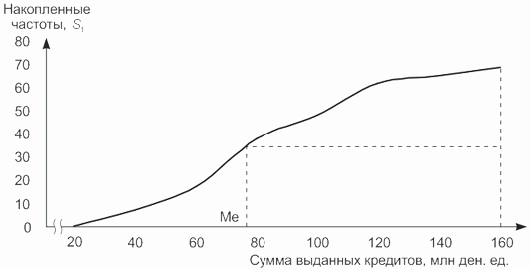
Рис.
8.5.
Определение медианы по кумуляте
Структурные средние – мода, медиана, квантиль, дециль
Краткая теория
Наиболее широкое применение в статистике имеют структурные
средние, к числу которых относятся мода и медиана (непараметрические средние).
Мода – величина признака (варианта), которая
встречается в ряду распределения с наибольшей частотой (весом). К моде (Мо)
прибегают для выявления величины признака, имеющей наибольшее распространение
(цена на рынке, по которой было совершено наибольшее число продаж данного
товара, номер обуви, который пользуется наибольшим спросом у покупателей и т.
д.). Мода используется только в совокупностях большой численности. В дискретном
ряду мода находится как варианта, имеющая наибольшую частоту. В интервальном
ряду сначала находится модальный интервал, то есть интервал, обладающий наибольшей частотой, а
затем – приближенное значение модальной величины признака по формуле:
– нижняя граница модального интервала
– величина модального интервала
– частота интервала, предшествующего
модальному
– частота модального интервала
– частота интервала, следующего за модальным
Квантили –
величины, разделяющие совокупность на определенной количество равных по
численности элементов частей. Самый известный квантиль – медиана, делящая совокупность на две равные части. Кроме медианы часто используются квартили, делящие ранжированный ряд на 4 равные части, децили -10 частей и перцентили – на 100
частей.
Медиана –
величина признака у единицы, находящейся в середине ранжированного
(упорядоченного) ряда. Если ряд распределения представлен конкретными
значениями признака, то медиана (Me) находится как
серединное значение признака.
Если ряд распределения дискретный, то медиана находится как
серединное значение признака (например, если число значений нечетное – 45, то
соответствует 23 значению признака в ряду
значений, расположенных в порядке возрастания, если число значений четное – 44,
то медиана соответствует полусумме 22 и 23 значений
признака).
Если ряд распределения интервальный, то первоначально
находят медианный интервал, который содержит единицу, находящуюся в середине
ранжированного ряда. Для определения этого интервала сумму частот
делят пополам и на основании последовательного накопления (суммирования)
частот интервалов, начиная с первого, находят интервал, где расположена
медиана. Значение медианы в интервальном ряду вычисляют по формуле:
– нижняя граница медианного интервала
– величина медианного интервала
– сумма
частот ряда
– сумма накопленных частот в интервалах,
предшествующих медианному
– частота медианного интервала
Квартили – это значения
признака в ранжированном ряду, выбранные таким образом, что 25% единиц
совокупности будут меньше величины
, 25% единиц будут заключены между
и
; 25% –
между
и
,
остальные 25% превосходят
. Квартили определяются по формулам,
аналогичным формуле для расчета медианы. Для интервального ряда:
Децилем
называется структурная переменная, делящая распределение на 10 равных частей по
числу единиц в совокупности. Децилей 9, а децильных
групп 10. Децили определяются по формулам, аналогичным формуле для расчета
медианы и квартилей.
В целом общая формула для расчета квантилей в интервальном
ряду такова:
– порядковый номер квантиля
– размерность квантиля (на сколько частей эти
квартили делят совокупность)
– нижняя граница квантильного
интервала
– ширина квантильного
интервала
– накопленная частота предквантильного
интервала
Для дискретного ряда номер квантиля можно
найти по формуле:
Примеры решения задач
Задача 1
(дискретный ранжированный ряд)
В
результате исследований установлен среднемесячный доход жильцов одного
подъезда:
|
1.5 |
1.8 |
2 |
2.5 |
2.8 |
2.8 |
2.8 |
3.0 |
3.6 |
3.8 |
|
3.9 |
4 |
5.8 |
5.9 |
6 |
6 |
6 |
6.8 |
7 |
7 |
Определите:
Модальный
и медианный доход, квартили и децили дохода.
Решение
Имеем уже ранжированный ряд – значения дохода жильцов распределены по возрастанию.
Мода
– наиболее часто встречающееся значение. В данном случае имеем ряд с двумя
модами.
и
Медиана
– такое значение признака, которое делит упорядоченное множество данных
пополам.
Квартили
– значения признака в ранжированном ряду, выбранные таким образом, что 25%
единиц совокупности будут меньше величины
; 25% единиц будут
заключены между
и
; 25% – между
и
; остальные 25%
превосходят
.
Дицили делят ряд на 10 равных частей:
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 2
(интервальный ряд)
Для
определения среднего размера вклада в кредитном учреждении были получены
следующие данные:
| Размер вклада, тыс.р. | до 10.0 | 10.0-16.0 | 16.0-22.0 | 22.0-28.0 | 28.0-34.0 | Свыше 34.0 |
|
Удельный вес вкладов, % |
5.0 | 8.0 | 15.0 | 22.0 | 30.0 | 20.0 |
Рассчитайте
структурные средние (моду, медиану,
квартили).
Решение
Вычислим моду размера вклада:
Мода – варианта, которой соответствует наибольшая частота.
Мода вычисляется по формуле:
–
начало модального интервала
–
величина интервала
–
частота модального интервала
–
частота интервала, предшествующего модальному
–
частота интервала, следующего за модальным
Таким образом, наибольшее
количество вкладов имеют размер 30,7 тыс.р.
Медиана – варианта, находящаяся в середине ряда распределения.
Расчет медианы производится по формуле:
-начало
(нижняя граница) медианного интервала
-величина интервала
-сумма всех частот ряда
-частота медианного интервала
-сумма накопленных частот вариантов до
медианного
Таким образом, половина вкладов имеет размер до 28 тыс.р.,
другая половина – более 28 тыс.р.
Вычислим квартили:
Таким
образом 25% вкладов меньше 20,8 тыс.р., 25% вкладов
лежат в интервале от 20,8 тыс.р. до 28 тыс.р., 25% лежат в интервале от 28 тыс.р.
до 33 тыс.р., 25% больше величины в 33 тыс.р.
Задача 3
Постройте
графики для вариационного ряда. На графике покажите моду, медиану, среднюю, квартили.
| Возраст детей (лет) | Число детей (доли) |
| 0-3 | 0.15 |
| 3-6 | 0.2 |
| 6-9 | 0.4 |
| 9-12 | 0.2 |
| 12-15 | 0.05 |
Решение
Вычислим
среднюю
: Для этого просуммируем
произведения середин интервалов и соответствующих частот, и полученную сумму
разделим на сумму частот.
Вычисление моды интервального ряда на графике
Построим
гистограмму.
Мода определяется по
гистограмме распределения. Для этого выбирается самый высокий прямоугольник,
который в данном случае является модальным. Затем правую вершину модального
прямоугольника соединяют с правым верхним углом предыдущего прямоугольника. А
левую вершину модального прямоугольника – с левым верхним углом последующего
прямоугольника. Далее из точки их пересечения опускают перпендикуляр на ось
абсцисс.
Абсцисса точки пересечения
этих прямых и будет модой распределения
Гистограмма
По
гистограмме получаем, что
Вычисление медианы и квартилей интервального ряда на графике
Построим
кумулятивную кривую частот (график накопленных частот)
Кумулятивная кривая частот
На получившимся графике
накопленных частот из последней получившейся точки (в нашем примере) проведем
линию перпендикулярную к оси
она так же
является максимальной высотой. Поделим ее на 4 части. Через полученные точки
строим параллельную оси
линии которая должна пересекать высоту к оси
и кумуляту. От
места пересечения кумуляты опускаем перпендикуляры. Получившиеся точки есть квартили
и медиана (квартиль при
).
Вывод к задаче
Таким образом
средний возраст детей 6,9 лет. Наибольшее количество детей имеют возраст 7,5
лет. Четверть детей младше 4,5 лет, а самая старшая четверть детей старше 9,1
лет. Половина детей имеет возраст менее 7,3 лет, другая половина – более 7,3
лет.
Имеются данные о распределении населения России по среднедушевому денежному доходу за 2015 год.
| Среднедушевой денежный доход в месяц, руб. | Население в % к итогу | Накопленные частоты |
|---|---|---|
| До 5000 | 2,4 | 2,4 |
| 5000 – 7000 | 3,8 | 6,2 |
| 7000 – 10000 | 8,0 | 14,2 |
| 10000 – 14000 | 12,1 | 26,3 |
| 14000 – 19000 | 14,4 | 40,7 |
| 19000 – 27000 | 18,2 | 58,9 |
| 27000 – 45000 | 22,5 | 81,4 |
| свыше 45000 | 18,6 | 100 |
| Итого | 100 | – |
Рассчитайте:
1. Структурные средние: медиану, первый и третий квартили, первый и девятый децили.
2. Децильный коэффициент дифференциации доходов населения.
Решение:
1. Структурные средние.
1) Медиана – это варианта, расположенная в середине ранжированного ряда. Медиана интервального вариационного ряда распределения определяется по формуле:
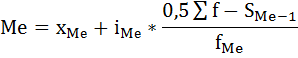
где
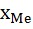 – начальное значение интервала, содержащего медиану;
– начальное значение интервала, содержащего медиану;
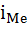 – величина медианного интервала;
– величина медианного интервала;
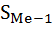 – сумма накопленных частот, предшествующих медианному интервалу;
– сумма накопленных частот, предшествующих медианному интервалу;
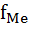 – частота медианного интервала.
– частота медианного интервала.
Определим, прежде всего, медианный интервал. Сумма накопленных частот, превышающая половину всех значений (58,9), соответствует интервалу 19 000 – 27 000. Это и есть медианный интервал, в котором находится медиана. Определим её значение по приведённой выше формуле, если
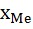 = 19 000,
= 19 000, 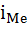 = 8 000, Σf = 100,
= 8 000, Σf = 100, 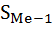 = 40,7,
= 40,7, 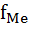 = 18,2:
= 18,2:
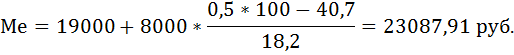
Это так называемый медианный доход – показатель уровня дохода индивида, находящегося в середине ранжированного ряда распределения.
Таким образом, половина населения имеет среднедушевой доход ниже 23 087,91 руб., а вторая половина – вышее 23 087,91 руб.
2) Рассчитаем первый и третий квартили:
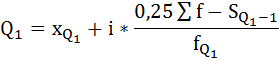
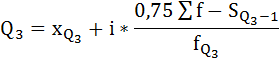
где
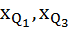 – начальные значения квартильных интервалов, первого и третьего соответственно;
– начальные значения квартильных интервалов, первого и третьего соответственно;
i – величина квартильного интервала;
Σf – сумма частот ряда;
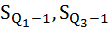 – накопленные частоты интервала, предшествующего квартильному;
– накопленные частоты интервала, предшествующего квартильному;
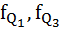 – частота квартильного интервала.
– частота квартильного интервала.
Определим интервалы, в которых находятся 1 и 3 квартиль. По ряду накопленных частот (третья графа в таблице) видно, что варианта, отсекающая 1/4 численности частот, находится в интервале от 10 000 до 14 000.
А варианта, отсекающая 3/4 численности частот, находится в интервале от 27 000 до 45 000.
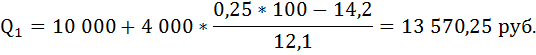
То есть у 25% населения душевой доход не превышает 13 570,25 руб.
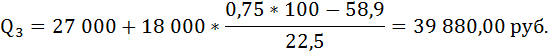
То есть у 25% населения душевой доход выше, чем 39 880,00 руб.
3) Децили делят ряд распределения признака по частоте на 10 равных частей.
Рассчитаем первый и девятый децили.
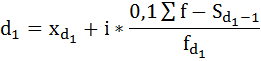
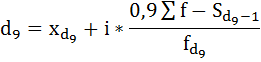
где
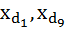 – начальные значения децильных интервалов, первого и девятого соответственно;
– начальные значения децильных интервалов, первого и девятого соответственно;
i – величина децильного интервала;
Σf – сумма частот ряда;
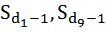 – накопленные частоты интервала, предшествующего децильному;
– накопленные частоты интервала, предшествующего децильному;
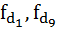 – частота децильного интервала.
– частота децильного интервала.
Определим интервалы, в которых находятся 1 и 9 дециль. По ряду накопленных частот (третья графа в таблице) видно, что варианта, отсекающая 1/10 численности частот находится в интервале от 7 000 до 10 000.
А варианта, отсекающая 9/10 численности частот находится в интервале от 45 000 и выше.
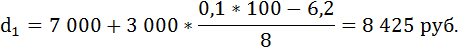
Следовательно, 10% самых бедных имеют среднедушевые доходы менее 8425 руб., а остальные 90% – выше этой суммы.
Последний интервал является открытым (не имеет верхней границы). Величину данного интервала принимают равной величине предыдущего интервала.
i = 45 000 – 27 000 = 18 000.
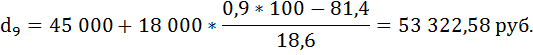
У 10% самого обеспеченного населения среднедушевые доходы превышают 53 322,58 руб.
2. Децильный коэффициент дифференциации доходов населения определяется по формуле:
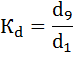
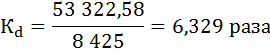
Минимальные доходы 10% самого богатого населения России в 2015 году превысили максимальные доходы 10% наименее обеспеченного населения в 6, 329 раз.
Источник данных: Россия в цифрах. 2016: Крат.стат.сб./Росстат-М.,2016 – 543 с.

- Что такое децильная формула?

Формула дециля (Содержание)
- формула
- Примеры
Что такое децильная формула?
Дециль, как звучит его название, является статистическим термином, который делит данные на десять определенных интервалов. Он в основном делит точки данных на набор данных в 10 равных частях в числовой строке. Этот тип ранжирования данных используется во многих областях, таких как финансы, экономика и т. Д. Мы должны помнить одну вещь: точки данных могут быть случайными, и мы должны поместить эти числа в строку сначала в числовой строке в порядке возрастания, а затем разделите их в децилях. Как только мы разделим данные, ранжирование по децилям может быть дано:
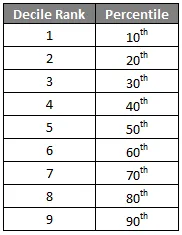
Как и другие инструменты квартиль и процентиль, дециль также является методом, который делит данные на более мелкие части, которые легче измерять, анализировать и понимать.
Формула для дециля:
Допустим, у нас есть набор данных с N точками данных:
X – (X1, X2, X3 ……… .. XN)
Формула для децилей дается:
D i = (N + 1) * i / 10
D1 = (N + 1) * 1/10
D2 = (N + 1) * 2/10
И так до
D9 = (N + 1) * 9/10
Из приведенной выше формулы видно, что D5 = (N + 1) * 5/10 = (N + 1) / 2, что является медианой. Таким образом, 5- й дециль представляет собой медиану.
Для сгруппированных данных:
Di = L + (h / f) * (i * (N / 10) – C)
Где:
я = 1, 2, 3, 4, 5…, 9
- L – нижняя граница группы
- h – ширина
- f – частота
- N – общее количество точек данных
- C – накопленная частота, предшествующая этому классу
Примеры формул дециля (с шаблоном Excel)
Давайте рассмотрим пример, чтобы лучше понять расчет децилей.
Вы можете скачать этот шаблон Excel с формулой дециля здесь – Шаблон Excel с формулой дециля
Децильная формула – пример № 1
Допустим, у нас есть наборы данных, которые содержат 39 точек данных. Рассчитайте децили.
Набор данных:

Решение:
Прежде всего, мы должны расположить это в порядке возрастания, т.е. от низшего к высшему.
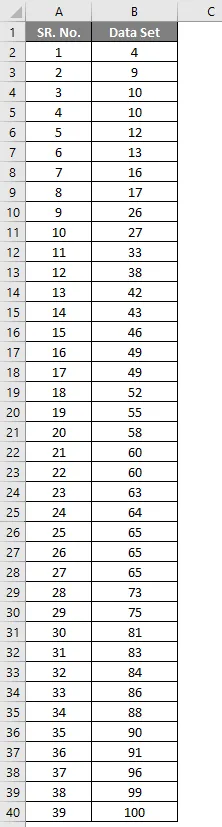
Дециль рассчитывается по формуле, приведенной ниже
D i = (N + 1) * i / 10
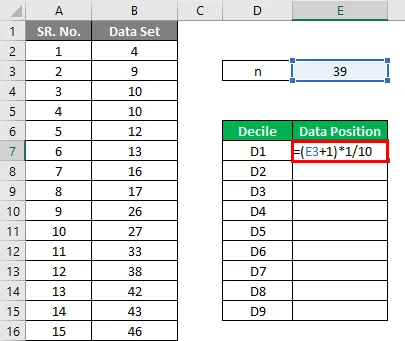
Результат будет таким, как указано ниже.
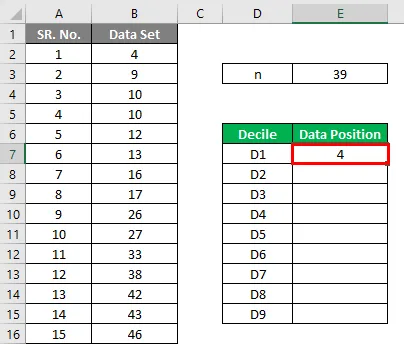
Аналогичным образом рассчитайте для всех точек.
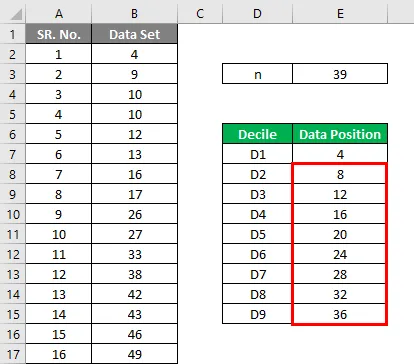
Сейчас
- D1 = (39 + 1) * 1/10 = 40/10 = 4- я точка данных = 10
- D2 = (39 + 1) * 2/10 = 80/10 = 8- я точка данных = 17
- D3 = (39 + 1) * 3/10 = 120/10 = 12- я точка данных = 38
- D4 = (39 + 1) * 4/10 = 160/10 = 16- я точка данных = 49
- D5 = (39 + 1) * 5/10 = 200/10 = 20- я точка данных = 58
- D6 = (39 + 1) * 6/10 = 240/10 = 24- я точка данных = 64
- D7 = (39 + 1) * 7/10 = 280/10 = 28- я точка данных = 73
- D8 = (39 + 1) * 8/10 = 320/10 = 32- я точка данных = 84
- D9 = (39 + 1) * 9/10 = 360/10 = 36- я точка данных = 91
Если вы видите набор данных, медиана этого набора: (n + 1) / 2 = 40/2 = 20- е значение, т.е. 58, это то же самое, что и D5.
Децильная формула – пример № 2
Предположим, ниже приведена таблица частот, которая у вас есть, для которой вам нужно рассчитать децили.
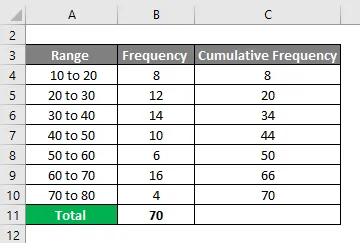
Из приведенного выше изображения, мы дали следующую информацию.
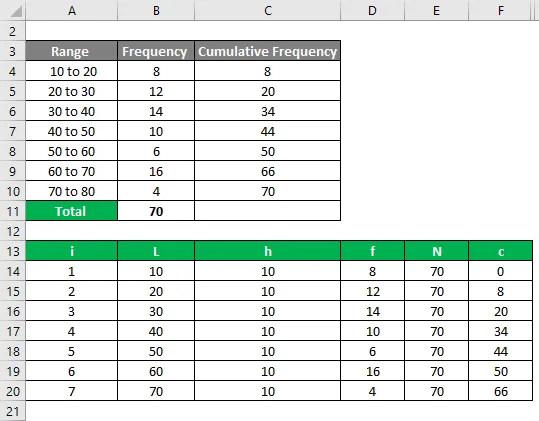
Дециль рассчитывается по формуле, приведенной ниже
Di = L + (h / f) * (I * (N / 10) – C)
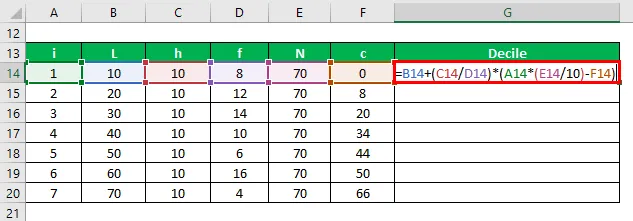
Результат будет как указано ниже
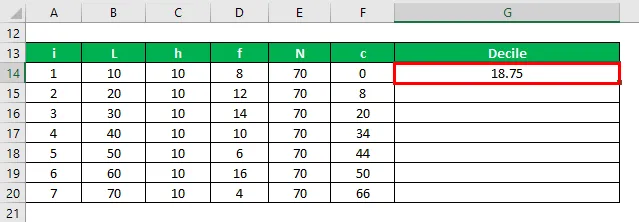
Аналогичным образом рассчитайте для других значений
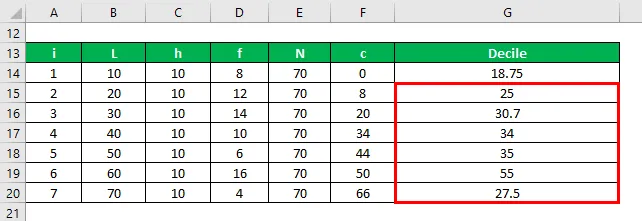
Di = L + (h / f) * (i * (N / 10) – C)
- D1 = 10 + (10/8) * (1 * (70/10) – 0) = 18, 75
- D2 = 20 + (10/12) * (2 * (70/10) – 8) = 25
- D3 = 30 + (10/14) * (3 * (70/10) – 20) = 30, 7
- D4 = 40 + (10/10) * (4 * (70/10) – 34) = 34
- D5 = 50 + (10/6) * (5 * (70/10) – 44) = 35
- D6 = 60 + (10/16) * (6 * (70/10) – 50) = 55
- D7 = 70 + (10/4) * (7 * (70/10) – 66) = 27, 5
объяснение
Мы знаем, что квартили делят данные на четыре равные группы, дециль делит данные на десять равных частей. Дециль, как обсуждалось выше, ранжирует набор данных от самого низкого до самого высокого. Это делается по шкале от 1 до 10, где каждое число в основном указывает на увеличение на 10 процентных пунктов. Таким образом, 1-й дециль имеет 10% точек данных под ним, D2 имеет 20% точек данных под ним и так далее. Таким образом, ранжирование по децилям является еще одним методом классификации данных, таких как квартиль или процентиль.
Актуальность и использование формулы дециля
Как обсуждалось выше, Decile помогает нам очень быстро разделить данные на десять частей и, в конечном итоге, облегчает понимание данных в этих частях. В финансах децили используются для анализа эффективности различных фондов путем их ранжирования и измерения производительности одного фонда по сравнению с аналогичными фондами. Например, вы являетесь аналитиком и оцениваете набор взаимных фондов, поэтому любой фонд, который занимает 6 место по шкале децилей, означает, что он входит в верхние 60% фондов. Таким образом, в основном мы можем использовать децили и разделять эти средства на наиболее эффективные и худшие за определенный период.
Рекомендуемые статьи
Это руководство по формуле децилей. Здесь мы обсудим, как рассчитать децили, а также практические примеры и загружаемый шаблон Excel. Вы также можете посмотреть следующие статьи, чтобы узнать больше –
- Калькулятор формулы Quartile Deviation
- ВВП на душу населения с примерами
- Как рассчитать процент прибыли с помощью формулы?
- Расчет чистого операционного дохода с помощью шаблона Excel

 ,
, ,
,