Как найти дефекты массы ядер

В уроке 2 «Изотопы элементов» из курса «Химия для чайников» рассмотрим что такое изотопы элементов и как правильно их обозначают; кроме того мы научимся определять массовое число, дефект массы и энергию связи ядра. Данный урок полностью опирается на основы химии, изложенные в первом уроке, в котором мы рассмотрели строение атома и атомного ядра, поэтому настоятельно вам рекомендую его изучить от корки до корки.

Что такое изотоп?

Хотя все атомы одного элемента имеют одинаковое число протонов, эти атомы могут отличаться числом имеющихся у них нейтронов. Такие различные атомы одного и того же элемента называются изотопами. Количество протонов, а также количество электронов у изотопа и исходного элемента совпадает. По этой причине в природе существует гораздо больше химических элементов, чем указано в таблице Менделеева, которая систематизирует элементы по числу протонов (порядковый номер).

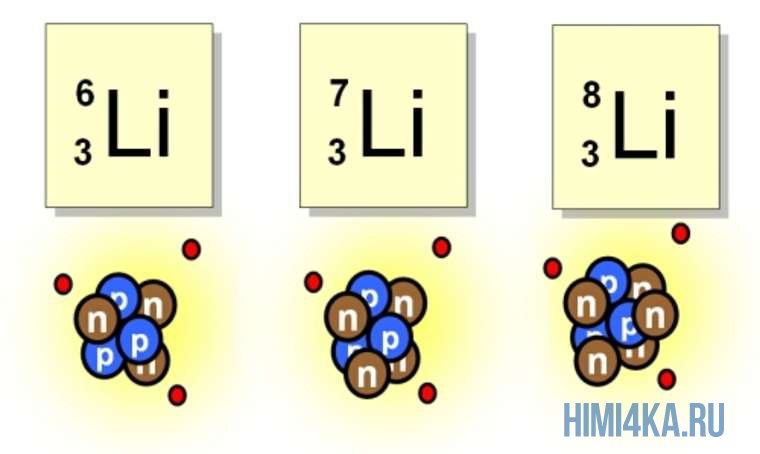
Например, все атомы Li имеют 3 протона, но в природе существуют изотопы, содержащие от 3 до 5 нейтронов. Для обозначения изотопа, слева от символа элемента подписывают нижним индексом его порядковый номер, а верхним — массовое число. Массовое число — это суммарное число нуклонов (протонов и нейтронов) в атомном ядре, численно близкое к атомной массе элемента. Нижний индекс, обозначающий порядковый номер элемента, указывать не обязательно, так как все атомы лития имеют в своем ядре по 3 протона. Также, обсуждая эти изотопы, можно пользоваться записью «литий-6» и «литий-8».

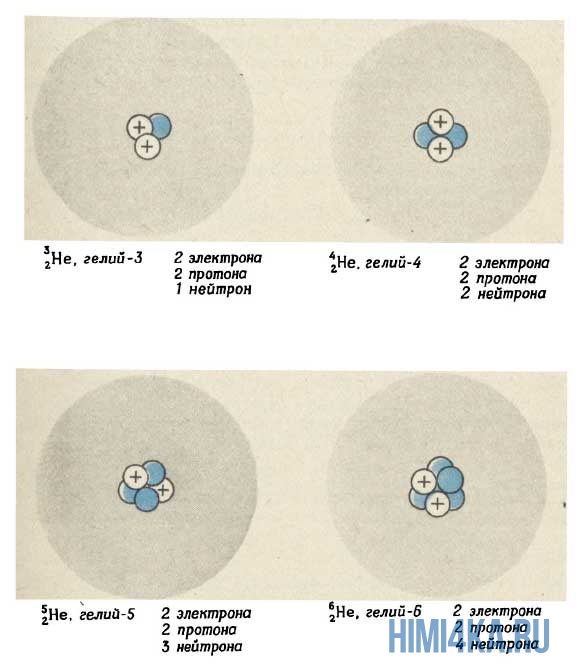
На рисунке выше изображен состав четырех изотопов гелия (Не). Все атомы гелия содержат два протона (и, следовательно, два электрона), но число нейтронов у них может быть разным. В природе большинство атомов гелия имеет два нейтрона (гелий-4) и реже одного раза на миллион встречаются атомы гелия с одним нейтроном (гелий-3). Другие изотопы гелия — гелий-5 , гелий-6 и гелий-8 (не показанный на рисунке) — неустойчивы и обнаруживаются лишь на очень непродолжительное время в ядерных реакциях (подробнее об этом будем говорить еще не скоро). Размеры ядер на рисунке очень сильно увеличены. Если бы они были такими, как это показано на рисунке, диаметр атома должен был достигать примерно 0,5 км.

Пример 1. Сколько протонов, нейтронов и электронов содержится в атоме урана-238? Запишите символ этого изотопа.

Решение: Порядковый номер урана (см. таблицу Менделеева) равен 92, а массовое число изотопа равно 238 (по условию). Следовательно, он содержит 92 протона, 92 электрона и 238 — 92 = 146 нейтронов. Его символ ²³⁸U.

Дефект массы и энергия связи ядра

Затронув тему изотопов, нельзя пройти мимо феномена дефект массы ядра. Когда из отдельных нуклонов образуется атомное ядро, часть их массы превращается в энергию. Другими словами, вот взяли вы щепотку протонов и нейтронов, хорошенько их смяли вместе, и получили ядро, но его масса будет меньше массы исходных компонентов. Это и есть дефект масс. Формула для расчета дефекта массы ядра:

• ∆m=(Zm_p+Nm_n)-M_я

где M_я – масса ядра, Z – число протонов в ядре, N – число нейтронов в ядре, m_p – масса протона, m_n – масса нейтрона.

Если к атому подвести энергию (которая эквивалентна дефекту масс), то можно разделить его ядро обратно на нуклоны. Эта энергия носит название энергия связи ядра. Формула для расчета энергии связи ядра:

• ∆E_св=∆mc²

где с — скорость света, ∆m — дефект массы ядра

Проверьте себя, как вы усвоили понятия дефект массы и энергия связи ядра, самостоятельно решив задачу пользуясь формулами выше.

Пример 2. Если образовать атом углерода-12 из субатомных частиц, какое значение будет иметь дефект масс? 

Теперь нам известно, что каждый изотоп элемента характеризуется порядковым номером (суммарным числом протонов), массовым числом (суммарным числом протонов и нейтронов) и атомной массой (массой атома, выраженной в атомных единицах массы). Поскольку дефект массы при образовании атома очень мал, массовое число обычно совпадает с атомной массой изотопа, округленной до ближайшего целого числа. (Например, атомная масса хлора-37 равна 36,966, что после округления дает 37.) Если в природе встречается несколько изотопов одного элемента, то экспериментально наблюдаемая атомная масса (естественная атомная масса) равна средневзвешенному значению атомных масс отдельных изотопов. Это средневзвешенное значение определяется соответственно относительному содержанию изотопов в природе. Хлор существует в природе в виде смеси из 75,53% хлора-35 (атомная масса 34,97 а.е.м.) и 24,47% хлора-37 (36,97 а.е.м.), поэтому средневзвешенное значение масс этих изотопов равно

• (0,7553·34,97 а.е.м.) + (0,2447·36,97 а.е.м.) = 35,46 а.е.м.

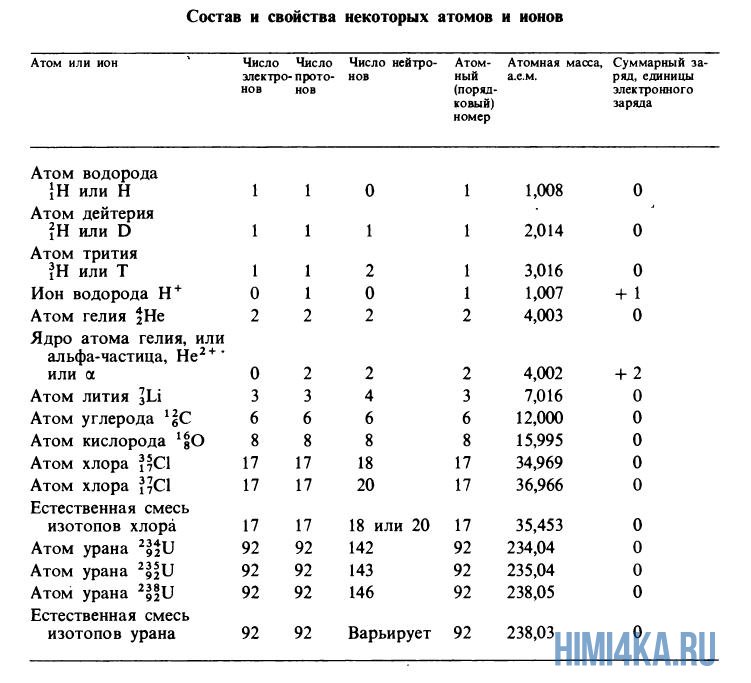
Атомные массы, указанные в таблице Менделеева представляют собой во всех случаях средневзвешенные значения атомных масс изотопов, встречающихся в природе, и именно этими значениями мы будем пользоваться в дальнейшем, за исключением тех случаев, когда будет обсуждаться какой-нибудь конкретный изотоп. Все изотопы одного элемента в химическом отношении ведут себя практически одинаково. На рисунке ниже изображены состав и свойства некоторые атомов, ионов и изотопов элементов.

Пример 3. Магний (Mg) в основном состоит из трех естественных изотопов: 78,70% всех атомов магния имеют атомную массу 23,985 а.е.м., 10,13% — 24,986 а.е.м. и 11,17% — 25,983 а.е.м. Сколько протонов и нейтронов содержится в каждом из этих трех изотопов? Чему равно средневзвешенное значение их атомных масс?

Решение: Все изотопы магния содержат по 12 протонов. Изотоп с атомной массой 23,985 а.е.м. имеет массовое число 24 (суммарное число протонов и нейтронов), следовательно, он имеет 24 — 12 = 12 нейтронов. Символ этого изотопа ²⁴Mg. Аналогично находим, что изотоп с атомным весом 24,986 а.е.м. имеет массовое число 25, содержит 13 нейтронов и имеет символ ²⁵Mg. Третий изотоп (25,983 а.е.м.) имеет массовое число 26, содержит 14 нейтронов и имеет символ ²⁶Mg. Средняя атомная масса магния находится следующим образом:

• (0,7870·23,985 а.е.м.) + (0,1013·24,986 а.е.м.) + (0,1117·25,983 а.е.м.) = 24,31 а.е.м.

Надеюсь урок 2 «Изотопы элементов» помог вам понять что из себя представляют изотопы. Если у вас возникли вопросы, пишите их в комментарии.

Дефе́кт ма́ссы (англ. mass defect) ΔM — разность между суммой масс отдельных составляющих какой-либо связанной физической системы взаимодействующих объектов (тел, частиц), находящихся в свободном состоянии, и массой само́й этой системы. В таком определении знак дефекта масс положителен; иногда дефект масс определяют как разность между массой системы и суммой масс компонент, в этом случае знак отрицателен^[1]. С точностью до коэффициента c² дефект массы равен энергии связи E_св системы:

Так, дефект масс атомного ядра — связанной системы из Z протонов и N нейтронов — равен

где m_p и m_n — массы свободных протона и нейтрона, соответственно,

M(Z, N) — масса ядра.

Например, масса M_d дейтрона (ядра атома дейтерия, тяжёлого изотопа водорода ²H), состоящего из одного протона и одного нейтрона, равна 2,013 553 а.е.м.^[2] (1875,613 МэВ/c² в энергетическом эквиваленте)^[3]. Масса свободного протона равна 1,007 276 а.е.м.^[4] (938,272 МэВ/c²)^[5], нейтрона — 1,008 665 а.е.м.^[6] (939,565 МэВ/c²)^[7]. Дефект масс будет равен

ΔM_d = m_p + m_n − M_d = 0,002 388 а.е.м. = 2,224 МэВ/c².

В результате слияния одного моля протонов (масса 1,007 276 г) и одного моля нейтронов (масса 1,008 665 г) образуется 1 моль дейтронов массой 2,013 553 г, что на 0,002 388 г меньше, чем сумма масс исходных компонентов. Указанный дефект массы выделится как энергия, равная энергии связи одного дейтрона (E_св(d) = 2,224 МэВ), умноженной на число Авогадро (количество дейтронов в одном моле): 2,224 МэВ · N_A = 214,6 ГДж (эквивалентно теплоте сгорания 5 тонн бензина).

Для атомных ядер понятие дефекта массы тесно связано с понятием упаковочного коэффициента (упаковочного множителя) f или удельной энергии связи ε_св, т.е. дефекта массы или энергии связи, приходящихся на один нуклон:

f = ΔM / A,

ε_св = E_св / A,

где A = Z + N — массовое число, общее количество нуклонов (протонов и нейтронов) в ядре. Удельная энергия связи и упаковочный коэффициент характеризуют устойчивость ядра.

Можно определить также относительный дефект массы системы — безразмерную величину, представляющую собой отношение дефекта массы ΔM к сумме масс M_i компонентов системы: Δμ = ΔM/ΣM_i. Типичные значения относительного дефекта массы для атомных ядер средней массы составляют 0,008—0,009, для атомов (без учёта дефекта массы ядра) ~10⁻⁸…10⁻⁶. Астрономические объекты могут иметь существенный гравитационный дефект масс. Так, для звезды, близкой по массе к Солнцу, относительный гравитационный дефект массы составляет ~10⁻⁶, для белого карлика ~10⁻³…10⁻⁴, для нейтронной звезды ~10⁻¹. Наибольший относительный дефект масс среди гравитационно связанных объектов характерен для чёрных дыр; он может достигать десятков процентов^[1]. Так, при слиянии двух чёрных дыр суммарной массой 65 M_⊙, которое вызвало гравитационно-волновой всплеск GW150914, зафиксированный 14 сентября 2015 года, образовалась чёрная дыра массой 62 M_⊙; дефект массы в 3 M_⊙ был излучён в форме гравитационных волн^[8].

Дефект массы всегда возникает в результате превращения энергии связи в энергию излучения (электромагнитного, нейтринного, гравитационного), покидающего образовавшуюся связанную систему^[1].

См. также[править | править код]

• Эквивалентность массы и энергии

Примечания[править | править код]

Ссылки[править | править код]

• Астронет. Масса и энергия связи ядра
• Сивухин Д. В. Общий курс физики, т.5, ч. 2

Устойчивость атомных ядер основывается на действии неких колоссальных многократно превосходящих силы кулоновского отталкивания протонов сил, удерживающих нейтроны и протоны внутри ядра.

Приведенные выше силы, удерживающие нуклоны в ядре, носят название ядерных. Они представляют собой проявление самого интенсивного из всех известных в физике видов взаимодействия, то есть, так называемого сильного взаимодействия.

Ядерные силы превышают электростатические силы приблизительно в сотню раз и на десятки порядков обгоняют силы гравитационного взаимодействия нуклонов. Короткодействующий характер ядерных сил представляет собой их крайне важную особенность. Опыты Резерфорда, направленные на изучение рассеяния α-частиц показали, что обсуждаемый тип сил заметно проявляется только на расстояниях близких к размерам ядра, то есть на расстоянии в 10–12–10–13 см. На более протяженных расстояниях становится наблюдаемым действие сравнительно медленно спадающих кулоновских сил.

Основываясь на опытных данных, можно заявить, что протоны в ядре в отношении сильного взаимодействия ведут себя ровно так же, как и нейтроны. Из этого факта исходит вывод о том, что ядерные силы не имеют зависимости от наличия или отсутствия у частиц электрического заряда.

Дефект массы

Энергия связи каждого ядра может быть определена при помощи точного измерения его массы. В наше время физики обладают знаниями, позволяющими им измерять массы частиц, будь то электроны, протоны, нейтроны, ядра или что-то подобное, с чрезвычайно высокой точностью.

Благодаря дефекту массы, используя формулу Эйнштейна E=mc2, можно высчитать энергию, выделившуюся при образовании приведенного ядра, то есть энергию связи ядра Eсв:

Eсв=∆Mc2=Zmp+Nmn-Mяс  .

Данная энергия выделяется в процессе образования ядра в виде излучения γ-квантов.

Как пример высчитаем энергию связи ядра гелия He24, в чей состав входят пара протонов и два нейтрона. Масса ядра гелия Mя=4,00260 а. е. м. Сумма масс двух протонов с двумя нейтронами эквивалентна 2mp+2mn=4, 03298 а. е. м. Таким образом, дефект массы ядра гелия равняется ΔM=0,03038 а. е. м. Процесс расчета по формуле Eсв ΔMc2 приводит нас к следующему значению энергии связи ядра He24 : Eсв=28,3 МэВ. Это колоссальная величина. Образование всего 1 г гелия приводит к выделению энергии приближенной к 13,6 эВ. Приблизительно такая же энергия излучается в процессе сгорания практически целого вагона с каменным углем. Энергия связи ядра на много порядков превосходит энергию связи электронов с атомом. Для атома водорода H11 энергия ионизации равняется 13,6 эВ.

В таблицах обычно указана удельная энергия связи, то есть, энергия связи на один нуклон. Для ядра гелия удельная энергия связи примерно равна 7,1 МэВ/нуклон. На рисунке 6.6.1 проиллюстрирован график зависимости удельной энергии связи от массового числа A. Как мы можем наблюдать на графике, удельная энергия связи нуклонов у различных атомных ядер разнится. В случае легких ядер удельная энергия связи изначально резко увеличивается от 1,1 МэВ/нуклон у дейтерия до7,1 МэВ/нуклон у гелия He24. После ряда скачкообразных изменений удельная энергия медленно повышается до максимальной величины 8,7 МэВ/нуклон у элементов с массовым числом A=50–60, а затем все так же медленно падает у тяжелых элементов. К примеру, у урана U92238 она равняется 7,6 МэВ/нуклон.

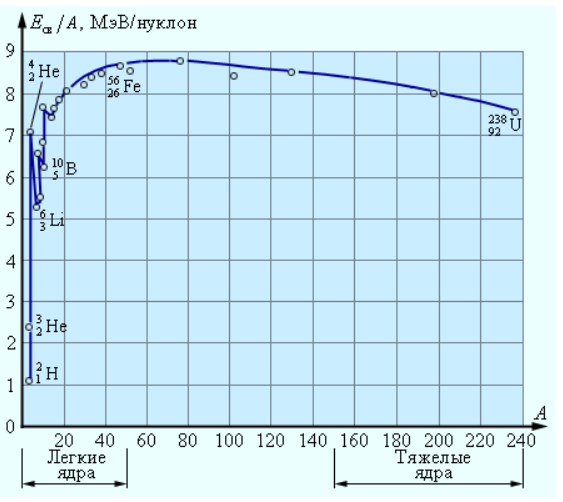
Рисунок 6.6.1. Удельная энергия связи ядер.

Понижение удельной энергии связи в процессе перехода к тяжелым элементам основывается на повышении энергии кулоновского отталкивания протонов. В тяжелых ядрах связь между нуклонами слабеет, вследствие чего структура ядер теряет значительную часть своей прочности. Числа протонов Z и нейтронов N выходят эквивалентными в случае стабильных легких ядер, когда роль кулоновского взаимодействия мала, в качестве примера можно привести He24, Li36, B510. Под воздействием ядерных сил формируются протон-нейтронные пары. Однако тяжелым ядрам, содержащим немалое число протонов, по причине увеличения энергии кулоновского отталкивания для обеспечения устойчивости необходимы дополнительные нейтроны. На рисунке 6.6.2 изображена диаграмма, демонстрирующая количество протонов и нейтронов в стабильных ядрах. У ядер, идущих следом за висмутом (Z>83), по причине большого числа протонов полная стабильность оказывается принципиально невозможной.

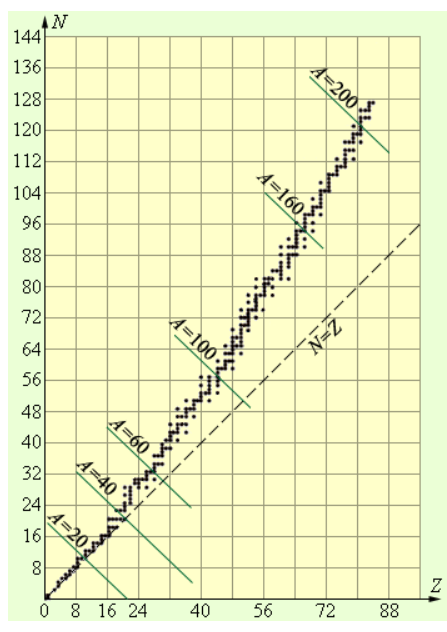
Рисунок 6.6.2. Количество протонов и нейтронов в стабильных ядрах.

Ядерные превращения

На рисунке 6.6.1 можно увидеть, что с энергетической точки зрения большей устойчивостью обладают ядра элементов из средней части системы Менделеева. Данный факт означает, что существуют две возможности получения положительного энергетического выхода в процессе ядерных превращений:

1. Деление тяжелых ядер на более легкие.
2. Слияние легких ядер в более тяжелые.

Оба приведенных процесса выделяют колоссальное количество энергии. В условиях современной физики, как деление тяжелых ядер на более легкие, так и слияние легких в тяжелые осуществлены на практике: реакции деления и термоядерные реакции.

Произведем некоторые оценки. Пускай, к примеру, ядро урана U92238 делится на два эквивалентных друг другу ядра с массовыми числами 119. У приведенных ядер, как видно из рисунка 6.6.1, удельная энергия связи около 8,5 МэВ/нуклон. Удельная энергия связи ядра урана 7,6 МэВ/нуклон. Соответственно, при делении ядра урана излучается энергия, равняющаяся 0,9 МэВ/нуклон или больше 200МэВ на один атом урана.

Исследуем следующий пример. Пускай в неких условиях два ядра дейтерия H12 формируют одно ядро гелия He24. Удельная энергия связи ядер дейтерия равняется значению 1,1 МэВ/нуклон, а удельная энергия связи ядра гелия 7,1 МэВ/нуклон. Соответственно, в процессе синтеза единого ядра гелия из двух ядер дейтерия произведется энергия, эквивалентная 6 МэВ/нуклон или 24 МэВ на атом гелия.

Стоит отметить, что в сравнении с делением тяжелых элементов синтез легких провоцирует излучение энергии на один нуклон большее примерно в шесть раз.

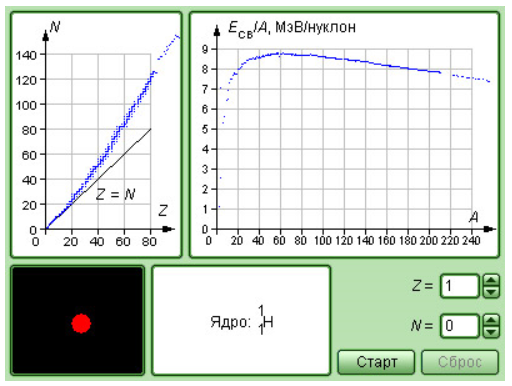
Рисунок 6.6.3. Модель энергии связи ядер.