Груз массой 45 кг с
помощью динамометра тянут равномерно по горизонтальной плоскости. Определите
деформацию пружины динамометра, если ее жесткость равна 7,8 кH/м, сила упругости направлена под углом 30 градусов к горизонту,
а коэффициент трения скольжения груза по поверхности равен 0,26.
Решение.
Деформация пружины x связана
с ее жесткостью l и модулем силы упругости F
соотношением F = kx (закон
Гука), откуда x = F/k. Силу F можно найти с помощью
второго закона Ньютона.
На груз действуют сила
тяжести mg, сила упругости пружины F,
сила нормальной реакции опоры N и сила трения Fтр . По второму закону
Ньютона получаем.
Запишем теперь его в
проекциях на координатные оси OX
и OY.
Кроме того, Fтр = mN. Решаем полученную систему уравнений и находим F.
Ответ: x = 15 мм.
Источник: Подготовка к тестированию по физике. Шепелевич. В. Г.
Сила упругости. Закон Гука
- Виды деформаций
- Закон Гука
- Измерение силы с помощью динамометра
- Задачи
п.1. Виды деформаций
Под действием силы все тело или отдельные его части приходят в движение.
При движении одних частей тела относительно других происходит изменение формы и размеров.
Деформация – это изменение взаимного положения частиц тела, связанное с их перемещением друг относительно друга под действием приложенной силы, при котором тело изменяет свою форму и размеры.
 |
К простейшим видам деформации относятся:
|
Различают упругие (обратимые) и неупругие (необратимые) деформации.
Деформация является упругой, если, после прекращения действия вызвавших её сил, тело полностью восстанавливает свою форму и размеры.
Например, если немного согнуть школьную линейку, растянуть пружину или надавить на воздушный шарик, после прекращения действия силы линейка выпрямится, пружина сожмется, и шарик опять станет круглым. Эти деформации – упругие, они обратимы.
Если же приложенная сила окажется слишком большой, линейка сломается, пружина так и останется растянутой, а шарик лопнет. Эти деформации – неупругие, они необратимы.
Все здания и сооружения вокруг нас рассчитываются так, чтобы их «нагруженные» части испытывали только упругие деформации; это обеспечивает надёжность и долговечность конструкций.
Восстановление формы и размера тела при упругой деформации происходит под действием силы упругости, которая возникает благодаря межатомным и межмолекулярным взаимодействиям.
Сила упругости уравновешивает действие внешней силы и направлена в сторону, противоположную смещению частиц.
Например (см. рисунок):
- при растяжении сила упругости стремится сжать тело;
- при сжатии сила упругости стремится распрямить тело.
п.2. Закон Гука
 |
Проведем серию опытов с пружиной. Пусть при действии на пружину силой (F) мы получаем деформацию (удлинение) (Delta l). При этом в пружине возникают силы упругости, стремящиеся вернуть её в исходное положение, (overrightarrow{F_{text{упр}}}=-overrightarrow{F}). Если приложенную силу увеличить в 2 раза, то деформация также увеличится в 2 раза. Увеличение силы в 3 раза приводит к росту деформации в 3 раза и т.д. Опыты показывают, что во всех случаях деформация будет прямо пропорциональна приложенной силе. |
Следовательно, сила упругости также будет прямо пропорциональна деформации: $$ F_{text{упр}}simDelta l $$
Для каждого тела отношение силы упругости к величине деформации при малых упругих деформациях является постоянной величиной $$ k=frac{F_{text{упр}}}{Delta l}=const $$ которая называется коэффициентом упругости или жесткостью.
Жесткость тела зависит от формы, размеров и материала, из которого оно изготовлено.
В системе СИ жесткость измеряется в ньютонах на метр, (frac{text{Н}}{text{м}}).
Закон Гука
Сила упругости, возникающая во время упругой деформации тела, прямо пропорциональна удлинению (величине деформации): $$ F_{text{упр}}=kDelta l $$ Сила упругости всегда направлена противоположно деформации.
п.3. Измерение силы с помощью динамометра
 |
Динамометр– это прибор для измерения силы.
Простейший пружинный динамометр состоит из пружины с крючком и дощечки со шкалой (проградуированной в ньютонах). |
В технике используются динамометры более сложных конструкций.
Но принцип действия – использование закона Гука – во многих из них сохраняется.
п.4. Задачи
Задача 1. Резиновая лента удлинилась на 10 см под действием силы 50 Н. Какова жесткость ленты?
Дано:
(Delta l=10 text{см}=0,1 text{м})
(F=50 text{Н})
__________________
(k-?)
Жесткость ленты $$ k=frac{F}{Delta l} $$ $$ k=frac{50}{0,1}=500 left(frac{text{Н}}{text{м}}right) $$ Ответ: 500 Н/м
Задача 2. Под действием силы 300 Н пружина динамометра удлинилась на 0,6 см. Каким будет удлинение пружины под действием силы 700 Н? Ответ запишите в миллиметрах.
Дано:
(F_1=300 text{Н})
(Delta l_1=0,6 text{см}=6cdot 10^{-3} text{м})
(F_2=700 text{Н})
__________________
(Delta l_2-?)
Жесткость пружины begin{gather*} k=frac{F_1}{Delta l_1}=frac{F_2}{Delta l_2}Rightarrow Delta l_2=frac{F_2}{F_1}Delta l_1\[6pt] Delta l_2=frac{700}{300}cdot 6cdot 10^{-3}=14cdot 10^{-3} (text{м})=14 (text{мм}) end{gather*} Ответ: 14 мм
Задача 3. Пружина без груза имеет длину 30 см и коэффициент жесткости 20 Н/м. Найдите длину растянутой пружины, если на нее действует сила 5 Н. Ответ запишите в сантиметрах.
Дано:
(l_0=30 text{cм}=0,3 text{м})
(k=20 text{Н/м})
(F=5 text{Н})
__________________
(l-?)
Удлинение пружины под действием силы: $$ Delta l=frac Fk $$ Длина растянутой пружины begin{gather*} l=l_0+Delta l=l_0+frac Fk\[6pt] l=0,3+frac{5}{20}=0,3+0,25=0,55 (text{м})=55 (text{cм}) end{gather*} Ответ: 55 cм
Задача 4*. Грузовик взял на буксир легковой автомобиль массой 1,5 т с помощью троса. Двигаясь равноускоренно, они проехали путь 600 м за 50 с. На сколько миллиметров удлинился во время движения трос, если его жесткость равна (3cdot 10^5 text{Н/м})?
Дано:
(m=1,5 text{т}=1500 text{кг})
(s=600 text{м})
(t=50 text{c})
(v_0=0)
(k=3cdot 10^5 text{Н/м})
__________________
(Delta l-?)
Сила упругости, возникающая в тросе, уравновешивает силу тяги, передвигающую автомобиль с постоянным ускорением: $$ F_{text{упр}}=kDelta l=F_{text{т}}=ma $$ Перемещение из состояния покоя $$ s=frac{at^2}{2}Rightarrow a=frac{2s}{t^2} $$ Получаем: begin{gather*} kDelta l=mcdotfrac{2s}{t^2}Rightarrow Delta l=frac mkcdot frac{2s}{t^2}\[6pt] Delta l=frac{1500}{3cdot 10^5}cdot frac{2cdot 600}{50^2}=2,4cdot 10^{-3} (text{м})=2,4 (text{мм}) end{gather*} Ответ: 2,4 мм
Конспект по физике для 7 класса «Закон Гука. Динамометр». ВЫ УЗНАЕТЕ: Как формулируется закон Гука. Что такое коэффициент упругости пружины. Каким прибором измеряется сила. ВСПОМНИТЕ: Что такое сила? Каковы единицы силы? Что такое сила тяжести? Как рассчитать силу тяжести? Что такое сила упругости?
Конспекты по физике Учебник физики Тесты по физике
Закон Гука. Динамометр
Английский физик Роберт Гук, современник И. Ньютона, в 1660 г. экспериментально установил, как зависит сила упругости от деформации.
ЗАКОН ГУКА
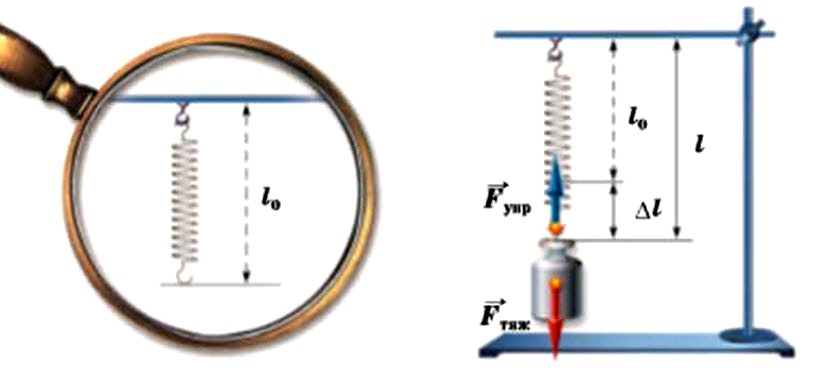
Проведём следующий опыт. К штативу подвесим пружину и измерим её длину. Пусть длина нерастянутой пружины равна l0. Если теперь к ней подвесить грузик, то пружина растянется и её длина станет равна l. Растяжение пружины равно Δl = l – l0. Чем тяжелее грузик, тем сильнее растягивается пружина и тем больше значение Δl.
Каждый раз при подвешивании груза пружина растягивается до определённого состояния, после чего движение груза прекращается и система приходит в состояние равновесия. Это означает, что сила тяжести, действующая на груз, компенсируется силой упругости, возникающей в пружине. Сила тяжести определяется по формуле Fтяж = mg. Следовательно, чем больше масса груза, тем больше значение силы тяжести, действующей на него, и соответственно больше значение силы упругости, уравновешивающей её. Тщательные измерения в данном опыте показывают, что растяжение пружины прямо пропорционально значению силы упругости.
Опыт подтверждает закон, названный в честь учёного, открывшего его,
законом Гука
: модуль силы упругости при растяжении (или сжатии) тела прямо пропорционален изменению длины тела.
Коэффициент пропорциональности в законе Гука называют коэффициентом упругости тела (стержня, пружины и т. п.). Он зависит от формы и размеров тела, а также от материала, из которого оно изготовлено. Коэффициент упругости в СИ выражается в ньютонах на метр (Н/м).
УПРУГАЯ И ПЛАСТИЧЕСКАЯ ДЕФОРМАЦИИ
Деформации, которые полностью исчезают, как только прекращается действие деформирующей силы, называют упругими. Деформации, которые не исчезают после прекращения действия деформирующей силы, называют пластическими. Если пружину растянуть, а затем отпустить, то она примет первоначальную форму. Но эту же пружину можно растянуть настолько, что после того, как её отпустят, она так и останется растянутой. Закон Гука справедлив только для упругой деформации, для пластических деформаций он не выполняется.
ДИНАМОМЕТР
Закон Гука лежит в основе действия прибора для измерения силы — динамометра (от греч. dinamis — сила и metron — мера). Принцип действия пружинного динамометра основан на сравнении любой силы с силой упругости пружины. На практике используют динамометры самого разного тина.
ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ЗАКОНА ГУКА
Простейший пружинный динамометр (динамометр Бакушинского) состоит из пружины с двумя крючками, укреплённой на дощечке. Дощечка снабжена шкалой, а к нижнему концу пружины прикреплён указатель.
Построим график зависимости силы упругости от деформации пружины динамометра.
Для этого будем последовательно подвешивать к динамометру грузики определённой массы и измерять соответствующие значения силы упругости и растяжения пружины. Так как сила тяжести, действующая на тело массой 1 кг, равна 9,8 Н, то сила, равная 1 Н, будет действовать на тело, которое в 9,8 раза легче. Масса этого тела 102 г. Под влиянием силы тяжести, действующей на груз, пружина динамометра растягивается на Δl1 = 2,5 см. Нанесём на график соответствующую точку (зелёным цветом). Подвесим к крючку ещё один такой же груз и повторим описанный опыт. Суммарная масса груза в этом случае равна 204 г, а деформация — Δl2 = 5 см. Нанесём соответствующую точку на координатную плоскость. Проделаем аналогичные действия для трёх грузов. Можно увидеть, что все три точки лежат на одной прямой.
Как по графику определить значение коэффициента упругости пружины? По закону Гука k = Fупр / Δl. Если взять любую точку, лежащую на прямой, и определить её координаты, то на оси абсцисс мы получим значение Δl, а по оси ординат — значение Fупр. Поделив одно значение на другое, получим искомую величину.
Повторив описанный опыт с другой пружиной, получим график другой прямой (синего цвета), которая отличается от предыдущей углом наклона к оси абсцисс. Чем больше коэффициент упругости пружины, тем угол наклона больше.
Вы смотрели Конспект по физике для 7 класса «Закон Гука. Динамометр»: Как формулируется закон Гука. Что такое коэффициент упругости пружины. Каким прибором измеряется сила. Что такое сила? Каковы единицы силы? Что такое сила тяжести? Как рассчитать силу тяжести? Что такое сила упругости?
Вернуться к Списку конспектов по физике (В оглавление).
Афонин А., Капшай В., Капшай М., Шолох В. Что покажет динамометр? //Квант. — 1992. — № 2. — С. 47-51.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
Задачи о показаниях измерительных приборов часто кажутся простыми. Дело, вероятно, в том, что, когда вводится новая физическая величина, всегда сразу же дается рецепт, с помощью какого устройства и как именно следует эту величину измерять. В дальнейшем, считая вопрос исчерпанным, к тонкостям процесса измерения возвращаются редко.
Это относится и к измерениям с помощью простейших приборов, например — пружинного динамометра.
Хорошо известно, что если к обоим концам динамометра приложены одинаковые по модулю силы F0, то динамометр покажет именно это значение силы. При этом пружина динамометра растянется, и ее абсолютное удлинение Δl0 определится соотношением 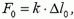
Задача 1. 3а один конец пружинного динамометра тянут с силой F1 = 50 H, за другой — с силой F2 = 70 H. Что покажет динамометр?
На вопрос этой задачи отвечают обычно, что динамометр покажет либо F2, либо F1. Встречаются также ответы F2 + F1 и F2 – F1. На самом деле ни один из этих ответов не является верным. А что же верно? Об этом — чуть позже.
С помощью пружинного динамометра можно также определить массу m тела, поскольку нетрудно измерить силу тяжести, равную m·g. Вроде бы тоже все просто. Однако…
Задача 2. Как определить массу пружины динамометра, имея в своем распоряжении только этот динамометр?
Оказывается, обе сформулированные задачи тесно связаны друг с другом, хотя на первый взгляд это может показаться и странным. Скоро вы в этом убедитесь. Но прежде рассмотрим еще одну, несколько более простую задачу и решим ее.
Задача 3. За один конец динамометра тянут с силой, равной F. Что покажет динамометр?
Для начала попытаемся четко понять, что означает этот вопрос.
Ясно, что, глядя на динамометр, мы можем сказать только, растянулась его пружина или нет и если растянулась, то насколько. Мы можем также измерить величину абсолютного удлинения пружины в единицах длины, например в сантиметрах. Определить же значение силы можно лишь после предварительной градуировки шкалы динамометра в единицах силы, например в ньютонах, с помощью закона Гука.
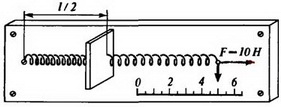
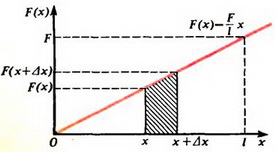
Очень важными являются также следующие два условия: 1) во время измерения динамометр покоится в некоторой инерциальной системе отсчета; 2) пружина динамометра растягивается равномерно по всей длине. Проще всего эти два условия обеспечиваются равенством сил, действующих на оба конца пружины динамометра. В важности второго условия нетрудно убедиться с помощью следующего рассуждения. Допустим, мы закрепили одну половину пружины (соединенную со шкалой) так, что она вообще не будет деформироваться и перемещаться, а за свободный конец второй половины пружины тянем с силой F (рис. 1). Что в этом случае покажет динамометр? Очевидно, половина пружины под действием силы F удлинится на столько же, на сколько удлинится вся пружина под действием силы F/2. Таким образом, стрелка динамометра покажет силу F/2.
Рис. 1.
Итак, если сила натяжения постоянна вдоль пружины и равна F, динамометр покажет F. Если же сила натяжения равна нулю на одной половине пружины и F на другой, динамометр покажет F/2. А что если сила натяжения будет изменяться вдоль пружины еще каким-нибудь, более сложным образом? Какой будет суммарная деформация всей пружины (ведь именно она «ответственна» за показание стрелки динамометра)? Как, наконец, создать неравномерную силу натяжения, не закрепляя части пружины?
Оказывается, в условиях задачи 3 реализуется именно такая ситуация. Так что же происходит, если сила F действует только на один конец динамометра?
Во-первых, динамометр движется и движется равноускоренно (других сил нет). Его ускорение равно 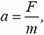
Во-вторых, различные участки пружины будут деформироваться по-разному, поскольку сила натяжения будет изменяться вдоль пружины. Определим эту силу, считая, что пружина расположена горизонтально и сила F действует на ее правый конец.
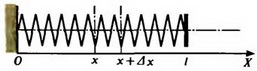
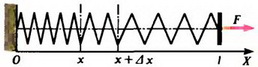
Для дальнейшего удобства «пронумеруем» точки (витки) пружины с помощью непрерывно изменяющейся величины x следующим образом (рис. 2).
а
б
Рис. 2.
Вместо того, например, чтобы говорить «точка пружины, которая находится на расстоянии x от левого конца пружины в недеформированном состоянии», будем говорить кратко «точка x». Очевидно, что x изменяется в пределах от 0 до l, где l — длина недеформированной пружины. Силу натяжения в точке x обозначим F(x); при этом понятно, что F(0) = 0 и F(l) = F. Заметим, что масса участка пружины от точки 0 до точки x равна 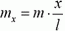
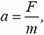
Эта сила линейно зависит от параметра точки пружины x (рис. 3).
Рис. 3.
Теперь задача сводится к тому, чтобы, зная силу натяжения в каждой точке пружины, определить деформацию всей пружины. Для этого поступим так. Выделим малый (по сравнению с l) участок недеформированной пружины между точками x и x + Δх (рис. 2, а). Длину этого участка Δx будем обозначать также b. На левый конец этого участка действует сила натяжения 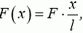
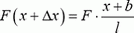
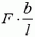
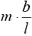
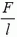
Так как силы 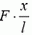
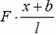
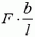
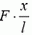
Если бы на оба конца пружины действовала сила F0, в каждой точке x сила натяжения также равнялась бы F0, и пружина была бы растянута равномерно. Абсолютное удлинение всей пружины было бы равно
где k — жесткость пружины, а относительное удлинение —
При этом относительное удлинение любого участка было бы таким же.
Например, для участка длиной b
В случае же, когда сила натяжения зависит от x, относительное удлинение участка длиной b будет другим:
Это означает, что участки возле правого конца пружины растягиваются больше, возле левого — меньше (см. рис. 2, б и рис. 4).
Рис. 4.
Абсолютное удлинение этого участка есть
Заметим, что величина абсолютного удлинения участка Δx, с точностью до постоянного коэффициента 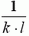
Для того чтобы найти абсолютное удлинение всей пружины, разделим ее на n кусков малой длины точками x1 = 0, x2, …, xn, xn+1 = l. Будем считать, что
(n велико). Абсолютное удлинение i-гo участка выразится формулой
а абсолютное удлинение всей пружины —
Устремим теперь длину каждого участка к нулю (а их число к бесконечности). Тогда получим
Ясно, что эта сумма, с точностью до коэффициента , равна сумме площадей трапеций, подобных заштрихованной на рисунке 3, а ее предел — площади прямоугольного треугольника с катетами F и l. Следовательно,
Для тех, кто знаком с понятием определенного интеграла, запишем
Итак, абсолютное удлинение Δl всей пружины, на один конец которой действует сила F, найдено. Можно сказать, что это удлинение будет таким же, если на оба конца динамометра действует так называемая эффективная сила 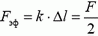
Разобравшись с задачей 3, вернемся к задаче 1. Если на правый конец динамометра действует сила F1, а на левый F2, то пружина движется с ускорением
Для участка пружины от 0 до x имеем
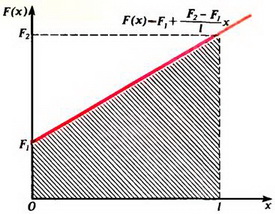
следовательно, сила натяжения в точке x равна
Абсолютное удлинение можно найти с помощью тех же рассуждений, что и раньше. Так, с одной стороны, абсолютное удлинение пружины равно площади заштрихованной на рисунке 5 трапеции (деленной на k·l).
Рис. 5.
С другой стороны, его можно выразить в виде интеграла:
Таким образом, динамометр, на концы которого действуют различные силы F1 и F2 растягивается так, как если бы на оба его конца действовала одна и та же сила 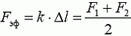
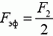
Теперь рассмотрим задачу 2. Так можно ли сделать какие-нибудь измерения с помощью одного только динамометра? Оказывается, можно. Сначала расположим динамометр горизонтально и убедимся, что его стрелка находится на нулевом делении. Затем расположим динамометр вертикально, держа за верхний конец пружины, который прикреплен к шкале. В таком положении стрелка динамометра (нижний конец пружины) покажет не ноль — пружина растянется под действием силы тяжести. Но на сколько? Что же теперь покажет динамометр?
Заметим, что в вертикальном положении на концы пружины действуют различные силы. На верхнем конце сила натяжения пружины равна mg, где m — масса пружины, на нижнем сила натяжения равна нулю. Кроме того, сила натяжения на расстоянии x от нижнего конца пружины равна 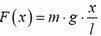
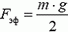
Вывод: масса пружины динамометра равна 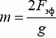
В заключение — несколько задач для самостоятельного решения.
Упражнения
1. Динамометр подвешен вертикально за верхний конец (за который пружина прикреплена к шкале). К его нижнему концу подвешен (верхним концом) второй динамометр, а к нижнему концу второго — третий. Все динамометры одинаковые. Верхний динамометр показывает силу F. Что показывают второй и третий динамометры? Массой шкал пренебречь.
2. Пружина в горизонтальном положении имеет длину 1 м. Подвешенная за один конец, она растягивается до 1,2 м. Другая такая же пружина имеет в горизонтальном положении длину 2 м. До какой длины она растянется, если ее тоже подвесить за один конец?
3. Пружина динамометра может как растягиваться, так и сжиматься, подчиняясь в обоих случаях закону Гука. За один конец динамометра тянут с силой 70 Н, другой толкают в том же направлении с силой 50 Н. Что покажет динамометр?
4. Стержень, изготовленный из упругого материала (металл, резина), аналогичен пружине. Если на его торцы действуют одинаковые растягивающие силы F, то относительное удлинение стержня равно 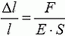
5. Стальной стержень (см. предыдущую задачу), поставленный «на попа», имеет длину 1 м. Какой будет длина стержня, если его подвесить за верхний конец?
Ответы
1) 3F/5; F/5. 2) 2,8 м. 3) 10 H. 4) 74,1 м. 5) 1 + 3,6·10-7 м.
для школьников и умных взрослых)) Как определить коэффициент жесткости пружины динамометра?
Анжелика Иванова
Мастер
(1872),
закрыт
12 лет назад
RIPvanWINKLE
Искусственный Интеллект
(158188)
12 лет назад
F=-kx-отсюда и k=-F/x Показания динамометра делим на удлинение пружины… Линейкой можно измерить…
Анжелика ИвановаМастер (1872)
12 лет назад
А можно еще вопрос? Почему закон Бука справедлив для простых упругих деформаций.
RIPvanWINKLE
Искусственный Интеллект
(158188)
Анжелика Иванова, При небольших деформациях не возникает остаточных деформаций, т. е. пружина возвращается после растяжение в первоначальное состояние.
Валентина ???
Гений
(71098)
12 лет назад
Подвесить груз известной массы, заметить растяжение, приравнять силу тяжести к силе упругости
mg=kx
и выразить к
RIPvanWINKLEИскусственный Интеллект (158188)
12 лет назад
Зачем груз известной массы,когда динамометр ПРОГРАДУИРОВАН в Ньютонах,которые нам и нужны?
Валентина ???
Гений
(71098)
Можно и так. А у вас минус надо убрать. Модули сил равны при равновесии груза.
Анжелика ИвановаМастер (1872)
12 лет назад
А можно еще вопрос? Почему закон Бука справедлив для простых упругих деформаций.
RIPvanWINKLE
Искусственный Интеллект
(158188)
Закон Гука(Г),при неупругих пружина вытягивается и не возвращается в первоначальную форму.-В учебнике ведь всё написано!-В этом-то не ленись!!!!