Как найти деформирующую силу

Сила: что это за величина

В повседневной жизни мы часто встречаем, как любое тело деформируется (меняет форму или размер), ускоряется или замедляется, падает. В общем, чего только с разными телами в реальной жизни не происходит. Причиной любого действия или взаимодействия является сила.

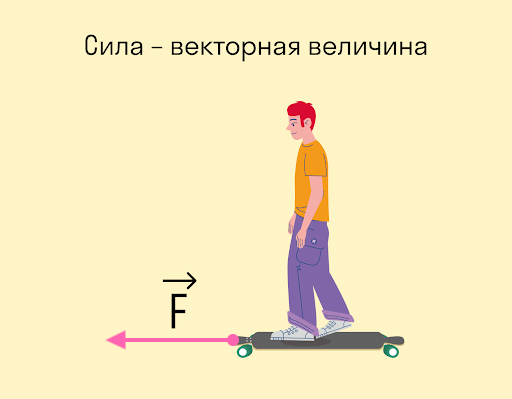
Сила — это физическая векторная величина, которая является мерой действия одного тела на другое.

Она измеряется в ньютонах — это единица измерения названа в честь Исаака Ньютона.

Сила — величина векторная. Это значит, что, помимо модуля, у нее есть направление. От того, куда направлена сила, зависит результат действия этой силы.

Вот стоите вы на лонгборде: можете оттолкнуться вправо, а можете влево — в зависимости от того, в какую сторону оттолкнетесь, результат будет разный. В данном случае результат выражается в направлении движения.

Деформация

Деформация — это изменение формы и размеров тела (или части тела) под действием внешних сил

Происходит деформация из-за различных факторов: при изменении температуры, влажности, фазовых превращениях и других воздействиях, вызывающих изменение положения частиц тела.

На появление того или иного вида деформации большое влияние оказывает характер приложенных к телу сил. Одни процессы деформации связаны с преимущественно перпендикулярно (нормально) приложенной силой, а другие — преимущественно с силой, приложенной по касательной.

По характеру приложенной к телу нагрузки виды деформации подразделяют следующим образом:

• Деформация растяжения

• Деформация сжатия

• Деформация сдвига

• Деформация при кручении

• Деформация при изгибе

Сила упругости: Закон Гука

Давайте займемся баскетболом. Начнем набивать мяч о пол, он будет чудесно отскакивать. Этот удар можно назвать упругим. Если при ударе деформации не будет совсем, то он будет называться абсолютно упругим.

Если вы перепутали мяч и взяли пластилиновый, он деформируется при ударе и не оттолкнется от пола. Такой удар будет называться абсолютно неупругим.

Деформацию тоже можно назвать упругой (при которой тело стремится вернуть свою форму и размер в изначальное состояние) и неупругой (когда тело не может вернуться в исходное состояние).

При деформации возникает сила упругости— это та сила, которая стремится вернуть тело в исходное состояние, в котором оно было до деформации.

Сила упругости, возникающая при упругой деформации растяжения или сжатия тела, пропорциональна абсолютному значению изменения длины тела. Выражение, описывающее эту закономерность, называется законом Гука.

Какой буквой обозначается сила упругости?

Важно раз

Изменение длины может обозначаться по-разному в различных источниках.

Варианты обозначений: x, ∆x, ∆l.

Это равноценные обозначения — можно использовать любое удобное.

Важно два

Поскольку сила упругости всегда направлена против деформации (она же стремится все «распрямить»), в Законе Гука должен быть знак минус. Часто его и можно встретить в разных учебниках. Но поскольку мы учитываем направление этой силы при решении задач, знак минус можно не ставить.

Задачка

На сколько удлинится рыболовная леска жесткостью 0,3 кН/м при равномерном (без ускорения) поднятии вверх рыбы весом 300 г?

Решение:

Сначала определим силу тяжести. Не забываем массу представить в единицах СИ – килограммах.

m = 300 г = 0,3 кг

Если принять ускорение свободного падения равным 10 м/с*с, то модуль силы тяжести равен :

F = mg = 0,3*10 = 3 Н.

Вспомним закон Гука:

И выразим из него модуль удлинения лески:

Так как одна сила уравновешивает другую, мы можем их приравнять:

Подставим числа, жесткость лески при этом выражаем в ньютонах:

= 0,01 м = 1 см

Ответ: удлинение лески равно 1 см.

Параллельное и последовательное соединение пружин

В Законе Гука есть такая величина, как коэффициент жесткости— это характеристика тела, которая показывает его способность сопротивляться деформации. Чем больше коэффициент жесткости, тем больше эта способность, а как следствие из Закона Гука — и сила упругости.

Чаще всего эта характеристика используется для описания жесткости пружины. Но если мы соединим несколько пружин, то их суммарная жесткость нужно будет рассчитать. Разберемся, каким же образом.

Последовательное соединение системы пружин

Последовательное соединение характерно наличием одной точки соединения пружин.

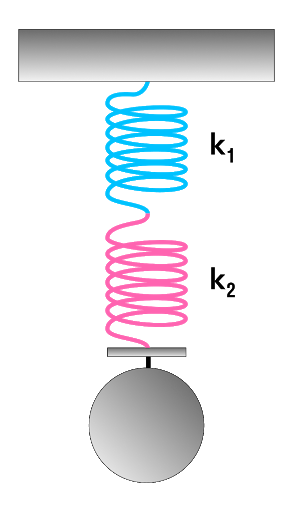
При последовательном соединении общая жесткость системы уменьшается. Формула для расчета коэффициента упругости будет иметь следующий вид:

Параллельное соединение системы пружин

Последовательное соединение характерно наличием двух точек соединения пружин.

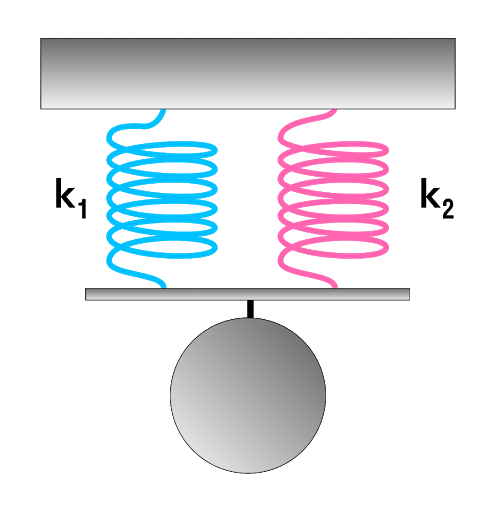
В случае когда пружины соединены параллельно величина общего коэффициента жесткости системы будет увеличиваться. Формула для расчета будет выглядеть так:

Задачка

Какова жесткость системы из двух пружин, жесткости которых k₁ = 100 Н/м, k₂ = 200 Н/м, соединенных: а) параллельно; б) последовательно?

Решение:

а) Рассмотрим параллельное соединение пружин.

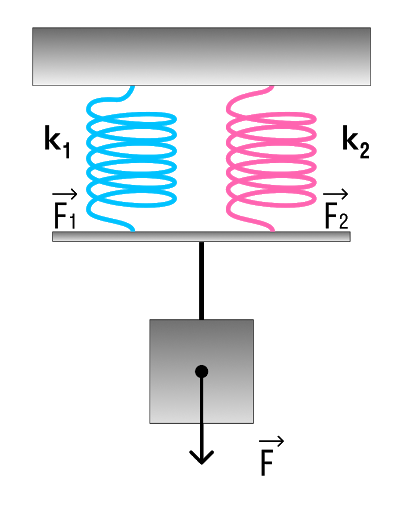
При параллельном соединении пружин общая жесткость

k = k₁ + k₂ = 100 + 200 = 300 Н/м

б) Рассмотрим последовательное соединение пружин.

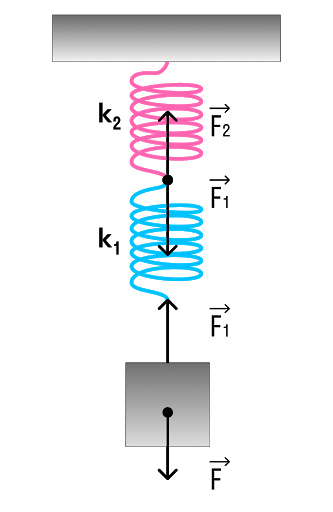
При последовательном соединении общая жесткость двух пружин

66,7 Н/м

График зависимости силы упругости от жесткости

Закон Гука можно представить в виде графика. Это график зависимости силы упругости от изменения длины и по нему очень удобно можно рассчитать коэффициент жесткости. Давай рассмотрим на примере задач.

Задачка 1

Определите по графику коэффициент жесткости тела.

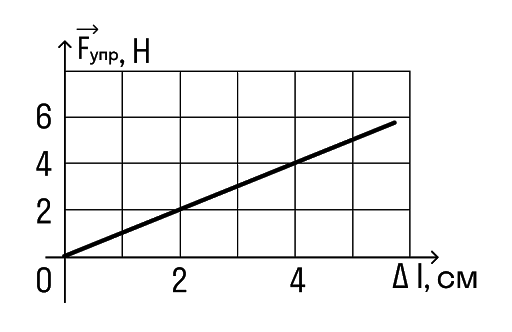
Решение:

Из Закона Гука выразим коэффициент жесткости тела:

F = kx

Снимем значения с графика. Важно выбрать одну точку на графике и записать для нее значения обеих величин.

Например, возьмем вот эту точку.

В ней удлинение равно 2 см, а сила упругости 2 Н.

Переведем сантиметры в метры:

2 см = 0,02 м

И подставим в формулу:

=100 Н/м

Ответ:жесткость пружины равна 100 Н/м

Онлайн-уроки физики в Skysmart не менее увлекательны, чем наши статьи!

Задачка 2

На рисунке представлены графики зависимости удлинения от модуля приложенной силы для стальной (1) и медной (2) проволок равной длины и диаметра. Сравнить жесткости проволок.

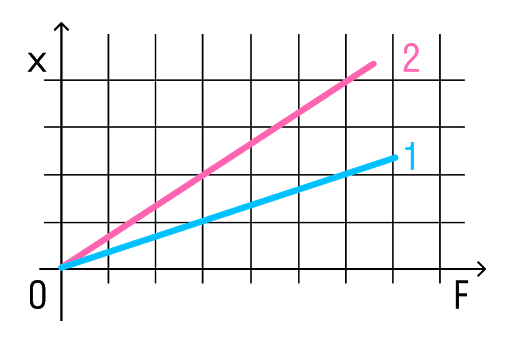
Решение:

Возьмем точки на графиках, у которых будет одинаковая сила, но разное удлинение.

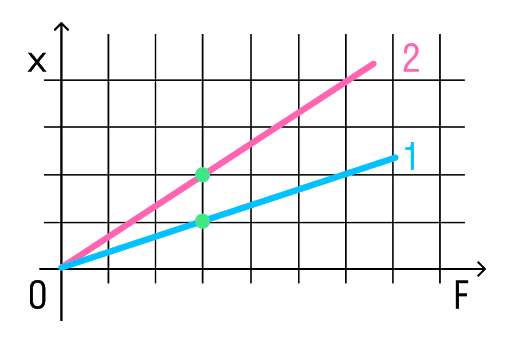
Мы видим, что при одинаковой силе удлинение 2 проволоки (медной) больше, чем 1 (стальной). Если выразить из Закона Гука жесткость, то можно увидеть, что она обратно пропорциональна удлинению.

Значит жесткость стальной проволоки больше.

Ответ: жесткость стальной проволоки больше медной.

---

---

Содержание:

Деформация тела:

Вспомните ненастный день: дует порывистый ветер, гнутся деревья. Чем сильнее ветер, тем больше гнутся деревья. А вот физики говорят, что деревья деформируются. Когда ветер стихает, деревья возвращаются в свое первоначальное положение — деформация исчезает. Но если ветер достаточно сильный, то ветви деревьев и даже их стволы могут сломаться.

Виды деформации

Уже отмечалось, что результатом действия силы на тело может быть как изменение скорости движения тела, так и его деформация. Например, если толкнуть мячик, то он придет в движение, а некоторые его части при толчке сместятся относительно друг друга — мячик деформируется.

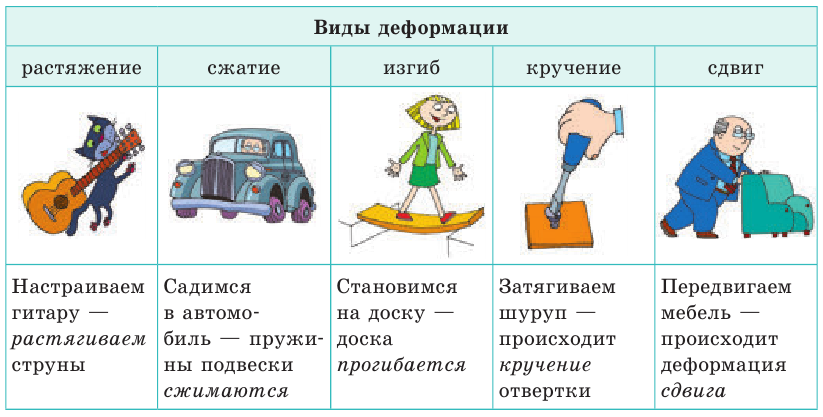
Деформация — изменение формы и (или) размеров тела. В зависимости от того, как именно части тела смещаются относительно друг друга, различают деформации растяжения, сжатия, изгиба, кручения, сдвига (см. таблицу).

Различия упругих и пластических деформаций

Возьмите эспандер (или ластик) и сожмите его — эспандер согнется. Но если прекратить сжимать эспандер, он полностью восстановит свою форму — деформация исчезнет (рис. 19.1). Деформации, которые полностью исчезают после прекращения действия на тело внешних сил, называют упругими.

Делая глиняную фигурку, мастер мнет руками комок глины, и глина сохранит форму, которую придаст ей мастер (рис. 19.2). Тяжелый пресс на монетном дворе чеканит монеты из металлических заготовок, — после прекращения действия пресса монета не восстановит свою прежнюю форму куска металла. И глина, и металл «не помнят» своей формы до деформации и не восстанавливают ее. Деформации, которые сохраняются после прекращения действия на тело внешних сил, называют пластическими. Попробуйте привести другие примеры упругих и пластических деформаций.

Определение силы упругости

При деформации всегда возникает сила, стремящаяся восстановить то состояние тела, в котором оно находилось до деформации. Эту силу называют силой упругости (рис. 19.3).

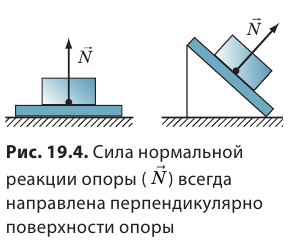
Сила упругости — это сила, которая возникает во время деформации тела и направлена в сторону, противоположную направлению смещения частей этого тела при деформации. Обычно силу упругости обозначают символом 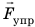, но в некоторых случаях используют и другие символы. Если тело давит на опору, то опора деформируется (прогибается). Деформация опоры вызывает появление силы упругости, действующей на тело перпендикулярно поверхности опоры. Эту сила называют силой нормальной реакции опоры и обозначаются символом 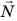(рис. 19.4).

Если тело растягивает подвес (нить, жгут, шнур), то возникает сила упругости, направленная вдоль подвеса. Эту силу называют силой натяжения подвеса и обозначают символом 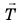(рис. 19.5).

Закон Гука

Научное исследование процессов растяжения и сжатия тел начал Роберт Гук (рис. 19.6) в XVII в. Результатом работы ученого стал закон, который позже получил название закон Гука: При малых упругих деформациях растяжения или сжатия сила упругости прямо пропорциональна удлинению тела и всегда пытается вернуть тело в недеформированное состояни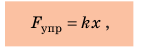е: где 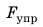— сила упругости; x — удлинение тела; k — коэффициент пропорциональности, который называют жесткостью тела.

Удлинение — это физическая величина, которая характеризует деформации растяжения и сжатия и равна изменению длины тела в результате деформации. Удлинение х определяется по формуле: 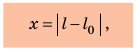где l — длина деформированного тела; — длина недеформированного тела (рис. 19.7). Жесткость тела можно определить, воспользовавшись законом Гука: 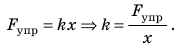Единица жесткости в СИ — ньютон на метр: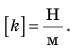

Жесткость — это характеристика тела, поэтому она не зависит ни от силы упругости, ни от удлинения. Жесткость зависит от формы и размеров тела, а также от материала, из которого тело изготовлено. Сила упругости прямо пропорциональна удлинению тела, поэтому график зависимости 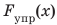— прямая (рис. 19.8). Чем больше жесткость тела, тем выше расположен график. Воспользовавшись графиками на рис. 19.8, определите жесткость тел І–ІІІ и убедитесь в справедливости последнего утверждения.

• Заказать решение задач по физике

Почему возникает сила упругости

Вы хорошо знаете, что все тела состоят из частиц (атомов, молекул, ионов). В твердых телах частицы колеблются около положений равновесия и взаимодействуют межмолекулярными силами притяжения и отталкивания. В положениях равновесия данные силы уравновешены. При деформации тела во взаимном расположении его частиц происходят изменения. Если расстояние между частицами увеличивается, то межмолекулярные силы притяжения становятся больше сил отталкивания. Если же частицы сближаются, то больше становятся межмолекулярные силы отталкивания. Другими словами: при деформации частицы «стремятся» вернуться в положение равновесия. Силы, возникающие при изменении положения одной частицы, очень малы. Но когда тело деформируется, изменяется взаимное расположение огромного количества частиц. В результате сложение сил дает заметную равнодействующую, которая противостоит деформации тела. Это и есть сила упругости. Итак, сила упругости — проявление действия межмолекулярных сил.

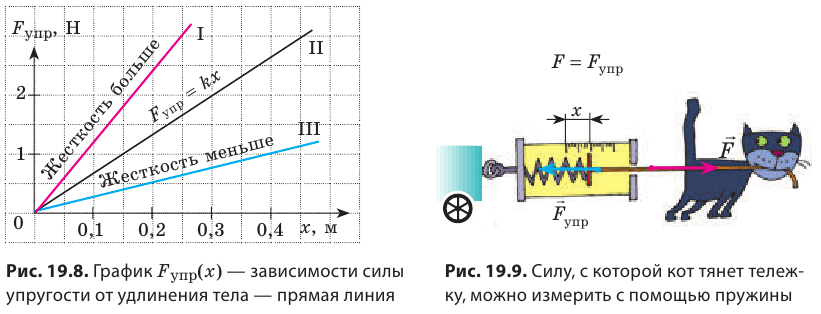
Приборы для измерения силы

Сила — это физическая величина, поэтому ее можно измерить. Приборы для измерения силы называют динамометрами. Основная составляющая простейших динамометров — пружина. Рассмотрим принцип действия таких динамометров на простом примере. Чтобы с помощью пружины, жесткость k которой известна, измерить силу F, с которой кот тянет тележку (рис. 19.9), необходимо:

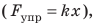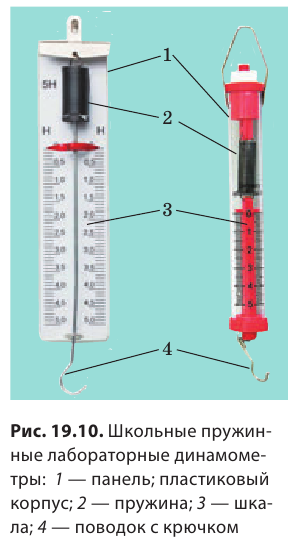
1) измерить удлинение x пружины; 2) воспользовавшись законом Гука, определить силу упругости которая действует на кота со стороны пружины и по значению равна силе F тяги кота: 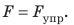Понятно, что каждый раз измерять удлинение пружины и рассчитывать силу неудобно. Поэтому пружину закрепляют на панели со шкалой, проградуированной в единицах силы. Именно так устроены простейшие школьные лабораторные динамометры (рис. 19.10). Существуют и другие виды пружинных динамометров (см., например, рис. 19.11).

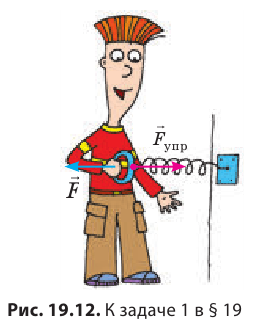
Пример №1

Действуя на пружину силой 40 Н, мальчик растянул ее на 8 см. Определите жесткость пружины. Какую силу нужно приложить мальчику, чтобы растянуть эту пружину еще на 6 см? Деформацию пружины считайте малой упругой. Анализ физической проблемы. Сила, которую прикладывает мальчик, по значению равна силе упругости, возникающей при растяжении пружины: F= уFпр (рис. 19.12). Деформация является малой упругой, поэтому воспользуемся законом Гука. Задачу будем решать в единицах СИ.

Дано:

,,

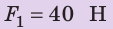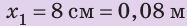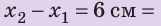
Найти:

,

Решение:

1. Вычислим жесткость пружины: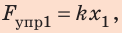

поэтому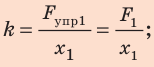

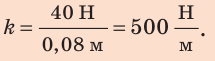
2. Найдем силу, которую нужно приложить мальчику, чтобы дополнительно растянуть пружину:

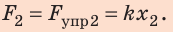
По условию 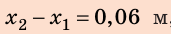,поэтому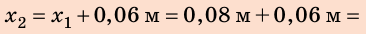 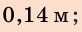следовательно,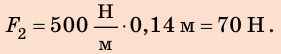

Анализ результатов. Для удлинения пружины на 8 см мальчик прикладывал силу 40 Н; для удлинения пружины еще на 6 см ему нужно увеличить силу на 30 Н — это правдоподобный результат.

Ответ: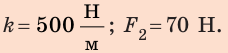

Пример №2

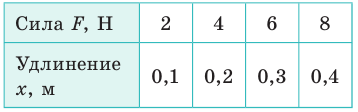
Выполняя экпериментальное задание, девочка увеличивала нагрузку на резиновый шнур. Каждый раз она измеряла силу, действующую на шнур, и соответствующее удлинение шнура. Воспользовавшись таблицей, составленной девочкой, постройте график уFпр(x). С помощью графика определите: 1) жесткость шнура; 2) удлинение шнура, когда к нему приложена сила 5 Н; 3) силу, которую нужно приложить к шнуру, чтобы его удлинение было равно 6 см.

Анализ физической проблемы. При растяжении шнура возникает сила упругости, которая по значению равна силе, действующей на шнур: 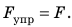Для построения графика зависимости 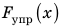начертим две взаимно перпендикулярных оси. На горизонтальной оси будем откладывать удлинение x шнура, а на вертикальной — соответствующее значение силы упругости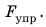

Решение:

Построив указанные в таблице точки (см. рисунок), увидим, что все они принадлежат одной прямой, значит, для любой точки графика имеем: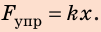

1) Выбрав точку А графика, найдем жесткость шнура: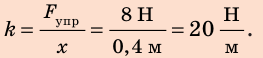

2) Удлинение шнура в результате действия силы 5 Н найдем по графику: если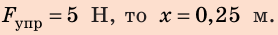

3) Силу, которую нужно приложить к шнуру, чтобы его удлинение было равно 0,06 м, найдем по закону Гука: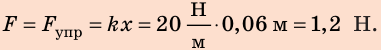

Ответ: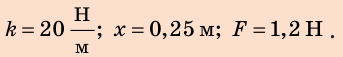

Итоги:

Деформацией называют изменение формы и (или) размеров тела. Если после прекращения действия на тело внешних сил деформация полностью исчезает, то это упругая деформация; если деформация сохраняется, то это пластическая деформация.

Сила упругости 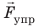— это сила, которая возникает во время деформации тела и направлена в сторону, противоположную направлению смещения частей этого тела при деформации.

Сила упругости — проявление действия межмолекулярных сил. При малых упругих деформациях растяжения и сжатия выполняется закон Гука: сила упругости прямо пропорциональна удлинению тела и всегда пытается вернуть тело в недеформированное состояние: 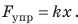Приборы для измерения силы называют динамометрами. Простейшие из них — пружинные динамометры.

Обычно при изучении закон Гука не вызывает особых сложностей. Запомнить, что деформация в упругом теле пропорциональна приложенной к нему силе, совсем не сложно.

Чаще всего, этого знания вполне достаточно для школьного курса, чтобы забыть про Гука навсегда :)… Чтобы он лучше запомнился, глянем на портрет.

Однако, если вы изучаете физику по углубленной программе или если ваш преподаватель хочет добиться демонстрации понимания этого закона на более высоком уровне, то сказанного явно недостаточно. Кроме того, при поступлении в технический институт, знаний этих тоже мало. Ведь на законе Гука держится великий и ужасный сопромат! Да и при изучении механики – это один из самых важных законов.

Давайте изложим основные постулаты Гука в простой и понятной читателю форме, ну а если вопросы останутся – пишем их в комментариях или в личку.

Введение и основные понятия

Наверняка вы в детстве играли с такой штукой, которая называется лук со стрелами. Принцип работы этого устройства очень прост. Есть согнутая палка, чаще всего из ивы, и есть тетива, которая связывает концы палки. Когда мы натягиваем тетиву стрелой, то сила упругости палки заставляет её возвращаться к прежнему состоянию и передавать энергию стреле.

Как вы догадываетесь, ключевое слово тут – сила упругости. Это такая сила, которая возникает в теле при попытке это тело согнуть или изменить его форму, то есть деформировать. Кстати, про силу полезно прочитать вот это. Обусловлена она внутренним взаимодействием частичек.

И тут тоже появилось новое слово – деформация. Думаю, пояснять что это такое, не нужно.

А вот сказать, что деформация бывает обратимая (упругая) и необратимая, важно. Ведь закон Гука работает в случаях существования упругой деформации.

Упругая деформация – это такая деформация, после которой тело возвращается к своим первоначальным геометрическим характеристикам, после снятия внешнего воздействия.

Простейшие виды деформации – это растяжение и сжатие. Сразу вспоминаем пружину. Ну и в учебнике физики вы как раз-таки встретите закон Гука, который раскрывается на примере пружины.

Формулировка закона Гука

Формулируется закон так:

Деформация, возникающая в упругом теле, пропорциональна приложенной к этому телу силе.

Если записывать его в виде формулы, то имеем следующее:

F = -kx ,

где F – сила упругости в теле, k – коэффициент упругости или жесткости, x – линейное изменение размеров тела.

Почему тут минус? Да его можно и не писать, если понимать логику. Вспоминаем, что сила есть вектор. Так как сила, возникающая в теле, противонаправлена силе приложенной, то формула записывается с минусом.

Иногда вместо k или x используют другие обозначения, но смысл от этого не меняется.

Разбираемся с новыми буквами

У нас появилась сила упругости в теле. Именно она в формуле – это F. Вспоминаем, что по третьему закону Ньютона (обязательно читаем), она равна силе или векторной сумме сил, воздействующей на тело. Мы считаем именно эту силу. Поэтому, если, скажем, предстоит решить задачу, где книга лежит на столе, а стол гнется, то мы считаем, что сила упругости в столе, равна нашему любимому m*g, так как книга притягивается к полу и вызывает изгиб стола.

k – это жесткость тела. Зависит она от материала и характеристик тела. Очевидно, что деревянная доска и железная труба будут иметь разные жесткости.

Стоит отметить, что это величина расчётная, но в начале изучения вы будете брать её из табличек и считать константой. А вот дальше нужно будет вспомнить/изучить, такую штуку, как модуль упругости первого рода или модуль Юнга. Это уже основы сопротивления материалов и начнется “О Боже, профессор нинада!”)

х – это линейное удлинение. Считается очень просто. Сколько стало минус сколько было :). В сложных случаях считается тоже посложнее, но нужны просто знания геометрии.

Новые важные понятия и обобщенный закон Гука

Про обобщенный закон Гука следует написать отдельную статью. Здесь же отмечу, что искушенный читатель наверняка заметил – пока речь идёт только об одноосном деформировании. Мы работаем с пружиной, которую можно растянуть вдоль оси икс или сжать вдоль оси икс. А что, если пружина будет растягиваться и сгибаться одновременно…

Реальные тела обычно деформируются во все стороны. В дело вступают сразу три направления.

В этом случае нужно использовать обобщенный закон Гука. Используются так называемые тензоры. Это большая тема, а тут отметим, что если вас вдруг спросили, а какие ограничения есть у стандартного закона Гука, то обязательно не забудьте сказать, что деформация должна происходить вдоль одной оси.

Ещё при разговоре об ограничениях выполнения закона стоит отметить про предел пропорциональности. Это максимальное механическое нагружение, до которого выполняется закон Гука. Смотрим на график. По оси Ыгрик у нас отложено механическое напряжение (читай как сила для упрощения), а по оси Ыкс – изменение размеров. Пока у нас есть линейная зависимость, отмеченная красной прямой линией, закон Гука будет выполняться.

Все тела ведут себя по разному и при достижении точки А одни тела развалятся/сломаются, а другие необратимо удлинятся/сожмутся. В конкретном примере тело расслюнявило, но оно не сломалось. Связь между силой и деформацией стала нелинейной.

Закон Гука выполняется только при малых деформациях и далеко не для всех материалов! Так, для многих полимеров закон Гука не будет выполняться. Выполняется он только, напомним, в линейных системах.

Как же описывать связь силы упругости и деформации в нелинейных системах, т.е. когда деформация не мала. Или что делать, когда закон Гука неприменим. Очень хорошо, что вы об этом задумались! Но это большая и сложная тема. Всё опять сводится к закону Гука в обобщенной форме и условно принимается, что деформация мала. Примерно так :)…

Но вообще, при больших деформациях следует использовать иные способа расчёта.

На все тела, которые находятся на Земле, действует сила тяжести. Все они стремятся под ее действием упасть вниз. Но не похоже, чтобы все в мире лежало на земле.

На еду в вашей тарелке действует сила тяжести, но она же не проваливается сквозь тарелку. На учебник на вашей парте тоже действует сила тяжести. Но стол от этого не придавливается к полу.

Значит, существует некая сила, уравновешивающая силу тяжести. На данном уроке мы узнаем, что же это за сила.

Определение силы упругости

Начнем с рассмотрения простого опыта (рисунок 1).

На два бруска положим доску. На доску поставим гирю. Мы увидим, что доска прогнется. Что же здесь происходит со стороны физики?

На гирю действует сила тяжести, она начинает двигаться вниз и прогибает доску. Доска деформируется из-за взаимодействия с гирей. Значит, возникает еще одна сила, с которой доска в ответ действует на гирю. 

Сила тяжести, действующая на гирю, направлена вертикально вниз, а другая сила направлена вертикально вверх. Поэтому она и уравновесила силу тяжести. Нашу искомую силу называют силой упругости.

Сила упругости — это сила, возникающая в теле в результате его деформации и стремящаяся вернуть тело в исходное положение.

Сила упругости  — векторная величина:

• обозначается как $vec{F}_{упр}$
• ее модуль обозначается как $F_{упр}$

В ситуации на рисунке 1, опора (доска) прогибается. Чем сильнее этот прогиб, тем больше сила упругости. Когда сила упругости и сила тяжести становятся равны, то опора и тело останавливаются. Так они приходят в равновесие.

Деформация и ее виды

Рассмотрим следующий случай (рисунок 2). Подвесим тело на нити.

В таких конструкциях нить часто называют подвесом. Когда мы подвесили тело, нить начала растягиваться — в ней возникла сила упругости.

Чем больше нить растягивается, тем больше становится сила упругости. Как и в случае с опорой, как только сила упругости станет равной силе тяжести, растяжение прекратится. 

Когда возникает сила упругости?
Получается, что сила упругости возникает при деформации тел. Если исчезает деформация, то исчезает и сила упругости.

Что называют деформацией тела?

Деформация тела — это любое изменение его формы и размеров.

Какие виды деформаций вы знаете?
Иногда после таких взаимодействий тело, испытывающее деформацию, меняет свои форму и размеры — происходит неупругая (пластическая) деформация. А иногда возвращается в исходное состояние. Тогда деформация называется упругой (рисунок 3).

Дадим определения

Упругая деформация — это деформация, при которой после прекращения воздействия деформирующей силы тело полностью восстановило свою форму и объем.

Пластическая деформация — это деформация, сохраняющаяся после прекращения действия деформирующей силы.

Упругая деформация бывает различных видов:

1. Растяжения (рисунок 2)
2. Сжатия (рисунок 4)

1. Сдвига (при такой деформации нагрузка прикладывается параллельно основанию тела, и одна часть тела сдвигается относительно другой (рисунок 5));

1. Изгиба (рисунок 1);
2. Кручения (рисунок 6).

Примеры деформации разных видов

1. Играем на гитаре — кратковременно растягиваем струны

2. Садимся в автомобиль — пружины подвески сжимаются

3. Сидим на тонкой доске — доска прогибается

4. Затягиваем шуруп — происходит кручение отвертки (хоть мы и не видим деформацию отвертки)

5. Двигаем расшатанный стул — происходит сдвиг сиденья относительно пола

Закон Гука

От чего же зависит сила упругости? Роберт Гук, современник Ньютона, ответил на этот вопрос (рисунок 8).

Рассмотрим опыт, изображенный на рисунке 9. 

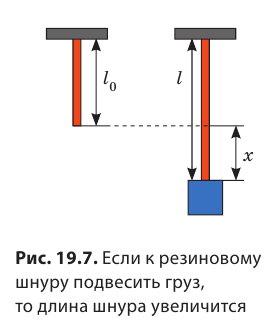
У нас есть штатив, к которому мы прикрепим резиновый шнур. Измерим его длину и обозначим как $l_0$.

Далее подвесим к шнуру чашку с гирей. Шнур удлинится. Снова измерим его длину — теперь она имеет значение $l$.

Шнур изменил свою длину после наших действий. Это изменение (удлинение шнура) мы можем найти по формуле:
$Delta l = l- l_0$,
где $Delta l$ — изменение длины. Знак $Delta$ (греческая буква “дельта”) используется как символ для обозначения изменения между значениями какой-либо величина.

Если мы будем менять гири на чашке, то будет меняться длина шнура, то есть его удлинение (деформация) $Delta l$.

Так мы подошли к закону Гука. Как он формулируется?

Изменение длины тела при растяжении или сжатии прямо пропорционально модулю силы упругости:
$F_{упр} = k Delta l$

Здесь $Delta l$ — изменение длины тела, $k$ — коэффициент пропорциональности, который называется жесткостью. Жесткость тела зависит от материала, формы и размеров тела.