Действующее (эффективное) значение переменного тока равно величине такого постоянного тока, который за время, равное одному периоду переменного тока, произведёт такую же работу (тепловой или электродинамический эффект), что и рассматриваемый переменный ток.
В современной литературе чаще используется математическое определение этой величины — среднеквадратичное значение переменного тока. Иначе говоря, действующее значение переменного тока можно определить по формуле:
Действующее значение в типичных случаях[править | править код]
Приведены формулы для электрического тока. Аналогичным образом определяются действующие значения ЭДС и напряжения.
Синусоида[править | править код]
Для синусоидального тока:
где
— амплитудное значение тока.
Прямоугольная форма[править | править код]
Для тока, имеющего форму однополярного прямоугольного импульса, действующее значение тока зависит от скважности:
где
— коэффициент заполнения (величина, обратная скважности).
В частности, для тока, имеющего форму однополярного меандра (коэффициент заполнения 0,5):
Для тока, имеющего форму двухполярного меандра:
Треугольная форма[править | править код]
Для тока треугольной и пилообразной формы (независимо от того, меняется ли направление тока):
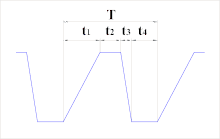
Трапециевидная форма[править | править код]
Для тока трапециевидной формы действующее значение можно определить разбив период на отрезки положительного фронта, действия максимального значения и отрицательного фронта:
где
— длительность положительного фронта;
— длительность действия максимального значения;
— длительность отрицательного фронта;
— длительность полного периода.
Дугообразная форма[править | править код]
Для тока имеющего форму дуги (половины окружности):
Дополнительные сведения[править | править код]
В англоязычной технической литературе для обозначения действующего значения употребляется термин effective value — эффективное значение. Также применяется аббревиатура RMS или rms — root mean square — среднеквадратичное (значение).
Электроизмерительные приборы (амперметры, вольтметры) для измерения в цепях переменного тока обычно градуируются так, чтобы их показания соответствовали действующему значению синусоидального тока или напряжения. При измерении несинусоидальных токов и напряжений приборы различных систем могут давать разные показания[1].
См. также[править | править код]
- Список параметров напряжения и силы электрического тока
Примечания[править | править код]
- ↑ 11.8. Показания приборов различных систем в цепях несинусоидального тока. StudFiles. Дата обращения: 16 февраля 2019.
Литература[править | править код]
- «Справочник по физике», Яворский Б. М., Детлаф А. А., изд. «Наука», 1979 г.1
- Курс физики. А. А. Детлаф, Б. М. Яворский М.: Высш. шк., 1989. § 28.3, п.5
- «Теоретические основы электротехники», Л. А. Бессонов: Высш. шк., 1996. § 7.8 — § 7.10
Ссылки[править | править код]
- Действующие значения тока и напряжения
- Среднеквадратичное значение
-
Действующее значение переменного тока
При анализе цепей
переменного тока принято пользоваться
так называемым действующим
(средним квадратичным за период) значением
переменного тока.
На рисунке 7 показано
графическое изображение синусоидального
переменного тока i
= Imsinωt.

Рис. 7
Маленькой буквой
i
обозначается мгновенное значение тока.
Мгновенное значение i
– это текущее значение синусоидальной
функции времени.
В частности, как это видно из рисунка
7, в момент времени t1
= 0 мгновенное значение i(t1)
= 0; при t2
= Т/4
i(t2)
= +Im;
при t3
= Т/2
i(t3)
= 0; при t4
= 3Т/2
i(t4)
= –Im;
при t5
= Т
i(t5)
= 0 и т.д.
Амплитудное
значение Im
– это максимальное значение синусоиды
тока (рис. 7).
Действующим
значением переменного тока
(в том числе синусоидального) называется
такой условный
постоянный ток I,
который в резисторе с сопротивлением
R
за время периода Т реального переменного
тока i
выделяет такое же количество тепла, как
и реальный переменный ток.
С учетом того, что
все законы
электротехники
(в том числе и закон Джоуля–Ленца),
сформулированные для цепей постоянного
тока, справедливы
в цепях переменного тока только для
мгновенных значений,
можно написать соответствующие
зависимости.
Количество тепла,
выделяемое условным постоянным током
I,
согласно закону Джоуля–Ленца [2]:
(4)
а выделяемое
синусоидальным током:
(5)
Приравняв правые
части равенств (4) и (5), после сокращения
на константу R
получим:
(6)
.
Проделав
соответствующие преобразования, подробно
рассмотренные в [1], получим
,
то есть действующее
значение синусоидального тока в
меньше
амплитудного.
По аналогии для действующих
значений напряжения и э.д.с. можно
записать соответственно
Действующие
значения являются средними квадратичными
за период Т
в отличии от средних арифметических
значений.
Как
известно среднее арифметическое значение
синусоидального тока за период равно
нулю:
поскольку вычисление
определенного интеграла в заданных
пределах сводится к определению суммы
площадей положительной и отрицательной
полуволн синусоиды, равновеликих по
величине, но противоположных по знаку.
На практике
используется среднее
значение синусоидального тока за
положительную половину периода
[1].
(7)
где ω
= 2π/Т
– угловая частота.
Коэффициентом
формы Кф
какой либо периодически изменяющейся
величины называется
отношение действующего значения к
среднему.
Для
синусоидального тока
-
Изображение синусоидальных функций вращающимися векторами
Как
известно [1], синусоидальные функции
времени можно графически изображать
не только синусоидами (рис. 6, 7), но и
вращающимися векторами.
В курсе тригонометрии
приводится следующий способ построения
графика синусоиды.
Радиус-вектор,
длина которого равна амплитуде синусоиды
Im
(рис. 8), вращают против часовой стрелки,
проектируя его на вертикальную ось с
одновременной разверткой по горизонтальной
оси, на которой откладывают соответствующие
углы поворота.
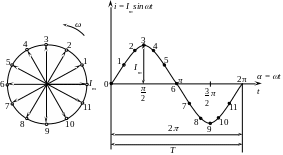
Рис. 8
На
рисунке 8 показано построение одного
периода синусоиды тока i
=
Imsint
в пределах от t
= 0 (t
= 0) до t
= T
(t
= 2π).
График на рисунке 8 соответствует случаю
равенства нулю ψІ
= 0 начальной фазы, то есть синусоида
начинается с нуля, уходя в область
положительных значений.
Начальной фазой
ψ синусоидальной
функции называется
значение фазового угла в момент времени
t
= 0.

Рис. 9
На рисунке 9
приведено построение полного цикла
T
(2π)
синусоиды i
= Imsin(t
+ ψІ),
у которой начальная фаза ψІ
> 0, то есть радиус-вектор Im
в момент времени t
= 0 повернут относительно горизонтального
положения на угол ψІ
= π/6
в положительном (против часовой стрелки)
направлении.
На рисунке 10
показана векторная диаграмма напряжения
Um
и тока Im
с различными начальными фазами ψU
и ψI
соответственно для промежутка времени
t
= 0 с последующей разверткой в графики
синусоид u
= Umsin(t
+ ψU)
и i
= Imsin(t
+ ψI).
Введем понятия о
сдвиге фаз
синусоид одной и той же частоты во
времени. Применительно к рисунку 10 углом
сдвига φ
между напряжением и током называется
разность начальных фаз
соответствующих синусоид: φ
= ψU
– ψI.
С учетом положительного
направления вращения векторов
> 0 (против часовой стрелки) является
очевидным, что вектор
напряжения
Um
опережает
вектор тока
Im
на угол
φ.
Поскольку время t
на оси абсцисс (рис. 10) отсчитывается
слева направо, то сравнивая моменты
прохождения одинаковых фаз синусоид
напряжения и тока, можно убедиться, что
напряжение опережает ток во времени на
угол φ.

Рис. 10
К
ак
видно из рисунка 10 синусоида напряжения
по сравнению с синусоидой тока проходит
раньше на угол φ
через нулевые значения и фазу положительной
амплитуды.
Как
уже упоминалось, все основные законы
электротехники, сформулированные
применительно к цепям постоянного тока
[2], для цепей переменного тока справедливы
только для мгновенных токов, напряжений
и э.д.с. Рассмотрим простейший электрический
узел (рис. 11), являющийся одним из участков
цепи синусоидального тока.
Стрелками условно показаны направления
токов, чтобы было возможно пользоваться
правилом знаков (плюс – минус) при
алгебраических операциях с мгновенными
значениями синусоидальных функций
времени. Предположим, что заданы синусоиды
токов i1
= Im1sin(t
+ ψ1)
и i2
= Im2sin(t
+ ψ2),
а необходимо определить синусоиду
суммарного тока i.
Составим уравнения по первому закону
Кирхгофа в алгебраической форме для
мгновенных значений:
i
(8)
–
i1
–
i2
= 0
i = i1
+ i2
= Im1sin(t
+ ψ1)
+ Im2sin(t
+ ψ2)
= Imsin(t
+ ψ),
то
есть решение сводится к определению
амплитуды Im
и начальной фазы ψ
суммарной синусоиды i.
Эта задача решается
аналитически с достаточно высокой
точностью получаемых результатов. Такой
метод
расчета, основанный на алгебраических
операциях с мгновенными значениями
синусоид, называется аналитическим.
Недостатком этого метода является
усложнение расчетных операций, если
число слагаемых синусоид увеличивается.
Поэтому был предложен графический
метод,
основанный на геометрическом сложении
векторов, изображающих синусоидальные
токи, напряжения и э.д.с. одинаковой
частоты
(метод
векторных диаграмм).
Покажем этот метод
применительно к простейшему электрическому
узлу (рис. 11), рассмотренному
выше с позиций аналитического метода.
Изобразим
слагаемые синусоиды для момента времени
t
= 0 в виде векторов
и
с учетом начальных фаз ψ1
и ψ2
и соблюдением одинаковых масштабов
(рис. 12). Очевидно проекции этих векторов
на вертикальную ось i
(ось мгновенных значений) при вращении
их против часовой стрелки с угловой
скоростью w
и при одновременной развертке по
горизонтальной оси времени t
(или фазового угла wt)
позволяют построить графики соответствующих
синусоид. Осуществим векторное
суммирование
по правилу треугольника или диагонали
параллелограмма (рис. 12). Поскольку
векторы
и
построены для момента времени t
= 0, то их проекции на вертикальную ось
i1
= Im1sinψ1
и i2
= Im2sinψ2
представляют собой мгновенные значения
при t
= 0. Спроецировав
на ту же ось вектор
,
получим мгновенное
значение тока
i
=
Imsinψ,
которое
в соответствии с теоремой
о векторной сумме
равно алгебраической сумме проекций
слагаемых векторов
i
= i1
+ i2.
Таким образом можно
утверждать, что можно
заменить алгебраические операции с
мгновенными значениями синусоид
геометрическим сложением векторов,
изображающих эти синусоиды.
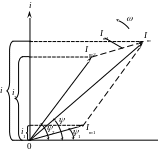
Рис. 12
Векторной
диаграммой называется совокупность
векторов, изображающих синусоидальные
функции токов, напряжений и э.д.с.
одинаковой частоты, которая,
как правило, представляет
собой графическое решение первого или
второго закона Кирхгофа.
В
отличие
от аналитического метода метод векторных
диаграмм (графический) является более
простым и наглядным.
Недостатком этого метода является
невысокая точность результатов при
необходимости в численных расчетах.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Что такое действующее значение напряжения
Содержание
- 1 Как измеряется
- 1.1 Практический пример
- 2 Импульсный электрический заряд
- 2.1 Расчёт кривой
- 2.2 Вычисления
- 3 Сила переменного тока
- 4 Вывод
- 5 Видео по теме
Всем нам известно о 220 вольт в бытовой розетке. Но если подключить к ней вольтметр, напряжение каждый раз будет разным. При этом зачастую напряжение может быть даже больше данной величины. Постараемся в данном материале разобраться — почему это происходит, что такое действующее значение переменного тока, и как его можно рассчитать с помощью различных вариантов.
Как измеряется
Электродинамические параметры в сети постоянно изменяются. Это связано с тем, что они представлены синусоидальным однополярным импульсом разной амплитуды. При измерении напряжения в цепи переменного тока, каждый раз будет получен разный результат. А при вычислении усреднённого параметра, он всегда будет составлять 0.
Получается, что математически вычислить данный параметр невозможно. Есть возможность получить только усреднённый параметр, который зависит от полупериода синусоидальной волны. Однако использовать его на практике или для каких-то вычислений нельзя.
Для решения этой проблемы и стали применять такое понятие, как действующее значение для расчёта силы тока и напряжения. Параметр определяется по характеристикам постоянного тока в цепи, генерирующей тепловую энергию такого же объёма, как и при подаче в цепь переменного тока.
Практический пример
Определение выше будет непонятным для человека, который не имеет особых познаний в области электротехники и электродинамики. Чтобы понять его смысл, предлагается рассмотреть следующий пример:
- Доступны две идентичные электроцепи (длина, элементы цепи и сечение проводников у них совпадают).
- В каждую включён одинаковый резистор — электронный компонент, который изменяет свое сопротивление в зависимости от подаваемого тока.
- Обе цепи подключаются к источникам электроэнергии, имеющим одинаковое напряжение.
Но между цепями есть одна разница. На первую электроцепь подаётся постоянный, а на вторую — переменный ток. По одной из них пойдёт стабильный электроток, а по другой потечет импульсный электрозаряд, который постоянно изменяется и имеет синусоидальной график.
Чтобы найти количества тепла в цепи с сопротивлением, используется такая формула:
После произведения ряда замеров и вычислений можно увидеть, что выделяемое тепло в этих двух электроцепях имеет одинаковую величину. Например, в цепи с постоянным током при подаче напряжения 30 вольт выделяется тепло 200 Джоуль (или Дж). Если вторая цепь имеет идентичные характеристики, то выделение тепла в ней также составит 200 Дж. Получается, что напряжение 30В в этих электроцепях — это и есть эффективное напряжение.
Импульсный электрический заряд
Вышеприведенный пример позволяет только определить действующее и среднее значение напряжения переменного тока. Но на практике такой метод также не применяется, из–за того, что получить доступ к источнику переменного напряжения не всегда представляется возможным. Поэтому параметры цепи рассчитываются с помощью формул, которые основаны на синусоидальных кривых.
Стоит отметить, что действующее напряжение не всегда формируется путём плавного изменения определённого импульсного электрозаряда. Кривая зачастую имеет форму, отличную от привычной нам синусоиды:
- Прямоугольную (меандр);
- треугольную;
- трапециевидную
- и другие.
То есть график электротока может иметь отличную, но при этом стабильную форму. Наглядным примером такого варианта является кривая осциллографа, регистрирующая ритмы сердцебиения человека.
Но независимо от действующего в сети импульсного заряда, во время расчётов используется именно синусоида. Это объясняется тем, что погрешности в расчетах будут крайне малыми. Поэтому ими можно пренебречь, ведь они не скажутся на конечном результате:
- Частота импульса в жилых домах составляет 50 Гц. За 1 сек электрический импульс проходит через фазу 100 раз. Это означает, что работающая от сети лампочка за секунду 100 раз загорается и тухнет, а электрический заряд при этом изменяется довольно плавно. Но человек этого не замечает из-за невосприимчивости человеческого зрения к сверхбыстрым колебаниям.
- Одинаковая площадь фигур. Независимо от формы кривой периода, описывающей переменный электроток идентичных параметров, площадь их фигур всегда будет одинаковой. Следовательно, при любых расчетах получится одно и то же эффективное значение переменного синусоидального тока. Поэтому эффективные значения не зависят от формы кривой. На них оказывает влияние именно величина амплитуды.
Форма кривой импульса важна только для сверхточных расчётов в лабораторных условиях. Также она учитывается для работы суперкомпьютеров. В остальных случаях синусоида позволит вычислить действующее значение переменного синусоидального тока.
Расчёт кривой
Синусоида — это периодическая функция, которую можно всегда описать с помощью уравнения. Если взять её за основу, то на входе имеются следующие исходные данные:
- Т — амплитуда;
- φ — начальная фаза;
- ωt — угловая скорость.
По этим входным характеристикам находим другие переменные параметры:
- Uт — амплитудное напряжение;
- Uм — действующие в момент измерения значения напряжения;
- ωt + φ — фактическая фаза в точке измерения.
Т.к. начальная фаза равняется нулю, на выходе формула кривой будет иметь следующий вид:
Uм = Uт·sin(ωt + φ) = Uт·sin(ωt)
Теперь необходимо обратиться к закону выделения тепла, который еще называется законом Джоуля-Ленца. Согласно него квадрат напряжения — это произведение выделяемого тепла на сопротивление проводника.
| Формулы для расчета тепловой энергии в электроцепях: | |
| с постоянным током | с переменным током |
| Q = U2/R | Q = Uм2/R |
- Uм — величина постоянного напряжения;
- Uм — величина действующего напряжения;
- R — сопротивление проводника.
Мы видим, что при расчетах количества тепла в цепи переменного тока, пользуется именно действующим значением переменного тока.
Из данных формул вытекают два важных нюанса, на которые стоит обратить внимание:
- В расчетах используется среднеквадратичное значение напряжения (СКЗ). Это связано с тем, что величина напряжения постоянно изменяется и можно получить только какую-то усредненную величину.
- Амплитуда постоянного тока довольно условная величина. Ее используют в расчетах, чтобы только описать период синусоиды переменного электрозаряда.
Вычисления
Волны синусоид будут одинаковыми. Однако в пределах периода в каждой точке измерения напряжения будут отличаться. Поэтому, чтобы уравнять между собой среднеквадратичное напряжение постоянного и переменного электротока по тепловыделению, требуется рассчитать объём выделенного тепла в течение времени, равного 1 периоду:
В уравнение теперь можно подставить выражение расчёта мгновенного напряжения
Uм = Uт·sin(ωt + ф) = Uт·sin(ωt)
После математического преобразования можно рассчитать действующее значение электрического напряжения:
U = Uт / √2 = 0,707·Uм
Теперь найдем амплитудное напряжение по формуле:
Uт = U·√2
Амплитудное напряжение так же имеет и другое название – максимально возможное эффективное мгновенное значение напряжения.
Сила переменного тока
С помощью амперметра находим амплитудную силу тока в цепи. Используя её вместе с периодом, который равен 1/50 секунд, можно применить описанную выше формулу, чтобы рассчитать среднеквадратичное значение напряжения. В результате этого будет получена действующие значения силы тока.
Действующее значение тока можно рассчитать, когда других исходных параметров нет, но нам известно эффективное значение величины напряжения в цепи. Следовательно, можно воспользоваться всем нам известным законом Ома вычисления значения силы тока:
U = I·R и I = U/R
где:
- U — будет действующим напряжением переменного синусоидального тока;
- R — сопротивление проводника, которое всегда можно узнать в любом справочнике, зная состав материала проводника.
Ранее электропроводку делали из алюминия и меди, которые отличались довольно высоким сопротивлением. Эффективное значение реальной силы тока этих металлов было меньше 6.5А. По этой причине в старых домах зачастую срабатывает автоматический выключатель, если одновременно подключить в сеть несколько приборов. Сегодня открыты сложные сплавы с низким сопротивлением. Они позволяют достичь с действующее значение силы переменного тока около 16А даже в обычных современных многоквартирных домах.
С уменьшением сопротивления проводника, прямопропорционально возрастает мощность и тепловыделение. При том надо помнить о том, что у каждого сплава есть свой определенный температурный предел. Поэтому в жилых сетях сила тока часто не превышает 20 ампер, а при резком ее скачке, например, при неполадках на подстанции, электронная часть устройств просто сгорает. Для предотвращения таких случаев и подключаются автоматы, которые при регистрации высоких действующих значений размыкают цепь на данном участке. Более мощные источники электроэнергии встречаются только в промышленных трехфазных сетях с напряжением 380В.
Вывод
Мы рассмотрели в данной статье — что называют действующим значением силы тока и напряжения, а так же как определяют эти значения переменного тока в электроцепи. Это эффективные значения переменного тока, под действием которого выделяется точно такое же количества тепла, как и в цепи постоянного тока, имеющей аналогичные характеристики.
Видео по теме
Какое напряжение между фазой и нулём в отечественной электросети: 220 или 310? На самом деле и одно и другое! Всё дело в том, что в наших сетях протекает синусоидальный ток, а у синусоиды есть ряд характеристик и особенностей, которые мы попытаемся рассмотреть простым языком в этой статье.
Речь далее пойдет только о синусоидальном переменном токе или напряжении. Для тока другой формы всё сказанное далее, в принципе, справедливо, но будут отличаться формулы для вычисления и, соответственно, числовые значения.
Синусоида, её амплитуда и другие характеристики
Все мы знаем, что между фазой и нулём 220 вольт (230В по ГОСТу), но многие знают что выпрямленное и сглаженное сетевое напряжение превышает 300 вольт, да и конденсаторы в фильтры выпрямителей подбирают не ниже чем 400 вольт, откуда они берутся? Для начала рассмотрим график, на котором изображено синусоидальное напряжение в привычной всем розетке 220В.
На рисунке 1 по вертикали размечено напряжение в вольтах, а по горизонтали время. Обратите внимание, что напряжение в электросети периодично изменяется от -310 вольт, до + 310 вольт, каждый период изменений длится 20 миллисекунд, после чего повторяется.
Точно описать любую величину, изменяющуюся по синусоидальному закону можно с помощью трёх характеристик:
- Амплитуда — это высота синусоиды от нуля до верхней или нижней точки. В нашем случае это 310В. Обозначается буквами Im или Um, для тока и напряжения соответственно.
- Период — расстояние между двумя соседними максимумами или минимумами синусоиды. В электросетях РФ он равен 20 миллисекунд, так как стандартная частота — 50 Гц. Обозначается буквой T.
- Начальный фазовый угол — это величина, которая отражает насколько сдвинута синусоида по горизонтали относительно начального момента времени наблюдения (нулевой секунды). Если проще, то на графике выше фаза в начале графика начинается с 0, значит она не сдвинута, если бы начиналась с другой величины — то была бы сдвинутой на определенный угол.
При рассмотрении однофазной сети начальный фазовый угол нас не интересует, он используется при исследовании трёхфазного напряжения.
Рассмотрим этот график еще раз, но отметим на нём амплитуду и период.
График описывает формула синусоидального напряжения (для тока аналогично, но U меняется на I):
Из этого следует, что величина напряжения (или тока) в каждый конкретный момент времени разная, такая величина называется мгновенной. Соответственно и мгновенная мощность, выделяемая на активной нагрузке (R) в каждый момент будет разной:
Это подходящая формула для описания мгновенного состояния электрической цепи, но совершенно неудобная и неподходящая для измерения параметров и описания электрических цепей в общем. Поэтому используют какие-то усреднённые значения электрической мощности, напряжения и тока.
В литературе принято объяснять смысл действующих и амплитудных значений на примере силы тока. К тому же по определения, формулы и их смысл аналогичны, и для напряжения, и для тока. Поэтому я немного отойду от синусоидального напряжения, и далее пойдет речь о токе.
Действующее, среднеквадратичное, эффективное?
Теперь вы знаете, что амплитуда фазного напряжения в электросети равна 310В, но что такое 220В и откуда они берутся? Дело в том, что — 220В это действующее напряжение, его же называют среднеквадратичным или эффективным.
Это значит, что если на лампочку накаливания или нагревательную спираль подать переменный ток с действующим значением (силой) в 1 ампер, то на ней выделится та же мощность (количество тепла), как если бы через неё протекал постоянный ток в 1 ампер.
Для нахождения среднего значения переменного синусоидального тока за половину периода, необходимо проинтегрировать формулу этого тока, при этом пределами интегрирования выбирается половина периода:
Как отмечалось выше, формула для среднего переменного синусоидального напряжения (как и для ЭДС) будет аналогичной:
Но это средние величины, которые на практике не используется так часто, как действующие величины. Действующее напряжение или ток, находится подобным образом, при вычислениях интегрируется та же формула, но возведенная в квадрат, после чего извлекается корень. Пределы интегрирования уже не половина, а целый период. Кстати, поэтому действующее значение называется еще и «среднеквадратичным». Формулу действующего значения переменного синусоидального тока:
Действующий ток (Iд) или напряжение (Uд), в корень из двух раз меньше, чем амплитудное. Чтобы его вычислить, нужно амплитудное значение разделить на 1.41, или умножить на 0.707.
Uд=Um/1.41=0.707*Um
И наоборот, чтобы узнать амплитудное значение при известном действующем, нужно умножить его на 1.41 или разделить на 0.707. Приведем пример, из графика на рисунке 1, мы узнали, что амплитуда напряжения в однофазной электросети 310 вольт, найдем его действующее значение:
Uд=Um/1.41=310/1.41=219,8~220В
Мы получили привычные нам 220В. Как отмечалось ранее, действующие значения напряжения и тока удобно использовать для расчетов и описания электрических цепей, поэтому и говорят «в розетке 220В», «линейное напряжение 380В» и так далее.
Повторим пройденное: непрерывное тепловое воздействие переменного синусоидального тока на какую-то активную нагрузку за определенный период времени будет численно равно тепловому воздействию постоянного тока за тот же период, при условии, что величина постоянного тока была в 1.41 раз меньше амплитуды переменного. То есть за то же время выделится столько же теплоты.
В таком случае, при активной нагрузке (резисторы, ТЭНы, нихромовые спирали, лампы накаливания), можно приравнять действующее значение переменного тока или напряжения, к такому же по величине постоянному току или напряжению.
Какое напряжение измеряет мультиметр, амперметр или вольтметр?
В подавляющем большинстве случаев если на измерительном приборе вы выбираете режим измерения переменного тока или напряжения (U~, I~), вы измерите именно действующие значения. Однако есть и специфичные приборы, измеряющие амплитудные значения параметров в электрической сети, а также на электронных осциллографах могут выводится и действующие, и амплитудные величины измеряемых сигналов. Измерение амплитудных значений может обозначаться как Im.
При этом далеко не все приборы могут измерять переменный ток по форме отличный от синусоидального — пилообразный, прямоугольный и так далее. Вы могли видеть, что на хороших мультиметрах написано загадочное «TRUE RMS», что расшифровывается как: «True Root Mean Sqare», а переводится как — истинное среднеквадратичное значение. Такие измерительные приборы показывают действующие значения напряжений и токов любых форм (не только синусоидальных).
В завершение этой статьи, предлагаю вам закрепить знания и ознакомиться с прекрасным советским плакатом, на эту тему
Теория / 4.3. Действующее и среднее значения переменного тока
Основной задачей расчета электрической цепи является определение тока. В цепях постоянного тока,
если нет регулирующих устройств, ток остается неизменным и его легко рассчитать
или измерить. В цепях переменного тока ток непрерывно меняется по величине и по
направлению. Если, допустим, что каким-либо путем нам удалось определить одно
мгновенное значение тока, то это не даст оценки действия всех остальных
значений.
Поэтому
переменный ток оценивается по его действию, которое эквивалентно
действию некоторого постоянного тока. В качестве критерия такой эквивалентности
принято считать тепловое действие тока.
Действующее значение переменного
тока численно равно такому постоянному току, который в элементе цепи за время,
равное периоду Т, выделяет такое же количество тепла, какое в том же элементе за то же время при тех
же условиях выделяет переменный ток.
Определим количество тепла, которое выделяется за
период Т постоянным током.
По закону Джоуля – Ленца:
Для переменного тока
По определению количество тепла, выделяемое постоянным
и переменным токами, должно быть одинаково.
Тогда действующее значение тока определится выражением
Полученное выражение справедливо для любого
переменного тока независимо от его формы.
Определим действующее значение синусоидального тока. Представим
мгновенное значение тока в виде
тогда будет
справедливо соотношение:
Используя правила тригонометрических преобразований, выразим
Действующее значение синусоидального тока в корень из 2 раз меньше его амплитудного
значения.
То же самое можно сказать о напряжении и ЭДС:
Действующие значения токов, напряжений и ЭДС обозначаются прописной буквой без индекса. Все расчеты в
цепях переменного тока выполняются для действующих значений токов, напряжений и
ЭДС.
Действующее значение переменного тока можно измерить
приборами любой системы, кроме магнитоэлектрической.
Отношение амплитуды к действующему значению тока
называется коэффициентом амплитуды.
Для синусоидальных токов коэффициент амплитуды всегда
равен корню из 2.
В ряде случаев при анализе электрических цепей
переменного тока необходимо определить среднее значение переменного тока.
Средним значением переменного тока называется среднее арифметическое из
всех мгновенных значений за половину периода.
Для синусоидальных
величин среднее значение всегда оценивается
за половину периода, так как
мгновенные значения полпериода положительны, а полпериода – отрицательны, в
результате среднее значение за период равно нулю.
Найдем среднее значение переменного тока:
Отношение действующего значения к среднему называется коэффициентом
формы кривой.
Подставив эти значения в формулу коэффициента формы,
получим для синусоидального тока
Таким образом, действующие
значения тока, напряжения и э.д.с. связаны со средними значениями
соотношениями: