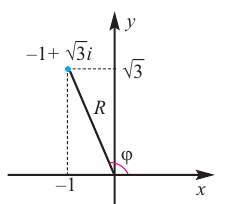
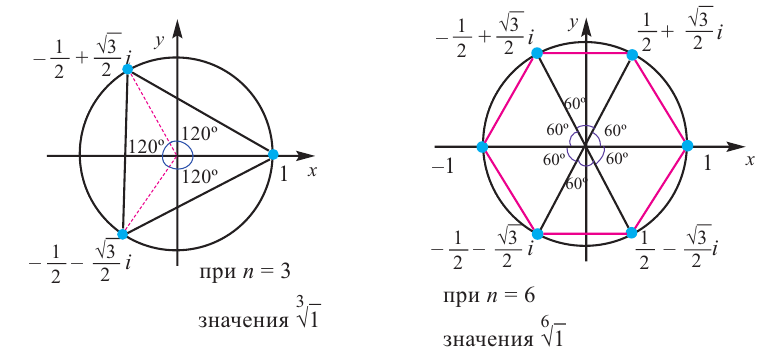
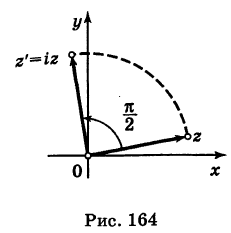
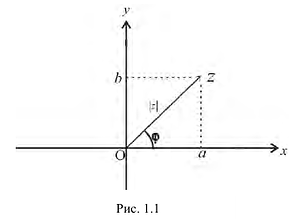
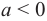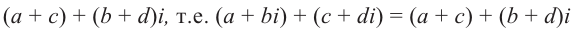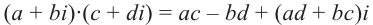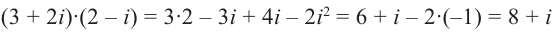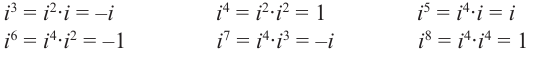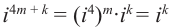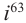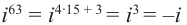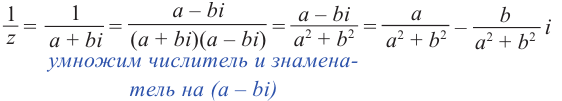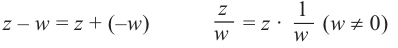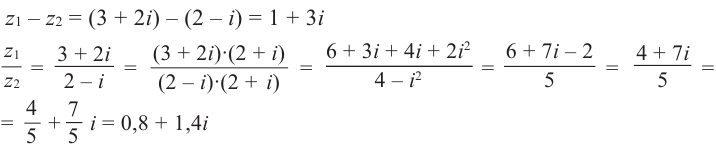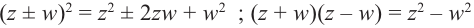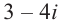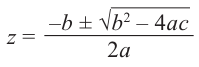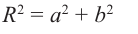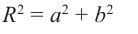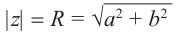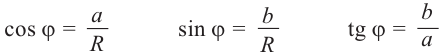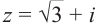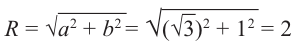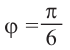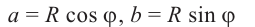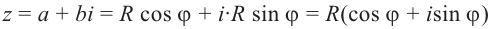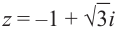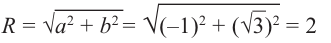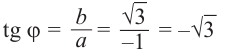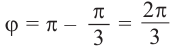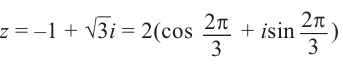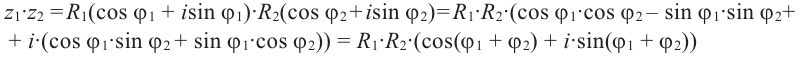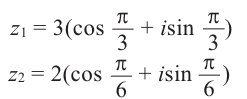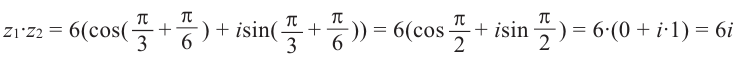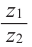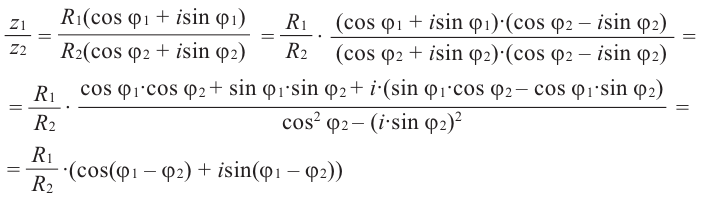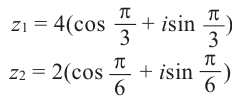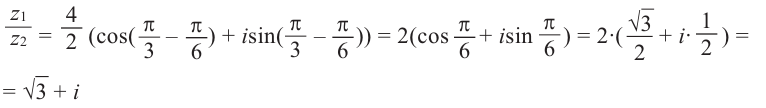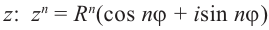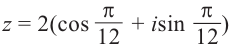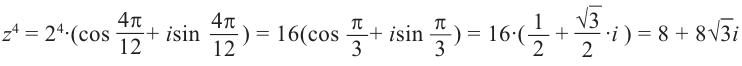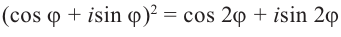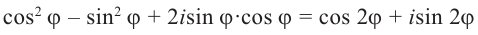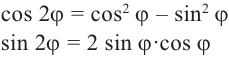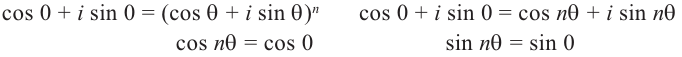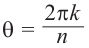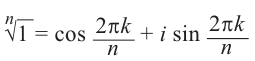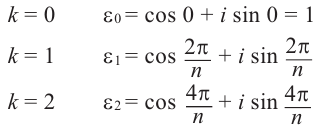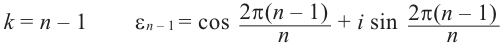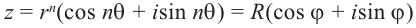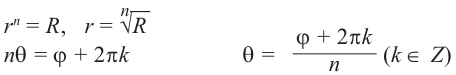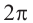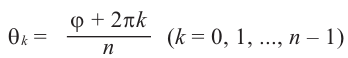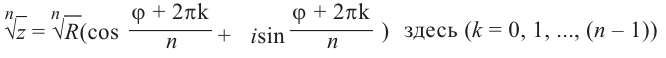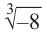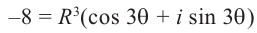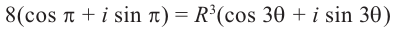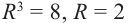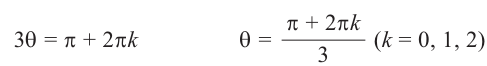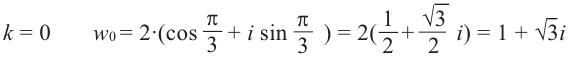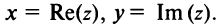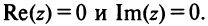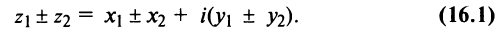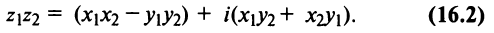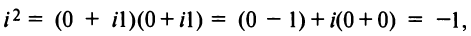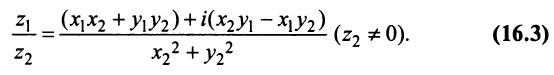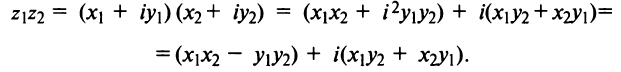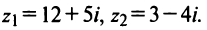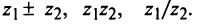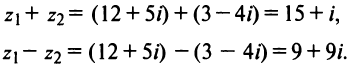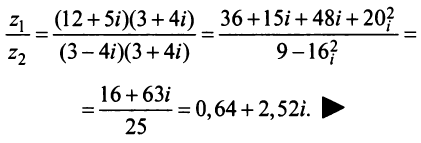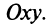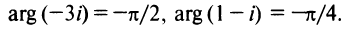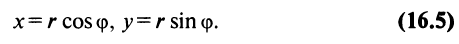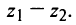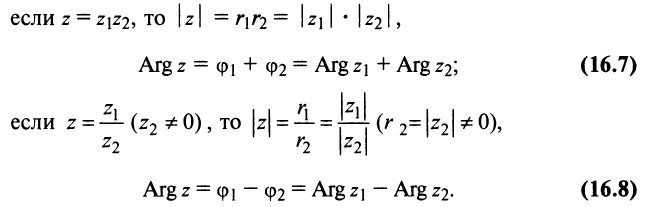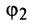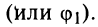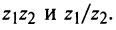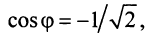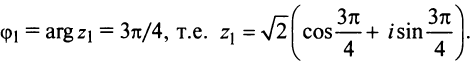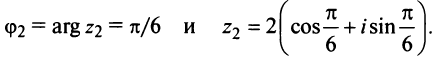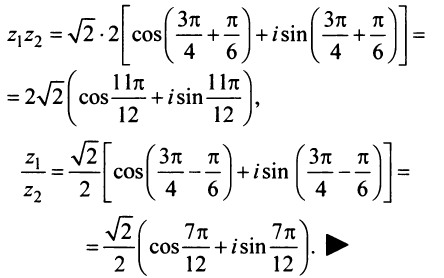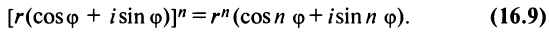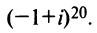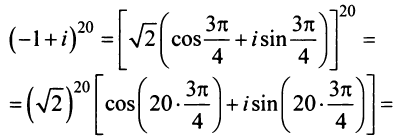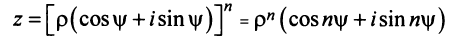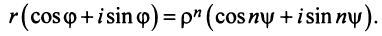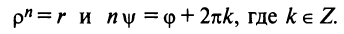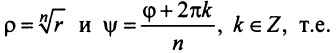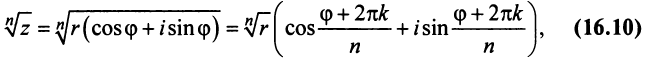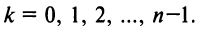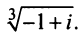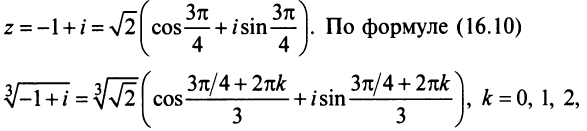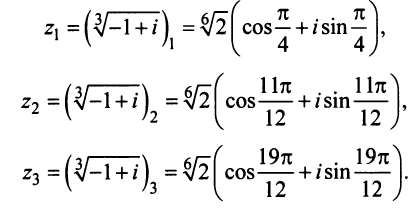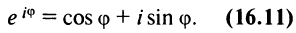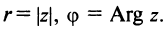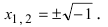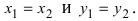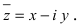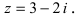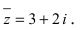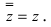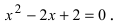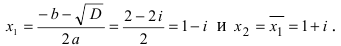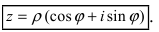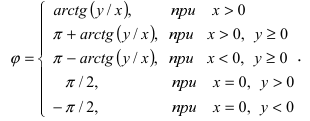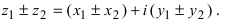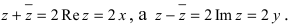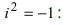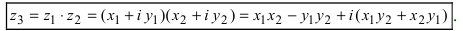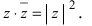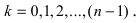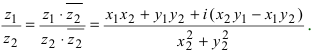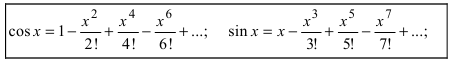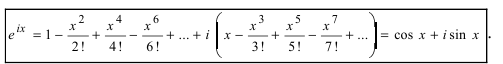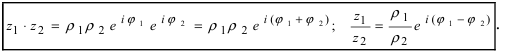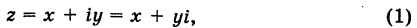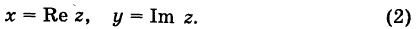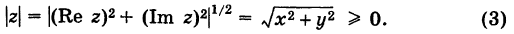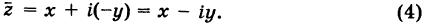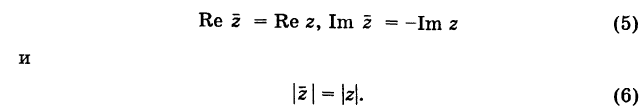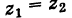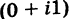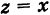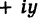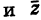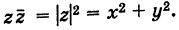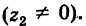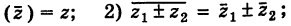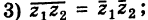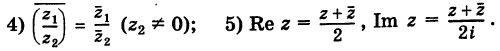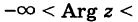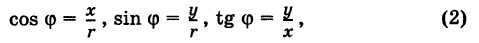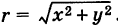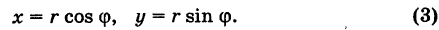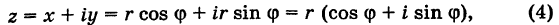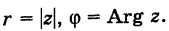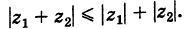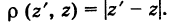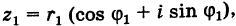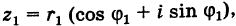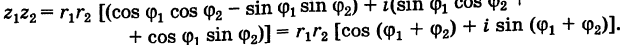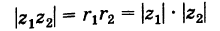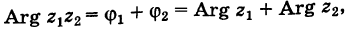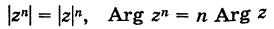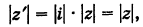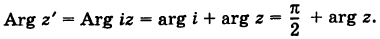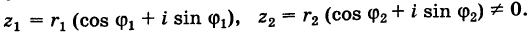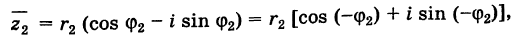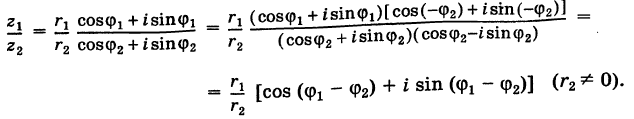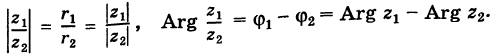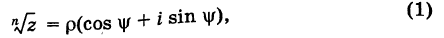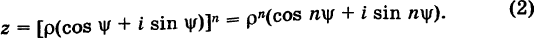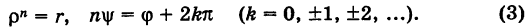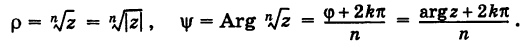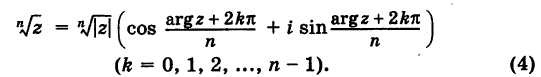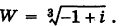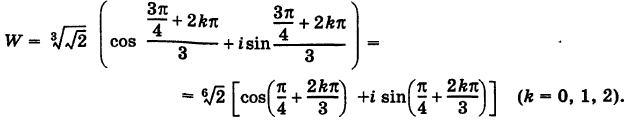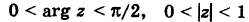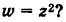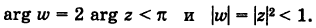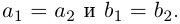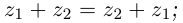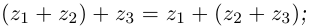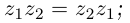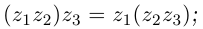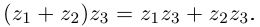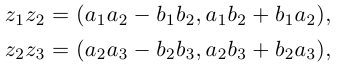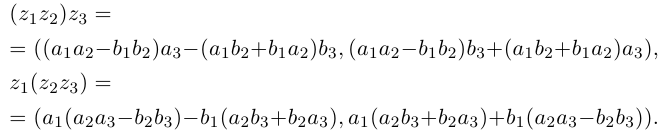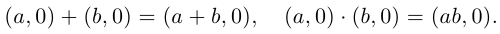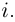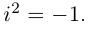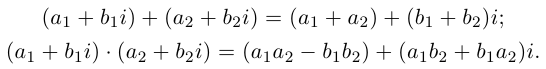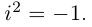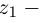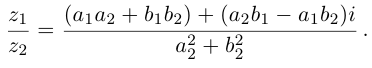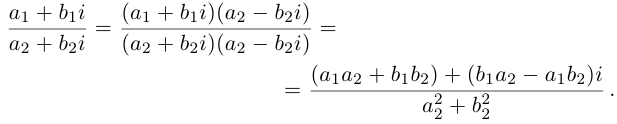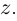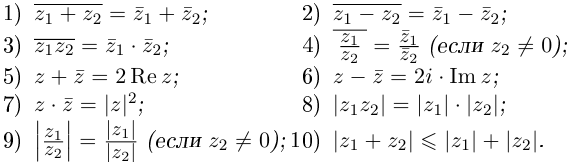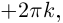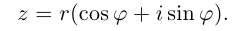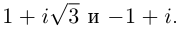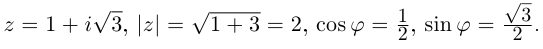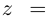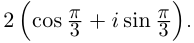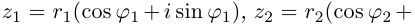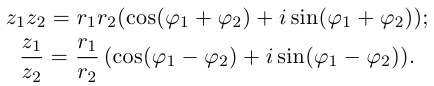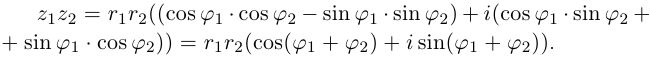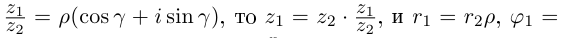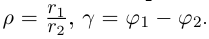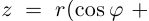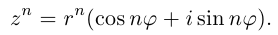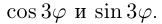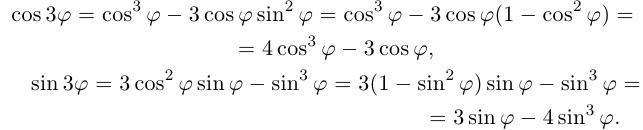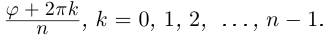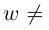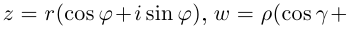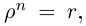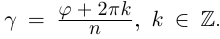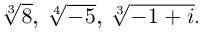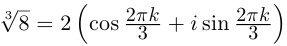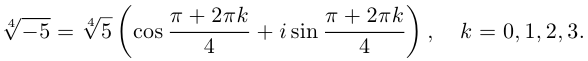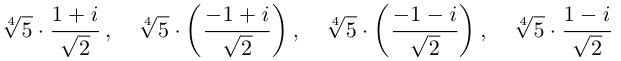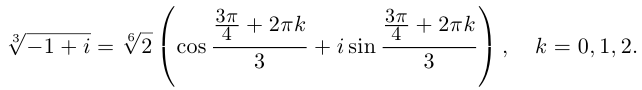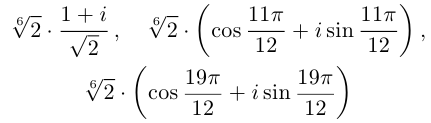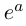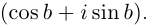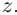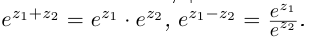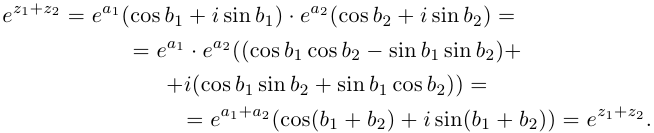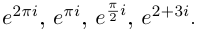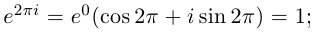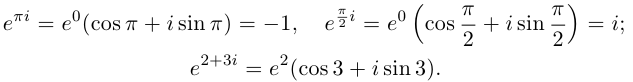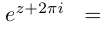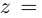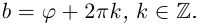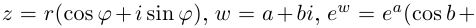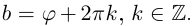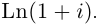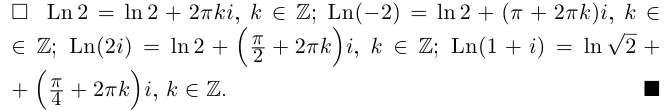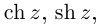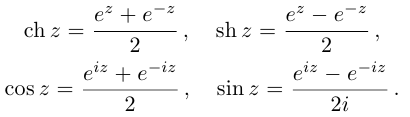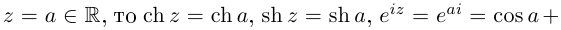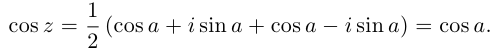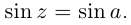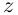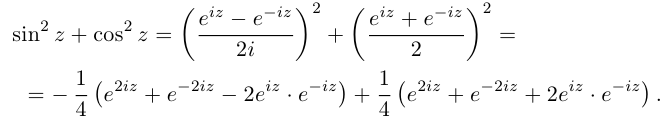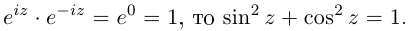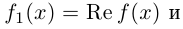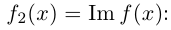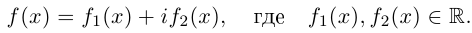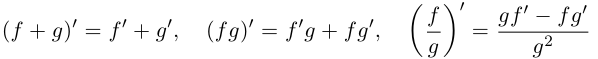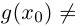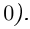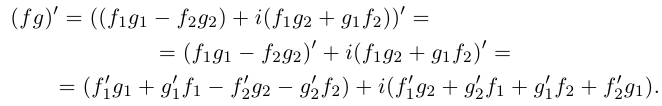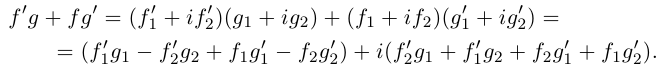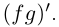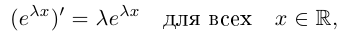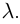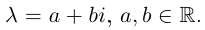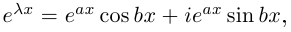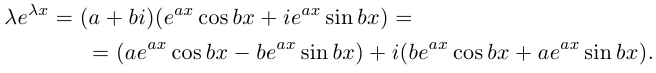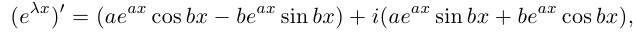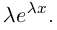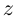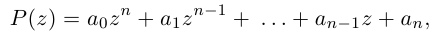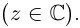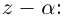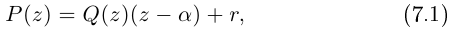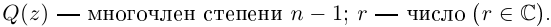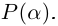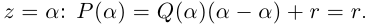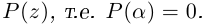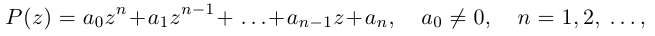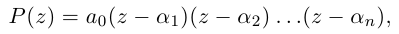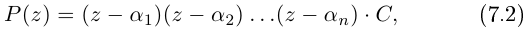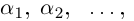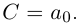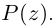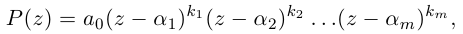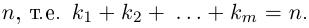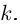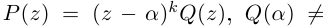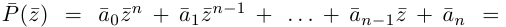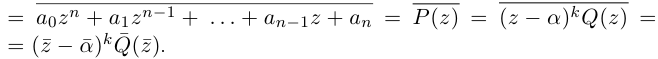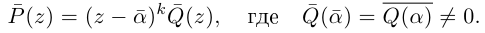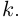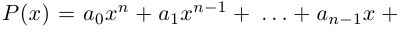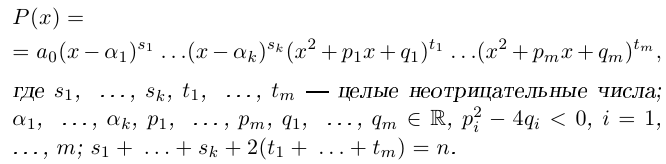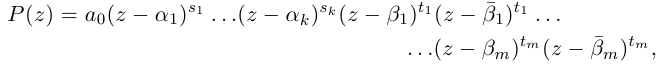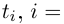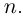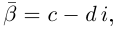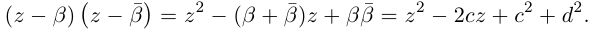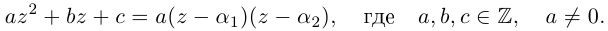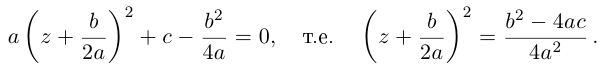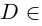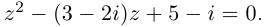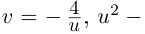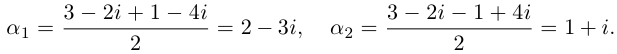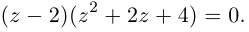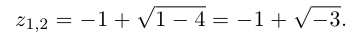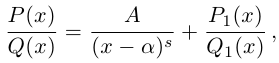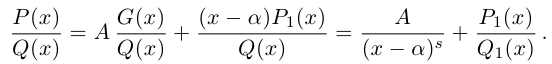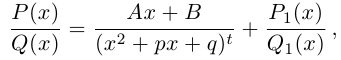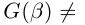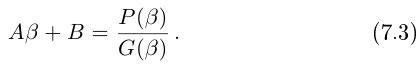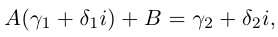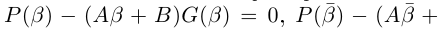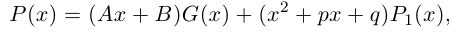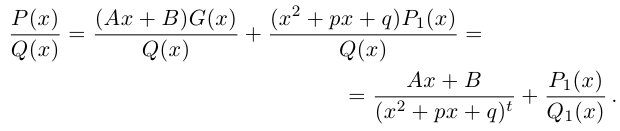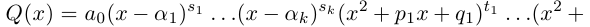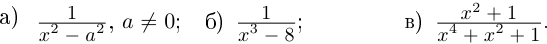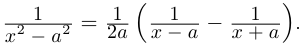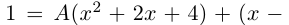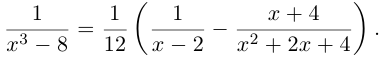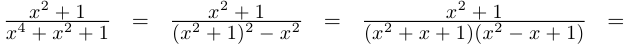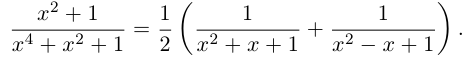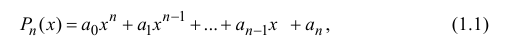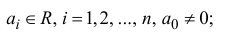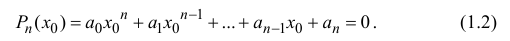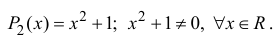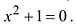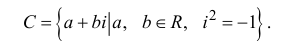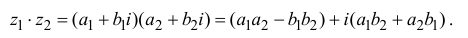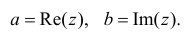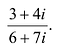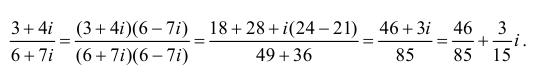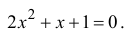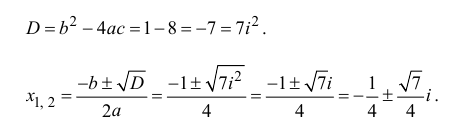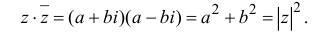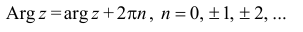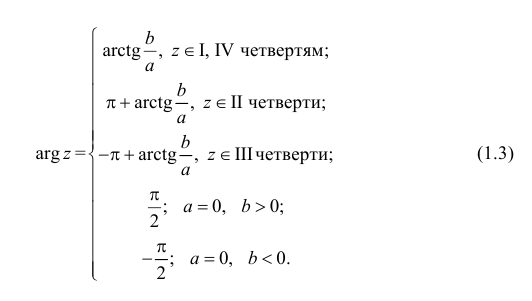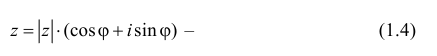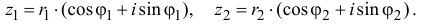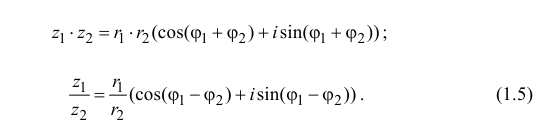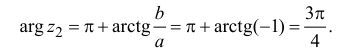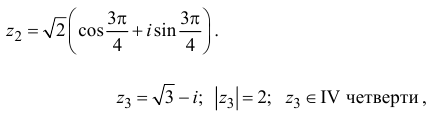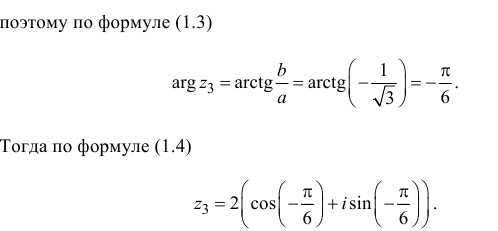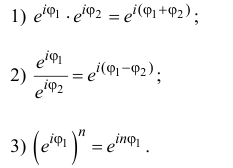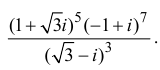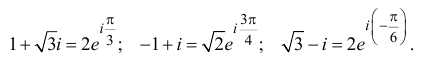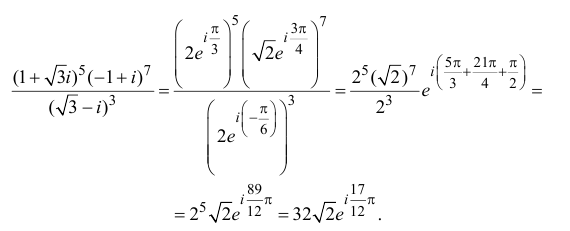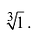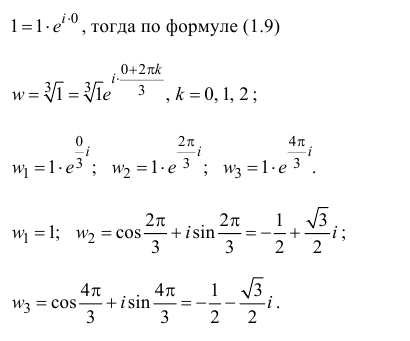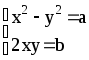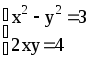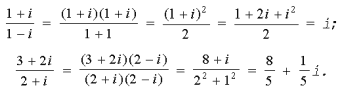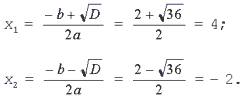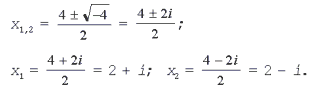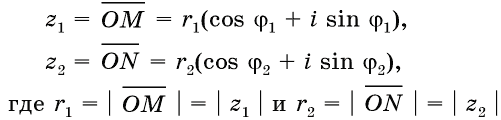Действия над комплексными числами.
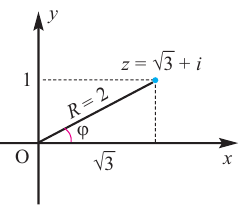
Комплексные числа – числа вида $x+iy,$ где $x,yin mathbb{R,}$ а
$,i,$ такое число, что $ i^2=-1.$ Множество комплексных чисел
обозначается $mathbb{C}.$
Действия над комплексными числами.
Сложение комплексных чисел:
$$(x_1+iy_1)+(x_2+iy_2)=(x_1+x_2)+i(y_1+y_2).$$
Умножение двух комплексных чисел:
$$(x_1+iy_1)(x_2+iy_2)=x_1x_2-y_1y_2+(x_1y_2+x_2y_1)i.$$
Умножение комплексного числа на действительное:
$$lambda(x+iy)=lambda x+ilambda y.$$
Деление комплексных чисел:
$$frac{x_1+iy_1}{x_2+iy_2}=frac{(x_1+iy_1)(x_2-iy_2)}{(x_2+iy_2)(x_2-iy_2)}=frac{x_1x_2+y_1y_2+i(y_1x_2-x_1y_2)}{x_2^2+y_2^2}=$$ $$frac{x_1x_2+y_1y_2}{x_2^2+y_2^2}+frac{y_1x_2-x_1y_2}{x_2^2+y_2^2}i.$$
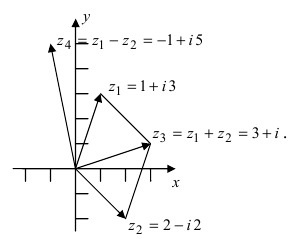
Действительные числа $x$ и $y$ комплексного числа $z=x+iy,$ называются действительной и мнимой частью числа $z$ и обозначаются, соответственно, $Re z=x$ и $Im z=y.$
Два комплексных числа $z_1=x_1+iy_1$ и $z_2=x_2+iy_2$ называются равными в том и только том случае, если $x_1=x_2,$ $y_1=y_2.$
Запись $z=x+iy$ называют алгебраической формой комплексного числа $z.$
Числа $z_1=x+iy$ и $z_2=x-iy$ называют сопряженными.
Примеры:
Выполнить действия над комплексными числами, представив результат в алгебраичекой форме:
1.421. $(2+3i)(3-i).$
Решение:
$(2+3i)(3-i)=6-2i+9i-3i^2=6+7i+3=9+7i.$
Ответ: $9+7i.$
1.424. $(2i-i^2)^2+(1-3i)^3.$
Решение.
$(2i-i^2)^2+(1-3i)^3=(2i+1)^2+1-3(3i)^2+3(3i)-(3i)^3=$ $=4i^2+4i+1-27i^2+9i-27i^3=-4+4i+1+27-9i+27i=24+22i.$
Ответ: $24+22i.$
1.425. $frac{2-i}{1+i}.$
Решение.
$$frac{2-i}{1+i}=frac{(2-i)(1-i)}{(1+i)(1-i)}=frac{2-2i-i+i^2}{1-i^2}=frac{2-3i-1}{1+1}=frac{1-3i}{2}=frac{1}{2}-frac{3}{2}i.$$
Ответ: $frac{1}{2}-frac{3}{2}i.$
{jumi[*4]}
1.428. $frac{(1+i)(3+i)}{3-i}-frac{(1-i)(3-i)}{3+i}.$
Решение.
$$frac{(1+i)(3+i)}{3-i}-frac{(1-i)(3-i)}{3+i}=frac{(1+i)(3+i)(3+i)}{(3-i)(3+i)}-$$ $$-frac{(1-i)(3-i)(3-i)}{(3+i)(3-i)}=frac{9+15i+7i^2+i^3}{9-i^2}-frac{9-15i+7i^2-i^3}{9-i^2}=$$ $$=frac{9+15i-7-i-9+15i+7-i}{10}=frac{28}{10}i=frac{14}{5}i.$$
Ответ: $frac{14}{5}i.$
Найти действительные решения следующего уравнения:
1. 430. $(1+i)x+(-2+5i)y=-4+17i.$
Решение.
$(1+i)x+(-2+5i)y=-4+17iRightarrow$
$x+xi-2y+5yi=-4+17iRightarrow$
$(x-2y)+(x+5y)i=-4+17iRightarrow$
$$left{begin{array}{lcl}x-2y=-4\x+5y=17end{array}right.Rightarrowleft{begin{array}{lcl}x=2y-4\2y-4+5y=17end{array}right.Rightarrowleft{begin{array}{lcl}x=2\y=3end{array}right. .$$
Ответ: $x=2; y=3.$
Домашнее задание.
Выполнить действия над комплексными числами, представив результат в алгебраичекой форме:
1.422. $(1+2i)^2.$
Ответ: $-3+4i.$
1.423. $(1-i)^3-(1+i)^3.$
Ответ: $-4i.$
1.426. $frac{1}{1+4i}+frac{1}{4-i}.$
Ответ: $frac{5}{17}-frac{3}{17}i.$
1.427. $left(frac{1-i}{1+i}right)^3.$
Ответ: $i.$
Найти действительные решения следующего уравнения:
1.431. $12((2x+i)(1+i)+(x+y)(3-2i))=17+6i.$
Ответ: $x=1/3; y=1/4.$
Решить следующие системы линейных уравнений:
1.432. $(3-i)z_1+(4+2i)z_2=1+3i;$
$(4+2i)z_1-(2+3i)z_2=7.$
Ответ: $z_1=1; z_2=i.$
1.433. $(2+i)z_1+(2-i)z_2=6;$
$(3+2i)z_1+(3-2i)z_2=8.$
Ответ: $z_1=2+i; z_2=2-i.$
правильно?
раскроем скобки:
[math]6x+8ix-4y-3iy=5+2i[/math]
перегруппируем слагаемые:
[math]left( 6x-4y right)+left( 8x-3y right)i=5+2i[/math]
По определению равенства двух комплексных чисел приравняем действительную и мнимую части. Получим систему двух уравнений:
[math]left{!begin{aligned}& 6x-4y=5 \& 8x-3y=2 end{aligned}right.[/math]
решим способом подстановки:
[math]x=frac{ 5+4y }{ 6 }[/math]
[math]8 cdot frac{ 5+4y }{ 6 } -3y=2[/math]
[math]frac{ 4(5+4y) -3y-2}{ 3 } =0[/math]
[math]7y+14=0[/math]
[math]y=-2[/math]
[math]x=frac{ 5+4 cdot (-2) }{ 6 } =-frac{ 1 }{ 2 }[/math]
Ответ: [math]x=-frac{ 1 }{ 2 }, y=-2[/math]
Содержание:
Хроника возникновения комплексных чисел:
Исследование.
1) Подтвердите примерами справедливость следующих высказываний. Если высказывание ложно, то сделайте так, чтобы оно стало истинным.
- а) Если а и b – натуральные числа, то корень уравнения х + а = b также является натуральным числом.
- б) Если а и b -целые числа, то корень уравнения ах = b также является целым числом
- в) Если а неотрицательное рациональное число, то корень уравнения х1 = а также является рациональным числом.
- г) Если а неотрицательное действительное число, то корень уравнения х2 = а также является действительным числом.
2) Существует ли действительное число квадрат которого равен -1?
3)
- а) Существуют ли действительные корни уравнения х2 = а при
- б) Можно ли решить эту задачу расширив множество действительных чисел?
4) Существует ли однозначное соответствие между множеством действительных чисел и множеством точек на числовой оси? А какие числа соответствуют точкам на координатной плоскости?
На множестве действительных чисел уравнение х2 = -1 не имеет решений. Значит, мы должны расширить множество действительных чисел так, чтобы корни этого уравнения входили в него. Для этого введём новое число и примем, что оно является корнем уравнения х2 + 1 = 0, т.е. 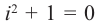
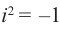
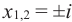
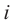
Расширим множество действительных чисел так, чтобы в него входили все действительные числа и число 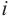
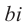
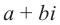
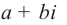
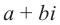
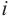
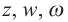
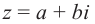
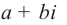
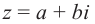
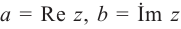
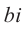
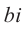
Следствие: для комплексных чисел а + 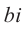
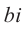
а + 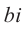
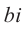
Пример. Из равенства 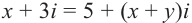
Решение: Из равенства действительных и мнимых частей получаем: х = 5
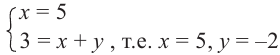
Суммой комплексных чисел 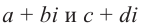
Действия над комплексными числами
Произведением комплексных чисел 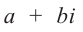
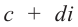
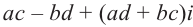
Значит, два комплексных числа умножаются по правилу умножения многочленов при условии, что 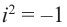
Пример №1
Рассмотрим частные случаи степеней мнимых единиц:
Как видно, натуральные степени мнимой единицы 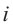
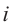
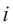
Пример №2
Вычислите: а) 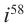
Решение: а) 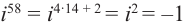
Число 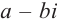
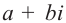
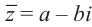
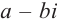
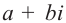
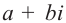
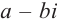
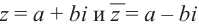
Произведение взаимно сопряжённых комплексных чисел является действительным числом: 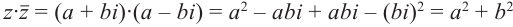
В частном случае, сопряжённым для действительного числа является само число, для мнимого – произведение числа и (-1).
Для каждого комплексного числа 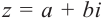
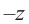
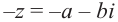
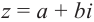
Вычитание и частное комплексных чисел определяется равенствами:
Для нахождения отношения комплексных чисел, удобнее числитель и знаменатель умножить на число, сопряжённое для знаменателя .
Пример №3
Найдём разность и отношение чисел 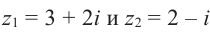
Решение:
Все свойства арифметических операций для действительных чисел, справедливы для комплексных чисел. Как следствие, получаем, что любые алгебраические тождества справедливы для множества комплексных чисел. Например, для комплексных чисел 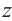
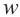
Квадратный корень комплексного числа
Число, квадрат которого равен 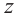
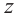
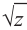
Пример №4
Найдём квадратный корень комплексного числа
Решение: Пусть 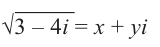
Из равенства действительных и мнимых частей имеем:
Отсюда получаем решение (2; -1) и (-2; 1). Значит,
Примечание: В отличии от действительных чисел, говоря о квадратном корне комплексного числа, имеется в виду каждое из двух значений, различающихся знаками. Корни квадратного уравнения 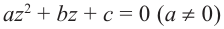
Пример №5
Решим уравнение 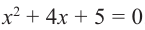
Решение:
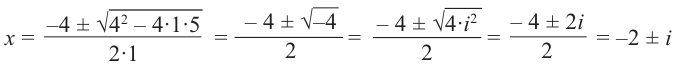
Легко можно проверить, что также в силе остаётся и теорема Виета. Для квадратного уравнения с действительными коэффициентами комплексные корни являются сопряжёнными числами. Комплексное число 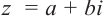
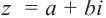
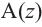
Пример:
Точки, соответствующие комплексно сопряжённым числам располагаются симметрично оси абсцисс.
Модуль и аргумент комплексного числа
Тригонометрическая форма комплексного числа
Пусть на комплексной плоскости комплексному числу 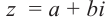
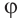
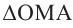
Отсюда:
Расстояние, от начала координат до точки соответствующей комплексному числу, называется модулем комплексного числа и обозначается как: 
Угол, образованный конечной стороной угла поворота луча ОМ,
называется аргументом 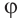
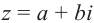
Из 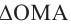
Модуль числа 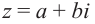
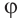
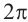
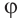
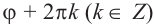
Для аргумента комплексного числа, обычно берётся угол принадлежащий промежутку [0; 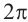
Пример №6
Найдём модуль и аргумент комплексного числа
Решение: Из того, что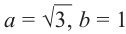
и принимая внимание, что угол 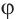
получим:
Из формул 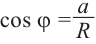
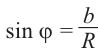
Тогда
Для комплексного числа 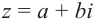
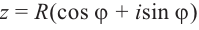
В частном случае для модуля и аргумента числа 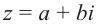
Пример №7
Запишем комплексное число
в тригонометрической форме.
Решение:
Так как угол 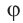
Действия над комплексными числами, заданными в тригонометрической форме
Найдём произведение комплексных чисел, заданных в тригонометрической форме 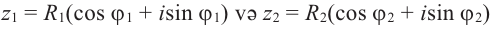
Чтобы найти произведение комплексных чисел, заданных в тригонометрической форме, надо перемножить их модули и сложить их аргументы.
Пример:
Теперь найдём отношение
Модуль отношение равен отношению модулей делимого и делителя, а аргумент равен разности аргументов делимого и делителя.
Пример:
Возвести число 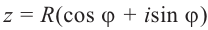
Модуль степени комплексного числа с натуральным показателем равен степени модуля основания, а аргумент равен аргументу основания умноженному на показатель степени n.
Пример:
Формулу 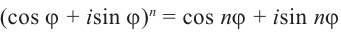
Отсюда
Из равенства двух комплексных чисел имеем:
Аналогичным образом можно написать формулы для 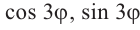
Корень n-ой степени комплексного числа
Найдём значение выражения 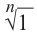
Запишем в виде 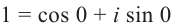
виде 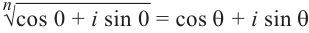
Возведём каждую из двух сторон в n-ую степень:
Если два комплексных числа, заданных в тригонометрической форме равны, то их модули равны, а аргументы отличаются на 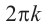
Это значит,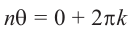
Таким образом,
Отсюда при 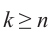
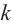

Обозначим корни 
Как видно, модули корней 
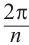

Корнем 
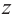
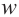
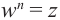
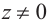


Запишем 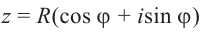
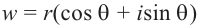
Для 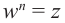
Из равенства двух комплексных чисел получим:
Значения при 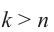

Поэтому, должно соблюдаться следующее:
Формула корни n-ой степени комплексного числа
Если 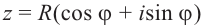
Пример №8
Найдём все значения
Решение: пусть 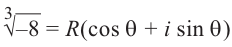
Отсюда
При
При
При
Для чего нужны комплексные числа
Комплексные числа возникают в связи с задачей решения квадратных уравнений. Так, оставаясь в множестве действительных чисел, невозможно решить квадратное уравнение, дискриминант которого меньше нуля.
Комплексные числа необходимы в различных приложениях математики. В частности, теория функций комплексной переменной является действенным инструментом при использовании математических методов в различных областях науки.
Арифметические операции над комплексными числами
Комплексным числом называется выражение вида 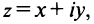
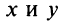
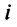
Число 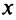
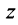
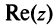
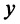
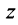
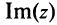
Действительное число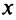
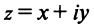
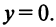
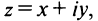
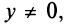
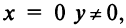
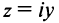
Числа 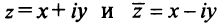
Два комплексных числа 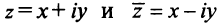
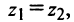
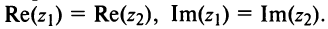
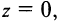
Арифметические операции на множестве комплексных чисел определяются следующим образом.
1.Сложение (вычитание) комплексных чисел
2. Умножение комплексных чисел
В частности,
т.е. мнимая единица есть число, квадрат которого равен — 1.
3. Деление двух комплексных чисел
Нетрудно убедиться в том, что все арифметические операции (16.1)-(16.3) над комплексными числами определяются естественным образом из правил сложения и умножения многочленов 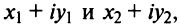
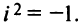
Пример №9
Даны комплексные числа
Найти
Решение:
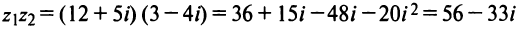
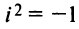
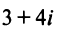
Если для геометрического изображения действительных чисел используются точки числовой прямой, то для изображения комплексных чисел служат точки координатной плоскости
Плоскость называется комплексной, если каждому комплексному числу 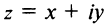
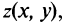
Оси 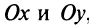
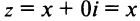
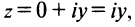
Тригонометрическая и показательная формы комплексного числа
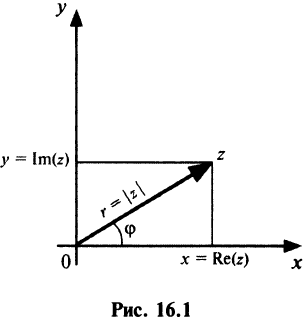
С каждой точкой 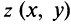
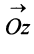
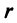
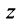
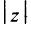
Угол 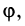
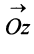
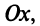
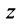
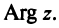
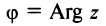
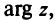
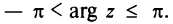
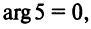
Очевидно (см. рис. 16.1), что
Следовательно, комплексное число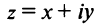
Представление комплексного числа в виде (16.6), где 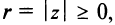
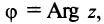
Сформулируем некоторые свойства арифметических операций над комплексными числами.
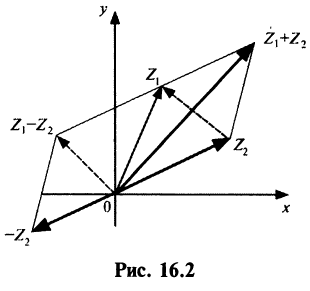
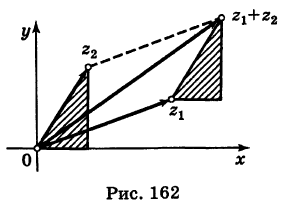
1. При сложении (вычитании) комплексных чисел их радиусы-векторы складываются (вычитаются) по правилу параллелограмма.
На рис. 16.2 показаны радиусы-векторы комплексных чисел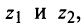
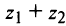
2. Модуль произведения (частного) двух комплексных чисел равен произ ведению (частному) модулей этих чисел, а его аргумент — сумме (разности) аргументов этих чисел, т.е.
Геометрически умножение числа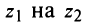
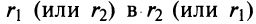
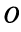
Пример №10
Комплексные числа 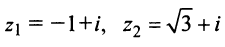
Решение:
По формуле (16.4) найдем модуль комплексного числа 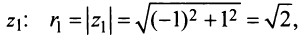
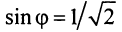
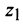
Аналогично 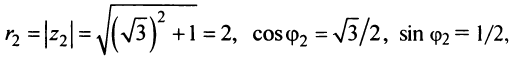
Теперь по формулам (16.7) и (16.8)
Так как в соответствии с формулами (16.7) и (16.8) при умножении комплексных чисел их модули перемножаются, а аргументы складываются, легко получить формулу возведения комплексного числа в натуральную степень 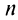
Пример №11
Найти
Решение:
По формуле Муавра (16.9)
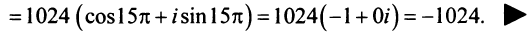
Пусть
Тогда, используя определение корня и формулу Муавра (16.9), получим
или
Отсюда следует, что
Итак,
где
При 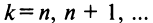
Таким образом, корень 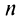
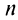
Пример №12
Найти
Решение:
В примере 16.2 было получено
откуда получаем три значения корня
На комплексной плоскости найденные значения корня представляют равноотстоящие друг от друга точки 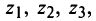
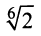
Связь между тригонометрическими и показательными функциями выражается формулой Эйлера.
Отсюда следует показательная форма комплексного числа.
где
В заключение отметим, что в показательной форме, так же как и в тригонометрической, легко проводить операции умножения, деления, возведения в степень, извлечение корня из комплексных чисел.
Формы записи комплексного числа
Решение простейшего квадратного уравнения 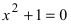
Определение: Выражение 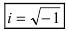
Определение: Комплексным числом называется выражение вида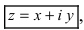
Определение: Приведенная форма записи комплексного числа называется алгебраической.
Определение: Два комплексных числа 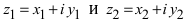
Определение: Комплексное число называется нулевым, если вещественная и мнимая части равны нулю.
Определение: Комплексно-сопряженным к комплексному числу 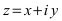
Пример №13
Записать комплексно-сопряженное число к комплексному числу
Решение:
Согласно определению комплексно-сопряженного числа получаем
Замечание: Двойное комплексное сопряжение приводит к исходному комплекс- ному числу, т.е.
Решение квадратных уравнений с отрицательным дискриминантом невозможно в области вещественных чисел, так как нельзя извлекать корень четной степени из отрицательного числа на множестве действительных чисел. Однако это ограничение снимается в области комплексных чисел.
Пример №14
Решить квадратное уравнение
Решение:
Вычислим дискриминант уравнения 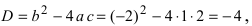
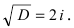
Замечание: Решение квадратного уравнения с отрицательным дискриминантом всегда состоит из комплексно-сопряженных корней.
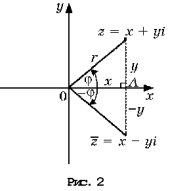
Комплексное число 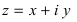
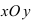
Рис. 2. Изображение комплексного числа на комплексной плоскости.
Пример №15
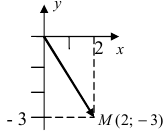
Изобразить на комплексной плоскости число z = 2-3i (Рис. 3).
Решение:
Рис. 3. Изображение комплексного 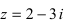
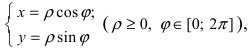
Определение: Полученная форма записи комплексного числа называется тригонометрической.
Обратный переход от полярной системы отсчета к декартовой системе координат осуществляется по формулам: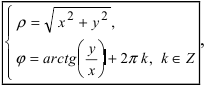
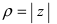
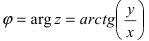
Замечание: Аргумент комплексного числа 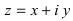
Действия с комплексными числами
1. Для того чтобы сложить (найти разность) два комплексных числа 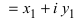
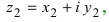
Пример №16
Найти сумму и разность чисел 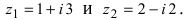
Решение:
Найдем сумму заданных комплексных чисел 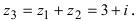
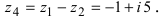
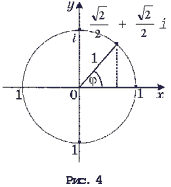
Рис. 4. Изображение комплексных чисел на комплексной плоскости.
Замечание: Отметим, что
2. Для того чтобы найти произведение двух комплексных чисел 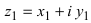
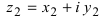
Замечание: Отметим, что
Замечание: Произведение комплексных чисел в тригонометрической форме записи имеет вид 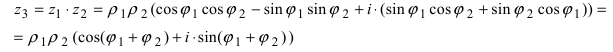
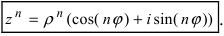
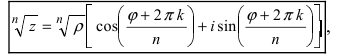
3. Деление комплексного числа 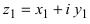
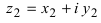
Замечание: Деление этих чисел в тригонометрической форме записи имеет вид: 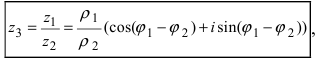
Показательная форма записи комплексного числа
Известно, что любую дифференцируемую функцию можно представить по формуле Тейлора-Маклорена (см. Лекцию № 22, Первый семестр), например,
Последняя формула называется формулой Эйлера. Используя эту формулу,
запишем комплексное число 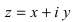
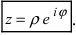
Комплексные числа и арифметические операции
Как известно, под комплексным числом понимается выражение вида
где х и у — действительные числа, a i — мнимая единица.
Числа вида 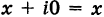
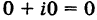
Действительные числа х и у называются соответственно действительной и мнимой частями числа z и обозначаются следующим образом:
Под модулем комплексного числа z понимается неотрицательное число
Сопряженным числом 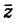
Таким образом,
На множестве комплексных чисел следующим образом определено отношение равенства двух чисел, а также операции сложения, вычитания, умножения и деления.
I. Пусть z1=x1+iy1 и z2=x2+iy2.Тогда
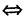
В частности, z = 0 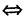
II. z1±z2= (x1± x2) + i(y1 ± y2)-
Отсюда следует, что
Re (z1 ± z2) – Re z1 ± Re z2,
Im (z1 ± z2) – Imz1 ± 1mz2
III. z1z2 = (x1x2 – y1y2) + i(x1y2+x2y1).
Отсюда, в частности, получаем важное соотношение
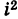
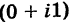
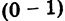
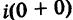
Заметим, что правило умножения III получается формально путем умножения двучленов 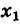
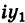
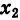
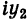
Очевидно также, что для 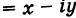
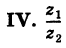
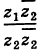
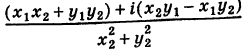
Легко проверить следующие свойства:
1)
- Заказать решение задач по высшей математике
Комплексная плоскость
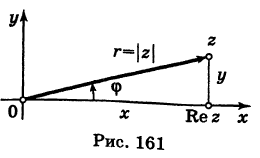
Рассмотрим плоскость с прямоугольной системой координат Оху. Каждому комплексному числу z = х + iy может быть поставлена в соответствие точка плоскости z(x, у) (рис. 161), причем это соответствие взаимно однозначно. Плоскость, на которой реализовано такое соответствие, называют комплексной плоскостью, и вместо комплексных чисел говорят о точках комплексной плоскости.
На оси Ох расположены действительные числа: z =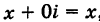
Заметим, что г = |z| представляет собой расстояние точки г от начала координат.
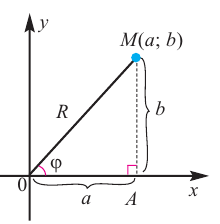
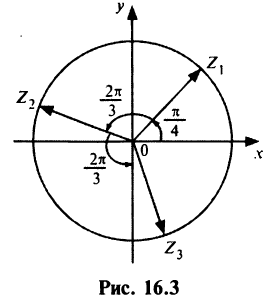
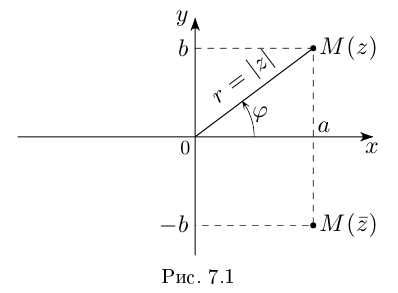
С каждой точкой z связан радиус-вектор этой точки Oz; угол, образованный радиусом-вектором точки z с осью Ох, называется аргументом ф = Arg z этой точки. Здесь 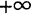
Для аргумента ср имеем (рис. 161)
где
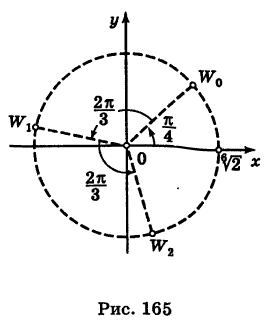
Примеры: 1) arg 2 = 0; 2) arg (-1) = 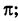
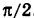
Модуль г и аргумент ф комплексного числа z можно рассматривать (рис. 161) как полярные координаты точки z. Отсюда получаем
Таким образом, имеем тригонометрическую форму комплексного числа
где
Теорема: При сложении комплексных чисел их радиусы-векторы складываются (по правилу параллелограмма).
Действительно, если число 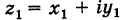
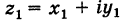
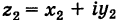
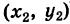
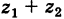
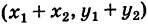
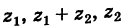
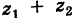
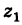
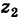
Следствие. Так как 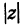
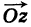
Теорема: При вычитании комплексных чисел их радиусы-векторы вычитаются. Так как 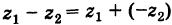

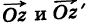
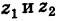
Следствие. Расстояние между двумя точками 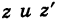
Теоремы о модуле и аргументе
Теорема: Модуль произведения комплексных чисел равен произведению модулей этих чисел, а аргумент произведения равен сумме аргументов сомножителей. Действительно, если
то имеем
Отсюда
и
где значения многозначной функции Arg, стоящие в левой и правой частях равенства (1), следует подбирать соответствующим образом. Это замечание надо иметь в виду и для дальнейшего.
Следствие. Модуль целой положительной степени комплексного числа равен такой же степени модуля этого числа, а аргумент степени равен аргументу числа, умноженному на показатель степени, т. е.
(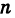
Доказательство непосредственно вытекает из рассмотрения произведения равных сомножителей.
Пример №17
Построить точку 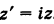
Решение:
Имеем
Следовательно, при умножении на i вектор 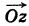
Теорема: Модуль частного двух комплексных чисел равен частному модулей этих чисел, а аргумент частного равен разности аргументов делимого и делителя. Пусть
Так как
то на основании теоремы 1 имеем
Отсюда
Извлечение корня из комплексного числа
Пусть
где 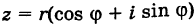
Отсюда получаем
Таким образом,
Заметим, что здесь под 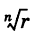
Здесь в качестве числа k достаточно брать лишь значения 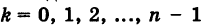
Из формулы (4) следует, что корень 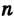
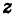
Пример №18
Найти
Решение:
Так как 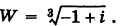
Отсюда
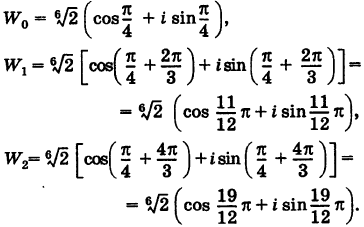
Точки 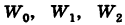
Понятие функции комплексной переменной
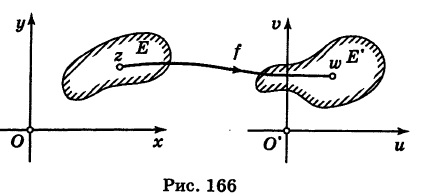
Пусть даны две комплексные плоскости Оху (плоскость г) и O’uv (плоскость w).
Определение: Если каждой точке z 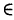
с областью определения Е, значения которой принадлежат множеству Е’ (рис. 166). Если множество значений функции f(z) исчерпывает все множество Е то Е’ называется множеством значений (областью изменения) функции f(z). В этом случае пишут
Множества Е и Е’ можно изображать на одной комплексной плоскости.
Таким образом, каждая комплексная функция реализует однозначное в одну сторону отображение одного множества на другое. Благодаря этому комплексные функции находят свое применение в таких науках, как гидродинамика и аэродинамика, так как с их помощью удобно описывать «историю» движения объема жидкости (или газа).
Раздел математики, изучающий свойства комплексных функций, носит название теории функций комплексной переменной.
Пример:
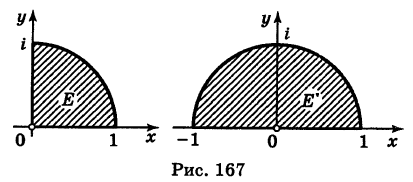
Во что переходит сектор Е
(рис. 167, а) при отображении
Решение:
Имеем
Поэтому отображенная область E’ представляет собой полукруг (рис. 167, б).
Определение комплексных чисел
Определение комплексного числа и основные функции комплексной переменной
Определение 7.1. Множеством комплексных чисел 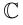
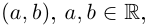
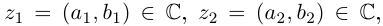
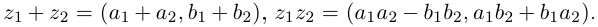
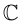
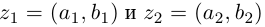
Операции сложения и умножения на множестве 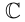
Лемма 7.1. Для любых комплексных чисел 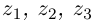
- 1)
- 2)
- 3)
- 4)
- 5)
□ Докажем, например, свойство 4 (свойство 5 доказывается аналогично, свойства 1, 2, 3 очевидны).
Пусть 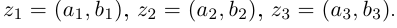
Два последних комплексных числа совпадают. После раскрытия скобок оказывается, что оба они равны
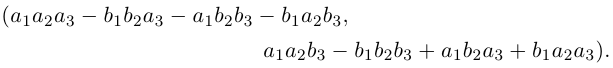
Определение 7.2. Комплексное число 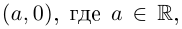
Это определение оправдывается тем, что установлено взаимно однозначное соответствие между множеством пар 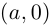
Такое соответствие в высшей алгебре называется изоморфизмом.
Определение 7.3. Комплексное число (0,1) обозначается буквой
Легко видеть, что 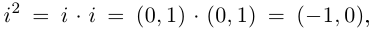
Далее, так как 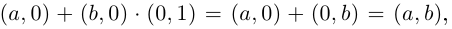
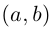
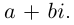
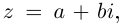
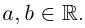
Иными словами, комплексные числа можно складывать и умножать, пользуясь известными законами сложения и умножения (лемма 7.1), имея в виду, что
Определение 7.4. Разностью двух комплексных чисел 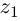
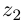
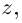
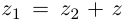
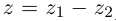
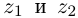
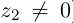
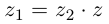
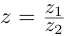
Проверим, что эти операции однозначно определены.
□ Пусть 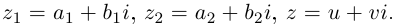
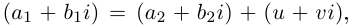
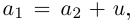
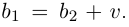
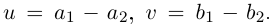
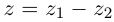
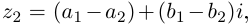
Для частного имеем: 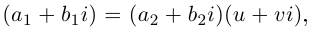
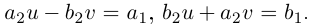
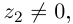
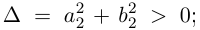
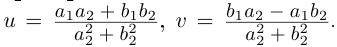
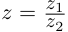
Такое деление можно осуществлять непосредственно:
Комплексное число 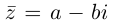
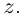
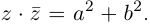
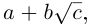
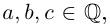

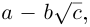
Определение 7.5. Пусть 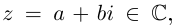
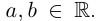
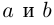
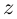
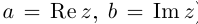
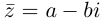
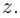
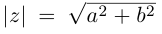
Лемма 7.2. Для любых комплексных чисел 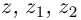
Доказать эти утверждения будет предложено самостоятельно в качестве упражнения.
Множество комплексных чисел 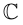
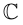
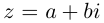
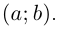
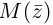
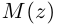
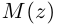
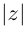
Аргументом числа 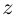
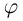
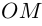
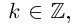
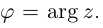
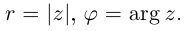
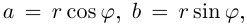
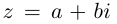
Пример:
Записать в тригонометрической форме числа
□ 1)
При записи комплексного числа в тригонометрической форме обычно берут одно фиксированное («наиболее простое») значение аргумента. Возьмём 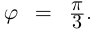
2) 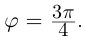
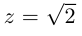
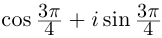
Комплексные числа, записанные в тригонометрической форме, удобно умножать и делить. При умножении модули чисел перемножаются, аргументы складываются. При делении модули делятся, аргументы вычитаются.
Лемма 7.3. Пусть 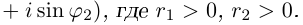
Если
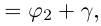
Степень с целым показателем для комплексных чисел определяется так же, как и для действительных. Поэтому мы можем сформулировать
Следствие (формула Муавра). Если 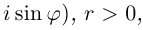
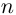
Иными словами, при возведении комплексного числа в целую степень модуль числа возводится в эту степень, а аргумент умножается на показатель степени.
Пример:
Применяя формулу Муавра, получить известные формулы тригонометрии для
□ Имеем: 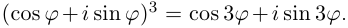
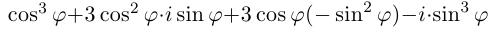
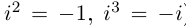
Определение 7.6. Пусть 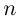
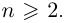
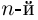
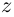
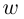
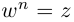
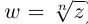
Лемма 7.4. Если 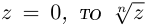
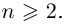
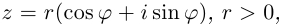
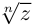
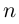
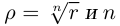
□ Правая часть леммы очевидна, так как 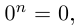
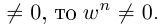
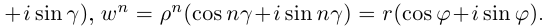
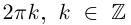
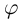
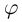
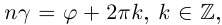
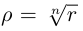
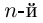
При замене 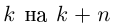
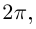
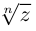
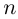
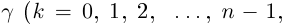
Замечание. 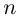
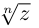
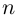
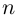
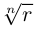
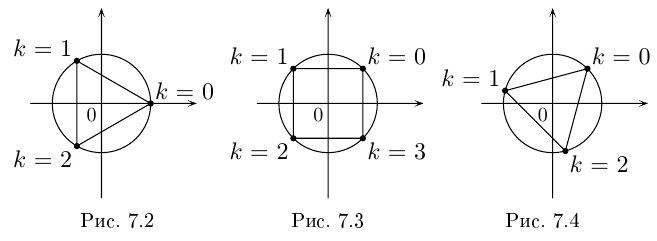
Пример №19
Найти все значения
□ 1) 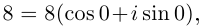
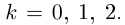
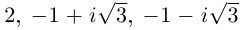
Первое из них — арифметическое значение кубического корня из положительного числа 8.
2) 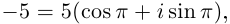
Получим 4 значения:
(см. рис. 7.3). 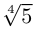
3) 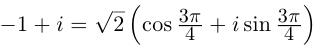
Получим 3 значения:
(см. рис. 7.4). ■
Определение 7.7. Пусть 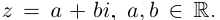
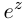
Если 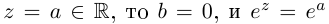
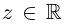
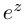
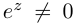
Лемма 7.5. Для любых 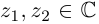
□ Пусть 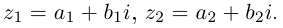
Далее, так как 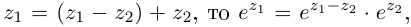
Пример №20
Вычислить
□ Имеем:
Так как при всех 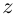
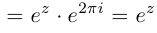
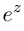
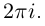
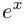
Определение 7.8. Логарифмом комплексного числа 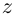
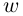
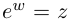
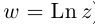
Лемма 7.6. Если 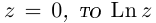
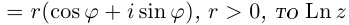
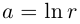
□ Первая часть леммы следует из того, что 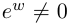
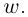
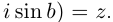
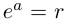
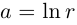
Таким образом, множество значений функции 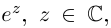
Пример №21
Найти все значения 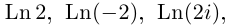
Определение 7.9. Для любых 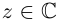
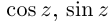
Если
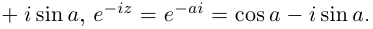
Аналогично,
Отметим также, что все известные формулы тригонометрии сохраняются для комплексных значений аргументов (при этом 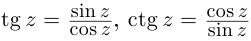
Так как
Легко видеть, что 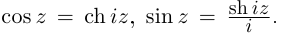
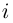
Комплекснозначные функции действительной переменной
Рассмотрим функцию 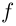
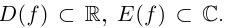
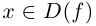
Так как 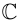
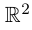
Определение 7.10. Комплекснозначная функция действительной переменной 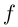
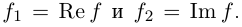
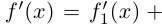
Для комплекснозначных функций сохраняются формулы производной суммы, произведения и частного.
Лемма 7.7. Если комплекснозначные функции действительной переменной 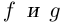
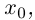
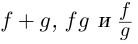
в точке 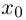
□ Докажем лемму для случая производной произведения. Утверждение для производной суммы доказывается проще, а для производной частного — несколько сложнее, но, по сути дела, аналогично.
Пусть 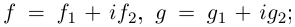
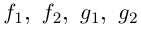
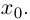
Функция 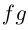
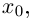
Легко видеть, что это выражение совпадает с
Пример №22
Доказать, что при любом 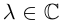
т.е. привычная для действительных 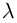
□ Пусть
Тогда
С другой стороны,
что совпадает с
Отметим, что производная комплекснозначной функции берётся по действительной переменной. Принципиально иная ситуация возникает при рассмотрении комплекснозначных функций комплексной переменной и при дифференцировании их по комплексной переменной. Здесь имеют место совершенно неожиданные эффекты (например, если функция дифференцируема в окрестности точки, то она имеет производные всех порядков в этой окрестности), которые студенты обычно изучают на III курсе (курс ТФКП — теория функций комплексной переменной).
Многочлены
Функция комплексной переменной
где 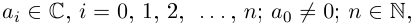
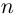
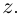
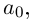
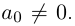
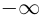
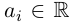
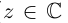
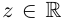
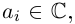
Если 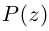
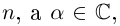
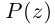
где
Теорема 7.1 (Безу). Остаток от деления многочлена 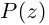
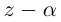
□ Из (7.1) имеем при
Следствие. Многочлен 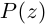

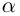
□ Утверждение немедленно следует из теоремы Безу.
Таким образом, число 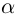
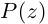
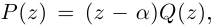
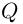
Теорема 7.2 (основная теорема алгебры). Любой многочлен степени 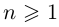
В настоящее время мы не располагаем математическим аппаратом для доказательства этой теоремы, поэтому примем её без доказательства. Доказана она будет очень просто в курсе ТФКП (и даже двумя способами — как простое следствие из теоремы Лиувилля или теоремы Руше).
Теорема 7.3. Многочлен с комплексными коэффициентами
раскладывается в произведение линейных множителей
где 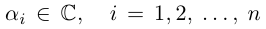
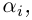
□ По основной теореме алгебры 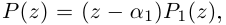
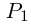
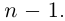
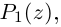
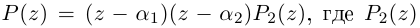
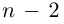
где 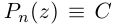
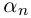
Если раскрыть скобки в правой части (7.2), то коэффициент при 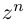
Определение 7.11. Комплексное число 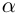
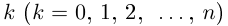
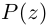
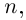
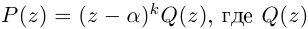
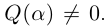
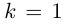
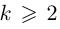
Если 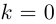
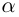
В общем случае, учитывая кратность корней, многочлен 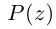
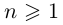
где все комплексные числа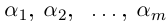
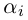
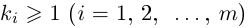
Лемма 7.8. Пусть 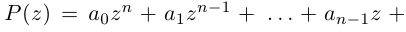
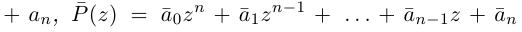
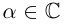
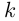
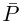
□ Так как 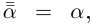
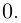
Так как 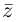
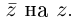
Это и означает, что 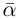
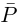
Следствие. Если 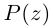
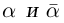
□ Это очевидно из леммы 7.8, так как 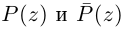
Теорема 7.4. Многочлен степени 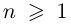
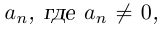
□ По теореме 7.3 и лемме 7.8
где 
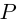


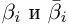

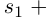
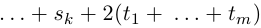
Пусть 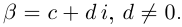
Получили квадратный трёхчлен с действительными коэффициентами 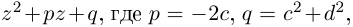
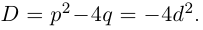
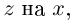
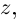
Теорема 7.4 является примером утверждения, в формулировке которого отсутствуют комплексные числа (чисто действительное утверждение), а естественное доказательство его получается с выходом во множество комплексных чисел. Таких утверждений можно встретить немало в различных математических курсах и прикладных науках.
Кстати, квадратный трехчлен с комплексными коэффициентами имеет такой же вид разложения на линейные множители, как и квадратный трёхчлен с действительными корнями в элементарной алгебре:
Корни 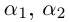
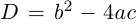
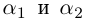
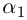
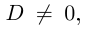
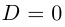
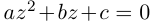
Если 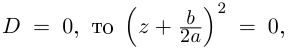
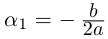
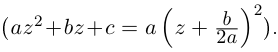
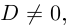
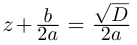
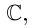
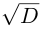
Пример №23
Решить уравнение
□ 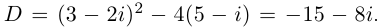
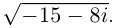
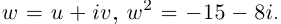
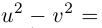
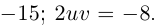
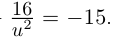
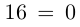
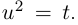
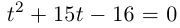
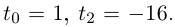
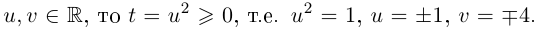
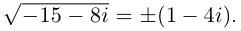
Пример №24
Найти все значения 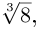
□ Левая часть раскладывается на множители:
Поэтому один из корней равен 2. Квадратный трёхчлен 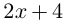
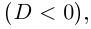
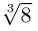
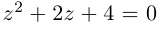
Во множестве комплексных чисел 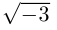
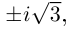
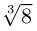
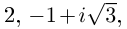
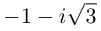
Разложение правильной дроби в сумму простейших дробей
Мы будем рассматривать действительные дробно-рациональные функции 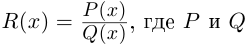
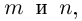
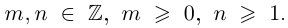
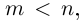
Лемма 7.9. Если 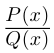
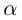
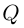
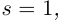
где 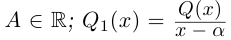
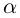
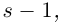
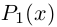
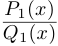
□ Так как 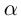
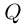
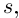
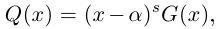
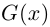
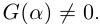
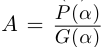
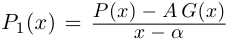
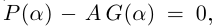
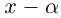
Так как степень G меньше степени Q и степень Р меньше степени Q, то степень числителя последней дроби меньше степени Q; значит, степень 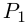
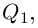
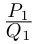
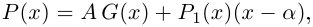
Утверждение леммы, очевидно, сохраняется, если все числа и многочлены считать комплексными.
Лемма 7.10. Пусть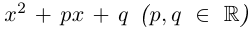
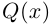
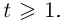
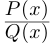
где 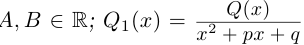
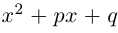
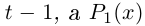
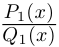
□ Пусть 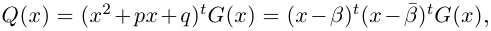
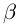
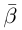
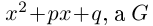
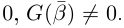
Такие числа А и В определены единственным образом, так как если 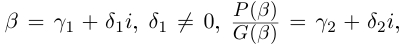
и числа А, В находятся из системы 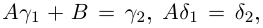
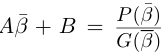
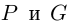
Рассмотрим многочлен 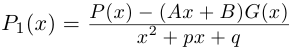
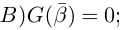
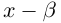
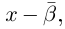
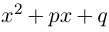
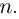
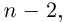
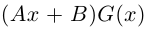
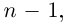
Значит, степень 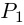
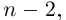
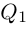
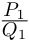
откуда
Последовательно выделяя из многочлена 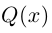
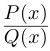
(здесь
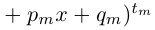
Все слагаемые последней суммы называются простейшими дробями. Все коэффициенты, обозначенные символом 
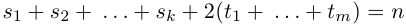
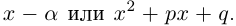
Теорема 7.5. Любая правильная рациональная дробь с действительными коэффициентами раскладывается в сумму простейших дробей.
Пример №25
Разложить в сумму простейших дробей:
а) 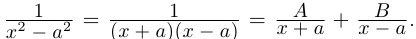
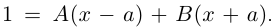
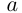
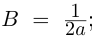
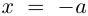
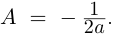
б)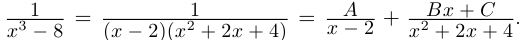
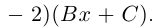
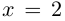
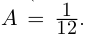
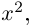
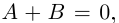
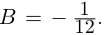
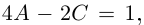
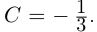
в)
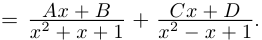
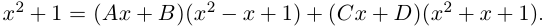
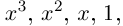
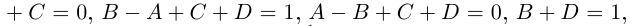
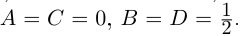
Вычисление комплексного числа
Определение 1.1. Многочленом (полиномом) степени n с действительными коэффициентами называется любое выражение вида
где
х – переменная.
Корнем многочлена (1.1) называется любое число 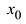
Нетрудно заметить, что некоторые многочлены вообще не имеют
действительных корней, например:
Расширим множество действительных чисел. Добавим к этому
множеству символ i , такой что 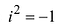
Тогда ±i – два корня уравнения
Определение 1.2. Множеством комплексных чисел называется множество
Суммой двух комплексных чисел 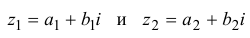
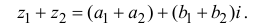
Произведением двух комплексных чисел 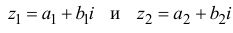
Для числа z= a +bi число а называется действительной частью,
число b – мнимой частью. Обозначения:
Относительно операций «+» и « · » комплексные числа С обладают
такими же свойствами, как и действительные числа. Эти операции
коммутативны и ассоциативны; для них существуют обратные операции:
вычитание и деление (кроме деления на 0).
Пример №26
Найти
Решение:
Теорема 1.1 (основная теорема алгебры). Любое уравнение вида (1.2)
имеет решение во множестве С.
Пример №27
Решить уравнение
Решение:
Определение 1.3. Для комплексного числа z =a +bi число z =a -bi называется комплексно-сопряженным, число 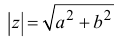
Если рассмотреть плоскость с декартовой системой координат ( O,x,y ) и на оси Ох отложить а – действительную часть z, а на оси Oy – b – мнимую часть z, то получим взаимно однозначное соответствие между множеством С всех
комплексных чисел и множеством точек плоскости.
Такая плоскость называется комплексной плоскостью, рис. 1.1.
При этом 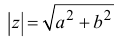
Определение 1.4. Аргументом комплексного числа z =a +bi называется
угол 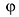
направлением оси Ох Аргумент будем обозначать Argz . Аргумент
определен с точностью до 2 πn. При этом значение 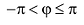
главным и обозначается argz.
Замечание.
При этом
Если 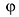
тригонометрическая форма комплексного числа.
Теорема 1.2. Пусть
Доказательство
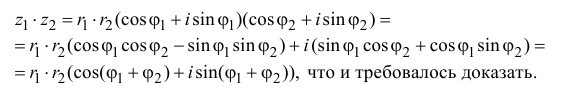
Из формул (1.5) следует, в частности, что 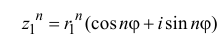
Пример №28
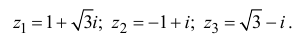
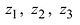
Решение:
поэтому по формуле (1.3)
Тогда по формуле (1.4)
поэтому по формуле (1.3)
Тогда
Из формул (1.5), (1.6) видно, что аргумент 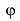
умножении, делении, возведении в степень ведет себя как показатель
степени. Обозначим 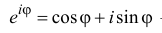
Тогда из теоремы 1.2 следует, что
Учитывая (1.7), формулу (1.4) для z можно переписать в виде 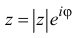
Пример №29
Вычислить
Решение:
Согласно примеру 1.3
Поэтому
Определение 1.5. Корнем n-й степени из числа z 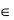
число 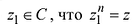
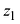
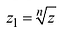
Из формулы (1.8) видно что 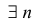
если 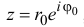
Пример №30
Найти
Решение:
- Координаты на прямой
- Координаты на плоскости
- Линейная функция
- Квадратичная функция
- Степенные ряды
- Элементы матричного анализа
- Уравнение линии
- Функции нескольких переменных
Множество
всевозможных пар действительных чисел
называется множеством комплексных
чисел, если выполняются условия:
1) определено
сравнение (a,b)=(c,d)
Û
a=c Ù
b=d
2) определено
cложение
(a,b)+(c,d)=(a+c,b+d)
3) определено
умножение (a,b)(c,d)=(ac-bd,ad+bc)
При этом число
(0,0) называется нулём и обозначается 0,
число (1,0) называется единицей и
обозначается 1, число (0,1) называется
мнимой единицей и обозначается i.
Комплексные числа (a,b)
можно
обозначать в виде
a+ib. При
таких обозначениях арифметические
операции над комплексными числами
выполняются по обычным алгебраическим
правилам, но при этом i2
заменяется
на -1. Число a-ib
называется
комплексно сопряжённым к числу a+ib.
Модулем комплексного
числа u=a+ib
называется
действительное число
.
При этом можно записатьu=|u|(cosj+isinj)
(тригонометрическая форма записи), где
j
– некоторый угол из промежутка [0;2p)
называемый
аргументом числа u.
Справедливы свойства:
|u|³0
|-u|=|u|
|uv|=|u||v|
|u+v|£|u|+|v|
(неравенство
треугольника
для
модуля)
|u-v|³|u|-|v|
(следствие
из неравенства треугольника)
un=|u|n(cosnj+isinnj) (формула
возведения в степень)
(формула
извлечения корня n-ой
степени)
Для вычисления
квадратного
корня
кроме общего способа можно использовать
специальный приём.
Пусть
требуется вычислить квадратный корень
из числа a+ib.
Обозначим
этот корень через x+iy.
По
определению квадратного корня a+ib
= (x+iy)2.
Раскрывая
скобки и сравнивая получаем систему
Её решения дадут
нам два значения квадратного корня.
Пример 1.
(1+i)(5-i)=5+5i-i-i2=5+5i-i+1=6+4i
(i2
заменили
на -1)
Ответ:
6+4i
Пример 2.
(домножили
числитель и знаменатель на 1-i
(сопряжённое
к 1+i)
и затем i2
заменили
на -1)
Ответ:
1+i
Пример
3.
(1-i)5
=
((cos(7p/4)+isin(7p/4))5
=
4(cos(35p/4)+isin(35p/4))
=
=
4(-
/2+i
/2)
= -4+4i (перешли
к тригонометрической форме записи и
воспользовались формулой возведения
в степень)
Ответ:
-4+4i
Пример 4.
Вычислить
.
Решение: ,обозначим
значения корня (их четыре) через u0,
u1,
u2,
u3.
По
формуле извлечения корня
.
При к=0 получаем
u0=cos(p/8)+isin(p/8)
При к=1 получаем
u1=cos(5p/8)+isin(5p/8)
При к=2 получаем
u2=cos(9p/8)+isin(9p/8)
При к=3 получаем
u3=cos(13p/8)+isin(13p/8)
Ответ:
{ cos(p/8)+isin(p/8);
cos(5p/8)+isin(5p/8);
cos(9p/8)+isin(9p/8);
cos(13p/8)+isin(13p/8)
}
Пример 5.
Вычислить
.
Составим систему
Û
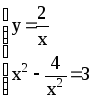
x4-3x2-4=0.
Обозначим t=x2
Þ
t2-3t-4=0
Þ
t1=-1,
t2=4
Þ
x2=4
Þ
x1=-2,
y1=-1
и
x2=2,
y2=1
Ответ:
{ -2-i; 2+i }
Пример
6.
Решить уравнение
x2
+ 4x + 5 = 0. Находим
D
= 16 – 4×5
= -4 < 0 Þ
корни
комплексные:
Ответ:
{ -2-i ; -2+i }
666
Вычислить:
1. (1+2i)(2+i) 2.
(1+2i):(2+i) 3.
4.
5.
Решить уравнения:
6. x2
– 16x + 65 = 0 7. 9x2
+ 6x + 5 = 0
8.
x4
+ 2x2
– 3 = 0 9. x4
+ 6x2
+ 25 = 0
Вычислить:
10. (2+i)(3-i) 11.
(4+2i):(3-i) 12.
13.
Решить уравнения:
14. x2
+ 12x + 40
= 0 15.
x4
– 4x2
– 5
= 0
16. x4
–
6x2
+
25
= 0
555 Решение алгебраических уравнений.
Поиск рациональных
корней алгебраических уравнений с
целыми коэффициентами основан на
теореме:
если рациональное число –
корень такого уравнения, то его числитель
– множитель свободного члена, а знаменатель
– множитель коэффициента при старшей
степени. Для подстановки чисел в уравнение
можно применять схему Горнера. В
комплексной области любое алгебраическое
уравнение n-ой
степени имеет ровно n
корней.
Схема Горнера.
Вычисления по
схеме Горнера заносим в таблицу из двух
строк. Слева от таблицы пишем проверяемое
число. В первой строке записываем
коэффициенты исходного уравнения,
включая нулевые. Затем в первую ячейку
второй строки переписываем число из
верхней ячейки, во вторую ячейку второй
строки записываем сумму верхнего числа
и предыдущего, умноженного на проверяемое
число и т.д. Если в последней ячейке
получится 0, то проверяемое число –
корень, а остальные числа – коэффициенты
алгебраического уравнения с уменьшенной
на один степенью. Решая это уравнение
получим остальные корни.
Пример 7.
Решить уравнение
x3
+ x – 2 = 0. Рациональные
корни этого уравнения ищем среди чисел
±1,
±2.
Проверяем число 1:
|
1 |
1 |
0 |
1 |
-2 |
|
1 |
1 |
2 |
0 |
Так как в последней
ячейке ноль, то x1=1.
Остальные
корни ищем из уравнения x2
+ x + 2 = 0
(его коэффициенты берём из второй
строки).
D = 1 – 8 = – 7 < 0 Þ
Ответ:
666
Решить уравнения:
17. x3
– x2
– 2x + 2 = 0 18. x3
+ x2
– 2 = 0
19.
x5
– 4x3
– 8x2
+ 32 = 0 20. x3
– 12x2
+ 47x -60 = 0
21.
x4
– 10x3
+ 35x2
– 50x + 24 = 0
555
|
Выучить |
|
|u+v|£|u|+|v| |u-v|³|u|-|v| u=|u|(cosj+isinj) un=|u|n(cosnj+isinnj) |
Ответы.
1. 5i
2. 0,8+0,6i 3. 3+i; -3-i
4.
2(cos(p/10+2kp/5)+isin(p/10+2kp/5)),
k=0,1,2,3,4
5.
Ö2(cos(p/36+2kp/3)+isin(p/36+2kp/3)),
k=0,1,2 6. 8±i
7. -1/3±2i/3
8.
±1;
±iÖ3
9. 1±2i;
-1±2i
10. 7+i 11. 1+i 12. ±(3-i)
13.
2(cos(3p/8+kp/2)+isin(3p/8+kp/2)),
k=0,1,2,3 14. -6±2i
15. ±i;
±Ö5
16. 2±i;
-2±i
17. 1;
±Ö2
18. 1; -1±i
19. ±2;
-1±iÖ3
20. 3; 4; 5 21. 1;2;3;4
Вычислить u+v,
u-v, uv,
,
3.1
u=3-4i
v=8+6i 3.2
u=21+20i
v=9-40i
3.3
u=-16+30i v=-21-20i 3.4
u=-9-40i
v=21-20i
3.5
u=24+10i
v=-15+8i 3.6
u=-21+20i
v=-8-6i
3.7
u=24-10i
v=-21-20i 3.8
u=3+4i
v=-5+12i
3.9
u=21-20i
v=7+24i 3.10 u=-7+24i
v=24-10i
3.11 u=-7+24i
v=-16+30i 3.12 u=7+24i
v=-5+12i
3.13 u=-7-24i
v=5+12i 3.14
u=21-20i
v=-16-30i
3.15 u=-16-30i
v=16+30i 3.16 u=3-4i
v=7-24i
3.17 u=16+30i
v=-15+8i 3.18 u=-8-6i
v=16-30i
3.19 u=24+10i
v=8+6i 3.20 u=-3+4i
v=7-24i
3.21 u=21+20i
v=16+30i 3.22 u=5-12i
v=9-40i
3.23 u=5-12i
v=8+6i 3.24 u=-9+40i
v=-16+30i
3.25 u=5-12i
v=-7-24i 3.26
u=-16-30i
v=21+20i
3.27 u=-16+30i
v=15-8i 3.28 u=-7-24i
v=-8-6i
3.29 u=21-20i
v=-5-12i 3.30
u=-8-6i
v=-15-8i
3.31 u=-16-30i
v=-3+4i 3.32
u=7+24i v=-9+40i
3.33 u=-24-10i
v=21-20i 3.34
u=-7-24i v=8+6i
3.35 u=15-8i
v=8-6i
Возвести в степень,
преобразовав в тригонометрическую
форму
и
вычислить корень этой же степени:
4.1
(-Ö3+i)3 4.2
(-1+iÖ3)7 4.3
(-1+i)7
4.4
(1-iÖ3)5 4.5
(1+iÖ3)3 4.6
(Ö3-i)3
4.7
(Ö3+i)3 4.8
(-1+i)3 4.9
(-Ö3-i)3
4.10 (-Ö3+i)7 4.11
(-Ö3+i)3 4.12
(1-i)5
4.13 (1+iÖ3)5 4.14
(1-iÖ3)3 4.15
(1-iÖ3)7
4.16 (-Ö3-i)3 4.17
(-1+iÖ3)3 4.18
(-1+i)7
4.19 (1-i)7 4.20
(1-iÖ3)3 4.21
(1-i)3
4.22 (-1+iÖ3)5 4.23
(-1-i)5 4.24
(-Ö3-i)3
4.25 (Ö3-i)5 4.26
(1+i)7 4.27
(1-i)7
4.28 (-Ö3+i)3 4.29
(-1-i)7 4.30
(1+i)3
4.31 (-1+iÖ3)3 4.32
(-Ö3-i)3 4.33
(-1-iÖ3)5
4.34 (-1+i)5 4.35
(-1-iÖ3)7
Найти действительные
и комплексные корни уравнений:
5.1 x4+10x3+37x2+58x+30=0
75x3-35x2-8x+4=0
5.2
x4-5x3-6x2+84x-144=0 12x3-68x2+115x-50=0
5.3
x4-9x3+30x2-52x+48=0 18x3-15x2-100x+125=0
5.4
x4-2x3-7x2+18x-18=0 18x3-33x2-28x-5=0
5.5
x4+8x3+22x2+28x+16=0 75x3-140x2+87x-18=0
5.6
x4-9x3+30x2-46x+24=0 12x3+40x2+39x+9=0
5.7
x4-9x3+25x2-9x-44=0 12x3+20x2+4x-4=0
5.8
x4+5x3+x2-3x+36=0 20x3+60x2+60x+20=0
5.9
x4-5x3-8x2+82x-120=0 20x3+76x2+64x-16=0
5.10 x4-7x3+16x2
– 24=0 75x3+40x2-33x-18=0
5.11
x4+7x3+11x2-25x-66=0 12x3-56x2+80x-32=0
5.12
x4-6x3+10x2+6x-11=0 12x3+4x2-5x-2=0
5.13
x4-3x3-11x2+13x+60=0 75x3+35x2-123x+45=0
5.14
x4-3x3-10x2+6x+72=0 45x3+57x2+23x+3=0
5.15
x4-3x3-8x2+22x-24=0 18x3+33x2-28x+5=0
5.16
x4-7x3+20x2-32x+24=0 12x3+8x2-20x-16=0
5.17
x4+5x3-2x2-42x-72=0 45x3+42x2-4x-8=0
5.18
x4-6x3+14x2-18x+9=0 12x3+32x2+23x+5=0
5.19
x4-11x3+46x2-90x+72=0 45x3-141x2+95x+25=0
5.20
x4+2x3-14x2-32x-32=0 20x3-104x2+145x-25=0
5.21
x4-10x3+37x2-62x+40=0 20x3-76x2+64x+16=0
5.22
x4-11x3+48x2-96x+72=0 50x3-85x2-92x-20=0
5.23 x4
– 3x2+14x-12=0 12x3-80x2+175x-125=0
5.24
x4+7x3+18x2+28x+16=0 12x3-76x2+155x-100=0
5.25
x4+2x3-10x2-44x-48=0 20x3+44x2+28x+4=0
5.26
x4+8x3+25x2+36x+18=0 20x3+68x2+69x+18=0
5.27
x4-7x3+16x2-18x+8=0 18x3+27x2
– 9=0
5.28
x4-5x3-2x2+42x-72=0 50x3+55x2-28x+3=0
5.29
x4-3x3-3x2+31x-42=0 18x3+60x2+56x+16=0
5.30
x4-4x3-8x2+72x-96=0 75x3+170x2+128x+32=0
5.31 x4
– 10x2-20x-16=0 75x3-20x2-17x-2=0
5.32
x4+13x3+66x2+156x+144=0 20x3+104x2+145x+25=0
5.33 x4-4x3
+ 8x-32=0 50x3+110x2+78x+18=0
5.34
x4-8x3+23x2-34x+24=0 18x3-93x2+152x-80=0
5.35
x4-8x3+24x2-32x+15=0 20x3+44x2+28x+4=0
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Развитие понятия числа является
важнейшей сквозной методико-содержательной
линией школьного курса математики, проходящий в
той или иной степени через все классы средней
школы. В приложении «Математика» неоднократно
публиковались статьи о методике изучения
различных числовых систем в школе. В частности, в
1995–96 гг. были опубликованы три лекции академика
РАО, профессора Г. Глейзера:
Лекция 1. Натуральные числа,
1995, № 47.
Лекция 2. Рациональные числа, 1995, № 48.
Лекция 3. Действительные числа, 1996, № 3.
Публикуемая ниже статья завершает цикл этих
лекций.
Введение
Начнем с нескольких
напоминаний.
Одна из причин введения
рациональных чисел обусловлена требованием,
чтобы всякое линейное уравнение ax = b (где a № 0) было
разрешимо. В области целых чисел линейное
уравнение разрешимо лишь в том случае, когда b
делится нацело на a.
Одна из причин расширения
множества рациональных чисел до множества
действительных чисел была связана с
разрешимостью квадратных уравнений, например,
уравнения вида x2 = 2. На множестве
рациональных чисел это уравнение не разрешимо,
так как среди рациональных нет числа, квадрат
которого равен двум. Как известно, – число иррациональное. На
множестве же действительных чисел уравнение x2
= 2 разрешимо, оно имеет два решения x1 = и x2 = –
.
И все же нельзя считать, что на
множестве действительных чисел разрешимы все
квадратные уравнения. Например, квадратное
уравнение x2 = – 1 на множестве
действительных чисел решений не имеет, так как
среди действительных чисел нет такого числа,
квадрат которого отрицателен.
Таким образом, действительных
чисел явно недостаточно, чтобы построить такую
теорию квадратных уравнений, в рамках которой
каждое квадратное уравнение было бы разрешимо.
Это соображение приводит к необходимости
вводить новые числа и расширять множество
действительных чисел до множества комплексных
чисел, в котором было бы разрешимо любое
квадратное уравнение.
Вспомним о едином принципе
расширения числовых систем и поступим в
соответствии с этим принципом.
Если множество А расширяется
до множества В, то должны быть выполнены
следующие условия:
1. Множество А есть
подмножество В.
2. Отношения элементов множества А (в частности,
операции над ними) определяются также и для
элементов множества В; смысл этих отношений для
элементов множества А, рассматриваемых уже как
элементы множества В, должен совпадать с тем,
какой они имели в А до расширения.
3. В множестве В должна выполняться операция,
которая в А была невыполнима или не всегда
выполнима.
4. Расширение В должно быть минимальным из всех
расширений данного множества А, обладающих
первыми тремя свойствами, причем это расширение
В должно определяться множеством А однозначно (с
точностью до изоморфизма).
Итак, расширяя множество
действительных чисел до множества новых чисел,
названных комплексными, необходимо, чтобы:
а) комплексные числа
подчинялись основным свойствам действительных
чисел, в частности, коммутативному,
ассоциативному и дистрибутивному законам;
б) в новом числовом множестве были разрешимы
любые квадратные уравнения.
Множество действительных
чисел недостаточно обширно, чтобы в нем были бы
разрешимы все квадратные уравнения. Поэтому,
расширяя множество действительных чисел до
множества комплексных чисел, мы потребуем, чтобы
в нем можно было бы построить полную и
законченную теорию квадратных уравнений.
Другими словами, мы расширим множество
действительных чисел до такого множества, в
котором можно будет решить любое квадратное
уравнение. Так, уравнение x2 = – 1 не имеет
решений во множестве действительных чисел
потому, что квадрат действительного числа не
может быть отрицательным. В новом числовом
множестве оно должно иметь решение. Для этого
вводится такой специальный символ i, называемый
мнимой единицей, квадрат которого равен – 1.
Ниже будет показано, что
введение этого символа позволит осуществить
расширение множества действительных чисел,
пополнив его мнимыми числами вида bi (где b –
действительное число) таким образом, чтобы в
новом числовом множестве (множестве комплексных
чисел) при сохранении основных законов
действительных чисел были разрешимы любые
квадратные уравнения.
Основные
определения. Операции над комплексными числами
1. Существует элемент i (мнимая
единица) такой, что i2 = – 1.
2. Символ a + bi называют
комплексным числом с действительной частью a и
мнимой частью bi, где a и b – действительные числа, b
– коэффициент мнимой части.
Комплексное число a + 0i
отождествляется с действительным числом a, т.е. a +
0i = a, в частности, 0 + 0i = 0. Числа вида bi (b № 0) называют чисто
мнимыми.
Например, комплексное число 2 +
3i имеет действительную часть – действительное
число 2 и мнимую часть 3i, действительное число 3 –
коэффициент мнимой части.
Комплексное число 2 – 3i имеет
действительную часть число 2, мнимую часть – 3i,
число – 3 – коэффициент при мнимой части.
3. Правило равенства. Два
комплексных числа равны тогда и только тогда,
когда равны их действительные части и равны
коэффициенты мнимых частей.
Т.е., если a + bi = c +di, то a = c, b = d: и,
обратно, если a = c, b = d, то a + bi = c +di.
4. Правило сложения и
вычитания комплексных чисел.
(a + bi) + (c + di) = (a + c) + (b +
d)i.
Например:
(2 + 3i) + (5 + i) = (2 + 5) + (3 + 1)i
= 7 + 4i;
(– 2 + 3i) + (1 – 8i) = (– 2 + 1)
+ (3 + (– 8))i = – 1 – 5i;
(– 2 + 3i) + (1 – 3i) = (– 2 + 1)
+ (3 + (– 3))i =
= – 1 + 0i = – 1.
Вычитание комплексных чисел
определяется как операция, обратная сложению, и
выполняется по формуле:
(a + bi) – (c + di) = (a – c) + (b
– d)i.
Например:
(5 – 8i) – (2 + 3i) = (3 – 2) +
(– 8 – 3)i = 1 – 11i;
(3 – 2i) – (1 – 2i) = (3 – 1) +
((– 2) – (– 2))i = 2 + 0i = 2.
5. Правило умножения
комплексных чисел.
(a + bi)(c + di) = (aс + bd) + (ad +
bc)i.
Из определений 4 и 5 следует,
что операции сложения, вычитания и умножения над
комплексными числами осуществляются так, как
будто мы выполняем операции над многочленами,
однако с условием, что i2 = – 1.
Действительно: (a + bi)(c + di) = ac + adi
+ bdi2 = (ac – bd) + (ad + bc)i.
Например, (– 1 + 3i)(2 + 5i) = – 2 – 5i +
6i + 15i2 = – 2 – 5i + 6i – 15 = – 17 + i; (2 + 3i)(2 – 3i) = 4
– 6i + 6i – 9i2 = 4 + 9 = 13.
Из второго примера следует,
что результатом сложения, вычитания,
произведения двух комплексных чисел может быть
число действительное. В частности, при умножении
двух комплексных чисел a + bi и a – bi, называемых
сопряженными комплексными числами, в результате
получается действительное число, равное сумме
квадратов действительной части и коэффициента
при мнимой части. Действительно:
(a + bi)(a – bi) = a2 –
abi + abi – b2i2 = a2 + b2.
Произведение двух чисто
мнимых чисел – действительное число.
Например: 5i•3i = 15i2 = –
15; – 2i•3i = – 6i2 = 6, и вообще bi•di = bdi2
= – bd.
6. Деление комплексного числа a
+ bi на комплексное число c + di № 0 определяется как операция
обратная умножению и выполняется по формуле:
.
Формула теряет смысл, если c + di
= 0, так как тогда c2 + d2 = 0, т. е. деление
на нуль и во множестве комплексных чисел
исключается.
Обычно деление комплексных
чисел выполняют путем умножения делимого и
делителя на число, сопряженное делителю.
Например,
Опираясь на введенные
определения нетрудно проверить, что для
комплексных чисел справедливы коммутативный,
ассоциативный и дистрибудивный законы. Кроме
того, применение операций сложения, умножения,
вычитания и деления к двум комплексным числам
снова приводит к комплексным числам. Тем самым
можно утверждать, что множество комплексных
чисел образует поле. При этом, так как
комплексное число a + bi при b = 0 отождествляется с
действительным числом a = a + 0i, то поле комплексных
чисел включает поле действительных чисел в
качестве подмножества.
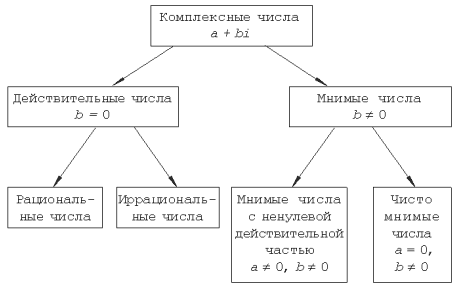
Приведем классификацию
комплексных чисел:
Решение квадратных
уравнений
Одна из причин введения
комплексных чисел состояла в том, чтобы добиться
разрешимости любого квадратного уравнения, в
частности уравнения
x2 = – 1.
Покажем, что расширив поле
действительных чисел до поля комплексных чисел,
мы получили поле, в котором каждое квадратное
уравнение разрешимо, т.е. имеет решение. Так,
уравнение x2 = – 1 имеет два решения: x1
= i, x2 = – i.
Это нетрудно установить
проверкой: i•i = i2 = – 1, (– i)•(– i) = i2
= – 1.
Перейдем теперь к вопросу о
решении полного квадратного уравнения.
Квадратным уравнением называют уравнение вида:
ax2 + bx + c = 0 (a № 0),
где x – неизвестная, a, b, c –
действительные числа, соответственно первый,
второй коэффициенты и свободный член, причем a № 0. Решим это
уравнение, выполнив над ним ряд несложных
преобразований.
· Разделим все члены
уравнения на a № 0 и перенесем свободный член в
правую часть уравнения:
Теперь можно исследовать
полученное решение. Оно зависит от значения
подкоренного выражения, называемого
дискриминантом квадратного уравнения. Если b2
– 4ac > 0, то
есть действительное число и квадратное
уравнение имеет действительные корни. Если же – мнимое число,
квадратное уравнение имеет мнимые корни.
Результаты
исследования представлены ниже в таблице:
Итак, введение комплексных
чисел позволяет разработать полную теорию
квадратных уравнений. В поле комплексных чисел
разрешимо любое квадратное уравнение.
Примеры.
1. Решите уравнение x2 – 2x
– 8 = 0.
Решение. Найдем
дискриминант D = b2 – 4ac = (– 2)2 –
4•1•(– 8) = 36 > 0.
Уравнение имеет два
действительных корня:
2. Решите уравнение x2 + 6x +
9 = 0.
Решение. D = 62 – 4•1•9 = 0,
уравнение имеет два равных действительных корня:
3. Решите уравнение x2 – 4x
+ 5 = 0.
Решение. D = 16 – 4•1•5 = – 4 < 0,
уравнение имеет мнимые корни:
Геометрическая
интерпретация комплексных чисел
Известно, что отрицательные
числа были введены в связи с решением линейных
уравнений с одной переменной. В конкретных
задачах отрицательный ответ истолковывался как
значение направленной величины (положительные и
отрицательные температуры, передвижения в
противоположных направлениях, прибыль и долг и
т.п.). Однако еще в ХVI веке многие математики не
признавали отрицательных чисел. Только с
введением координатной прямой и координатной
плоскости отчетливо проявился смысл
отрицательных чисел, и они стали такими же
«равноправными» и понятными, как и натуральные
числа. Аналогично обстоит дело с комплексными
числами. Смысл их отчетливо проявляется при
введении их геометрической интерпретации.
интерпретация комплексных чисел состоит в том,
что каждому комплексному числу z = x + yi ставится в
соответствие точка (x, y) координатной плоскости
таким образом, что действительная часть
комплексного числа представляет собой абсциссу,
а коэффициент при мнимой части – ординату точки.
Таким образом,
устанавливается взаимно однозначное
соответствие между множеством комплексных чисел
и множеством точек координатной плоскости.
Подобным образом было установлено соответствие
между множеством действительных чисел и
множеством точек числовой прямой.
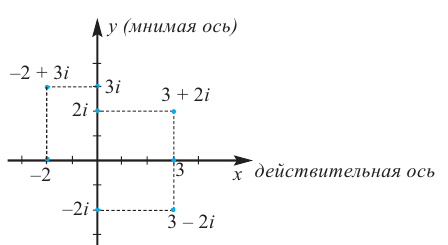
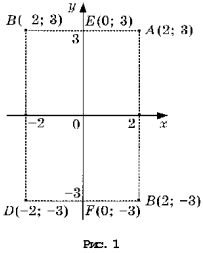
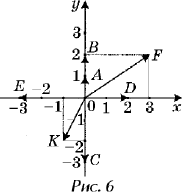
На рисунке 1 изображена
координатная плоскость. Числу 2 + 3i соответствует
точка A(2, 3) плоскости; числу 2 – 3i – точка B(2, – 3);
числу – 2 + 3i – точка C(– 2, 3); числу – 2 – 3i – точка
D(– 2; – 3). Числу 3i соответствует точка E(0, 3); а
числу – 3i – точка F(0, – 3). Итак, каждому
комплексному числу соответствует единственная
точка координатной плоскости и, обратно, каждой
точке координатной плоскости соответствует
единственное комплексное число, при этом двум
различным комплексным числам соответствуют две
различные точки координатной плоскости. Ясно,
что действительным числам x + 0i соответствуют
точки оси абсцисс, а чисто мнимым числам 0 + yi, где y
№ 0 –
точки оси ординат. Поэтому ось Oy называют мнимой,
а ось Ox – действительной. Сопряженным
комплексным числам соответствуют точки, симметричные
относительно оси абсцисс (рис. 2).
Тригонометрическая
форма комплексного числа
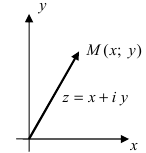
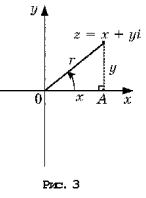
Точка координатной плоскости,
соответствующая комплексному числу z = x + yi, может
быть указана по-другому: ее координатами могут
быть расстояние r от начала координат и величина
угла j между положительной полуосью Ox и лучом Oz
(рис. 3).
Расстояние r от начала системы
координат до точки, соответствующей
комплексному числу z, называют модулем этого
числа. Тогда по теореме Пифагора (рис. 2)
имеем: r2 = x2 + y2 = (x + yi)(x – yi)
= z•z.
Отсюда найдем модуль
комплексного числа как арифметическое
(неотрицательное) значение корня:
Если комплексное число z
изображается точкой оси абсцисс (т.е. является
действительным числом), то его модуль совпадает с
абсолютным значением. Все комплексные числа,
имеющие модуль 1, изображаются точками единичной
окружности – окружности с центром в начале
системы координат, радиуса 1 (рис. 4).
лучом Oz называют аргументом комплексного числа z
= x + yi (рис. 3).
Сопряженные комплексные
числа имеют
один и тот же модуль и аргументы, отличающиеся знаком: j = – j.
В отличие от модуля аргумент
комплексного числа определяется неоднозначно.
Аргумент одного и того же комплексного числа
может иметь бесконечно много значений,
отличающихся друг от друга на число, кратное 360°.
Например, число z (рис. 3) имеет модуль r, аргумент
же этого числа может принимать значения j; j + 360°; j + 720°; j + 1080°; … или
значения j – 360°; j –720°; j – 1080°; … Данное значение модуля r и любое из
приведенных выше значений аргумента определяют
одну и ту же точку плоскости, соответствующую
числу z.
Пусть точке с координатами (x;
y) соответствует комплексное число z = x + yi. Запишем
это комплексное число через его модуль и
аргумент. Воспользуемся определением
тригонометрических функций синуса и косинуса
(рис. 3):
x = r cos j; y = r sin j.
Тогда число z выражается через
модуль и аргумент следующим образом: z = x + yi =
r(cos j + i sin
j).
Выражение z = r(cos j + i sin j) называют
тригонометрической формой комплексного числа, в
отличии от выражения z = x + yi, называемого
алгебраической формой комплексного числа.
Приведем примеры обращения
комплексных чисел из алгебраической формы в
тригонометрическую:
Для числа i имеем r = 1, j = 90°, поэтому
i = 1(cos 90° + i sin 90°);
Для числа – 1 имеем r = 1, j = 180°,
поэтому – 1 = 1(cos 180° + i sin 180°);
Для числа 1 + i имеем поэтому
Для числа имеем r = 1, j = 45°, поэтому
Для числа имеем r = 2, j = 120°, поэтому
Справедливость приведенных
равенств нетрудно проверить путем подстановки в
их правой части числовых значений
тригонометрических функций. Итак, для того, чтобы
комплексное число, заданное в алгебраической
форме, обратить в тригонометрическую форму,
необходимо найти его модуль r и аргумент j,
пользуясь формулами:
Комплексные числа и
векторы
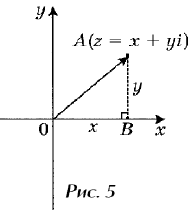
геометрической интерпретации комплексных чисел.
Каждой точке (x , y) координатной плоскости,
изображающей комплексное число
z = x + yi, соответствует единственный вектор,
отложенный от начала системы координат и обратно
(рис. 5). При этом двум различным точкам
координатной плоскости будут соответствовать
два таких различных вектора.
Таким образом, может быть
установлено взаимно однозначное соответствие
между множеством точек координатной плоскости
(комплексными числами) и множеством векторов,
отложенных от начала системы координат.
Если z = x + yi (рис. 5), то вектор , отложенный от
начала системы координат до точки, изображающей
число z, будет иметь координаты (x; y). Известно, что
равные векторы имеют равные координаты.
Итак, мы рассмотрели два
способа интерпретации комплексных чисел: их
можно изображать либо точками координатной
плоскости, либо векторами, отложенными от начала
системы координат. При этом любые два равных
вектора (имеющих одно и то же направление и
равные длины) изображают одно и то же комплексное
число, а векторы, отличные либо длиной, либо
направлением, изображают разные числа. На
рисунке 6 с помощью векторов изображены
различные комплексные числа: изображает число 2 + 0i;
– число – 3 + 0i;
– число 0 + i;
– число 0 + 2i;
– число 0 – 3i;
– число 3 + 2i;
– число – 1 – 2i.
Ясно, что любой ненулевой
вектор, лежащий на оси Oy (или параллельный ей),
изображает чисто мнимое число yi, причем y > 0,
если направление вектора совпадает с
направлением оси, y < 0, если направление вектора
противоположно направлению оси. Вследствие
этого ось Oy называют мнимой. Все векторы, лежащие
на оси Ox (или параллельные ей) изображают
действительные числа, поэтому ее называют
действительной осью.
Векторная интерпретация
комплексных чисел позволяет уяснить
геометрический смысл операций над комплексными
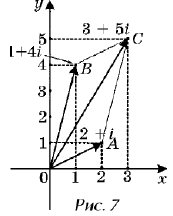
числами. Например, сумма двух комплексных чисел 2
+ i и 1 + 4i равна 3 + 5i. Каждое из слагаемых изображает
соответствующий вектор, отложенный от начала O
координат (рис. 7):
= 2 + i;
= 1 + 4i.
Сумма этих векторов – вектор = 3 + 5i, изображается
диагональю параллелограмма, построенного на
векторах и .
себе геометрический смысл умножения двух
комплексных чисел, воспользуемся их
тригонометрической формой. Пусть векторы изображают
соответственно комплексные числа:
соответственно модули этих
чисел, а j1
и j2
– их аргументы. Найдем произведение этих чисел:
z1z2 = r1r2(cosj1 + i sin j1)(cos j2 + i sin j2) = r1r2(cos
j1cos
j2
– sin j1
sin j2)
+ i = (cos j1sin
j2 +
sin j1cos
j2).
школы теоремами сложения синуса и косинуса:
cos j1cos j2 – sin j1 sin j2 = cos(j1 + j2);
cos j1sin j2 + sin j1cos j2 = sin(j1 + j2).
Тогда произведение данных
комплексных чисел равно комплексному числу:
z1z2 = r1r2(cos(j1 + j2) + isin(j1 + j2)).
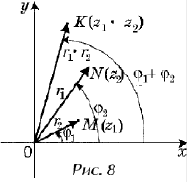
Последнее соотношение
позволяет сформулировать правило умножения
комплексных чисел: при умножении двух
комплексных чисел их модули перемножаются, а их
аргументы складываются. Это проиллюстрировано
на рисунке 8.
комплексных чисел связано с поворотом
(вращением). Так, произведение z1z2
изображается вектором представляющим собой образ вектора
, повернутого на
угол j2
(или образ вектора , повернутого на угол j1), при этом модуль вектора
равен произведению модулей данных векторов.
Связь произведения
комплексных чисел с вращением становится более
наглядной, если рассматривать произведение
различных комплексных чисел (векторов) на
комплексное число i, у которого модуль равен 1, а
аргумент 90°. Например, найдем произведение
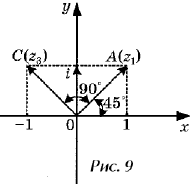
комплексных чисел z1 = 1 + i и z2 = i.
z = z1z2 = (1 +
i)i = i + i2 = – 1 + i.
Числа z1 и z2
соответственно изображают векторы и (рис.9). Мы
видим, что модуль комплексного числа z равен
модулю числа z1:
Аргумент же комплексного
числа z равен 45° + 90° = 135°, в то время, как аргумент
комплексного числа z1 равен 45°. Т.е. вектор ,
изображающий число z, есть образ вектора ,
изображающего число z1 при повороте на 90°.