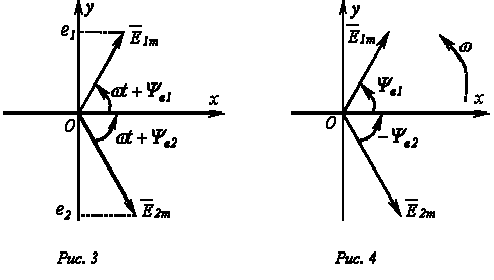Переменный
ток долгое время не находил практического
применения. Это было связано с тем,
что первые генераторы электрической
энергии вырабатывали постоянный ток,
который вполне удовлетворял технологическим
процессам электрохимии, а двигатели
постоянного тока обладают хорошими
регулировочными характеристиками.
Однако по мере развития производства
постоянный ток все менее стал удовлетворять
возрастающим требованиям экономичного
электроснабжения. Переменный ток дал
возможность эффективного дробления
электрической энергии и изменения
величины напряжения с помощью
трансформаторов. Появилась возможность
производства электроэнергии на крупных
электростанциях с последующим экономичным
ее распределением потребителям,
увеличился радиус электроснабжения.
В
настоящее время центральное производство
и распределение электрической энергии
осуществляется в основном на переменном
токе. Цепи с изменяющимися – переменными
– токами по сравнению с цепями постоянного
тока имеют ряд особенностей. Переменные
токи и напряжения вызывают переменные
электрические и магнитные поля. В
результате изменения этих полей в цепях
возникают явления самоиндукции и
взаимной индукции, которые оказывают
самое существенное влияние на процессы,
протекающие в цепях, усложняя их анализ.
Переменным
током (напряжением, ЭДС и т.д.)
называется
ток (напряжение, ЭДС и т.д.), изменяющийся
во времени. Токи, значения которых
повторяются через равные промежутки
времени в одной и той же последовательности,
называются периодическими,
а
наименьший промежуток времени, через
который эти повторения наблюдаются, –
периодом
Т.
Для периодического тока имеем
|
|
(1) |
Величина,
обратная периоду, есть частота,
измеряемая
в герцах (Гц):
|
|
(2) |
Диапазон
частот, применяемых в технике: от
сверхнизких частот (0.01¸10 Гц – в системах
автоматического регулирования, в
аналоговой вычислительной технике) –
до сверхвысоких (3000 ¸ 300000 МГц –
миллиметровые волны: радиолокация,
радиоастрономия). В РФ промышленная
частота f
= 50Гц.
Мгновенное
значение переменной величины есть
функция времени. Ее принято обозначать
строчной буквой:
i
– мгновенное значение тока
![]() ;
;
u
–
мгновенное значение напряжения
![]() ;
;
е
–
мгновенное значение ЭДС
![]() ;
;
р–
мгновенное значение мощности
![]() .
.
Наибольшее
мгновенное значение переменной величины
за период называется амплитудой (ее
принято обозначать заглавной буквой с
индексом
m).
![]() –
–
амплитуда тока;
![]() –
–
амплитуда напряжения;
![]() –
–
амплитуда ЭДС.
Действующее значение переменного тока
Значение
периодического тока, равное такому
значению постоянного тока, который за
время одного периода произведет тот же
самый тепловой или электродинамический
эффект, что и периодический ток, называют
действующим
значением периодического
тока:
|
|
(3) |
Аналогично
определяются действующие значения ЭДС
и напряжения.
Синусоидально изменяющийся ток
Из
всех возможных форм периодических токов
наибольшее распространение получил
синусоидальный ток. По сравнению с
другими видами тока синусоидальный ток
имеет то преимущество, что позволяет в
общем случае наиболее экономично
осуществлять производство, передачу,
распределение и использование
электрической энергии. Только при
использовании синусоидального тока
удается сохранить неизменными формы
кривых напряжений и токов на всех
участках сложной линейной цепи. Теория
синусоидального тока является ключом
к пониманию теории других цепей.
Изображение синусоидальных эдс, напряжений и токов на плоскости декартовых координат
Синусоидальные
токи и напряжения можно изобразить
графически, записать при помощи уравнений
с тригонометрическими функциями,
представить в виде векторов на декартовой
плоскости или комплексными числами.
Приведенным
на рис. 1, 2 графикам двух синусоидальных
ЭДС е1
и
е2
соответствуют
уравнения:
![]()
![]() .
.
Значения
аргументов синусоидальных функций
![]() и
и![]() называютсяфазами
называютсяфазами
синусоид,
а значение фазы в начальный момент
времени (t=0):
![]() и
и
![]() –начальной
–начальной
фазой (
![]()
![]() ).
).
Величину
![]() ,
,
характеризующую скорость изменения
фазового угла, называютугловой
частотой. Так
как фазовый угол синусоиды за время
одного периода Т
изменяется на
![]() рад.,
рад.,
то угловая частота есть![]() ,
,
гдеf–
частота.
При
совместном рассмотрении двух синусоидальных
величин одной частоты разность их
фазовых углов, равную разности начальных
фаз, называют углом
сдвига фаз.
Для
синусоидальных ЭДС е1
и
е2
угол
сдвига фаз:
![]() .
.
Векторное изображение синусоидально изменяющихся величин
На
декартовой плоскости из начала координат
проводят векторы, равные по модулю
амплитудным значениям синусоидальных
величин, и вращают эти векторы против
часовой стрелки (в
ТОЭ данное направление принято за
положительное)
с угловой частотой, равной w.
Фазовый угол при вращении отсчитывается
от положительной полуоси абсцисс.
Проекции вращающихся векторов на ось
ординат равны мгновенным значениям ЭДС
е1
и
е2
(рис.
3). Совокупность векторов, изображающих
синусоидально изменяющиеся ЭДС,
напряжения и токи, называют векторными
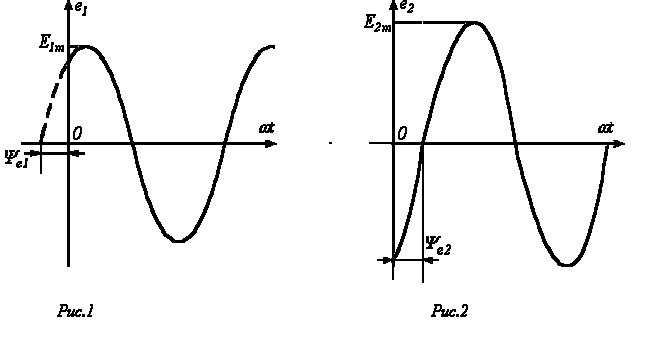
диаграммами. При
построении векторных диаграмм векторы
удобно располагать для начального
момента времени (t=0),
что
вытекает из равенства угловых частот
синусоидальных величин и эквивалентно
тому, что система декартовых координат
сама вращается против часовой стрелки
со скоростью w.
Таким образом, в этой системе координат
векторы неподвижны (рис. 4). Векторные
диаграммы нашли широкое применение при
анализе цепей синусоидального тока. Их
применение делает расчет цепи более
наглядным и простым. Это упрощение
заключается в том, что сложение и
вычитание мгновенных значений величин
можно заменить сложением и вычитанием
соответствующих векторов.
|
|
Пусть,
например, в точке разветвления цепи
(рис. 5) общий ток
![]() равен
равен
сумме токов![]() и
и![]() двух
двух
ветвей: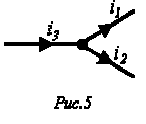
![]() .
.
Каждый
из этих токов синусоидален и может быть
представлен уравнением
![]() и
и![]() .
.
Результирующий
ток также будет синусоидален:
![]() .
.
Определение
амплитуды![]() и начальной фазы
и начальной фазы![]() этого
этого
тока путем соответствующих тригонометрических
преобразований получается довольно
громоздким и мало наглядным, особенно,
если суммируется большое число
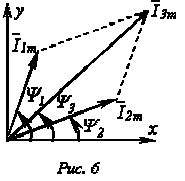
синусоидальных величин. Значительно
проще это осуществляется с помощью
векторной диаграммы. На рис. 6 изображены
начальные положения векторов токов,
проекции которых на ось ординат дают
мгновенные значения токов дляt=0.
При
вращении этих векторов с одинаковой
угловой скоростью w
их
взаимное расположение не меняется, и
угол сдвига фаз между ними остается
равным
![]() .
.
Так
как алгебраическая сумма проекций
векторов на ось ординат равна мгновенному
значению общего тока, вектор общего
тока равен геометрической сумме векторов
токов:
![]() .
.
Построение
векторной диаграммы в масштабе позволяет
определить значения
![]() и
и![]() из
из
диаграммы, после чего может быть записано
решение для мгновенного значения![]() путем
путем
формального учета угловой частоты:![]() .
.
Действующее (эффективное) значение переменного тока равно величине такого постоянного тока, который за время, равное одному периоду переменного тока, произведёт такую же работу (тепловой или электродинамический эффект), что и рассматриваемый переменный ток.
В современной литературе чаще используется математическое определение этой величины — среднеквадратичное значение переменного тока. Иначе говоря, действующее значение переменного тока можно определить по формуле:
Действующее значение в типичных случаях[править | править код]
Приведены формулы для электрического тока. Аналогичным образом определяются действующие значения ЭДС и напряжения.
Синусоида[править | править код]

Для синусоидального тока:
где
— амплитудное значение тока.
Прямоугольная форма[править | править код]
Для тока, имеющего форму однополярного прямоугольного импульса, действующее значение тока зависит от скважности:
где
— коэффициент заполнения (величина, обратная скважности).
В частности, для тока, имеющего форму однополярного меандра (коэффициент заполнения 0,5):
Для тока, имеющего форму двухполярного меандра:
Треугольная форма[править | править код]
Для тока треугольной и пилообразной формы (независимо от того, меняется ли направление тока):
Трапециевидная форма[править | править код]
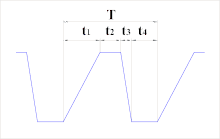
Для тока трапециевидной формы действующее значение можно определить разбив период на отрезки положительного фронта, действия максимального значения и отрицательного фронта:
где
— длительность положительного фронта;
— длительность действия максимального значения;
— длительность отрицательного фронта;
— длительность полного периода.
Дугообразная форма[править | править код]
Для тока имеющего форму дуги (половины окружности):
Дополнительные сведения[править | править код]
В англоязычной технической литературе для обозначения действующего значения употребляется термин effective value — эффективное значение. Также применяется аббревиатура RMS или rms — root mean square — среднеквадратичное (значение).
Электроизмерительные приборы (амперметры, вольтметры) для измерения в цепях переменного тока обычно градуируются так, чтобы их показания соответствовали действующему значению синусоидального тока или напряжения. При измерении несинусоидальных токов и напряжений приборы различных систем могут давать разные показания[1].
См. также[править | править код]
- Список параметров напряжения и силы электрического тока
Примечания[править | править код]
- ↑ 11.8. Показания приборов различных систем в цепях несинусоидального тока. StudFiles. Дата обращения: 16 февраля 2019.
Литература[править | править код]
- «Справочник по физике», Яворский Б. М., Детлаф А. А., изд. «Наука», 1979 г.1
- Курс физики. А. А. Детлаф, Б. М. Яворский М.: Высш. шк., 1989. § 28.3, п.5
- «Теоретические основы электротехники», Л. А. Бессонов: Высш. шк., 1996. § 7.8 — § 7.10
Ссылки[править | править код]
- Действующие значения тока и напряжения
- Среднеквадратичное значение
Для школьников.
Генераторы переменного тока, о принципе работы которых говорилось ранее, вырабатывают переменный синусоидальный ток.
Характеристики переменного тока
Как любая колеблющаяся величина переменный ток характеризуется периодом и частотой.
Периодом переменного тока Т называется промежуток времени, в течение которого сила тока совершает одно полное колебание:
Частотой переменного тока называется число периодов за единицу времени:
Частота переменного тока всех электростанций равна 50 Гц или период промышленного тока равен 0,02 с.
Круговая или циклическая частота переменного тока:
Так как величина и направление мгновенных значений переменного тока всё время меняются, то введено понятие действующего значения тока, путём сравнения теплового действия постоянного и переменного токов.
Действующее значение силы переменного тока численно равно такому постоянному току, который проходя через одинаковое сопротивление, что и переменный, выделяет в нём за время периода одинаковое количество теплоты.
Например, если говорим, что сила переменного тока равна 2 А – это значит, что тепловое действие этого переменного тока такое же, как и постоянного тока силой 2 А. За равные промежутки времени они выделяют одинаковое количество теплоты.
Действующие значения силы переменного тока, а также действующие значения ЭДС и напряжения переменного тока связаны с их максимальными (амплитудными) значениями, обозначенными с индексом “нуль”, следующими соотношениями:
В генераторах, установленных на электростанциях, всегда возникает переменная ЭДС, изменяющаяся во времени по синусоидальному закону. Если принять начальную фазу за нуль, то мгновенные значения ЭДС связаны с её максимальными (амплитудными) значениями следующей зависимостью:
Такая же зависимость существует между мгновенными значениями напряжений на зажимах источника и его максимальным значением:
Если к генератору переменной ЭДС, на зажимах которого существует напряжение
подключить внешнюю цепь, то в ней будет течь синусоидальный ток, мгновенные значения которого связаны с амплитудным значением тока следующей зависимостью:
Здесь угол “фи” есть разность (сдвиг) фаз между током и напряжением.
Разность фаз может быть положительной и отрицательной величиной – это зависит от вида нагрузки во внешней цепи (от того, содержит ли внешняя цепь активное, индуктивное, емкостное сопротивления).
Для цепи только с активным сопротивлением угол “фи” равен нулю, то есть колебания тока и напряжения совпадают по фазе (показано на рисунках ниже).
Какой физический смысл имеет активное сопротивление?
Вспомним электрическую цепь постоянного тока.
К понятию электрического сопротивления и к закону Ома для участка цепи (не содержащего источника тока) пришли через опыты.
А именно, к участку цепи прикладывали постоянное напряжение U и измеряли проходящий по участку ток. Оказалось, что ток всегда пропорционален напряжению.
Коэффициент пропорциональности между ними назвали сопротивлением R участка цепи прохождению по нему тока.
Так опытным путём был получен один из основных законов постоянного тока – закон Ома.
Сопротивление проводника зависит от материала, из которого он изготовлен, от температуры и определяется его размерами.
Для однородного проводника в виде проволоки, трубки, бруска, пластины
Электронная теория сопротивление проводника току объясняет столкновениями упорядоченно движущихся электронов с ионами кристаллической решётки проводника.
При изучении цепей постоянного тока R называли просто сопротивлением.
При переходе к цепям переменного тока его стали называть активным сопротивлением, потому что оно активно (постоянно) потребляет электрическую энергию от источника тока, превращая её в другие виды энергии, преимущественно в тепловую.
Так, при прохождении тока (постоянного или переменного) через нить лампочки накаливания, выделяется тепло, нить накаляется и излучает свет.
В цепях переменного тока, кроме активного сопротивления R, имеют место индуктивное и емкостное сопротивления, которые в отличие от активного сопротивления, не поглощают энергию, а лишь передают её от электрического поля магнитному, и наоборот.
Индуктивному и емкостному сопротивлениям будут посвящены следующие две статьи.
Теперь рассмотрим случай, когда в цепи переменного тока содержится только активное сопротивление:
В цепи, содержащей только активное сопротивление, ток и напряжение колеблются в одинаковой фазе, то есть ток следует за напряжением, проходя одновременно с ним через максимумы и нулевые значения.
На рисунке ниже показаны кривые зависимости мгновенных значений тока и напряжения от времени за период.
Величины с нулевыми индексами в формулах соответствуют максимальным значениям тока и напряжения.
Связь между действующими (эффективными) значениями тока и напряжения (без индексов) и максимальными значениями тока и напряжения подчиняется закону Ома:
(Хотя закон Ома был установлен для цепей постоянного тока, но он справедлив и для переменного тока небольшой частоты. Для тока, имеющего частоту 50 Гц, используемого на производстве и в быту, закон Ома справедлив.)
На следующем рисунке показаны графики изменения во времени мгновенных значений напряжения, силы тока и мощности переменного тока для цепи, содержащей только активные сопротивления:
(О мощности тока прочтёте, пройдя по этой ссылке)
На рисунке выше оси времени отложены положительные значения тока и напряжения (когда ток течёт в направлении от источника к потребителю энергии), а ниже оси времени – их отрицательные значения (когда ток течёт в обратном направлении).
Мгновенная мощность получается путём перемножения мгновенных значений напряжения и тока, она всегда положительна (произведение отрицательным мгновенных значений тока и напряжения даёт положительную мощность).
Это означает, что цепи переменного тока, имеющие только активное сопротивление, всё время потребляют электроэнергию. Заштрихованная площадь пропорциональна мощности, потребляемой активным сопротивлением цепи за период.
(Для сведения – если мощность отрицательна, то это означает, что энергия из цепи поступает обратно в источник. К активному сопротивлению это не относится.)
Напряжение на активном сопротивлении (активное напряжение) равно произведению тока на активное сопротивление:
Активная мощность равна произведению тока на активное напряжение в этом сопротивлении:
Активная мощность характеризует скорость необратимого превращения электрической энергии в другие виды энергии (тепловую, световую и др.)
Пример
Активное сопротивление 4 Ом включено в цепь переменного тока напряжением 120 В. Определить силу тока, активное напряжение и активную мощность для этого сопротивления.
Решение.
В условии задачи дано действующее напряжение. Тогда действующее значение тока в цепи:
Активное напряжение:
По расчётам активное напряжение в данном примере получается равным 120 В. Это значит, что всё приложенное к зажимам цепи напряжение является активным напряжением.
Активная мощность, найденная по формуле данной ниже, равна 3600 Вт.
Ответ: 30 А; 120 В; 3600 Вт.
Таким образом, если внешняя цепь состоит только из активных сопротивлений, то колебания тока и напряжения в ней совпадают по фазе, а мощность цепи всегда положительна. Это значит, что активное сопротивление активно поглощает мощность (электрическую энергию) источника, превращая её в тепло или работу (если цепь содержит двигатель).
К.В. Рулёва, к. ф.-м. н., доцент. Подписывайтесь на канал. Ставьте лайки. Спасибо.
Предыдущая запись : Двигатели постоянного и переменного тока. Вращающееся магнитное поле.
Следующая запись : Конденсатор в цепи переменного тока. Емкостное сопротивление.
Ссылки на занятия до электростатики даны в Занятии 1 .
Ссылки на занятия (статьи), начиная с электростатики, даны в конце Занятия 45.
Ссылки на занятия (статьи), начиная с теплового действия тока, даны в конце Занятия 58.
Ссылки на занятия, начиная с переменного тока, даны в конце Занятия 70 .
Содержание:
Однофазные электрические цепи переменного тока:
Для получения, передачи и распределения электрической энергии применяются в основном устройства переменного тока: генераторы, трансформаторы, линии электропередачи и распределительные цепи переменного тока.
Постоянный ток, необходимый в некоторых областях народного хозяйства (транспорт, связь, электрохимия и др.), получают выпрямлением переменного тока.
Переменным электрическим током называют ток, периодически изменяющийся по величине и направлению.
Основное достоинство переменного тока заключается в возможности трансформировать напряжение. Кроме того, электрические машины переменного тока надежней в работе, проще по устройству и эксплуатации.
Говоря о переменном токе, обычно имеют в виду синусоидальный переменный ток, т. е. ток, изменяющийся по синусоидальному закону. При синусоидальном токе ЭДС электромагнитной индукции, самоиндукции и взаимоиндукции изменяются по синусоидальному закону.
Синусоидальный переменный ток проходит в замкнутой линейной электрической цепи под действием синусоидальной ЭДС.
Рассмотрим получение синусоидальной ЭДС. Если в однородном магнитном поле с индукцией В равномерно со скоростью V вращается рамка (рис. 10.1), то в каждой активной стороне этой рамки длиной 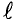
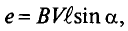
где а – угол, под которым активный проводник рамки пересекает магнитное поле (угол между 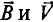 ), или угол поворота рамки относительно нейтральной плоскости
), или угол поворота рамки относительно нейтральной плоскости 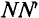 как углы со взаимно перпендикулярными сторонами.
как углы со взаимно перпендикулярными сторонами.
Плоскость 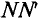 называется нейтральной, т. к. ЭДС в рамке, расположенной в этой плоскости, равна нулю (а = 0, следовательно, sin а = 0).
называется нейтральной, т. к. ЭДС в рамке, расположенной в этой плоскости, равна нулю (а = 0, следовательно, sin а = 0).
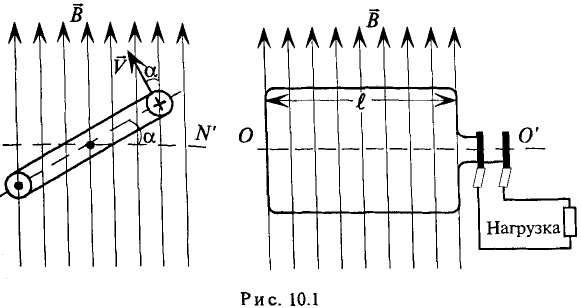
как 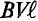 — величина постоянная по условию, то е пропорциональна sin а, т. е. ЭДС в этой рамке, при вращении ее вокруг оси изменяется по синусоидальному закону. Если к этой рамке включить нагрузку (потребитель), то в замкнутой цепи (рис. 10.1) идет ток, который, как и ЭДС, изменяется по синусоидальному ну. Поэтому такой ток и называется синусоидальным.
— величина постоянная по условию, то е пропорциональна sin а, т. е. ЭДС в этой рамке, при вращении ее вокруг оси изменяется по синусоидальному закону. Если к этой рамке включить нагрузку (потребитель), то в замкнутой цепи (рис. 10.1) идет ток, который, как и ЭДС, изменяется по синусоидальному ну. Поэтому такой ток и называется синусоидальным.
Синусоидальная ЭДС 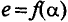 изображена на графике рис. 10.2. график принято называть «волновая диаграмма». (Если изменяющаяся величина изображена в зависимости от времени то ее называют «временная диаграмма».) На этой диаграмме синусоида ограничивает величины ЭДС (ординаты) при раз-личных углах поворота рамки относительно нейтральной плоскости NN”. Как видно, синусоидальная ЭДС изменяется по величине и направлению.
изображена на графике рис. 10.2. график принято называть «волновая диаграмма». (Если изменяющаяся величина изображена в зависимости от времени то ее называют «временная диаграмма».) На этой диаграмме синусоида ограничивает величины ЭДС (ординаты) при раз-личных углах поворота рамки относительно нейтральной плоскости NN”. Как видно, синусоидальная ЭДС изменяется по величине и направлению.
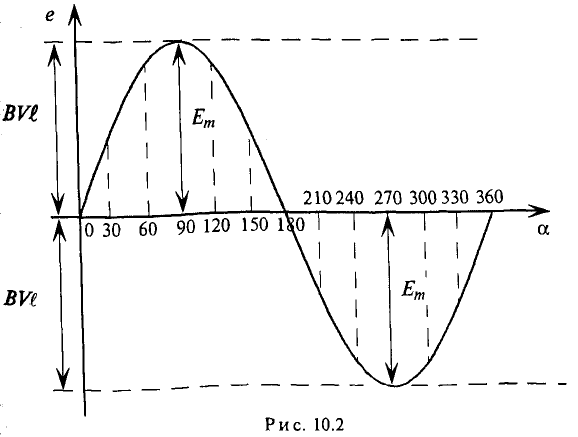
Величины, характеризующие синусоидальную ЭДС
Амплитуда — это максимальное значение периодически изменяющейся величины.
Обозначаются амплитуды прописными буквами с индексом m, т. е. 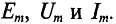
Нетрудно видеть (рис. 10.2), что ЭДС достигает своих амплитудных значений тогда, когда рамка повернется на угол а = 90° или на угол а = 270°, так как 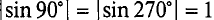 . Следовательно,
. Следовательно, 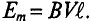
Тогда 
Период – это время, в течение которого переменная величина делает полный цикл своих изменений, после чего изменения повторяются в той же последовательности.
Обозначается период буквой Т и измеряется в секундах, с (сек) т.е. 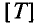 = с.
= с.
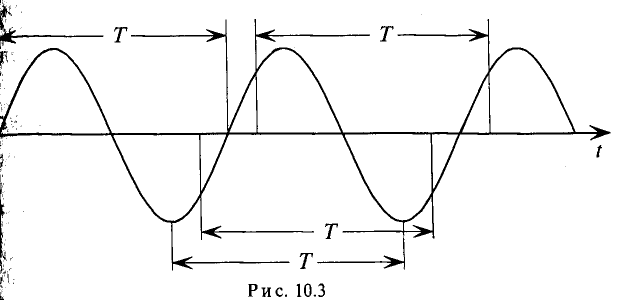
Значение ЭДС через каждый период определяется следующим равенством (рис. 10.3):
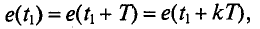
где к – целое число.
На рис. 10.3 изображена временная диаграмма синусоидальной ЭДС при вращении рамки в магнитном поле.
Частота – число периодов в единицу времени, т. е. величина, обратная периоду.
Обозначается частота буквой 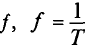 , и измеряется в герцах (Гц):
, и измеряется в герцах (Гц):
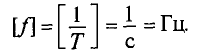
Стандартной частотой в электрических сетях России является частота 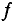 = 50 Гц. Для установок электронагрева пользуются частотами
= 50 Гц. Для установок электронагрева пользуются частотами 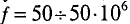 Гц (
Гц (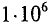 Гц = 1 МГц – мегагерц).
Гц = 1 МГц – мегагерц).
При частоте 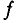 =50 Гц, т.е. 50 периодов в секунду, период
=50 Гц, т.е. 50 периодов в секунду, период
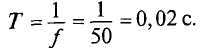
Угловая частота (угловая скорость) характеризуется углом поворотом рамки в единицу времени.
Обозначается угловая частота буквой 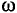 (омега):
(омега):

Измеряется угловая частота в единицах радиан в секунду, так как угол измеряется в радианах (рад).
Так, время одного периода Т рамка повернется на угол 360° = рад. Следовательно, угловую частоту можно выразить следующим образом:

Мгновенное значение — это значение переменной величины в й конкретный момент времени.
Мгновенные значения обозначаются строчными буквами..
Из выражения (10.2) следует, что угол поворота рамки 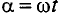 , мгновенные значения синусоидальных величин можно записать так:
, мгновенные значения синусоидальных величин можно записать так:
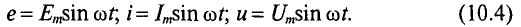
Таким образом, любая синусоидальная величина характеризуется амплитудой и угловой частотой, которые являются постоянными для данной синусоиды. Следовательно, по формулам (10.4) можно определить синусоидальную величину в любой конкретный момент времени t, если известны амплитуда и угловая частота.
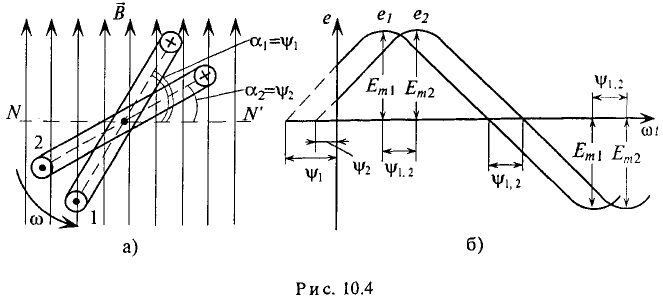
Фаза и сдвиг фаз
Если в магнитном поле вращаются две жестко скрепленные между собой под каким-то углом одинаковые рамки (рис. 10.4а), т.е. амплитуды ЭДС 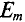 и угловые частоты со их одинаковы, то мгновенное значение их ЭДС можно записать в виде
и угловые частоты со их одинаковы, то мгновенное значение их ЭДС можно записать в виде
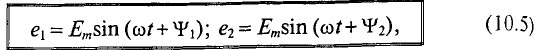
где 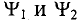 — углы, определяющие значения синусоидальных величин
— углы, определяющие значения синусоидальных величин 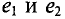 в начальный момент времени (t = 0), т.е.
в начальный момент времени (t = 0), т.е.
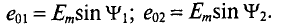
Поэтому эти углы 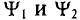 называют начальными фазами синусоид.
называют начальными фазами синусоид.
Начальные фазы 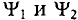 этих ЭДС различны.
этих ЭДС различны.
Таким образом, согласно (10.5) каждая синусоидальная величина характеризуется амплитудой 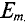 , угловой частотой со и начальной фазой
, угловой частотой со и начальной фазой  . Для каждой синусоиды эти величины
. Для каждой синусоиды эти величины 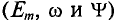 являются постоянными. В выражениях (10.4) начальные фазы
являются постоянными. В выражениях (10.4) начальные фазы  синусоид равны нулю (
синусоид равны нулю ( = 0).
= 0).
Величина 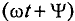 называется фазой синусоиды.
называется фазой синусоиды.
Разность начальных фаз двух синусоидальных величин одинаковой частоты определяет угол сдвига фаз этих величин:

При вращении против часовой стрелки (рис. 10.4а) ЭДС в первой рамке достигает амплитудного и нулевого значения раньше, чем во второй, т. е. 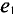 опережает по фазе
опережает по фазе 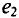 или
или 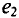 отстает по фазе
отстает по фазе 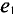 (рис. 10.46). Угол сдвига фаз
(рис. 10.46). Угол сдвига фаз 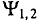 показывает, на какой угол синусоидальная величина опережает или отстает от другой, достигает своих амплитудных и нулевых значений раньше позже).
показывает, на какой угол синусоидальная величина опережает или отстает от другой, достигает своих амплитудных и нулевых значений раньше позже).
Две синусоидальные величины одинаковой частоты, достигаю-одновременно своих амплитудных (одного знака) и нулевых сечений, считаются совпадающими по фазе (рис. 10.5а).
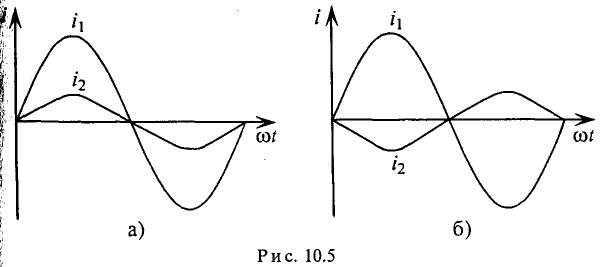
Если две синусоиды одинаковой частоты достигают одновременно своих нулевых и амплитудных значений разных знаков (рис. 10.56), то они находятся в противофазе.
Время, на которое одна синусоидальная величина опережает и отстает от другой, характеризует время сдвига фаз 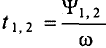 , которое можно выразить через период Т и частоту
, которое можно выразить через период Т и частоту 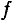 синусоиды следующим образом:
синусоиды следующим образом:
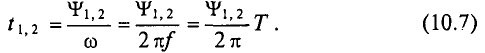
Среднее и действующее значения переменного тока
Кроме амплитудных и мгновенных значений переменный ток, напряжение, ЭДС характеризуются еще средними и действующими (эффективными) значениями.
Среднее значение переменного тока
Среднее значение переменного тока равно величине такого постоянного тока, при котором через поперечное сечение провод-проходит то же количество электричества Q, что и при переменном токе.
Таким образом, среднее значение переменного тока эквивалентно постоянному току по количеству электричества Q, проходящему через поперечное сечение проводника в определенный промежуток времени.
Средние значения переменных величин обозначаются прописными буквами с индексом «с», т. е. 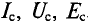 .
.
Если ток изменяется по синусоидальному закону, то за половину периода через поперечное сечение проводника проходит определенное количество электричества Q в определенном направлении, а за вторую половину периода через то же сечение проходит то же количество электричества в обратном направлении. Таким образом, среднее значение синусоидального тока за период равно нулю, т. е. 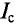 = 0.
= 0.
Поэтому для синусоидального переменного тока определяется его среднее значение за половину периода Т/2, т. е.
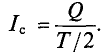
Из выражения (2.1) значение переменного тока 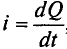 , откуда
, откуда 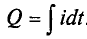 . Следовательно, среднее значение синусоидального тока
. Следовательно, среднее значение синусоидального тока 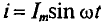 с начальной фазой
с начальной фазой  = 0 за полупериод определяется (рис. 10.6) выражением
= 0 за полупериод определяется (рис. 10.6) выражением
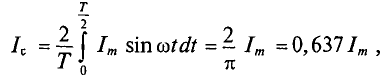
где 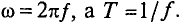
Графически среднее за полупериод значение синусоидального тока равно высоте прямоугольника с основанием, равным Т/2, и площадью, равной площади, ограниченной кривой тока и осью абсцисс за половину периода (рис. 10.6).
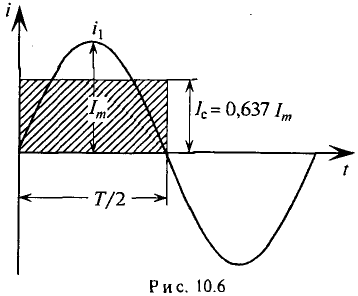
Под средним значением переменной величины понимают постоянную составляющую этой величины.
Средние значения синусоидального напряжения и ЭДС за полупериод можно определить по аналогии с током.
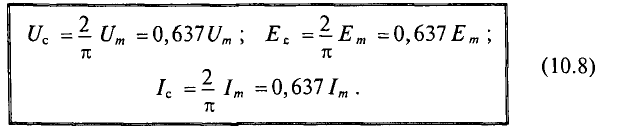
Действующее значение переменного тока
Действующее (или эффективное) значение переменного тока — значение переменного тока, эквивалентное постоянному току тепловому действию.
Действующее значения переменных величин обозначается прочими буквами без индексов: I, U, Е.
Действующее значение переменного тока I равно величине такого постоянного тока, которое за время, равное одному периоду первого тока Т, выделит в том же сопротивлении R такое же количество тепла, что и переменный ток i:
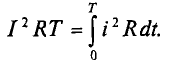
Откуда действующее значение переменного тока
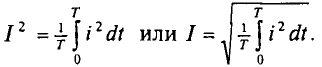
Если переменный ток изменяется по синусоидальному закону с начальной фазой, равной нулю, т.е. 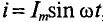 , то действующее сечение такого синусоидального тока будет равно
, то действующее сечение такого синусоидального тока будет равно
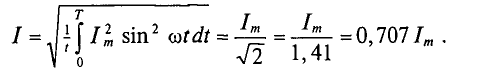
Действующее значение синусоидального тока в 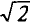 =1 ,41 раза меньше его амплитудного значения. Так же можно определить действующие значения синусоидального напряжения и ЭДС.
=1 ,41 раза меньше его амплитудного значения. Так же можно определить действующие значения синусоидального напряжения и ЭДС.
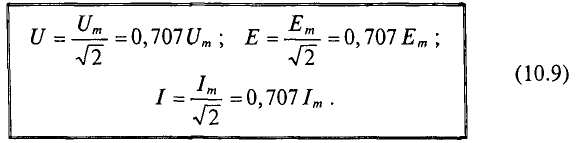
Номинальные значения тока и напряжения в электрических цепей и устройствах выражаются их действующими значениями.
Так, например, стандартные напряжения электрических сетей U= 127 В или U = 220 В выражают действующие значения этих напряжений. А изоляцию необходимо рассчитывать на амплитудное значение этих напряжений, т. е.
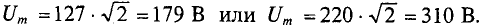
При расчете цепей переменного тока и их исследованиях чаще всего пользуются действующими (эффективными) значениями тока, напряжения и ЭДС.
На шкалах измерительных приборов переменного тока указывается действующие значение переменного тока или напряжения.
Именно действующие значения тока, напряжения и ЭДС указываются в технической документации, если нет специальных оговорок.
Коэффициенты формы и амплитуды
Отклонения кривых тока, напряжения и ЭДС от синусоиды характеризуются коэффициентами формы 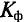 и амплитуды
и амплитуды 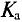 .
.
Коэффициент формы 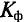 определяется отношением действующего значения переменной величины к ее среднему значению:
определяется отношением действующего значения переменной величины к ее среднему значению:

Коэффициент формы необходимо учитывать при проектировании и изучении выпрямительных устройств и электрических машин.
Для синусоидальных величин коэффициент формы будет равен
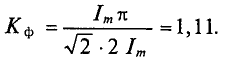
Коэффициент амплитуды 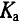 определяется отношением амплитудного значения переменной величины к ее действующему значению:
определяется отношением амплитудного значения переменной величины к ее действующему значению:

Для синусоидальных величин коэффициент амплитуды равен
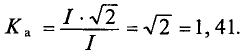
Чем больше коэффициент формы и коэффициент амплитуды отличается от значений 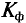 = 1,11 и
= 1,11 и 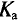 = 1,41, тем больше рассматриваемая кривая отличается от синусоиды. Так, например, если
= 1,41, тем больше рассматриваемая кривая отличается от синусоиды. Так, например, если 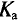 = 1,41, то исследуемая кривая имеет более острую форму, чем синусоида, а если
= 1,41, то исследуемая кривая имеет более острую форму, чем синусоида, а если 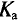 < 1,41, то более тупую.
< 1,41, то более тупую.
График прямоугольной формы имеет коэффициент амплитуды 1.
Векторные диаграммы
Для наглядности синусоидальные величины изображают векторами, вращающимися против часовой стрелки со скоростью, равной угловой частоте со этих синусоид. Так как эти векторы изображают синусоиды в начальный момент времени (t = 0), то они подвижны. Длина вектора в выбранном масштабе определяется амплитудой синусоиды, а угол поворота вектора против часовой стрелки относительно положительного направления оси абсцисс начальной фазе синусоиды. Таким образом, вектор учитывают все значения, характеризующие синусоидальную величину – амплитуду, угловую частоту и начальную фазу, пример, три синусоидальные ЭДС одинаковой частоты
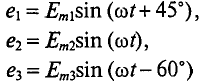
можно изобразить векторами (рис. 10.7).
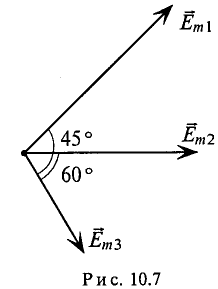
Совокупность нескольких векторов, изображающих синусоидальные величины одинаковой частоты в начальный момент времени, называется векторной диаграммой.
На векторной диаграмме (рис. 10.7) на-ю видны величины синусоид (ампли-), их начальные фазы и углы сдвига между ними. Очевидно, наибольшую амплитуду имеет ЭДС 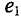 , а наименьшую ЭДС
, а наименьшую ЭДС 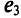 ЭДС
ЭДС 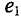 опережает по фазе
опережает по фазе 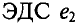 угол 45°, а ЭДС
угол 45°, а ЭДС 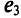 отстает от ЭДС
отстает от ЭДС 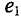 по фазе на угол 105° и т. д. Начало отсчета времени можно выбирать произвольно, т. е. один из векторов векторной диаграммы направляется произвольно, а остальные векторы (соответствующих длин) изображаются отношению к нему под углами, равными углам сдвига фаз между ними (рис. 10.8). При указанном ЭДС могут быть записаны так:
по фазе на угол 105° и т. д. Начало отсчета времени можно выбирать произвольно, т. е. один из векторов векторной диаграммы направляется произвольно, а остальные векторы (соответствующих длин) изображаются отношению к нему под углами, равными углам сдвига фаз между ними (рис. 10.8). При указанном ЭДС могут быть записаны так:

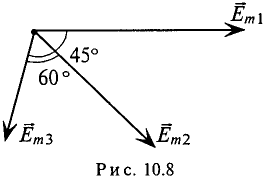
При этом амплитуды ЭДС и углы сдвига фаз остаются неизменными (как и угловая частота), а меняются только начальные фазы синусоид, изображенных на векторной диаграмме (рис. 10.7). В расчетах, если специально не оговорено, начальные фазы не играют роли.
Сложение синусоидальных величин
Сложение и вычитание синусоидальных величин одинаковой частоты можно осуществлять аналитически и графически. В результате такого сложения (вычисления) получается синусоида с той же частотой, с определенной амплитудой и определенной начальной фазой.
Аналитическое сложение предусматривает сложение мгновенных значений синусоидальных величин, выраженных аналитически, т. е.
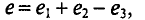
где 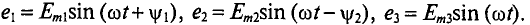
Тогда
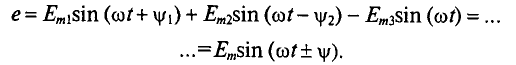
Математический анализ позволяет определить суммарную ЭДС е и ее аналитическое выражение.
Графическое сложение можно осуществлять по: 1) волновым (временном) диаграммам и 2) векторным диаграммам.
1. Графическое сложение по временным диаграммам (рис. 10.9) осуществляется следующим образом: ординаты суммарной синусоиды определяются сложением ординат слагаемых синусоид в различные моменты времени.
Как видно, в рассматриваемом примере амплитуда суммарной синусоиды не равна алгебраической сумме амплитуд слагаемых синусоид. Начальная фаза суммарной синусоиды также не является результатом арифметических действий, т.е. по временным диаграммам производятся только графические действия.
2. Графическое сложение по векторным диаграммам осуществляется в следующей последовательности. Прежде всего необходимо построить векторную диаграмму слагаемых синусоидальных величин (рис. 10.10а).
Определение вектора, изображающего суммарную синусоиду, осуществляется сложением векторов слагаемых синусоид по правилу многоугольника, т. е. из какой-либо точки О изображают вектор, соответствующий первой слагаемой синусоиде 10.106), из конца этого вектора изображают вектор, соответствующий второй слагаемой синусоиде, и т.д.
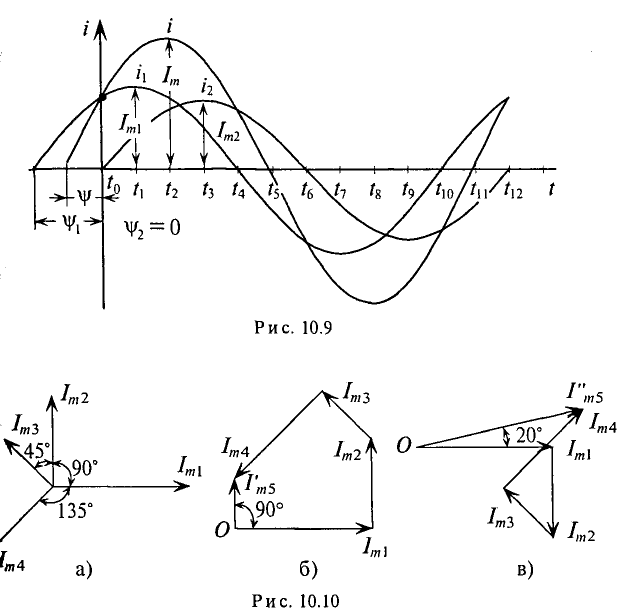
Вектор, соответствующий суммарной синусоиде, проводят из и О к концу последней слагаемой синусоиды.
Тот вектор (рис. 10.106), в масштабе изображения слагаемых синусоид, соответствует амплитуде суммарной синусоиды 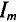 . Угол поворота этого вектора против часовой стрелки относительно положительного направления оси абсцисс соответствует положительному значению начальной фазы
. Угол поворота этого вектора против часовой стрелки относительно положительного направления оси абсцисс соответствует положительному значению начальной фазы 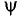 суммарной синусоиды, угловая частота суммарной синусоиды равна частоте слагаемых синусоид.
суммарной синусоиды, угловая частота суммарной синусоиды равна частоте слагаемых синусоид.
Вычитание синусоидальной величины равносильно умножение этой величины на отрицательную единицу (—1), что соответствует повороту вектора этой величины на 180″ (рис. 10.10 в).
Сложение и вычитание синусоидальных величин по векторный диаграммам рассматривается в примере 10.1.
Пример 10.1
Заданы мгновенные значения четырех токов:

Определить:
1)суммарный ток при условии 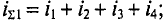
2)суммарный ток при условии 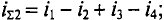
3)частоту f всех синусоид.
Решение
Для построения векторной диаграммы слагаемых токов задаются определенным масштабом токов 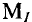 (например,
(например, 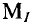 = 1 А/см). В этом масштабе построена векторная диаграмма токов на рис. 10.10а.
= 1 А/см). В этом масштабе построена векторная диаграмма токов на рис. 10.10а.
1. Для определения суммарного тока производится сложение векторов по правилу многоугольника (рис. 10.106). Суммарный ток в результате сложения будет равен 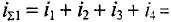
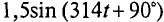 . Амплитуда суммарного тока
. Амплитуда суммарного тока 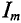 = 1,5 А определена из многоугольника в выбранном масштабе, а начальная фаза его измерена транспортиром
= 1,5 А определена из многоугольника в выбранном масштабе, а начальная фаза его измерена транспортиром  = 90°.
= 90°.
2. Построение многоугольника для заданного условия показано на рис. 10.10в. Из многоугольника определяется результирующий ток
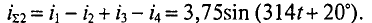
3. Частота слагаемых и результирующих токов будет равна
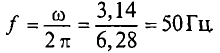
В заключение можно сделать вывод, что самым удобным и, следовательно, распространенным методом сложения синусоидальных величин является метод графического сложения по векторным диаграммам. Этот метод и будет использован при расчете электрических цепей однофазного и трехфазного тока, изменяющегося по синусоидальному закону.
Так как действующие значения синусоидальных величин пропорциональны их амплитудным значениям (см. (10.9)), то вектор, отражающий в определенном масштабе амплитудное значение, в этом масштабе представляет действующее значение той же вены. Исходя из этого, в дальнейшем на векторных диаграммах будут изображаться векторы, в определенном масштабе представляющие не амплитудное, а действующее значение синусоидальной вены, которое чаще всего используется при расчетах цепей переменного тока.
- Однофазные цепи синусоидального тока
- Законы и правила Кирхгофа для электрических цепей
- Линии с распределенными параметрами
- Идеализированные пассивные элементы
- Закон Ома для замкнутой цепи
- Энергия и мощность электрического тока
- Закон Джоуля — Ленца для тока
- Режимы работы электрических цепей
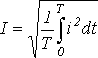 ,
,