Что такое действующее значение напряжения
Содержание
- 1 Как измеряется
- 1.1 Практический пример
- 2 Импульсный электрический заряд
- 2.1 Расчёт кривой
- 2.2 Вычисления
- 3 Сила переменного тока
- 4 Вывод
- 5 Видео по теме
Всем нам известно о 220 вольт в бытовой розетке. Но если подключить к ней вольтметр, напряжение каждый раз будет разным. При этом зачастую напряжение может быть даже больше данной величины. Постараемся в данном материале разобраться — почему это происходит, что такое действующее значение переменного тока, и как его можно рассчитать с помощью различных вариантов.
Как измеряется
Электродинамические параметры в сети постоянно изменяются. Это связано с тем, что они представлены синусоидальным однополярным импульсом разной амплитуды. При измерении напряжения в цепи переменного тока, каждый раз будет получен разный результат. А при вычислении усреднённого параметра, он всегда будет составлять 0.

Получается, что математически вычислить данный параметр невозможно. Есть возможность получить только усреднённый параметр, который зависит от полупериода синусоидальной волны. Однако использовать его на практике или для каких-то вычислений нельзя.
Для решения этой проблемы и стали применять такое понятие, как действующее значение для расчёта силы тока и напряжения. Параметр определяется по характеристикам постоянного тока в цепи, генерирующей тепловую энергию такого же объёма, как и при подаче в цепь переменного тока.
Практический пример
Определение выше будет непонятным для человека, который не имеет особых познаний в области электротехники и электродинамики. Чтобы понять его смысл, предлагается рассмотреть следующий пример:
- Доступны две идентичные электроцепи (длина, элементы цепи и сечение проводников у них совпадают).
- В каждую включён одинаковый резистор — электронный компонент, который изменяет свое сопротивление в зависимости от подаваемого тока.
- Обе цепи подключаются к источникам электроэнергии, имеющим одинаковое напряжение.

Но между цепями есть одна разница. На первую электроцепь подаётся постоянный, а на вторую — переменный ток. По одной из них пойдёт стабильный электроток, а по другой потечет импульсный электрозаряд, который постоянно изменяется и имеет синусоидальной график.
Чтобы найти количества тепла в цепи с сопротивлением, используется такая формула:

После произведения ряда замеров и вычислений можно увидеть, что выделяемое тепло в этих двух электроцепях имеет одинаковую величину. Например, в цепи с постоянным током при подаче напряжения 30 вольт выделяется тепло 200 Джоуль (или Дж). Если вторая цепь имеет идентичные характеристики, то выделение тепла в ней также составит 200 Дж. Получается, что напряжение 30В в этих электроцепях — это и есть эффективное напряжение.
Импульсный электрический заряд
Вышеприведенный пример позволяет только определить действующее и среднее значение напряжения переменного тока. Но на практике такой метод также не применяется, из–за того, что получить доступ к источнику переменного напряжения не всегда представляется возможным. Поэтому параметры цепи рассчитываются с помощью формул, которые основаны на синусоидальных кривых.
Стоит отметить, что действующее напряжение не всегда формируется путём плавного изменения определённого импульсного электрозаряда. Кривая зачастую имеет форму, отличную от привычной нам синусоиды:
- Прямоугольную (меандр);
- треугольную;
- трапециевидную
- и другие.

То есть график электротока может иметь отличную, но при этом стабильную форму. Наглядным примером такого варианта является кривая осциллографа, регистрирующая ритмы сердцебиения человека.

Но независимо от действующего в сети импульсного заряда, во время расчётов используется именно синусоида. Это объясняется тем, что погрешности в расчетах будут крайне малыми. Поэтому ими можно пренебречь, ведь они не скажутся на конечном результате:
- Частота импульса в жилых домах составляет 50 Гц. За 1 сек электрический импульс проходит через фазу 100 раз. Это означает, что работающая от сети лампочка за секунду 100 раз загорается и тухнет, а электрический заряд при этом изменяется довольно плавно. Но человек этого не замечает из-за невосприимчивости человеческого зрения к сверхбыстрым колебаниям.

- Одинаковая площадь фигур. Независимо от формы кривой периода, описывающей переменный электроток идентичных параметров, площадь их фигур всегда будет одинаковой. Следовательно, при любых расчетах получится одно и то же эффективное значение переменного синусоидального тока. Поэтому эффективные значения не зависят от формы кривой. На них оказывает влияние именно величина амплитуды.

Форма кривой импульса важна только для сверхточных расчётов в лабораторных условиях. Также она учитывается для работы суперкомпьютеров. В остальных случаях синусоида позволит вычислить действующее значение переменного синусоидального тока.
Расчёт кривой
Синусоида — это периодическая функция, которую можно всегда описать с помощью уравнения. Если взять её за основу, то на входе имеются следующие исходные данные:
- Т — амплитуда;
- φ — начальная фаза;
- ωt — угловая скорость.

По этим входным характеристикам находим другие переменные параметры:
- Uт — амплитудное напряжение;
- Uм — действующие в момент измерения значения напряжения;
- ωt + φ — фактическая фаза в точке измерения.
Т.к. начальная фаза равняется нулю, на выходе формула кривой будет иметь следующий вид:
Uм = Uт·sin(ωt + φ) = Uт·sin(ωt)
Теперь необходимо обратиться к закону выделения тепла, который еще называется законом Джоуля-Ленца. Согласно него квадрат напряжения — это произведение выделяемого тепла на сопротивление проводника.
| Формулы для расчета тепловой энергии в электроцепях: | |
| с постоянным током | с переменным током |
| Q = U2/R | Q = Uм2/R |
- Uм — величина постоянного напряжения;
- Uм — величина действующего напряжения;
- R — сопротивление проводника.
Мы видим, что при расчетах количества тепла в цепи переменного тока, пользуется именно действующим значением переменного тока.

Из данных формул вытекают два важных нюанса, на которые стоит обратить внимание:
- В расчетах используется среднеквадратичное значение напряжения (СКЗ). Это связано с тем, что величина напряжения постоянно изменяется и можно получить только какую-то усредненную величину.
- Амплитуда постоянного тока довольно условная величина. Ее используют в расчетах, чтобы только описать период синусоиды переменного электрозаряда.
Вычисления
Волны синусоид будут одинаковыми. Однако в пределах периода в каждой точке измерения напряжения будут отличаться. Поэтому, чтобы уравнять между собой среднеквадратичное напряжение постоянного и переменного электротока по тепловыделению, требуется рассчитать объём выделенного тепла в течение времени, равного 1 периоду:
![]()
В уравнение теперь можно подставить выражение расчёта мгновенного напряжения
Uм = Uт·sin(ωt + ф) = Uт·sin(ωt)

После математического преобразования можно рассчитать действующее значение электрического напряжения:
U = Uт / √2 = 0,707·Uм
Теперь найдем амплитудное напряжение по формуле:
Uт = U·√2
Амплитудное напряжение так же имеет и другое название – максимально возможное эффективное мгновенное значение напряжения.
Сила переменного тока
С помощью амперметра находим амплитудную силу тока в цепи. Используя её вместе с периодом, который равен 1/50 секунд, можно применить описанную выше формулу, чтобы рассчитать среднеквадратичное значение напряжения. В результате этого будет получена действующие значения силы тока.
Действующее значение тока можно рассчитать, когда других исходных параметров нет, но нам известно эффективное значение величины напряжения в цепи. Следовательно, можно воспользоваться всем нам известным законом Ома вычисления значения силы тока:
U = I·R и I = U/R
где:
- U — будет действующим напряжением переменного синусоидального тока;
- R — сопротивление проводника, которое всегда можно узнать в любом справочнике, зная состав материала проводника.
Ранее электропроводку делали из алюминия и меди, которые отличались довольно высоким сопротивлением. Эффективное значение реальной силы тока этих металлов было меньше 6.5А. По этой причине в старых домах зачастую срабатывает автоматический выключатель, если одновременно подключить в сеть несколько приборов. Сегодня открыты сложные сплавы с низким сопротивлением. Они позволяют достичь с действующее значение силы переменного тока около 16А даже в обычных современных многоквартирных домах.

С уменьшением сопротивления проводника, прямопропорционально возрастает мощность и тепловыделение. При том надо помнить о том, что у каждого сплава есть свой определенный температурный предел. Поэтому в жилых сетях сила тока часто не превышает 20 ампер, а при резком ее скачке, например, при неполадках на подстанции, электронная часть устройств просто сгорает. Для предотвращения таких случаев и подключаются автоматы, которые при регистрации высоких действующих значений размыкают цепь на данном участке. Более мощные источники электроэнергии встречаются только в промышленных трехфазных сетях с напряжением 380В.
Вывод
Мы рассмотрели в данной статье — что называют действующим значением силы тока и напряжения, а так же как определяют эти значения переменного тока в электроцепи. Это эффективные значения переменного тока, под действием которого выделяется точно такое же количества тепла, как и в цепи постоянного тока, имеющей аналогичные характеристики.
Видео по теме
Среднеквадратичное значение
В зарубежной терминологии применяется аббревиатура RMS (rms) – root mean square.
В математике для набора чисел x1, x2, …, xn количеством n среднеквадратичное значение (rms) определяется выражением:

Например, для чисел 2,3 и 6 среднеквадратичным значением будет квадратный корень из (2²+3²+6²)/3. √(49/3) = 4.04
Среднеквадратичным значением двух или нескольких чисел
является квадратный корень из среднеарифметического значения квадратов этих чисел.
Для любой непрерывной функции в интервале T1 – T2 среднеквадратичное значение можно рассчитать по формуле:

Среднеквадратичное значение применяется в расчётах, где существует пропорциональная зависимость не самих переменных значений, а их квадратов.
Действующее значение напряжения и тока
В качестве примера можно рассмотреть квадратичную зависимость мощности или работы электрического тока от значений тока или напряжения.
P = I²R; A = I²Rt; P = U²/R; A = U²t/R
Величина постоянного напряжения или тока является его среднеквадратичным значением.
Среднеквадратичное значение переменного тока равно величине постоянного тока,
действие которого произведёт такую же работу в активной (резистивной) нагрузке за время периода.
Определяющим фактором здесь является среднее (среднеарифметическое) значение мощности Pavg
или работы Aavg,
пропорциональное квадрату значения тока.
Так же среднеквадратичное значение переменного напряжения за период равносильно
по своему воздействию на активную нагрузку такому же значению постоянного напряжения.
P = UI = Pavg = UrmsIrms
Среднеквадратичное значение переменного напряжения или тока часто называют действующим или эффективным.
Величину переменного напряжения или тока, в большинстве случаев,
выражают его среднеквадратичным значением и измеряют приборами электромагнитного типа или специальными среднеквадратичными измерителями – True RMS.
Примечание:
Электромагнитные приборы используют для измерения переменного тока и напряжения в промышленных установках.
Усилие, создаваемое измерительной катушкой в электромагнитном приборе, пропорционально квадрату тока, поэтому не меняется по направлению.
Угол отклонения стрелки определится некоторым средним усилием F, которое будет пропорционально среднеквадратичному значению тока.
Расчёт действующего значения
В качестве примера рассчитаем среднеквадратичное значение синусоидального напряжения.

Запишем выражение Urms с применением интеграла функции
U = Uampsin(t) для одного периода 2π :

Показать расчёт
Скрыть расчёт

Вынесем Uamp из под знака радикала.
Воспользуемся табличным интегралом  ,
,
перепишем и решим последнее выражение с применением формулы Ньютона-Лейбница:

Так как sin(2π), sin(4π) и sin(0) равны нулю, вычисляем RMS синусоиды следующим образом:

В результате решения в итоге получим:
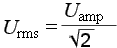
Расчёт RMS для напряжения или тока треугольной и пилообразной формы можно рассмотреть на примере одного периода T
для функции  , представленной на рисунке:
, представленной на рисунке:

Выразим Urms искомой функции с помощью определённого интеграла:

Показать расчёт
Скрыть расчёт

Используя табличный интеграл 
и формулу Ньютона-Лейбница, получаем:

В итоге преобразований получим:

Ток или напряжение любой сложной формы можно рассмотреть, как набор функций в пределах периода.
Тогда значением RMS будет квадратный корень из среднеарифметического значения интегралов для квадрата каждой функции, ограниченной её интервалом времени в периоде.
Например, для множества функций F1(t) , F2(t) , … , Fn(t)
в соответствующих им интервалах времени (0 – T1), (T1 – T2), …, (Tn – T),
составляющих период T, действующее напряжение (RMS) определится выражением:

Для вариантов однополярного или двуполярного напряжения пилообразной и треугольной формы в периоде 2T или 4T, представленных на рисунке ниже,
T и U amp имеют те же расчётные величины,
что и в рассмотренном случае c функцией  ,
,
а интегралы, определённые в интервалах, равных T, для квадратов используемых функций 
 ,
,
будут иметь одно и то же значение 

Следовательно, вышеуказанные варианты однополярного или двуполярного напряжения пилообразной и треугольной формы будут иметь
среднеквадратичное значение  .
.
В заключении рассмотрим пример вычисления действующего значения положительных прямоугольных импульсов длительностью Ti .

Выразим Urms одного периода T, как квадратный корень из среднеарифметического значения интегралов,
определённых в интервалах 0 – Ti и Ti – T для квадратов всех значений периода.

В результате получаем значение RMS, равное произведению амплитуды импульсов Uamp на квадратный корень из
коэффициента заполнения (Ti / T).

В качестве дополнительного материала предлагаем рассмотреть расчёт средеквадратичного значения напряжения накала кинескопа цветного телевизора, исходя из амплитуды и формы напряжения.
Замечания и предложения принимаются и приветствуются!
Особенности измерения переменных напряжений и токов
В радиолюбительской практике приходится сталкиваться с необходимостью измерения переменных напряжений и токов не только синусоидальной формы, но и сигналов другой формы: прямоугольных импульсов, выходных напряжений одно- и двухполупериодных выпрямителей, выходных напряжений тиристорных регуляторов и пр. Форма сигнала существенно влияет на показания измерительного прибора. Дело в том, что шкалы большинства вольтметров переменного напряжения (как цифровых, так и стрелочных) градуируются в действующих значениях переменного напряжения. При этом в большинстве таких приборов в основу измерения переменного напряжения (или тока) положен способ измерения средневыпрямленного значения напряжения или тока.

Основные параметры переменного напряжения
Дадим некоторые определения. Переменное напряжение характеризуется следующими основными параметрами: амплитудным (пиковым) значением Ua, средним значением Ucp, средневыпрямленным значением Ucpв, действующим (среднеквадратическим, эффективным) значением Uд.
Амплитудное значение—это наибольшее или наименьшее за период значение величины.
Среднее значение за период — это среднеинтегральное за период значение величины, которое математически может быть определено следующим образом:
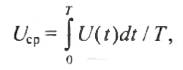
где U(t) — мгновенное значение напряжения.
Для двухполярных напряжений, форма которых симметрична относительно горизонтальной оси (например, для синусоидального) Ucp = 0. Часто говорят также, что среднее значение напряжения — это его постоянная составляющая. Очевидно, что для синусоидального симметричного напряжения постоянная составляющая равна нулю. Именно поэтому вольтметр постоянного напряжения, включенный для измерения такого напряжения, покажет нулевое значение. Это связано с тем, что любой вольтметр постоянного тока представляет собой выпрямитель с инерционным элементом. В стрелочных приборах функцию инерционного элемента выполняет магнитоэлектрический прибор. В цифровых вольтметрах такую функцию выполняет либо фильтр нижних частот, образованный резистором и конденсатором, либо усреднение производится самим аналого-цифровым преобразователем измерительного прибора.
Средневыпрямленное значение за период — это среднеинтегральное за период значение модуля величины, которое математически может быть определено по формуле:
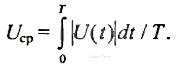
Эту величину несложно измерить, применив двухполупериодный выпрямитель. Эта величина характеризует перенос заряда электрическим током и геометрически равна высоте прямоугольника, у которого основание равно длине одного полупериода, а площадь прямоугольника равна площади под одной полуволной синусоиды.
Действующим (среднеквадратическим, эффективным) значением переменной величины называют такое постоянное значение этой величины, которое производит такое же тепловое действие, как и переменная величина. Поскольку тепловое действие электрического тока пропорционально квадрату тока (или напряжения), действующее значение можно определить как корень квадратный из среднего за период квадрата мгновенного значения величины, т. е.
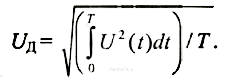
Все вышеуказанные значения напряжений связаны между собой коэффициентами амплитуды Ка и формы Кф. При этом Ка = Uа/ Uд, Кф= Uд /Ucpв. Иногда для удобства расчетов вводят коэффициент усреднения Ку = Ка Кф = Uа/ Ucpв. Эти коэффициенты позволяют определять любой параметр переменного напряжения, если известны форма напряжения и один из его параметров.
Формы и параметры, наиболее часто встречающиеся в практике радиолюбителя электрических сигналов различной формы, показаны на рис. 1 и в табл.1.
Напомним, что скважностью Q импульсов называют отношение периода следования импульсов к длительности одного импульса.
Особый интерес представляет измерение выходного напряжения регулятора с фазоимпульсным управлением (рис. 1, з). Его форма характеризуется углом α включения коммутирующего элемента (обычно это триодный или симметричный тиристор). Значение угла α может находиться в пределах от 0 до 180°. Коэффициенты формы и амплитуды являются функциями этого угла:
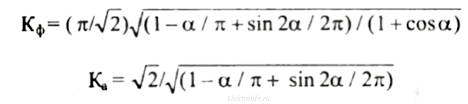
при 0 < α < 90° и
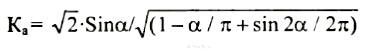
при 90° < α < 180°.
В данных формулах значение угла α измеряется в радианах (один радиан равен примерно 57,3°). Для удобства расчетов в приведенной ниже таблице 2 даны значения Кф, Ка и Ку для различных значений угла α, измеренного в градусах.
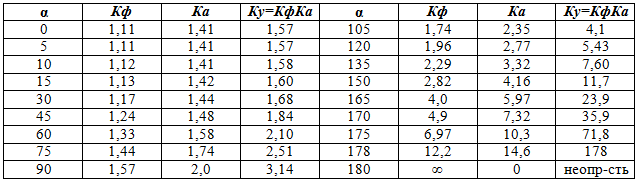
Из таблицы хорошо видно, что с увеличением угла значения Кф и Ка все более и более отклоняются от значений, приведенных в табл. 1 для синусоидального напряжения (1,11 и 1,41 соответственно).
Методика измерения переменных напряжений
В радиолюбительской практике возникает необходимость измерить действующее или среднее (средневыпрямленное), реже — амплитудное (пиковое) значения напряжений.
Приборы для измерения переменных напряжений отличаются принципом действия. Так, в приборах электромагнитной системы отклонение стрелки пропорционально действующему значению переменного напряжения или тока. При этом форма напряжения значения не имеет. Следовательно, для измерения действующих значений переменного напряжения произвольной формы желательно применять приборы электромагнитной системы. На шкалы таких приборов наносится соответствующий знак (рис. 2, а).
Приборы магнитоэлектрической системы реагируют на средневыпрямленное значение измеряемой величины и имеют на шкалах знак, показанный на рис. 2, б. Такие приборы весьма широко распространены и на их основе изготавливается подавляющее большинство авометров (тестеров). Практически все цифровые авометры широкого применения также реагируют на средневыпрямленное значение измеряемой величины. Отсюда следует, что для измерения средневыпрямленных значений переменных величин желательно применять именно такие приборы, поскольку форма сигнала на показания прибора не влияет.
Шкалы всех вольтметров, независимо от принципа действия прибора, градуируются в действующих значениях синусоидального напряжения. Это объясняется тем, что эти вольтметры чаще всего применяются для измерения синусоидальных напряжений как наиболее часто встречающихся в практике. Поэтому, если измеряется синусоидальное напряжение, прибор показывает значение Uд. Если же форма напряжения отличается от синусоидальной, потребуется пересчет показаний с учетом коэффициентов формы и амплитуды. Исключение составляют пиковые вольтметры, шкалы которых градуируются в амплитудных значениях Ua. При отсутствии такого вольтметра его несложно сделать самостоятельно, добавив к вольтметру постоянного тока диодный выпрямитель и конденсатор (рис. 3).
С учетом вышеизложенного, последовательность измерений переменной величины может быть следующей.
-
С помощью осциллографа определяется форма измеряемого сигнала и по таблице 1 и рисунку 1 определяются коэффициенты формы и амплитуды. Для выходного напряжения фазоимпульсного (рис. 1, з) регулятора необходимо определить угол включения α, который приблизительно можно оценить осциллографом.
-
Выясняют принцип действия измерительного прибора, и в каких значениях проградуирована его шкала.
-
Считывают показания со шкалы прибора и корректируют их с учетом Ка и Кф.
Примеры
Пример 1. Измеряется синусоидальное напряжение вольтметром переменного тока магнитоэлектрической системы. Шкала отградуирована в действующих значениях. Показание вольтметра равно 100 В. Из табл. 1 определяем Ка = 1,41 и Кф = 1,11. По формулам Ka = Ua/ Uд, Кф = Uд / Ucpв вычисляем: амплитудное значение напряжения Ua = Ка • Uд = 1,41 • 100 = 141 (В) и средневыпрямленное значение Ucpв = Uд / Кф = 100:1,11 =90 (В).
Пример 1. Измеряется синусоидальное напряжение вольтметром переменного тока магнитоэлектрической системы. Шкала отградуирована в действующих значениях. Показание вольтметра равно 100 В. Из табл. 1 определяем Ка = 1,41 и Кф = 1,11. По формулам Ka = Ua/ Uд, Кф = Uд / Ucpв вычисляем: амплитудное значение напряжения Ua = Ка • Uд = 1,41 • 100 = 141 (В) и средневыпрямленное значение Ucpв = Uд / Кф = 100:1,11 =90 (В).
Пример 2. Цифровым вольтметром постоянного тока, у которого измерительный узел реагирует на средневыпрямленное значение напряжения, измеряется напряжение на выходе двухполупериодного
выпрямителя (рис. 1, б). Прибор показывает 50 В. Из табл. 1 определяем коэффициенты формы и амплитуды для измеряемого двухполупериодного напряжения: Ка = 1,41 и Кф= 1,11. Находим действующее значение измеряемого напряжения Uд = КфUcpв = 1,11• 50 = 55,5 (В), а затем амплитудное значение Ua = Ка Uд = 1,41•55,5 = 78,3 (В). Чтобы убедиться в правильности расчетов, понадобятся квадратичный вольтметр и осциллограф (или пиковый вольтметр). Подключенный к входу двухполупериодного выпрямителя квадратичный вольтметр должен показать 55,5 В. Определенная по изображению на экране осциллографа амплитуда напряжения должна составить примерно 78,3 В. При отсутствии осциллографа можно измерить амплитудное значение напряжения пиковым вольтметром, воспользовавшись приведенной на рис. 3 схемой. Показание вольтметра в этом случае также должно составить 78,3 В.
Если переменное напряжение той же величины (55,5 В действующего значения) будет подано на однополупериодный выпрямитель, то подключенный к нагрузке вольтметр постоянного тока покажет вдвое меньшее, по сравнению с предыдущим случаем, значение — 25 В.
Пример 3. Используется тот же вольтметр, что и в примере 2. Измеряемое напряжение имеет форму, показанную на рис. 1, з. Угол α = 90° (определен с помощью осциллографа). Показание вольтметра равно 40 В, то есть (Ucpв = 40 В. Из табл. 2 определяем коэффициенты формы и амплитуды для измеряемого напряжения для указанного угла α: Ка = 2,0 и Кф = 1,57. Находим действующее значение измеряемого напряжения Uд = КфUcpв = 1,57•40 = 62,8 (В), а затем амплитудное значение Ua = Ка Uд = 2•62,8 = 125,6 (В).
Пример 4. Измеряемое напряжение имеет форму, аналогичную показанной на рис. 1.з, но вторая полуволна имеет отрицательную полярность (то есть речь идет о переменном напряжении). Фазовый угол α = 90° (определен с помощью осциллографа). Для измерения переменного напряжения используется квадратичный вольтметр, шкала которого проградуирована в действующих значениях напряжения. Вольтметр доказывает 62,8 В. Следовательно, действующее значение напряжения и составляет эти самые 62,8 В. Из табл. 2 определяем коэффициенты формы и амплитуды измеряемого напряжения для указанного угла α: Ка = 2,0, Кф = 1,57. Находим средневыпрямленное значение измеряемого напряжения Ucpв = Uд / Кф = 62,8:1,57 = 40 (В), а затем амплитудное значение Ua = Ка Uд = 2,0•62,8 = 125,6 (В).
Как видим, в двух последних примерах напряжение было измерено вольтметрами разного принципа действия, но результаты оказались одинаковыми. Это подтверждает правильность измерений и расчетов, а также свидетельствует о том, что средневыпрямленное и действующее значения переменного напряжения не зависят от знака этого напряжения.
Итоги
Исходя из рассмотренных выше примеров, можно сформулировать последовательность действий по измерению переменных напряжений:
1) Зная принцип действия прибора и способ градуировки шкалы прибора, вычисляется значение той величины, на которую непосредственно реагирует измерительный узел прибора (для квадратичного вольтметра — действующее значение напряжения, для вольтметра на базе прибора магнитоэлектрической системы — средневыпрямленное значение и т. п.).
2) Зная форму сигнала, по таблице определяются коэффициенты формы и напряжения.
3) Вычисляются искомые значения напряжения.
Все, что было сказано выше относительно измерения напряжений, в полной мере может быть применено и к измерению переменных токов. Однако далеко не все ампервольтомметры (тестеры) широкого применения имеют предел измерения переменного тока, а если таковой предел имеется, то максимальное значение тока не превышает обычно 10 А. Казалось бы, можно использовать режим измерения постоянного тока (имеется в каждом ампервольтомметре) и, добавив мостовой выпрямитель, измерять переменный ток. Однако при этом на диодах выпрямителя будет выделяться значительная мощность, а падение напряжения на измерительной цепи значительно возрастет (до 2…3 В), что может привести к снижению точности измерений за счет влияния измерительной цепи на работу устройства.
Действующее напряжение и амплитудное напряжение — что это, и в чем отличие

Все знают, что действующее напряжение в розетке 220 Вольт (230 по новым нормам, но для данной темы это не имеет особого значения). Это легко проверить при помощи мультиметра, который измерит разность потенциалов между фазой и рабочим нулевым проводником. То есть, при идеальных условиях, потенциал на нулевом проводе 0, а на фазном 220 Вольт. На самом деле все немного не так — переменный ток имеет синусоидальную форму с потенциалом на пиках 310 и -310 Вольт (амплитудное напряжение). Для того чтобы это увидеть, необходимо воспользоваться осциллографом.
Синусоида действующего и амплитудного напряжения
Понятно, что данный материал в большей степени ориентирован на простую аудиторию, у которой не то, что осциллографа нет, даже мультиметр наверняка не у каждого есть. Поэтому все примеры будут браться из среды программы Electronics Workbench, доступной каждому.
И первое, что нам нужно посмотреть — это синусоиду напряжения фазы из розетки. Для этого в программе отрисуем трехфазную сеть и подключим осциллограф к одной из фаз:
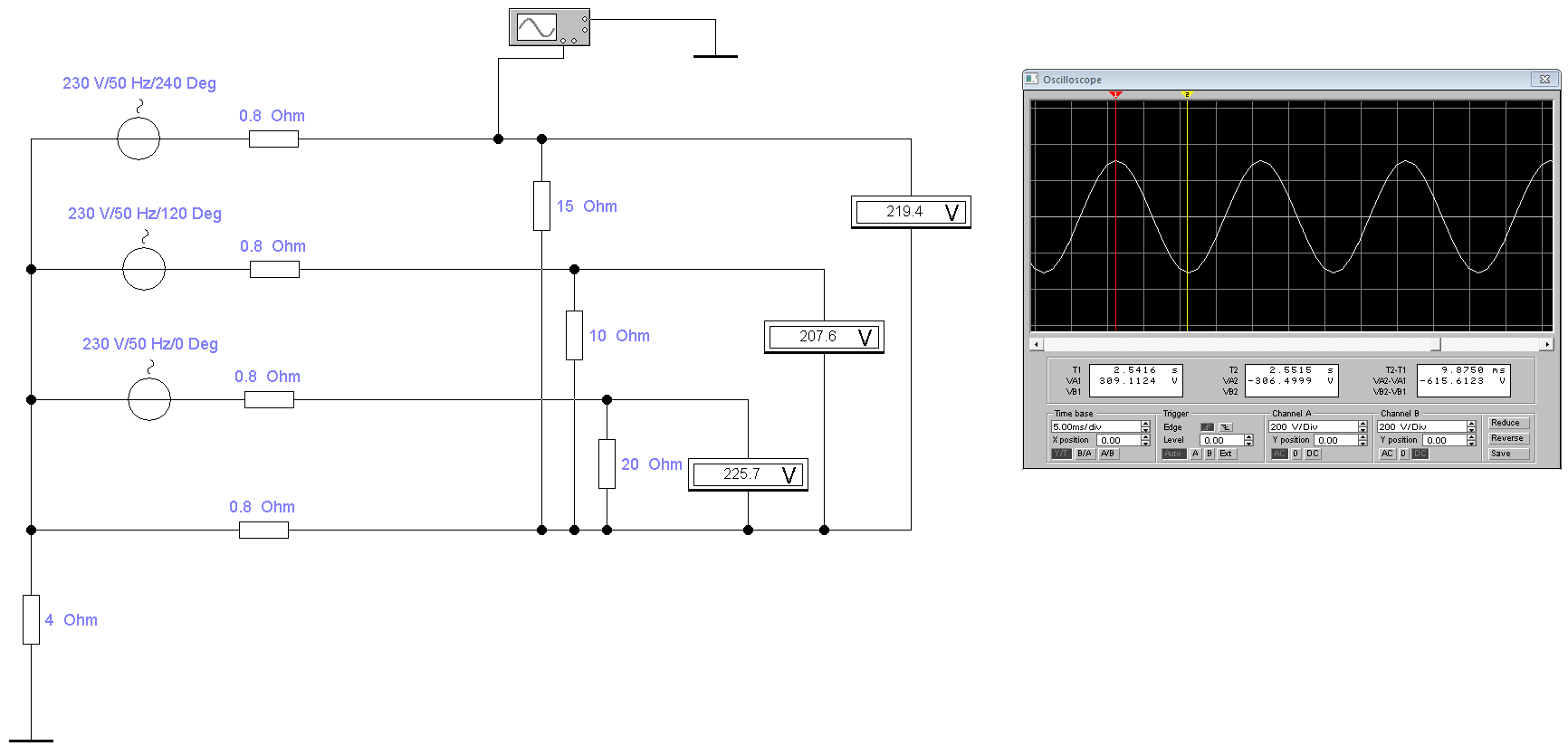
Как видно при показании вольтметра 219,4 Вольт между одной из фаз и PEN проводником, осциллограф показал синусоиду с амплитудой 309,1 Вольт. Это значение напряжения называется максимальным (амплитудным). А 219,4 Вольт, которые показывает вольтметр — это действующее напряжение. Его также называют среднеквадратичным или эффективным. И прежде чем перейти к рассмотрению данной особенности, кратко, простыми словами пройдемся по отрисованной схеме трехфазной сети и разберемся в природе синусоиды.
Начнем со схемы:
- Слева на право — три источника переменного напряжения с фазовыми углами 0, 120, 240 градусов и соединенными звездой.
- Резистор 4 Ом — это заземление нейтрали трансформатора.
- Резисторы по 0,8 Ом — условное сопротивление проводов, зависящее от сечения провода и длины линии.
- Резисторы 15, 10 и 20 Ом — нагрузка потребителей по трем фазам.
- К одной из фаз подключен осциллограф, показывающий амплитуду 309,1 Вольт.
Теперь рассмотрим синусоиду. Переменное напряжение в отличие от постоянного, график которого прямая на осциллографе, непрерывно изменяется как по величине, так и по направлению. Причем изменения эти происходят периодически, то есть точно повторяются через равные промежутки времени.
Переменное напряжение генерируется на электростанциях и посредством повышающих и понижающих распределительных трансформаторов попадает к конечному потребителю. При этом трансформация по пути никак не сказывается на синусоиде напряжения.
Видео — действующее напряжение и амплитудное
С полным и наглядным изложением рассматриваемого вопроса вы можете ознакомиться в следующем видео:
Работа генератора трехфазного переменного тока
Рассмотрим упрощенно работу генератора трехфазного переменного тока. Обмотки статора (фазы А, В и С) генератора расположены под углом 120 градусов относительно друг друга. Ротор с магнитом вращаясь индуцирует в обмотках статора периодически изменяющиеся ЭДС. Выглядит это следующим образом:
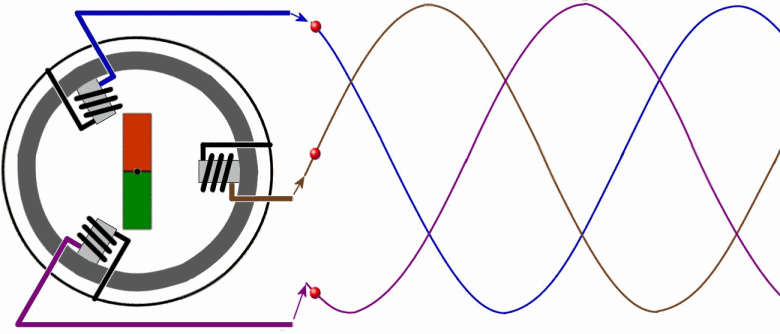
Такое вращение происходит с частотой 50 оборотов в секунду, то есть с частотой 50 Герц. Это значит, что электроны движутся в течение 1 секунды 50 раз в одном направлении (положительный полупериод синусоиды), и 50 — в обратном (отрицательный полупериод), 100 раз проходя чрез нулевое значение. Получается, что к примеру обычная лама накаливания, включенная в сеть с такой частотой, будет затухать и вспыхивать примерно 100 раз за секунду, однако мы этого не замечаем в силу особенностей своего зрения.
Определение действующего напряжения
Теперь непосредственно о том, почему произошел переход от максимального, амплитудного значения напряжения 310 Вольт к действующему 220 Вольт. Ответ можно найти в самом определении.
Действующее (эффективное или среднеквадратичное) значение напряжения — это такое напряжение постоянного тока, которое на такой же резистивной нагрузке выделит такую же мощность, как измеряемое переменное напряжение. Соответственно, действующее значение силы тока — такое значение силы постоянного тока, при прохождении которого через резистивную нагрузку выделится такая же мощность, что и при прохождении измеряемого тока.
Можно сформулировать и немного иначе. Действующее значение переменного тока равно величине такого постоянного тока, который за время, равное одному периоду переменного тока, произведет такую же работу (тепловой или электродинамический эффект), что и рассматриваемый переменный ток.
Общая формула расчета действующего напряжения произвольной формы следующая:
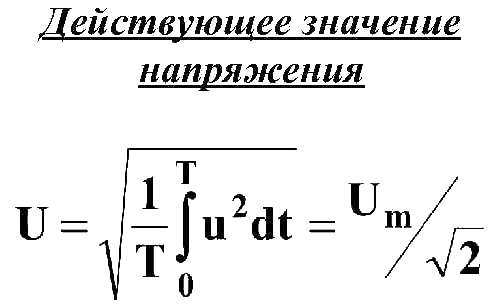
Объяснение действующего напряжения
Определение и формула — это хорошо. Но лучше все понять на наглядном примере. Объяснить все можно через мощность. Причем есть сложный для восприятия способ и более простой, который мы и рассмотрим далее.
Нам нужно взять один период синусоиды переменного напряжения, на этом промежутке построить синусоиду переменного тока и проанализировать мощность. Начнем с периода синусоиды переменного напряжения. Здесь же построим синусоиду переменного тока с учетом условной резистивной нагрузки (например, лампочки). По закону Ома сила тока равна напряжению, деленному на сопротивление.
Точные значения в конкретный момент при данном объяснении не принципиальны, поэтому все построения приблизительные. Естественно нужно понимать, что деля напряжение на сопротивление, мы получим синусоиду переменного тока с амплитудой в R раз меньшей, чем у напряжения. R – это значение сопротивления.
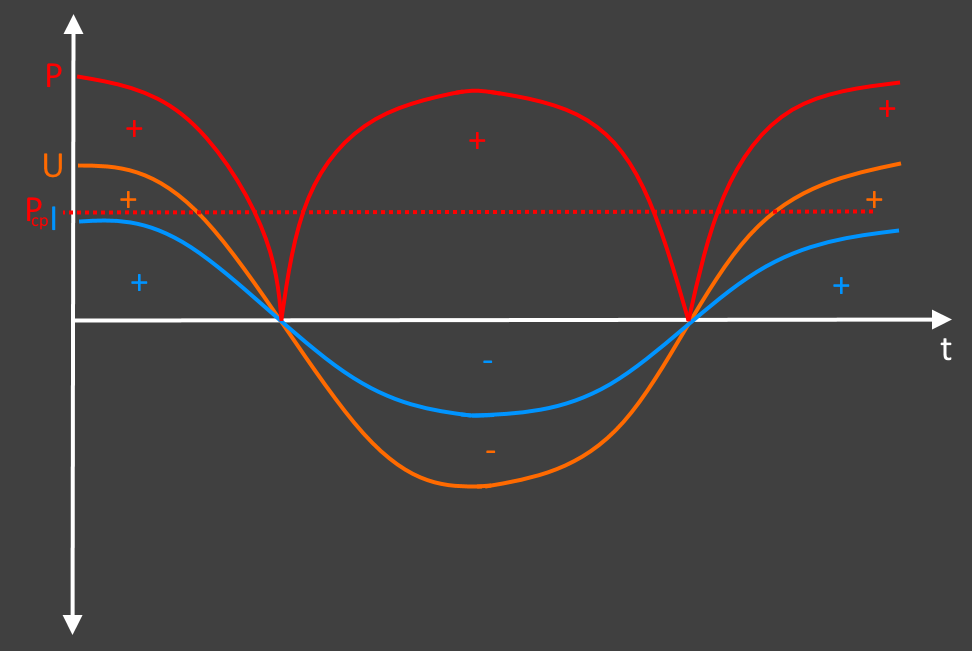
Теперь по двум синусоидам строим график мощности по формуле мощность равна силе тока умноженной на напряжение (P = I × U). Так как напряжение и ток имеют общие нулевые точки, то график мощности не будет заходить в отрицательную область. То есть сила тока со знаком «+» и напряжение со знаком «+» дадут мощность со знаком «+», так же как и сила тока со знаком «-» и напряжение со знаком «-» дадут мощность со знаком «+».
Анализируя полученный график можно отметить, что мощность пульсирующая. Она поднимается до максимального значения и падает до нуля, потом опять поднимается и снова падает. Как на эти колебания мощности реагируют электроприборы? Никак. Поскольку частота переменного тока 50 Герц, то эти колебания происходят очень быстро. Электроприборы откликаются не на максимальные и минимальные значения мощности, а на усредненные. То есть берется максимальное значение мощности и делится на два. Это значение называется действующим и находится по следующей формуле:
Pд = (Imax × Umax) / 2, где Pд — мощность действующая, Imax — сила тока максимальная, Umax — напряжение максимальное.
Двойку можно представить в виде корень из двух умножить на корень из двух. Получаем Действующее значение мощности = сила тока максимальная деленная на корень из двух умноженная на напряжение максимальное деленное на корень из двух (Pд = (Imax/√2) × (Umax/√2)).
Соответственно сила тока максимальная деленная на корень из двух — это действующее значение силы переменного тока, а напряжение максимальное деленное на корень из двух – это действующее значение переменного напряжения.
И действительно, если мы возьмем максимальное напряжение из предыдущего примера 309,1 Вольт и разделим на корень из двух, то получим действующее напряжение (то, которое показывает вольтметр) 219,4 Вольт.
Метод измерения действующего значения напряжения с применением МК
Время на прочтение
5 мин
Количество просмотров 100K
В данном посте речь пойдет об одном из вариантов измерения действующего значения напряжения и частоты сети на 8-ми битном микроконтроллере PIC18. При желании, можно метод перенести на любой другой МК, вплоть до всеми любимых ARDUINO (если они поддерживают реализацию прерываний по таймеру с частотой 5-10 кГц).
Также, рассматриваемый метод позволяет измерять частоту сетевого напряжения без использования внешних дополнительных средств, таких как компараторы. Но, при этом приходится жертвовать либо временными ресурсами МК, либо точностью измерения частоты.
Почему важно измерять действующее значение, а не какое либо другое, например, средневыпрямленное? Большинство “китайских” электронных вольтметров измеряют сетевое напряжение по средневыпрямленному значению. Методика измерения следующая: за период сетевого напряжения делается выборка из N значений амплитуды напряжения, результаты суммируются (без знака), делятся на N (усредняются), после чего полученный результат умножается на коэффициент

Указанный коэффициент определяет зависимость действующего значения синусоидального (!) сигнала от средневыпрямленного.
Такая методика измерения проста, не требует много ресурсов микроконтроллера (как временных, так и ресурсов памяти). Основным недостатком такой методики измерения является большая ошибка измерения на несинусоидальных сигналах.
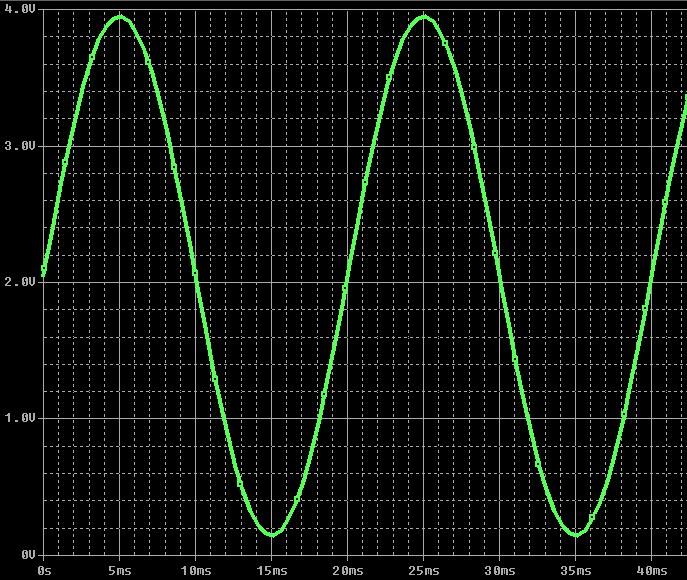
Как все знают, изменение сигнала сетевого напряжения подчиняется синусоидальному закону (вследствие применения синхронных генераторов на электростанции), с частотой изменения сигнала 50 Гц (60 Гц). Однако, на практике вследствие влияния сторонних факторов (в основном подключение к сети мощных нелинейных нагрузок), а также применения инверторов с квазисинусоидальным выходным напряжением (см. рисунок), синусоида напряжения либо значительно искажается, либо заменятся прямоугольными импульсами. В таких случаях указанный выше метод измерения даст очень большую погрешность (например, в квазисинусоидальных инверторах выходное напряжение, измеренное “китайским» вольтметром может быть равно 180-200В, в то время как действующее напряжение будет равно 220В ).
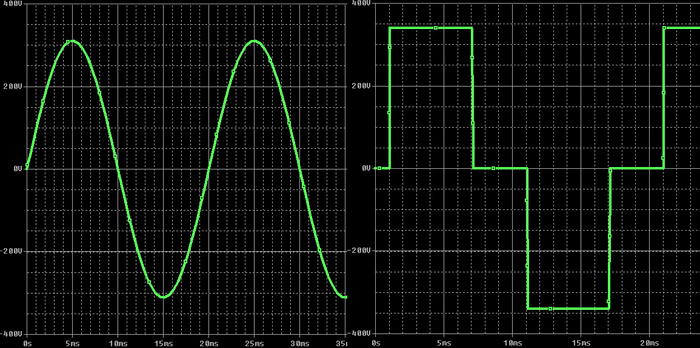
Например, напряжение у меня дома
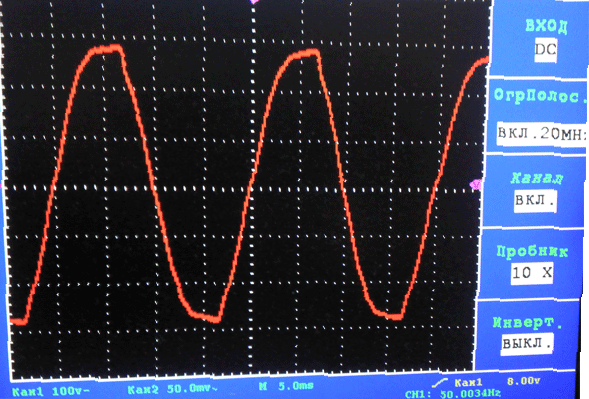
Почему важно измерять именно действующее значение напряжения (тока)? Потому что именно действующие (еще называют его эффективными) значения напряжения и тока определяют работу электрической системы (грубо говоря, электронагреватель выделяет тепло в прямой зависимости от действующих значений напряжения и тока сети).
Действующее значение измеряемой периодической величины рассчитывается по формуле
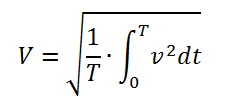
Или после дискретизации получим
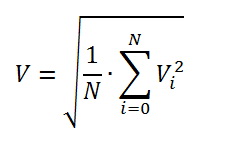
Т.е. нам нужно делать выборку ряда значений за период сетевого напряжения, просуммировать значения квадратов точек выборки, поделить на количество точек за период (при определении количества точек выборки не забываем про теорему Котельникова-Шеннона), и взять квадратный корень из полученного результата.
Вроде бы ничего сложного, если бы не но:
1) Каждый период точки выборки набираются заново, что увеличивает погрешность измерения;
2) В реальной сети, около нуля напряжения, могут встречаться как “нулевые полки”, так и повторные переходы через ноль напряжения, что значительно внесет погрешность в измерение.
С первым пунктом будем бороться измерением измерением суммы квадратов точек выборки за каждый полупериод, после чего суммируя n-ую сумму квадратов с (n+1)-й и откидывая (n-1)-ую.
Со вторым пунктом будем бороться введением зон нечувствительности по напряжению (введем границы напряжения перехода через ноль с положительной и отрицательной сторон) обычно 5-10 В в обе стороны, а также зон нечувствительности по частоте (ограничим допустимую частоту сигнала напряжения).
Таким образом, мы получим рассчитанное значение действующего значения сетевого напряжения за период на каждом полупериоде сетевого напряжения.
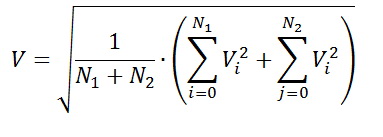
Частота напряжения вычисляется по формуле:

где Fд — частота дискретизации (для удобства и увеличения точности измерения частоты выбрана равной 10 кГц (период выборки — 100 мкс)).
Теперь рассмотрим структурную схему измерительной части (в реальной схеме следует добавить фильтрующие и защитные элементы).
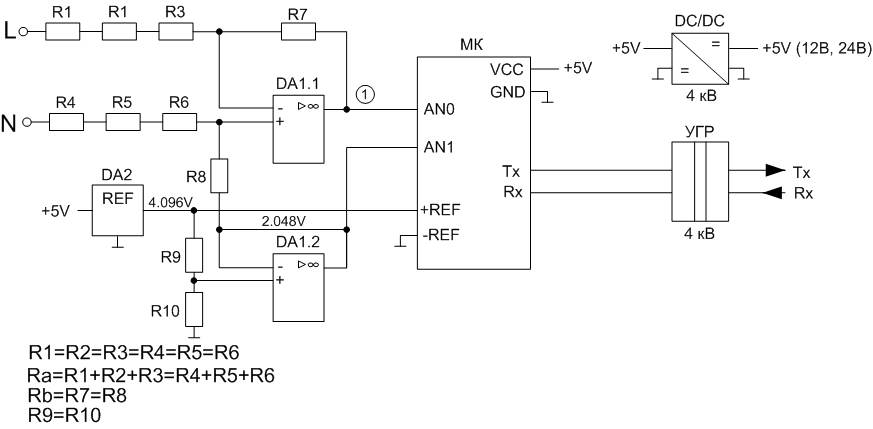
Внимание! В данном методе измерения не реализована гальваническая развязка микроконтроллера от сети. Гальваноразвязка реализуется на стороне цифрового интерфейса передачи данных от микроконтроллера.
На входе установлен дифференциальный операционный усилитель с делителем напряжения, опертым на половину опорного напряжения (2,048 В). Поскольку, для уменьшения размеров лучше применять маломощные резисторы, устанавливаем их минимум 3 шт. равными по сопротивлению — чтобы увеличить суммарное пробивное напряжения резисторов. При этом нужно подсчитать мощность потерь при максимальном входном напряжении (P=U^2/R) — чтобы не превышала допустимой мощности резисторов. Плечи дифференциального усилителя тоже делаем равными. Тогда, напряжение в точке 1 рассчитывается по формуле:
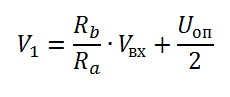
А напряжение в точке 1 будет иметь вид:
Также, половина опорного напряжения подается на один из каналов АЦП. Это позволяет в постоянном режиме (например, один раз за период) определять положение уровня нуля измеряемого напряжения.
Т.е. мы обошлись операционным усилителем с однополярным питанием, и наш входной сигнал в точке 1 изменяется от 0 до Uоп. Такой способ дает достаточно точные результаты, по сравнению, например, с выпрямлением напряжения с помощью диодов.
Расчет делителя и коэффициента АЦП сводится к следующему:

где A и В — замеры АЦП (за вычетом измеренного значения нуля сигнала — AN1) для текущего и предыдущего полупериодов; N1, N2 — число замеров для текущего и предыдущего полупериодов; Nadс — разрядность АЦП; U’оп — опорное напряжение за вычетом зон нелинейности (нечувствительности) операционного усилителя (обычно 0,6 В).
Расчет делителя удобно проводить считая сигнал постоянным, приведенным к амплитуде синусоидального, а не синусоидальным. Тогда действующее значение сигнала равно амплитудному и равно значению каждого замера.
Например, нужно рассчитать делитель для измерения максимального значения 420В переменного тока:

Сопротивление Ra выбирается в диапазоне от 500 кОм до 1500 кОм. По выбранному сопротивлению Ra рассчитывается Rb.
В итоге, алгоритм расчета действующего значения напряжения и частоты примет вид:
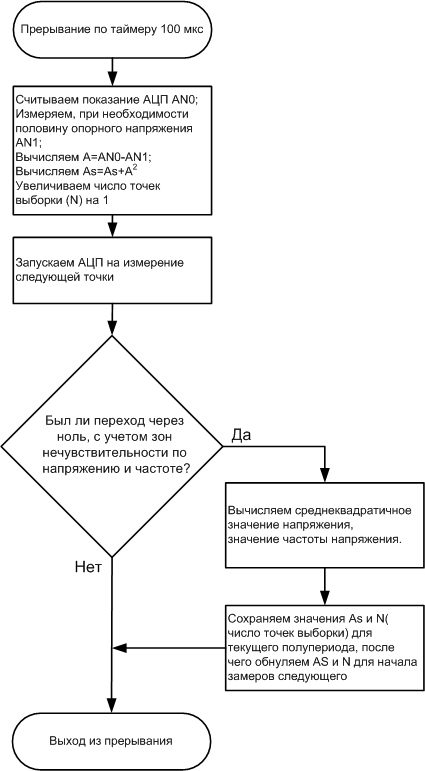
При этом часть затратных расчетов (деление, извлечение корня) можно перенести из прерывания в основную программу.
При расчете действующих значений на 8-ми битном МК целесообразно пользоваться целочисленными методами (с использованием масштабных коэффициентов) не прибегая к расчетам с плавающей запятой, а также упрощать по возможности арифметические операции (деление, изъятие квадратного корня и проч.). Это значительно экономит ресурсы МК.
