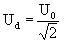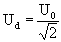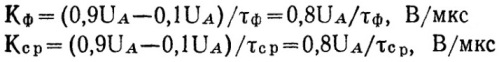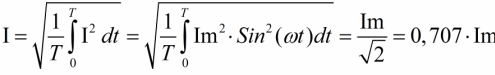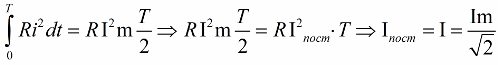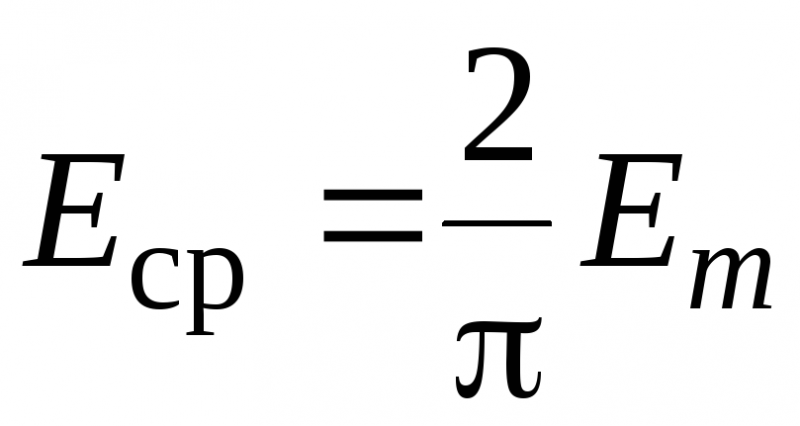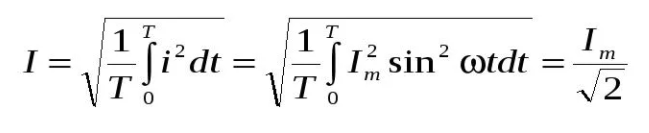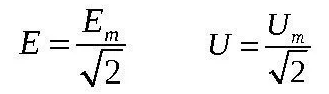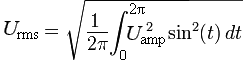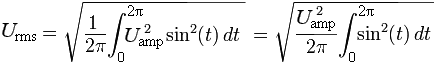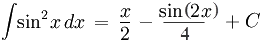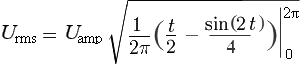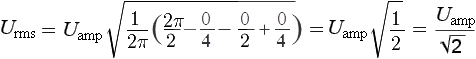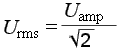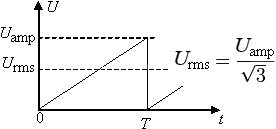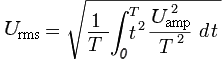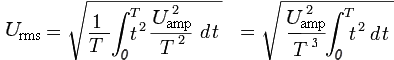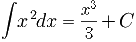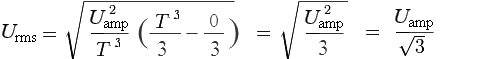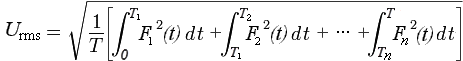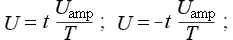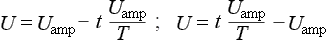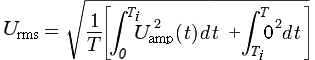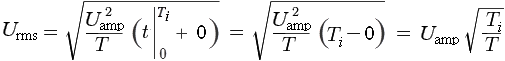Среднеквадратичное значение
В зарубежной терминологии применяется аббревиатура RMS (rms) – root mean square.
В математике для набора чисел x1, x2, …, xn количеством n среднеквадратичное значение (rms) определяется выражением:
Например, для чисел 2,3 и 6 среднеквадратичным значением будет квадратный корень из (2²+3²+6²)/3. √(49/3) = 4.04
Среднеквадратичным значением двух или нескольких чисел
является квадратный корень из среднеарифметического значения квадратов этих чисел.
Для любой непрерывной функции в интервале T1 – T2 среднеквадратичное значение можно рассчитать по формуле:
Среднеквадратичное значение применяется в расчётах, где существует пропорциональная зависимость не самих переменных значений, а их квадратов.
Действующее значение напряжения и тока
В качестве примера можно рассмотреть квадратичную зависимость мощности или работы электрического тока от значений тока или напряжения.
P = I²R; A = I²Rt; P = U²/R; A = U²t/R
Величина постоянного напряжения или тока является его среднеквадратичным значением.
Среднеквадратичное значение переменного тока равно величине постоянного тока,
действие которого произведёт такую же работу в активной (резистивной) нагрузке за время периода.
Определяющим фактором здесь является среднее (среднеарифметическое) значение мощности Pavg
или работы Aavg,
пропорциональное квадрату значения тока.
Так же среднеквадратичное значение переменного напряжения за период равносильно
по своему воздействию на активную нагрузку такому же значению постоянного напряжения.
P = UI = Pavg = UrmsIrms
Среднеквадратичное значение переменного напряжения или тока часто называют действующим или эффективным.
Величину переменного напряжения или тока, в большинстве случаев,
выражают его среднеквадратичным значением и измеряют приборами электромагнитного типа или специальными среднеквадратичными измерителями – True RMS.
Примечание:
Электромагнитные приборы используют для измерения переменного тока и напряжения в промышленных установках.
Усилие, создаваемое измерительной катушкой в электромагнитном приборе, пропорционально квадрату тока, поэтому не меняется по направлению.
Угол отклонения стрелки определится некоторым средним усилием F, которое будет пропорционально среднеквадратичному значению тока.
Расчёт действующего значения
В качестве примера рассчитаем среднеквадратичное значение синусоидального напряжения.

Запишем выражение Urms с применением интеграла функции
U = Uampsin(t) для одного периода 2π :
Показать расчёт
Скрыть расчёт

Вынесем Uamp из под знака радикала.
Воспользуемся табличным интегралом 
перепишем и решим последнее выражение с применением формулы Ньютона-Лейбница:

Так как sin(2π), sin(4π) и sin(0) равны нулю, вычисляем RMS синусоиды следующим образом:

В результате решения в итоге получим:
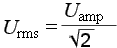
Расчёт RMS для напряжения или тока треугольной и пилообразной формы можно рассмотреть на примере одного периода T
для функции 
Выразим Urms искомой функции с помощью определённого интеграла:
Показать расчёт
Скрыть расчёт
Используя табличный интеграл
и формулу Ньютона-Лейбница, получаем:
В итоге преобразований получим:
Ток или напряжение любой сложной формы можно рассмотреть, как набор функций в пределах периода.
Тогда значением RMS будет квадратный корень из среднеарифметического значения интегралов для квадрата каждой функции, ограниченной её интервалом времени в периоде.
Например, для множества функций F1(t) , F2(t) , … , Fn(t)
в соответствующих им интервалах времени (0 – T1), (T1 – T2), …, (Tn – T),
составляющих период T, действующее напряжение (RMS) определится выражением:
Для вариантов однополярного или двуполярного напряжения пилообразной и треугольной формы в периоде 2T или 4T, представленных на рисунке ниже,
T и U amp имеют те же расчётные величины,
что и в рассмотренном случае c функцией 
а интегралы, определённые в интервалах, равных T, для квадратов используемых функций 
будут иметь одно и то же значение
Следовательно, вышеуказанные варианты однополярного или двуполярного напряжения пилообразной и треугольной формы будут иметь
среднеквадратичное значение 
В заключении рассмотрим пример вычисления действующего значения положительных прямоугольных импульсов длительностью Ti .
Выразим Urms одного периода T, как квадратный корень из среднеарифметического значения интегралов,
определённых в интервалах 0 – Ti и Ti – T для квадратов всех значений периода.
В результате получаем значение RMS, равное произведению амплитуды импульсов Uamp на квадратный корень из
коэффициента заполнения (Ti / T).
В качестве дополнительного материала предлагаем рассмотреть расчёт средеквадратичного значения напряжения накала кинескопа цветного телевизора, исходя из амплитуды и формы напряжения.
Замечания и предложения принимаются и приветствуются!
Что такое действующее значение напряжения
Содержание
- 1 Как измеряется
- 1.1 Практический пример
- 2 Импульсный электрический заряд
- 2.1 Расчёт кривой
- 2.2 Вычисления
- 3 Сила переменного тока
- 4 Вывод
- 5 Видео по теме
Всем нам известно о 220 вольт в бытовой розетке. Но если подключить к ней вольтметр, напряжение каждый раз будет разным. При этом зачастую напряжение может быть даже больше данной величины. Постараемся в данном материале разобраться — почему это происходит, что такое действующее значение переменного тока, и как его можно рассчитать с помощью различных вариантов.
Как измеряется
Электродинамические параметры в сети постоянно изменяются. Это связано с тем, что они представлены синусоидальным однополярным импульсом разной амплитуды. При измерении напряжения в цепи переменного тока, каждый раз будет получен разный результат. А при вычислении усреднённого параметра, он всегда будет составлять 0.
Получается, что математически вычислить данный параметр невозможно. Есть возможность получить только усреднённый параметр, который зависит от полупериода синусоидальной волны. Однако использовать его на практике или для каких-то вычислений нельзя.
Для решения этой проблемы и стали применять такое понятие, как действующее значение для расчёта силы тока и напряжения. Параметр определяется по характеристикам постоянного тока в цепи, генерирующей тепловую энергию такого же объёма, как и при подаче в цепь переменного тока.
Практический пример
Определение выше будет непонятным для человека, который не имеет особых познаний в области электротехники и электродинамики. Чтобы понять его смысл, предлагается рассмотреть следующий пример:
- Доступны две идентичные электроцепи (длина, элементы цепи и сечение проводников у них совпадают).
- В каждую включён одинаковый резистор — электронный компонент, который изменяет свое сопротивление в зависимости от подаваемого тока.
- Обе цепи подключаются к источникам электроэнергии, имеющим одинаковое напряжение.
Но между цепями есть одна разница. На первую электроцепь подаётся постоянный, а на вторую — переменный ток. По одной из них пойдёт стабильный электроток, а по другой потечет импульсный электрозаряд, который постоянно изменяется и имеет синусоидальной график.
Чтобы найти количества тепла в цепи с сопротивлением, используется такая формула:
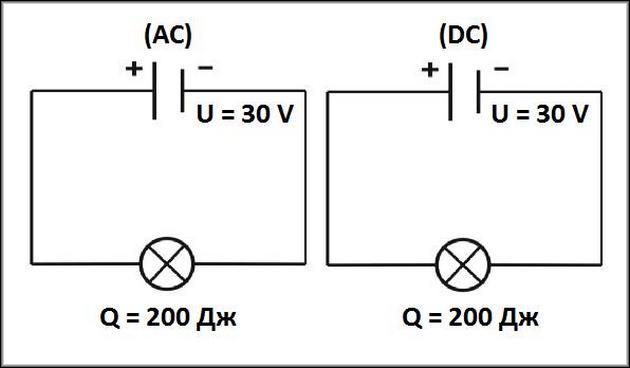
После произведения ряда замеров и вычислений можно увидеть, что выделяемое тепло в этих двух электроцепях имеет одинаковую величину. Например, в цепи с постоянным током при подаче напряжения 30 вольт выделяется тепло 200 Джоуль (или Дж). Если вторая цепь имеет идентичные характеристики, то выделение тепла в ней также составит 200 Дж. Получается, что напряжение 30В в этих электроцепях — это и есть эффективное напряжение.
Импульсный электрический заряд
Вышеприведенный пример позволяет только определить действующее и среднее значение напряжения переменного тока. Но на практике такой метод также не применяется, из–за того, что получить доступ к источнику переменного напряжения не всегда представляется возможным. Поэтому параметры цепи рассчитываются с помощью формул, которые основаны на синусоидальных кривых.
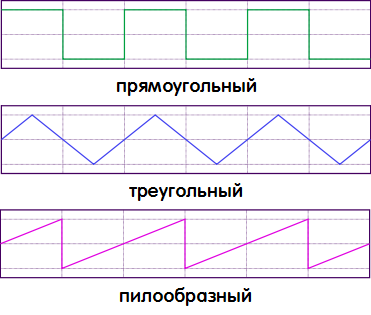
Стоит отметить, что действующее напряжение не всегда формируется путём плавного изменения определённого импульсного электрозаряда. Кривая зачастую имеет форму, отличную от привычной нам синусоиды:
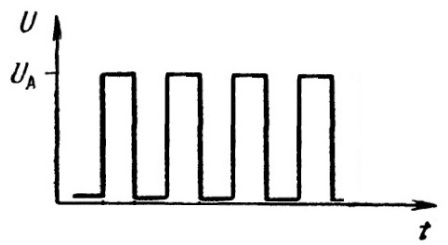
- Прямоугольную (меандр);
- треугольную;
- трапециевидную
- и другие.
То есть график электротока может иметь отличную, но при этом стабильную форму. Наглядным примером такого варианта является кривая осциллографа, регистрирующая ритмы сердцебиения человека.
Но независимо от действующего в сети импульсного заряда, во время расчётов используется именно синусоида. Это объясняется тем, что погрешности в расчетах будут крайне малыми. Поэтому ими можно пренебречь, ведь они не скажутся на конечном результате:
- Частота импульса в жилых домах составляет 50 Гц. За 1 сек электрический импульс проходит через фазу 100 раз. Это означает, что работающая от сети лампочка за секунду 100 раз загорается и тухнет, а электрический заряд при этом изменяется довольно плавно. Но человек этого не замечает из-за невосприимчивости человеческого зрения к сверхбыстрым колебаниям.
- Одинаковая площадь фигур. Независимо от формы кривой периода, описывающей переменный электроток идентичных параметров, площадь их фигур всегда будет одинаковой. Следовательно, при любых расчетах получится одно и то же эффективное значение переменного синусоидального тока. Поэтому эффективные значения не зависят от формы кривой. На них оказывает влияние именно величина амплитуды.
Форма кривой импульса важна только для сверхточных расчётов в лабораторных условиях. Также она учитывается для работы суперкомпьютеров. В остальных случаях синусоида позволит вычислить действующее значение переменного синусоидального тока.
Расчёт кривой
Синусоида — это периодическая функция, которую можно всегда описать с помощью уравнения. Если взять её за основу, то на входе имеются следующие исходные данные:
- Т — амплитуда;
- φ — начальная фаза;
- ωt — угловая скорость.
По этим входным характеристикам находим другие переменные параметры:
- Uт — амплитудное напряжение;
- Uм — действующие в момент измерения значения напряжения;
- ωt + φ — фактическая фаза в точке измерения.
Т.к. начальная фаза равняется нулю, на выходе формула кривой будет иметь следующий вид:
Uм = Uт·sin(ωt + φ) = Uт·sin(ωt)
Теперь необходимо обратиться к закону выделения тепла, который еще называется законом Джоуля-Ленца. Согласно него квадрат напряжения — это произведение выделяемого тепла на сопротивление проводника.
| Формулы для расчета тепловой энергии в электроцепях: | |
| с постоянным током | с переменным током |
| Q = U2/R | Q = Uм2/R |
- Uм — величина постоянного напряжения;
- Uм — величина действующего напряжения;
- R — сопротивление проводника.
Мы видим, что при расчетах количества тепла в цепи переменного тока, пользуется именно действующим значением переменного тока.
Из данных формул вытекают два важных нюанса, на которые стоит обратить внимание:
- В расчетах используется среднеквадратичное значение напряжения (СКЗ). Это связано с тем, что величина напряжения постоянно изменяется и можно получить только какую-то усредненную величину.
- Амплитуда постоянного тока довольно условная величина. Ее используют в расчетах, чтобы только описать период синусоиды переменного электрозаряда.
Вычисления
Волны синусоид будут одинаковыми. Однако в пределах периода в каждой точке измерения напряжения будут отличаться. Поэтому, чтобы уравнять между собой среднеквадратичное напряжение постоянного и переменного электротока по тепловыделению, требуется рассчитать объём выделенного тепла в течение времени, равного 1 периоду:
В уравнение теперь можно подставить выражение расчёта мгновенного напряжения
Uм = Uт·sin(ωt + ф) = Uт·sin(ωt)
После математического преобразования можно рассчитать действующее значение электрического напряжения:
U = Uт / √2 = 0,707·Uм
Теперь найдем амплитудное напряжение по формуле:
Uт = U·√2
Амплитудное напряжение так же имеет и другое название – максимально возможное эффективное мгновенное значение напряжения.
Сила переменного тока
С помощью амперметра находим амплитудную силу тока в цепи. Используя её вместе с периодом, который равен 1/50 секунд, можно применить описанную выше формулу, чтобы рассчитать среднеквадратичное значение напряжения. В результате этого будет получена действующие значения силы тока.
Действующее значение тока можно рассчитать, когда других исходных параметров нет, но нам известно эффективное значение величины напряжения в цепи. Следовательно, можно воспользоваться всем нам известным законом Ома вычисления значения силы тока:
U = I·R и I = U/R
где:
- U — будет действующим напряжением переменного синусоидального тока;
- R — сопротивление проводника, которое всегда можно узнать в любом справочнике, зная состав материала проводника.
Ранее электропроводку делали из алюминия и меди, которые отличались довольно высоким сопротивлением. Эффективное значение реальной силы тока этих металлов было меньше 6.5А. По этой причине в старых домах зачастую срабатывает автоматический выключатель, если одновременно подключить в сеть несколько приборов. Сегодня открыты сложные сплавы с низким сопротивлением. Они позволяют достичь с действующее значение силы переменного тока около 16А даже в обычных современных многоквартирных домах.
С уменьшением сопротивления проводника, прямопропорционально возрастает мощность и тепловыделение. При том надо помнить о том, что у каждого сплава есть свой определенный температурный предел. Поэтому в жилых сетях сила тока часто не превышает 20 ампер, а при резком ее скачке, например, при неполадках на подстанции, электронная часть устройств просто сгорает. Для предотвращения таких случаев и подключаются автоматы, которые при регистрации высоких действующих значений размыкают цепь на данном участке. Более мощные источники электроэнергии встречаются только в промышленных трехфазных сетях с напряжением 380В.
Вывод
Мы рассмотрели в данной статье — что называют действующим значением силы тока и напряжения, а так же как определяют эти значения переменного тока в электроцепи. Это эффективные значения переменного тока, под действием которого выделяется точно такое же количества тепла, как и в цепи постоянного тока, имеющей аналогичные характеристики.
Видео по теме
Действующее значение напряжения для прямоугольных импульсов
Расчет действующего значения выходного напряжения
преобразователя в зависимости от формы сигнала
При использовании ветрогенераторов в качестве источника энергии необходимо иметь промежуточный накопитель энергии. Как правило, для этого используется аккумуляторная батарея с довольно низким выходным постоянным напряжением – 12 или 24 В . В то же время большинство потребительских нагрузок рассчитаны на подключение к сетям переменного тока напряжением 110 – 380 В частотой 45 – 65 Гц . Поэтому требуется преобразователь постоянного напряжения аккумуляторной батареи ( наиболее распространены автомобильные аккумуляторы напряжением 12 В) в переменное напряжение ( чаще всего 220 В 50 Гц) [1, 2].
Нагрузки, подключаемые в сеть переменного тока, могут не иметь блока питания и иметь индуктивный характер (вибрационный насос, электромагнит, электродвигатель ) или резистивный характер (лампа накаливания, нагревательный прибор ).
При наличии блока питания он может быть трансформаторным или бестрансформаторного типа.
Синусоидальная форма выходного сигнала преобразователя при малом коэффициенте гармоник соответствует паспортным требованиям нагрузок, подключаемых в сеть переменного тока , в частности, по соотношению амплитудного и действующего значений напряжения . Однако преобразователь с синусоидальной формой выходного сигнала сложен в конструировании и изготовлении. Желательно упростить преобразователь за счет использования других форм выходного сигнала, поняв условия, при которых такой преобразователь может использоваться для возможно большего количества типов нагрузок.
Форма выходного сигнала наиболее просто реализуемых преобразователей может быть прямоугольной, прямоугольной с паузой, трапецеидальной .
При этом возникает проблема выбора параметров сигнала, в частности, амплитудного значения напряжения. Для нагрузок с бестрансформаторным блоком питания , построенном по схеме выпрямитель-фильтр-преобразователь, максимальное амплитудное значение любого сигнала независимо от его формы может составлять 310 В, причем, как правило, это значение может быть существенно уменьшено .
Для нагрузок резистивного типа (ламп накаливания), рассчитанных на синусоидальное напряжение с действующим значением 220 В, амплитудное напряжение 310 В для сигнала прямоугольной формы без паузы является чрезмерным ( действующее значение сигнала прямоугольной формы равно его амплитудному значению, в данном случае 310 В), и его необходимо уменьшить .
Рассмотрим случай трансформаторного блока питания . Полоса пропускания трансформаторов по частоте весьма широкая (до тысяч герц), поэтому напряжение на выходе трансформатора будет иметь прямоугольную форму. Так как стоящие дальше по схеме стабилизаторы рассчитаны на использование переменного напряжения с амплитудным значением (приведенным ко входу) 310 В, то применение прямоугольного напряжения с амплитудным значением 310 В будет перегружать трансформатор, а при меньших значениях амплитуды ухудшатся условия работы стабилизаторов.
Величину действующего напряжения для периодического сигнала Ud = U(t) с периодом T и круговой частотой w = 2 p /T можно рассчитать по формуле:
Для синусоидального сигнала с периодом T, круговой частотой w = 2 p /T и амплитудным значением U0:
Для прямоугольного сигнала с периодом T, круговой частотой w = 2 p /T и амплитудным значением U0:
Для прямоугольного сигнала с паузой ( период T , круговая частота w = 2 p /T, длительность импульса положительной и отрицательной полярности t , длительность паузы T/2 – t ) с амплитудным значением U0:

Для трапецеидального сигнала с периодом T, круговой частотой w = 2 p /T и амплитудным значением U0:
Здесь t – длительность вершины импульса.
При t = T/8 ( четвертой части полупериода) действующее значение напряжения Ud будет таким же, как для случая синусоидального сигнала с такой же амплитудой U0:
Принимая в качестве критерия соотношение для амплитудного и действующего значения выходного напряжения преобразователя как для случая синусоидального сигнала (2)
можно сделать вывод, что приемлемой формой выходного сигнала преобразователя является прямоугольная с паузой, когда длительность как отрицательного, так и положительного импульса равна длительности паузы (половина полупериода), или трапецеидальная, когда длительность плоской вершины импульса составляет четвертую часть полупериода . Выходной сигнал трапецеидальной формы предпочтительнее, так как коэффициент гармоник для него меньше.
Таким образом, возможно конструирование преобразователя с выходным сигналом трапецеидальной формы частотой 50 Гц, у которого длительность плоской вершины импульса составляет четвертую часть полупериода. Амплитуда выходного напряжения должна быть около 310 В. Действующее значение напряжения при этом будет равно 220 В. Такой преобразователь подходит по своим параметрам для большинства применяемых типов нагрузок.
- Амплитуда — максимальное абсолютное значение.
- Электрическое напряжение — разность электрических потенциалов в соответствующих точках.
11.12.2003
12.01.2006
17.04.2006
17.06.2010
Источник
Электрические и временные параметры прямоугольных импульсов
Периодические и непериодические сигналы, форма которых отличается от синусоидальной, обычно называют импульсными сигналами . Процессы генерации, преобразования, а также вопросы практического применения импульсных сигналов относятся сегодня ко многим областям электроники.
Так, например, ни один современный блок питания не обходится без расположенного на его печатной плате генератора прямоугольных импульсов, такого например как на микросхеме TL494, выдающей импульсные последовательности с параметрами, подходящими для текущей нагрузки.
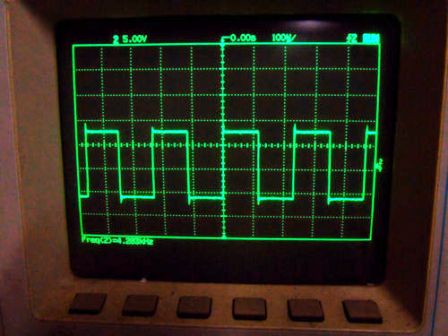
Поскольку импульсные сигналы могут иметь различную форму, то и называют различные импульсы в соответствии с похожей по форме геометрической фигурой: прямоугольные импульсы, трапецеидальные импульсы, треугольные импульсы, пилообразные импульсы, ступенчатые, и импульсы разных других форм. Между тем, наиболее часто практически применяются именно прямоугольные импульсы . О их параметрах и пойдет речь в данной статье.
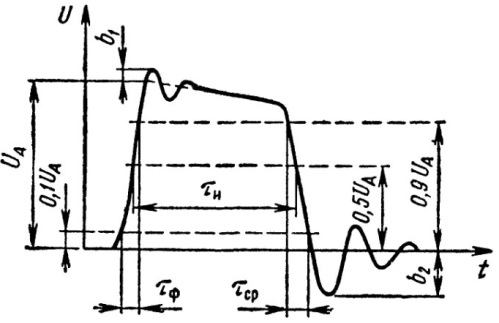
Конечно, термин «прямоугольный импульс» несколько условен. В силу того что ничего идеального в природе не бывает, как не бывает и идеально прямоугольных импульсов. На самом деле реальный импульс, который принято называть прямоугольным, может иметь и колебательные выбросы (на рисунке показаны как b1 и b2), обусловленные вполне реальными емкостными и индуктивными факторами.
Выбросы эти могут, конечно, отсутствовать, однако существуют электрические и временные параметры импульсов, отражающие в числе прочего «неидеальность их прямоугольности».
Прямоугольный импульс имеет определенную полярность и рабочий уровень. Чаще всего полярность импульса положительна, поскольку подавляющее большинство цифровых микросхем питаются положительным, относительно общего провода, напряжением, и следовательно мгновенное значение напряжения в импульсе всегда больше нуля.
Но есть, например, компараторы, питаемые двухполярным напряжением, в таких схемах можно встретить разнополярные импульсы. Вообще микросхемы, питаемые напряжением отрицательной полярности, не так широко применяются, как микросхемы с обычным положительным питанием.
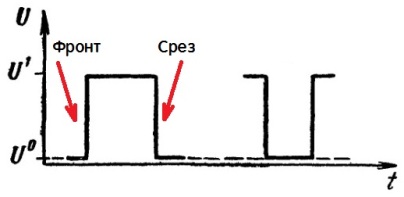
В последовательности импульсов рабочее напряжение импульса может принимать низкий или высокий уровень, причем один уровень с течением времени сменяет другой. Уровень низкого напряжения обозначают U0, уровень высокого U1. Наибольшее мгновенное значение напряжения в импульсе Ua или Um, относительно начального уровня, называется амплитудой импульса .
Разработчики импульсных устройств зачастую оперируют активными импульсами высокого уровня, такими как показанный на рисунке слева. Но иногда практически целесообразно применить в качестве активных импульсы низкого уровня, для которых исходное состояние — высокий уровень напряжения. Импульс низкого уровня показан на рисунке справа. Называть импульс низкого уровня «отрицательным импульсом» — безграмотно.
Перепад напряжения в прямоугольном импульсе называют фронтом, который представляет собой быстрое (соизмеримое по времени со временем протекания переходного процесса в цепи) изменение электрического состояния.
Перепад с низкого уровня к высокому уровню, то есть положительный перепад, называют передним фронтом или просто фронтом импульса. Перепад от высокого уровня к низкому, или отрицательный перепад, называют срезом, спадом или просто задним фронтом импульса.
Передний фронт обозначают в тексте 0.1 или схематически _|, а задний фронт 1.0 или схематически |_.
В зависимости от инерционных характеристик активных элементов, переходный процесс (перепад) в реальном устройстве всегда занимает некоторое конечное время. Поэтому полная длительность импульса включает в себя не только времена существования высокого и низкого уровней, но также времена длительности фронтов (фронта и среза), которые обозначаются Тф и Тср. Практически в любой конкретной схеме время фронта и спада можно увидеть при помощи осциллографа.
Так как в реальности моменты начала и окончания переходных процессов в перепадах очень точно выделить непросто, то принято считать за длительность перепада промежуток времени, во время которого напряжение изменяется от 0,1Ua до 0,9Ua (фронт) или от 0,9Ua до 0,1Ua (срез). Так и крутизна фронта Кф и крутизна среза Кс.р. задаются в соответствии с данными граничными состояниями, и измеряются в вольтах в микросекунду (в/мкс). Непосредственно длительностью импульса называют промежуток времени, отсчитываемый от уровня 0,5Ua.
Когда рассматривают в общем процессы формирования и генерации импульсов, то фронт и срез принимают по длительности за ноль, поскольку для грубых расчетов эти малые временные промежутки оказываются не критичны.
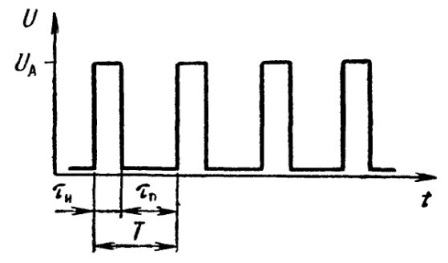
Импульсная последовательность — это импульсы, следующие друг за другом в определенном порядке. Если паузы между импульсами и длительности импульсов в последовательности равны между собой, то это периодическая последовательность. Период следования импульсов Т — это сумма длительности импульса и паузы между импульсами в последовательности. Частота f следования импульсов — это величина обратная периоду.
Периодические последовательности прямоугольных импульсов, кроме периода Т и частоты f, характеризуются еще парой дополнительных параметров: коэффициентом заполнения DC и скважностью Q. Коэффициент заполнения — это отношение времени длительности импульса к его периоду.
Скважность — это отношение периода импульса ко времени его длительности. Периодическая последовательность скважности Q=2, то есть такая, у которой время длительности импульса равно времени паузы между импульсами или у которой коэффициент заполнения равен DC=0,5, называется меандром.
Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!
Подписывайтесь на наш канал в Telegram!
Просто пройдите по ссылке и подключитесь к каналу.
Не пропустите обновления, подпишитесь на наши соцсети:
Источник
Среднеквадратичное значение
В зарубежной терминологии применяется аббревиатура RMS (rms) — root mean square.
В математике для набора чисел x1, x2, . xn количеством n среднеквадратичное значение (rms) определяется выражением:
Например, для чисел 2,3 и 6 среднеквадратичным значением будет квадратный корень из (2²+3²+6²)/3. √(49/3) = 4.04
Среднеквадратичным значением двух или нескольких чисел является квадратный корень из среднеарифметического значения квадратов этих чисел.
Для любой непрерывной функции в интервале T1 — T2 среднеквадратичное значение можно рассчитать по формуле:
Среднеквадратичное значение применяется в расчётах, где существует пропорциональная зависимость не самих переменных значений, а их квадратов.
Действующее значение напряжения и тока
В качестве примера можно рассмотреть квадратичную зависимость мощности или работы электрического тока от значений тока или напряжения.
P = I²R; A = I²Rt; P = U²/R; A = U²t/R
Величина постоянного напряжения или тока является его среднеквадратичным значением.
Среднеквадратичное значение переменного тока равно величине постоянного тока, действие которого произведёт такую же работу в активной (резистивной) нагрузке за время периода.
Определяющим фактором здесь является среднее (среднеарифметическое) значение мощности P avg или работы A avg, пропорциональное квадрату значения тока.
Так же среднеквадратичное значение переменного напряжения за период равносильно по своему воздействию на активную нагрузку такому же значению постоянного напряжения.
Среднеквадратичное значение переменного напряжения или тока часто называют действующим или эффективным.
Величину переменного напряжения или тока, в большинстве случаев, выражают его среднеквадратичным значением и измеряют приборами электромагнитного типа или специальными среднеквадратичными измерителями — True RMS.
Примечание:
Электромагнитные приборы используют для измерения переменного тока и напряжения в промышленных установках. Усилие, создаваемое измерительной катушкой в электромагнитном приборе, пропорционально квадрату тока, поэтому не меняется по направлению.
Угол отклонения стрелки определится некоторым средним усилием F, которое будет пропорционально среднеквадратичному значению тока.
Расчёт действующего значения
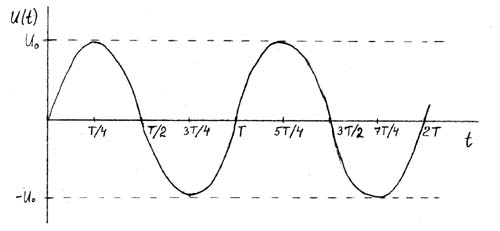
В качестве примера рассчитаем среднеквадратичное значение синусоидального напряжения.
Запишем выражение U rms с применением интеграла функции U = U ampsin(t) для одного периода 2π :
Вынесем U amp из под знака радикала. Воспользуемся табличным интегралом 
Так как sin(2π), sin(4π) и sin(0) равны нулю, вычисляем RMS синусоиды следующим образом:
В результате решения в итоге получим:
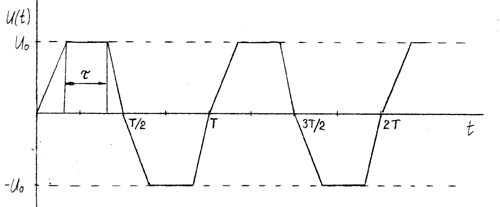
Расчёт RMS для напряжения или тока треугольной и пилообразной формы можно рассмотреть на примере одного периода T для функции 
Выразим U rms искомой функции с помощью определённого интеграла:
Используя табличный интеграл 
В итоге преобразований получим:
Ток или напряжение любой сложной формы можно рассмотреть, как набор функций в пределах периода. Тогда значением RMS будет квадратный корень из среднеарифметического значения интегралов для квадрата каждой функции, ограниченной её интервалом времени в периоде.
Например, для множества функций F1(t) , F2(t) , . , F n(t) в соответствующих им интервалах времени (0 — T1), (T1 — T2), . (T n — T), составляющих период T, действующее напряжение (RMS) определится выражением:
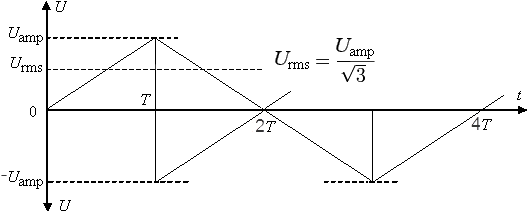
Для вариантов однополярного или двуполярного напряжения пилообразной и треугольной формы в периоде 2T или 4T, представленных на рисунке ниже, T и U amp имеют те же расчётные величины, что и в рассмотренном случае c функцией 

Следовательно, вышеуказанные варианты однополярного или двуполярного напряжения пилообразной и треугольной формы будут иметь среднеквадратичное значение 
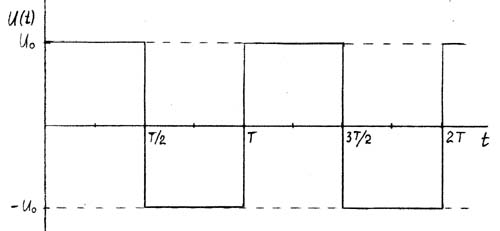
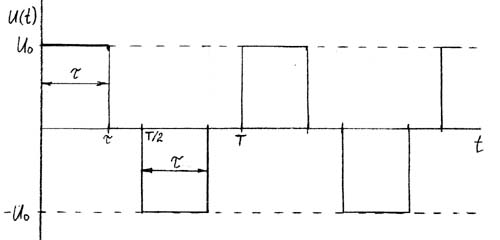
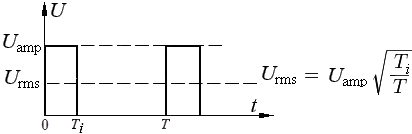
В заключении рассмотрим пример вычисления действующего значения положительных прямоугольных импульсов длительностью T i .
Выразим U rms одного периода T, как квадратный корень из среднеарифметического значения интегралов, определённых в интервалах 0 — T i и T i — T для квадратов всех значений периода.
В результате получаем значение RMS, равное произведению амплитуды импульсов U amp на квадратный корень из коэффициента заполнения (T i / T).
В качестве дополнительного материала предлагаем рассмотреть расчёт средеквадратичного значения напряжения накала кинескопа цветного телевизора, исходя из амплитуды и формы напряжения.
Замечания и предложения принимаются и приветствуются!
Источник
Определение действующего напряжения
Теперь непосредственно о том, почему произошел переход от максимального, амплитудного значения напряжения 310 Вольт к действующему 220 Вольт. Ответ можно найти в самом определении.
Действующее (эффективное или среднеквадратичное) значение напряжения — это такое напряжение постоянного тока, которое на такой же резистивной нагрузке выделит такую же мощность, как измеряемое переменное напряжение. Соответственно, действующее значение силы тока — такое значение силы постоянного тока, при прохождении которого через резистивную нагрузку выделится такая же мощность, что и при прохождении измеряемого тока.
Можно сформулировать и немного иначе. Действующее значение переменного тока равно величине такого постоянного тока, который за время, равное одному периоду переменного тока, произведет такую же работу (тепловой или электродинамический эффект), что и рассматриваемый переменный ток.
Общая формула расчета действующего напряжения произвольной формы следующая:
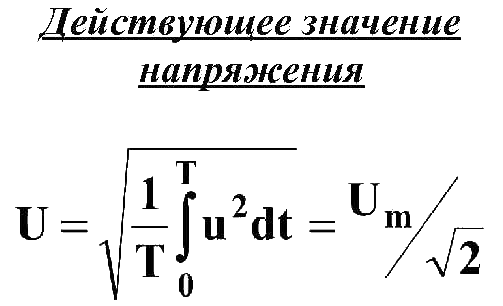
Объяснение действующего напряжения
Определение и формула — это хорошо. Но лучше все понять на наглядном примере. Объяснить все можно через мощность. Причем есть сложный для восприятия способ и более простой, который мы и рассмотрим далее.
Нам нужно взять один период синусоиды переменного напряжения, на этом промежутке построить синусоиду переменного тока и проанализировать мощность. Начнем с периода синусоиды переменного напряжения. Здесь же построим синусоиду переменного тока с учетом условной резистивной нагрузки (например, лампочки). По закону Ома сила тока равна напряжению, деленному на сопротивление.
Точные значения в конкретный момент при данном объяснении не принципиальны, поэтому все построения приблизительные. Естественно нужно понимать, что деля напряжение на сопротивление, мы получим синусоиду переменного тока с амплитудой в R раз меньшей, чем у напряжения. R – это значение сопротивления.
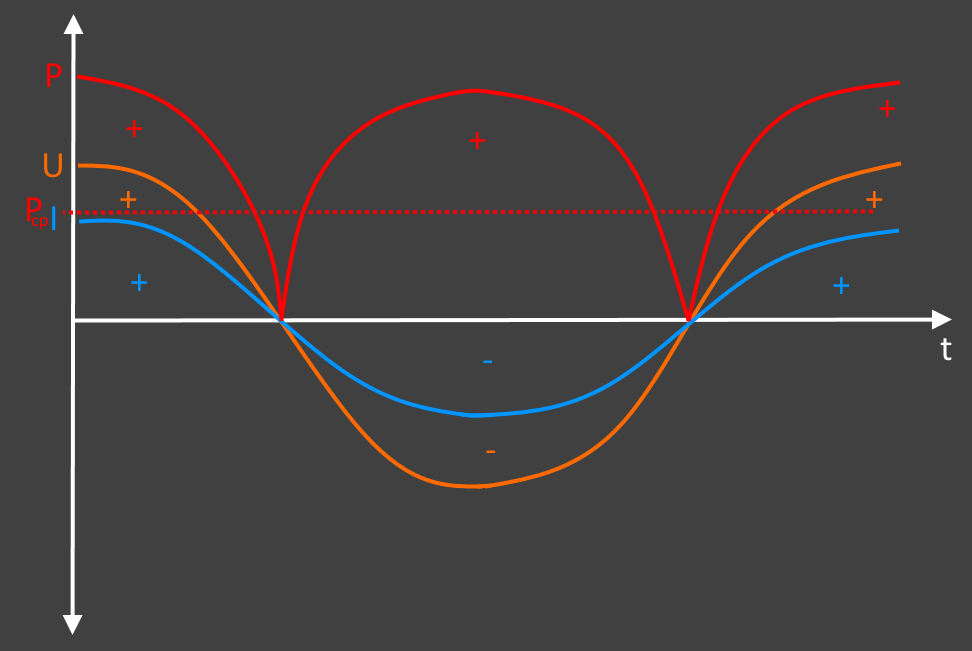
Теперь по двум синусоидам строим график мощности по формуле мощность равна силе тока умноженной на напряжение (P = I × U). Так как напряжение и ток имеют общие нулевые точки, то график мощности не будет заходить в отрицательную область. То есть сила тока со знаком «+» и напряжение со знаком «+» дадут мощность со знаком «+», так же как и сила тока со знаком «-» и напряжение со знаком «-» дадут мощность со знаком «+».
Анализируя полученный график можно отметить, что мощность пульсирующая. Она поднимается до максимального значения и падает до нуля, потом опять поднимается и снова падает. Как на эти колебания мощности реагируют электроприборы? Никак. Поскольку частота переменного тока 50 Герц, то эти колебания происходят очень быстро. Электроприборы откликаются не на максимальные и минимальные значения мощности, а на усредненные. То есть берется максимальное значение мощности и делится на два. Это значение называется действующим и находится по следующей формуле:
Pд = (Imax × Umax) / 2, где Pд — мощность действующая, Imax — сила тока максимальная, Umax — напряжение максимальное.
Двойку можно представить в виде корень из двух умножить на корень из двух. Получаем Действующее значение мощности = сила тока максимальная деленная на корень из двух умноженная на напряжение максимальное деленное на корень из двух (Pд = (Imax/√2) × (Umax/√2)).
Соответственно сила тока максимальная деленная на корень из двух — это действующее значение силы переменного тока, а напряжение максимальное деленное на корень из двух – это действующее значение переменного напряжения.
И действительно, если мы возьмем максимальное напряжение из предыдущего примера 309,1 Вольт и разделим на корень из двух, то получим действующее напряжение (то, которое показывает вольтметр) 219,4 Вольт.
Действующее значение тока
Применив метод интегрирования к квадратам амплитудной силы тока и синусу круговой частоты и выведя среднеквадратичные величины, можно получить действующее значение силы тока:
Сравнивая тепловые эффекты постоянного и переменного электротоков, взятые за одинаковый временной отрезок и при одинаковой активной нагрузке, можно обнаружить, что равенство тепловых характеристик проводников того и другого типа достигается в том случае, если сила линейного тока будет меньше максимальных силовых значений в цепи переменного тока в 1,414 раз.
Какие коэффициенты характеризуют переменное напряжение
Помимо базовых параметров переменного тока, в электротехнике принято производить измерения электросигналов, включая выходные напряжения выпрямителей и импульсы различной формы.
Амплитудное значение напряжения
Под амплитудным или пиковым напряжением подразумевают максимальный показатель U за один период синусоиды:
Um = max(|u(t)|)
Для измерения данного параметра обычно используют вольтметр импульсного типа или осциллограф.
Мгновенное значение тока
Параметр обозначает силу тока или напряжение в конкретный временной момент (u(t), i(t)). В зависимости от динамики электрического сигнала, для определения мгновенных значений могут применяться малоинерционные вольтметры, а также шлейфовые или электронно-лучевые осциллографы.
Среднее значение
Под средним значением синусоидально изменяющейся величины понимают ее среднее значение за полпериода.
Среднее значение тока: 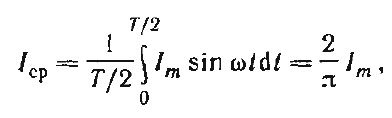
т. е. среднее значение синусоидального тока составляет 2/π = 0,638 от амплитудного. Аналогично, Eср = 2Ем/π ; Ucp = 2Uм/π.
Среднеквадратичное значение напряжения
Итак, что же у нас получилось? Как и постоянное напряжение, так и переменное напряжение зажигали одну и ту же лампочку, которая кушала одну и ту же мощность. Значит эта осциллограмма
и вот эта осциллограмма
Чем то похожи? Но чем???
Среднеквадратичноезначениенапряжения — это такое значение переменного напряжения, при котором нагрузка потребляет столько же силы тока, как и при постоянном напряжении. То есть лампочка у нас потребляла 1,71 Ампер и при постоянном токе и при переменном. То есть, в двух этих случаях, мощность, которую потребляла лампочка, была одинакова.
Также среднеквадратичное напряжение еще называют действующим или эффективным значением напряжения. С помощью несложных умозаключений, инженеры-электрики пришли к выводу действующее (оно же среднеквадратичное) напряжение синусоидального сигнала любой частоты равняется максимальной его амплитуде, поделенной на корень из двух

Стоп! Мы ведь не разобрали, что такое максимальная амплитуда! На осциллограмме максимальная амплитуда выглядит примерно вот так:

Если даже посчитать по клеточкам и посмотреть, чему равняется одна клеточка по вертикали (смотрим внизу слева, она равняется 5 Вольт), то Umax = 17 Вольт. Делим это значение на корень из двух. Я беру это значение как 1,41. Получаем, что среднеквадратичное значение равняется 17/1,41=12,06 Вольт. Ну что, все верно
Значит, когда нам говорят, что напряжение в розетке равняется 220 Вольт, то мы то знаем, что на самом деле это среднеквадратичное напряжение. Максимальная амплитуда этих 220 Вольт равняется 220х1,41=310 Вольт.
Где же среднеквадратичное напряжение и максимальная амплитуда сигнала прячутся на табличке измерений? Да вот же они!
Vk — это и есть среднеквадратичное напряжение этого сигнала.
Ma — это и есть Umax.
Конечно, 16,6/1,41=11,8 Вольт, а он пишет 12,08 Вольт.
Средневыпрямленное значение
Величина определяется как взятое по модулю среднеарифметическое всех мгновенных значений напряжения. Для одного периода средневыпрямленная величина равна сумме площадей сверху и снизу оси времени. Хотя параметр не находит практического применения, именно он фиксируется по факту большинством измеряющих устройств магнитоэлектрического принципа действия, несмотря на то, что их шкалы имеют градацию для действительных значений. При этом эффективные и средневыпрямленные значения оказываются близки друг к другу только в случае синусоидального напряжения.
Синусоида, её амплитуда и другие характеристики
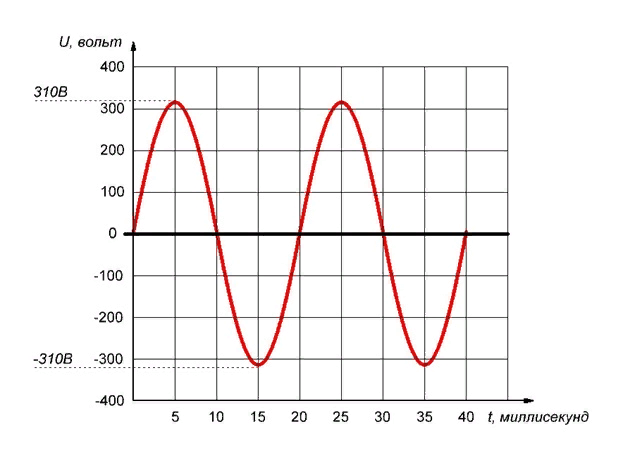
Все мы знаем, что между фазой и нулём 220 вольт (230В по ГОСТу), но многие знают что выпрямленное и сглаженное сетевое напряжение превышает 300 вольт, да и конденсаторы в фильтры выпрямителей подбирают не ниже чем 400 вольт, откуда они берутся? Для начала рассмотрим график, на котором изображено синусоидальное напряжение в привычной всем розетке 220В.
Рисунок 1 — график синусоидально изменяющегося напряжения Рисунок 1 — график синусоидально изменяющегося напряжения
На рисунке 1 по вертикали размечено напряжение в вольтах, а по горизонтали время. Обратите внимание, что напряжение в электросетипериодично изменяется от -310 вольт, до + 310 вольт, каждый период изменений длится 20 миллисекунд, после чего повторяется.
Точно описать любую величину, изменяющуюся по синусоидальному закону можно с помощью трёх характеристик:
- Амплитуда — это высота синусоиды от нуля до верхней или нижней точки. В нашем случае это 310В. Обозначается буквами Im или Um, для тока и напряжения соответственно.
- Период — расстояние между двумя соседними максимумами или минимумами синусоиды. В электросетях РФ он равен 20 миллисекунд, так как стандартная частота — 50 Гц. Обозначается буквой T.
- Начальный фазовый угол — это величина, которая отражает насколько сдвинута синусоида по горизонтали относительно начального момента времени наблюдения (нулевой секунды). Если проще, то на графике выше фаза в начале графика начинается с 0, значит она не сдвинута, если бы начиналась с другой величины — то была бы сдвинутой на определенный угол.
При рассмотрении однофазной сети начальный фазовый угол нас не интересует, он используется при исследовании трёхфазного напряжения.
Рассмотрим этот график еще раз, но отметим на нём амплитуду и период.
Рисунок 2 — амплитуда и период синусоидального напряжения Рисунок 2 — амплитуда и период синусоидального напряжения
График описывает формула синусоидального напряжения (для тока аналогично, но U меняется на I):
где: Um – амплитуда; ω – угловая частота (равна 2×pi×f); t – время, ф — начальная фаза где: Um – амплитуда; ω – угловая частота (равна 2×pi×f); t – время, ф — начальная фаза
Из этого следует, что величина напряжения (или тока) в каждый конкретный момент времени разная, такая величина называется мгновенной. Соответственно и мгновенная мощность, выделяемая на активной нагрузке (R) в каждый момент будет разной:
Это подходящая формула для описания мгновенного состояния электрической цепи, но совершенно неудобная и неподходящая для измерения параметров и описания электрических цепей в общем. Поэтому используют какие-то усреднённые значения электрической мощности, напряжения и тока.
В литературе принято объяснять смысл действующих и амплитудных значений на примере силы тока. К тому же по определения, формулы и их смысл аналогичны, и для напряжения, и для тока. Поэтому я немного отойду от синусоидального напряжения, и далее пойдет речь о токе.
Формула действующего значение тока
Синусоидальные гармоники являются типичной характеристикой переменного тока. В этом отношении по синусоиде происходит изменение электродвижущей силы и тока при определенной нагруженности цепи. При этом динамика ЭДС может быть описана следующими параметрами:
• Период — время, за которое электродинамические показатели изменяются по полному циклу. Он напрямую связан с частотой вращения роторного механизма генератора электротока.
• Частота — определяется как число периодов за одну единицу времени. Современные стандарты для электросетей предписывают частоту переменного тока в 50 герц. Это означает, что за 1 секунду ток меняет направление 50 раз, а один период длится 20 миллисекунд.
• Амплитуда — максимальная величина гармоники переменного тока. В строгом смысле параметр применим исключительно к синусоидальному изменению. С некоторыми допущениями амплитуда может быть определена и для других форм электросигнала. За один период электродвижущая сила дважды доходит до пиковых значений и обозначается как Em+ и Em- соответственно положению полупериодов.
• Угловая частота — скорость колебательного движения, измеряемая в радианах в секунду. При этом один период синусоиды приравнивается к значению 2π. Общая формула угловой частоты: ω = 2π / Т.
• Фаза колебаний — стадия синусоидальной волны, принимаемая как аргумент функции тока, которая отсчитывается от среднего нулевого значения. Величина фазы колебаний, используемая для определения синуса или косинуса фазового угла, описывается формулой φ = ωt.
Как в случае со среднеквадратичными значениями тока и напряжения, через основные характеристики определяется и среднее значение ЭДС, которое сводится к следующему выражению:
Среднеквадратичные показатели переменного тока определяется как отношение амплитудного значения тока к корню из 2.
Схожим образом обозначаются эффективные значения напряжения и ЭДС.
Действительные значения синусоидального тока помогают производить практическую оценку и описание электроцепей. Несмотря на сложность составляющих понятий, эти величины сводятся к простым выражениям. Номинальное напряжение электрических сетей и приборов представляет собой как раз среднеквадратичное значение. Умножив указанный вольтаж на корень из 2, можно узнать амплитудное значение напряжения электроустройств.
Какое напряжение измеряет мультиметр, амперметр или вольтметр?
В подавляющем большинстве случаев если на измерительном приборе вы выбираете режим измерения переменного тока или напряжения (U~, I~), вы измерите именно действующие значения. Однако есть и специфичные приборы, измеряющие амплитудные значения параметров в электрической сети, а также на электронных осциллографах могут выводится и действующие, и амплитудные величины измеряемых сигналов. Измерение амплитудных значений может обозначаться как Im.
При этом далеко не все приборы могут измерять переменный ток по форме отличный от синусоидального — пилообразный, прямоугольный и так далее. Вы могли видеть, что на хороших мультиметрах написано загадочное «TRUE RMS», что расшифровывается как: «True Root Mean Sqare», а переводится как — истинное среднеквадратичное значение. Такие измерительные приборы показывают действующие значения напряжений и токов любых форм (не только синусоидальных).
Работа генератора трехфазного переменного тока
Рассмотрим упрощенно работу генератора трехфазного переменного тока. Обмотки статора (фазы А, В и С) генератора расположены под углом 120 градусов относительно друг друга. Ротор с магнитом вращаясь индуцирует в обмотках статора периодически изменяющиеся ЭДС. Выглядит это следующим образом:
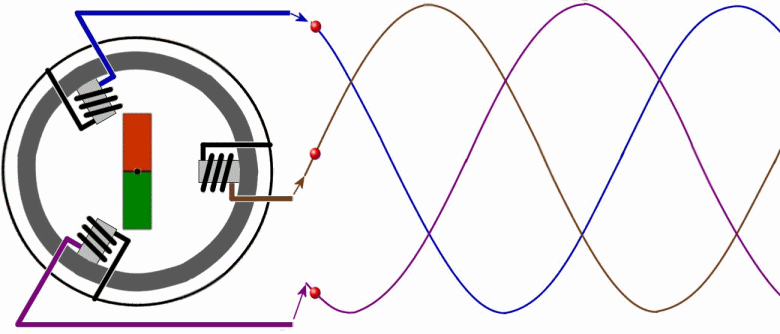
Такое вращение происходит с частотой 50 оборотов в секунду, то есть с частотой 50 Герц. Это значит, что электроны движутся в течение 1 секунды 50 раз в одном направлении (положительный полупериод синусоиды), и 50 — в обратном (отрицательный полупериод), 100 раз проходя чрез нулевое значение. Получается, что к примеру обычная лама накаливания, включенная в сеть с такой частотой, будет затухать и вспыхивать примерно 100 раз за секунду, однако мы этого не замечаем в силу особенностей своего зрения.
Расчёт действующего значения
В качестве примера рассчитаем среднеквадратичное значение синусоидального напряжения.
Запишем выражение Urms с применением интеграла функции U = Uampsin(t) для одного периода 2π :
Показать расчётСкрыть расчёт
Вынесем Uamp из под знака радикала. Воспользуемся табличным интегралом
, перепишем и решим последнее выражение с применением формулы Ньютона-Лейбница:
Так как sin(2π), sin(4π) и sin(0) равны нулю, вычисляем RMS синусоиды следующим образом:
В результате решения в итоге получим:
Расчёт RMS для напряжения или тока треугольной и пилообразной формы можно рассмотреть на примере одного периода T для функции
, представленной на рисунке:
Выразим Urms искомой функции с помощью определённого интеграла:
Показать расчёт
Скрыть расчёт
Используя табличный интеграл
и формулу Ньютона-Лейбница, получаем:
В итоге преобразований получим:
Ток или напряжение любой сложной формы можно рассмотреть, как набор функций в пределах периода. Тогда значением RMS будет квадратный корень из среднеарифметического значения интегралов для квадрата каждой функции, ограниченной её интервалом времени в периоде.
Например, для множества функций F1(t) , F2(t) , … , Fn(t) в соответствующих им интервалах времени (0 – T1), (T1 – T2), …, (Tn – T), составляющих период T, действующее напряжение (RMS) определится выражением:
Для вариантов однополярного или двуполярного напряжения пилообразной и треугольной формы в периоде 2T или 4T, представленных на рисунке ниже, T и Uamp имеют те же расчётные величины, что и в рассмотренном случае c функцией
, а интегралы, определённые в интервалах, равных T, для квадратов используемых функций
, будут иметь одно и то же значение
Следовательно, вышеуказанные варианты однополярного или двуполярного напряжения пилообразной и треугольной формы будут иметь среднеквадратичное значение
.
В заключении рассмотрим пример вычисления действующего значения положительных прямоугольных импульсов длительностью Ti .
Выразим Urms одного периода T, как квадратный корень из среднеарифметического значения интегралов, определённых в интервалах 0 – Ti и Ti – T для квадратов всех значений периода.
В результате получаем значение RMS, равное произведению амплитуды импульсов Uamp на квадратный корень из коэффициента заполнения (Ti / T).
В качестве дополнительного материала предлагаем рассмотреть расчёт средеквадратичного значения напряжения накала кинескопа цветного телевизора, исходя из амплитуды и формы напряжения.
Практический пример
Определение выше будет непонятным для человека, который не имеет особых познаний в области электротехники и электродинамики. Чтобы понять его смысл, предлагается рассмотреть следующий пример:
- Доступны две идентичные электроцепи (длина, элементы цепи и сечение проводников у них совпадают).
- В каждую включён одинаковый резистор — электронный компонент, который изменяет свое сопротивление в зависимости от подаваемого тока.
- Обе цепи подключаются к источникам электроэнергии, имеющим одинаковое напряжение.
Но между цепями есть одна разница. На первую электроцепь подаётся постоянный, а на вторую — переменный ток. По одной из них пойдёт стабильный электроток, а по другой потечет импульсный электрозаряд, который постоянно изменяется и имеет синусоидальной график.
Чтобы найти количества тепла в цепи с сопротивлением, используется такая формула:
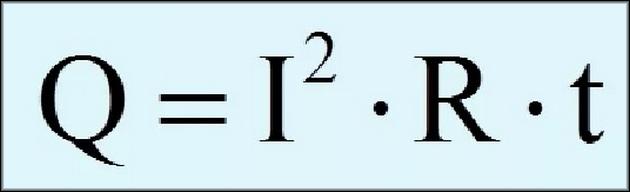
После произведения ряда замеров и вычислений можно увидеть, что выделяемое тепло в этих двух электроцепях имеет одинаковую величину. Например, в цепи с постоянным током при подаче напряжения 30 вольт выделяется тепло 200 Джоуль (или Дж). Если вторая цепь имеет идентичные характеристики, то выделение тепла в ней также составит 200 Дж. Получается, что напряжение 30В в этих электроцепях — это и есть эффективное напряжение.
Дополнительные сведения
В англоязычной технической литературе для обозначения действующего значения употребляется термин effective value — эффективное значение. Также применяется аббревиатура RMS или rms — root mean square — среднеквадратичное (значение).
Электроизмерительные приборы (амперметры, вольтметры) для измерения в цепях переменного тока обычно градуируются так, чтобы их показания соответствовали действующему значению синусоидального тока или напряжения. При измерении несинусоидальных токов и напряжений приборы различных систем могут давать разные показания.
Вывод
Мы рассмотрели в данной статье — что называют действующим значением силы тока и напряжения, а так же как определяют эти значения переменного тока в электроцепи. Это эффективные значения переменного тока, под действием которого выделяется точно такое же количества тепла, как и в цепи постоянного тока, имеющей аналогичные характеристики.
Предыдущая
РазноеЗачем нужны сервисы приема СМС и с чем их едят
Следующая
РазноеИмпульсный и аналоговый блоки питания, принципы работы и основные отличия. Что такое импульсный блок питания (ИБП) и как он работает
Действующее (эффективное) значение переменного тока равно величине такого постоянного тока, который за время, равное одному периоду переменного тока, произведёт такую же работу (тепловой или электродинамический эффект), что и рассматриваемый переменный ток.
В современной литературе чаще используется математическое определение этой величины — среднеквадратичное значение переменного тока. Иначе говоря, действующее значение переменного тока можно определить по формуле:
Действующее значение в типичных случаях[править | править код]
Приведены формулы для электрического тока. Аналогичным образом определяются действующие значения ЭДС и напряжения.
Синусоида[править | править код]
Для синусоидального тока:
где
— амплитудное значение тока.
Прямоугольная форма[править | править код]
Для тока, имеющего форму однополярного прямоугольного импульса, действующее значение тока зависит от скважности:
где
— коэффициент заполнения (величина, обратная скважности).
В частности, для тока, имеющего форму однополярного меандра (коэффициент заполнения 0,5):
Для тока, имеющего форму двухполярного меандра:
Треугольная форма[править | править код]
Для тока треугольной и пилообразной формы (независимо от того, меняется ли направление тока):
Трапециевидная форма[править | править код]
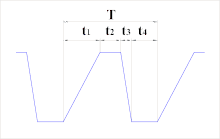
Для тока трапециевидной формы действующее значение можно определить разбив период на отрезки положительного фронта, действия максимального значения и отрицательного фронта:
где
— длительность положительного фронта;
— длительность действия максимального значения;
— длительность отрицательного фронта;
— длительность полного периода.
Дугообразная форма[править | править код]
Для тока имеющего форму дуги (половины окружности):
Дополнительные сведения[править | править код]
В англоязычной технической литературе для обозначения действующего значения употребляется термин effective value — эффективное значение. Также применяется аббревиатура RMS или rms — root mean square — среднеквадратичное (значение).
Электроизмерительные приборы (амперметры, вольтметры) для измерения в цепях переменного тока обычно градуируются так, чтобы их показания соответствовали действующему значению синусоидального тока или напряжения. При измерении несинусоидальных токов и напряжений приборы различных систем могут давать разные показания[1].
См. также[править | править код]
- Список параметров напряжения и силы электрического тока
Примечания[править | править код]
- ↑ 11.8. Показания приборов различных систем в цепях несинусоидального тока. StudFiles. Дата обращения: 16 февраля 2019.
Литература[править | править код]
- «Справочник по физике», Яворский Б. М., Детлаф А. А., изд. «Наука», 1979 г.1
- Курс физики. А. А. Детлаф, Б. М. Яворский М.: Высш. шк., 1989. § 28.3, п.5
- «Теоретические основы электротехники», Л. А. Бессонов: Высш. шк., 1996. § 7.8 — § 7.10
Ссылки[править | править код]
- Действующие значения тока и напряжения
- Среднеквадратичное значение