Действующее (эффективное) значение переменного тока равно величине такого постоянного тока, который за время, равное одному периоду переменного тока, произведёт такую же работу (тепловой или электродинамический эффект), что и рассматриваемый переменный ток.
В современной литературе чаще используется математическое определение этой величины — среднеквадратичное значение переменного тока. Иначе говоря, действующее значение переменного тока можно определить по формуле:
Действующее значение в типичных случаях[править | править код]
Приведены формулы для электрического тока. Аналогичным образом определяются действующие значения ЭДС и напряжения.
Синусоида[править | править код]

Для синусоидального тока:
где
— амплитудное значение тока.
Прямоугольная форма[править | править код]
Для тока, имеющего форму однополярного прямоугольного импульса, действующее значение тока зависит от скважности:
где
— коэффициент заполнения (величина, обратная скважности).
В частности, для тока, имеющего форму однополярного меандра (коэффициент заполнения 0,5):
Для тока, имеющего форму двухполярного меандра:
Треугольная форма[править | править код]
Для тока треугольной и пилообразной формы (независимо от того, меняется ли направление тока):
Трапециевидная форма[править | править код]
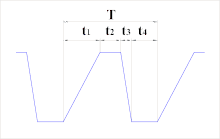
Для тока трапециевидной формы действующее значение можно определить разбив период на отрезки положительного фронта, действия максимального значения и отрицательного фронта:
где
— длительность положительного фронта;
— длительность действия максимального значения;
— длительность отрицательного фронта;
— длительность полного периода.
Дугообразная форма[править | править код]
Для тока имеющего форму дуги (половины окружности):
Дополнительные сведения[править | править код]
В англоязычной технической литературе для обозначения действующего значения употребляется термин effective value — эффективное значение. Также применяется аббревиатура RMS или rms — root mean square — среднеквадратичное (значение).
Электроизмерительные приборы (амперметры, вольтметры) для измерения в цепях переменного тока обычно градуируются так, чтобы их показания соответствовали действующему значению синусоидального тока или напряжения. При измерении несинусоидальных токов и напряжений приборы различных систем могут давать разные показания[1].
См. также[править | править код]
- Список параметров напряжения и силы электрического тока
Примечания[править | править код]
- ↑ 11.8. Показания приборов различных систем в цепях несинусоидального тока. StudFiles. Дата обращения: 16 февраля 2019.
Литература[править | править код]
- «Справочник по физике», Яворский Б. М., Детлаф А. А., изд. «Наука», 1979 г.1
- Курс физики. А. А. Детлаф, Б. М. Яворский М.: Высш. шк., 1989. § 28.3, п.5
- «Теоретические основы электротехники», Л. А. Бессонов: Высш. шк., 1996. § 7.8 — § 7.10
Ссылки[править | править код]
- Действующие значения тока и напряжения
- Среднеквадратичное значение
Что такое действующее значение напряжения
Содержание
- 1 Как измеряется
- 1.1 Практический пример
- 2 Импульсный электрический заряд
- 2.1 Расчёт кривой
- 2.2 Вычисления
- 3 Сила переменного тока
- 4 Вывод
- 5 Видео по теме
Всем нам известно о 220 вольт в бытовой розетке. Но если подключить к ней вольтметр, напряжение каждый раз будет разным. При этом зачастую напряжение может быть даже больше данной величины. Постараемся в данном материале разобраться — почему это происходит, что такое действующее значение переменного тока, и как его можно рассчитать с помощью различных вариантов.
Как измеряется
Электродинамические параметры в сети постоянно изменяются. Это связано с тем, что они представлены синусоидальным однополярным импульсом разной амплитуды. При измерении напряжения в цепи переменного тока, каждый раз будет получен разный результат. А при вычислении усреднённого параметра, он всегда будет составлять 0.

Получается, что математически вычислить данный параметр невозможно. Есть возможность получить только усреднённый параметр, который зависит от полупериода синусоидальной волны. Однако использовать его на практике или для каких-то вычислений нельзя.
Для решения этой проблемы и стали применять такое понятие, как действующее значение для расчёта силы тока и напряжения. Параметр определяется по характеристикам постоянного тока в цепи, генерирующей тепловую энергию такого же объёма, как и при подаче в цепь переменного тока.
Практический пример
Определение выше будет непонятным для человека, который не имеет особых познаний в области электротехники и электродинамики. Чтобы понять его смысл, предлагается рассмотреть следующий пример:
- Доступны две идентичные электроцепи (длина, элементы цепи и сечение проводников у них совпадают).
- В каждую включён одинаковый резистор — электронный компонент, который изменяет свое сопротивление в зависимости от подаваемого тока.
- Обе цепи подключаются к источникам электроэнергии, имеющим одинаковое напряжение.

Но между цепями есть одна разница. На первую электроцепь подаётся постоянный, а на вторую — переменный ток. По одной из них пойдёт стабильный электроток, а по другой потечет импульсный электрозаряд, который постоянно изменяется и имеет синусоидальной график.
Чтобы найти количества тепла в цепи с сопротивлением, используется такая формула:

После произведения ряда замеров и вычислений можно увидеть, что выделяемое тепло в этих двух электроцепях имеет одинаковую величину. Например, в цепи с постоянным током при подаче напряжения 30 вольт выделяется тепло 200 Джоуль (или Дж). Если вторая цепь имеет идентичные характеристики, то выделение тепла в ней также составит 200 Дж. Получается, что напряжение 30В в этих электроцепях — это и есть эффективное напряжение.
Импульсный электрический заряд
Вышеприведенный пример позволяет только определить действующее и среднее значение напряжения переменного тока. Но на практике такой метод также не применяется, из–за того, что получить доступ к источнику переменного напряжения не всегда представляется возможным. Поэтому параметры цепи рассчитываются с помощью формул, которые основаны на синусоидальных кривых.
Стоит отметить, что действующее напряжение не всегда формируется путём плавного изменения определённого импульсного электрозаряда. Кривая зачастую имеет форму, отличную от привычной нам синусоиды:
- Прямоугольную (меандр);
- треугольную;
- трапециевидную
- и другие.

То есть график электротока может иметь отличную, но при этом стабильную форму. Наглядным примером такого варианта является кривая осциллографа, регистрирующая ритмы сердцебиения человека.

Но независимо от действующего в сети импульсного заряда, во время расчётов используется именно синусоида. Это объясняется тем, что погрешности в расчетах будут крайне малыми. Поэтому ими можно пренебречь, ведь они не скажутся на конечном результате:
- Частота импульса в жилых домах составляет 50 Гц. За 1 сек электрический импульс проходит через фазу 100 раз. Это означает, что работающая от сети лампочка за секунду 100 раз загорается и тухнет, а электрический заряд при этом изменяется довольно плавно. Но человек этого не замечает из-за невосприимчивости человеческого зрения к сверхбыстрым колебаниям.

- Одинаковая площадь фигур. Независимо от формы кривой периода, описывающей переменный электроток идентичных параметров, площадь их фигур всегда будет одинаковой. Следовательно, при любых расчетах получится одно и то же эффективное значение переменного синусоидального тока. Поэтому эффективные значения не зависят от формы кривой. На них оказывает влияние именно величина амплитуды.

Форма кривой импульса важна только для сверхточных расчётов в лабораторных условиях. Также она учитывается для работы суперкомпьютеров. В остальных случаях синусоида позволит вычислить действующее значение переменного синусоидального тока.
Расчёт кривой
Синусоида — это периодическая функция, которую можно всегда описать с помощью уравнения. Если взять её за основу, то на входе имеются следующие исходные данные:
- Т — амплитуда;
- φ — начальная фаза;
- ωt — угловая скорость.

По этим входным характеристикам находим другие переменные параметры:
- Uт — амплитудное напряжение;
- Uм — действующие в момент измерения значения напряжения;
- ωt + φ — фактическая фаза в точке измерения.
Т.к. начальная фаза равняется нулю, на выходе формула кривой будет иметь следующий вид:
Uм = Uт·sin(ωt + φ) = Uт·sin(ωt)
Теперь необходимо обратиться к закону выделения тепла, который еще называется законом Джоуля-Ленца. Согласно него квадрат напряжения — это произведение выделяемого тепла на сопротивление проводника.
| Формулы для расчета тепловой энергии в электроцепях: | |
| с постоянным током | с переменным током |
| Q = U2/R | Q = Uм2/R |
- Uм — величина постоянного напряжения;
- Uм — величина действующего напряжения;
- R — сопротивление проводника.
Мы видим, что при расчетах количества тепла в цепи переменного тока, пользуется именно действующим значением переменного тока.

Из данных формул вытекают два важных нюанса, на которые стоит обратить внимание:
- В расчетах используется среднеквадратичное значение напряжения (СКЗ). Это связано с тем, что величина напряжения постоянно изменяется и можно получить только какую-то усредненную величину.
- Амплитуда постоянного тока довольно условная величина. Ее используют в расчетах, чтобы только описать период синусоиды переменного электрозаряда.
Вычисления
Волны синусоид будут одинаковыми. Однако в пределах периода в каждой точке измерения напряжения будут отличаться. Поэтому, чтобы уравнять между собой среднеквадратичное напряжение постоянного и переменного электротока по тепловыделению, требуется рассчитать объём выделенного тепла в течение времени, равного 1 периоду:
![]()
В уравнение теперь можно подставить выражение расчёта мгновенного напряжения
Uм = Uт·sin(ωt + ф) = Uт·sin(ωt)

После математического преобразования можно рассчитать действующее значение электрического напряжения:
U = Uт / √2 = 0,707·Uм
Теперь найдем амплитудное напряжение по формуле:
Uт = U·√2
Амплитудное напряжение так же имеет и другое название – максимально возможное эффективное мгновенное значение напряжения.
Сила переменного тока
С помощью амперметра находим амплитудную силу тока в цепи. Используя её вместе с периодом, который равен 1/50 секунд, можно применить описанную выше формулу, чтобы рассчитать среднеквадратичное значение напряжения. В результате этого будет получена действующие значения силы тока.
Действующее значение тока можно рассчитать, когда других исходных параметров нет, но нам известно эффективное значение величины напряжения в цепи. Следовательно, можно воспользоваться всем нам известным законом Ома вычисления значения силы тока:
U = I·R и I = U/R
где:
- U — будет действующим напряжением переменного синусоидального тока;
- R — сопротивление проводника, которое всегда можно узнать в любом справочнике, зная состав материала проводника.
Ранее электропроводку делали из алюминия и меди, которые отличались довольно высоким сопротивлением. Эффективное значение реальной силы тока этих металлов было меньше 6.5А. По этой причине в старых домах зачастую срабатывает автоматический выключатель, если одновременно подключить в сеть несколько приборов. Сегодня открыты сложные сплавы с низким сопротивлением. Они позволяют достичь с действующее значение силы переменного тока около 16А даже в обычных современных многоквартирных домах.

С уменьшением сопротивления проводника, прямопропорционально возрастает мощность и тепловыделение. При том надо помнить о том, что у каждого сплава есть свой определенный температурный предел. Поэтому в жилых сетях сила тока часто не превышает 20 ампер, а при резком ее скачке, например, при неполадках на подстанции, электронная часть устройств просто сгорает. Для предотвращения таких случаев и подключаются автоматы, которые при регистрации высоких действующих значений размыкают цепь на данном участке. Более мощные источники электроэнергии встречаются только в промышленных трехфазных сетях с напряжением 380В.
Вывод
Мы рассмотрели в данной статье — что называют действующим значением силы тока и напряжения, а так же как определяют эти значения переменного тока в электроцепи. Это эффективные значения переменного тока, под действием которого выделяется точно такое же количества тепла, как и в цепи постоянного тока, имеющей аналогичные характеристики.
Видео по теме
Понятие
действующего значения тока вводится в
связи с необходимостью производства
измерений. Что измерять у переменного
тока? Если бы мы имели дело только с
синусоидами – кривыми одной формы, то
можно было бы измерять амплитуды. Но на
практике встречаются самые разные
кривые, и может оказаться так, что два
различных по форме тока имеют одинаковые
амплитуды, хотя очевидно, что на
электрическую цепь они будут оказывать
разное воздействие.
Поэтому
наиболее целесообразно оценивать
величину тока по той работе, которую он
совершает. При такой оценке действие
переменного тока сравнивается с
аналогичным действием постоянного
тока. Например, если некоторый переменный
ток выделяет на участке цепи такое же
количество тепла, что и постоянный ток
силой 10 ампер, то говорят, что величина
этого переменного тока составляет 10
ампер. Это значение тока и называют
действующим.
Итак,
действующим
значением переменного тока называется
численное значение такого постоянного
тока, который за время, равное одному
периоду, выделяет в сопротивлении такое
же количество тепла, что и ток переменный.
Таким
образом, для оценки величины переменного
тока мы должны сделать следующее.
1.
Определить количество теплоты,
выделяющейся в сопротивлении R
за время Т
при протекании переменного тока i.
Это количество теплоты равно
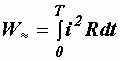
.
`
2. Подобрать такой постоянный ток I,
который за то же время Т
в том же сопротивлении R
выделяет такое же количество тепла. При
постоянном токе оно равно
![]()
.
3.
Приравнять W
и
W=:
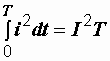
,
откуда
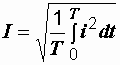
.
(2.5)
Последняя
формула и определяет действующее
значение переменного тока.
Пример
2.1.
На вход некоторой цепи подается импульсное
напряжение треугольной формы (рис. 2.4,
а).
Чему равно его действующее значение?
Р
е ш е н и е.
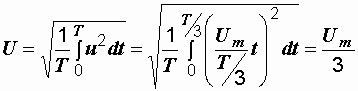
.

Рис.
2.4. Переменные напряжения различной
формы
Пример
2.2.
На рис. 2.4, б
показана кривая напряжения на выходе
схемы однофазного однополупериодного
выпрямления. Чему равно действующее
значение напряжения, если его амплитудное
значение Um
составляет 311 В?
Р
е ш е н и е.

155,5
В.
Пример
2.3.
Определить действующее значение
синусоидального тока
![]()
.
Р
е ш е н и е.

.
Рассмотренные
примеры показывают, что действующее
значение переменного тока зависит от
его формы.
У
синусоидального тока оно равно амплитуде,
деленной на
![]()
.
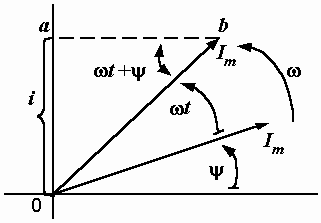
2.4. Представление синусоидальной функции времени вращающимся вектором. Векторные диаграммы
Пусть
в прямоугольной системе координат
имеется вектор длиной Im,
расположенный под углом к горизонтальной
оси (рис. 2.5). Заставим этот вектор
вращаться против часовой стрелки c
угловой скоростью . Тогда за время t
он повернется на угол t.
|
Рис. 2.5. Вращающийся |
Проекцию вектора на вертикальную ось |
Обычно
вектор при этом показывается не в
произвольный момент времени t,
а в начальный (t
= 0), когда его угол наклона к горизонтальной
оси равен начальной фазе.
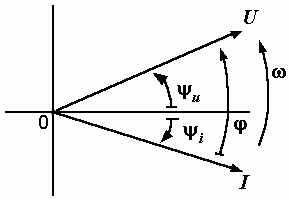
Теперь по уравнениям (2.3)
построим векторную диаграмму двух
векторов – тока и напряжения (рис. 2.6).
|
Рис. |
Длины векторов равны |
Векторная
диаграмма дает наглядное представление
об отставании одних величин и опережении
других. Если вращать картинку, показанную
на рис. 2.6, против часовой стрелки, то
вектор тока будет отставать от напряжения
на угол
. Так как при вращении длины векторов и
угол между ними не меняются, то в том
случае, когда начальные фазы напряжения
и тока нас не интересуют, мы можем
изображать диаграмму без осей и
располагать ее так, как нам удобно (рис.
2.7).
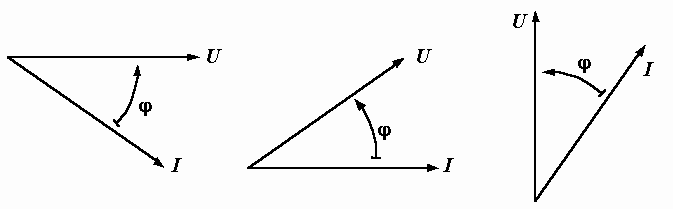
Рис.
2.7. Варианты построения векторной
диаграммы
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Какое напряжение между фазой и нулём в отечественной электросети: 220 или 310? На самом деле и одно и другое! Всё дело в том, что в наших сетях протекает синусоидальный ток, а у синусоиды есть ряд характеристик и особенностей, которые мы попытаемся рассмотреть простым языком в этой статье.
Речь далее пойдет только о синусоидальном переменном токе или напряжении. Для тока другой формы всё сказанное далее, в принципе, справедливо, но будут отличаться формулы для вычисления и, соответственно, числовые значения.
Синусоида, её амплитуда и другие характеристики
Все мы знаем, что между фазой и нулём 220 вольт (230В по ГОСТу), но многие знают что выпрямленное и сглаженное сетевое напряжение превышает 300 вольт, да и конденсаторы в фильтры выпрямителей подбирают не ниже чем 400 вольт, откуда они берутся? Для начала рассмотрим график, на котором изображено синусоидальное напряжение в привычной всем розетке 220В.
На рисунке 1 по вертикали размечено напряжение в вольтах, а по горизонтали время. Обратите внимание, что напряжение в электросети периодично изменяется от -310 вольт, до + 310 вольт, каждый период изменений длится 20 миллисекунд, после чего повторяется.
Точно описать любую величину, изменяющуюся по синусоидальному закону можно с помощью трёх характеристик:
- Амплитуда — это высота синусоиды от нуля до верхней или нижней точки. В нашем случае это 310В. Обозначается буквами Im или Um, для тока и напряжения соответственно.
- Период — расстояние между двумя соседними максимумами или минимумами синусоиды. В электросетях РФ он равен 20 миллисекунд, так как стандартная частота — 50 Гц. Обозначается буквой T.
- Начальный фазовый угол — это величина, которая отражает насколько сдвинута синусоида по горизонтали относительно начального момента времени наблюдения (нулевой секунды). Если проще, то на графике выше фаза в начале графика начинается с 0, значит она не сдвинута, если бы начиналась с другой величины — то была бы сдвинутой на определенный угол.
При рассмотрении однофазной сети начальный фазовый угол нас не интересует, он используется при исследовании трёхфазного напряжения.
Рассмотрим этот график еще раз, но отметим на нём амплитуду и период.
График описывает формула синусоидального напряжения (для тока аналогично, но U меняется на I):
Из этого следует, что величина напряжения (или тока) в каждый конкретный момент времени разная, такая величина называется мгновенной. Соответственно и мгновенная мощность, выделяемая на активной нагрузке (R) в каждый момент будет разной:
Это подходящая формула для описания мгновенного состояния электрической цепи, но совершенно неудобная и неподходящая для измерения параметров и описания электрических цепей в общем. Поэтому используют какие-то усреднённые значения электрической мощности, напряжения и тока.
В литературе принято объяснять смысл действующих и амплитудных значений на примере силы тока. К тому же по определения, формулы и их смысл аналогичны, и для напряжения, и для тока. Поэтому я немного отойду от синусоидального напряжения, и далее пойдет речь о токе.
Действующее, среднеквадратичное, эффективное?
Теперь вы знаете, что амплитуда фазного напряжения в электросети равна 310В, но что такое 220В и откуда они берутся? Дело в том, что — 220В это действующее напряжение, его же называют среднеквадратичным или эффективным.
Это значит, что если на лампочку накаливания или нагревательную спираль подать переменный ток с действующим значением (силой) в 1 ампер, то на ней выделится та же мощность (количество тепла), как если бы через неё протекал постоянный ток в 1 ампер.
Для нахождения среднего значения переменного синусоидального тока за половину периода, необходимо проинтегрировать формулу этого тока, при этом пределами интегрирования выбирается половина периода:
Как отмечалось выше, формула для среднего переменного синусоидального напряжения (как и для ЭДС) будет аналогичной:
Но это средние величины, которые на практике не используется так часто, как действующие величины. Действующее напряжение или ток, находится подобным образом, при вычислениях интегрируется та же формула, но возведенная в квадрат, после чего извлекается корень. Пределы интегрирования уже не половина, а целый период. Кстати, поэтому действующее значение называется еще и «среднеквадратичным». Формулу действующего значения переменного синусоидального тока:
Действующий ток (Iд) или напряжение (Uд), в корень из двух раз меньше, чем амплитудное. Чтобы его вычислить, нужно амплитудное значение разделить на 1.41, или умножить на 0.707.
Uд=Um/1.41=0.707*Um
И наоборот, чтобы узнать амплитудное значение при известном действующем, нужно умножить его на 1.41 или разделить на 0.707. Приведем пример, из графика на рисунке 1, мы узнали, что амплитуда напряжения в однофазной электросети 310 вольт, найдем его действующее значение:
Uд=Um/1.41=310/1.41=219,8~220В
Мы получили привычные нам 220В. Как отмечалось ранее, действующие значения напряжения и тока удобно использовать для расчетов и описания электрических цепей, поэтому и говорят «в розетке 220В», «линейное напряжение 380В» и так далее.
Повторим пройденное: непрерывное тепловое воздействие переменного синусоидального тока на какую-то активную нагрузку за определенный период времени будет численно равно тепловому воздействию постоянного тока за тот же период, при условии, что величина постоянного тока была в 1.41 раз меньше амплитуды переменного. То есть за то же время выделится столько же теплоты.
В таком случае, при активной нагрузке (резисторы, ТЭНы, нихромовые спирали, лампы накаливания), можно приравнять действующее значение переменного тока или напряжения, к такому же по величине постоянному току или напряжению.
Какое напряжение измеряет мультиметр, амперметр или вольтметр?
В подавляющем большинстве случаев если на измерительном приборе вы выбираете режим измерения переменного тока или напряжения (U~, I~), вы измерите именно действующие значения. Однако есть и специфичные приборы, измеряющие амплитудные значения параметров в электрической сети, а также на электронных осциллографах могут выводится и действующие, и амплитудные величины измеряемых сигналов. Измерение амплитудных значений может обозначаться как Im.
При этом далеко не все приборы могут измерять переменный ток по форме отличный от синусоидального — пилообразный, прямоугольный и так далее. Вы могли видеть, что на хороших мультиметрах написано загадочное «TRUE RMS», что расшифровывается как: «True Root Mean Sqare», а переводится как — истинное среднеквадратичное значение. Такие измерительные приборы показывают действующие значения напряжений и токов любых форм (не только синусоидальных).
В завершение этой статьи, предлагаю вам закрепить знания и ознакомиться с прекрасным советским плакатом, на эту тему
Демьян Бондарь
Эксперт по предмету «Электроника, электротехника, радиотехника»
преподавательский стаж — 5 лет
Задать вопрос автору статьи
Действующее значение переменного тока. Характеристики переменного тока
Определение 1
Действующее или эффективное значение переменного тока – это значение переменного электрического тока равное величине постоянного тока, который проделает такую же работу, сопровождающуюся тепловым эффектом или электродинамическим эффектом, что и рассматриваемый переменный ток за время равное одному периоду переменного тока.
К основным характеристикам переменного тока относятся:
- Амплитуда, являющаяся максимальным значением периодически изменяющегося тока.
- Период, который является временем, в течении которого электрическим током совершается полный цикл изменений, после чего они повторяются в той же последовательности.
- Частота, которая обратна периоду, то есть показывает количество завершенных циклов изменений за единицу времени.
- Мгновенное значение, являющееся значением переменного тока в конкретный момент времени.
- Угловая скорость или угловая частота, которая характеризуется углом поворота рамки за единицу времени.
В современной литературе обычно используется математическое определение действующего значения переменного тока, которое звучит следующим образом: действующее значение переменного тока – среднеквадратичное значение переменного тока. Таким образом эта величина рассчитывается по следующей формуле:
Рисунок 1. Формула. Автор24 — интернет-биржа студенческих работ
Существует пять типичных случаев переменного электрического тока:
- Синусоида.
- Прямоугольная форма.
- Треугольная форма.
- Трапециевидная форма.
- Дугообразная форма.
Для синусоидального тока формула для расчета действующего значения выглядит следующим образом:
Рисунок 2. Формула. Автор24 — интернет-биржа студенческих работ
«Действующее и среднее значение переменного тока» 👇
где Im – амплитудное значение тока.
Для электрического тока, который имеет форму однополярного прямоугольного импульса используется следующая формула для расчета действующего значения.
Рисунок 3. Формула. Автор24 — интернет-биржа студенческих работ
где D – коэффициент заполнения.
Если коэффициент заполнения равен 0,5, то есть ток имеет форму однополярного меандра, то формула выглядит так:
$I = Im* √0.5 = 0.707*Im$
В том случае, когда у тока форма двуxполярного меандра, то:
$I = Im$
Для токов пилообразной и треугольной формы расчет действующего значения осуществляется по формуле:
Рисунок 4. Формула. Автор24 — интернет-биржа студенческих работ
Посредством разбивки периода на отрезки действия максимального значения, положительного фронта и отрицательного фронта, получается формула для расчета действующего значения переменного тока трапециевидной формы:
Рисунок 5. Формула. Автор24 — интернет-биржа студенческих работ
где: t1, t2, t3 – соответственно продолжительность положительного фронта, действия максимального значения и отрицательного фронта; Т – длительность полного периода.
Для тока, который имеет форму дуги или половины окружности, формула для расчета действующего значения имеет следующий вид:
Рисунок 6. Формула. Автор24 — интернет-биржа студенческих работ
Для измерения тока в цепях переменного тока большинство электроизмерительных приборов, таких как вольтметры и амперметры, градуируются таким образом, чтобы показания соответствовали эффективному значению переменного тока или напряжения.
Среднее значение переменного тока. Коэффициенты амплитуды и формы
Определение 2
Среднее значение переменного тока – это значение переменного тока равное величине постоянного тока, при котором через поперечное сечение проводника проходит такое же количество электричества, что и в случае переменного тока.
Среднее значение переменного тока эквивалентно постоянному по величине электричества, которое проходит через поперечное сечение проводника за определенный промежуток времени. если электрический ток изменяется согласно синусоидальному закону, то за пол через поперечное сечение проводника проходит определенное количество электричества и в определенном направлении. Таким образом его среднее значение за один период равно нулю:
$Iс=0$
Поэтому в данном случае среднее значение переменного синусоидального тока определяется за половину периода, и формула выглядит следующим образом:
$Ic = Q / (T/2)$
где: Q – количество электричества; Т – длительность периода.
Рассмотрим рисунок, который представлен ниже.
Рисунок 7. Переменный ток. Автор24 — интернет-биржа студенческих работ
В общем виде значение переменного тока рассчитывается по формуле:
$i = dQ / dt$
Отсюда получается, что
$Q = idt$
Таким образом среднее значение синусоидального переменного тока за половину период и с начальной фазой равной нулю на представленном выше рисунке рассчитывается по формуле:
Рисунок 8. Формула. Автор24 — интернет-биржа студенческих работ
Где: w – угловая скорость; $Т = 1/f; w = 2*п*f; п = 3,14; f $- частота электрического тока.
Графически среднее значение синусоидального переменного тока является высотой прямоугольника, основание которого равняется половине периода, а площадь ограниченна кривой электрического тока и осью абсцисс за половину периода.
Средним значением переменной величины является постоянная составляющая данной величины. Поэтому, чтобы рассчитать среднее значение переменного напряжения и электродвижущей силы можно использовать формулы:
$Uc = (2/п )* Um$
$Ec = (2/п)*Em$
где: Um – амплитудное значение напряжения; Еm – амплитудное значение электродвижущей силы.
Отклонения кривых электрического тока от синусоиды характеризуется коэффициентами формы и амплитуды. Отношением действующего значения переменной величины к ее среднему значению определяется коэффициент формы, то есть:
$Кф = I/Ic$
Коэффициент формы должен учитываться в процессе проектирования и изучения выпрямительных устройств и электрических машин. Для синусоиды коэффициент формы рассчитывается следующим образом:
$Кф = (Im*п) / (√2*2*Im) = 1.11$
Чтобы рассчитать коэффициент амплитуды, используется формула:
$Ка = Im / I$
где I – действующее значение переменного тока.
Для синусоидальной величины формула имеет следующий вид:
$Ка = (I*√2) / I = /2 = 1,41$
Чем больше значение коэффициентов амплитуды и формы отличаются от иx значения для синусоидальных величин, тем больше кривая электрического тока отличается от синусоиды.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме