Как найти действующую силу тока по амплитудному

Переменный электрический ток

Переменный ток (AC – Alternating Current) – электрический ток, меняющий свою величину и направление с течением времени.

Часто в технической литературе переменным называют ток, который меняет только величину, но не меняет направление, например, пульсирующий ток.
Необходимо помнить при расчётах, что переменный ток в этом случае является лишь составляющей частью общего тока.
Такой вариант можно представить как переменный ток AC с постоянной составляющей DC.
Либо как постоянный ток с переменной составляющей, в зависимости от того, какая составляющая наиболее важна в контексте.

DC – Direct Current – постоянный ток, не меняющий своей величины и направления.

В реальности постоянный ток не может сохранять свою величину постоянной, поэтому существует условно в тех случаях, где можно пренебречь изменениями его постоянной величины, либо в качестве составляющей (DC) для периодически меняющегося электрического тока любой формы. Тогда величина DC будет равна среднему значению тока за период, и будет являться нулевой линией для переменной составляющей AC.

При синусоидальной форме тока, например в электросети, постоянная составляющая DC равна нулю.

Постоянный ток с переменной составляющей в виде пульсаций показан синей линией на верхнем графике рисунка.
Запись AC+DC в данном случае не является математической суммой, а лишь указывает на две составляющие тока. Суммируются мощности.

Величина тока будет равна квадратному корню из суммы квадратов двух величин – значения постоянной составляющей DC и среднеквадратичного значения переменной составляющей AC.

Термины AC и DC применимы как для тока, так и для напряжения.

Параметры переменного тока и напряжения

Величина переменного тока, как и напряжения, постоянно меняется во времени. Количественными показателями для измерений и расчётов применяются их следующие параметры:

Период T – время, в течении которого происходит один полный цикл изменения тока в оба направления относительно нуля или среднего значения.

Частота  f – величина, обратная периоду, равная количеству периодов за одну секунду.

Один период в секунду это один герц (1 Hz). Частота f = 1/T

Циклическая частота  ω – угловая частота, равная количеству периодов за 2π секунд.

ω = 2πf = 2π/T

Обычно используется при расчётах тока и напряжения синусоидальной формы. Тогда в пределах периода можно не рассматривать частоту и время, а исчисления производить в радианах или градусах. T = 2π = 360°

Начальная фаза  ψ – величина угла от нуля (ωt = 0) до начала периода.
Измеряется в радианах или градусах. Показана на рисунке для синего графика синусоидального тока.

Начальная фаза может быть положительной или отрицательной величиной, соответственно справа или слева от нуля на графике.

Мгновенное значение – величина напряжения или тока измеренная относительно нуля в любой выбранный момент времени t.

i = i(t);   u = u(t)

Последовательность всех мгновенных значений в любом интервале времени можно рассмотреть как функцию изменения тока или напряжения во времени.
Например, синусоидальный ток или напряжение можно выразить функцией:

i = I_ampsin(ωt);   u = U_ampsin(ωt)

С учётом начальной фазы:

i = I_ampsin(ωt + ψ);   u = U_ampsin(ωt + ψ)

Здесь I_amp и U_amp – амплитудные значения тока и напряжения.

Амплитудное значение – максимальное по модулю мгновенное значение за период.

I_amp = max|i(t)|;   U_amp = max|u(t)|

Может быть положительным и отрицательным в зависимости от положения относительно нуля.

Часто вместо амплитудного значения применяется термин амплитуда тока (напряжения) – максимальное отклонение от нулевого значения.

Среднее значение (avg) – определяется как среднеарифметическое всех мгновенных значений за период T.

Среднее значение является постоянной составляющей DC напряжения и тока.
Для синусоидального тока (напряжения) среднее значение равно нулю.

Средневыпрямленное значение – среднеарифметическое модулей всех мгновенных значений за период.

Для синусоидального тока или напряжения средневыпрямленное значение равно среднеарифметическому за положительный полупериод.

Среднеквадратичное значение (rms) – определяется как квадратный корень из среднеарифметического квадратов всех
мгновенных значений за период.

Для синусоидального тока и напряжения амплитудой I_amp (U_amp)
среднеквадратичное значение определится из расчёта:

---

Коэффициент амплитуды и коэффициент формы

---

Действующие значения тока и напряжения

Переменный синусоидальный ток в течение периода имеет различные мгновенные значения. Естественно поставить вопрос, какое же значение тока будет измеряться амперметром, включенным в цепь?

При расчетах цепей переменного тока, а также при электрических измерениях неудобно пользоваться мгновенными или амплитудными значениями токов и напряжений, а их средние значения за период равны нулю. Кроме того, об электрическом эффекте периодически изменяющегося тока (о количестве выделенной теплоты, о совершенной работе и т. д.) нельзя судить по амплитуде этого тока.

Наиболее удобным оказалось введение понятий так называемых действующих значений тока и напряжения . В основу этих понятий положено тепловое (или механическое) действие тока, не зависящее от его направления.

Действующее значение переменного тока — это значение постоянного тока, при котором за период переменного тока в проводнике выделяется столько же теплоты, сколько и при переменном токе.

Для оценки действия, производимого переменным током, мы сравним его действия с тепловым эффектом постоянного тока.

Мощность Р постоянного тока I , проходящего через сопротивление r , будет Р = Р 2 r .

Мощность переменного тока выразится как средний эффект мгновенной мощности I 2 r за целый период или среднее значение от ( Im х sin ω t ) 2 х r за то же время.

Пусть среднее значение t2 за период будет М. Приравнивая мощность постоянного тока и мощность при переменном токе, имеем: I 2 r = Mr, откуда I = √ M ,

Величина I называется действующим значением переменного тока.

Среднее значение i2 при переменном токе определим следующим образом.

Построим синусоидальную кривую изменения тока. Возведя в квадрат каждое мгновенное значение тока, получим кривую зависимости Р от времени.

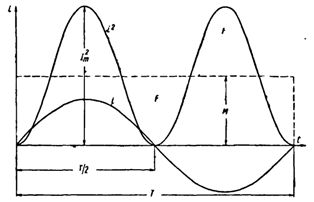
Обе половины этой кривой лежат выше горизонтальной оси, так как отрицательные значения тока (- i ) во второй половине периода, будучи возведены в квадрат, дают положительные величины.

Построим прямоугольник с основанием Т и площадью, равной площади, ограниченной кривой i 2 и горизонтальной осью. Высота прямоугольника М будет соответствовать среднему значению Р за период. Это значение за период, вычисленное при помощи высшей математики, будет равно 1/2I 2 m . Следовательно, М = 1/2I 2 m

Так как действующее значение I переменного тока равно I = √ M , то окончательно I = Im / √ 2

Аналогично зависимость между действующим и амплитудным значениями для напряжения U и Е имеет вид:

Действующие значения переменных величин обозначаются прописными буквами без индексов ( I , U, Е).

На основании сказанного выше можно сказать, что действующее значение переменного тока равно такому постоянному току, который, проходя через то же сопротивление, что и переменный ток, за то же время выделяет такое же количество энергии.

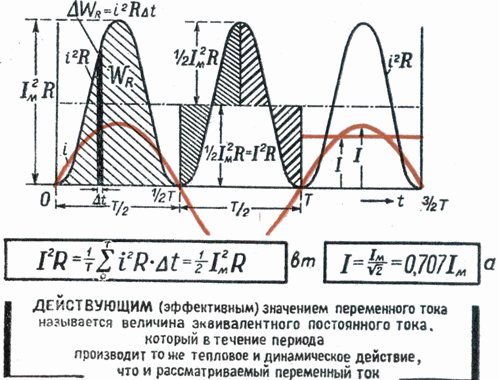
Электроизмерительные приборы (амперметры, вольтметры), включенные в цепь переменного тока, показывают действующие значения тока или напряжения.

При построении векторных диаграмм удобнее откладывать не амплитудные, а действующие значения векторов. Для этого длины векторов уменьшают в √ 2 раз. От этого расположение векторов на диаграмме не изменяется.

Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!

Подписывайтесь на наш канал в Telegram!

Просто пройдите по ссылке и подключитесь к каналу.

Не пропустите обновления, подпишитесь на наши соцсети:

Источник

Параметры переменного напряжения

Как вы помните из предыдущей статьи, переменное напряжение — это напряжение, которое меняется со временем. Оно может меняться с каким-то периодом, а может быть хаотичным. Но не стоит также забывать, что и переменное напряжение обладает своими особенными параметрами.

Среднее значение напряжения

Среднее значение переменного напряжения Uср — это, грубо говоря, площадь под осциллограммой относительно нуля за какой-то промежуток времени. Чтобы это понять, давайте рассмотрим вот такую осциллограмму.

Например,чему равняется среднее значение напряжения за эти два полупериода? В данном случае ноль вольт. Почему так? Площади S1 и S2 равны. Но все дело в том, что площадь S2 берется со знаком «минус». А так как площади равны, то в сумме они дают ноль: S1+(-S2)=S1-S2=0. Для бесконечного по времени синусоидального сигнала среднее значение напряжения также равняется нулю.

То же самое касается и других сигналов, например, двухполярного меандра. Меандр — это прямоугольный сигнал, у которого длительности паузы и импульса равны. В этом случае его среднее напряжение также будет равняться нулю.

Средневыпрямленное значение напряжения

Чаще всего используют средневыпрямленное значение напряжения Uср. выпр. То есть площадь сигнала, которая «пробивает пол» берут не с отрицательным знаком, а с положительным.

средневыпрямленное значение напряжения будет уже равняться не нулю, а S1+S2=2S1=2S2. Здесь мы суммируем площади, независимо от того, с каким они знаком.

На практике средневыпрямленное значение напряжения получить легко, использовав диодный мост. После выпрямления синусоидального сигнала, график будет выглядеть вот так:

Для того, чтобы примерно узнать, чему равняется средневыпрямленное напряжение, достаточно узнать максимальную амплитуду синусоидального сигнала Umax и сосчитать ее по формуле:

Среднеквадратичное значение напряжения

Чаще всего используют среднеквадратичное значение напряжения или его еще по-другому называют действующим. В литературе обозначается просто буквой U. Чтобы его вычислить, тут уже простым графиком не отделаешься. Среднеквадратичное значение — это значение постоянного напряжения, который, проходя через нагрузку (скажем, лампу накаливания), выделяет за тот же промежуток времени такое же количество мощности, какое выделит в этой нагрузке переменное напряжение. В английском языке среднеквадратичное напряжение обозначается так: RMS (rms) — root mean square.

Связь между амплитудным и среднеквадратическим значением устанавливается через коэффициент амплитуды K_a:

Вот некоторые значения коэффициента амплитуды K_a для некоторых сигналов переменного напряжения:

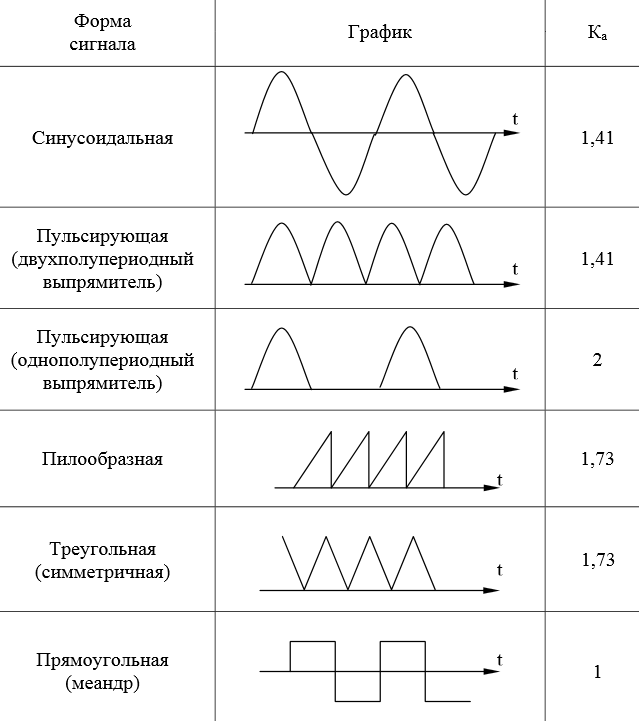
Более точные значения 1,41 и 1,73 — это √2 и √3 соответственно.

Как измерить среднеквадратичное значение напряжения

Для правильного замера среднеквадратического значения напряжения у нас должен быть мультиметр с логотипом T-RMS. RMS — как вы уже знаете — это среднеквадратическое значение. А что за буква «T» впереди? Думаю, вы помните, как раньше была мода на одно словечко: «тру». «Она вся такая тру…», «Ты тру или не тру?» и тд. Тру (true) — с англ. правильный, верный.

Так вот, T-RMS расшифровывается как True RMS — «правильное среднеквадратическое значение». Мои токоизмерительные клещи могут замерять этот параметр без труда, так как на них есть логотип «T-RMS».

мультиметр с True RMS

Проведем небольшой опыт. Давайте соберем вот такую схемку:

Выставим на моем китайском генераторе частоты треугольный сигнал с частотой, ну скажем, 100 Герц

генератор частоты

А вот осциллограмма этого сигнала. Внизу, в красной рамке, можно посмотреть его параметры

треугольный сигнал

И теперь вопрос: чему будет равно среднеквадратическое напряжение этого сигнала?

Так как один квадратик у нас равняется 1 Вольт (мы это видим внизу осциллограммы в красной рамке), то получается, что амплитуда Umax этого треугольного сигнала равняется 4 Вольта. Для того, чтобы рассчитать среднеквадратическое напряжение, мы воспользуемся формулой:

Итак, смотрим нашу табличку и находим интересующий нас сигнал:

Для нас не важно, пробивает ли сигнал «пол» или нет, главное, чтобы сохранялась форма сигнала. Видим, что наш коэффициент амплитуды K_a= 1,73.

Подставляем его в формулу и вычисляем среднеквадратическое значение нашего треугольного сигнала

Проверяем нашим прибором, так ли оно на самом деле?

Супер! И в правду Тrue RMS.

Замеряем это же самое напряжение с помощью моего китайского мультиметра

Он меня обманул :-(. Он умеет измерять только среднеквадратическое значение синусоидального сигнала, а у нас сигнал треугольный.

Самый интересный сигнал в плане расчетов — это двуполярный меандр, ну тот есть тот, который «пробивает пол».

Его амплитудное Umax, средневыпрямленное Uср.выпр. и среднеквадратичное напряжение U равняется одному и тому же значению. В данном случае это 1 Вольт.

Вот вам небольшая картинка, чтобы не путаться

среднее, среднеквадратичное и пиковое значения напряжения

• Сред. — средневыпрямленное значение сигнала. Это и есть площадь под кривой
• СКЗ — среднеквадратичное напряжение. Как мы видим, для синусоидальных сигналов, оно будет больше, чем средневыпрямленное.
• Пик. — амплитудное значение сигнала
• Пик-пик. — размах или двойная амплитаду. Или иначе, амплитуда от пика до пика.

Так что же все-таки показывает мультиметр при измерении переменного напряжения? Показывает он НЕ амплитудное, НЕ среднее и НЕ среднее выпрямленное напряжение, а среднее квадратическое, то есть действующее напряжение! Об этом всегда помним.

Источник

Действующее напряжение и амплитудное напряжение — что это, и в чем отличие

Все знают, что действующее напряжение в розетке 220 Вольт (230 по новым нормам, но для данной темы это не имеет особого значения). Это легко проверить при помощи мультиметра, который измерит разность потенциалов между фазой и рабочим нулевым проводником. То есть, при идеальных условиях, потенциал на нулевом проводе 0, а на фазном 220 Вольт. На самом деле все немного не так — переменный ток имеет синусоидальную форму с потенциалом на пиках 310 и -310 Вольт (амплитудное напряжение). Для того чтобы это увидеть, необходимо воспользоваться осциллографом.

Синусоида действующего и амплитудного напряжения

Понятно, что данный материал в большей степени ориентирован на простую аудиторию, у которой не то, что осциллографа нет, даже мультиметр наверняка не у каждого есть. Поэтому все примеры будут браться из среды программы Electronics Workbench, доступной каждому.

И первое, что нам нужно посмотреть — это синусоиду напряжения фазы из розетки. Для этого в программе отрисуем трехфазную сеть и подключим осциллограф к одной из фаз:

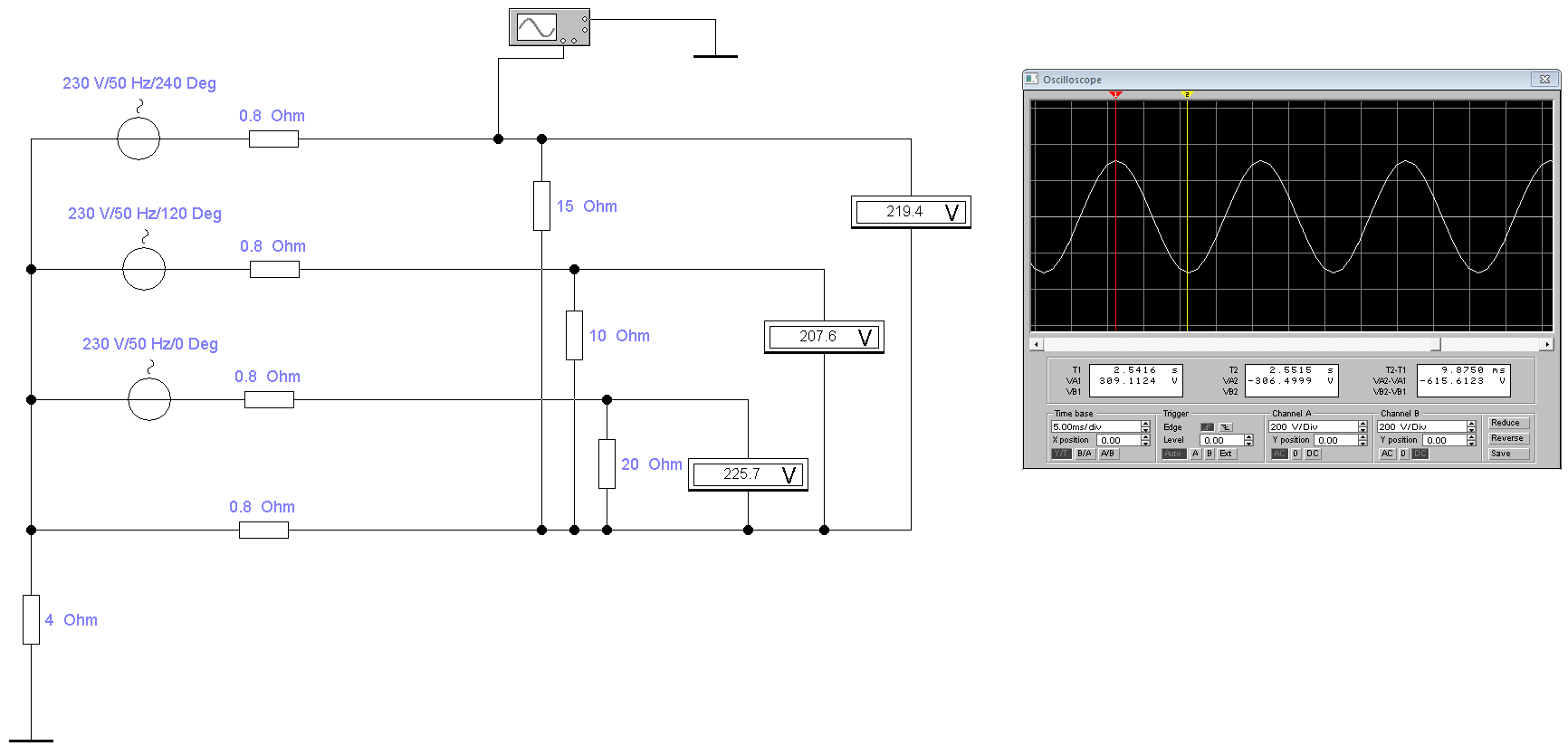
Как видно при показании вольтметра 219,4 Вольт между одной из фаз и PEN проводником, осциллограф показал синусоиду с амплитудой 309,1 Вольт. Это значение напряжения называется максимальным (амплитудным). А 219,4 Вольт, которые показывает вольтметр — это действующее напряжение. Его также называют среднеквадратичным или эффективным. И прежде чем перейти к рассмотрению данной особенности, кратко, простыми словами пройдемся по отрисованной схеме трехфазной сети и разберемся в природе синусоиды.

Начнем со схемы:

• Слева на право — три источника переменного напряжения с фазовыми углами 0, 120, 240 градусов и соединенными звездой.
• Резистор 4 Ом — это заземление нейтрали трансформатора.
• Резисторы по 0,8 Ом — условное сопротивление проводов, зависящее от сечения провода и длины линии.
• Резисторы 15, 10 и 20 Ом — нагрузка потребителей по трем фазам.
• К одной из фаз подключен осциллограф, показывающий амплитуду 309,1 Вольт.

Теперь рассмотрим синусоиду. Переменное напряжение в отличие от постоянного, график которого прямая на осциллографе, непрерывно изменяется как по величине, так и по направлению. Причем изменения эти происходят периодически, то есть точно повторяются через равные промежутки времени.

Переменное напряжение генерируется на электростанциях и посредством повышающих и понижающих распределительных трансформаторов попадает к конечному потребителю. При этом трансформация по пути никак не сказывается на синусоиде напряжения.

Видео — действующее напряжение и амплитудное

С полным и наглядным изложением рассматриваемого вопроса вы можете ознакомиться в следующем видео:

Работа генератора трехфазного переменного тока

Рассмотрим упрощенно работу генератора трехфазного переменного тока. Обмотки статора (фазы А, В и С) генератора расположены под углом 120 градусов относительно друг друга. Ротор с магнитом вращаясь индуцирует в обмотках статора периодически изменяющиеся ЭДС. Выглядит это следующим образом:

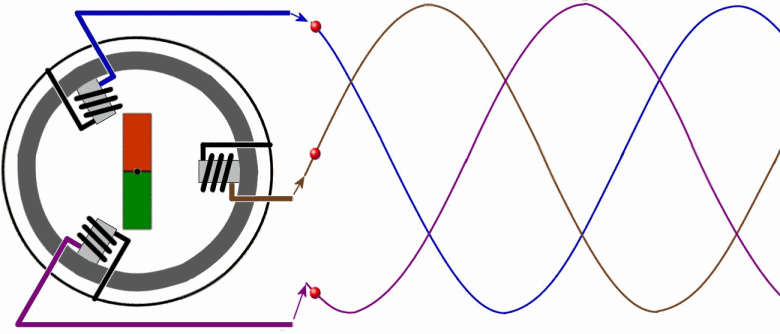
Такое вращение происходит с частотой 50 оборотов в секунду, то есть с частотой 50 Герц. Это значит, что электроны движутся в течение 1 секунды 50 раз в одном направлении (положительный полупериод синусоиды), и 50 — в обратном (отрицательный полупериод), 100 раз проходя чрез нулевое значение. Получается, что к примеру обычная лама накаливания, включенная в сеть с такой частотой, будет затухать и вспыхивать примерно 100 раз за секунду, однако мы этого не замечаем в силу особенностей своего зрения.

Определение действующего напряжения

Теперь непосредственно о том, почему произошел переход от максимального, амплитудного значения напряжения 310 Вольт к действующему 220 Вольт. Ответ можно найти в самом определении.

Действующее (эффективное или среднеквадратичное) значение напряжения — это такое напряжение постоянного тока, которое на такой же резистивной нагрузке выделит такую же мощность, как измеряемое переменное напряжение. Соответственно, действующее значение силы тока — такое значение силы постоянного тока, при прохождении которого через резистивную нагрузку выделится такая же мощность, что и при прохождении измеряемого тока.

Можно сформулировать и немного иначе. Действующее значение переменного тока равно величине такого постоянного тока, который за время, равное одному периоду переменного тока, произведет такую же работу (тепловой или электродинамический эффект), что и рассматриваемый переменный ток.

Общая формула расчета действующего напряжения произвольной формы следующая:

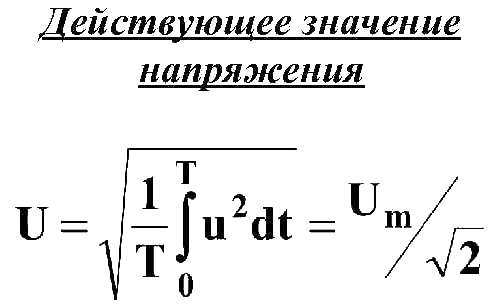
Объяснение действующего напряжения

Определение и формула — это хорошо. Но лучше все понять на наглядном примере. Объяснить все можно через мощность. Причем есть сложный для восприятия способ и более простой, который мы и рассмотрим далее.

Нам нужно взять один период синусоиды переменного напряжения, на этом промежутке построить синусоиду переменного тока и проанализировать мощность. Начнем с периода синусоиды переменного напряжения. Здесь же построим синусоиду переменного тока с учетом условной резистивной нагрузки (например, лампочки). По закону Ома сила тока равна напряжению, деленному на сопротивление.

Точные значения в конкретный момент при данном объяснении не принципиальны, поэтому все построения приблизительные. Естественно нужно понимать, что деля напряжение на сопротивление, мы получим синусоиду переменного тока с амплитудой в R раз меньшей, чем у напряжения. R – это значение сопротивления.

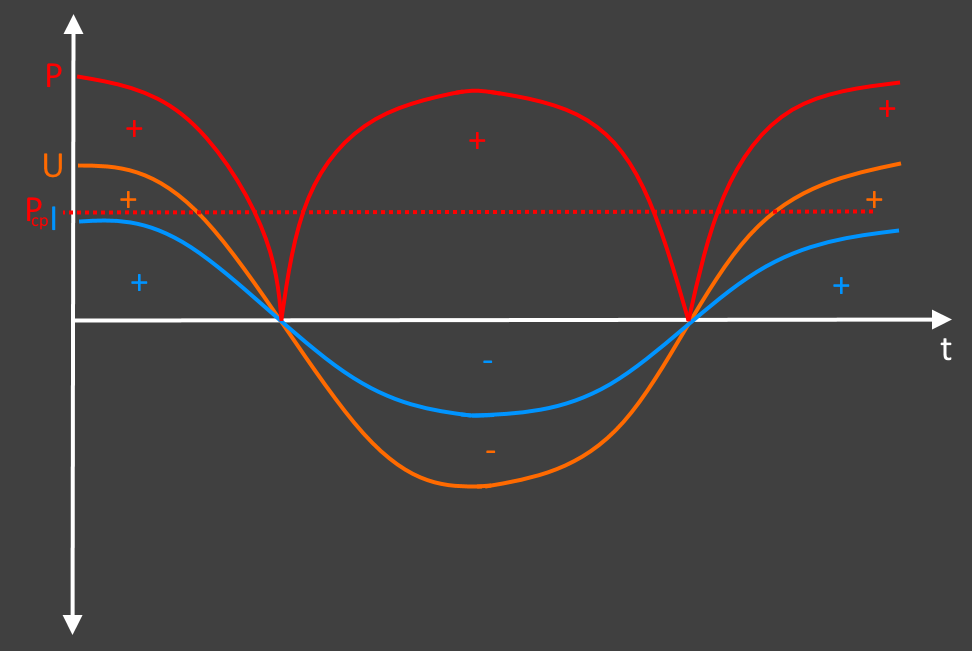
Теперь по двум синусоидам строим график мощности по формуле мощность равна силе тока умноженной на напряжение (P = I × U). Так как напряжение и ток имеют общие нулевые точки, то график мощности не будет заходить в отрицательную область. То есть сила тока со знаком «+» и напряжение со знаком «+» дадут мощность со знаком «+», так же как и сила тока со знаком «-» и напряжение со знаком «-» дадут мощность со знаком «+».

Анализируя полученный график можно отметить, что мощность пульсирующая. Она поднимается до максимального значения и падает до нуля, потом опять поднимается и снова падает. Как на эти колебания мощности реагируют электроприборы? Никак. Поскольку частота переменного тока 50 Герц, то эти колебания происходят очень быстро. Электроприборы откликаются не на максимальные и минимальные значения мощности, а на усредненные. То есть берется максимальное значение мощности и делится на два. Это значение называется действующим и находится по следующей формуле:

Pд = (Imax × Umax) / 2, где Pд — мощность действующая, Imax — сила тока максимальная, Umax — напряжение максимальное.

Двойку можно представить в виде корень из двух умножить на корень из двух. Получаем Действующее значение мощности = сила тока максимальная деленная на корень из двух умноженная на напряжение максимальное деленное на корень из двух (Pд = (Imax/√2) × (Umax/√2)).

Соответственно сила тока максимальная деленная на корень из двух — это действующее значение силы переменного тока, а напряжение максимальное деленное на корень из двух – это действующее значение переменного напряжения.

И действительно, если мы возьмем максимальное напряжение из предыдущего примера 309,1 Вольт и разделим на корень из двух, то получим действующее напряжение (то, которое показывает вольтметр) 219,4 Вольт.

Источник

Вынужденные
Электромагнитные Колебания

Вынужденными
электромагнитными колебаниями называют
периодические изменения силы тока и
напряжения в электрической цепи,
происходящие под действием переменной
ЭДС от внешнего источника. Внешним
источником ЭДС в электрических цепях
являются генераторы переменного тока,
работающие на электростанциях.

Принцип
действия генератора переменного тока
легко показать при рассмотрении
вращающейся рамки провода в магнитном
поле.

В
однородное магнитное поле с индукцией
В помещаем прямоугольную рамку,
образованную проводниками (abсd).

Пусть
плоскость рамки перпендикулярна индукции
магнитного поля В и ее площадь равна S.

Магнитный
поток в момент времени t₀ =
0 будет равен Ф = В*8.

При
равномерном вращении рамки вокруг оси
OO₁ с
угловой скоростью w магнитный поток,
пронизывающий рамку, будет изменяться
с течением времени по закону:

Изменение
магнитного потока возбуждает в рамке
ЭДС индукцию, равную

где
Е₀=
ВSw – амплитуда ЭДС.

Если
с помощью контактных колец и скользящих
по ним щеток соединить концы рамки с
электрической цепью, то под действием
ЭДС индукции, изменяющейся со временем
по гармоническому закону, в электрической
цепи возникнут вынужденные гармонические
колебания силы тока – переменный
ток.

На
практике синусоидальная ЭДС возбуждается
не путем вращения рамки в магнитном
поле, а путем вращения магнита или
электромагнита (ротора) внутри статора
– неподвижных обмоток, навитых на
сердечники из магнитомягкого материала.
В этих обмотках находится переменная
ЭДС, что позволяет избежать снятия
напряжения с помощью контактных колец. 

Переменный
Ток

Рассмотрим
процессы, происходящие в проводнике,
включенном в цепь переменного тока.

Если
индуктивность проводника настолько
мала, что при включении его в цепь
переменного тока индукционными полями
можно пренебречь по сравнению с внешним
электрическим полем, то движение
электрических зарядов в проводнике
определяется действием только внешнего
электрического поля, напряженность
которого пропорциональна напряжению
на концах проводника.

При
изменении напряжения по гармоническому
закону U = U_m cos
wt напряженность электрического поля в
проводнике изменяется по такому же
закону.

Под
действием переменного электрического
поля в проводнике возникает переменный
электрический ток, частота и фаза
колебаний которого совпадает с частотой
и фазой колебаний напряжения:

где
i – мгновенное значение силы тока, I_m–
амплитудное значение силы тока.

Колебания
силы тока в цепи являются вынужденными
электрическими колебаниями, возникающими
под действием приложенного переменного
напряжения.

Амплитуда
силы тока равна: 

При
совпадении фаз колебаний силы тока и
напряжения мгновенная мощность
переменного тока равна:

Среднее
значение квадрата косинуса за период
равно 0,5. В результате средняя мощность
за период

Для
того чтобы формула для расчета мощности
переменного тока совпадала по форме с
аналогичной формулой для постоянного
тока (Р = PR), вводится понятие действующих
значений силы тока и напряжения. Из
равенства мощностей получим

Действующим
значением силы тока называют величину,
в корень из 2 раз меньшую ее амплитудного
значения:

Действующее
значение силы тока равно силе такого
постоянного тока, при котором средняя
мощность, выделяющаяся в проводнике в
цепи переменного тока, равна мощности,
выделяющейся в том же проводнике в цепи
постоянного тока.

Действующее
значение переменного напряжения в
корень из 2 раз меньше его амплитудного
значения:

Средняя
мощность переменного тока при совпадении
фаз колебаний силы тока и напряжения
равна произведению действующих значений
силы тока и напряжения:

Сопротивление
элемента электрической цепи, в которой
происходит превращение электрической
энергии во внутреннюю энергию,
называют активным
сопротивлением.
Активное сопротивление участка цепи
можно определить как частное от деления
средней мощности на квадрат действующего
значения силы тока:

Активным
сопротивлением R называется физическая
величина, равная отношению мощности к
квадрату силы тока ,
что получается из выражения для
мощности .
При небольших частотах практически не
зависит от частоты и совпадает с
электрическим сопротивлением проводника.

Пусть
в цепь переменного тока включена катушка.
Тогда при изменении силы тока по закону в
катушке возникает ЭДС самоиндукции .
Т.к. электрическое сопротивление катушки
равно нулю, то ЭДС равна минус напряжению
на концах катушки, созданному внешним
генератором (??? Каким еще генератором???) .
Следовательно, изменение силы тока
вызывает изменение напряжения, но со
сдвигом по фазе .
Произведение является
амплитудой колебаний напряжение, т.е. .
Отношение амплитуды колебаний напряжения
на катушке к амплитуде колебаний тока
называется индуктивным сопротивлением .

Пусть
в цепи находится конденсатор. При его
включение он четверть периода заряжается,
потом столько же разряжается, потом то
же самое, но со сменой полярности. При
изменении напряжения на конденсаторе
по гармоническому закону заряд
на его обкладках равен .
Ток в цепи возникает при изменении
заряда: ,
аналогично случаю с катушкой амплитуда
колебаний силы тока равна .
Величина, равная отношению амплитуды
к силе тока, называется емкостным
сопротивлением .

АКТИВНОЕ
СОПРОТИВЛЕНИЕ.  ДЕЙСТВУЮЩИЕ ЗНАЧЕНИЯ
СИЛЫ ТОКА И НАПРЯЖЕНИЯ

Перейдем
к более детальному рассмотрению
процессов, которые происходят в цепи,
подключенной к источнику переменного
напряжения.

Сила
тока в цени с резистором. Пусть
цепь состоит из соединительных проводов
и нагрузки с малой индуктивностью и
большим сопротивлением R (рис. 4.10). Эту
величину, которую мы до сих пор называли
электрическим сопротивлением или просто
сопротивлением, теперь будем называть
активным сопротивлением.
 

Сопротивление R
называется активным, потому что при
наличии нагрузки, обладающей этим
сопротивлением, цепь поглощает энергию,
поступающую от  генератора. Эта
энергия превращается во внутреннюю
энергию проводников — они  нагреваются.  
Будем  считать, что напряжение на
зажимах цепи меняется по гармоническому
закону:

u = U_m cos t.

Как
и в случае постоянного тока, мгновенное
значение силы тока прямо пропорционально
мгновенному значению напряжения. Поэтому
для нахождения мгновенного значения
силы тока можно применить закон
Ома:

 
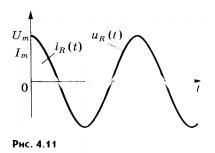
В
проводнике с активным сопротивлением
колебания силы тока совпадают по фазе
с колебаниями напряже ния (рис. 4.11), а
амплитуда силы тока определяется
равенством

Мощность
в цепи с резистором. В
цепи переменного тока промышленной
частоты (v = 50 Гц) сила тока и напряжение
изменяются сравнительно быстро. Поэтому
при прохождении тока по проводнику,
например по нити электрической лампочки,
количество выделенной энергии также
будет быстро меняться со временем. Но
этих быстрых изменений мы не замечаем.

Как
правило, нам нужно бывает знать среднюю
мощ ностъ тока на участке цепи за большой
промежуток времени, включающий много
периодов. Для этого достаточно найчи
среднюю мощность за один период. Под
средней за период, мощностью переменного
тока понимают отношение суммарной энергии,
поступающей в цепь за период, к периоду.

Мощность
в цепи постоянного тока на участке с
сопротивлением R определяется формулой

P
= I²R.      
(4.18)

На протяжении очень малого
интервала времени переменный ток можно
считать практически постоянным. 

Поэтому
мгновенная моoность в цепи переменного
тока на участке, имеющем активное
сопротивление R, определяется формулой

P
= i²R.                                        
     (4.19)

Найдем среднее
значение мощности за период. Для этого
сначала преобразуем формулу (4.19),
подставляя в нее выражение (4.16) для силы
тока и используя известное из математики
соотношение 

График
зависимости мгновенной мощности от
времени изображен на рисунке 4.12, а.
Согласно графику (рис. 4.12, б.), на протяжении
одной восьмой периода, когда ,
мощность в любой момент времени больше,
чем  . 
Зато на протяжении следующей восьмой
части периода, когда cos 2t
< 0, мощность в любой момент времени
меньше    чем  .
Среднее за период значение cos 2t
равно нулю, а значит равно нулю второе
слагаемое в уравнении (4.20).

Средняя
мощность  равна,
таким образом, первому члену в формуле
(4.20):

Действующие
значения силы тока и напряжения. Из
формулы (4.21) видно, что величина  
есть среднее за период значение квадрата
силы тока:
 

 
Величина,
равная квадратному корню из среднего
значения квадрата силы тока, называется
действующим значением силы неременного
тока. Действующее зртачепие силы
неременного тока обозначается через
I:

Действующее
значение силы переменного тока равно
силе такого постоянного тока, при котором
в проводнике выделяется то же
количество теплоты,
что и при переменном токе за то же время.

Действующее
значение переменного напряжения
определяется аналогично действующему
значению силы тока:

Заменяя
в формуле (4.17) амплитудные значения силы
тока и напряжения на их действующие
значения, получаем
Это
закон Ома для участка цепи переменного
тока с резистором.

Как
и при механических колебаниях, в случае
электрических колебаний обычно нас не
интересуют значения силы тока, напряжения
и других величин в каждый момент времени.
Важны общие характеристики колебаний,
такие, как амплитуда, период, частота,
действующие значения силы тока и
напряжения, средняя мощность. Именно
действующие значения силы тока и
напряжения регистрируют амперметры
ивольтметры переменного
тока.

Кроме
того, действующие значения удобнее
мгновенных значений еще и потому, что
именно они непосредственно определяют
среднее значение мощности Р переменного
тока:

P
= I²R
= UI.

Колебания
силы тока в цепи с резистором совпадают
по фазе с колебаниями напряжения, а
мощность определяется действующими
значениями силы тока и напряжения.

Переменный
ток оценивается его действием,
эквивалентной действия постоянного
тока.

Активным
сопротивлением называют
такое сопротивление проводника, в
котором электрическая энергия необратимо
превращается во внутреннюю. Пусть
напряжение в цепи переменного тока
изменяется по гармоничным законом. Под
действием переменного электрического
поля в проводнике возникает переменный
ток, частота и фаза колебаний которого
совпадает с частотой и фазой колебания
напряжения. Амплитудное значение силы
тока равна отношению амплитудного
значения напряжения к сопротивлению
проводника. Мощность тока равна
произведению силы тока и напряжения.
Тогда активное сопротивление можно
определить как отношение мощности
переменного тока на участке цепи к
квадрату действующей силы тока.

Действующим
значением силы тока
называется сила постоянного тока,
благодаря которой в проводнике выделяется
за одинаковое время такое же количество
теплоты, что и переменным током. Найти
действующее значение силы тока можно
как отношение амплитудного значения
силы тока до квадратного корня из
двух.

Действующее
значение напряжения также в корень из
двух меньше его амплитудного значения.

При
изучении вынужденных механических
колебаний мы ознакомились с
явлением резонанса.
Резонанс наблюдается в том случае, когда
собственная частота колебаний системы
совпадает с частотой изменения внешней
силы. Если трение мало, то амплитуда
установившихся вынужденных колебаний
при резонансе резко увеличивается.
Совпадение вида уравнений для описания
механических и электромагнитных
колебаний (позволяет сделать заключение
о возможности резонанса также и в
электрической цепи, если эта цепь
представляет собой колебательный
контур, обладающий определенной
собственной частотой колебаний.

При
механических колебаниях резонанс
выражен отчетливо при малых значениях
коэфициента трения .
В электрической цепи роль коэффициента
трения выполняет ее активное сопротивление
R. Ведь именно наличие этого сопротивления
в цепи приводит к превращению энергии
тока но внутреннюю энергию проводника
(проводник нагревается). Поэтому резонанс
в электрическом колебательном кон-lype
должен быть выражен отчетливо при малом
активном сопротивлении R.

Мы
с вами уже знаем, что если активное
сопротивление мало, то собственная
циклическая частота колебаний в контуре
определяется формулой

Сила
тока при вынужденных
колебаниях должна
достигать максимальных значений, когда
частота переменного напряжения,
приложенного к контуру, равна собственной
частоте колебательного контура:

Резонансом
в электрическом колебательном
контуре называется
явление резкого возрастания амплитуды
вынужденных колебаний силы тока при
совпадении частоты внегннего переменного
напряжения с собственной частотой
колебательного контура.

Амплитуда
силы тока при резонансе. Как
и в случае механического резонанса, при
резонансе в колебательном контуре
создаются оптимальные условия для
поступления энергии от внешнего источника
в контур. Мощность в контуре максимальна
в том случае, когда сила тока совпадает
по фазе с напряжением. Здесь наблюдается
полная аналогия с механическими
колебаниями: при резонансе в механической
колебательной системе внешняя сила
(аналог напряжения в цепи) совпадает по
фазе со скоростью (аналог силы тока).

Не
сразу после включения внешнего переменного
напряжения в цепи устанавливается
резонансное значение силы тока. Амплитуда
колебаний силы тока нарастает постепенно
— до тех пор, пока энергия, выделяющаяся
за период на резисторе, не сравняется
с энергией,
поступающей в контур за это же
время:

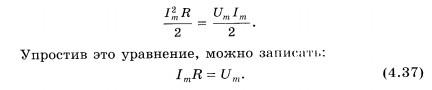
 Отсюда
амплитуда установившихся колебаний
силы тока при резонансе определяется
уравнением
 
 При
R  0
резонансное значение силы тока
неограниченно возрастает: (I_m)_рез  .
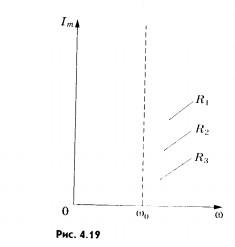
Наоборот, с увеличением R максимальное
значение силы тока уменьшается, и при
больших R говорить о резонансе уже не
имеет смысла. Зависимость амплитуды
силы тока от частоты при различных
сопротивлениях (R₁ <
R₂ <
R₃)
показана на рисунке 4.19.

Одновременно
с увеличением силы тока при резонансе
резко возрастают напряжения на
конденсаторе и катушке индуктивности.
Эти напряжения при ма.пом активном
сопротивлении во много раз превышают
внешнее напряжение.

Использование
резонанса в радиосвязи. Явление
электрического резонанса широко
используется при осуществлении
радиосвязи. Радиоволны от различных
передающих станций возбуждают в антенне
радиоприемника переменные токи различных
частот, так как каждая передающая
радиостанция работает на своей частоте.
С антенной индуктивно связан колебательный
контур (рис. 4.20). Вследствие электромагнитной
индукции в контурной катушке возникают
переменные ЭДС соответствующих частот
и вынужденные колебания силы тока тех
же частот. Но только при резонансе
колебания силы тока в контуре и напряжения
в нем будут значительными, т. е. из
колебаний различных частот, возбуждаемых
в антенне, контур выделяет только те,
частота которых равна его собственной
частоте. Настройка контура на нужную
частоту  обычно
осуществляется путем изменения
емкости конденсатора.
В этом обычно состоит настройка
радиоприемника на определенную
радиостанцию.

Необходимость
учета возможности резонанса в электрической
цепи. В некоторых случаях резонанс в
электрической цепи может принести
большой вред. Если цепь не рассчитана
на работу в условиях резонанса, то его
возникновеие может привести к аварии.

Чрезмерно
большие токи могут перегреть провода.
Большие напряжения приводят к пробою
изоляции.

Такого
рода аварии нередко случались еще
сравнительно недавно, когда плохо
представляли себе законы электрических
колебаний и не умели правильно
рассчитывать электрические
цепи.

При
вынужденных электромагнитных колебаниях
возможен резонанс — резкое возрастание
амплитуды колебаний силы тока и напряжения
при совпадении частоты внешнего
переменного напряжения с собственной
частотой колебаний. На явлении резонанса
основана вся радиосвязь.

Изучение
цепей переменного тока с активным,
емкостным и индуктивным сопротивлениями
происходит в следующей логической
последовательности: сначала дается
понятие о том или ином виде сопротивлений
в цепи переменного тока (сравнение с
его поведением в цепи постоянного тока),
затем фазовые соотношения, формула
соответствующего сопротивления,
преобразования энергии в цепи, содержащей
только активное, емкостное или индуктивное
сопротивление.

Последовательность
изучения сопротивлений в цепи переменного
тока может быть и несколько иной. 

Понятие
действующего значения силы тока и
напряжения можно ввести так: вначале
выводят выражение для расчета мгновенных
значений мощности на активном
сопротивлении, отсюда находят среднее
значение мощности за период и выясняют,
что  есть
среднее значение квадрата силы тока за
период. Вводят определение: корень
квадратный из этой величины называют
действующим значением переменного
тока. Название связано с тем, что при
прохождении такого тока по участку с
активным сопротивлением выделяется
мощность

Такая
же мощность выделяется в цепи постоянного
тока, величина которого равна действующему
значению переменного тока. Итак,
действующим значением переменного тока
является такое значение постоянного
тока, которое в резисторе R выделяет
такое же количество теплоты, что и
переменный ток.

Очень
важно отметить, что шкалы электроизмерительных
приборов, для измерения переменных силы
тока и напряжения градуируют именно в
действующих значениях этих
величин.

Рассмотрение
цепи переменного тока со смешанным
сопротивлением начинают с эксперимента
— измеряют напряжение на каждом из
последовательно включенных элементов
цепи (лампе, катушке и батарее
конденсаторов), подключенных к источнику
переменного напряжения. Обращают
внимание на следующие опытные факты:

1.
Общее напряжение не равно сумме напряжений
на отдельных участках, как это имело
место для цепей постоянного тока.

2.
Напряжение на участке, включающем в
себя катушку и конденсатор, равно не
сумме, а разности напряжений на каждом
из них в отдельности. Объяснить этот
результат можно предложить самим
учащимся; им известно, что на индуктивности
напряжение опережает ток на π/2, а на
электроемкости отстает от него на ту
же величину. Так как мгновенное значение
силы тока в цепи всюду одно и то же, то
ясно, что колебания напряжения на
индуктивности и электроемкости происходят
со сдвигом фаз, равным π, т. е. их фазы
противоположны.

3.
Полное сопротивление цепи меньше суммы
всех включенных в нее сопротивлений
(активного, индуктивного и емкостного).
Учащихся нужно убедить, что чем меньше
сдвиг фаз между током и напряжением,
тем большую часть мощности, подводимой
к цепи, используют полезно, необратимо
превращая в другие виды энергии.

Далее
рассматривают устройство и работу
трансформатора. На примере однофазного
трансформатора показывают его действие
(повышение и понижение напряжения) и
устройство. Вначале рассматривают режим
холостого хода, а затем нагруженного
трансформатора. В качестве нагрузки
целесообразно использовать реостат,
так как им проще изменять нагрузку.
Показывают, что при увеличении нагрузки
возрастает сила
тока как во вторичной, так и в первичной
обмотке трансформатора. Учащимся
предлагают самим с энергетических
позиций объяснить возрастание силы
тока в первичной цепи (увеличение
потребления энергии на нагрузке
естественно должно сопровождаться
увеличением потребления энергии
первичной обмоткой от генератора).

Для
изучения электромагнитных колебаний
широко используется школьный прибор-
звуковой генератор школьный ГЗШ. Он
перекрывает диапазон генерируемых
частот синусоидальных колебаний от 20
до 20000 Гц с диапазонами: «X1» (от 20 до 200
Гц), «X10» (от 200 до 2000 Гц), «X100» ( от 2000 до
20000 Гц), питается от сети переменного
тока напряжением 220 В. На лицевую панель
генератора выведены тумблёр включения
генератора в сеть, сигнальная лампочка,
переключатель поддиапазонов на три
фиксированных положения, отмеченных
«X1», «X10», «X100», диск с неравномерной
шкалой деления (от 20 до 200) ручка переменного
резистора, позволяющая менять амплитуду
выходного сигнала, выходные зажимы,
рассчитанные на подключение цепей с
разным сопротивлением (5, 600, 5000 Ом). Если
для опытов необходимы частоты 20 – 200
Гц, то переключатель устанавливают в
положение «X1» если 200 – 2000 Гц – в положение
«X10», а для частот 2000 – 20000 Гц используют
положение «X100». Плавную регулировку
частоты осуществляют поворотом
диска. 

Так
же широко используются выпрямители
ВУП-1 и ВУП-2

ВУП-2
предназначен для обеспечения питанием
демонстрационных установок в опытах
по электричеству.

Технические
данные: Прибор позволяет получить на
выходных зажимах: выпрямленное напряжение
350В при максимальной силе тока
220мА;

постоянное
отфильтрованное напряжение 250В при
максимальной нагрузке 50мА; регулируемое
напряжение от 0 до 250В постоянного тока
до 50мА; регулируемое напряжение от 0 до
+100В и от 0 до-100В постоянного тока до
10мА; напряжение 6.3В переменного тока до
3А.

Еще
один источник питания без которого
практически невозможно осуществлять
многие опыты по электричеству
РНШ.

Регулятор
напряжения школьный предназначен для
плавного регулирования напряжения
однофазного переменного тока с частотой
50 Гц, при проведении лабораторных и
демонстрационных опытов в физических
кабинетах школ. Прибор присоединяется
к сети выводным шнуром. Прибор можно
включить в сеть напряжением 127 и 220В.
Рабочее напряжение снимается с зажимов,
обозначенных «Выходное напряжение».

В
целях правильной эксплуатации регулятора
напряжения в паспорте прибора приведена
таблица допустимых значений электрической
мощности нагрузки регулятора при разных
напряжениях, подаваемых на нагрузку, и
при сетевых напряжениях 127 и
220В.

Установленный
в регуляторе напряжения вольтметр имеет
неравномерную шкалу. Достоверный отсчет
можно вести только при 50В. В случае
необходимости снимать с регулятора
более низкие напряжения нужно параллельно
выходным зажимам подключать дополнительный
вольтметр с соответствующим пределом
измерения.

Регулятор
напряжения может быть использован как
для повышения, так и для понижения
напряжений переменного тока, при разных
демонстрационных и лабораторных
опытах

Для
наглядного отображения электромагнитных
колебаний применяют школьные осциллографы
ОДШ-2 и ОЭШ-70. 

Наиболее
широко при­меняют осциллографы для
исследования периодических процессов,
а также для изучения вольтамперных
характеристик диода и трио­да, петли
гистерезиса и др. В простейшем случае
осциллограф состоит из четырех блоков:
блока электронно-лучевой трубки ЭЛТ,
генератора развертки ГР, усилителя
исследуемого сигнала УС и блока питания
БП . Основным элементом первого блока
является электронно-лучевая трубка, на
экране которой формируется картина
исследуемого сиг­нала (осциллограмма).
Нить накала НН подогревает ка­тод К,
с поверхности которого вылетают
элект­роны. Электроны, пролетев через
отверстия уп­равляющего электрода,
фокусирующего ци­линдра ФЦ и анода
А, а также между пласти­нами XX и УУ,
попадают на экран и вызывают его свечение.
Изменением разности потенциалов между
катодом и управляющим электродом мож­но
менять число электронов в пучке, а это
по­зволяет регулировать яркость
изображения на экране. Чем больше по
модулю отрицательный потенциал на
управляющем электроде относи­тельно
катода, тем меньше электронов пройдет
через управляющий электрод и достигнет
анода. Осциллограф снабжен ручкой
«яркость» для уп­равления потоком
электронов в пучке.

Электрическое
поле между фокусирующим цилиндром и
анодом способно фокусировать рас­ходящийся
электронный пучок. Обычно на передней
стенке смонтированы выключатель сети,
сигнальная лампочка, за­жимы «Вход
У», «Вход X» и делитель входного сигнала.
На боко­вую панель выведены ручки
управления электронным пучком,
«Синхронизация», «Внутр. — от сети —
внешн.», «Уси­ление», ручки развертки,
«Диапазоны 0, 30, 150, 500 Гц, 2, 8, 16 кГц»,
«Частота плавно», а также ручки усиления
сигнала «Уси­ление У», «Усиление X».
Осциллограф ОДШ-2 отличается от ОЭШ-70
конструктивно и внешним оформлением.
На переднюю панель выведен не только
экран электронно-лучевой трубки, но и
основные ручки уп­равления. Верхний
ряд ручек предназначен для управления
элек­тронным пучком: «Яркость»,
«Фокус», «Вверх-вниз», «Влево-вправо».
Во втором ряду сверху смонтированы
ручки управления уси­лителем «Усиление
У» и делитель напряжения 1:1, 1:10, 1:30, 1:1OO,
1:1000, а также выключатель сети с сигнальной
лампоч­кой. В третьем ряду сверху
расположены ручки и кнопки генера­тора
развертки: «Частота плавно», «Вкл. 1, 2,
3, 4», «Усиление X». Кнопочный переключатель
позволяет менять пилообразное напря­жение
частотой от 20 Гц до 20 кГц. Генератор
развертки рабо­тает только при нажатой
кнопке «Вкл». В нижнем ряду располо­жены
зажимы «Вход У», «Вход X», «Внешн. синхр»,
кнопки син­хронизации «Внешн.»,
«Внутр.» и ручка синхронизации.

На
боковую панель осциллографа ОДШ-2
выведены ручки уп­равления двухканальным
коммутатором с двумя входами. Комму­татор
позволяет наблюдать на экране осциллографа
одновремен­но сигналы от двух источников
переменного тока. Если частоты источников
одинаковы, то по полученным осциллограммам
мож­но судить о сдвиге фаз поданных
сигналов. Например, на один вход можно
подать сигнал, пропорциональный
напряжению на конденсаторе, а на другой
— пропорциональный силе тока, текущего
через конденсатор. Тогда на экране
осциллографа можно наблю­дать две
синусоиды, сдвинутые по фазе на 90°.
Применяя комму­татор, можно сравнивать
частоту исследуемого сигнала со
стан­дартной частотой, если эти сигналы
отличаются по частоте. На задней стенке
осциллографов ОДШ-2 и ОЭШ-70 смонтиро­ваны
гнезда, позволяющие подавать исследуемый
сигнал непосред­ственно на пластины
электронно-лучевой трубки. Возможность
подавать исследуемый сигнал непосредственно
на пластины позво­ляет применить
осциллограф и для цепей постоянного
тока. По­давая сигнал постоянного
напряжения на пластины XX (или УУ) при
отключенной развертке, можно наблюдать
смещение светя­щейся точки по
горизонтали (или вертикали), причем
отклонение этой точки пропорционально
приложенному напряжению. Следо­вательно,
осциллограф можно применить как вольтметр
с боль­шим внутренним сопротивлением.

Для
усиления электромагнитных колебаний
применяют усилители низкой частоты.
Усилитель низкой частоты –
электронный прибор. Предназначенный
для усиления электрических колебаний
звуковой частоты от 20 Гц до 20 кГц. Обычно
усилитель состоит из нескольких блоков:
предварительного усилителя напряжения,
усилителя мощности, согласующего
выходного трансформатора и блока
питания. Для школ выпускаются усилители
разной конструкции и отличающиеся по
внешнему виду.

Усилитель
УНЧ-3 на
лицевой панели имеет ручку регулятора
громкости и сигнальную лампочку. Ручкой
регулятора громкости производят также
включение и выключение сети. В крайнем
левом положении ручки при повороте
против часовой стрелки прибор отключен.
Включение осуществляют поворотом ручки
по часовой стрелке после щелчка. Так
как усилитель собран на электронных
лампах, то он начинает работать после
их прогрева. 

На
боковой стенке смонтированы три входных
гнезда: для подключения М – микрофона,
АД – адаптера, Л – линии. Нижние гнёзда
соединены с корпусом прибора. На задней
стенке имеются две пары гнёзд: Гр – для
подключения громкоговорителя (низкоомный
выход) и Л – высокоомный выход. Здесь
же имеются вывод сетевого шнура с вилкой
и октальная панель, в которую вставлена
специальная вилка с предохранителем
(на 0,5 А) для сети с напряжением 220 В. Вилку
можно устанавливать в двух положениях:
«220 В» и «127 В».

Усилитель
УНЧ-5 собран на транзисторах. На лицевой
панели усилителя смонтирован выключатель
сети с индикаторной лампочкой, гнезда
выхода, гнезда входа для микрофона и
звукоснимателя, разъем для подключения
микрофона, ручки регулировки тембра по
низкой и высокой частоте, ручка регулировки
уровня сигнала, индикатор перегрузки.
На задней стенке имеются вывод сетевого
шнура с вилкой и предохранитель (на 0,5
А).

На
вход усилителя могут подаваться сигналы
не только с микрофона и звукоснимателя,
но и от других датчиков электрических
колебаний напряжением от нескольких
милливольт до вольт (сигналы с элементов
цепи переменного тока, звукового
генератора и т.д.). К выходу усилителя
можно подключить не только громкоговоритель,
но и другие приборы: осциллограф,
измерительные приборы переменного
тока, головные телефоны и пр. Потребляемая
усилителем мощность не более 40 Вт,
выходная – около 5 Вт.

Запрещается
при эксплуатации усилителя менять
предохранитель, разбирать и ремонтировать
прибор, включенный в сеть.

Усилитель
на вертикальной панели входит в комплект
демонстрационных приборов по радиотехнике.
Слева смонтированы универсальные зажимы
входа усилителя. Первая лампа работает
в режиме усиления напряжения, вторая –
как усилитель мощности. В анодную цепь
второй лампы включен согласующий
трансформатор, вторичная обмотка
которого соединена с зажимами низкого
и высокого выходного напряжения. Три
нижних зажима служат для подключения
питания от ВУП –2, на два нижних зажима
подаётся напряжение переменного тока
6,3 В для питания накала ламп, а на средний
и третий снизу – напряжение постоянного
тока 250 В для анодной цепи ламп, причём
на третий снизу зажим подаётся
положительный потенциал. Подключение
блока питания и сборку установок с
усилителем на панели запрещается
выполнять при включённом в сеть
выпрямителе ВУП-2.

В
демонстрационных установках предпочтение
следует отдавать усилителю УНЧ-5.

Ранее мы познакомились с постоянным электрическим током — направленным движением зарядов, для которого сила тока постоянна. В случае, если значение силы тока непостоянно, тогда ток будем называть переменным.

Для школьной физики переменный ток рассматривается в двух, в общем-то, похожих случаях:

• вынужденные колебания (на вход цепи подаётся внешняя разность потенциалов/ток, которые изменяются гармонически).
• колебания в LC (состоящем из катушек индуктивности и конденсаторов) или LCR (состоящем их катушек индуктивности, конденсаторов и сопротивлений) контурах.

Рассмотрение свободных колебаний в случае переменного тока аналогично постоянному. Точно так же существует закон Ома для цепи переменного тока, рассчитываются мощности и энергии (работы) для такого случая.

Для школы характерно описание переменного тока через гармонические законы. Переменными параметрами в цепи могут быть ЭДС (), напряжение на элементе (), сила тока (), заряд конденсатора (). Рассмотрим ЭДС источника гармонический колебаний:

(1)

• где

Аналогичным образом можно ввести колебания напряжения  на элементе:

(2)

• где

Таким же образом вводится и колебание силы тока:

(3)

• где

И, аналогично, заряд на конденсаторе:

(4)

• где

Важно: нужно помнить, что тригонометрически можно превратить синус в косинус:

(5)

• где
  • — новая начальная фаза колебания.

Вывод: таким образом, рассмотрение переменного тока в случае формульных задач, связанных с соотношениями (1) — (4), касается анализа сомножителей и слагаемых, входящих в само соотношение.