Как найти декартово множество - Сайт, где вы сможете решить свои вопросы

Декартово произведение двух множеств

Понятие декартова произведения
Табличное представление декартовых произведений
Координатная плоскость как декартово произведение
Примеры

Понятие декартова произведения

Множество всех возможных пар, составленных из элементов множества A и B, называется декартовым произведением этих множеств:

$$ A times B = {(a,b)| a in Bbb A, b in Bbb B } $$

Мощность декартова произведения равно произведению мощностей исходных множеств: $|A times B| = |A| cdot |B|$. Это справедливо как для конечных, так и бесконечных множеств.

Декартово произведение некоммутативно: $A times B neq B times A$

Произведение $A times A = A^2$ называют декартовым квадратом.

Например:

Если A = {1;3;5}, B = {2;4}, их декартово произведение – это множество пар:

$A times B$ = {(1;2),(1;4),(3;2),(3;4),(5;2),(5;4)}

Мощность декартова произведения $n(A times B) = 6 = underbrace{n(A)}_{3text{}} cdot underbrace{n(B)}_{2text{}} $

Произведение в другом порядке:

$B times A$ = {(2;1),(2;3),(2;5),(4;1),(4;3),(4;5)}

Множества $A times B$ и $B times A$ отличаются.

Табличное представление декартовых произведений

Таблица умножения или таблица квадратов натуральных чисел являются примером функций, заданных на декартовых произведениях.

Например, таблица квадратов натуральных чисел:

961

1024

1089

1156

1225

1681

1764

1849

1936

2025

2601

2704

2809

2916

3025

Соответствует декартову произведению двух множеств

A = {1;2;3;4;5} и B{1;2;3;4;5}

На котором задана функциональная зависимость:

$$f(A times B) = {f(a,b) | f(a,b) = (10a+b)^2, a in Bbb A, b in Bbb B}$$

Второй пример – турнирная таблица встреч команд-участников чемпионата

Для пяти команд, если встречи две и на первом месте в паре – команда-хозяин, получаем:

–

(1;2)

(1;3)

(1;4)

(1;5)

(2;1)

–

(2;3)

(2;4)

(2;5)

(3;1)

(3;2)

–

(3;4)

(3;5)

(4;1)

(4;2)

(4;3)

–

(4;5)

(5;1)

(5;2)

(5;3)

(5;4)

–

В этом случае:

$$ f(A times B) = {(a,b)|a neq b,a in Bbb A, b in Bbb B} $$

Координатная плоскость как декартово произведение

Координатная плоскость является декартовым квадратом множества действительных чисел: $ Bbb R times Bbb R = Bbb R^2$. Точки, соответствующие полученным парам чисел, полностью заполняют плоскость.

Принадлежность точки координатной плоскости можно записать: $ (x,y) in Bbb R^2$

Множество $ Bbb R^2$ является континуальным и эквивалентно $ Bbb R^2 sim Bbb R sim [0;1]$

Бесконечный квадрат имеет столько же точек, сколько единичный отрезок (!)

Примеры

Пример 1. Найдите декартовы произведения и декартовы квадраты множеств:

а) A = {0;1}, B = {3;5;7}

$ A times B$ = {(0;3),(0;5),(0;7),(1;3),(1;5),(1;7)}

$ B times A$ = {(3;0),(3;1),(5;0),(5;1),(7;0),(7;1)}

$ A^2$ = {(0;0),(0;1),(1;0),(1;1)}

$B^2 $ = {(3;3),(3;5),(3;7),(5;3),(5;5),(5;7),(7;3),(7;5),(7;7) }

б) A = {a;b;c}, B = {e;f}

$ A times B$ = {(a;e),(a;f),(b;e),(b;f),(c;e),(c;f)}

$ B times A$ = {(e;a),(e;b),(e;c),(f;a),(f;b),(f;c)}

$ A^2$ = {(a;a),(a;b),(a;c),(b;a),(b;b),(b;c),(c;a),(c;b),(c;c) }

$B^2 $ = {(e;e),(e;f),(f;e),(f;f)}

Пример 2. Отметьте на координатной плоскости точки множеств $A times B$ и $B times A$, найдите их пересечение, если

а) A = {2;3;5}, B = {-2;3}

Точки $ A times B$ синие, точки B×A красные, точка пересечения $ A times B cap B times A$ = {(3,3)} зелёная.

б) A = {-1;2}, B = {0;2;4}

Точки $ A times B$ синие, точки B×A красные, точка пересечения $ A times B cap B times A$ = {(2,2)} зелёная.

Источник

Прямо́е, или дека́ртово произведе́ние двух множеств — множество, элементами которого являются все возможные упорядоченные пары элементов исходных множеств. Предполагается, что впервые «декартово» произведение двух множеств ввёл Георг Кантор^[1]^[2].

Понятие прямого произведения естественно обобщается на произведение множеств с дополнительной структурой (алгебраической, топологической и так далее), поскольку произведение множеств часто наследует структуры, имевшиеся на исходных множествах.

Прямое произведение в теории множеств[править | править код]

Произведение двух множеств[править | править код]

Произведение множества {в, и, к} на множество цветов радуги

в	в	в	в	в	в	в	в
и	и	и	и	и	и	и	и
к	к	к	к	к	к	к	к

Пусть даны два множества и . Прямое произведение множества и множества есть такое множество , элементами которого являются упорядоченные пары (x,y) для всевозможных xin X и yin Y . Упорядоченную пару, образованную из элементов и , принято записывать, используя круглые скобки: (a,b) . Элемент называют первой координатой (компонентой) пары, а элемент – второй координатой (компонентой) пары.

Прямое произведение двух множеств наглядно можно представить в виде таблицы, строки которой определяют элементы первого множества, а столбцы, соответственно, второго. Все клетки данной таблицы в таком случае будут элементами декартова произведения.

Слово «упорядоченная» значит, что для xne y , . Так, пары (a,b) и равны в том и только том случае, если a=c и b=d .

Важность «порядка» можно показать на примере обычной записи чисел: используя две цифры 3 и 5, можно записать четыре двузначных числа: 35, 53, 33 и 55. Несмотря на то, что числа 35 и 53 записаны с помощью одних и тех же цифр, эти числа различные. В том случае, когда важен порядок следования элементов, в математике говорят об упорядоченных наборах элементов.

В упорядоченной паре (a,b) может быть, что a=b . Так, запись чисел 33 и 55 можно рассматривать как упорядоченные пары (3; 3) и (5; 5).

Отображения произведения множеств в его множители — и — называют координатными функциями.

Аналогично определяется произведение конечного семейства множеств.

Комментарии[править | править код]

Строго говоря, тождество ассоциативности не имеет места, но в силу существования естественного взаимно однозначного соответствия (биекции) между множествами и этим различием можно зачастую пренебречь.

Декартова степень[править | править код]

{0, 1, 2}³, 3³ = 27 элементов
000	001	002	010	011	012	020	021	022
100	101	102	110	111	112	120	121	122
200	201	202	210	211	212	220	221	222

-я декартова степень множества определяется для целых неотрицательных , как -кратное декартово произведение на себя^[3] ^[4]:

$begin{matrix} underbrace{Xtimes Xtimes ldots times X}. \ n end{matrix}$

Обычно обозначается как X^n или $X^{times n}$ .

При положительных декартова степень X^n состоит из всех упорядоченных наборов элементов из длины .
Так, вещественное пространство $mathbb {R} ^{3}$ — множество кортежей из трех вещественных чисел — есть 3-я степень множества вещественных чисел

При n=0 , декартова степень X^0, по определению, содержит единственный элемент — пустой кортеж.

Прямое произведение семейства множеств[править | править код]

В общем случае, для произвольного семейства множеств (не обязательно различных) ${X_i}_{iin I}$ (множество индексов может быть бесконечным) прямое произведение $X = prod_{iin I} X_i$ определяется как множество функций, сопоставляющих каждому элементу iin I элемент множества $X_{i}$ :

${displaystyle X=prod _{iin I}X_{i}={fcolon Ito bigcup limits _{iin I}X_{i}mid f(i)in X_{i},iin I}.}$

Отображения называются проекциями, и определяются следующим образом: .

В частности, для конечного семейства множеств ${A_1, dots ,A_n}$ любая функция $f:{1,dots ,n} to bigcuplimits_{i = 1}^n A_i$ с условием эквивалентна некоторому кортежу длины , составленному из элементов множеств ${A_i}_{i = 1}^n$ , так, что на -ом месте кортежа стоит элемент множества $A_{i}$ . Поэтому декартово (прямое) произведение конечного числа множеств ${A_i}_{i = 1}^n$ может быть записано так:

$A_1 times dots times A_n = {(a_1, dots ,a_n) mid a_i in A_i, i in {1, dots ,n}}.$

Теоретико-множественные операции с прямыми произведениями[править | править код]

Пусть заданы прямые произведения ${displaystyle A=A_{1}times dots times A_{n}}$ и ${displaystyle B=B_{1}times dots times B_{n}}$ . Тогда

, если и только если ${displaystyle A_{i}subseteq B_{i}}$ для всех ^[5];
${displaystyle Acap B=(A_{1}cap B_{1})times dots times (A_{n}cap B_{n})}$ , при этом, если существует хотя бы один , такой что ${displaystyle A_{i}cap B_{i}=varnothing }$ , то ^[5];
${displaystyle Acup Bsubseteq (A_{1}cup B_{1})times dots times (A_{n}cup B_{n})}$ , при этом равенство возможно лишь в следующих случаях^[6]:

– или ;

– для всех ${displaystyle i=1,2,ldots ,nquad A_{i}=B_{i}quad }$ за исключением одного из .

4. Дополнение прямого произведения ${displaystyle A=A_{1}times dots times A_{n}}$ можно вычислить^[7], если задан универсум ${displaystyle U=X_{1}times dots times X_{n}}$ . Для упрощения выражений введем следующие обозначения . Обозначим прямое произведение в виде ограниченного прямыми скобками кортежа, в котором располагаются множества, из которых сформировано прямое произведение, например:

${displaystyle A=A_{1}times A_{2}times dots times A_{n}=[A_{1}quad A_{2}quad dots quad A_{n}]}$

С учетом этого объединение прямых произведений, заданных в одном и том же универсуме, можно выразить в виде матрицы, ограниченной прямыми скобками, в которой строки представляют прямые произведения, участвующие в объединении:

${displaystyle Acup B=(A_{1}times A_{2}times dots times A_{n})cup (B_{1}times B_{2}times dots times B_{n})=left[{begin{array}{cccc}A_{1}&A_{2}&dots &A_{n}\B_{1}&B_{2}&dots &B_{n}end{array}}right]}$

Тогда дополнением прямого произведения будет следующее объединение прямых произведений, выраженное в виде матрицы размерности :

${displaystyle {overline {A}}=left[{begin{array}{ccccc}{overline {A_{1}}}&X_{2}&dots &X_{n-1}&X_{n}\X_{1}&{overline {A_{2}}}&dots &X_{n-1}&X_{n}\dots &dots &dots &dots &dots \X_{1}&X_{2}&dots &{overline {A_{n-1}}}&X_{n}\X_{1}&X_{2}&dots &X_{n-1}&{overline {A_{n}}}end{array}}right]}$

Диагональные компоненты этой матрицы ${displaystyle {overline {A_{i}}}}$ равны соответственно ${displaystyle X_{i}setminus A_{i}}$ .

Прямое произведение отображений[править | править код]

Пусть — отображение из в , а — отображение из в . Их прямым произведением называется отображение из в : .

Аналогично вышеизложенному, данное определение обобщается на многократные и бесконечные произведения.

Воздействие на математические структуры[править | править код]

Прямое произведение групп[править | править код]

Прямое (декартово) произведение двух групп (G,*) и — это группа из всех пар элементов (g,h) с операцией покомпонентного умножения: . Эта группа обозначается как . Ассоциативность операции умножения в группе следует из ассоциативности операций перемножаемых групп. Сомножители и изоморфны двум нормальным подгруппам своего произведения, ${(g,1_H)mid gin G}$ и ${(1_G,h)mid hin H}$ соответственно. Пересечение этих подгрупп состоит из одного элемента , который является единицей группы-произведения. Координатные функции произведения групп являются гомоморфизмами.

Это определение распространяется на произвольное число перемножаемых групп. В случае конечного числа прямое произведение изоморфно прямой сумме. Отличие возникает при бесконечном числе множителей.

В общем случае, $overline{prod_{iin I}} G_i={fcolon Itobigcup_{iin I} G_i}$ , где и . (Операция в правой части — это операция группы $G_{i}$ ). Единицей группы-произведения будет последовательность, составленная из единиц всех перемножаемых групп: . Например, для счётного числа групп: $overline{prod_{iinmathbb{N}}} mathbb{Z}_2=(2^mathbb{N},; operatorname{xor})$ , где в правой части стоит множество всех бесконечных двоичных последовательностей.

Подгруппа на множестве всех , носитель которых (то есть множество $mathrm{supp},(f) = {iin Imid f(i)ne 1_i}$ ) конечен, называется прямой суммой. Например, прямая сумма того же самого набора множеств $prod_{iinmathbb{N}} mathbb{Z}_2 = (mathbb{N},; operatorname{xor})$ содержит все двоичные последовательности с конечным числом единиц, а их можно трактовать как двоичные представления натуральных чисел.

Декартово произведение индексированной системы групп есть её прямое произведение в категории Grp.

Прямая сумма индексированной системы групп есть её копроизведение в категории Grp.

Прямое произведение других алгебраических структур[править | править код]

Аналогично произведению групп можно определить произведения колец, алгебр, модулей и линейных пространств, причём в определении прямого произведения 1_i (см. выше) следует заменить нулём.
Определение произведения двух (или конечного числа) объектов совпадает с определением прямой суммы. Однако, вообще говоря, прямая сумма отличается от прямого произведения: например, прямое произведение счётного множества копий есть пространство всех последовательностей действительных чисел, тогда как прямая сумма — пространство тех последовательностей, у которых только конечное число членов ненулевые (так называемых финитных последовательностей).

Прямое произведение векторных пространств[править | править код]

Декартово произведение двух векторных пространств и над общим полем — это множество упорядоченных пар векторов , то есть теоретико-множественное декартово произведение множеств векторов из и , с линейностью, заданной покоординатно: , .

Данное определение распространяется на любую индексированную систему линейных (векторных) пространств: декартовым произведением индексированной системы векторных пространств над общим полем является теоретико‑множественное декартово произведение множеств векторов сомножителей, на котором задана покоординатная линейность, то есть при суммировании суммируются все проекции, при умножении на число все проекции умножаются на это число: ${displaystyle c=a+bleftrightarrow forall i:c_{i}=a_{i}+b_{i}}$ , ${displaystyle b=mathrm {alpha } aleftrightarrow forall i:b_{i}=mathrm {alpha } a_{i}}$ .

Декартово произведение индексированной системы линейных пространств есть её прямое произведение в категории ${displaystyle operatorname {Vec} _{F}}$ , где есть подлежащее поле системы.

Прямая сумма векторных пространств есть такое подмножество их декартова произведения, элементы которого имеют лишь конечное число отличных от нуля проекций
${displaystyle bigoplus {A}=left{ain prod {A}mid leftvert left{iin operatorname {dom} Amid a_{i}neq 0right}rightvert <aleph _{0}right}}$ , где есть индексное множество индексированной системы .
Для конечного числа слагаемых прямая сумма не отличается от декартова произведения.

Прямая сумма индексированной системы линейных пространств есть её копроизведение в категории ${displaystyle operatorname {Vec} _{F}}$ , где есть подлежащее поле системы.

Прямое произведение топологических пространств[править | править код]

Пусть и — два топологических пространства. Топология декартова произведения задаётся на их теоретико‑множественном произведении, как бесструктурных множеств, базой, состоящей из всевозможных произведений , где — открытое подмножество и — открытое подмножество .

Определение легко обобщается на случай произведения нескольких пространств.

Для произведения бесконечного набора сомножителей определение усложняется: пусть есть индексированная система топологических пространств, — бесструктурное произведение элементов , как множеств. Определим цилиндр, восставленный над ${displaystyle Usubseteq X_{i}}$ , как множество всех точек из , чьи ‑е проекции лежат в , т. е. ${displaystyle operatorname {Cyl} left(i,;Uright)=left{xin Bmid x_{i}in Uright}}$ , где и есть индексное множество индексированной системы . Топология произведения будет задана на предбазе из цилиндров, восставленных надо всеми открытыми множествами всех топологий из набора : ${displaystyle left{operatorname {Cyl} left(i,;Uright)mid iin operatorname {dom} Xland Uin operatorname {T} left(X_{i}right)right}}$ , где ${displaystyle operatorname {T} left(X_{i}right)}$ есть совокупность всех отрытых множеств (топология) пространства $X_{i}$ , то есть задаваться базой, составленной из всевозможных пересечений конечного числа открытых цилиндров. Данная топология является «контрвариантно» наведённой проекторами — это минимальная топология на теоретико‑множественном декартовом произведении, при которой все проекторы непрерывны (такая топология аналогична компактно-открытой топологии пространств отображений, если считать индексное множество имеющим дискретную топологию).

Декартово произведение индексированной системы топологических пространств есть её прямое произведение в категории .

Прямая сумма топологий строится на бесструктурной прямой сумме пространств, как множеств точек. Открытыми в ней являются все множества, пересечения которых со всеми слагаемыми открыты. Данная топология является «ковариантно» наведённой копроекторами — это максимальная топология на теоретико‑множественной прямой сумме, при которой все копроекторы (т. е. вложения слагаемых в сумму) непрерывны.

Прямая сумма индексированной системы топологических пространств есть её копроизведение в категории .

Теорема Тихонова утверждает компактность произведений любого количества компактных пространств; однако для бесконечных произведений её не удаётся доказать без использования аксиомы выбора (или равносильных ей утверждений теории множеств).

Также теорема Александрова показывает, что любое топологическое пространство можно вложить в (бесконечное) произведение связных двоеточий, если только выполнена аксиома Колмогорова.

Прямое произведение графов[править | править код]

	—	
	—	
		
	—	

Множество вершин прямого произведения двух графов и задаётся как произведение вершин графов сомножителей.
Рёбрами будут соединены следующие па́ры вершин:

Иначе говоря, множество рёбер произведения графов является объединением двух произведений: рёбер первого на вершины второго, и вершин первого на рёбра второго.

Вариации и обобщения[править | править код]

Идея прямого произведения получила дальнейшее развитие в теории категорий, где она послужила основой для понятия произведения объектов. Неформально, произведение двух объектов и — это наиболее общий объект в данной категории, для которого существуют проекции на и . Во многих категориях (множеств, групп, графов, …) произведением объектов является именно их прямое произведение. Важно, что в большинстве случаев важно не столько конкретное определение прямого произведения, сколько указанное выше свойство универсальности. Различные определения будут давать при этом изоморфные объекты.

См. также[править | править код]

Дизъюнктное объединение
Полупрямое произведение
Прямая сумма
Тензорное произведение
Декартовы координаты
Операции над множествами
Комбинаторика

Примечания[править | править код]

↑ Бурбаки, 2013, с. 307.
↑ Cantor, 1932, с. 286—287.
↑ Бурбаки, 2013, с. 115.
↑ Эдельман, 1975, с. 10.
↑ ¹ ² Бурбаки, 2013, с. 117.
↑ Кулик, 2020, с. 77.
↑ Кулик, 2020, с. 83.

Литература[править | править код]

Бурбаки Н. Основные структуры анализа. Книга 1. Теория множеств. — М.: Книга по требованию, 2013. — 460 с.
Кулик Б.А. Логика и математика: просто о сложных методах логического анализа. — СПб.: Политехника, 2020. — 141 с. — ISBN 978-5-7325-1166-6.
Эдельман С.Л. Математическая логика. — М.: Высшая школа, 1975. — 176 с.
Cantor G. Gesammelte Abhandlungen. — Berlin: Springer, 1932. — 486 с.

Источник

Содержание

Декартово
произведение множеств.
Свойства
операции декартова произведения.
Кортеж.
Длина кортежа.

Основная
литература 7,
10, 11, 16, 23, 33, 34;

Дополнительная
литература 17,
18, 27, 50, 81, 84, 82, 86, 87

1. Декартово произведение множеств

Используя
две цифры, например, 3 и 5, можно записать
четыре двузначных числа: 35, 53, 33 и 55.
Несмотря на то, что числа 35 и 53 записаны
с помощью одних и тех же цифр, эти числа
различные. В том случае, когда важен
порядок следования элементов, в математике
говорят об упорядоченных наборах
элементов. В рассмотренном примере мы
имели дело с упорядоченными
парами.

Упорядоченную
пару, образованную из элементов a
и b,
принято записывать, используя круглые
скобки: (a;
b).
Элемент a
называют первой
координатой (компонентой) пары,
а элемент b
– второй
координатой (компонентой) пары.

Пары
(а; b)
и (с; d)
равны в том и только том случае, когда
а = с и b
= d.

В
упорядоченной паре (а; в) может быть, что
а = в. Так, запись чисел 33 и 55 можно
рассматривать как упорядоченные пары
(3; 3) и (5; 5).

Упорядоченные
пары можно образовывать как из элементов
одного множества, так и двух множеств.

Пример

Даны
множества А=1,2,3,
В=3,5.
Образовать упорядоченные пары так,
чтобы первая компонента принадлежала
множеству А, а вторая – множеству В.

Перечислив
все такие пары, получим множество: (1;
3), (1; 5), (2; 3), (2; 5), (3;3), (3;5).

Видим,
что имея два множества А и В, мы получили
новое множество, элементами которого
являются упорядоченные пары чисел. Это
множество называют декартовым
произведением множеств А и В.

Определение.
Декартовым
произведением множеств А и В называется
множество всех пар, первая компонента
которых принадлежит множеству А, а
вторая компонента принадлежит множеству
В.

Декартово
произведение множеств А и В обозначают
А.
Используя это обозначение, определение
произведения можно записать так:

х;
у) 
х 
и у 
.

Пример

Найти
декартово произведение множеств А и В,
если:

а)
А = m,
p,
e,
f,
k;
b)
A
= B=3,
5.

Решение.
а) Действуем согласно определению –
образуем все пары, первая компонента
которых выбирается из А, а вторая – из
В: А 


(m;
p);
(m;
f);
(m;
k);
(p;
e);
(p;
f);(p;
k).

b)
Декартово произведение равных множеств
находят, образуя всевозможные пары из
элементов данного множества: А 
А = (3;
3); (3; 5); (5; 3); (5; 5).

2. Свойства операции нахождения декартова произведения

Так
как декартовы произведения А
и ВА
состоят из различных элементов, то
операция нахождения декартова
произведения множеств свойством
коммутативности не обладает.
Аналогично
рассуждая, можно доказать, что для этой
операции не выполняется и свойство
ассоциативности.
Но
она дистрибутивна относительно
объединения и вычитания множеств, т.е.
для любых множеств А, В и С выполняются
равенства:

  С



С



С,



С 


С


С.

Пример

Проверьте
справедливость свойства дистрибутивности
декартова произведения относительно
объединения, если: А = 3;
4; 5,
В = 5;
7,
С = 7;
8.

Решение.
Найдем объединение множеств А и В: 
= 3;
4; 5;7.
Далее перечислим элементы множества


С, используя определение декартова
произведения: 

С = (3;
7), (3; 8), (4; 7), (4; 8), (5; 7), (5; 8), (7; 7), (7; 8).

Чтобы
найти элементы множества 

С



С,
перечислим сначала элементы множеств
А 
С и В 
С:

А

С = (3;
7), (3; 8), (4; 7), (4; 8), (5; 7), (5; 8)

В

С = (5;
7), (5; 8), (7; 7), (7; 8).

Найдем
объединение полученных декартовых
произведений:

  С



С
= (3;
7), (3; 8), (4; 7), (4; 8), (5; 7), (5; 8), (7; 7), (7; 8).

Видим,
что множества 

С и 

С



С
состоят из одних и тех же элементов,
следовательно, для данных множеств А,
В и С справедливо равенство 

С 


С



С.

Выясним
теперь, как можно
наглядно
представить декартово произведение
множеств.

Если
множества А
и В
конечны и содержат небольшое число
элементов, то можно изобразить декартово
произведение этих множеств при помощи
таблицы
или
графа.

Пример

Д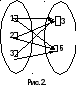екартово
произведение множеств А =1;
2; 3
и В = 3;
5
можно представить так, как показано на
рисунке 1 и 2

	3	5
1	(1,3)	(1,5)
2	(2,3)	(2,3)
3	(3,3)	(3,3)

Рис.
1

Декартово
произведение двух числовых множеств
(конечных и бесконечных) можно изображать
на координатной плоскости, так как
каждая пара чисел может быть единственным
образом изображена точкой на этой
плоскости.

Способ
наглядного представления декартова
произведения двух числовых множеств
удобно использовать в случае, когда
хотя бы одно из них бесконечное.

Пример

Изобразите
на координатной плоскости декартово
произведение 

В, если:

а)
А = 1;
2; 3
и В = 3;
5;

б)
А = 1;
3,
В = 3;
5;

в)
А = R,
В = 3;
5;

г)
А = R,
В = R.

Решение

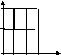
а)
Так как множество А состоит из трех
элементов, а множество В содержит все
действительные числа о т 3 до 5, включая
и сами эти числа, то декартово произведение


В будет состоять из бесконечного
множества пар, первая компонента которых
либо 1, либо 2, либо 3, а вторая – любое
действительное число из промежутка 3;
5.
Такое множество пар действительных
чисел на координатной плоскости
изобразится тремя отрезками.

1
2 3 х

б)
В этом случае бесконечны оба множества
А и В. Поэтому первой координатой может
быть любое число из промежутка 1;
3,
и, следовательно, точки, изображающие
элементы декартова произведения данных
множеств А и В, образуют квадрат. Чтобы
подчеркнуть, что элементы декартова
произведения изображаются и точками,
лежащими внутри квадрата, этот квадрат
можно заштриховать.

1
2 х

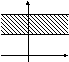
в)
Этот случай отличается от предыдущих
тем, что множество А состоит из всех
действительных чисел, т.е. абсцисса
точек, изображающих элементы множества


В, принимает все действительные значения,
в то время как ордината выбирается из
промежутка 3;
5.
Множество таких точек образует полосу.

г)
Декартово произведение RR
состоит из всевозможных действительных
чисел. Точки, изображающие эти пары,
сплошь заполняют координатную плоскость.
Таким образом, декартово произведение
RR
содержит столько же элементов, сколько
точек находится на координатной
плоскости.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Cartesian product of the sets and

In mathematics, specifically set theory, the Cartesian product of two sets A and B, denoted A × B, is the set of all ordered pairs (a, b) where a is in A and b is in B.^[1] In terms of set-builder notation, that is

{displaystyle Atimes B={(a,b)mid ain A {mbox{ and }} bin B}.}

^[2]^[3]

A table can be created by taking the Cartesian product of a set of rows and a set of columns. If the Cartesian product rows × columns is taken, the cells of the table contain ordered pairs of the form (row value, column value).^[4]

One can similarly define the Cartesian product of n sets, also known as an n-fold Cartesian product, which can be represented by an n-dimensional array, where each element is an n-tuple. An ordered pair is a 2-tuple or couple. More generally still, one can define the Cartesian product of an indexed family of sets.

The Cartesian product is named after René Descartes,^[5] whose formulation of analytic geometry gave rise to the concept, which is further generalized in terms of direct product.

Set-theoretic definition[edit]

A rigorous definition of the Cartesian product requires a domain to be specified in the set-builder notation. In this case the domain would have to contain the Cartesian product itself. For defining the Cartesian product of the sets and , one such domain is the set where denotes the power set. Then the Cartesian product of the sets and would be defined as^[6]

Examples[edit]

A deck of cards[edit]

An illustrative example is the standard 52-card deck. The standard playing card ranks {A, K, Q, J, 10, 9, 8, 7, 6, 5, 4, 3, 2} form a 13-element set. The card suits {♠, ♥, ♦, ♣} form a four-element set. The Cartesian product of these sets returns a 52-element set consisting of 52 ordered pairs, which correspond to all 52 possible playing cards.

Ranks × Suits returns a set of the form {(A, ♠), (A, ♥), (A, ♦), (A, ♣), (K, ♠), …, (3, ♣), (2, ♠), (2, ♥), (2, ♦), (2, ♣)}.

Suits × Ranks returns a set of the form {(♠, A), (♠, K), (♠, Q), (♠, J), (♠, 10), …, (♣, 6), (♣, 5), (♣, 4), (♣, 3), (♣, 2)}.

These two sets are distinct, even disjoint, but there is a natural bijection between them, under which (3, ♣) corresponds to (♣, 3) and so on.

A two-dimensional coordinate system[edit]

Cartesian coordinates of example points

The main historical example is the Cartesian plane in analytic geometry. In order to represent geometrical shapes in a numerical way, and extract numerical information from shapes’ numerical representations, René Descartes assigned to each point in the plane a pair of real numbers, called its coordinates. Usually, such a pair’s first and second components are called its x and y coordinates, respectively (see picture). The set of all such pairs (i.e., the Cartesian product ℝ×ℝ, with ℝ denoting the real numbers) is thus assigned to the set of all points in the plane.^{[citation needed]}

Most common implementation (set theory)[edit]

A formal definition of the Cartesian product from set-theoretical principles follows from a definition of ordered pair. The most common definition of ordered pairs, Kuratowski’s definition, is . Under this definition, (x,y) is an element of , and is a subset of that set, where represents the power set operator. Therefore, the existence of the Cartesian product of any two sets in ZFC follows from the axioms of pairing, union, power set, and specification. Since functions are usually defined as a special case of relations, and relations are usually defined as subsets of the Cartesian product, the definition of the two-set Cartesian product is necessarily prior to most other definitions.

Non-commutativity and non-associativity[edit]

Let A, B, C, and D be sets.

The Cartesian product A × B is not commutative,

^[4]

because the ordered pairs are reversed unless at least one of the following conditions is satisfied:^[7]

A is equal to B, or
A or B is the empty set.

For example:

A = {1,2}; B = {3,4}

A × B = {1,2} × {3,4} = {(1,3), (1,4), (2,3), (2,4)}

B × A = {3,4} × {1,2} = {(3,1), (3,2), (4,1), (4,2)}

A = B = {1,2}

A × B = B × A = {1,2} × {1,2} = {(1,1), (1,2), (2,1), (2,2)}

A = {1,2}; B = ∅

A × B = {1,2} × ∅ = ∅

B × A = ∅ × {1,2} = ∅

Strictly speaking, the Cartesian product is not associative (unless one of the involved sets is empty).

If for example A = {1}, then (A × A) × A = {((1, 1), 1)} ≠ {(1, (1, 1))} = A × (A × A).

Intersections, unions, and subsets[edit]

Example sets

A = {y ∈ ℝ : 1 ≤ y ≤ 4}, B = {x ∈ ℝ : 2 ≤ x ≤ 5},
and C = {x ∈ ℝ : 4 ≤ x ≤ 7}, demonstrating
A × (B∩C) = (A×B) ∩ (A×C),
A × (B∪C) = (A×B) ∪ (A×C), and

A × (B C) = (A×B) (A×C)

Example sets

A = {x ∈ ℝ : 2 ≤ x ≤ 5}, B = {x ∈ ℝ : 3 ≤ x ≤ 7},
C = {y ∈ ℝ : 1 ≤ y ≤ 3}, D = {y ∈ ℝ : 2 ≤ y ≤ 4}, demonstrating

(A∩B) × (C∩D) = (A×C) ∩ (B×D).

(A∪B) × (C∪D) ≠ (A×C) ∪ (B×D) can be seen from the same example.

The Cartesian product satisfies the following property with respect to intersections (see middle picture).

(Acap B)times (Ccap D)=(Atimes C)cap (Btimes D)

In most cases, the above statement is not true if we replace intersection with union (see rightmost picture).

In fact, we have that:

For the set difference, we also have the following identity:

Here are some rules demonstrating distributivity with other operators (see leftmost picture):^[7]

${displaystyle {begin{aligned}Atimes (Bcap C)&=(Atimes B)cap (Atimes C),\Atimes (Bcup C)&=(Atimes B)cup (Atimes C),\Atimes (Bsetminus C)&=(Atimes B)setminus (Atimes C),end{aligned}}}$

${displaystyle (Atimes B)^{complement }=left(A^{complement }times B^{complement }right)cup left(A^{complement }times Bright)cup left(Atimes B^{complement }right)!,}$

where ${displaystyle A^{complement }}$ denotes the absolute complement of A.

Other properties related with subsets are:

{displaystyle {text{if both }}A,Bneq emptyset {text{, then }}Atimes Bsubseteq Ctimes D!iff !Asubseteq C{text{ and }}Bsubseteq D.}

^[8]

Cardinality[edit]

The cardinality of a set is the number of elements of the set. For example, defining two sets: A = {a, b} and B = {5, 6}. Both set A and set B consist of two elements each. Their Cartesian product, written as A × B, results in a new set which has the following elements:

A × B = {(a,5), (a,6), (b,5), (b,6)}.

where each element of A is paired with each element of B, and where each pair makes up one element of the output set.
The number of values in each element of the resulting set is equal to the number of sets whose Cartesian product is being taken; 2 in this case.
The cardinality of the output set is equal to the product of the cardinalities of all the input sets. That is,

|A × B| = |A| · |B|.^[4]

In this case, |A × B| = 4

Similarly

|A × B × C| = |A| · |B| · |C|

and so on.

The set A × B is infinite if either A or B is infinite, and the other set is not the empty set.^[9]

Cartesian products of several sets[edit]

n-ary Cartesian product[edit]

The Cartesian product can be generalized to the n-ary Cartesian product over n sets X₁, …, X_n as the set

${displaystyle X_{1}times cdots times X_{n}={(x_{1},ldots ,x_{n})mid x_{i}in X_{i} {text{for every}} iin {1,ldots ,n}}}$

of n-tuples. If tuples are defined as nested ordered pairs, it can be identified with (X₁ × ⋯ × X_n−1) × X_n. If a tuple is defined as a function on {1, 2, …, n} that takes its value at i to be the ith element of the tuple, then the Cartesian product X₁×⋯×X_n is the set of functions

${displaystyle {x:{1,ldots ,n}to X_{1}cup cdots cup X_{n} | x(i)in X_{i} {text{for every}} iin {1,ldots ,n}}.}$

n-ary Cartesian power[edit]

The Cartesian square of a set X is the Cartesian product X² = X × X.
An example is the 2-dimensional plane R² = R × R where R is the set of real numbers:^[1] R² is the set of all points (x,y) where x and y are real numbers (see the Cartesian coordinate system).

The n-ary Cartesian power of a set X, denoted $X^{n}$ , can be defined as

${displaystyle X^{n}=underbrace {Xtimes Xtimes cdots times X} _{n}={(x_{1},ldots ,x_{n}) | x_{i}in X {text{for every}} iin {1,ldots ,n}}.}$

An example of this is R³ = R × R × R, with R again the set of real numbers,^[1] and more generally Rⁿ.

The n-ary Cartesian power of a set X is isomorphic to the space of functions from an n-element set to X. As a special case, the 0-ary Cartesian power of X may be taken to be a singleton set, corresponding to the empty function with codomain X.

Infinite Cartesian products[edit]

It is possible to define the Cartesian product of an arbitrary (possibly infinite) indexed family of sets. If I is any index set, and ${displaystyle {X_{i}}_{iin I}}$ is a family of sets indexed by I, then the Cartesian product of the sets in ${displaystyle {X_{i}}_{iin I}}$ is defined to be

${displaystyle prod _{iin I}X_{i}=left{left.f:Ito bigcup _{iin I}X_{i} right| forall iin I. f(i)in X_{i}right},}$

that is, the set of all functions defined on the index set I such that the value of the function at a particular index i is an element of X_i. Even if each of the X_i is nonempty, the Cartesian product may be empty if the axiom of choice, which is equivalent to the statement that every such product is nonempty, is not assumed.

For each j in I, the function

${displaystyle pi _{j}:prod _{iin I}X_{i}to X_{j},}$

defined by $pi _{j}(f)=f(j)$ is called the jth projection map.

Cartesian power is a Cartesian product where all the factors X_i are the same set X. In this case,

$prod _{iin I}X_{i}=prod _{iin I}X$

is the set of all functions from I to X, and is frequently denoted X^I. This case is important in the study of cardinal exponentiation. An important special case is when the index set is , the natural numbers: this Cartesian product is the set of all infinite sequences with the ith term in its corresponding set X_i. For example, each element of

$prod _{n=1}^{infty }mathbb {R} =mathbb {R} times mathbb {R} times cdots$

can be visualized as a vector with countably infinite real number components. This set is frequently denoted $mathbb {R} ^{omega }$ , or $mathbb {R} ^{mathbb {N} }$ .

Other forms[edit]

Abbreviated form[edit]

If several sets are being multiplied together (e.g., X₁, X₂, X₃, …), then some authors^[10] choose to abbreviate the Cartesian product as simply ×X_i.

Cartesian product of functions[edit]

If f is a function from X to A and g is a function from Y to B, then their Cartesian product f × g is a function from X × Y to A × B with

{displaystyle (ftimes g)(x,y)=(f(x),g(y)).}

This can be extended to tuples and infinite collections of functions.
This is different from the standard Cartesian product of functions considered as sets.

Cylinder[edit]

Let be a set and . Then the cylinder of with respect to is the Cartesian product of and .

Normally, is considered to be the universe of the context and is left away. For example, if is a subset of the natural numbers , then the cylinder of is .

Definitions outside set theory[edit]

Category theory[edit]

Although the Cartesian product is traditionally applied to sets, category theory provides a more general interpretation of the product of mathematical structures. This is distinct from, although related to, the notion of a Cartesian square in category theory, which is a generalization of the fiber product.

Exponentiation is the right adjoint of the Cartesian product; thus any category with a Cartesian product (and a final object) is a Cartesian closed category.

Graph theory[edit]

In graph theory, the Cartesian product of two graphs G and H is the graph denoted by G × H, whose vertex set is the (ordinary) Cartesian product V(G) × V(H) and such that two vertices (u,v) and (u′,v′) are adjacent in G × H, if and only if u = u′ and v is adjacent with v′ in H, or v = v′ and u is adjacent with u′ in G. The Cartesian product of graphs is not a product in the sense of category theory. Instead, the categorical product is known as the tensor product of graphs.

References[edit]

^ ^a ^b ^c Weisstein, Eric W. “Cartesian Product”. mathworld.wolfram.com. Retrieved September 5, 2020.
^ Warner, S. (1990). Modern Algebra. Dover Publications. p. 6.
^ Nykamp, Duane. “Cartesian product definition”. Math Insight. Retrieved September 5, 2020.
^ ^a ^b ^c “Cartesian Product”. web.mnstate.edu. Archived from the original on July 18, 2020. Retrieved September 5, 2020.
^ “Cartesian”. Merriam-Webster.com. 2009. Retrieved December 1, 2009.
^ Corry, S. “A Sketch of the Rudiments of Set Theory” (PDF). Retrieved May 5, 2023.
^ ^a ^b Singh, S. (August 27, 2009). Cartesian product. Retrieved from the Connexions Web site: http://cnx.org/content/m15207/1.5/
^ Cartesian Product of Subsets. (February 15, 2011). ProofWiki. Retrieved 05:06, August 1, 2011 from https://proofwiki.org/w/index.php?title=Cartesian_Product_of_Subsets&oldid=45868
^ Peter S. (1998). A Crash Course in the Mathematics of Infinite Sets. St. John’s Review, 44(2), 35–59. Retrieved August 1, 2011, from http://www.mathpath.org/concepts/infinity.htm
^ Osborne, M., and Rubinstein, A., 1994. A Course in Game Theory. MIT Press.

External links[edit]

Cartesian Product at ProvenMath
“Direct product”, Encyclopedia of Mathematics, EMS Press, 2001 [1994]
How to find the Cartesian Product, Education Portal Academy

Источник

КАРТА – СХЕМА
УЧЕБНОГО ЗАНЯТИЯ

продолжительность – 90 минут

Тема занятия: Декартово произведение и разбиение множеств на классы

Цели занятия:

·
расширить знания студентов с темы действия с
множествами, рассмотреть Декартово произведение, разбиение множеств на классы;

·
способствовать развитию памяти, внимания,
логического мышления;

·
создать условия для применения полученных знаний
при выполнении расчетных заданий.

Необходимое аппаратное и программное обеспечение:

·
компьютер;

·
экран;

·
проектор.

Дидактическое
обеспечение:

1.
Карточки с заданиями самостоятельной работы

2.
Стойлова АП.
Математика : учебник для студ. учреждений высш.образования / Л.П. Стойлова. –
4-е изд., стер. – М. : Издательский центр “Академия”, 2014.

3.
Информационные источники:

Стойлова АП. Математика : учебник для студ. учреждений высш.образования
/ Л.П. Стойлова. – 4-е изд., стер. – М. : Издательский центр
“Академия”, 2014.

Тип и вид учебного занятия:

·
лекция.

ОРГАНИЗАЦИОННАЯ СТРУКТУРА УРОКА

Этапы урока	Содержание и виды деятельности преподавателя	Примечания
1. Организационный этап	Приветствие, выявление отсутствующих, информирование о теме и целях занятия.
2. Актуализация ЗУН	Устный опрос. – Что такое множество? Что означает задать множество? – Способы задания множеств – Что такое подмножество? -какие действия выполняем над множествами? – Что такое пересечение? Объединение? – Какие свойства пересечения, объединения? Самостоятельная работа (с взаимопроверкой) 1. Даны множества: А = {2; 3; 8}, В = {2; 3; 8; 11}, С = {5; 11}. Найдите: а) А∩В; б) А∩С; в) С∩В. 2. Даны множества: А = {2; 3; 8}, В = {2; 3; 8; 11}, С = {5; 11}. Найдите: а) АUВ; б) АUС; в) СUВ. 3. Даны множества: А = {a, b, c, d}, B = {c, d, e, f}, C = {c, e, g, k}. Найдите а)(А∩В)∩С; б) )(АВ)С; в) (А В)∩С
3. Изучение нового материала	Теоретические сведения. – Декартово произведение. – разбиение множеств на классы
4. Первичное закрепление	Практическое выполнение заданий
5. Информация о домашнем задании	Самостоятельная работа	Методические рекомендации для самостоятельной работы
6. Подведение итогов урока	Подведение итогов работы группы, отдельных студентов. Корректирование пробелов знаний. Рефлексия

Декартово произведение

В
начальных классах ученики решают задачу: используя цифры 1, 2, 3
образовать всевозможные двузначные числа.

Путем
перебора дети получают:

11 12 13

21 22 23

31 32 33

Запись
каждого числа состоит из двух цифр, причем существенен порядок их следования.
Например, из цифр 1, 2 образованы числа 12 и 21.

В
том случае, когда важен порядок следования элементов множества, в математике
говорят об упорядоченных наборах элементов. В данной задаче – упорядоченные
пары (а; b), образованные из элементов а и b. Это (1;
2), (1; 3), (1; 4) и т.д. Первый элемент а называют первой
координатой пары, элемент b – второй.

Значит,
в нашей задаче мы оперировали множеством А={1, 2, 3} и образовывали
всевозможные пары.

Рассмотрим
другой пример. Пусть А={1, 2, 3}, B={4, 5}. Образуем всевозможные пары (а;b)
так, что аА, bВ.
Получим некоторое новое множество {(1; 5), (1; 4), (2; 4), (2; 5), (3;
4), (3; 5)}, элементами которого являются упорядоченные пары чисел. Это
новое множество называют декартовым произведением множеств А и В.

Декартовым произведением множеств А и В называется множество пар, первая компонента которых принадлежит
множеству А, вторая множеству В. Обозначают АВ. Таким
образом АВ =
{(x;y) | xA, yB}.

Операцию
нахождения декартового произведения множеств А и В называют декартовым
умножением этих множеств.

Рассмотрим
следующий пример. Известно, что АВ={(2,
3), (2, 5), (2, 6), (3, 3), (3, 5), (3, 6)}. Установим,
из каких элементов состоят множества А и В. Так как первая
компонента пары декартового произведения принадлежит множеству А, а
вторая – множеству В, то данные множества имеют следующий
вид: А={2, 3}, B={3, 5, 6}.

Перечислим
элементы, принадлежащие множеству АВ, если

А={a, b, c, d}, B=A. Декартово произведение АВ={(a,
a), (a, b), (a, c),
(a, d), (b, a), (b, b), (b, c), (b, d), (c, a), (c, b), (c, c), (c, d), (d, a),
(d, b) ,(d, c), (d, d)}.

Количество пар в декартовом прoизведении АВ
будет равно произведению числа элементов множества А и числа элементов
множества В: n(АВ)=n(A)n(B).

В
математике рассматривают не только упорядоченные пары, но и наборы из трех,
четырех и т.д. элементов. Такие упорядоченные наборы называют кортежами. Так, набор (1, 5, 6) есть кортеж длины 3, так как в нем
три элемента.

Используя
понятие кортежа, можно определить понятие декартового произведения n множеств.

Декартовым произведением множеств А, А,…, A называют множество кортежей длины n, образованных так, что первая
компонента принадлежит множеству А,
вторая – А, …, n-ая
– множеству А: АА…A.

Пусть
даны множества А={2,
3}; А={3,
4, 5}; A={7,
8}. Декартово произведение ААА={
(2, 3, 7), (2, 3, 8), (2, 4, 7), (2, 4, 8), (2, 5, 7),
(2, 5, 8),(3, 3, 7), (3, 4, 7), (3, 3, 8), (3, 4, 8), (3, 5, 7), (3, 5, 8)}.

Понятие разбиения множества
на классы

Понятие множества и операций над множествами позволяют
уточнить представление о классификации.

Классификация – это действие
распределения объектов по классам на основании сходств внутри класса и их
отличия от других объектов. Классификация широко применяется в математике.

Например, натуральные числа делятся на четные и нечетные;
углы бывают острые, тупые и прямые и т.д.

Любая классификация связана с разбиением некоторого
множества объектов на подмножества.

Считают, что множество Х разбито на классы Х, Х,…, Х,
если:

1) подмножества Х, Х,…, Х попарно
не пересекаются;

2) объединение этих подмножеств
совпадает с множеством Х.

Если не выполнено хотя бы одно из этих условий,
классификацию считают неправильной.

Например: а) Множество треугольников Х разбито на
три класса: остроугольные, прямоугольные и тупоугольные. Действительно,
выделенные подмножества попарно не пересекаются, а их объединение совпадает с
множеством Х; b) Из множества треугольников Х выделили подмножества
равнобедренных, равносторонних и разносторонних треугольников. Так как
множества равнобедренных и равносторонних треугольников пересекаются, значит,
не выполнено первое условие классификации, и разбиения множества Х на
классы мы не получили.

Так как разбиение множества на классы связано с выделением
его подмножеств, то классификацию можно выполнять при помощи свойств элементов
множеств.

Рассмотрим, например, множество натуральных чисел. Его
элементы обладают различными свойствами. Нас интересуют числа со свойством
«быть кратным 3». Это свойство позволяет выделить из множества N
подмножество, состоящее из чисел, кратных 3. Тогда про остальные
натуральные числа можно сказать, что они не кратны 3, т.е. получаем еще
одно подмножество множества N. Так как выделенные подмножества не
пересекаются, а их объединение совпадает с множеством N, то имеем
разбиение данного множества на два класса.

Вообще, если на множестве Х задано одно свойство,
то это множество разбивается на два класса. Первый – это класс объектов,
обладающих данным свойством, а второй – дополнение первого класса до множества Х.
Во втором классе содержатся такие объекты множества Х, которые заданным
свойством не обладают. Такую классификацию называют дихотомической.

Рассмотрим ситуацию, когда для элементов множества заданы
два свойства. Например, свойства натуральных чисел: «быть кратным 3» и «быть
кратным 5». При помощи этих свойств из множества N можно выделить два
подмножества: А – множество чисел, кратных 3 и В – множество
чисел, кратных 5. Эти множества пересекаются, но ни одно из них не является
подмножеством другого (рис. 13). Разбиения на подмножества А и В в
данном случае на произошло. Но круг, изображающий множество N, можно
рассматривать как состоящий из четырех непересекающихся областей. Каждая
область изображает некоторое подмножество множество N. Множество I
состоит из чисел, кратных 3 и 5, множество I – из чисел, кратных 3 и не кратных
5, множество III – из чисел, кратных 5 и не кратных 3, множество IV – из
чисел, не кратных 3 и не кратных 5. Объединение этих четырех множеств есть множество N.

Таким образом, выделение двух свойств привело к разбиению
множества N натуральных чисел на четыре класса.

Не следует думать, что задание двух свойств элементов множества всегда приводит
к разбиению этого множества на четыре класса. Например, при помощи таких двух
свойств «быть кратным 3» и «быть кратным 6» множество натуральных чисел
разбивается на три класса (рис. 14): I – класс чисел, кратных 6; II – класс
чисел, кратных 3, но не кратных 6; III – класс чисел, не кратных 3.

Примеры

Приведем несколько примеров
разбиения:

1. Множество четырехугольников разбито
на два класса:
трапеции и прямоугольники. Данные подмножества попарно не пересекаются, а их
объединения совпадают с множеством .

2. Множество четырехугольников разбито
на три класса:
квадраты, параллелограммы, прямоугольники. Так как прямоугольник и квадрат –
частные случаи параллелограмма, то данные подмножества пересекаются, значит, не
выполнено первое условие классификации, и разбиение множества не получено.

3. Дано множество прямых в
пространстве, которое разбито на классы по их взаимному расположению:
параллельные, пересекающиеся, скрещивающиеся. Данные подмножества попарно
не пересекаются, а их объединения совпадают с множеством .

4. Дано множество , которое
можно разделить на два класса: и , где –
множество натуральных четных чисел, а – множество натуральных нечетных
чисел.

5. Множество разбито на
три класса: , и . множество
чисел, которые делятся на , – множество чисел,
которые делятся на , множество чисел,
которые делятся на . Но существуют числа, которые могут
делится одновременно и на , и . Отсюда
следует, что подмножества пересекаются, и разбиение не получено.

Практические задания

Пример 1. Даны множества: А₁=
{2, 3}, А₂= {3, 4, 5}, А₃ = {6, 7}. Найти А₁´
А₂ ´А₃.

Решение. Элементами множества А₁´
А₂ ´А₃ будут кортежи длины 3 такие, что первая их
компонента принадлежит множеству А_1,вторая – множеству А₂,
третья – множеству А₃.

А₁´ А₂ ´А₃={(2, 3, 6), (2,3,7), (2,4,6), (2,4,7), (2,5,6), (2,5,7), (3,3,6),
(3,3,7),(3,4,6), (3,4,7), (3,4,7),(3,5,6), (3,5,7)}.

Пример 2. Пусть на множестве Х={3, 5, 7} задано отношение «меньше» (т.е. первый
элемент меньше второго, второй меньше третьего). Записать декартово
произведение X´X. Из этого множества следует выбрать элементы, которые должны
удовлетворять отношению «меньше».

Решение.

Декартово
произведение X ´ Х может быть записано в виде множества из упорядоченных пар:

X ´ Х=
{(3;3),(3;5),(3;7),(5;3),(5;5),(5;7),(7;3),(7;5),(7;7)}.

Из этого множества
выбираются элементы, которые удовлетворяют отношению «меньше». В результате
получится новое множество из упорядоченных пар:

W={(3;5),(3;7),(5;7)}.

В новом множестве
все пары являются элементами декартова произведения X´X. Отношение «меньше» на
множестве Х является подмножеством декартова произведения X´X. Бинарное отношение
на множестве Х есть подмножество декартова произведения WÌ X´X.

2) Декартово
произведение двух множеств X ´ Y.

Пример 3.

Пусть заданы два
множества: X= {2, 6, 1}, Y= {7, 4,
8}.

Записать декартово
произведение X ´ Y .

Решение.

Декартово
произведение двух множеств равно:

X ´ Y={(2, 7), (2, 4), (2, 8), (6, 7), (6, 4), (6, 8), (1, 7), (1, 4), (1,
8)}.

Аналогично можно
найти декартово произведение трёх множеств: X ´ Y´ Z.

Источник

Декартово произведение двух множеств

Понятие декартова произведения

Табличное представление декартовых произведений

Координатная плоскость как декартово произведение

Примеры

Прямое произведение в теории множеств[править | править код]

Произведение двух множеств[править | править код]

Комментарии[править | править код]

Декартова степень[править | править код]

Прямое произведение семейства множеств[править | править код]

Теоретико-множественные операции с прямыми произведениями[править | править код]

Прямое произведение отображений[править | править код]

Воздействие на математические структуры[править | править код]

Прямое произведение групп[править | править код]

Прямое произведение других алгебраических структур[править | править код]

Прямое произведение векторных пространств[править | править код]

Прямое произведение топологических пространств[править | править код]

Прямое произведение графов[править | править код]

Вариации и обобщения[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

1. Декартово произведение множеств

2. Свойства операции нахождения декартова произведения

Set-theoretic definition[edit]

Examples[edit]

A deck of cards[edit]

A two-dimensional coordinate system[edit]

Most common implementation (set theory)[edit]

Non-commutativity and non-associativity[edit]

Intersections, unions, and subsets[edit]

Cardinality[edit]

Cartesian products of several sets[edit]

n-ary Cartesian product[edit]

n-ary Cartesian power[edit]

Infinite Cartesian products[edit]

Other forms[edit]

Abbreviated form[edit]

Cartesian product of functions[edit]

Cylinder[edit]

Definitions outside set theory[edit]

Category theory[edit]

Graph theory[edit]

See also[edit]

References[edit]

External links[edit]

Примеры

Вам также может понравиться

Как исправить сзв стаж на одного сотрудника

Microsoft flight simulator как найти свой город

Как составить рифму для стихов

Добавить комментарий Отменить ответ