Операции над множествами: объединение, пересечение, дополнение и различие
17 авг. 2022 г.
читать 2 мин
Набор — это набор предметов.
Мы обозначаем набор с помощью заглавной буквы, а элементы в наборе определяем с помощью фигурных скобок. Например, предположим, что у нас есть некоторый набор под названием «A» с элементами 1, 2, 3. Мы запишем это так:
А = {1, 2, 3}
В этом руководстве объясняются наиболее распространенные операции с множествами, используемые в теории вероятностей и статистике.
Союз
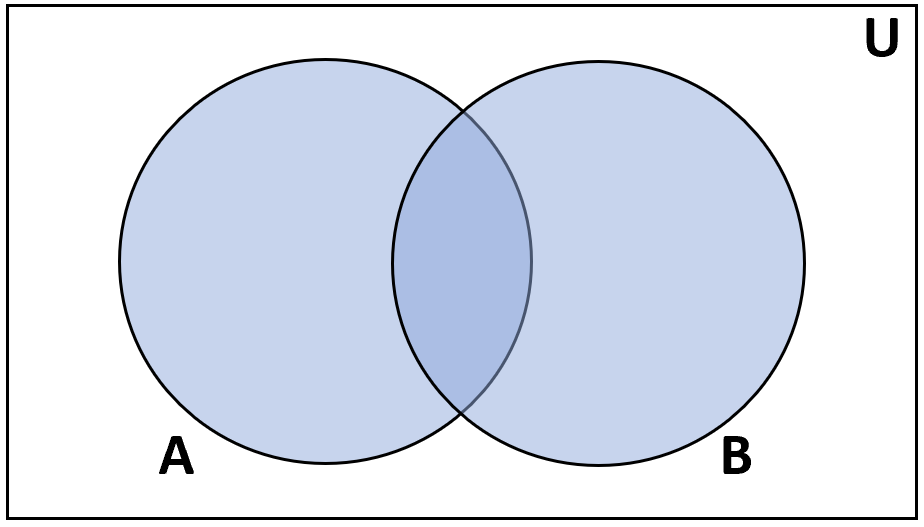
Определение: Объединение множеств A и B — это множество элементов, которые находятся либо в A, либо в B.
Обозначение: А ∪ В
Примеры:
- {1, 2, 3} ∪ {4, 5, 6} = {1, 2, 3, 4, 5, 6}
- {1, 2} ∪ {1, 2} = {1, 2}
- {1, 2, 3} ∪ {3, 4} = {1, 2, 3, 4}
Перекресток
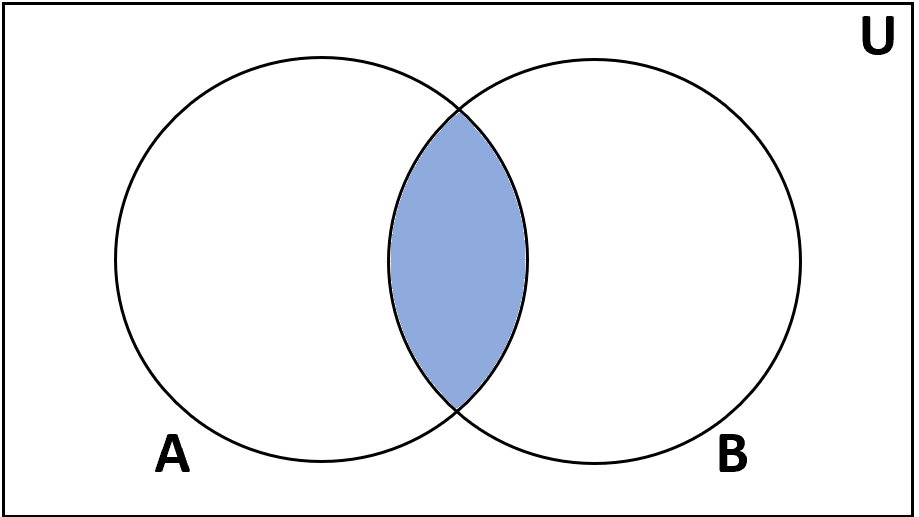
Определение: Пересечение множеств A и B — это множество элементов, которые находятся как в A, так и в B.
Обозначение: А ∩ В
Примеры:
- {1, 2, 3} ∩ {4, 5, 6} = {∅}
- {1, 2} ∩ {1, 2} = {1, 2}
- {1, 2, 3} ∩ {3, 4} = {3}
Дополнение
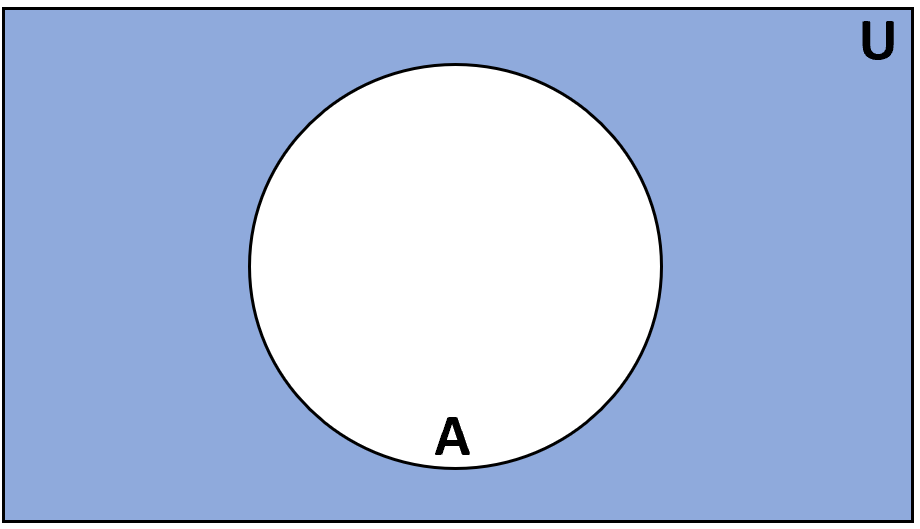
Определение: Дополнением множества A называется множество элементов, которые входят в универсальное множество U, но не входят в A.
Обозначение: A’ или A c
Примеры:
- Если U = {1, 2, 3, 4, 5, 6} и A = {1, 2}, то A c = {3, 4, 5, 6}
- Если U = {1, 2, 3} и A = {1, 2}, то A c = {3}
Разница
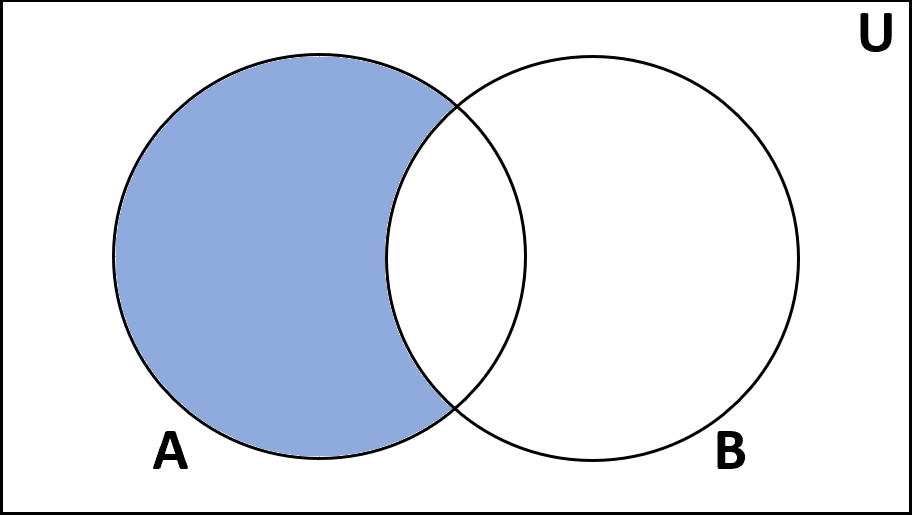
Определение: Разность множеств А и В — это множество элементов, которые есть в А, но отсутствуют в В.
Обозначение: А – Б
Примеры:
- {1, 2, 3} – {2, 3, 4} = {1}
- {1, 2} – {1, 2} = {∅}
- {1, 2, 3} – {4, 5} = {1, 2, 3}
Симметричная разница
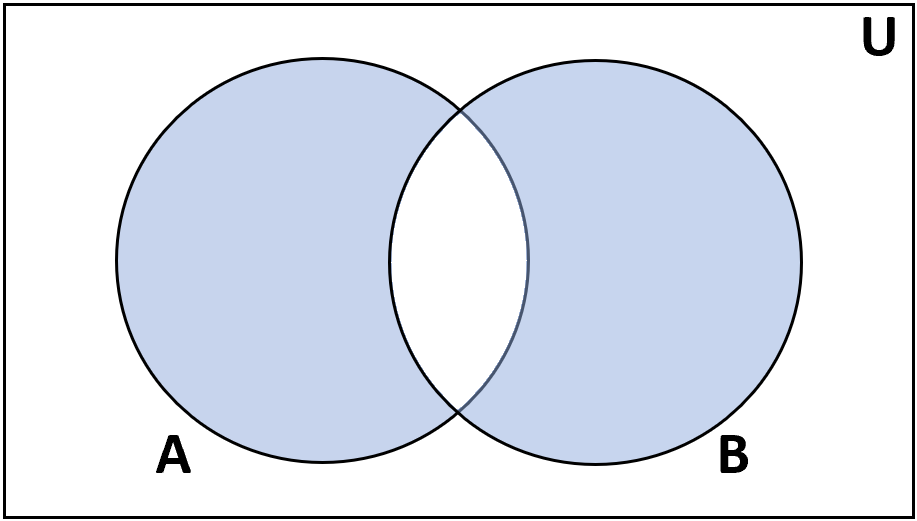
Определение: Симметричная разность множеств A и B — это множество элементов, которые находятся либо в A, либо в B, но не в обоих.
Обозначение: А Δ В
Примеры:
- {1, 2, 3} ∆ {2, 3, 4} = {1, 4}
- {1, 2} ∆ {1, 2} = {∅}
- {1, 2, 3} Δ {4, 5} = {1, 2, 3, 4, 5}
Декартово произведение
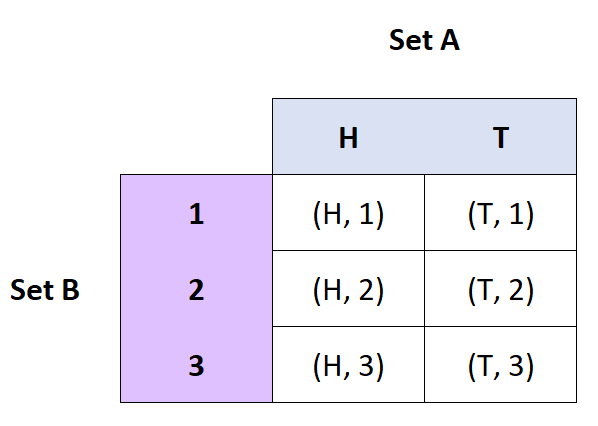
Определение: Декартово произведение множеств A и B — это множество упорядоченных пар из A и B.
Обозначение: А х В
Примеры:
- Если A = {H, T} и B = {1, 2, 3}, то A x B = {(H, 1), (H, 2), (H, 3), (T, 1), ( Т, 2), (Т, 3)}
- Если A = {T, H} и B = {1, 2, 3}, то A x B = {(T, 1), (T, 2), (T, 3), (H, 1), ( Н, 2), (Н, 3)}
Написано

Замечательно! Вы успешно подписались.
Добро пожаловать обратно! Вы успешно вошли
Вы успешно подписались на кодкамп.
Срок действия вашей ссылки истек.
Ура! Проверьте свою электронную почту на наличие волшебной ссылки для входа.
Успех! Ваша платежная информация обновлена.
Ваша платежная информация не была обновлена.
Декартово произведение множеств A
и B – это множество упорядоченных
пар, первый элемент которых принадлежит
A, а второй – принадлежит B.
![]()
Пример.
![]()
![]()
![]()
![]()
Свойства декартова произведения:
-

– некоммутативность -
 =
=
– ассоциативность
Свойство ассоциативности позволяет
использовать сокращенную запись для
декартова произведения нескольких
множеств:
![]()
![]()
-

– дистрибутивность относительно
объединения
![]()
– дистрибутивность относительно
пересечения
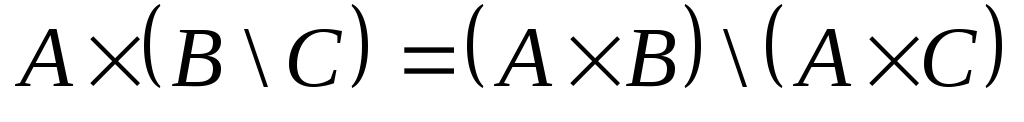
– дистрибутивность относительно разности
Доказательство: Докажем, например,
дистрибутивность декартова произведения
относительно операции пересечения
множеств.
-


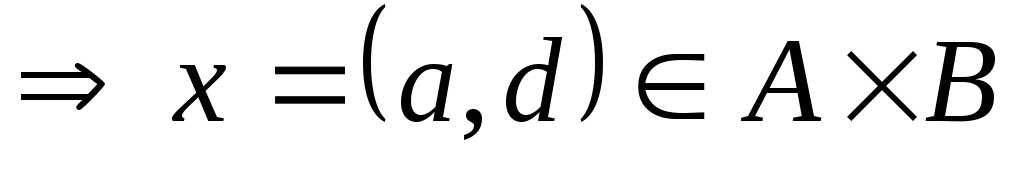 ;
;

-
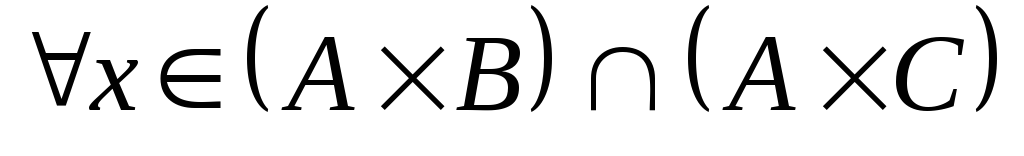 ,
, ,
,

Особым случаем декартова произведения
является произведение множества самого
на себя. В этом случае говорят о декартовом
квадрате множества или декартовой
n-ой степени множества А.
![]() ;
;
![]()
Пример.
![]()
![]()
Теорема. Если множество A содержит
n элементов, а B – m элементов,
т.е.:
![]()
![]() ,
,
то
![]()
содержит
![]()
элементов.
Соседние файлы в предмете Дискретная математика
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Решение некоторых математических задач предполагает нахождение пересечения и объединения числовых множеств. В статье ниже рассмотрим эти действия подробно, в том числе, на конкретных примерах. Полученный навык будет применим для решения неравенств с одной переменной и систем неравенств.
Простейшие случаи
Когда мы говорим о простейших случаях в рассматриваемой теме, то имеем в виду нахождение пересечения и объединения числовых множеств, представляющих из себя набор отдельных чисел. В подобных случаях будет достаточно использования определения пересечения и объединения множеств.
Объединение двух множеств – это множество, в котором каждый элемент является элементом одного из исходных множеств.
Пересечение множеств – это множество, которое состоит из всех общих элементов исходных множеств.
Из указанных определений логически следуют следующие правила:
– чтобы составить объединение двух числовых множеств, имеющих конечное количество элементов, необходимо записать все элементы одного множества и дописать к ним недостающие элементы из второго множества;
– чтобы составить пересечение двух числовых множеств, необходимо элементы первого множества один за другим проверить на принадлежность второму множеству. Те из них, которые окажутся принадлежащими обоим множествам и будут составлять пересечение.
Полученное согласно первому правилу множество будет включать в себя все элементы, принадлежащие хотя бы одному из исходных множеств, т.е. станет объединением этих множеств по определению.
Множество, полученное согласно второму правилу, будет включать в себя все общие элементы исходных множеств, т.е. станет пересечением исходных множеств.
Рассмотрим применение полученных правил на практических примерах.
Исходные данные: числовые множества А = {3, 5, 7, 12} и В = {2, 5, 8, 11, 12, 13}. Необходимо найти объединение и пересечение исходных множеств.
Решение
- Определим объединение исходных множеств. Запишем все элементы, к примеру, множества А: 3, 5, 7, 12. Добавим к ним недостающие элементы множества В: 2, 8, 11 и 13. В конечном итоге имеем числовое множество: {3, 5, 7, 12, 2, 8, 11, 13}. Упорядочим элементы полученного множества и получим искомое объединение: А∪B = {2, 3, 5, 7, 8, 11, 12, 13}.
- Определим пересечение исходных множеств. Согласно правилу, переберем один за другим все элементы первого множества A и проверим, входят ли они во множество B. Рассмотрим первый элемент – число 3: он не принадлежит множеству B, а значит не будет являться элементом искомого пересечения. Проверим второй элемент множества A, т.е. число 5: оно принадлежит множеству B, а значит станет первым элементом искомого пересечения. Третий элемент множества A – число 7. Оно не является элементом множества B, а, следовательно, не является элементом пересечения. Рассмотрим последний элемент множества A: число 1. Оно также принадлежит и множеству B, и соответственно станет одним из элементов пересечения. Таким образом, пересечение исходных множеств – множество, состоящее из двух элементов: 5 и 12, т.е. А∩В = {5, 12}.
Ответ: объединение исходных множеств – А∪B = {2, 3, 5, 7, 8, 11, 12, 13}; пересечение исходных множеств – А∩В = {5, 12}.
Все вышесказанное относится к работе с двумя множествами. Что же касается нахождения пересечения и объединения трех и более множеств, то решение этой задачи возможно свести к последовательному нахождению пересечения и объединения двух множеств. Например, чтобы определить пересечение трех множеств A, В и С, возможно сначала определить пересечение A и B, а затем найти пересечение полученного результата с множеством C. На примере это выглядит так: пусть будут заданы числовые множества: А = {3, 9, 4, 3, 5, 21}, В = {2,7, 9, 21} и С = {7, 9, 1, 3}. Пересечение первых двух множеств составит: А∩В = {9, 21}, а пересечение полученного множества с множеством А∩В = {9, 21}. В итоге: А∩В∩С = {9}.
Однако на практике, чтобы найти объединение и пересечение трех и более простейших числовых множеств, которые состоят из конечного количества отдельных чисел, удобнее применять правила, аналогичные указанным выше.
Т.е., чтобы найти объединение трех и более множеств указанного типа, необходимо к элементам первого множества добавить недостающие элементы второго множества, затем – третьего и т.д. Для пояснения возьмем числовые множества: А = {1, 2}, В = {2, 3}, С = {1, 3, 4, 5}. К элементам первого множества A добавится число 3 из множества B, а затем – недостающие числа 4 и 5 множества C. Таким образом, объединение исходных множеств: А∪В∪С = {1, 2, 3, 4, 5}.
Что же касается решения задачи на нахождение пересечения трех и более числовых множеств, которые состоят из конечного количества отдельных чисел, необходимо одно за другим перебрать числа первого множества и поэтапно проверять, принадлежит ли рассматриваемое число каждому из оставшихся множеств. Для пояснения рассмотрим числовые множества:
А = {3, 1, 7, 12, 5, 2} В = {1, 0, 2, 12} С = {7, 11, 2, 1, 6} D = {1, 7, 15, 8, 2, 6}.
Найдем пересечение исходных множеств. Очевидно, что множество B имеет меньше всего элементов, поэтому именно их мы будем проверять, определяя, входят ли они в остальные множества. Число 1 множества B является элементом и прочих множеств, а значит является первым элементом искомого пересечения. Второе число множества B – число 0 – не является элементом множества A, а, следовательно, не станет элементом пересечения. Продолжаем проверку: число 2 множества B является элементом прочих множеств и становится еще одной частью пересечения. Наконец, последний элемент множества B – число 12 – не является элементом множества D и не является элементом пересечения. Таким образом, получаем: A∩B∩C∩D = {1, 2}.
Координатная прямая и числовые промежутки как объединение их частей
Отметим на координатной прямой произвольную точку, например, с координатой -5,4. Указанная точка разобьет координатную прямую на два числовых промежутка – два открытых луча (-∞, -5,4) и (-5,4, +∞) и собственно точку. Нетрудно увидеть, что в соответствии с определением объединения множеств любое действительное число будет принадлежать объединению (-∞, -5,4)∪ {-5,4} ∪(-5,4, +∞). Т.е. множество всех действительных чисел R = (-∞; +∞) возможно представить в виде полученного выше объединения. И наоборот, полученное объединение будет являться множеством всех действительных чисел.
Отметим, что заданную точку возможно присоединить к любому из открытых лучей, тогда он станет простым числовым лучом (-∞, -5,4] или [-5,4, +∞). При этом множество R будет описываться следующими объединениями: (-∞, -5,4] ∪ (-5,4, +∞) или (-∞, -5,4) ∪ [-5,4, +∞)..
Подобные рассуждения действительны не только относительно точки координатной прямой, но и относительно точки на любом числовом промежутке. Т.е., если мы возьмем любую внутреннюю точку любого произвольного промежутка, его возможно будет представить, как объединение его частей, полученных после деления заданной точкой, и самой точки. К примеру, задан полуинтервал (7, 32] и точка 13, принадлежащая этому числовому промежутку. Тогда заданный полуинтервал можно представить в виде объединения (7, 13) ∪ {13} ∪ (13, 32] и обратно. Мы можем включить число 13 в любой из промежутков и тогда заданное множество (7, 32] можно представить, как (7, 13] ∪ (13, 32] или (7, 13] ∪ (13, 32]. Также мы можем взять в качестве исходных данных не внутреннюю точку заданного полуинтервала, а его конец (точку с координатой 32), тогда заданный полуинтервал можно представить, как объединение интервала (7, 32) и множества из одного элемента {32}. Таким образом: (7, 32] = (7, 32) ∪ {32}.
Еще один вариант: когда берется не одна, а несколько точек на координатной прямой или числовом промежутке. Эти точки разобьют координатную прямую или числовой промежуток на несколько числовых промежутков, а объединение этих промежутков будут составлять исходные множества. К примеру, на координатной прямой заданы точки с координатами -6, 0, 8, которые разобьют ее на промежутки: (-∞, -6), (-6,0), (0, 8), (8, +∞). При этом множество всех действительных чисел, олицетворением чего и является координатная прямая, возможно представить в виде объединения полученных промежутков и указанных чисел:
(-∞, -6) ∪ {-6} ∪(-6,0) ∪ {0} ∪ (0, 8) ∪ {8} ∪ (8, +∞).
Как определить пересечение и объединение при помощи изображений числовых множеств
С темой нахождения пересечения и объединения множеств возможно наглядно разобраться, если использовать изображения заданных множеств на координатной прямой (если только речь – не о простейших случаях, рассмотренных в самом начале статьи).
Мы рассмотрим общий подход, который позволяет определить результат пересечения и объединения двух числовых множеств. Опишем подход в виде алгоритма. Рассматривать его шаги будем постепенно, каждый раз приводя очередной этап решения конкретного примера.
Исходные данные: заданы числовые множества А = (7, +∞) и В = [-3, +∞). Необходимо найти пересечение и объединение данных множеств.
Решение
- Изобразим заданные числовые множества на координатных прямых. Их необходимо расположить друг над другом. Для удобства принято считать, что точки начала отсчета заданных множеств совпадают, и остается сохранным расположение точек друг относительно друга: любая точка с большей координатой лежит правее точки с меньшей координатой. При этом, если нам интересно объединение множеств, то координатные прямые объединяют слева квадратной скобкой совокупности; если интересует пересечение, то – фигурной скобкой системы.
В нашем примере для записи пересечения и объединения числовых множеств имеем: 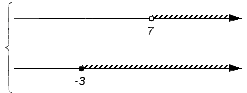 и
и 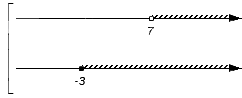
Изобразим еще одну координатную прямую, расположив ее под уже имеющимися. Она понадобится для отображения искомого пересечения или объединения. На этой координатной прямой отмечают все граничные точки исходных числовых множеств: сначала черточками, а позже, после выяснения характера точек с этими координатами, черточки будет заменены выколотыми или невыколотыми точками. В нашем примере это точки с координатами -3 и 7.
Получим:
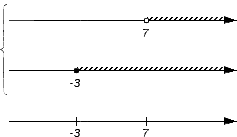 и
и 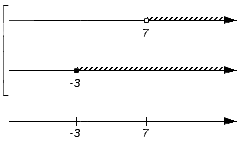
Точки, которые изображены на нижней координатной прямой в предыдущем шаге алгоритма, дают возможность рассматривать координатную прямую как набор числовых промежутков и точек (об этом мы говорили выше). В нашем примере координатную прямую представим в виде набора пяти числовых множеств: (-∞, -3), {-3}, (-3, 7), {7}, (7, +∞).
Теперь необходимо поочередно проверить принадлежность каждого из записанных множеств искомому пересечению или объединению. Получаемые выводы поэтапно отмечаются на нижней координатной прямой: когда промежуток является частью пересечения или объединения, над ним рисуется штриховка. Когда точка входит в пересечение или объединение, то штрих заменяется на сплошную точку; если точка не является частью пересечения или объединения – ее делают выколотой. В этих действиях нужно придерживаться таких правил:
-. промежуток становится частью пересечения, если он одновременно является частью множества A и множества B (или иными словами – если есть штриховка над этим промежутком на обеих координатных прямых, отображающих множества А и B);
– точка становится частью пересечения, если она является одновременно частью каждого из множеств А и В (иными словами – если точка является невыколотой или внутренней точкой какого-либо интервала обоих числовых множеств A и B);
– промежуток становится частью объединения, если он является частью хотя бы одного из множеств A или B (иными словами – если присутствует штриховка над этим промежутком хотя бы на одной из координатных прямых, отображающих множества A и B.
– точка становится частью объединения, если она является частью хотя бы одного из множеств A и B (иными словами – точка является невыколотой или внутренней точкой какого-либо интервала хотя бы одного из множеств A и B).
Кратко резюмируя: пересечением числовых множеств A и B служит пересечение всех числовых промежутков множеств A и B, над которыми одновременно присутствует штриховка, и всех отдельных точек, принадлежащих и множеству А, и множеству В. Объединением числовых множеств A и B служит объединение всех числовых промежутков, над которыми присутствует штриховка хотя бы у одного из множеств A или B, а также всех невыколотых отдельных точек.
- Вернемся к примеру, определим пересечение заданных множеств. Для этого поочередно проверим множества: (-∞, -3), {-3}, (-3, 7), {7}, (7, +∞). Начнем с множества (-∞, -3), наглядно выделив его на чертеже:
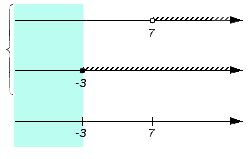
Этот промежуток не будет включен в пересечение, потому что не является частью ни множества A, ни множества B (нет штриховки). И так наш чертеж сохраняет свой изначальный вид:
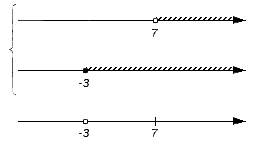
Рассмотрим следующее множество {-3}. Число -3 является частью множества B (невыколотой точкой), но не входит в состав множества A, а потому не станет частью искомого пересечения. Соответственно на нижней координатной прямой точку с координатой -3 делаем выколотой:
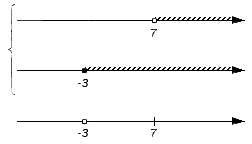
Оцениваем следующее множество (-3, 7).
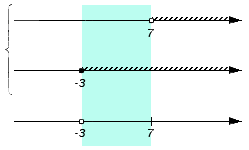
Оно является частью множества B (над интервалом присутствует штриховка), но не входит в множество A (над интервалом штриховка отсутствует): не будет входить в искомое пересечение, а значит на нижней координатной прямой не появляется никаких новых отметок:
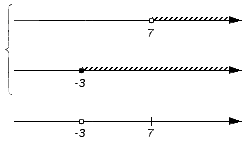
Следующее множество на проверку – {7}. Оно является составом множества B (точка с координатой 7 является внутренней точкой промежутка [-3, +∞) ), но не является частью множества A (выколотая точка), таким образом, рассматриваемый промежуток не станет частью искомого пересечения.. Отметим точку с координатой 7 как выколотую:
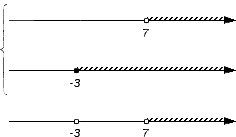
И, наконец, проверяем оставшийся промежуток (7, +∞).
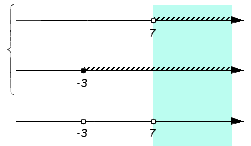
Промежуток входит в оба множества A и B (над промежутком присутствует штриховка), следовательно, становится частью пересечения. Штрихуем место над рассмотренным промежутком:
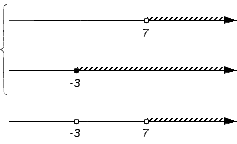
В конечном счете на нижней координатной прямой образовалось изображение искомого пересечения заданных множеств. Очевидно, что оно является множеством всех действительных чисел больше числа 7, т.е.: А∩В = (7, +∞).
- Следующим шагом определим объединение заданных множеств A и B. Последовательно проверим множества (-∞, -3), {-3}, (-3, 7), {7}, (7, +∞), устанавливая факт включения или невключения их в искомое объединение.
Первое множество (-∞, -3) не является частью ни одного из исходных множеств A и B (над промежутками нет штриховок), следовательно, множество (-∞, -3) не войдет в искомое объединение:
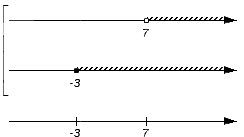
Множество {-3} входит в множество B, а значит будет входить в искомое объединение множеств A и B:
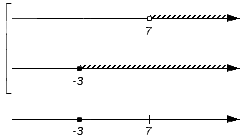
Множество (-3, 7) является составной частью множества B (над интервалом присутствует штриховка) и становится элементом объединения множеств A и B:
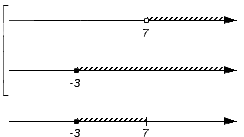
Множество 7 входит в числовое множество B, поэтому войдет и в искомое объединение:
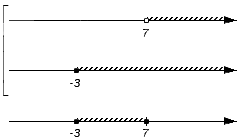
Множество (7, +∞), являясь элементом обоих множеств А и В одновременно, становится еще одной частью искомого объединения:
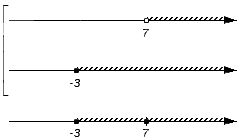
По итоговому изображению объединения исходных множеств А и В получаем: А∩В = [-3, +∞).
Имея некий практический опыт применения правил нахождения пересечений и объединений множеств, описанные проверки легко проводятся устно, что позволяет быстро записывать конечный результат. Продемонстрируем на практическом примере, как выглядит его решение без детальных пояснений.
Исходные данные: множества А =(-∞, -15)∪{-5}∪[0, 7)∪{12} и В =(-20, -10)∪{-5}∪(2, 3)∪{17}. Необходимо определить пересечение и объединение заданных множеств.
Решение
Отметим заданные числовые множества на координатных прямых, чтобы иметь возможность получить иллюстрацию искомых пересечения и объединения:


Ответ: А∩В = (-20,-15)∪{-5}∪(2, 3); А∪В = (-∞, -10)∪{-5}∪[0, 7]∪{12, 17}.
Также понятно, что при достаточном понимании процесса указанный алгоритм возможно подвергнуть оптимизации. К примеру, в процессе нахождения пересечения можно не тратить время на проверку всех промежутков и множеств, представляющих собой отдельные числа, ограничившись рассмотрением только тех промежутков и чисел, которые составляют множество А или В. Прочие промежутки в любом случае не войдут в пересечение, т.к. не являются частью исходных множеств. Составим иллюстрацию сказанного на практическом примере.
Исходные данные: множества А = {-2}∪[1, 5] и B = [-4, 3].
Необходимо определить пересечение исходных множеств.
Решение
Геометрически изобразим числовые множества А и В:
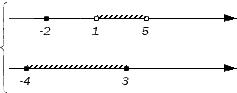
Граничные точки исходных множеств разобьют числовую прямую на несколько множеств:
(-∞, -4), {-4}, (-4, -2), {-2}, (-2, -1), {1}, (1, 3), {3}, (3, 5), {5}, (5, +∞).
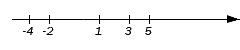
Легко заметить, что числовое множество A можно записать, объединив некоторые из перечисленных множеств, а именно: {-2}, (1, 3), {3} и (3, 5). Достаточно будет проверить эти множества на их включенность также в множество В для того, чтобы найти искомое пересечение. Те, что войдут в множество В и станут элементами пересечения. Проведем проверку.
Совершенно понятно, что {-2} является частью множества B , ведь точка с координатой -2 – внутренняя точка отрезка [-4, 3). Интервал (1, 3) и множество {3} также входят в множество В (над интервалом присутствует штриховка, а точка с координатой 3 является для множества В граничной и невыколотой). Множество (3, 5) не будет элементом пересечения, т.к. не входит в множество В (над ним не присутствует штриховка). Отметим все вышесказанное на чертеже:
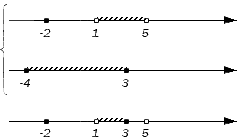
В итоге искомым пересечением двух заданных множеств будет объединение множеств, которое мы запишем так: {-2}∪(1, 3].
Ответ: А∩В = {-2}∪(1, 3].
В заключении статьи обговорим еще, как решить задачу о нахождении пересечения и объединения нескольких множеств (более 2). Сведем ее, как рекомендовалось ранее, к необходимости определения пересечения и объединения первых двух множеств, затем полученного результата с третьим множеством и так далее. А можно использовать описанный выше алгоритм с единственным только отличием, что проверку вхождения промежутков и множеств, представляющих собой отдельные числа, необходимо проводить не по двум, а всем заданным множествам. Рассмотрим на примере.
Исходные данные: множества А = (-∞, 12], В = (-3,25], D = (-∞, 25)ꓴ{40}. Необходимо определить пересечение и объединение заданных множеств.
Решение
Отображаем заданные числовые множества на координатных прямых и ставим с левой от них стороны фигурную скобку, обозначая пересечение, а также квадратную, обозначая объединение. Ниже отобразим координатные прямые с отмеченными штрихами граничными точками числовых множеств:
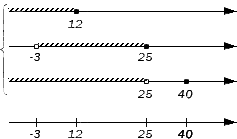
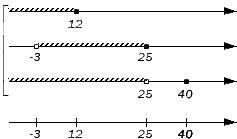
Таким образом, координатная прямая представлена следующими множествами: (-∞, -3), {-3}, (-3, 12), {12}, (12, 25), {25}, (25, 40), {40}, (40, +∞).
Начинаем искать пересечения, поочередно проверяя записанные множества на принадлежность каждому из исходных. Во все три заданных множества входит интервал (-3, 12) и множество {-12}: они и станут элементами искомого пересечения. Таким образом, получим: A∩B∩D = (-3, 12].
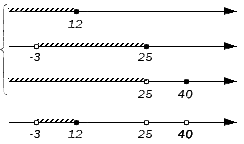
Объединение заданных множеств составят множества: (-∞, -3) – элемент множества А; {-3} – элемент множества А; (-3, 12) – элемент множества А; {12} – элемент множества А; (12, 25) – элемент множества В; {25} – элемент множества В и {40} – элемент множества D. Таким образом, получим: A∪B∪D = (-∞, 25] ∪ {40}.
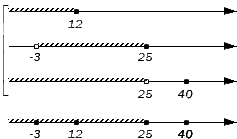
Ответ: A∩B∩D = (-3, 12]; A∪B∪D = (-∞, 25] ∪ {40}.
Отметим также, что искомое пересечение числовых множеств часто является пустым множеством. Происходит это в тех случаях, когда в заданные множества не включены элементы, одновременно принадлежащие им всем.
Исходные данные: А = [-7, 7]; В = {-15}∪[-12, 0)∪{5}; D = [-15, -10]∪[10, +∞); Е = (0, 27). Определить пересечение заданных множеств.
Решение
Отобразим исходные множества на координатных прямых и штрихами граничные точки этих множеств на дополнительной прямой.

Отмеченные точки разобьют числовую прямую на множества: (-∞, -15), {-15}, (-15, -12), {-12}, (-12, -10), {-10}, (-10, -7), {-7}, (-7, 0), {0}, (0, 5), {5}, (5, 7), {7}, (7, 10), {10}, (10, 27), {27}, (27, +∞).
Ни одно из них не является одновременно элементом всех исходных множеств, следовательно, пересечение заданных множеств есть пустое множество.
Ответ: A∩B∩D∩Е = Ø.
Множества удобно изображать в виде кругов, которые называют кругами Эйлера.
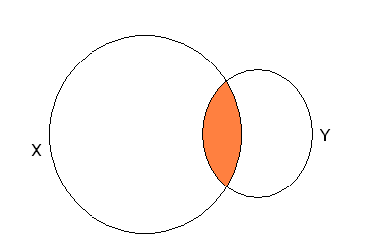
На рисунке множество пересечения множеств X и Y закрашено в оранжевый цвет.
Содержание:
Основные понятия:
Множество – одно из важнейших понятий математики. Вводится аксиоматически и не может быть определено через какие-либо элементарные понятия.
Кантор описывает множество следующим образом:
Множество S есть любое собрание определенных и различимых между собой объектов пашей интуиции и интеллекта, мыслимое как единое целое. Эти объекты называются элементами множества S
Термин «множество» характеризует совокупность, объединение некоторых объектов произвольной природы – элементов множества, которые обладают каким-либо общим для них свойством (признаком). Этот общий признак содержится в самом названии (задании) множества. Множество состоит из элементов и считается заданным, если о каждом из рассматриваемых объектов известно, входит он во множество или нет. Множество может быть задано либо перечислением его элементов, либо описанием свойств его элементов. Символическая запись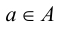
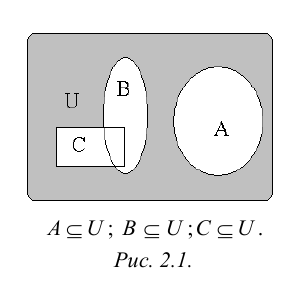
Рис. 2.1. Множество А называют подмножеством другого множества U или множество А включено во множество U, если каждый элемент множества А является одновременно элементом множества U. Это обозначается 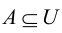 . Выделение подмножеств из множеств можно провести по различным признакам. В результате могут получиться как непересекающиеся подмножества (например, А и В ) так и подмножества, имеющие общие элементы ( В и С). Если множество состоит из конечного числа элементов, оно называется конечным. При этом число элементов множества может быть очень велико или вообще неизвестно. Множество может состоять также из бесконечного количества элементов, тогда оно называется бесконечным.
. Выделение подмножеств из множеств можно провести по различным признакам. В результате могут получиться как непересекающиеся подмножества (например, А и В ) так и подмножества, имеющие общие элементы ( В и С). Если множество состоит из конечного числа элементов, оно называется конечным. При этом число элементов множества может быть очень велико или вообще неизвестно. Множество может состоять также из бесконечного количества элементов, тогда оно называется бесконечным.
Свойства включения:
- Каждое множество есть подмножество самого себя
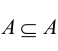 ;
; - Если
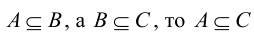 ;
; 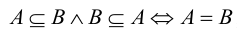 , т.е. множества А и В равны тогда и только тогда, когда эти множества состоят из одних и тех же элементов;
, т.е. множества А и В равны тогда и только тогда, когда эти множества состоят из одних и тех же элементов;- Каждый элемент множества А определяет некоторое подмножество множества А:
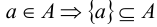
Множество, не содержащее ни одного элемента, называется пустым и обозначается 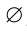 .
.
- Любое множество содержит
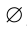 в качестве подмножества.
в качестве подмножества. - Каждое множество
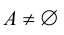 имеет, по крайней мере, два различных подмножества:
имеет, по крайней мере, два различных подмножества: 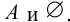 .
.
Множество 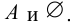 называют несобственными подмножествами множества А. Все остальные подмножества множества А называются собственными или истинными. В этом случае, когда
называют несобственными подмножествами множества А. Все остальные подмножества множества А называются собственными или истинными. В этом случае, когда 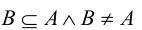 говорят, что В строго включено в А (обозначается
говорят, что В строго включено в А (обозначается 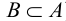 ):
):
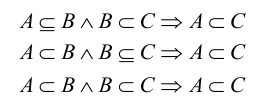
Множество всех подмножеств множества А называется множеством-степенью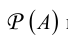 множества А.
множества А.
Если А не содержит элементов, т.е. 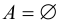 , то его единственным подмножеством является
, то его единственным подмножеством является 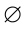 .
.
Если А – одноэлементное множество, т.е. 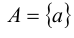 , то его подмножествами являются А и
, то его подмножествами являются А и 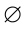 . Число этих подмножеств равно 2.
. Число этих подмножеств равно 2.
Если А – двухэлементное множество, т.е. 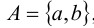 , то его подмножествами являются
, то его подмножествами являются 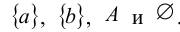 Число этих подмножеств равно 4.
Число этих подмножеств равно 4.
Несложно убедиться в том, что множество-степень 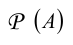 конечного n-элементного множества (А) состоит из 2″ подмножеств.
конечного n-элементного множества (А) состоит из 2″ подмножеств.
Основные операции над множествами
Суммой или объединением двух или произвольного (даже бесконечного) числа заданных множеств называется множество, состоящее из всех элементов, принадлежащих хотя бы одному из заданных множеств. Эта операция над множествами обозначается знаком 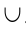 .
.
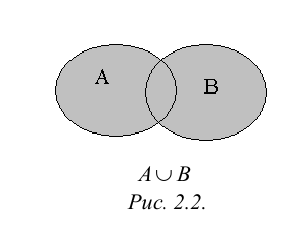
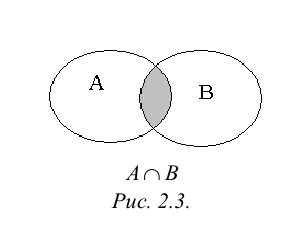
Произведением или пересечением двух или произвольного (даже бесконечного) числа заданных множеств называется множество, состоящее из всех элементов, принадлежащих каждому из заданных множеств. Эта операция над множествами обозначается знаком  . Если
. Если 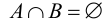 , то множества А и В называются непересекающимися.
, то множества А и В называются непересекающимися.
Два множества называются непересекающимися (или расчлененными) если 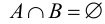 . Практический интерес представляют разбиения множества на взаимно непересекающиеся подмножества (эту задачу иногда называются классификацией). Разбиением множества А называется такая расчлененная система непустых подмножеств множества А, что каждый элемент множества А является элементом некоторого единственного множества этой системы. Возможность разбиения множества на непересекающиеся подмножества зависит от признака, по которому производится разбиение.
. Практический интерес представляют разбиения множества на взаимно непересекающиеся подмножества (эту задачу иногда называются классификацией). Разбиением множества А называется такая расчлененная система непустых подмножеств множества А, что каждый элемент множества А является элементом некоторого единственного множества этой системы. Возможность разбиения множества на непересекающиеся подмножества зависит от признака, по которому производится разбиение.
Разностью множеств А и В или дополнением В до А называется множество, состоящее только из тех элементов А, которые не входят в В. Эта операция над множествами обозначается знаком .
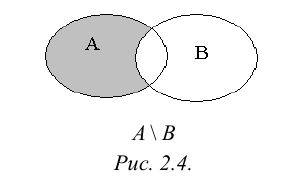
А В Рис. 2.4.
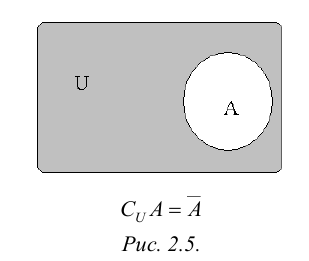
Часто все рассматриваемые множества считают подмножествами одного основного множества U. В таком случае разность U А (дополнение А до U) обозначают, как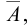 , а операцию называют взятием дополнения.
, а операцию называют взятием дополнения.
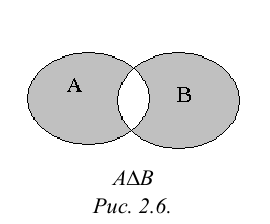
Симметрической разностью множеств А и В называется множество С: 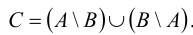 .
.
Обозначается симметрическая разность: 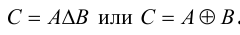 .
.
Для подмножеств данного множества U выполняются следующие законы:
Закон коммутативности (переместительный закон):
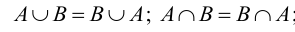
Закон ассоциативности (сочетательный закон) для любой тройки множеств А, В и С:
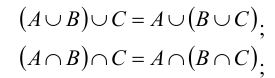
Закон дистрибутивности (распределительный закон) для любой тройки множеств А, В и С:
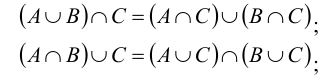
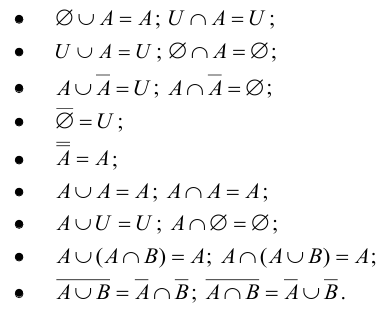
Если операции объединения множеств поставить в соответствие операцию сложения чисел, операции пересечения множеств – операцию умножения, универсальному множеству U – единицу, а пустому множеству – ноль, то возникает аналогия между множествами и числами. Операции объединения и пересечения множеств, как и действия над действительными числами, подчиняются законам коммутативности, ассоциативности и дистрибутивности. Можно также провести аналогию между свойствами логических операций, где логической эквивалентности соответствует операция равенства, а операциям конъюнкции и дизъюнкции – операции объединения и пересечения.
Свойства фигурируют попарно таким образом, что каждое получается из соседнего заменой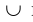 на
на  , U на
, U на 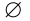 и наоборот. Такие выражения называются двойственными друг другу.
и наоборот. Такие выражения называются двойственными друг другу.
Принцип двойственности. Для любого тождества множеств двойственное ему выражение также является тождеством.
Очевидно, что операция разность не обладает свойствами коммутативности и ассоциативности, в то же время операция симметрическая разность и коммутативна, и ассоциативна.
Большое значение в современной математике имеет множественная операция декартово произведение. Если заданы два множества А и то из их элементов можно составить упорядоченные пары, взяв сначала какой-либо элемент первого множества, а затем -элемент второго множества. Декартовым произведением двух исходных множеств А и В называется множество С, составленное из упорядоченных пар (а,b). Декартово произведение множеств А и В обозначается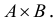 .
.
Очевидно, что 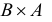 и
и 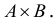 – различные множества, т.е. операция декартова произведения не коммутативна, но, в то же время, она обладает свойством ассоциативности.
– различные множества, т.е. операция декартова произведения не коммутативна, но, в то же время, она обладает свойством ассоциативности.
Отображения
Отображение – одно из основных понятий математики. Отображение есть какое-либо правило или закон соответствия множеств. Пусть X и Y – произвольные непустые множества. Говорят, что задано отображение 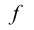 множества X на множество Y (запись:
множества X на множество Y (запись: 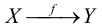 или
или 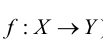 ) если каждому элементу х множества
) если каждому элементу х множества 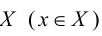 поставлен соответствие единственный, однозначно определенный элемент
поставлен соответствие единственный, однозначно определенный элемент 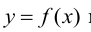 множества
множества 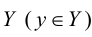 .
.
Элемент 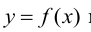 называется образом элемента х при отображении
называется образом элемента х при отображении 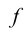 , а элемент
, а элемент 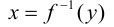 называется прообразом элемента у при этом отображении. Образом множества X элементов х при отображении
называется прообразом элемента у при этом отображении. Образом множества X элементов х при отображении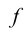 называется множество всех элементов вида
называется множество всех элементов вида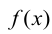 , принадлежащих области значений Y. Множество X всех элементов
, принадлежащих области значений Y. Множество X всех элементов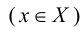 , образы которых
, образы которых 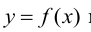 составляют область значений Y называется прообразом множества Y элементов
составляют область значений Y называется прообразом множества Y элементов 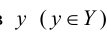 . Множество X называется областью определения отображения
. Множество X называется областью определения отображения 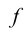 .
.
Отображение 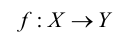 называется сюръективным, когда каждый элемент y множества
называется сюръективным, когда каждый элемент y множества 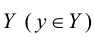 имеет хотя бы один прообраз х множества
имеет хотя бы один прообраз х множества 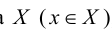 , т.е.
, т.е. 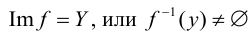 .
.
Отображение 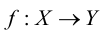 называется инъективным, когда каждый элемент
называется инъективным, когда каждый элемент 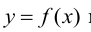 множества
множества 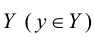 является образом лишь одного элемента х множества
является образом лишь одного элемента х множества 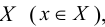 , т.е. образы любых двух различных элементов множества X различны, т.е. из
, т.е. образы любых двух различных элементов множества X различны, т.е. из 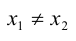 следует
следует 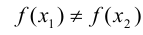 .
.
Отображение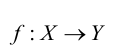 называется биективным или взаимно однозначным, когда оно одновременно ипъективно и сюръективно, т.е. каждый элемент множества Y является образом одного и только одного элемента множества X.
называется биективным или взаимно однозначным, когда оно одновременно ипъективно и сюръективно, т.е. каждый элемент множества Y является образом одного и только одного элемента множества X.
Равенство двух отображений 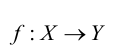 и
и 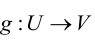 означает по определению, что их соответствующие области совпадают (X = U и Y= V), причем
означает по определению, что их соответствующие области совпадают (X = U и Y= V), причем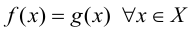 .
.
Произведение двух отображений 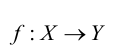 и
и 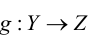 можно определить как отображение
можно определить как отображение 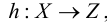 , которое каждому элементу х множества
, которое каждому элементу х множества 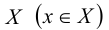 ставит в соответствие элемент
ставит в соответствие элемент 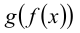 множества
множества 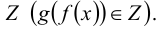 .
.
Отображение 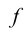 множества X на множество Y иначе называется функцией на множестве X со значениями во множестве Y. Если множества X и Y совпадают, то биективное отображение множества X на себя
множества X на множество Y иначе называется функцией на множестве X со значениями во множестве Y. Если множества X и Y совпадают, то биективное отображение множества X на себя 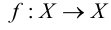 называется преобразованием множества X. Простейшее преобразование множества X – тождественное
называется преобразованием множества X. Простейшее преобразование множества X – тождественное 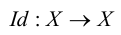 – определяется так:
– определяется так: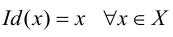 . Тождественное отображение
. Тождественное отображение 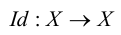 , переводящее каждый элемент
, переводящее каждый элемент 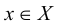 в себя, также называют единичным преобразованием. Если заданы преобразования
в себя, также называют единичным преобразованием. Если заданы преобразования 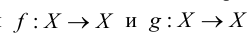 , то преобразование
, то преобразование 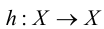 , являющееся результатом последовательного выполнения сначала преобразования
, являющееся результатом последовательного выполнения сначала преобразования 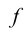 , а затем и преобразования g, называется произведением преобразований
, а затем и преобразования g, называется произведением преобразований 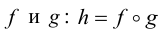 .
.
Для преобразований 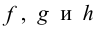 одного и того же множества X справедливы следующие законы:
одного и того же множества X справедливы следующие законы:
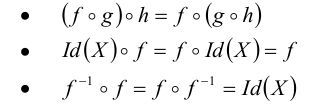
Коммутативный закон для произведения преобразований в общем случае не выполняется, т.е. 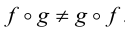 .
.
Если между двумя множествами можно задать биективное отображение (установить взаимно однозначное соответствие между их элементами), то такие множества называются эквивалентными или равномощными. Конечные множества равномощны только в том случае, когда число их элементов одинаково.
Бесконечные множества также можно сравнивать между собой.
Два множества имеют одинаковую мощность или называются эквивалентными (обозначение А = В), если между их элементами можно установить взаимно однозначное соответствие, т.е. если можно указать некоторое правило, в соответствии с которым каждому элементу одного из множеств соотносится один и только один элемент другого множества.
Если же подобное отображение невозможно, то множества имеют различную мощность; при этом оказывается, что в последнем случае, каким бы образом мы не пытались привести в соответствие элементы обоих множеств, всегда останутся лишние элементы и притом всегда от одного и того же множества, которому приписывается более высокое значение кардинального числа или говорят, что это множество имеет большую мощность.
Бесконечное множество и некоторое его подмножество могут быть эквивалентными.
Множество, эквивалентное множеству натуральных чисел, называется счетным множеством. Для того чтобы множество А было счетным, необходимо и достаточно, чтобы каждому элементу а множества А был поставлен в соответствие его порядковый номер 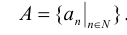 „ Из всякого бесконечного множества можно выделить счетное подмножество. Всякое подмножество счетного множества является счетным или конечным. Счетное множество является наиболее примитивно организованным бесконечным множеством. Декартово произведение двух счетных множеств является счетным. Объединение конечного или бесконечного числа конечных или счетных множеств является конечным или счетным множеством.
„ Из всякого бесконечного множества можно выделить счетное подмножество. Всякое подмножество счетного множества является счетным или конечным. Счетное множество является наиболее примитивно организованным бесконечным множеством. Декартово произведение двух счетных множеств является счетным. Объединение конечного или бесконечного числа конечных или счетных множеств является конечным или счетным множеством.
Отношения эквивалентности и упорядоченности
В математике понятие отношения используется для обозначения какой-либо связи между объектами. Отношение есть некоторое множество упорядоченных пар {х,у), где 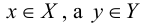 .
.
Часто приходится рассматривать несколько элементов множества как эквивалентные, потому что по определенным признакам один элемент может быть заменен другим. Так, например, по признаку величины дроби 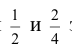 эквивалентны. Отношение эквивалентности рефлексивно, симметрично и транзитивно. Понятие эквивалентности подразумевает выполнение следующих условий:
эквивалентны. Отношение эквивалентности рефлексивно, симметрично и транзитивно. Понятие эквивалентности подразумевает выполнение следующих условий:
- каждый элемент эквивалентен самому себе;
- высказывание, что два элемента являются эквивалентными, не требует уточнения, какой из элементов рассматривается первым;
- два элемента, эквивалентные первому, эквивалентны между собой.
Пусть А – множество, в котором определено отношение эквивалентности. Подмножество элементов, эквивалентных элементу а, называется классом эквивалентности: все элементы этого класса эквивалентны между собой и всякий элемент а из А находится в одном и только в одном классе (если элементов, эквивалентных а, не существует, то а может быть и единственным элементом класса). Отношение эквивалентности в А определяет на А разбиение на классы эквивалентности, т.е. А становится объединением непересекающихся классов.
Особенности природы элементов множества в большинстве случаев позволяют установить между ними отношения полного (или совершенного) порядка. Это отношение по определению обладает следующими свойствами:
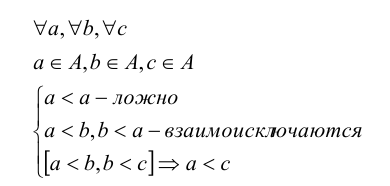
Если между элементами множества определено также и отношение эквивалентности, то между элементами устанавливается отношение неполного или нестрогого порядка:
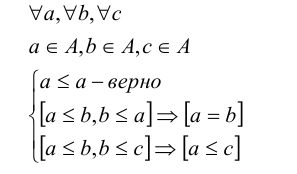
Возможны случаи, когда некоторые элементы множества не сравнимы. Такие множества называются частично упорядоченными.
Способы задания множеств
Как в повседневной, так и в научной жизни часто говорят о чертах какого-либо коллектива, совокупности некоторых объектов. Так, например, можно говорить о студентах группы некоторого института, о совокупности точек внутри некоторого круга и т.д.
Понятие множества в математике выведено из понятия совокупностей, образуемых из предметов, сведенных в одно целое. Предметы, собранные во множество, называются элементами множества. Понятие множество и элемент считаются основным понятиями и не сведены к другим понятиям путем применения формального определения. Таким образом, под множеством, мы будем понимать любое объединение в одно целое М определенных вполне различимых объектов m из нашего восприятия или мысли, которые называются элементами М
Каждое множество считается самостоятельной осмысленной вещыо, как бы осмысленной оболочкой его элементов. Множество
считается известным, если заданы его элементы; множество определяется раз и навсегда заданием его элементов; множества не зависят or времени.
Следовательно, множество однозначно определяется его элементами.
Множество, у которого ни один предмет не является элементом, называется пустым множеством. Пустое множество обозначается символом 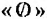 .
.
Для обозначения множеств обычно применяются заглавные латинские буквы. Выражение 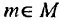 обозначает, что объект m является элементом М (читается: «m является элементом М или m принадлежит М»).
обозначает, что объект m является элементом М (читается: «m является элементом М или m принадлежит М»).
Выражение 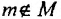 : «m не является элементом М или m не принадлежит М». Элементами множества могут быть и множссгва.
: «m не является элементом М или m не принадлежит М». Элементами множества могут быть и множссгва.
Справедлива следующая
Теорема 1.1.1. Два множества тождественны (равны) тогда и только тогда. если их элементы одинаковы.
Доказательство. Если два множества тождественны (равны), то на основе понятия тождественности элементы обоих множеств одинаковы.
С другой стороны, если о двух множествах нам известно, что их элементы тождественны, то эти два множссгва тождественны, так как множество однозначно определяется его элементами. 
В определениях, касающихся геометрических мест, всегда присутствует отождествление множеств, заданных двумя разнымиопределениями.
Например. Перпендикулярная липия, пересекающая отрезок прямой, является геометрическим местом точек, расположенных на одинаковом расстоянии от двух концов озрезка. Это означает следующее: В плоскости множество точек перпендикулярной линии, пересекающей в середине отрезок прямой, тождественно множеству точек, расположенных на одинаковом расстоянии от обоих концов отрезка.
Множество часто задается в следующем виде: элементы множества заключаются внутри фигурных скобок: {…}. Подобной записью может быть конкретное перечисление элементов множества или задание такого определения, которым элементы множества однозначно задаются.
Например:
- а) {гласные звуки слова «МАТЕМАТИКА»} – множество задано путем определения;
- б) {E, О, И, Я, О, Е}, {О, А, Е} – множество задано путем перечисления элементов.
Заметим, что один предмет в одном множестве является элементом только один раз, даже если предмет повторяется несколько раз.
Тождественные множества связываются знаком равенства (=):
{А, А, Е, Е|={А, Е}.
Множество А считается подмножеством В, если каждый элемент А является и элементом В, что обозначается выражением 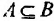 .
.
Понятие части (подмножества) в теории множеств отличается от обычного понятия части. В обычном понимании часть всегда меньше целого. А по понятию части в теории множеств целое также входит в понятие части, т.е. каждое множество является элементом самого себя, гак как каждый элемент А является элементом А, значит 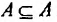 . Пустое множество является частью каждого множества.
. Пустое множество является частью каждого множества.
Множество А является действительным подмножеством множества B, если А является частью В, но не тождественно с ним, что обозначается 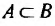 .
.
Примеры:
- Множество N неотрицательных целых чисел является действительной частью множества Z произвольных целых чисел:
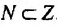 .
. - Множество Z действительная часть множества Q рациональных чисел:
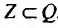
- Множество Q действительная часть множества R вещественных чисел
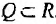
- Множество R действительная часть множества С комплексных чисел:
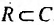
Не существует никакого ограничения в отношении того, насколько много (или мало) элементов может быть в одном множеств: в одном множестве может быть любое, даже бесконечное количество элементов.
Сравнивать множества можно, используя понятие взаимно однозначного соответствия между элементами.
Если каждому элементу множества А по некоторому закону ставится в соответствие определенный элемент множества В и если при этом каждый элемент множества В оказывается поставленным в соответствие одному и только одному элементу множества А, то говорят, что между А и В установлено взаимно однозначное соответствие.
Если между множествами А и В установить взаимно однозначное соответствие, то такие множества называются равиомощны-ми. Множество А называется бесконечным, если оно имеет ту же мощность, что и хотя бы одно из его действительных подмножеств, в противном случае А – конечное множество. Бесконечное множество А счётно, если можно установить взаимно однозначное соответствие между ним и множеством натуральных чисел.
Например, множество всех действительных чисел R и множество натуральных чисел N имеют разные мощности. Первое множество имеет мощность континуума, а второе – счетное множество.
Особую роль в теории множеств играет универсальное множество, которое часто называют просчранством. Это некоторое множество, фиксированное в рамках данной математической теории и содержащее в качестве элементов все объекты, рассматриваемые в этой теории.
Алгебраические операции над множествами
Определим операции, выполняемые над множествами.
а) Пересечением множеств Ми N называется множество, которое будет обозначаться М 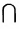 N, состоящее из элементов, принадлежащих как М, так и N, т.е. М
N, состоящее из элементов, принадлежащих как М, так и N, т.е. М 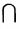 N =
N = 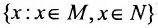 .
.
Эта запись означает, что пересечение M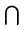 N двух множеств состоит из элементов х, одновременно принадлежащих как М, так и
N двух множеств состоит из элементов х, одновременно принадлежащих как М, так и
N. Например, если М = {0,1,2,3}, а N = {1,4,3,6}, то М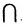 N = {1,3}. Основные тождества этой операции состоят в следующем:
N = {1,3}. Основные тождества этой операции состоят в следующем:
Если А 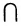 В = А, то действительны следующие соотношения:
В = А, то действительны следующие соотношения: 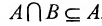 ,
,
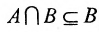 ,
,
А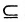 В.
В.
Вели 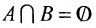 , т.е. если А и В не имеют общих элементов, то
, т.е. если А и В не имеют общих элементов, то
А и Б называются посторонними множествами.
Если есть совокупность множеств 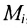 ,то пересечение всех множеств
,то пересечение всех множеств 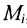 есть множество
есть множество 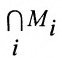 , которое состоит из элементов,
, которое состоит из элементов,
принадлежащих одновременно всем множествам совокупности 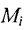 .
.
6) Объединением двух множеств А и В называется множество A 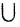 В, состоящее из элементов, по крайней мере, одного из множеств А и В, т. е.
В, состоящее из элементов, по крайней мере, одного из множеств А и В, т. е.
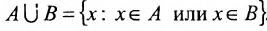 .
.
Эта запись означает, что объединение A 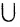 В двух множеств А и В состоит из элементов х, принадлежащих множеству А или множеству В, или множеством А и В одновременно. Например, если A={0,1,2,3} а B={4,5,6,}, то A
В двух множеств А и В состоит из элементов х, принадлежащих множеству А или множеству В, или множеством А и В одновременно. Например, если A={0,1,2,3} а B={4,5,6,}, то A 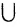 B = {0,1,2,3,4,5,6}.
B = {0,1,2,3,4,5,6}.
Легко увидеть, что если А и В являются ограниченными множествами без общих элементов, то количество элементов A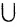 B = (количество элементов А) + (количество элементов В). На основе этих соотношений операция объединения часто называется суммированием множеств. Для операции объединения справедливы следующие тождества:
B = (количество элементов А) + (количество элементов В). На основе этих соотношений операция объединения часто называется суммированием множеств. Для операции объединения справедливы следующие тождества:
- A
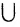 В = В
В = В 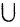 А (коммутативность).
А (коммутативность). - A
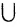 А = А (идемпотснция).
А = А (идемпотснция). - A
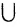
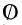 = А.
= А. - (A
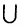 B)
B)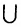 C = A
C = A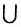 (B
(B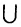 C) (ассоциативность).
C) (ассоциативность).
Так же действительны соотношения: 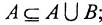
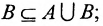
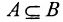 , тогда и только тогда, если A
, тогда и только тогда, если A 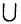 В=В.
В=В.
В общем случае, когда имеется совокупность множеств 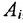 ,то объединение всех множеств
,то объединение всех множеств 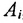 есть множество
есть множество 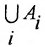 , которое состоит из элементов, принадлежащих хотя бы одному из множеств совокупности
, которое состоит из элементов, принадлежащих хотя бы одному из множеств совокупности 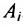 .
.
в) Множество элементов Е, не принадлежащих некоторой его части А, называется дополнением (разностью) к А в Е и обозначается через 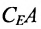 или СА или ЕА, т.е.
или СА или ЕА, т.е. 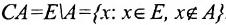 .
.
Например. Если областью существования функции 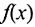 является А, а множество ее корней – В, то область существования функции
является А, а множество ее корней – В, то область существования функции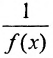 -множество АВ.
-множество АВ.
Для операции разности справедливы следующие соотношения:
- 1°.
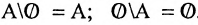 .
. - 2°.
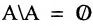 .
. - 3°.
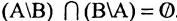 .
. - 4°.
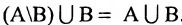 .
. - 5°.
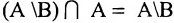 .
. - 6°.
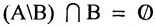 .
. - 7°.
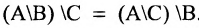 .
. - 8°.
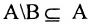 .
.
Два любых предмета а и b представляют собой упорядоченную пару, если предварительно задано, какой из них считается первым и какой вторым. Упорядоченные пары обозначаются символом (a, b), где а – первый элемент, b – второй {а и b могут быть тождественны).
г) Произведением А х В двух множеств А и В называется множество всевозможных упорядоченных пар (а, Ь), образованных из элементов а множества А и элементов b множества В, т.е. 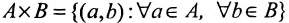 .
.
Пары (а, b) и (b, а) с 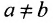 считаются различными. Это особенно важно иметь в виду, когда множества Aw В совпадают.
считаются различными. Это особенно важно иметь в виду, когда множества Aw В совпадают.
Пример:
Если А ={a,е,i}, а В={b,с}, то
А х В = {(a,b), (а,с), (e,b), (e,c), (i,b), (i,с)},
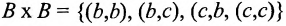 .
.
В координатной геометрии точки плоскости характеризуются парами чисел, а точки пространства – тремя числами. Это означает, что если R обозначает множество точек числовой оси, то R х R -множество точек плоскости, а (RxR)xR- множество точек пространства. Отсюда возникло обозначение 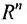 для произведения n множеств, идентичных множеству R всех вещественных чисел. Точка из
для произведения n множеств, идентичных множеству R всех вещественных чисел. Точка из 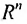 является, следовательно, упорядоченной системой произвольных вещественных чисел
является, следовательно, упорядоченной системой произвольных вещественных чисел 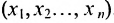 .
.
Справедливы следующие операции для декартового произведения множеств:
- 1°.
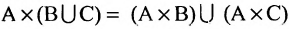 .
. - 2°.
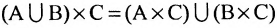 .
. - 3°.
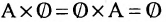 , т.к. пустое множество не имеет элементов.
, т.к. пустое множество не имеет элементов.
Понятие множества широко используется в экономических исследованиях. Так при изучении системы производства одного предприятия или нескольких, которые потребляют продукты: сырьё, энергию и трудовые ресурсы и производят в соответствии с некоторой технологией другие продукты-изделия, составляется математическая модель, где используется множество
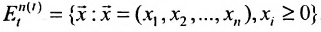 , которое характеризует производственный процесс. Элементами этого множества являются векторы
, которое характеризует производственный процесс. Элементами этого множества являются векторы 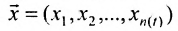 описывающие количество любого продукта, находящегося в системе.
описывающие количество любого продукта, находящегося в системе.
- Заказать решение задач по высшей математике
Выпуклые множества. Пересечение выпуклых множеств
В первом пункте мы определили множество, указали способы его задания. Теперь мы укажем некоторые дополнительные свойства множеств. Для этого введем ряд определений.
Окрестностью точки 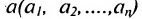 называется множество
называется множество
точек 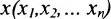 удовлетворяющих условию:
удовлетворяющих условию: 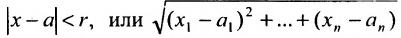 или
или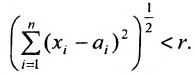
Таким образом, окрестность образуют все точки х, удаленные от точки а на расстояние меньшее r.
Точка 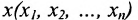 некоторого множества называется внутренней точкой этого множества, если она принадлежит множеству вместе с некоторой её окрестностью.
некоторого множества называется внутренней точкой этого множества, если она принадлежит множеству вместе с некоторой её окрестностью.
Точка пространства называется внешней по отношению к некоторому множеству точек, если она с некоторой окрестностью не принадлежит этому множеству.
Точка пространства называется граничной, если в любой её окрестности имеются точки как принадлежащие множеству так и не принадлежащие ему. Множество, содержащее все граничные точки, называется замкнутым.
Например, отрезок является замкнутым множеством.
Множество (тело) называется выпуклым, если оно вместе со своими двумя любыми точками Р и Q содержит все точки отрезка 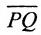 .
.
Примером выпуклого множества может служить отрезок. Из геометрии известны фигуры: треугольник, квадрат, прямоугольник, ромб, круг, эллипс. Множества точек, ограниченные эти фигурами, являются выпуклыми. В пространстве выпуклыми множествами являются: шар, эллипсоид, конус, цилиндр и другие.
Для выпуклых множеств, справедлива следующая теорема.
Теорема 1.3.1. Пересечение выпуклых множеств (тел) есть выпуклое множество, если оно не пусто.
Доказательство. Пусть имеется не пустое пересечение выпуклых множеств. Возьмём две произвольные точки Р u Q, принадлежащие этому пересечению. По определению пересечения эти точки принадлежат каждому из множеств, а так как эти множества выпуклы, то вместе с точками Р и Q им принадлежат и все точки отрезка PQ. Следовательно, все точки отрезка PQ принадлежат и пересечению, что и доказывает его выпуклость. 
Точка множество называется крайней, если она не является внутренней ни для какого отрезка, целиком принадлежащего множеству.
Так у выпуклого многоугольника крайними точками являются его вершины. Их конечное число. В пространстве многогранником называется множество с конечным числом крайних точек. Следовательно. выпуклый многогранник является замкнутым выпуклым множеством.
Высказывание
Математическая логика является современной формой так называемой формальной логики, применяющей математические методы для исследования своего предмета. В формальной логике и, соответственно, математической логике, собраны результаты законов структуры правильных выводов. Вывод является таким мыслительным процессом, в результате которого появляются новые открытия на основании уже имеющихся, без практических исследований. Рассмотрим пример вывода:
Предпосылки: Если будет раздача премии, то мы выполним план.
Будет раздача премии.
Окончательные выводы: Мы выполним план.
Если принять правильность предпосылок, то следует принять и правильность окончательного вывода. Обычно вместо предложений могут быть записаны любые такие изъявительные предложения, значения которых может быть правильно или ложно; следует оставить неизменённым только расположение слов «если» и «то» и расположение предложений, то есть структуру вывода. Структуру вывода можно выразить следующей схемой:
Если А, то В.
Путем изменения условий могут быть построены различные теории логики. Важнейшими главами математической логики является калькуляция высказываний и калькуляция предикатов.
Определение 1.4.1. Под термином высказывания подразумевается такое изъявительное предложение, которое является однозначно или правильным, или ложным.
Высказывание удовлетворяет условиям:
- а) оно не может быть одновременно и правильным и ложным (принцип непротиворечивости);
- б) исключено, чтобы оно было и неправильным и нсложным (принцип исключения третьей возможности).
Следовательно, каждое высказывание имеет значение 1 (истинно) или 0 (ложно).
В выводах могут фигурировать высказывания (либо в виде предпосылок, либо как окончательный вывод), возникшие из одного или нескольких высказываний, путем применения некоторого грамматического метода; они называются сложными высказываниями.
Определение 1.4.2. Под термином калькуляция высказываний подразумевается такой метод, с помощью которого из одного или нескольких высказываний получается такое высказывание, правильность или ложность которого однозначно определяется правильностью или ложсностью членов.
Операции над высказываниями
Отрицание, конъюнкция, дизъюнкция, импликация, эквивалентность
Простейшими примерами операций калькуляции высказываний является отрицание, конъюнкция, дизъюнкция, импликация, эквивалентность и т.д.
Определение 1.5.1. Под отрицанием высказывания А подразумевается высказывание «Неправильно, что А» или некоторая грамматически преобразованая форма данного высказывания.
По значению выражения «неправильно» отрицание А правильно тогда и только тогда, если самоё А неправильно; следовательно, отрицание действительно есть операция калькуляции высказываний.
Например: отрицание предложения «мотор работает» является предложение «мотор не работает».
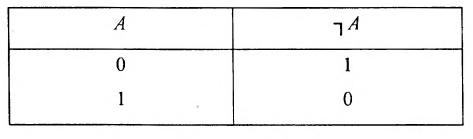
Отрицание является (унарной) одночленной операцией. Отрицание А обозначается символом 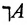 (читается «не А»). Таблица истинности для операции отрицания имеет вид: Таблица 1
(читается «не А»). Таблица истинности для операции отрицания имеет вид: Таблица 1
Закон двойного отрицания: 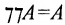 .
.
Здесь и в дальнейшем свойство высказываний «правильное» и «ложное» называется логическими значениями и обозначается 1 и О (п. и л.). Тогда операции, проводимые на логических значениях, называются логическими операциями. Для выражения любых логических значений вводятся логические переменные; они обозначаются символами 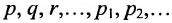 .
.
Следовательно, логические переменные могут принимать два значения 1 или 0. При использовании нескольких операций последовательно порядок выполнения отдельных операций обозначается скобками.
В общем случае, n-члснной логической операцией называется каждая такая функция, областью существования которой является упорядоченное множество всех выражений, образуемых из логических значений 1 и 0 с длиной выражения n, а значением её является одно из двух логических значений 1 и 0.
Определение 1.5.2. Под конъюнкцией двух высказываний А и В подразумевается высказывание «А и В».
По значению союза «и» конъюнкция является правильной тогда и только тогда, если оба её члена правильны, т.е. используя логические переменные можно записать:
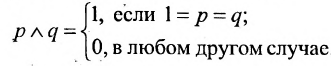
Таблица значений конъюнкции имеет вид:
Таблица 2
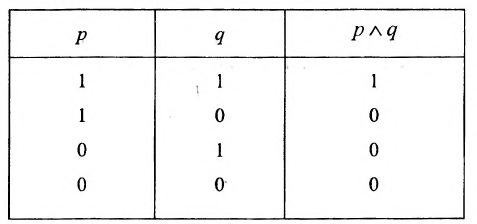
Справедлива следующая
Теорема 1.5.1. Любая логическая операция может быть выражена через операции отрицания и конъюнкции.
В области логических операций для контроля любого тождества составляется общая таблица операций, представленных по обеим сторонам знака =. Результат операций указывается в столбцах.
Пример:
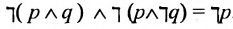 .
.
Решение:
Доказательство данного равенства проведём в табл. 3:
Таблица 3
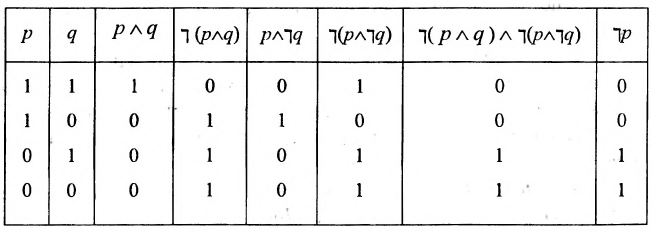
Определение 7.5.3. Под дизъюнкцией двух высказываний А и В подразумевается высказывание «А или В».
По значению союза «или» дизъюнкция является ложной, если оба её члена ложны, т.е. используя логические переменные можно записать:
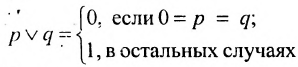 .
.
Дизъюнкция выражается с помощью операции конъюнкции и отрицания б следующей форме: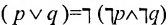
Таблица значений дизъюнкции имеет следующий вид:
Таблица 4
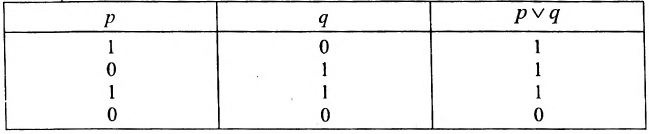
По аналогии с теоремой 3 можно сформулировать следующую теорему
Теорему 1.5.2. Каждая логическая операция может быть выражена с помощью только операций дизъюнкции и отрицания.
Например, операция конъюнкции выражается с помощью операций дизъюнкции и отрицания в виде: 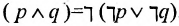 .
.
Определение 1.5.4. Операция, обозначаемая 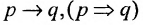 ,
,
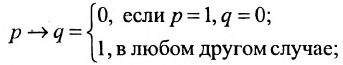
называется импликацией (с предварительным членом р и с последующим q).
Иначе её обозначение 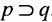 . Она выражается в следующем виде:
. Она выражается в следующем виде:
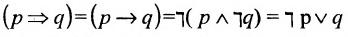 и читается: если р, то q из p следует q.
и читается: если р, то q из p следует q.
Таблица значений импликации имеет следующий вид: Таблица 5
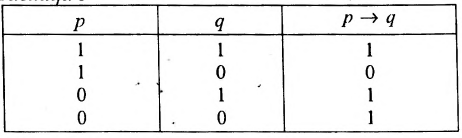
И конъюнкция, и дизъюнкция выражаются с помощью операций импликации и отрицания: 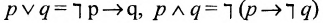 ,
,
Поэтому любая логическая операция может быть выражена ( помощью операций импликации и отрицания.
Выражения вида: «если А, то В», «неправильно, что: А и не В» «В если только А», «только тогда А, если В», «Достаточным условием В является А», «Необходимым условием А является В» соответственно обозначаются А 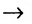 В или А
В или А  В.
В.
Определение 1.5.5. Операция, обозначаемая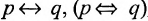 ,
,
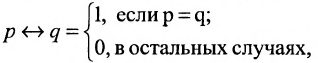
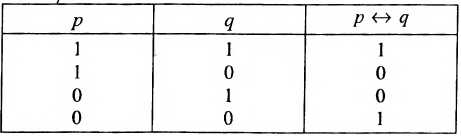
называется эквивалентностью (читается р эквивалентно q). Выражениями данной операции являются следующие: 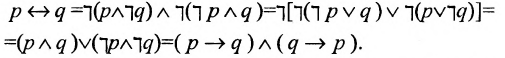
Так как высказывание 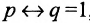 тогда и только тогда, когда
тогда и только тогда, когда
p=q, то данная логическая операция соответствует образованию
сложного предложения вида «А тогда и только тогда, когда В». Таблица значений эквивалентности имеет вид:
Таблица 6
Рассматриваются ещё:
операция Шеффера – отрицание операции конъюнкции 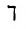
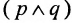 , обозначаемая
, обозначаемая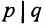 (р штрих q).
(р штрих q).
1) операция взаимоисключающего или (р или же q): 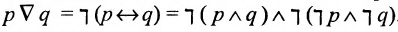 . Например, или ты вылечишься до завтрашнего дня, или мы тебя отвезём в больницу;
. Например, или ты вылечишься до завтрашнего дня, или мы тебя отвезём в больницу;
2) операция «ни-ни» (обозначается 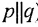 ) «ни А ни В»:
) «ни А ни В»: 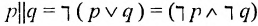 .
.
Предикаты и кванторы
Мри анализе вывода следует отмстить, что применяемые высказывания могут быть приведены из так называемых открытых предложений или предикатов, примерами которых служат: … является неделимым числом; … является столицей; … купил … за … рублей.
Если в эти схемы предложений вставить названия соответственно подобранных предметов (вместо пунктира), то получатся замкнутые предложения, высказывания. Такие предикаты выражаются однозначно в некоторых случаях, если вместо пунктира записываются буквы: x, у,z, … .
Кроме заполнения оставленных свободных мест названиями имеется и другой способ образования высказываний из предикатов: квантификация. Например, из открытого предложения «если х представляет собой дифференцируемую функцию, то функция х-непрерывная функция», подставив перед предложением «Для каждого л», получим следующее: Для каждого х, если х представляет собой дифференцируемую функцию, то x представляет собой непрерывную функцию. Текст «Для каждого x» обозначается символом 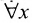 и называется универсальным квантором.
и называется универсальным квантором.
Существует ещё экзистенциальный квантор, который заменят текст «Имеется такое х» или «Существует такое х» и обозначается 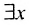 .
.
Для точного анализа вводятся следующие понятия:
Определение 1.6.1. n-мерным предикатом 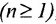 , определённым на непустом множестве H, называется такая функция, областью существования которой является множество упорядоченных n – членных знаков, образованных из элементов множества H, а значениями – логические значения.
, определённым на непустом множестве H, называется такая функция, областью существования которой является множество упорядоченных n – членных знаков, образованных из элементов множества H, а значениями – логические значения.
Предикаты обозначаются символами 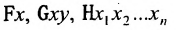 и т.д.
и т.д.
Жирными буквами обозначаются предикаты, а строчными буквами- аргументы предиката как функции; количеством последних определяется размерность предиката.
Например. Пусть Н- множество натуральных чисел, тогда предикат неделимого числа Fx определяется следующим образом:

Множества, операции над ними
Понятие множества является одним из основных в математике. Оно принадлежит к числу первичных, не определяемых через более простые.
Под множеством будем понимать совокупность объектов, объединенных по какому-либо признаку. Слова «совокупность», «набор», «система», «объединение» и другие являются синонимами слова «множество». Например, можно говорить о множестве студентов в институте, множестве букв в алфавите, множестве целых чисел и т. д. Из приведенных примеров следует, что множество может содержать как конечное, так и бесконечное число объектов некоторой природы. Объекты, из которых состоит множество, называются его элементами или точками. Принадлежность элемента 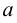 множеству
множеству 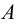 обозначают следующим образом:
обозначают следующим образом: 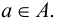 Если
Если 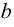 не является элементом множества
не является элементом множества 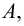 то пишут:
то пишут: 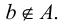 Если
Если 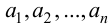 – некоторые элементы, то запись
– некоторые элементы, то запись 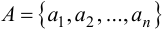 означает, что множество
означает, что множество 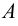 состоит из элементов
состоит из элементов 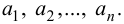
Два множества 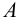 и
и 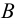 называют равными, если они состоят из одних и тех же элементов (обозначение:
называют равными, если они состоят из одних и тех же элементов (обозначение: 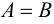 ). Множество
). Множество 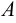 называется подмножеством множества
называется подмножеством множества 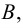 если все элементы множества
если все элементы множества 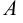 являются одновременно и элементами множества
являются одновременно и элементами множества 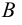 (обозначение:
(обозначение: 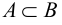 («множество
(«множество 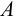 содержится в множестве
содержится в множестве 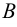 ») или
») или 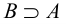 («множество
(«множество 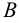 содержит множество
содержит множество 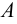 »). Например, так как всякое натуральное число
»). Например, так как всякое натуральное число 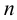 является целым, то
является целым, то 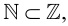 где
где 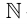 – множество натуральных чисел,
– множество натуральных чисел, 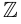 – множество целых чисел.
– множество целых чисел.
Множество, не содержащее ни одного элемента, будет называться пустым множеством и обозначаться 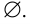 Это множество является подмножеством любого множества. Пусть
Это множество является подмножеством любого множества. Пусть 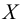 – множество, а
– множество, а 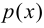 – какое-либо свойство элементов этого множества. Тогда запись
– какое-либо свойство элементов этого множества. Тогда запись 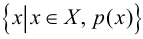 означает совокупность тех элементов множества
означает совокупность тех элементов множества 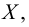 которые обладают свойством
которые обладают свойством 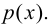 Например, если
Например, если 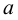 и
и 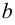 – два числа и
– два числа и 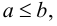 то встречавшиеся в элементарной математике отрезок, интервал и полуинтервалы можно записать в следующем виде:
то встречавшиеся в элементарной математике отрезок, интервал и полуинтервалы можно записать в следующем виде: 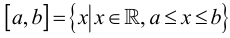 – отрезок;
– отрезок; 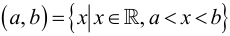 – интервал;
– интервал;
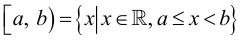 и
и 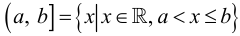 – полуинтервалы. Здесь
– полуинтервалы. Здесь 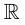 – множество действительных (вещественных) чисел.
– множество действительных (вещественных) чисел.
Множество 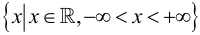 всех чисел называется также числовой прямой или числовой осью, а любое число – точкой этой прямой.
всех чисел называется также числовой прямой или числовой осью, а любое число – точкой этой прямой.
Пересечением множеств 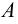 и
и 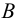 называется множество
называется множество 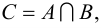 состоящее из всех элементов, одновременно принадлежащих как
состоящее из всех элементов, одновременно принадлежащих как 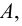 так и
так и 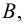 т.е.
т.е. 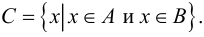
Объединением множеств 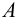 и
и 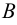 называется множество
называется множество 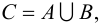 состоящее из всех элементов, принадлежащих хотя бы одному из двух данных множеств, т. е.
состоящее из всех элементов, принадлежащих хотя бы одному из двух данных множеств, т. е. 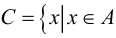 или
или 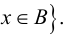
Разностью множеств 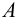 и
и 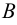 называется множество
называется множество 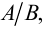 состоящее из тех элементов множества
состоящее из тех элементов множества 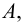 которые не принадлежат множеству
которые не принадлежат множеству 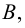 т.е.
т.е. 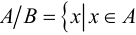 и
и 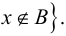
Пусть 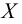 – некоторое основное множество, тогда дополнением множества
– некоторое основное множество, тогда дополнением множества 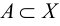 называется множество
называется множество 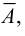 состоящее из всех элементов
состоящее из всех элементов 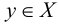 и не принадлежащих
и не принадлежащих 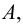 т. е.
т. е.
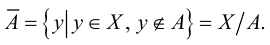
Таким образом, все элементы, которые не принадлежат множеству 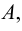 образуют множество
образуют множество 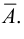 Следовательно,
Следовательно, 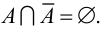
Логические символы
Многие математические понятия удобно записывать, пользуясь логической символикой. Так, символ 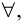 называемый квантором общности, используется вместо слов «для любого», «для всех», «для каждого», «какого бы ни было» и т. д., символ
называемый квантором общности, используется вместо слов «для любого», «для всех», «для каждого», «какого бы ни было» и т. д., символ 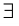 – квантор существования – вместо слов «существует», «найдется», «имеется» и т. д.
– квантор существования – вместо слов «существует», «найдется», «имеется» и т. д.
Часто используются также логические символы следствия 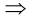 и равносильности
и равносильности 
Грани числовых множеств
Говорят, что множество 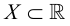 ограничено сверху (снизу), если существует такое число
ограничено сверху (снизу), если существует такое число 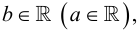 что
что 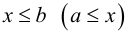 для любого
для любого 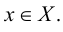 Число
Число 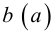 в этом случае называется верхней (нижней) гранью множества
в этом случае называется верхней (нижней) гранью множества 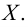
Множество, ограниченное и сверху, и снизу, называется ограниченным, т. е. существуют два числа 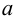 и
и 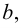 такие, что
такие, что 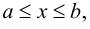
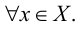 Эти неравенства показывают, что множество
Эти неравенства показывают, что множество 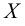 ограничено в том и только в том случае, если оно расположено на некотором конечном отрезке числовой прямой. Очевидно, что множество
ограничено в том и только в том случае, если оно расположено на некотором конечном отрезке числовой прямой. Очевидно, что множество 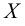 ограничено тогда и только тогда, когда существует положительное число
ограничено тогда и только тогда, когда существует положительное число 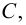 такое, что
такое, что
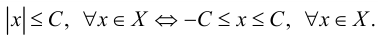
Множество, не ограниченное сверху или снизу, называется неограниченным.
Если число 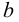 является верхней гранью множества
является верхней гранью множества 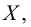 то и любое число больше
то и любое число больше 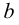 тоже является верхней гранью, и, если число
тоже является верхней гранью, и, если число 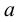 -нижняя грань множества
-нижняя грань множества 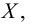 то всякое число, меньше
то всякое число, меньше 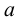 будет нижней гранью
будет нижней гранью 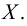
Наименьшая (наибольшая) из всех верхних (нижних) граней называется точной верхней (нижней) гранью множества и обозначается символом 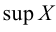 («супремум
(«супремум 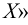 ) (
) (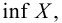 «инфимум
«инфимум 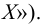
Точные верхняя и нижняя грани множества могут принадлежать или не принадлежать этому множеству. Если множество 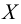 не ограничено сверху (снизу), то иногда используют обозначение
не ограничено сверху (снизу), то иногда используют обозначение 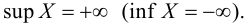
Теорема 1*. Всякое ограниченное сверху (снизу) числовое множество имеет точную верхнюю (нижнюю) грань.
Предельные точки числового множества. Открытые и замкнутые множества
Множество вещественных чисел 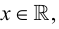 удовлетворяющих неравенству
удовлетворяющих неравенству 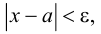 т.е.
т.е. 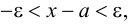 называется
называется 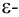 окрестностью точки
окрестностью точки 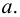
Множество вещественных чисел 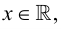 удовлетворяющих неравенству
удовлетворяющих неравенству 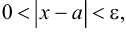 называется проколотой
называется проколотой 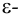 окрестностью точки
окрестностью точки 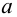 (точка
(точка 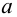 исключена из своей
исключена из своей 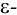 окрестности).
окрестности).
Геометрически 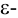 окрестность точки
окрестность точки 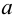 есть интервал
есть интервал 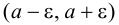 длиной
длиной 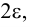 серединой которого является точка
серединой которого является точка 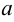 числовой прямой.
числовой прямой.
Точка 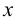 называется предельной точкой множества
называется предельной точкой множества 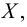 если в любой
если в любой 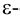 окрестности точки
окрестности точки 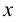 находятся точки из
находятся точки из 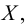 отличные от
отличные от 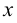 . Предельная точка может как принадлежать, так и не принадлежать множеству
. Предельная точка может как принадлежать, так и не принадлежать множеству 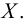
Точка 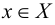 называется изолированной точкой этого множества, если в достаточно малой ее
называется изолированной точкой этого множества, если в достаточно малой ее 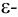 окрестности нет точек из
окрестности нет точек из 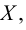 отличных от
отличных от 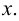
Точка 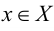 называется внутренней, если существует некоторая
называется внутренней, если существует некоторая 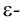 окрестность этой точки, целиком содержащаяся в множестве
окрестность этой точки, целиком содержащаяся в множестве 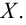
Множество, все точки которого являются внутренними, называется открытым; множество, содержащее все свои предельные точки, называется замкнутым. Открытым множеством является, например, интервал 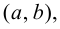 замкнутым множеством – отрезок
замкнутым множеством – отрезок 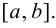
Точка 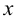 называется граничной точкой множества
называется граничной точкой множества 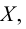 если любая
если любая 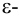 окрестность этой точки содержит точки, как принадлежащие множеству
окрестность этой точки содержит точки, как принадлежащие множеству 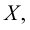 так и не принадлежащие ему. Множество всех граничных точек множества
так и не принадлежащие ему. Множество всех граничных точек множества 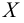 называется границей этого множества. Например, если
называется границей этого множества. Например, если 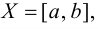 то все точки интервала
то все точки интервала 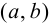 являются внутренними точками множества
являются внутренними точками множества 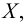 а граница этого множества состоит из двух точек:
а граница этого множества состоит из двух точек: 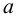 и
и 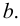
Если множество 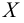 представляет собой область (открытое множество), то множество
представляет собой область (открытое множество), то множество 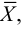 полученное присоединением к
полученное присоединением к 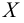 всех граничных точек этого множества, называется замкнутой областью.
всех граничных точек этого множества, называется замкнутой областью.
- Числовые множества
- Вектор – определение и основные понятия
- Прямая – понятие, виды и её свойства
- Плоскость – определение, виды и правила
- Степень с рациональным показателем
- Степень с действительным показателем
- Логарифм – формулы, свойства и примеры
- Корень из числа – нахождение и вычисление
