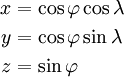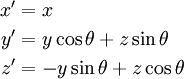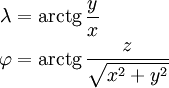Как найти декартовы координаты по сферическим

Сферические координаты (сферическая система координат)

Для введения сферической системы координат в пространстве выбирается плоскость (основная плоскость) и на ней задается полярная система координат с полюсом (начало сферической системы координат) и полярной осью . Через точку перпендикулярно основной плоскости проведем ось (ось аппликат) и выберем ее направление так, чтобы возрастание полярного угла со стороны положительного направления оси происходило против часовой стрелки (рис.2.36,а).

В сферической системе координат положение точки , не лежащей на оси аппликат, характеризуется расстоянием до начала координат, полярным углом точки – ортогональной проекции точки на основную плоскость, и углом между вектором и положительным направлением оси аппликат. Таким образом, сферические координаты точки – это упорядоченная тройка чисел – радиус , долгота и широта . У точек, принадлежащих оси аппликат, не определена долгота, их положение задается радиусом и широтой для положительной части оси и для отрицательной ее части. Начало координат задается нулевым значением радиуса . Иногда вместо угла широтой называют угол , принимающий значения .

Со сферической системой координат можно связать прямоугольную систему координат (рис.2.36,б), у которой начало и базисные векторы совпадают с началом сферической системы координат и единичными векторами на полярной оси и оси аппликат соответственно, а базисный вектор выбирается так, чтобы тройка была правой (при этом базис оказывается стандартным).

Наоборот, если в пространстве задана правая прямоугольная система координат, то, приняв положительную полуось абсцисс за полярную ось, получим сферическую систему координат (связанную с данной прямоугольной).

Переход от сферических координат к декартовым (прямоугольным)

Получим формулы, связывающие между собой прямоугольные координаты точки и её сферические координаты . По рис.2.36,б получаем

Эти формулы перехода позволяют найти прямоугольные координаты по известным сферическим координатам. Обратный переход выполняется по формулам

Формулы (2.22) определяют долготу с точностью до слагаемых , где . При из них следует, что . Главное значение долготы находится по формулам (см. рис.2.29).

Пример 2.13. В сферической системе координат :

а) построить координатные поверхности ;

б) найти сферические координаты точки , если известны её прямоугольные координаты ;

в) найти прямоугольные координаты точки , если известны её сферические координаты: .

Решение. а) Координатной поверхностью , т.е. геометрическим местом точек при фиксированном значении радиуса , является сфера с центром в начале координат (рис.2.37). Этим объясняется название сферической системы координат. Координатной поверхностью , т.е. геометрическим местом точек при фиксированном значении долготы , является полуплоскость, ограниченная осью аппликат (на рис.2.37 изображена полуплоскость ). Координатной поверхностью , т.е. геометрическим местом точек при фиксированном значении широты , является конус, ось которого совпадает с осью аппликат, а вершина – с началом координат. При получаем основную плоскость. На рис.2.37 изображены конус и основная плоскость .

б) Найдем сферические координаты точки . По формулам (2.22), учитывая рис.2.29 (см. пример 2.12), получаем

в) По формулам (2.21) получаем

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 25 декабря 2020 года; проверки требуют 4 правки.

Сферическая система координат — трёхмерная система координат, в которой каждая точка пространства определяется тремя числами , где  — расстояние до начала координат (радиальное расстояние), а и  — зенитный и азимутальный углы соответственно.

Понятия зенит и азимут широко используются в астрономии. Зенит — направление вертикального подъёма над произвольно выбранной точкой (точкой наблюдения), принадлежащей фундаментальной плоскости. В качестве фундаментальной плоскости в астрономии может быть выбрана плоскость, в которой лежит экватор, или плоскость, в которой лежит горизонт, или плоскость эклиптики и т. д., что порождает разные системы небесных координат. Азимут — угол между произвольно выбранным лучом фундаментальной плоскости с началом в точке наблюдения и другим лучом этой плоскости, имеющим общее начало с первым.

Если рассматривать сферическую систему координат относительно декартовой системы , фундаментальной плоскостью будет плоскость , зенитным углом точки, заданной радиус-вектором , будет угол между и осью , а азимутом — угол между проекцией на плоскость и осью . Это объясняет названия углов и то, что сферическая система координат может служить обобщением множества видов систем небесных координат.

Определения[править | править код]

Положение точки в сферической системе координат определяется тройкой , где

Угол называется зенитным, или полярным, также он может называться наклонением, или коширотой, а угол  — азимутальным. Углы и не определены при , также не определён угол при (то есть при или ).

Такое соглашение установлено в стандарте (ISO 31-11). Кроме того может использоваться соглашение, когда вместо зенитного угла , используется угол между радиус-вектором точки и плоскостью , равный . Он называется широтой и может быть обозначен той же буквой . Широта может изменяться в пределах . При этом соглашении углы и не имеют значения при , так же как и в первом случае, а не имеет значения при (то есть при или ).

Переход к другим системам координат[править | править код]

Декартова система координат[править | править код]

Если заданы сферические координаты точки , то переход к декартовым осуществляется по формулам:

Обратно, от декартовых к сферическим:

Якобиан преобразования к сферическим координатам равен

Таким образом, элемент объёма при переходе от декартовых к сферическим координатам будет выглядеть следующим образом:

Цилиндрическая система координат[править | править код]

Если заданы сферические координаты точки, то переход к цилиндрическим осуществляется по формулам:

Обратно от цилиндрических к сферическим:

Якобиан преобразования от сферических к цилиндрическим .

Дифференциальные характеристики[править | править код]

Вектор , проведённый из точки в точку , равен

где

ортогональные единичные векторы сферических координат в направлении увеличения , соответственно, а  — единичные векторы декартовых координат. Сферические координаты являются ортогональными, поэтому метрический тензор имеет в них диагональный вид:

• 
• Квадрат дифференциала длины дуги:

• Коэффициенты Ламе:

• Символы Кристоффеля :

Остальные равны нулю.

Математическое моделирование Земли[править | править код]

Сферическая географическая система координат[править | править код]

Сферическая географическая система координат строится следующим образом^[1]:

Вектор магнитной индукции магнитного поля Земли имеет компоненты

где  — магнитное наклонение;  — магнитное склонение.

Компоненты вектора ускорения свободного падения равны

Наконец, компоненты вектора угловой скорости вращения Земли такие:

В сферических географических координатах оптимально решать уравнения, описывающие поведение нейтральных частиц околоземного пространства^[1].

Сферическая геомагнитная система координат[править | править код]

Сферическая геомагнитная система координат строится следующим образом^[1]:

Географические координаты северного магнитного полюса равны

В сферической геомагнитной системе координат склонение и

Формулы, связывающие географические и геомагнитные сферические координаты^[1]:

В сферических геомагнитных координатах проще, чем в сферических географических координатах, описывать влияние геомагнитного поля на заряженные частицы околоземного пространства^[1].

См. также[править | править код]

• Углы Эйлера
• Гиперсферические координаты

Примечания[править | править код]

Ссылки[править | править код]

• Weisstein, Eric W. Сферические координаты (англ.) на сайте Wolfram MathWorld.

Сферические координаты (сферическая система координат)

Для введения сферической системы координат в пространстве выбирается плоскость ( основная плоскость ) и на ней задается полярная система координат с полюсом ( начало сферической системы координат ) и полярной осью . Через точку перпендикулярно основной плоскости проведем ось ( ось аппликат ) и выберем ее направление так, чтобы возрастание полярного угла со стороны положительного направления оси происходило против часовой стрелки (рис.2.36,а).

В сферической системе координат положение точки , не лежащей на оси аппликат, характеризуется расстоянием до начала координат, полярным углом точки – ортогональной проекции точки на основную плоскость, и углом между вектором и положительным направлением оси аппликат. Таким образом, сферические координаты точки – это упорядоченная тройка чисел – радиус , долгота и широта . У точек, принадлежащих оси аппликат, не определена долгота, их положение задается радиусом и широтой для положительной части оси и для отрицательной ее части. Начало координат задается нулевым значением радиуса . Иногда вместо угла широтой называют угол , принимающий значения .

Со сферической системой координат можно связать прямоугольную систему координат (рис.2.36,б), у которой начало и базисные векторы совпадают с началом сферической системы координат и единичными векторами на полярной оси и оси аппликат соответственно, а базисный вектор выбирается так, чтобы тройка была правой (при этом базис оказывается стандартным).

Наоборот, если в пространстве задана правая прямоугольная система координат, то, приняв положительную полуось абсцисс за полярную ось, получим сферическую систему координат ( связанную с данной прямоугольной ).

Переход от сферических координат к декартовым (прямоугольным)

Получим формулы, связывающие между собой прямоугольные координаты точки и её сферические координаты . По рис.2.36,б получаем

Эти формулы перехода позволяют найти прямоугольные координаты по известным сферическим координатам. Обратный переход выполняется по формулам

Формулы (2.22) определяют долготу с точностью до слагаемых , где . При из них следует, что . Главное значение долготы находится по формулам (см. рис.2.29).

Пример 2.13. В сферической системе координат :

а) построить координатные поверхности ;

б) найти сферические координаты точки , если известны её прямоугольные координаты ;

в) найти прямоугольные координаты точки , если известны её сферические координаты: .

Решение. а) Координатной поверхностью , т.е. геометрическим местом точек при фиксированном значении радиуса , является сфера с центром в начале координат (рис.2.37). Этим объясняется название сферической системы координат. Координатной поверхностью , т.е. геометрическим местом точек при фиксированном значении долготы , является полуплоскость, ограниченная осью аппликат (на рис.2.37 изображена полуплоскость ). Координатной поверхностью , т.е. геометрическим местом точек при фиксированном значении широты , является конус, ось которого совпадает с осью аппликат, а вершина – с началом координат. При получаем основную плоскость. На рис.2.37 изображены конус и основная плоскость .

б) Найдем сферические координаты точки . По формулам (2.22), учитывая рис.2.29 (см. пример 2.12), получаем

Системы координат

Декартова система координат.

Фиксируем в пространстве точку (O) и рассмотрим произвольную точку (M). Радиус-вектором точки (M) по отношению к точке (O) называется вектор (overrightarrow). Если в пространстве кроме точки (O) выбран некоторый базис, то точке (M) сопоставляется упорядоченная тройка чисел — компоненты ее радиус-вектора.

Декартовой системой координат в пространстве называется совокупность точки и базиса.

Точка носит название начала координат. Прямые, проходящие через начало координат в направлении базисных векторов, называются осями координат; первая — осью абсцисс, вторая — осью ординат, третья — осью аппликат. Плоскости, проходящие через оси координат, называются координатными плоскостями.

Пусть дана декартова система координат (O), (boldsymbol>), (boldsymbol>), (boldsymbol>). Компоненты (x), (y), (z) радиус-вектора (overrightarrow) точки (M) называются координатами точки (M) в данной системе координат:
$$
overrightarrow = xboldsymbol> + yboldsymbol> + zboldsymbol>.nonumber
$$
Первая координата называется абсциссой, вторая — ординатой, а третья — аппликатой.

Аналогично определяются координаты на плоскости и на прямой линии. Разумеется, точка на плоскости имеет только две координаты, а на прямой линии — одну.

Координаты точки пишут в скобках после буквы, обозначающей точку. Например, запись (A(2, 1/2)) означает, что точка (A) имеет координаты 2 и 1/2 в ранее выбранной декартовой системе координат на плоскости (рис. 2.1).

Рис. 2.1

Координаты точки, как и компоненты вектора, — величины безразмерные. В частности, они не зависят от выбранной единицы измерения длин. В самом деле, раскладывая векторы в теореме о линейной зависимости систем векторов, мы сводили дело к разложению вектора по коллинеарному с ним ненулевому вектору. А в этом случае компонента равна отношению длин, взятому с определенным знаком.
Легко видеть, что при заданной системе координат координаты точки определены однозначно. С другой стороны, если задана система координат, то для каждой упорядоченной тройки чисел найдется единственная точка, имеющая эти числа в качестве координат. Система координат на плоскости определяет такое же соответствие между точками плоскости и парами чисел. Задание системы координат на прямой линии сопоставляет каждой точке вещественное число и каждому числу — точку.

Рис. 2.2

Рассмотрим две точки (A) и (B), координаты которых относительно некоторой декартовой системы координат (O), (boldsymbol>), (boldsymbol>), (boldsymbol>) соответственно (x_<1>), (y_<1>), (z_<1>) и (x_<2>), (y_<2>), (z_<2>). Поставим себе задачу найти компоненты вектора (overrightarrow). Очевидно, что (overrightarrow = overrightarrow-overrightarrow) (рис. 2.2). Компоненты радиус-векторов (overrightarrow) и (overrightarrow) равны ((x_<1>), (y_<1>), (z_<1>)) и ((x_<2>), (y_<2>), (z_<2>)) по определению координат. Из ранее доказанного предположения следует, что (overrightarrow) имеет компоненты ((x_<2>-x_<1>), (y_<2>-y_<1>), (z_<2>-z_<1>)). Этим доказано следующее утверждение.

Чтобы найти координаты вектора, нужно из координат его конца вычесть координаты его начала.

Деление отрезка в заданном отношении.

Найдем координаты точки (M) на отрезке (AB), которая делит этот отрезок в отношении (lambda/mu), то есть удовлетворяет условию
$$
frac<|AM|> <|MB|>= frac<lambda><mu>, lambda > 0, mu > 0nonumber
$$
(рис. 2.3). Это условие можно переписать в виде
$$
muoverrightarrow = lambdaoverrightarrow.label
$$

Рис. 2.3

Обозначив через ((x_<1>), (y_<1>), (z_<1>)) и ((x_<2>), (y_<2>), (z_<2>)) соответственно координаты точек (A) и (B), а через ((x), (y), (z)) координаты точки (M), разложим обе части равенства по базису, причем компоненты векторов (overrightarrow) и (overrightarrow) найдем по предложению 1. Тогда
$$
mu(x-x_<1>) = lambda(x_<2>-x), mu(y-y_<1>) = lambda(y_<2>-y), mu(z-z_<1>) = lambda(z_<2>-z).nonumber
$$
Из этих равенств можно найти (x), (y) и (z), поскольку (lambda + mu neq 0):
$$
x = frac <mu x_<1>+ lambda x_<2>><lambda + mu>, y = frac <mu y_<1>+ lambda y_<2>><lambda + mu>, z = frac <mu z_<1>+ lambda z_<2>><lambda + mu>label
$$
Если в формулах eqref мы будем считать одно из чисел (lambda) или (mu) отрицательным, то из равенства eqref увидим, что (M) находится на той же прямой вне отрезка (AB), деля его в отношении |(lambda/mu)|. Поэтому из формул eqref можно найти координаты точки, делящей отрезок в заданном отношении как внутренним, так и внешним образом.

На плоскости и на прямой линии задача о делении отрезка решается точно так же, только из трех равенств в eqref остается соответственно два и одно равенство.

Декартова прямоугольная система координат.

Общие декартовы системы координат используются реже, чем специальный класс таких систем — декартовы прямоугольные системы координат.

Базис называется ортонормированным, если его векторы попарно ортогональны и по длине равны единице. Декартова система координат, базис которой ортонормирован, называется декартовой прямоугольной системой координат.

Нетрудно проверить, что координаты точки относительно декартовой прямоугольной системы координат в пространстве по абсолютной величине равны расстояниям от этой точки до соответствующих координатных плоскостей. Они имеют знак плюс или минус в зависимости от того, лежит точка по ту же или по другую сторону от плоскости, что и конец базисного вектора, перпендикулярного этой плоскости.

Аналогично находят координаты точки относительно декартовой прямоугольной системы координат на плоскости.

Полярная система координат.

Декартовы системы координат не единственный способ определять при помощи чисел положение точки на плоскости. Для этого используются многие другие типы координатных систем. Здесь мы опишем некоторые из них.

На плоскости часто употребляется полярная система координат. Она определена, если задана точка (O), называемая полюсом, и исходящий из полюса луч (l), который называется полярной осью. Положение точки (M) фиксируется двумя числами: радиусом (r = overrightarrow) и углом (varphi) между полярной осью и вектором (overrightarrow). Этот угол называется полярным углом (рис. 2.4).

Рис. 2.4

Мы будем измерять полярный угол в радианах и отсчитывать от полярной оси против часовой стрелки. У полюса (r = 0), а (varphi) не определено. У остальных точек (r > 0), а (varphi) определяется с точностью до слагаемого, кратного 2(pi). Это означает, что пары чисел ((r, varphi)), ((r, varphi + 2pi)) и вообще ((r), (varphi + 2kpi)), где (k) — любое целое число, представляют собой полярные координаты одной и той же точки.

Иногда ограничивают изменение полярного угла какими-нибудь условиями, например, (0 leq varphi 0), то паре ((r, varphi)) ставим в соответствие точку, радиус-вектор которой имеет длину (r) и составляет с полярной осью угол (varphi). При этом парам чисел ((r, varphi)) и ((r_<1>, varphi_<1>)) сопоставляется одна и та же точка, если (r = r_<1>), а (varphi = varphi_ <1>= 2pi k), где (k) — целое число.

Выберем на плоскости декартову прямоугольную систему координат, поместив ее начало в полюс (O) и приняв за базис векторы (boldsymbol>) и (boldsymbol>) длины (l), направленные соответственно вдоль полярной оси и под углом (pi/2) к ней (угол отсчитывается против часовой стрелки). Как легко видеть из рис. 2.4, декартовы координаты точки выражаются через ее полярные координаты формулами
$$
x = r cos varphi, y = r sin varphi.label
$$

Цилиндрические и сферические координаты.

В пространстве обобщением полярных систем координат являются цилиндрические и сферические системы координат. И для тех, и для других фигура, относительно которой определяется положение точки, состоит из точки (O), луча (l), исходящего из (O), и вектора (boldsymbol), равного по длине 1 и перпендикулярного к (l). Через точку (O) проведем плоскость (Theta), перпендикулярную вектору (boldsymbol). Луч (l) лежит в этой плоскости.

Пусть дана точка (M). Опустим из нее перпендикуляр (MM’) на плоскость (Theta).

Цилиндрические координаты точки (M) — это три числа (r), (varphi), (h). Числа (r) и (varphi) — полярные координаты точки (M’) по отношению к полюсу (O) и полярной оси (l), a (h) — компонента вектора (overrightarrow) по вектору (boldsymbol). Она определена, так как эти векторы коллинеарны (рис. 2.5).

Рис. 2.5

Сферические координаты точки — три числа ((r), (varphi), (theta)). Они определяются так: (r = |overrightarrow|). Как и для цилиндрических координат, (varphi) — угол вектора (overrightarrow>) с лучом (l), а (theta) — угол вектора (overrightarrow) с плоскостью (Theta) (рис. 2.6).

Рис. 2.6

[spoiler title=”источники:”]

http://univerlib.com/analytic_geometry/vector_algebra/coordinate_systems/

[/spoiler]

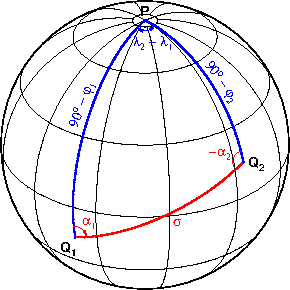
Обратная геодезическая задача — это нахождение начального направления и расстояния между двумя точками с известными координатами.

Общие положения

В качестве модели Земли принимается сфера с радиусом R, равным среднему радиусу земного эллипсоида. Аналогом прямой линии на плоскости является геодезическая линия на поверхности. На сфере геодезическая линия — дуга большого круга.

Введём следующие обозначения:

• φ — географическая широта,
• λ — географическая долгота,
• α — азимут дуги большого круга,
• σ — сферическое расстояние (длина дуги большого круга, выраженная в долях радиуса шара).

Линейное расстояние по дуге большого круга s связано со сферическим расстоянием σ формулой s = R σ.

Прямая и обратная геодезические задачи являются важными элементами более сложных геодезических задач.

Постановка задачи

Исходные данные

координаты пунктов Q₁ и Q₂ на сфере — φ₁, λ₁ и φ₂, λ₂.

Определяемые величины

расстояние между пунктами и начальный азимут направления с точки Q₁ на пункт Q₂ — σ, α₁.

На рисунке синим цветом выделены заданные элементы сферического треугольника, красным цветом неизвестные.

Алгоритм

Существует великое множество подходов к решению поставленной задачи. Рассмотрим простой и надёжный векторный метод.

Последовательность решения:

1. преобразовать углы φ₂ и λ₂ в декартовы координаты,
2. развернуть координатные оси вокруг оси Z на угол λ₁,
3. развернуть координатные оси вокруг оси Y на угол (90° − φ₁),
4. преобразовать декартовы координаты в сферические.

Можно устранить второй пункт, если в первом заменить долготу λ₂ на разность долгот (λ₂ − λ₁).

Пример реализации алгоритма в виде функции языка Си:

/*
 * Решение обратной геодезической задачи
 *
 * Аргументы исходные:
 *     pt1  - {широта, долгота} точки Q1
 *     pt2  - {широта, долгота} точки Q2
 *
 * Аргументы определяемые:
 *     azi  - азимут начального направления
 *     dist - расстояние (сферическое)
 */
void SphereInverse(double pt1[], double pt2[], double *azi, double *dist)
{
  double x[3], pt[2];
 
  SpherToCart(pt2, x);			// сферические -> декартовы
  Rotate(x, pt1[1], 2);			// первое вращение
  Rotate(x, M_PI_2 - pt1[0], 1);	// второе вращение
  CartToSpher(x, pt);	     		// декартовы -> сферические
  *azi = M_PI - pt[1];
  *dist = M_PI_2 - pt[0];
 
  return;
}

Следует заметить, что прямая и обратная задача математически идентичны, и алгоритмы их решения зеркально отражают друг друга.

Преобразование сферических координат в декартовы

В данном случае в качестве сферических координат φ, λ подставим φ₂, λ₂.

Реализация на Си:

/*
 * Преобразование сферических координат в вектор
 *
 * Аргументы исходные:
 *     y - {широта, долгота}
 *
 * Аргументы определяемые:
 *     x - вектор {x, y, z}
 */
void SpherToCart(double y[], double x[])
{
  double p;
 
  p = cos(y[0]);
  x[2] = sin(y[0]);
  x[1] = p * sin(y[1]);
  x[0] = p * cos(y[1]);
 
  return;
}

Вращение вокруг оси

Представим оператор вращения вокруг оси X на угол θ в следующем виде:

Операторы вращения вокруг осей Y и Z получаются перестановкой символов.

Реализация вращения вокруг i-ой координатной оси на Си:

/*
 * Вращение вокруг координатной оси
 *
 * Аргументы:
 *     x - входной/выходной 3-вектор
 *     a - угол вращения
 *     i - номер координатной оси (0..2)
 */
void Rotate(double x[], double a, int i)
{
  double c, s, xj;
  int j, k;
 
  j = (i + 1) % 3;
  k = (i - 1) % 3;
  c = cos(a);
  s = sin(a);
  xj = x[j] * c + x[k] * s;
  x[k] = -x[j] * s + x[k] * c;
  x[j] = xj;
 
  return;
}

Преобразование декартовых координат в сферические

В данном случае в роли сферических координат φ, λ окажутся углы (90° − σ), (180° − α₁).

Реализация на Си:

/*
 * Преобразование вектора в сферические координаты
 *
 * Аргументы исходные:
 *     x - {x, y, z}
 *
 * Аргументы определяемые:
 *     y - {широта, долгота}
 *
 * Возвращает:
 *     длину вектора
 */
double CartToSpher(double x[], double y[])
{
  double p;
 
  p = hypot(x[0], x[1]);
  y[1] = atan2(x[1], x[0]);
  y[0] = atan2(x[2], p);
 
  return hypot(p, x[2]);
}

Пример программной реализации

Исходники вышеприведённых функций можно найти в архиве Sph.zip в файле sph.c. Кроме того, в файл sph.h включены следующие определения:

#define A_E 6371.0				// радиус Земли в километрах
#define Degrees(x) (x * 57.29577951308232)	// радианы -> градусы
#define Radians(x) (x / 57.29577951308232)	// градусы -> радианы

Теперь напишем программу, которая обращается к функции SphereInverse для решения обратной задачи:

#include <stdio.h>
#include <stdlib.h>
#include "sph.h"
 
int main(int argc, char *argv[])
{
  char buf[1024];
  double pt1[2], pt2[2];
  double lat1, lon1, lat2, lon2, azi1, azi2, dist;
 
  while (fgets(buf, 1024, stdin) != NULL) {
    sscanf(buf, "%lf %lf %lf %lf", &lat1, &lon1, &lat2, &lon2);
    pt1[0] = Radians(lat1);
    pt1[1] = Radians(lon1);
    pt2[0] = Radians(lat2);
    pt2[1] = Radians(lon2);
    SphereInverse(pt2, pt1, &azi2, &dist);		// Решение обратной задачи
    SphereInverse(pt1, pt2, &azi1, &dist);		// Вычисление обратного азимута
    printf("%ft%ft%.4fn", Degrees(azi1), Degrees(azi2), dist * A_E);
  }
  return 0;
}

В архиве Sph.zip этот код находится в файле inv.c. Создадим исполняемый модуль inv компилятором gcc:

$ gcc -o inv inv.c sph.c -lm

Впрочем, в архиве есть Makefile. Для MS Windows готовую программу inv.exe можно найти в архиве Sph-win32.zip.

Программа читает данные из стандартного ввода консоли и отправляет результаты на стандартный вывод. Для чтения и записи файлов используются символы перенаправления потока «>» и «<» соответственно. Из каждой строки ввода программа считывает координаты двух точек φ₁, λ₁, φ₂, λ₂, которые должны быть в градусах, решает обратную задачу и записывает в строку вывода α₁, α₂, s (азимуты прямого и обратного направлений в градусах; расстояние между пунктами в километрах, а точнее, в единицах, определённых константой A_E).

Создадим файл inv.dat, содержащий одну строку данных:

30 0 52 54

После запуска программы

получим α₁, α₂, s:

44.804060 262.415109 5001.1309

В архиве Sph-py.zip находятся скрипты на языке Питон. Выполнение скрипта в командной консоли:

Решение обратной задачи средствами PROJ

В пакет PROJ входит программа geod, предназначенная для решения прямых и обратных геодезических задач на сфере. Так выглядит команда обработки файла inv.dat:

$ geod +a=6371000 +b=6371000 -I -f "%f" -F "%.4f" +units=km inv.dat

Параметр +a определяет радиус сферы, -I — решение обратных задач, -f — формат вывода угловых величин, -F — формат вывода длин линий, +units — единица измерения расстояний. В результате получим идентичный вывод:

44.804060 -97.584891 5001.1309

Различие значений α₂ на 360° объясняется тем, что inv выводит азимуты в диапазоне от 0° до 360°, а geod от −180° до +180°.

Альтернативные методы

Некоторые элементы альтернативных методов решения обратной задачи представлены в статье Вычисление расстояния и начального азимута между двумя точками на сфере.

В большинстве своём другие методы основаны на сферической тригонометрии. Многие из них используют вычисление σ или α₁ по таким функциям, как синус, косинус или гаверсинус. Это приводит к неоднозначности результатов вблизи особых значений, когда производная функции равна нулю. Такие методы не могут считаться универсальными.

К наиболее надёжным относится следующий способ:

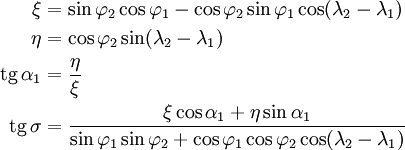
В сферической тригонометрии углы и стороны должны быть в диапазоне [0, 180°]. Алгоритмизация формул требует анализа и обработки случаев, когда входные величины не попадают в эти рамки.

Ссылки

• Вычисление расстояния и начального азимута между двумя точками на сфере
• Задачи на сфере: прямая геодезическая задача
• Задачи на сфере: угловая засечка
• Задачи на сфере: линейная засечка
• Краткий справочник по сферической тригонометрии
• man_geod – PROJ.4
• Earth radius
• Степанов Н. Н. Сферическая тригонометрия

Эти сферические координаты представляют собой набор точек местоположения в трехмерном пространстве , состоящий из радиальной координаты и две угловых координат называемых полярными координат и азимутальная координат.

На рисунке 1, который мы видим ниже, показаны сферические координаты (r, θ, φ) точки M. Эти координаты относятся к ортогональной системе декартовых осей X, Y, Z с началом O.

Рис. 1. Сферические координаты (r, θ, φ) точки M. (wikimedia commons)

В этом случае координата r точки M – это расстояние от этой точки до начала координат O. Полярная координата θ представляет собой угол между положительной полуосью Z и радиус-вектором OM. В то время как азимутальная координата φ – это угол между положительной полуосью X и радиус-вектором OM ‘, где M’ – ортогональная проекция M на плоскость XY.

Радиальная координата r принимает только положительные значения, но если точка находится в начале координат, тогда r = 0. Полярная координата θ принимает минимальное значение 0 ° для точек, расположенных на положительной полуоси Z, а максимальное значение 180 ° для точек находится на отрицательной полуоси Z. Наконец, азимутальная координата φ принимает минимальное значение 0 ° и максимальное значение 360 °.

0 ≤ г <∞

0 ≤ θ ≤ 180º

0 ≤ φ <360º

Изменение координат

Далее будут приведены формулы, позволяющие получить декартовы координаты (x, y, z) точки M, предполагая, что сферические координаты той же точки (r, θ, φ) известны:

х = г Sen (θ) Cos (φ)

у = г Sen (θ) Sen (φ)

z = r Cos (θ)

Таким же образом полезно найти отношения для перехода от декартовых координат (x, y, z) данной точки к сферическим координатам указанной точки:

г = √ (х ^ 2 + у ^ 2 + г ^ 2)

θ = Arctan (√ (x ^ 2 + y ^ 2) / z)

φ = Арктангенс (y / x)

Векторная база в сферических координатах

По сферическим координатам определяется ортонормированный базис базовых векторов, которые обозначаются Ur , Uθ , Uφ . На рисунке 1 показаны эти три единичных вектора, которые имеют следующие характеристики:

– Ur – единичный вектор, касательный к радиальной прямой θ = ctte и φ = ctte;

– Uθ – единичный вектор, касательный к дуге φ = ctte и r = ctte;

– Uφ – единичный вектор, касательный к дуге r = ctte и θ = ctte.

Элементы линий и объема в сферических координатах

Вектор положения точки в пространстве в сферических координатах записывается так:

г = г Ур

Но бесконечно малое изменение или смещение точки в трехмерном пространстве в этих координатах выражается следующим векторным соотношением:

d r = dr Ur + r dθ Uθ + r Sen (θ) d φ Uφ

Наконец, бесконечно малый объем dV в сферических координатах записывается так:

dV = r ^ 2 Sen (θ) dr dθ dφ

Эти соотношения очень полезны для вычисления линейных и объемных интегралов в физических ситуациях, обладающих сферической симметрией.

Связь с географическими координатами

Под географическими координатами понимаются те, которые служат для определения местоположения на поверхности земли. Эта система использует координаты широты и долготы для определения местоположения на поверхности Земли.

В географической системе координат предполагается, что земная поверхность имеет сферическую форму с радиусом Rt, даже если известно, что она сплющена на полюсах, и рассматривается набор воображаемых линий, называемых параллелями и меридианами.

Рис. 2. Долгота α и широта β наблюдателя на земной поверхности.

Широта β – это угол, образованный радиусом, который начинается от центра Земли до точки, которую вы хотите расположить. Она измеряется от экваториальной плоскости, как показано на рисунке 2. С другой стороны, долгота α – это угол, который образует меридиан точки, которая расположена, по отношению к нулевому меридиану (известному как меридиан Гринвича).

Широта может быть северной или южной широтой, в зависимости от того, находится ли место, где вы находитесь, в северном или южном полушарии. Точно так же долгота может быть западной или восточной в зависимости от того, находится ли местоположение к западу или востоку от нулевого меридиана.

Формулы для изменения с географической на сферическую

Чтобы получить эти формулы, прежде всего необходимо установить систему координат. Плоскость XY выбирается так, чтобы она совпадала с плоскостью экватора, положительная полуось X – это та, которая идет от центра Земли и проходит через нулевой меридиан. В свою очередь, ось Y проходит через меридиан 90º E. Земная поверхность имеет радиус Rt.

В этой системе координат преобразования из географического в сферический выглядят следующим образом:

αEβN → (Rt, θ = 90º-β, φ = α)

αOβN → (Rt, θ = 90º-β, φ = 360º-α)

αEβS → (Rt, θ = 90º + β, φ = α)

αOβS → (Rt, θ = 90º + β, φ = 360º-α)

Примеры

Пример 1

Географические координаты Пальма-де-Майорка (Испания):

38,847º восточной долготы и 39,570º северной широты. Для определения сферических координат, соответствующих Пальма-де-Майорка, применяется первая из формул, приведенных в предыдущем разделе:

38 847ºE 39 570ºN → (r = 6371 км, θ = 90º-39 570º, φ = 38 847º)

Итак, сферические координаты:

Пальма-де-Майорка: (r = 6371 км, θ = 50,43º, φ = 38,85º)

В предыдущем ответе r было принято равным среднему радиусу Земли.

Пример 2

Зная, что Мальвинские (Фолклендские) острова имеют географические координаты 59ºO 51,75ºS, определите соответствующие полярные координаты. Помните, что ось X идет от центра Земли к меридиану 0º и в экваториальной плоскости; ось Y также находится в экваториальной плоскости и проходит через западный меридиан 90º; наконец, ось Z на оси вращения Земли в направлении юг-север.

Чтобы найти соответствующие сферические координаты, воспользуемся формулами, представленными в предыдущем разделе:

59ºO 51,75ºS → (r = 6371 км, θ = 90º + 51,75º, φ = 360º-59º), то есть

Мальвинские острова: (r = 6371 км, θ = 141,75º, φ = 301º)

упражнения

Упражнение 1

Найдите декартовы координаты Пальмы-де-Майорки в декартовой системе координат XYZ, показанной на рисунке 2.

Решение: Ранее, в примере 1, сферические координаты были получены, начиная с географических координат Пальма-де-Майорка. Таким образом, представленные выше формулы можно использовать для перехода от сферической формы к декартовой:

x = 6371 км сен (50,43º) Cos (38,85º)

y = 6371 км сен (50,43º) сен (38,85º)

z = 6371 км Cos (50,43º)

Выполняя соответствующие расчеты, получаем:

Пальма-де-Майорка: (x = 3825 км, y = 3081 км, z = 4059)

Упражнение 2.

Найдите декартовы координаты Фолклендских островов в декартовой системе координат XYZ, показанной на рисунке 2.

Решение: Ранее в примере 2 сферические координаты были получены исходя из географических координат Мальвинских островов. Таким образом, представленные выше формулы можно использовать для перехода от сферической формы к декартовой:

x = 6371 км Сен (141,75º) Cos (301º)

y = 6371 км сен (141,75º) сен (301º)

z = 6371 км Cos (141,75º)

Выполняя соответствующие вычисления, получаем:

Фолклендские острова: (x = 2031 км, y = -3381 км, z = -5003)

Ссылки

1. Арфкен Г. и Вебер Х. (2012). Математические методы для физиков. Подробное руководство. 7-е издание. Академическая пресса. ISBN 978-0-12-384654-9
2. Расчет cc. Решенные задачи цилиндрических и сферических координат. Получено с: calculo.cc
3. Астрономическая мастерская. Широта и долгота. Получено с: tarifamates.blogspot.com/
4. Вайсштейн, Эрик У. «Сферические координаты». Из MathWorld-A Wolfram Web. Получено с: mathworld.wolfram.com
5. википедия. Сферическая система координат. Получено с: en.wikipedia.com
6. википедия. Векторные поля в цилиндрических и сферических координатах. Получено с: en.wikipedia.com