Загрузить PDF
Загрузить PDF
Смешанное число (смешанная дробь) — это дробь, которая записана в виде целого числа и правильной дроби.[1]
Смешанные числа можно делить — для этого сначала нужно преобразовать их в неправильные дроби. После преобразования смешанных чисел они делятся, как любые другие дроби.
-

1
Умножьте целое число на знаменатель дробной части.[2]
Сделайте это для обоих смешанных чисел. Запишите результат; он является частью нового числителя. -

2
Результат предыдущего умножения сложите с числителем дробной части.[3]
Сделайте это для обоих смешанных чисел. Полученная сумма является числителем неправильной дроби. -

3
Полученную сумму запишите над исходным знаменателем.[4]
Сделайте это для обеих дробей (не перепутайте соответствующие знаменатели). Получатся неправильные дроби, которые можно использовать для решения исходной задачи на деление. -

4
Преобразуйте целые числа в дроби. Если в задаче дано любое целое число, преобразуйте его в дробь. Для этого в числителе дроби запишите данное целое число, а в знаменателе запишите 1.[5]
- Например,
.
Реклама
- Например,
-

1
Перепишите исходное выражение деления. Для этого воспользуйтесь неправильными дробями, которые найдены в предыдущем разделе. Так как свойство коммутативности не применяется к операции деления, не перепутайте порядок расположения двух дробей.
- Например,
.
- Например,
-

2
Найдите дробь, обратную второй дроби.[6]
Для этого поменяйте местами числитель и знаменатель второй дроби.[7]
Затем операцию деления замените операцией умножения.[8]
-

3
Перемножьте числители. Сделайте это, как перемножаете два целых числа. Результат является числителем конечной дроби.[9]
-

4
Перемножьте знаменатели. Сделайте это, как перемножаете два целых числа. Результат является знаменателем конечной дроби.[10]
-

5
Упростите полученную дробь (если возможно). Чтобы упростить (сократить) дроби, нужно найти наибольший делитель (не равный 1) числителя и знаменателя, а затем разделить их на такой делитель. Более подробно об этом рассказано в статье «Как сокращать дроби».
Реклама
-

1
Разделите числитель на знаменатель. Если остатка нет, получится целое (а не смешанное) число; в этом случае решение задачи окончено. Но, скорее всего, при делении числителя на знаменатель получится остаток (пока забудьте про него). Целый результат деления числителя на знаменатель является целой частью смешанного числа.[11]
-

2
Остаток от деления числителя на знаменатель запишите в числителе дроби. Знаменатель оставьте прежним. Полученная дробь является дробной частью смешанного числа.[12]
-

3
Объедините целую и дробную части. Получится искомое смешанное число.
Реклама
Об этой статье
Эту страницу просматривали 74 228 раз.
Была ли эта статья полезной?
Деление смешанных чисел осуществляют по тому же принципу, что и умножение: сначала нужно перевести смешанную дробь в неправильную, а затем выполнять действие как с обыкновенной дробью.
Мы можем либо делить делимое на дробь, либо умножать его на дробь, обратную делителю.
Разберём подробнее все случаи.
Деление смешанного числа на натуральное
Можно сказать, что существует два способа разделить смешанное число на целое.
При делении смешанной дроби на натуральное число необходимо представить смешанную дробь в виде неправильной, а затем умножить её на число, обратное делителю.
Напомним, что любое целое число можно представить в виде неправильной дроби с единицей в роли знаменателя; если мы делаем из этой дроби обратную, то единица переносится в числитель, а знаменателем и будет наше число. Например, так:
$$4frac{2}{5} : 2 = frac{4 cdot 5 + 2}{5} cdot frac{1}{2} = frac{22 cdot 1}{5 cdot 2}$$
Существует и такая формулировка:
При делении смешанной дроби на натуральное число необходимо представить смешанную дробь в виде неправильной дроби, а затем умножить знаменатель на делитель, а числитель оставить без изменений.
$$4frac{2}{5} : 2 = frac{4 cdot 5 + 2}{5} : 2 = frac{22}{5 cdot 2}$$
Получается, что мы делаем одно и то же действие. Запись немного отличается, но считаем мы так же: после того, как мы перевели смешанное число в неправильную дробь, числитель уже не меняется, ведь для того, чтобы разделить дробь на целое число, нужно умножить её знаменатель на это число.
Это довольно простое действие, и, если числа, которыми мы оперируем, небольшие, то такой пример можно решить и устно:
$$4frac{2}{5} : 2 = frac{22}{10} = 2 frac{2}{10}$$
Деление целого числа на смешанную дробь
$$8 : 5frac{1}{4}$$
Такой пример выглядит сложнее. Но он решается по тому же принципу.
При делении целого числа на смешанную дробь, нужно перевести смешанное число в неправильную дробь, а затем умножить целое число на дробь, обратную данной неправильной дроби.
$$8 : 5frac{1}{6} = 8 : frac{31}{6} = 8 cdot frac{6}{31}$$
Мы перемещаем бывшее делимое, а теперь один из множителей, в числитель дроби и выполняем умножение:
$$8 cdot frac{6}{31} = frac{8 cdot 6}{31} = frac{48}{31} = 1frac{17}{31}$$
Давайте потренируемся.
Образавр пошёл за грибами и набрал две корзинки за полтора часа. Сколько корзинок он набрал за час?
Показать решение
Скрыть
Разделим количество корзинок на количество часов.
$$2 : 1frac{1}{2}$$
Делаем всё по привычному сценарию: переводим смешанную дробь в неправильную, «переворачиваем», умножаем.
$$2 : 1frac{1}{2} = 2 : frac{3}{2} = 2 cdot frac{2}{3} = frac{2 cdot 2}{3} = frac{4}{3} = 1frac{1}{3}$$
При желании можно проверить, умножив собранное за час количество корзинок на время сбора. Кстати, у нас получится умножение смешанных чисел.
Показать проверку
Скрыть
$$1frac{1}{3} cdot 1frac{1}{2} = frac{4}{3} cdot frac{3}{2} = frac{4 cdot 3}{3 cdot 2}$$
На этом этапе можно сократить дробь, убрав множитель $«3»$, так как он общий и для числителя, и для знаменателя:
$$frac{4 cdot 3}{3 cdot 2} = frac{4 }{2} = 2$$
Деление смешанного числа на дробь и дроби на смешанное число
Зная общий принцип, можете сформулировать, как происходит деление?
Показать правило
Скрыть
Опираясь на предыдущие правила, можно дать примерно такое определение:
Чтобы выполнить деление смешанного числа на дробь, нужно сначала представить делимое в виде неправильной дроби, а затем произвести действие с дробями: умножить делимое на дробь, обратную делителю.
Давайте для тренировки выполним такое упражнение: посмотрите на пример и найдите ошибку в вычислениях.
Показать правильный вариант
Скрыть
Хотя мы и заменяем деление дробей умножением, важно помнить, что в данном случае мы не можем свободно менять множители местами. В обратную дробь можно превращать только делитель. Правильное решение будет выглядеть так:
Деление смешанных чисел
И наконец разберём деление одного смешанного числа на другое. Правило для него то же самое, с той лишь разницей, что оба смешанных числа должны быть в виде неправильных дробей.
Мама купила четыре новые книги сказок, чтобы читать Тимоше по вечерам. За две недели и ещё один день она прочитала три книги, а четвёртую прочла на $frac{4}{7}$. Сколько книг читала мама за неделю?
Разделим количество книг на количество недель.
$$3frac{4}{7} : 2frac{1}{7}$$
Сначала переведём обе дроби в неправильные. У нас получится $frac{25 }{7}$ и $frac{15}{7}$. Произведём умножение делимого на дробь, обратную делителю. В данном примере мы можем сократить множители:
В предыдущих уроках было сказано, что дробь, состоящая из целой и дробной части, называется смешанной.
Все дроби, имеющие целую и дробную часть, носят одно общее название — смешанные числа.
Смешанные числа так же как и обыкновенные дроби можно складывать, вычитать, умножать и делить. В данном уроке мы рассмотрим каждое из этих действий по отдельности.
Сложение целого числа и правильной дроби
Встречаются задачи, в которых требуется сложить целое число и правильную дробь. Например, сложить число 2 и дробь ![]() . Чтобы решить этот пример, нужно число 2 представить в виде дроби
. Чтобы решить этот пример, нужно число 2 представить в виде дроби ![]() . Затем сложить дроби с разными знаменателями:
. Затем сложить дроби с разными знаменателями:
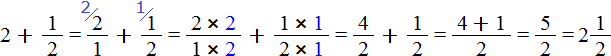
А теперь внимательно посмотрим на этот пример. Смотрим на его начало и на его конец. Начало у него выглядит так: ![]() , а конец так:
, а конец так: ![]() . Различие в том, что в первом случае число 2 и дробь
. Различие в том, что в первом случае число 2 и дробь ![]() соединяются знаком сложения, а во втором случае они записаны вместе. На самом деле это одно и то же. Дело в том, что
соединяются знаком сложения, а во втором случае они записаны вместе. На самом деле это одно и то же. Дело в том, что ![]() это свёрнутая форма записи смешанного числа, а
это свёрнутая форма записи смешанного числа, а ![]() — развёрнутая.
— развёрнутая.
Когда перед нами смешанное число вида ![]() , мы должны понимать, что знак сложения опущен.
, мы должны понимать, что знак сложения опущен.
Какой можно сделать вывод? Если потребуется сложить целое число и правильную дробь, можно опустить плюс и записать целое число и дробь вместе.
Значит значение выражения ![]() равно
равно ![]()
![]()
Если к двум целым пиццам прибавить половину пиццы, то получится две целые пиццы и ещё половина пиццы:
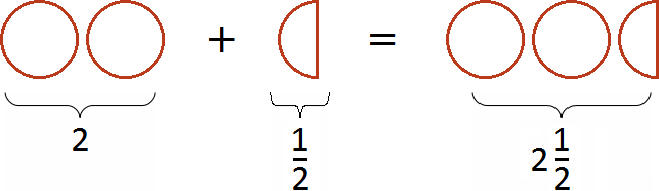
Пример 2. Найти значение выражения ![]()
Представим число 3 в виде дроби ![]() . Затем сложим дроби с разными знаменателями:
. Затем сложим дроби с разными знаменателями:
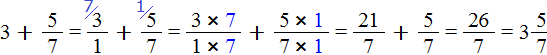
Это первый способ. Второй способ намного проще. Можно поставить знак равенства и записать целую и дробную часть вместе. То есть опустить знак сложения:
![]()
Пример 3. Найти значение выражения ![]()
Можно записать вместе число 2 и дробь ![]() , но этот ответ не будет окончательным, поскольку в дроби
, но этот ответ не будет окончательным, поскольку в дроби ![]() можно выделить целую часть.
можно выделить целую часть.
Поэтому в данном примере сначала нужно выделить целую часть в дроби ![]() . Пять вторых это две целых и одна вторая:
. Пять вторых это две целых и одна вторая:
![]()
Теперь в главном выражении ![]() вместо дроби
вместо дроби ![]() запишем смешанное число
запишем смешанное число ![]()
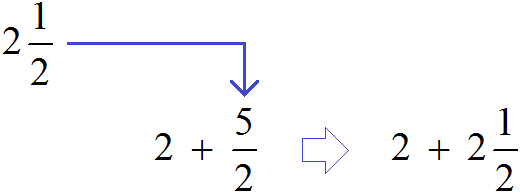
Получили новое выражение ![]() . В этом выражении смешанное число
. В этом выражении смешанное число ![]() запишем в развёрнутом виде:
запишем в развёрнутом виде:
![]()
Применим сочетательный закон сложения. Сложим две двойки, получим 4:
![]()
Теперь свернём полученное смешанное число:
![]()
Это окончательный ответ. Подробное решение этого примера можно записать следующим образом:
![]()
Сложение смешанных чисел
Встречаются задачи, в которых требуется сложить смешанные числа. Например, найти значение выражения ![]() . Чтобы решить этот пример, нужно целые и дробные части сложить по отдельности.
. Чтобы решить этот пример, нужно целые и дробные части сложить по отдельности.
Для начала запишем смешанные числа в развёрнутом виде:
![]()
Применим сочетательный закон сложения. Сгруппируем целые и дробные части по отдельности:
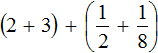
Вычислим целые части: 2 + 3 = 5. В главном выражении заменяем выражение в скобках (2 + 3) на полученную пятёрку:
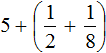
Теперь вычислим дробные части. Это сложение дробей с разными знаменателями. Как складывать такие дроби мы уже знаем:
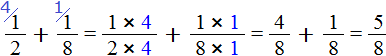
Получили ![]() . Теперь в главном выражении
. Теперь в главном выражении 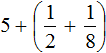 заменяем дробные части на полученную дробь
заменяем дробные части на полученную дробь ![]()
![]()
Теперь свернем полученное смешанное число:
![]()
Таким образом, значение выражения ![]() равно
равно ![]() . Попробуем изобразить это решение в виде рисунка. Если к двум целым и половине пиццы прибавить три целые и одну восьмую пиццы, то получится пять целых пицц и ещё пять восьмых пиццы:
. Попробуем изобразить это решение в виде рисунка. Если к двум целым и половине пиццы прибавить три целые и одну восьмую пиццы, то получится пять целых пицц и ещё пять восьмых пиццы:
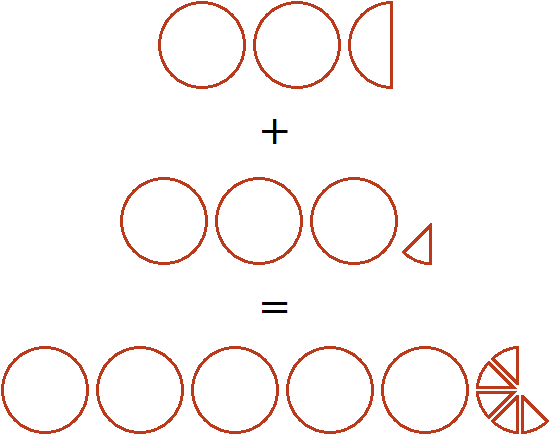
Подобные примеры нужно решать быстро, не останавливаясь на подробностях. Находясь в школе, нам пришлось бы записать решение этого примера следующим образом:
![]()
Если в будущем увидите такое короткое решение, не пугайтесь. Вы уже понимаете, что откуда взялось.
Пример 2. Найти значение выражения
Запишем смешанные числа в развёрнутом виде:
![]()
Сгруппируем целые и дробные части по отдельности:
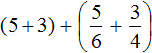
Вычислим целые части: 5 + 3 = 8. В главном выражении заменяем выражение в скобках (5 + 3) на полученное число 8
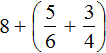
Теперь вычислим дробные части:
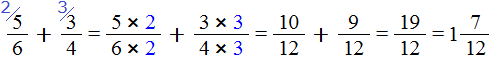
Получили смешанное число ![]() . Теперь в главном выражении
. Теперь в главном выражении 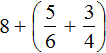 заменяем выражение в скобках на полученное смешанное число
заменяем выражение в скобках на полученное смешанное число ![]()
![]()
Получили выражение ![]() . В данном случае число 8 надо прибавить к целой части смешанного числа
. В данном случае число 8 надо прибавить к целой части смешанного числа ![]() . Для этого смешанное число
. Для этого смешанное число ![]() можно временно развернуть, чтобы было понятнее, что с чем складывать:
можно временно развернуть, чтобы было понятнее, что с чем складывать:
![]()
Сложим целые части. Получаем 9
![]()
Сворачиваем готовый ответ:
![]()
Таким образом, значение выражения равно
![]() .
.
Полное решение этого примера выглядит следующим образом:
![]()
Для решения подобных примеров существует универсальное правило. Выглядит оно следующим образом:
Чтобы сложить смешанные числа, надо:
- привести дробные части этих чисел к общему знаменателю;
- отдельно выполнить сложение целых и дробных частей.
Если при сложении дробных частей получилась неправильная дробь, выделить целую часть в этой дроби и прибавить ее к полученной целой части.
Применение готовых правил допустимо в том случае, если суть темы полностью понятна. Решение по-шаблону, поглядывая в другие подобные примеры, приводит к ошибкам на обнаружение которых уходит дополнительное время. Поэтому, сначала разумнее понять тему, а затем пользоваться готовым правилом.
Пример 3. Найти значение выражения ![]()
Воспользуемся готовым правилом. Приведём дробные части к общему знаменателю, затем по отдельности сложим целые и дробные части:
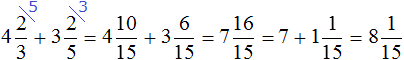
Сложение целого и смешанного числа
Встречаются задачи, в которых нужно сложить целое и смешанное число. Например, сложить 2 и смешанное число ![]() . В этом случае целые части складываются отдельно, а дробная часть остаётся без изменения:
. В этом случае целые части складываются отдельно, а дробная часть остаётся без изменения:
![]()
Здесь смешанная дробь ![]() была развёрнута в ходе решения, затем целые части были сгруппированы и сложены. В конце целая и дробная части были свёрнуты. В результате получили ответ
была развёрнута в ходе решения, затем целые части были сгруппированы и сложены. В конце целая и дробная части были свёрнуты. В результате получили ответ ![]() .
.
Попробуем изобразить это решение в виде рисунка. Если к двум целым пиццам прибавить три целые и треть пиццы, то получятся пять целых и треть пиццы:
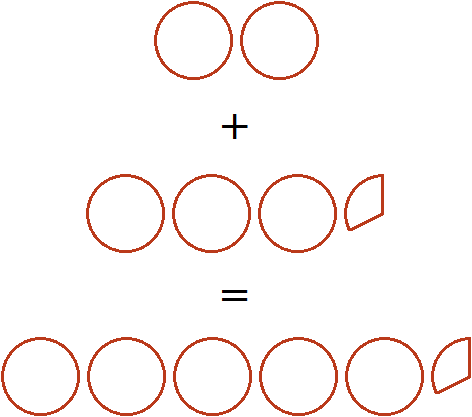
Пример 2. Найти значение выражения ![]()
В этом примере, как и в предыдущем, нужно сложить целые части:
![]()
Осталось свернуть целую и дробную части, но дело в том, что дробная часть ![]() представляет собой неправильную дробь. Сначала нужно выделить целую часть в этой неправильной дроби. Затем целую часть этой дроби прибавить к 4, а дробную часть оставить без изменения. Продолжим данный пример на новой строке:
представляет собой неправильную дробь. Сначала нужно выделить целую часть в этой неправильной дроби. Затем целую часть этой дроби прибавить к 4, а дробную часть оставить без изменения. Продолжим данный пример на новой строке:
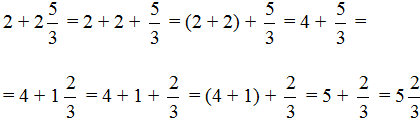
Вычитание дроби из целого числа
Встречаются задачи, в которых требуется вычесть дробь из целого числа. Например, вычесть из числа 1 дробь ![]() . Чтобы решить такой пример, нужно целое число 1 представить в виде дроби
. Чтобы решить такой пример, нужно целое число 1 представить в виде дроби ![]() , и выполнить вычитание дробей с разными знаменателями:
, и выполнить вычитание дробей с разными знаменателями:
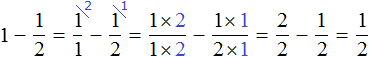
Если имеется одна целая пицца и мы вычтем из неё половину пиццы, то у нас получится половина пиццы:
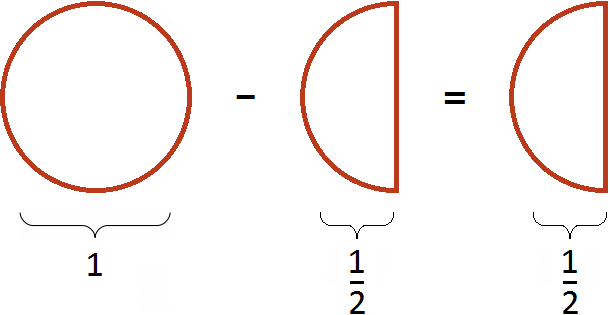
Пример 2. Найти значение выражения ![]() .
.
Представим число 2 в виде дроби ![]() , и выполним вычитание дробей с разными знаменателями:
, и выполним вычитание дробей с разными знаменателями:
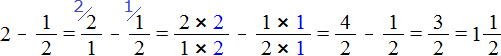
Если имеются две целые пиццы и мы вычтем из низ половину, то останется одна целая и половина пиццы:
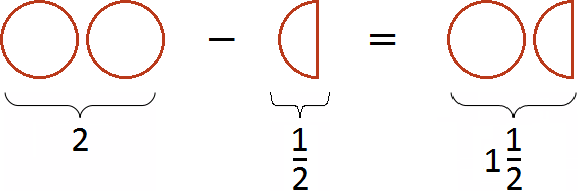
Такие примеры можно решать в уме. Достаточно суметь воспроизвести их в своём воображении. К примеру, найдём значение выражения ![]() , не приводя на бумаге никаких вычислений.
, не приводя на бумаге никаких вычислений.
Представим, что число 3 это три пиццы:

Нужно вычесть из них ![]() . Мы помним, что треть выглядит следующим образом:
. Мы помним, что треть выглядит следующим образом:

Теперь представим, во что превратятся три пиццы, если отрезать от них эту треть

Получилось ![]() (две целых и две трети пиццы).
(две целых и две трети пиццы).
Чтобы убедиться в правильности решения, можно найти значение выражения ![]() обычным методом, представив число 3 в виде дроби, и выполнив вычитание дробей с разными знаменателями:
обычным методом, представив число 3 в виде дроби, и выполнив вычитание дробей с разными знаменателями:
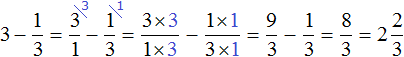
Пример 3. Найти значение выражения ![]()
Представим число 3 в виде дроби ![]() . Затем выполним вычитание дробей с разными знаменателями:
. Затем выполним вычитание дробей с разными знаменателями:
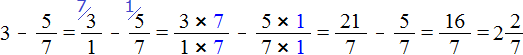
Вычитание смешанного числа из целого числа
Теперь мы готовы к тому, чтобы вычесть смешанное число из целого числа. Найдём значение выражения .
Чтобы решить этот пример, число 5 нужно представить в виде дроби, а смешанное число перевести в неправильную дробь. После перевода смешанного числа
в неправильную дробь, получим дробь
![]() . Теперь выполним вычитание дробей с разными знаменателями:
. Теперь выполним вычитание дробей с разными знаменателями:
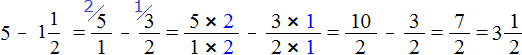
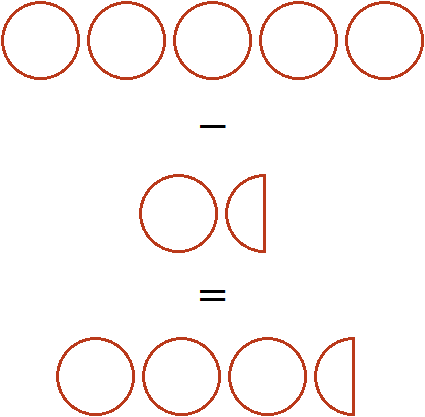
Если из пяти целых пицц вычесть одну целую и половину пиццы, то останутся три целые пиццы и половина пиццы:
Пример 2. Найти значение выражения ![]()
Представим 6 в виде дроби ![]() , а смешанное число
, а смешанное число ![]() , в виде неправильной дроби. После перевода смешанного числа
, в виде неправильной дроби. После перевода смешанного числа ![]() в неправильную дробь, получим дробь
в неправильную дробь, получим дробь ![]() . Теперь выполним вычитание дробей с разными знаменателями:
. Теперь выполним вычитание дробей с разными знаменателями:
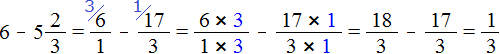
Примеры на вычитание дроби из числа или вычитание смешанной дроби из числа опять же можно выполнять в уме. Этот процесс легко поддаётся воображению.
К примеру, если нужно быстро найти значение выражения ![]() , то вовсе необязательно представлять число 2 в виде дроби и выполнять вычитание дробей с разными знаменателями. Число 2 можно вообразить, как две целые пиццы и далее представить, как от одной из них отрезали две третьих (два куска из трёх)
, то вовсе необязательно представлять число 2 в виде дроби и выполнять вычитание дробей с разными знаменателями. Число 2 можно вообразить, как две целые пиццы и далее представить, как от одной из них отрезали две третьих (два куска из трёх)

Тогда от той пиццы, от которой отрезали останется
![]() пиццы. Плюс одна из пицц останется нетронутой. Получится одна целая пицца и треть пиццы:
пиццы. Плюс одна из пицц останется нетронутой. Получится одна целая пицца и треть пиццы:
![]()
Если на рисунке вы закроете рукой две третьих пиццы (она закрашена), то сразу всё поймёте.
Вычитание смешанных чисел
Встречаются задачи, в которых требуется вычесть из одного смешанного числа другое смешанное число. Например, найдём значение выражения: ![]()
Чтобы решить этот пример, нужно смешанные числа ![]() и
и ![]() перевести в неправильные дроби, затем выполнить вычитание дробей с разными знаменателями:
перевести в неправильные дроби, затем выполнить вычитание дробей с разными знаменателями:
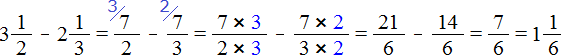
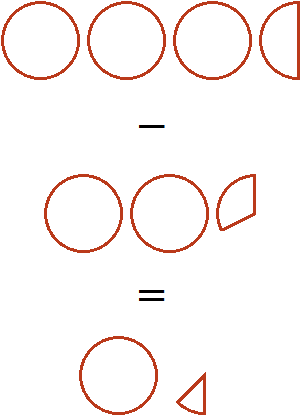
Если от трёх целых и половины пиццы вычесть две целые и треть пиццы, то останутся одна целая и одна шестая пиццы:
Пример 2. Найти значение выражения ![]()
Переводим смешанные числа ![]() и
и ![]() в неправильные дроби и выполняем вычитание дробей с разными знаменателями:
в неправильные дроби и выполняем вычитание дробей с разными знаменателями:
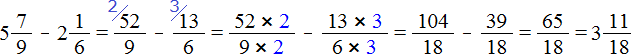
К вычитанию смешанных чисел мы ещё вернёмся. В вычитании дробей есть немало тонкостей, которым новичок пока не готов. Например, возможен случай, когда уменьшаемое может оказаться меньше вычитаемого. Это может вывести нас в мир отрицательных чисел, которых мы ещё не изучали.
А пока изучим умножение смешанных чисел. Благо оно не такое сложное, как сложение и вычитание.
Умножение целого числа на дробь
Чтобы целое число умножить на дробь, достаточно умножить это целое число на числитель дроби, а знаменатель оставить без изменения.
Например, умножим число 5 на дробь ![]() . Чтобы решить этот пример, нужно число 5 умножить на числитель дроби
. Чтобы решить этот пример, нужно число 5 умножить на числитель дроби ![]() , а знаменатель оставить без изменения:
, а знаменатель оставить без изменения:
![]()
В ответе получилась неправильная дробь. Выделим в ней целую часть:
![]()
Если имеются пять целых пицц и мы возьмём от этого количества половину, то у нас окажется две целые пиццы и половина пиццы:
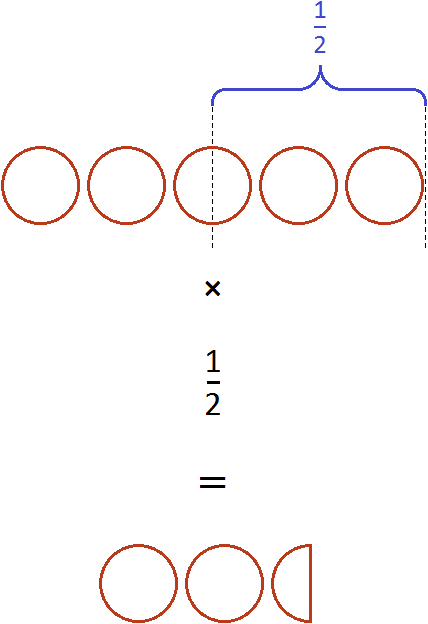
Пример 2. Найти значение выражения ![]()
Умножим число 3 на числитель дроби ![]()
![]()
В ответе получилась неправильная дробь ![]() , но мы выделили её целую часть и получили 2.
, но мы выделили её целую часть и получили 2.
Также, можно было сократить эту дробь. Получился бы тот же результат. Выглядело бы это следующим образом:
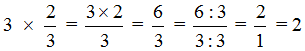
Если имеются три целые пиццы и мы возьмём от этого количества две третьих, то у нас окажется две целые пиццы:
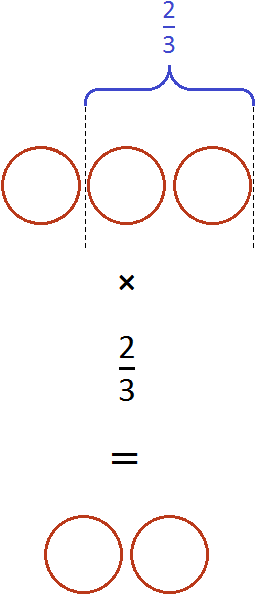
Пример 3. Найти значение выражения ![]()
Этот пример решается так же, как и предыдущие. Целое число и числитель дроби нужно перемножить:
![]()
Пример 4. Найти значение выражения ![]()
Умножим число 3 на числитель дроби ![]()
![]()
Умножение смешанного числа на дробь
Чтобы умножить смешанное число на дробь, нужно смешанное число перевести в неправильную дробь, затем выполнить перемножение обыкновенных дробей.
Пример 1. Найти значение выражения ![]()
Переведём смешанное число ![]() в неправильную дробь. После перевода это число превратится в дробь
в неправильную дробь. После перевода это число превратится в дробь ![]() . Затем можно будет умножить эту дробь на
. Затем можно будет умножить эту дробь на
![]()
Допустим, имеются одна целая и половина пиццы:

Умножить эти куски на означает взять от них две трети. Чтобы взять от них две трети, сначала разделим их на три равные части. Разделим пополам ту пиццу, которая слева. Тогда у нас получится три равных куска:
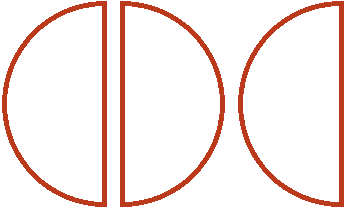
Теперь если мы возьмем (два куска из трёх имеющихся), то получим одну целую пиццу. Для наглядности закрасим эти два куска:
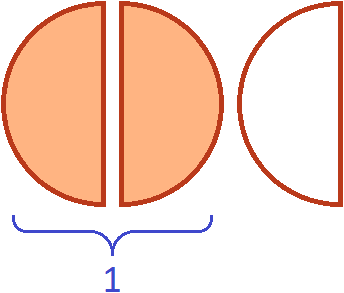
Поэтому значение выражения ![]() было равно 1
было равно 1
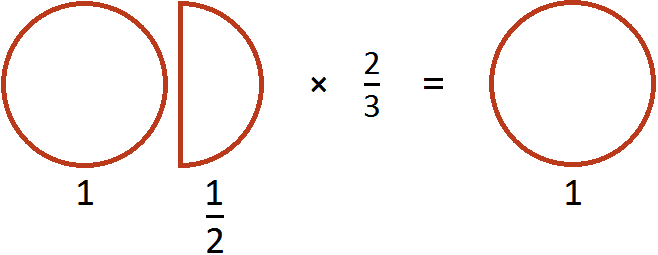
Умножение смешанных чисел
Встречаются задачи, в которых требуется перемножить смешанные числа. Например, перемножить ![]() и
и ![]() . Чтобы решить этот пример, нужно перевести эти смешанные числа в неправильные дроби, затем выполнить умножение неправильных дробей:
. Чтобы решить этот пример, нужно перевести эти смешанные числа в неправильные дроби, затем выполнить умножение неправильных дробей:
![]()
Попробуем разобраться в этом примере с помощью рисунка. Допустим, имеются одна целая и половина пиццы:
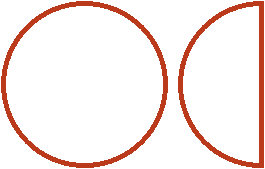
Теперь разберемся со смешанным множителем ![]() . Этот множитель означает, что одну целую и половину пиццы нужно взять 2 раза и еще
. Этот множитель означает, что одну целую и половину пиццы нужно взять 2 раза и еще ![]() раза.
раза.
С множителем 2 всё понятно, он означает что одну целую и половину пиццы нужно взять два раза. Давайте возьмём два раза целую пиццу и половину:
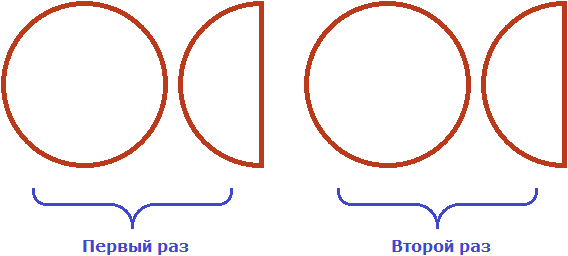
Но ещё осталось взять ![]() от изначальной целой пиццы и половины, ведь множителем было смешанное число
от изначальной целой пиццы и половины, ведь множителем было смешанное число ![]() . Для этого вернёмся к изначальной одной целой и половине пиццы, и разделим их на равные части так, чтобы можно было взять от них ровно половину. А половину мы сможем взять, если разделим целую пиццу на четыре части, а половину на две части:
. Для этого вернёмся к изначальной одной целой и половине пиццы, и разделим их на равные части так, чтобы можно было взять от них ровно половину. А половину мы сможем взять, если разделим целую пиццу на четыре части, а половину на две части:
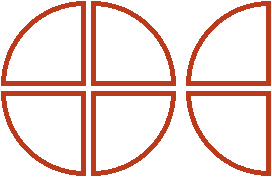
Мы разделили нашу целую пиццу и половину на равные части, и теперь можем сказать, что является половиной от этих кусков. Половиной от этих кусков является пиццы. Это можно хорошо увидеть, если мы упорядочим наши равные кусочки следующим образом:
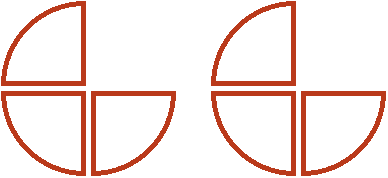
А если смотреть на изначальную целую пиццу и половину с точки зрения такого порядка, как на этом рисунке, то половиной от них является пиццы.
Поэтому значение выражения ![]() равно
равно ![]()
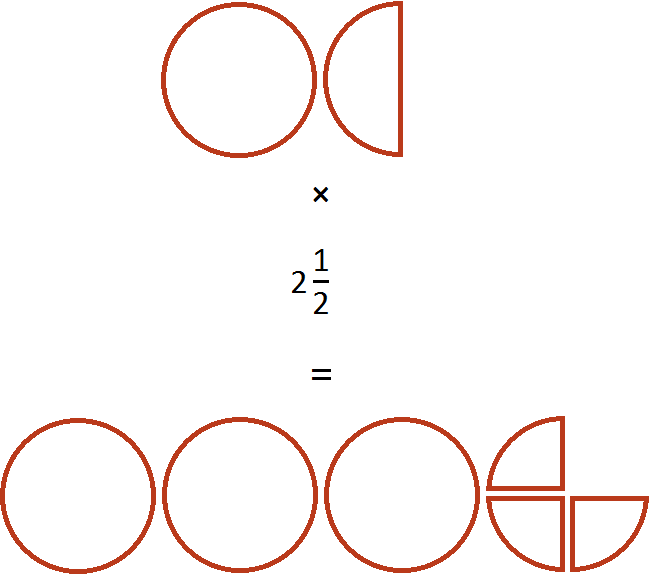
Пример 2. Найти значение выражения ![]()
Переводим смешанные числа в неправильные дроби и перемножаем эти неправильные дроби. Если в ответе получится неправильная дробь, выделим в ней целую часть:
![]()
Деление целого числа на дробь
Чтобы разделить целое число на дробь, нужно это целое число умножить на дробь, обратную делителю.
Например, разделим число 3 на дробь ![]() . Здесь число 3 — это делимое, а дробь
. Здесь число 3 — это делимое, а дробь ![]() — делитель.
— делитель.
Чтобы решить этот пример, нужно число 3 умножить на дробь, обратную дроби ![]() . А обратная дробь для дроби
. А обратная дробь для дроби ![]() это дробь
это дробь ![]() . Поэтому умножаем число 3 на дробь
. Поэтому умножаем число 3 на дробь ![]()
![]()
Допустим, имеются три целые пиццы:

Если мы зададим вопрос «cколько раз ![]() (половина пиццы) содержится в трёх пиццах», то ответом будет «шесть раз».
(половина пиццы) содержится в трёх пиццах», то ответом будет «шесть раз».
Действительно, если мы разделим каждую пиццу пополам, то у нас получится шесть половинок:
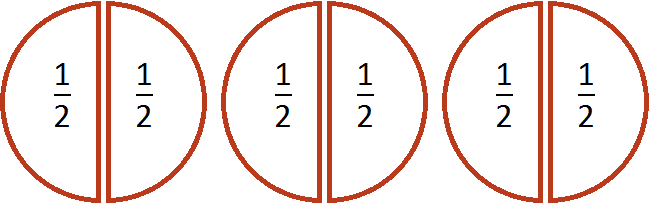
Поэтому значение выражения ![]() равно 6.
равно 6.
Пример 2. Найти значение выражения ![]()
Чтобы решить этот пример, нужно число 2 умножить на дробь, обратную дроби ![]() . А обратная дробь для дроби
. А обратная дробь для дроби ![]() это дробь
это дробь
![]()
Допустим, имеются две целые пиццы:

Зададим вопрос «Сколько раз ![]() пиццы содержится в этих двух пиццах?» Чтобы ответить на этот вопрос, выделим целую часть в дроби
пиццы содержится в этих двух пиццах?» Чтобы ответить на этот вопрос, выделим целую часть в дроби ![]() . После выделения целой части в этой дроби получим
. После выделения целой части в этой дроби получим ![]()
Теперь поставим вопрос так: «Сколько раз ![]() (одна целая и половина пиццы) содержится в двух пиццах?».
(одна целая и половина пиццы) содержится в двух пиццах?».
Чтобы ответить на этот вопрос, нужно найти в двух пиццах такое количество пиццы, которое изображено на следующем рисунке:

В двух пиццах одна целая и половина пиццы содержится один раз. Это можно увидеть, если вторую пиццу разделить пополам:
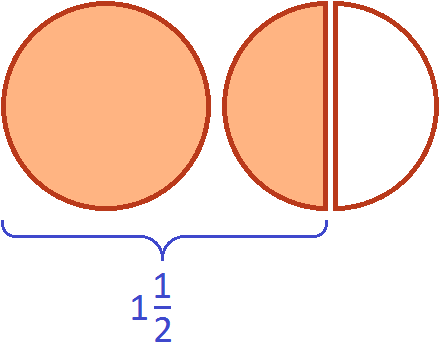
А оставшаяся половина это треть от ![]() , которая не вместилась. Третью она является по той причине, что в одной целой и половине пиццы целую часть пиццы можно разделить пополам. Тогда каждый кусок будет третью от этого количества:
, которая не вместилась. Третью она является по той причине, что в одной целой и половине пиццы целую часть пиццы можно разделить пополам. Тогда каждый кусок будет третью от этого количества:
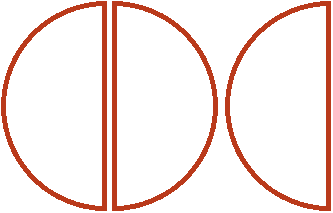
Поэтому значение выражения ![]() равно
равно ![]()
Пример 3. Найти значение выражения ![]()
Чтобы решить этот пример, нужно число 5 умножить на дробь, обратную дроби ![]() . А обратная дробь для дроби
. А обратная дробь для дроби ![]() это дробь
это дробь ![]() . Поэтому умножаем число 5 на
. Поэтому умножаем число 5 на ![]()
![]()
Дробь ![]() это 2 целых и
это 2 целых и ![]() . Проще говоря, две целые и четверть пиццы:
. Проще говоря, две целые и четверть пиццы:

А выражение ![]() определяет сколько раз
определяет сколько раз ![]() содержится в пяти целых пиццах. Ответом было смешанное число
содержится в пяти целых пиццах. Ответом было смешанное число ![]() .
.
То есть ![]() пиццы содержится в пяти целых пиццах
пиццы содержится в пяти целых пиццах ![]() раза.
раза.
Давайте нащупаем в пяти пиццах два раза по ![]()
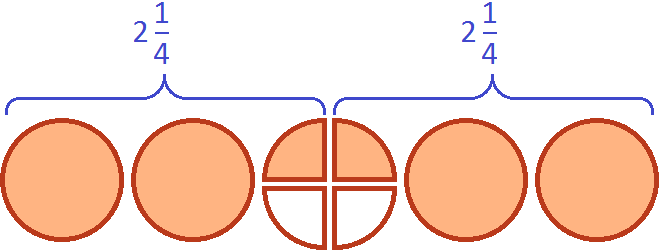
Белым цветом осталось не выделено две четверти. Эти две четверти представляют собой ![]() от
от ![]() , которые не вместились. Двумя девятыми они являются по той причине, что в
, которые не вместились. Двумя девятыми они являются по той причине, что в ![]() пиццы каждую целую пиццу можно разделить на четыре части. Тогда каждый кусок будет девятой частью от этого количества, а два куска соответственно двумя из девяти:
пиццы каждую целую пиццу можно разделить на четыре части. Тогда каждый кусок будет девятой частью от этого количества, а два куска соответственно двумя из девяти:
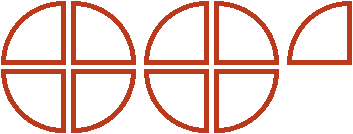
Поэтому значение выражения ![]() равно
равно ![]()
Деление дроби на целое число
Чтобы разделить дробь на целое число, нужно данную дробь умножить на число, обратное делителю. Таким делением мы занимались в прошлом уроке. Вспомним ещё раз.
Пример 1. Разделим дробь ![]() на число 2
на число 2
Чтобы разделить дробь ![]() на 2, нужно данную дробь умножить на число, обратное числу 2. А обратное числу 2 это дробь
на 2, нужно данную дробь умножить на число, обратное числу 2. А обратное числу 2 это дробь ![]()
![]()
Пусть имеется половина пиццы:

Разделим её поровну на две части. Тогда каждая получившаяся часть будет одной четвертой пиццы:
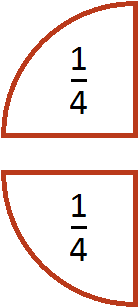
Поэтому значение выражения ![]() равно
равно ![]()
Пример 2. Найти значение выражения ![]()
Чтобы решить этот пример, нужно дробь ![]() умножить на число, обратное числу 2. Обратное числу 2 это дробь
умножить на число, обратное числу 2. Обратное числу 2 это дробь ![]()
![]()
Пример 3. Найти значение выражения ![]()
Умножаем первую дробь ![]() на число, обратное числу 3. Обратное числу 3 это дробь
на число, обратное числу 3. Обратное числу 3 это дробь ![]()
![]()
Деление целого числа на смешанное число
Встречаются задачи, в которых требуется разделить целое число на смешанное число. Например, разделим 2 на ![]() .
.
Чтобы решить этот пример, нужно делитель ![]() перевести в неправильную дробь. Затем умножить число 2 на дробь, обратную делителю.
перевести в неправильную дробь. Затем умножить число 2 на дробь, обратную делителю.
Переведём делитель ![]() в неправильную дробь, получим
в неправильную дробь, получим ![]() . Затем умножим 2 на дробь, обратную дроби
. Затем умножим 2 на дробь, обратную дроби ![]() . Обратная для дроби
. Обратная для дроби ![]() это дробь
это дробь
![]()
Допустим, имеются две целые пиццы:

Зададим вопрос «Сколько раз ![]() (одна целая и половина пиццы) содержится в двух целых пиццах?». Похожий пример мы решали ранее, когда учились делить целое число на дробь.
(одна целая и половина пиццы) содержится в двух целых пиццах?». Похожий пример мы решали ранее, когда учились делить целое число на дробь.
В двух пиццах одна целая и половина пиццы содержится один раз. Это можно увидеть, если вторую пиццу разделить пополам:

А оставшаяся половина это треть от ![]() , которая не вместилась. Третью она является по той причине, что в одной целой и половине пиццы целую часть пиццы можно разделить пополам. Тогда каждый кусок будет третью от этого количества:
, которая не вместилась. Третью она является по той причине, что в одной целой и половине пиццы целую часть пиццы можно разделить пополам. Тогда каждый кусок будет третью от этого количества:

Поэтому значение выражения ![]() равно
равно ![]()
Пример 2. Найти значение выражения ![]()
Переводим делитель ![]() в неправильную дробь, получаем
в неправильную дробь, получаем ![]() . Теперь умножаем число 5 на дробь, обратную дроби
. Теперь умножаем число 5 на дробь, обратную дроби ![]() . Обратная для дроби
. Обратная для дроби ![]() это дробь
это дробь ![]()
![]()
Сначала мы получили ответ ![]() , затем сократили эту дробь на 5, и получили
, затем сократили эту дробь на 5, и получили ![]() , но этот ответ нас тоже не устроил, поскольку он представлял собой неправильную дробь. Мы выделили в этой неправильной дроби целую часть. В результате получили ответ
, но этот ответ нас тоже не устроил, поскольку он представлял собой неправильную дробь. Мы выделили в этой неправильной дроби целую часть. В результате получили ответ ![]()
Деление смешанного числа на целое число
Чтобы разделить смешанное число на целое число, нужно смешанное число перевести в неправильную дробь, затем умножить эту дробь на число, обратное делителю.
Например, разделим ![]() на 2. Чтобы решить этот пример, нужно делимое
на 2. Чтобы решить этот пример, нужно делимое ![]() перевести в неправильную дробь. Затем умножить эту дробь на число, обратное делителю 2.
перевести в неправильную дробь. Затем умножить эту дробь на число, обратное делителю 2.
Переведём смешанное число ![]() в неправильную дробь, получим
в неправильную дробь, получим ![]() .
.
Теперь умножаем ![]() на число, обратное числу 2. Обратное числу 2 это дробь
на число, обратное числу 2. Обратное числу 2 это дробь ![]()
![]()
Допустим, имеется одна целая и половина пиццы:

Разделим это количество пиццы поровну на две части. Для этого сначала разделим на две части целую пиццу:

Затем разделим поровну на две части и половину:

Теперь если мы сгруппируем эти кусочки на две группы, то получим по пиццы в каждой группе:
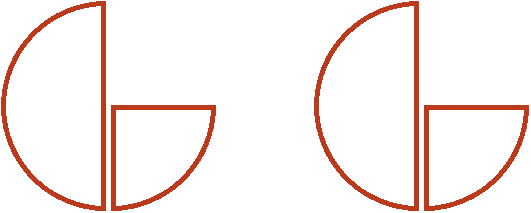
Поэтому значение выражения ![]() равно
равно
Пример 2. Найти значение выражения ![]()
Переведём делимое ![]() в неправильную дробь, получим
в неправильную дробь, получим ![]() . Теперь умножаем
. Теперь умножаем ![]() на число, обратное числу 4. Обратное числу 4 это дробь
на число, обратное числу 4. Обратное числу 4 это дробь ![]() .
.
![]()
Деление смешанных чисел
Чтобы разделить смешанные числа, нужно перевести их в неправильные дроби, затем выполнить обычное деление дробей. То есть умножить первую дробь на дробь, обратную второй.
Пример 1. Найти значение выражения ![]()
Переведём смешанные числа в неправильные дроби. Получим следующее выражение:
![]()
Как решать дальше мы уже знаем. Первую дробь ![]() нужно умножить на дробь, обратную второй. Обратная для второй дроби это дробь
нужно умножить на дробь, обратную второй. Обратная для второй дроби это дробь ![]() .
.
Дорешаем данный пример до конца:
![]()
Допустим, имеются две целые и половина пиццы:
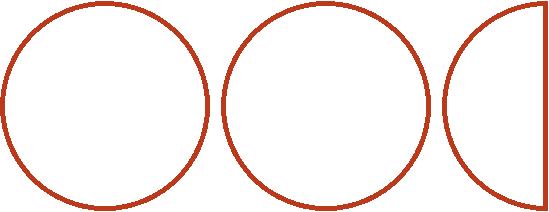
Если зададим вопрос «Сколько раз ![]() (одна целая и четверть пиццы) содержится в двух целых и половине пиццы», то ответом будет «два раза»:
(одна целая и четверть пиццы) содержится в двух целых и половине пиццы», то ответом будет «два раза»:
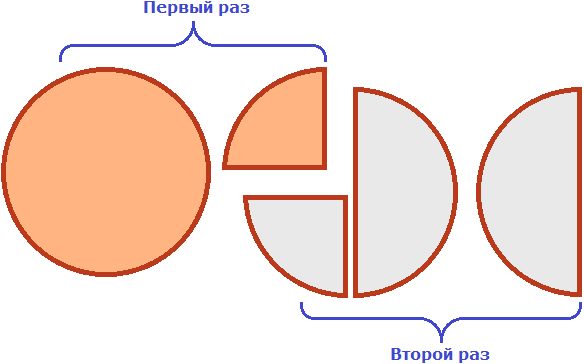
Пример 2. Найти значение выражения ![]()
Переведём смешанные числа в неправильные дроби. Получим следующее выражение:
![]()
Теперь умножаем первую дробь на дробь, обратную второй. Обратная для дроби это дробь ![]()
![]()
Сначала мы получили дробь![]() . Эту дробь мы сократили на 9. В результате получили дробь
. Эту дробь мы сократили на 9. В результате получили дробь ![]() , но такой ответ нас тоже не устроил и мы выделили в дроби
, но такой ответ нас тоже не устроил и мы выделили в дроби ![]() целую часть. В результате получили окончательный ответ
целую часть. В результате получили окончательный ответ ![]() .
.
Задания для самостоятельного решения
Задание 1. Найдите значение выражения:

Решение:
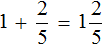
Задание 2. Найдите значение выражения:
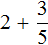
Решение:

Задание 3. Найдите значение выражения:

Решение:

Задание 4. Найдите значение выражения:

Решение:
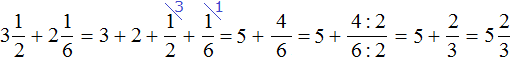
Задание 5. Найдите значение выражения:

Решение:

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже


Математика
5 класс
Урок № 76
Деление смешанных дробей
Перечень рассматриваемых вопросов:
– деление смешанной дроби на натуральное число;
– деление смешанных дробей;
– деление натурального числа на смешанную дробь;
– приёмы проверки результатов вычислений.
Тезаурус
Площадь прямоугольника – это произведение длины на ширину.
Скорость – это частное от деления расстояния на время движения.
Площадь прямоугольника – это произведение длины на ширину.
Обязательная литература
1. Никольский С. М. Математика. 5 класс: Учебник для общеобразовательных учреждений. / ФГОС // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. — М.: Просвещение, 2017. — 272 с.
Дополнительная литература
1. Чулков П. В. Математика: тематические тесты. 5 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. — М.: Просвещение, 2009. — 142 с.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин. — М.: Просвещение, 2014. — 95 с.
Теоретический материал для самостоятельного изучения
Вы уже научились сравнивать, складывать, вычитать, умножать и возводить в степень смешанные дроби. Сегодня мы рассмотрим деление смешанных дробей.
При делении обыкновенных дробей вы узнали правило: «Частным двух дробей является дробь, которая при умножении на делитель даёт делимое». Это правило справедливо и для смешанных дробей. Кроме правила вы узнали и формулу по которой находится частное двух дробей.

При выполнении деления делимое умножали на дробь, обратную делителю. Иначе говорят: «деление заменяем умножением, вторую дробь переворачиваем». Чтобы воспользоваться этой формулой при делении смешанных дробей, их нужно преобразовать в неправильные дроби.
Рассмотрим деление двух смешанных дробей:

- смешанные дроби преобразовали в неправильные;
- деление заменили умножением, делитель – обратным ему числом (перевернули дробь);
- записали произведение числителей и знаменателей одной дробью;
- сократили;
- выполнили отдельно умножение числителей и знаменателей;
- неправильную дробь представили смешанной дробью.
Проверим результат вычисления. Для этого нам нужно умножить частное на делитель. Если в результате этого произведение будет равно делимому, значит, вычисления выполнены верно.
В результате умножения частного на делитель у нас получилось число, равное делимому, значит, деление выполнено верно.
Иногда при делении смешанной дроби на натуральное число можно воспользоваться распределительным законом.

Здесь отдельно разделили целую и дробную части смешанной дроби на 3 и полученные результаты сложили.




Запомним алгоритм деления смешанных дробей:
- представить эти смешанные дроби неправильными дробями;
- делимое умножить на число обратное делителю;
- сократить, если это возможно;
- если в результате умножения получилась неправильная дробь, представить её смешанной дробью.
Тренировочные задания
№ 1. Решите уравнение и впишите верный ответ.


- Главная
- Справочники
- Справочник по математике 5-9 класс
- Обыкновенные дроби
- Деление обыкновенных дробей
Примеры:
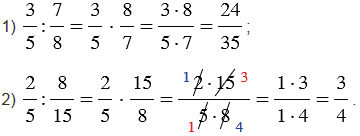
Обратите внимание, если возможно, то прежде, чем перемножить числа, выполняем сокращение (такой ход действий облегчит вычисления).
Деление смешанных чисел
Примеры:

Обратите внимание, если возможно, то прежде, чем перемножить числа, выполняем сокращение (такой ход действий облегчит вычисления).
Деление на натуральное число
При делении дроби на натуральное число, учитываем то, что любое натуральное число можно представить в виде дроби со знаменателем 1, затем пользуемся правилом деления дробей.
Примеры:
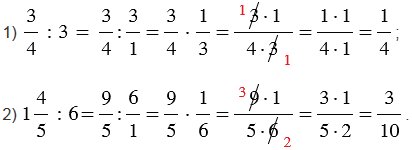
Обратите внимание, если возможно, то прежде, чем перемножить числа, выполняем сокращение (такой ход действий облегчит вычисления).
Нахождения числа по его дроби
Чтобы найти число по данному значению его дроби, надо это значение разделить на дробь
Примеры:
1) Найдите число, если 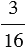 данного числа равны 27:
данного числа равны 27:
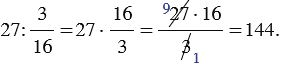
2) Найдите число, если 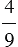 данного числа равны
данного числа равны 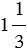 :
:
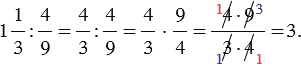
Советуем посмотреть:
Доли. Обыкновенные дроби
Сравнение дробей
Делители и кратные
Признаки делимости на 10, на 5 и на 2
Четные и нечетные числа
Признаки делимости на 9 и на 3
Простые и составные числа
Разложение на простые множители
Наибольший общий делитель
Наименьшее общее кратное
Деление и дроби
Сложение и вычитание дробей с одинаковыми знаменателями
Смешанное число
Сложение и вычитание смешанных чисел
Основное свойство дроби
Решето Эратосфена
Приведение дробей к общему знаменателю
Сравнение, сложение и вычитание дробей с разными знаменателями
Умножение обыкновенных дробей
Обыкновенные дроби
Правило встречается в следующих упражнениях:
6 класс
Номер 463,
Мерзляк, Полонский, Якир, Учебник
Номер 486,
Мерзляк, Полонский, Якир, Учебник
Номер 524,
Мерзляк, Полонский, Якир, Учебник
Номер 577,
Мерзляк, Полонский, Якир, Учебник
Номер 1048,
Мерзляк, Полонский, Якир, Учебник
Номер 1116,
Мерзляк, Полонский, Якир, Учебник
Номер 1345,
Мерзляк, Полонский, Якир, Учебник
Задание 637,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 818,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1449,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
7 класс
Номер 2,
Мерзляк, Полонский, Якир, Учебник
Номер 74,
Мерзляк, Полонский, Якир, Учебник
Номер 348,
Мерзляк, Полонский, Якир, Учебник
Номер 386,
Мерзляк, Полонский, Якир, Учебник
Номер 616,
Мерзляк, Полонский, Якир, Учебник
Номер 618,
Мерзляк, Полонский, Якир, Учебник
Номер 787,
Мерзляк, Полонский, Якир, Учебник
Номер 845,
Мерзляк, Полонский, Якир, Учебник
Номер 1119,
Мерзляк, Полонский, Якир, Учебник
Номер 1127,
Мерзляк, Полонский, Якир, Учебник
8 класс
Номер 13,
Мерзляк, Полонский, Якир, Учебник
Номер 91,
Мерзляк, Полонский, Якир, Учебник
Номер 118,
Мерзляк, Полонский, Якир, Учебник
Номер 140,
Мерзляк, Полонский, Якир, Учебник
Номер 205,
Мерзляк, Полонский, Якир, Учебник
Номер 223,
Мерзляк, Полонский, Якир, Учебник
Номер 278,
Мерзляк, Полонский, Якир, Учебник
Номер 315,
Мерзляк, Полонский, Якир, Учебник
Номер 402,
Мерзляк, Полонский, Якир, Учебник
Номер 482,
Мерзляк, Полонский, Якир, Учебник
