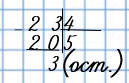Деление с остатком.
Рассмотрим простой пример:
15:5=3
В этом примере натуральное число 15 мы поделили нацело на 3, без остатка.
Иногда натуральное число полностью поделить нельзя нацело. Например, рассмотрим задачу:
В шкафу лежало 16 игрушек. В группе было пятеро детей. Каждый ребенок взял одинаковое количество игрушек. Сколько игрушек у каждого ребенка?
Решение:
Поделим число 16 на 5 столбиком получим:
Мы знаем, что 16 на 5 не делиться. Ближайшее меньшее число, которое делиться на 5 это 15 и 1 в остатке. Число 15 мы можем расписать как 5⋅3. В итоге (16 – делимое, 5 – делитель, 3 – неполное частное, 1 — остаток). Получили формулу деления с остатком, по которой можно сделать проверку решения.
16=5⋅3+1
a=b⋅c+d
a – делимое,
b – делитель,
c – неполное частное,
d – остаток.
Ответ: каждый ребенок возьмет по 3 игрушки и одна игрушка останется.
Остаток от деления
Остаток всегда должен быть меньше делителя.
Если при делении остаток равен нулю, то это значит, что делимое делиться нацело или без остатка на делитель.
Если при делении остаток больше делителя, это значит, что найденное число не самое большое. Существует число большее, которое поделит делимое и остаток будет меньше делителя.
Вопросы по теме “Деление с остатком”:
Остаток может быть больше делителя?
Ответ: нет.
Остаток может быть равен делителю?
Ответ: нет.
Как найти делимое по неполному частному, делителю и остатку?
Ответ: значения неполного частного, делителя и остатка подставляем в формулу и находим делимое. Формула:
a=b⋅c+d
(a – делимое, b – делитель, c – неполное частное, d – остаток.)
Пример №1:
Выполните деление с остатком и сделайте проверку: а) 258:7 б) 1873:8
Решение:
а) Делим столбиком:
258 – делимое,
7 – делитель,
36 – неполное частное,
6 – остаток. Остаток меньше делителя 6<7.
Подставим в формулу и проверим правильно ли мы решили пример:
7⋅36+6=252+6=258
б) Делим столбиком:
1873 – делимое,
8 – делитель,
234 – неполное частное,
1 – остаток. Остаток меньше делителя 1<8.
Подставим в формулу и проверим правильно ли мы решили пример:
8⋅234+1=1872+1=1873
Пример №2:
Какие остатки получаются при делении натуральных чисел: а) 3 б)8?
Ответ:
а) Остаток меньше делителя, следовательно, меньше 3. В нашем случае остаток может быть равен 0, 1 или 2.
б) Остаток меньше делителя, следовательно, меньше 8. В нашем случае остаток может быть равен 0, 1, 2, 3, 4, 5, 6 или 7.
Пример №3:
Какой наибольший остаток может получиться при делении натуральных чисел: а) 9 б) 15?
Ответ:
а) Остаток меньше делителя, следовательно, меньше 9. Но нам надо указать наибольший остаток. То есть ближайшее число к делителю. Это число 8.
б) Остаток меньше делителя, следовательно, меньше 15. Но нам надо указать наибольший остаток. То есть ближайшее число к делителю. Это число 14.
Пример №4:
Найдите делимое: а) а:6=3(ост.4) б) с:24=4(ост.11)
Решение:
а) Решим с помощью формулы:
a=b⋅c+d
(a – делимое, b – делитель, c – неполное частное, d – остаток.)
а:6=3(ост.4)
(a – делимое, 6 – делитель, 3 – неполное частное, 4 – остаток.) Подставим цифры в формулу:
а=6⋅3+4=22
Ответ: а=22
б) Решим с помощью формулы:
a=b⋅c+d
(a – делимое, b – делитель, c – неполное частное, d – остаток.)
с:24=4(ост.11)
(с – делимое, 24 – делитель, 4 – неполное частное, 11 – остаток.) Подставим цифры в формулу:
с=24⋅4+11=107
Ответ: с=107
Задача:
Проволоку 4м. нужно разрезать на куски по 13см. Сколько таких кусков получится?
Решение:
Сначала надо метры перевести в сантиметры.
4м.=400см.
Можно поделить столбиком или в уме получим:
400:13=30(ост.10)
Проверим:
13⋅30+10=390+10=400
Ответ: 30 кусков получиться и 10 см. проволоки останется.
- Главная
- Справочники
- Справочник по математике для начальной школы
- Деление
- Деление с остатком
Начнём рассмотрение новой темы с решения задачи.
Мама принесла 8 конфет и разделила их поровну между двумя детьми. Сколько конфет получил каждый?
8 : 2 = 4 (к.)
Каждый ребёнок получил по 4 конфеты.
На следующий день мама опять принесла 8 конфет, но в гостях у её детей была ещё одна подружка. Мама опять разделила конфеты поровну, но уже между тремя детьми. Сколько конфет получил каждый ребёнок?
Каждый получил по 2 конфеты и 2 конфеты остались лишними.
Как это записать?
8 : 3 = 2 (ост. 2)
Как сделать проверку?
2 • 3 + 2 = 8
Правило 1
Деление с остатком — это деление одного числа на другое, при котором остаток не равен нулю.
16 : 7 = 2 (ост. 2)
23 : 8 = 2 (ост. 7)
Правило 2
При делении с остатком остаток всегда должен быть меньше делителя.
43 : 8 = 5 (ост. 3)
остаток 3 < делимого 5
34 : 4 = 8 (ост. 2)
остаток 2 < делимого 4
Правило 3
Если делимое меньше делителя, в частном получается ноль, а остаток равен делимому.
7 : 10 = 0 (ост. 7)
6 : 9 = 0 (ост. 6)
Порядок решения
14 : 5 = 2 (ост. 4)
1. Нахожу наибольшее число до 14, которое делится на 5 без остатка. Это число 10.
10 : 5 = 2
2. Вычитаю из делимого найденное число: 14 − 10 = 4
3. Сравниваю остаток с делителем
4 < 5
Решение верно.
Проверка деления с остатком
1. Умножаю неполное частное на делитель.
2. Прибавляю остаток к полученному результату.
3. Сравниваю полученный результат с делимым, он должен быть МЕНЬШЕ.
Деление в столбик
В 23 содержится 5 раз по 4, и ещё остаётся 3.
Решение записывают так:
23 : 4 = 5 (ост. 3) или так:
, где 23 – делимое, 4 – делитель, 5 – неполное частное, а 3 – остаток.
Советуем посмотреть:
Табличное деление
Внетабличное деление
Деление суммы на число
Деление на однозначное число
Деление чисел, оканчивающихся нулями
Свойства деления
Деление
Правило встречается в следующих упражнениях:
2 класс
Страница 76. Урок 29,
Петерсон, Учебник, часть 3
Страница 77. Урок 29,
Петерсон, Учебник, часть 3
Страница 79. Урок 30,
Петерсон, Учебник, часть 3
Страница 80. Урок 30,
Петерсон, Учебник, часть 3
Страница 81. Урок 31,
Петерсон, Учебник, часть 3
Страница 82. Урок 31,
Петерсон, Учебник, часть 3
Страница 84. Урок 32,
Петерсон, Учебник, часть 3
Страница 87. Урок 33,
Петерсон, Учебник, часть 3
Страница 108. Повторение,
Петерсон, Учебник, часть 3
3 класс
Страница 30,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 32,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 34,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 47,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 51,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 24. Урок 8,
Петерсон, Учебник, часть 1
Страница 87. Урок 32,
Петерсон, Учебник, часть 1
Страница 92. Урок 34,
Петерсон, Учебник, часть 1
Страница 14. Урок 6,
Петерсон, Учебник, часть 3
Страница 71. Повторение,
Петерсон, Учебник, часть 3
4 класс
Страница 40,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 69,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 11. ПР 3. Вариант 2,
Моро, Волкова, Проверочные работы
Страница 61. ПР 1. Вариант 2,
Моро, Волкова, Проверочные работы
Страница 26,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 27,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 29,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 31,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 72,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 103,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
5 класс
Задание 533,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 545,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 679,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 879,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1024,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Номер 141,
Мерзляк, Полонский, Якир, Учебник
Номер 756,
Мерзляк, Полонский, Якир, Учебник
Номер 769,
Мерзляк, Полонский, Якир, Учебник
Номер 801,
Мерзляк, Полонский, Якир, Учебник
Номер 6,
Мерзляк, Полонский, Якир, Учебник
6 класс
Номер 350,
Мерзляк, Полонский, Якир, Учебник
Номер 365,
Мерзляк, Полонский, Якир, Учебник
Номер 435,
Мерзляк, Полонский, Якир, Учебник
Номер 764,
Мерзляк, Полонский, Якир, Учебник
Номер 1112,
Мерзляк, Полонский, Якир, Учебник
Номер 1143,
Мерзляк, Полонский, Якир, Учебник
Номер 1147,
Мерзляк, Полонский, Якир, Учебник
Задание 586,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 602,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 638,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
7 класс
Номер 32,
Мерзляк, Полонский, Якир, Учебник
Номер 330,
Мерзляк, Полонский, Якир, Учебник
Номер 385,
Мерзляк, Полонский, Якир, Учебник
Номер 573,
Мерзляк, Полонский, Якир, Учебник
Номер 580,
Мерзляк, Полонский, Якир, Учебник
Номер 582,
Мерзляк, Полонский, Якир, Учебник
Номер 606,
Мерзляк, Полонский, Якир, Учебник
Номер 773,
Мерзляк, Полонский, Якир, Учебник
Номер 784,
Мерзляк, Полонский, Якир, Учебник
Номер 871,
Мерзляк, Полонский, Якир, Учебник
8 класс
Номер 4,
Мерзляк, Полонский, Якир, Учебник
Номер 46,
Мерзляк, Полонский, Якир, Учебник
Номер 138,
Мерзляк, Полонский, Якир, Учебник
Номер 141,
Мерзляк, Полонский, Якир, Учебник
Номер 193,
Мерзляк, Полонский, Якир, Учебник
Номер 207,
Мерзляк, Полонский, Якир, Учебник
Номер 212,
Мерзляк, Полонский, Якир, Учебник
Номер 241,
Мерзляк, Полонский, Якир, Учебник
Номер 304,
Мерзляк, Полонский, Якир, Учебник
Номер 305,
Мерзляк, Полонский, Якир, Учебник
Математика, 4 класс. Урок № 54
Письменное деление на двузначное число с остатком.
Перечень вопросов, рассматриваемых в теме:
– Как делить многозначное число на двузначное с остатком?
– Как ким должен быть остаток от деления?
Глоссарий по теме:
Частное – результат деления одного числа на другое.
Неполное частное – результат деления с остатком, который показывает, какое максимальное число раз делитель содержится в делимом.
Остаток – число, которое получается в результате деления с остатком и показывает, какое минимальное число нужно вычесть из делимого, чтобы полученное число делилось нацело на делитель.
Основная и дополнительная литература по теме урока (точные библиографические данные с указанием страниц):
1.Петерсон Л.Г. Математика. 4 класс. 1 ч. – М.: 2013. – стр. 31-38.
2. Математика. Учебник для 4 кл. нач. шк. В 2 ч./М.И. Моро, М.А. Бантова – М.: Просвещение, 2017.
3. Математика. 4 класс. Учебник. Часть1/ Н.Б.Истомина, Т.Н.Миракова, Т.Б.Бука. Смоленск: Ассоциация XXI век, 2012. – стр. 38-52.
4. Математика. Учебник для 4 класса нач. шк. Часть 2/А.Л.Чекин. – М.: Академкнига/Учебник, 2016. – стр. 16-20.
Теоретический материал для самостоятельного изучения
|
|
Алгоритм деления: 1.Образую неполное делимое. 2.Определю количество цифр в частном. 3.Делю неполное делимое на делитель. 4.Умножаю делитель на пробную цифру. 5. Нахожу остаток от деления вычитанием. 6. Сравниваю остаток с делителем. |
При делении с остатком на двузначное число рассуждать будем так же, как и при делении без остатка.
Разделим 444 : 54.
Первое неполное делимое – это само число, 444. Поэтому в частном будет только одна цифра. Чтобы легче было найти цифру частного, будем делить 444 не на 54, а на 50. Для этого 44 разделим на 5, получим 8. Проверим, подходит ли она: 54 · 8 = 50 · 8 + 4 · 8 = 432, а 432 < 444.
Значит, пробная цифра 8 подходит. Записываем ее в частном. Закончим запись деления столбиком. Умножаем 54 на 8, будет 432. Находим остаток от деления. Он равен 12. 12 меньше, чем 54, то есть остаток меньше делителя. На этом деление закончено. При делении числа 444 на 54 получилось частное 8 и остаток 12.
Найдём значение частного 45598 : 58.
Выделим первое неполное делимое 455 сотен. Так как деление начинаем с сотен, в частном получим 3 цифры. Ищем первую цифру частного: 45 : 5 = 9
Получаем пробную цифру 9.
58 · 9 = 522, 522 > 455
Значит, 9 не подходит.
Пробуем цифру 8. Для проверки этой цифры используем другой способ. Будем умножать десятки:
5 дес. · 8= 40 дес.
8 · 8= 6 дес.
40 + 6 дес. > 45 дес. Значит, 8 это тоже много.
Пробуем следующую цифру 7.
5 дес. · 7 = 35 дес.
В запасе ещё: 45 дес. – 35 дес. = 10 дес. Этого точно хватит, так как при умножении 8 единиц на 7 получится 5 десятков. Значит, цифра 7 подходит. Записываем её в частном.
Умножаем 58 на 7, будет 406. Вычитаем 406 из 455, будет 49. Остаток 49 меньше делителя 58.
Второе неполное делимое 499 десятков. Ищем цифру частного: 49:5=9
Получаем пробную цифру 9.
Проверяем:
5 дес. · 9 = 45 дес.
45 + 7 дес. > 49 дес. Значит, в частном должно быть меньше 9.
Проверяем 8.
50 · 8 = 400
8 · 8 = 64
400 + 64 = 464
464 < 499, значит, цифра 8 подходит. Записываем её в частном.
Умножаем 58 на 8, будет 464. Вычитаем 464 из 49, будет 3. Остаток 35 меньше делителя 58.
Третье неполное делимое 358 едини. Ищем цифру частного: 35 : 5 = 7, получаем пробную цифру 7. Проверяем, но мы уже умножали 58 на 7, получили 406. Это больше, чем 358. Значит, 7 не подходит.
Проверим 6.
50 · 6 = 300
8 · 6 = 48
300 = 48 = 348
348 < 358, значит, цифра шесть подходит. Записываем её в частном.
Умножаем 58 на 6, будет 348. Вычитаем 348 из 358, будет 10. Остаток 10 меньше делителя 58. Неполных делимых больше нет. Деление окончено. В результате получили частное 786 и остаток 10.
Задания тренировочного модуля:
1. Не выполняя вычислений, найдите пропущенное делимое с помощью первого равенства.
|
903:7 = 129 |
1280:5 = 256 |
|
___ : 7 = 128 (ост.6) |
___ : 5 = 255 (ост.4) |
Правильный вариант: 902; 1279
2.Заполните таблицу.
|
Делимое |
2000 |
8300 |
|
|
Делитель |
12 |
300 |
9 |
|
Частное |
3 |
||
|
Остаток |
10 |
200 |
2 |
Правильный ответ:
|
Делимое |
46 |
2000 |
8300 |
|
Делитель |
12 |
300 |
9 |
|
Частное |
3 |
6 |
922 |
|
Остаток |
10 |
200 |
2 |
3. Выберите записи, которые соответствуют рисунку.
Варианты ответа:
13:4=3 (ост. 1)
17:3=5 (ост. 2)
16:5=3 (ост. 1)
3·5+1=16
5·3+1=16
16:3=5 (ост. 1)
Правильный вариант:
16:5=3 (ост. 1); 16:3=5 (ост. 1)
4. Раскрасьте карточки с выражениями, в значении частных которых будет остаток.
48:4
28:7
72:8
65:8
59:6
20:3
Правильный вариант:
65:8
59:6
20:3
Формула деления с остатком
Деление с остатком, как это?

Данную формулу так же можно прочитать следующим образом:
Разделить с остатком число a на число b – значит найти два таких числа c и n (частное и остаток), что:
Правило деления с остатком
Что бы разделить число с остатком, нужно:
1. Подобрать близкое к делимому число, которое меньше делимого и делителя на делитель без остатка;
2. Выполнить деление;
3. Найти остаток – из делимого вычесть число, которое разделили. Остаток всегда должен быть меньше делителя.
Примеры
19 : 4 = 4 (остаток 1), 19 = 4 • 4 + 3;
23 : 3 = 7 (остаток 2), 23 = 7 • 3 + 2.
Объясним правило на примере 19 : 4
1. Подбираем близкое к 19 число, которое меньше 19 и делится на 4 без остатка. Это число 16;
2. Делим 16 на 4, получаем 4;
3. Находим остаток: 19 – 16 = 3. Сравниваем остаток с делителем: 3 < 4. Значит, частное найдено верно.
4. Значит, 19 : 4 = 4 + 3 (остаток).
Проверка деления с остатком
Что бы проверить деление с остатком нужно:
1. Остаток сравнить с делителем (остаток должен быть меньше делителя);
2. Частное умножить на делитель и к полученному произведению прибавить остаток. Если получится делимое, то пример решен верно.
Пример №1
Проверяем:
1. 4 < 3;
2. 7 • 4 + 3 = 23.
Пример №2
Проверяем:
1. 5 < 15;
2. 3 • 15 + 5 = 50.