Следующее действие, которое можно выполнять с дробями это деление. Выполнять деление дробей достаточно просто главное знать несколько правил деления. Разберем правила деления и рассмотрим решение примеров на данную тему.
Деление дроби на дробь.
Чтобы делить дробь на дробь, нужно дробь, которая является делителем перевернуть, то есть получить обратную дробь делителю и потом выполнить умножение дробей.
(bf frac{a}{b} div frac{c}{d} = frac{a}{b} times frac{d}{c}\)
Пример:
Выполните деление обыкновенных дробей .
Деление дроби на число.
Чтобы разделить дробь на число, нужно знаменатель дроби умножить на число.
(bf frac{a}{b} div n = frac{a}{b} div frac{n}{1} = frac{a}{b} times frac{1}{n}\)
Рассмотрим пример:
Выполните деления дроби на натуральное число (frac{4}{7} div 3).
Как мы уже знаем, что любое число можно представить в виде дроби (3 = frac{3}{1} ).
(frac{4}{7} div 3 = frac{4}{7} div frac{3}{1} = frac{4}{7} times frac{1}{3} = frac{4 times 1}{7 times 3} = frac{4}{21}\)
Деление числа на дробь.
Чтобы поделить число на дробь, нужно знаменатель делителя умножить на число, а числитель делителя записать в знаменатель. То есть дробь делитель перевернуть.
Рассмотрим пример:
Выполните деление числа на дробь.
Деление смешанных дробей.
Перед тем как приступить к делению смешанных дробей, их нужно перевести в неправильную дробь, а дальше выполнить деление по правилу деления дроби на дробь.
Пример:
Выполните деление смешанных дробей.
(2frac{3}{4} div 3frac{1}{6} = frac{11}{4} div color{red} {frac{19}{6}} = frac{11}{4} times color{red} {frac{6}{19}} = frac{11 times 6}{4 times 19} = frac{11 times color{red} {2} times 3}{2 times color{red} {2} times 19} = frac{33}{38}\)
Деление числа на число.
Чтобы поделить простые числа, нужно представить их в виде дроби и выполнить деление по правилам деления дроби на дробь.
Пример:
(2 div 5 = frac{2}{1} div color{red} {frac{5}{1}} = frac{2}{1} times color{red} {frac{1}{5}} = frac{2 times 1}{1 times 5} = frac{2}{5}\)
Примечание к теме деление дробей:
На нуль делить нельзя.
Вопросы по теме:
Как делить дроби? Как разделить дробь на дробь?
Ответ: дроби делятся так, первую дробь делимое умножаем на дробь обратную дроби делителя.
Как делить дроби с разными знаменателями?
Ответ: не важно одинаковые или разные знаменатели у дробей, все дроби делятся по правилу деления дроби на дробь.
Пример №1:
Выполните деление и назовите делитель, дробь, обратную делителю: а) (frac{5}{9} div frac{8}{13}) б) (2frac{4}{5} div 1frac{7}{8})
Решение:
а) (frac{5}{9} div frac{8}{13} = frac{5}{9} times frac{13}{8} = frac{65}{72}\\)
( frac{8}{13}) – делитель, ( frac{13}{8}) – обратная дробь делителя.
б) (2frac{4}{5} div 1frac{7}{8} = frac{14}{5} div frac{15}{8} = frac{14}{5} times frac{8}{15} = frac{14 times 8}{5 times 15} = frac{112}{75} = 1frac{37}{75}\\)
( frac{15}{8}) – делитель, ( frac{8}{15}) – обратная дробь делителя.
Пример №2:
Вычислите деление: а) (5 div 1frac{1}{4}) б) (9frac{2}{3} div 8)
Решение:
а) (5 div 1frac{1}{4} = frac{5}{1} div frac{5}{4} = frac{5}{1} times frac{4}{5} = frac{color{red} {5} times 4}{1 times color{red} {5}} = frac{4}{1} = 4 \\)
б) (9frac{2}{3} div 8 = frac{29}{3} div frac{8}{1} = frac{29}{3} times frac{1}{8} = frac{29 times 1}{3 times 8} = frac{29}{24} = 1frac{5}{24}\\)
Математика
6 класс
Урок № 42
Деление дробей
Перечень рассматриваемых вопросов:
- деление рациональных чисел, правила знаков при делении.
Тезаурус
Частное двух дробей есть дробь, числитель которой равен произведению числителя первой дроби и знаменателя второй, а знаменатель – произведению знаменателя первой дроби и числителя второй дроби.
Частным двух дробей с одинаковыми знаками является положительная дробь, модуль которой равен частному модулей делимого и делителя.
Частное дробей с разными знаками есть отрицательная дробь, модуль которой равен частному модулей делимого и делителя.
Обязательная литература:
- Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017, стр. 258.
Дополнительная литература:
- Чулков П. В. Математика: тематические тесты.5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина — М.: Просвещение, 2009, стр. 142.
- Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин – М.: Просвещение, 2014, стр. 95.
Теоретический материал для самостоятельного изучения
На прошлом уроке мы изучали правила умножения дробей.
Сегодня рассмотрим правила деления.
Аналогично умножению, дроби с любыми знаками делят по тем же правилам, что и положительные дроби.
Частное двух дробей есть дробь, числитель которой равен произведению числителя первой дроби и знаменателя второй, а знаменатель – произведению знаменателя первой дроби и числителя второй дроби.
Найдём частное от деления двух дробей.
Запишем равенство, которое можно получить на основании правила деления.
Доказательство
Чтобы разделить дробь на целое, не равное нулю число, можно её знаменатель умножить на это число.
Найдём частное
Знак «–» перед дробью, можно записывать и в знаменателе, и в числители дроби, то есть верны равенства:
Используя свойство взаимно обратных дробей, что их произведение равно 1, можем сформулировать следующее утверждение:
Чтобы одну дробь разделить на другую, отличную от нуля, можно делимое умножить на дробь, обратную делителю.
Найдём частное
Правила знаков, при делении дробей
Правило деления дробей с одинаковыми знаками
Частным двух дробей с одинаковыми знаками является положительная дробь, равная частному модулей делимого и делителя.
Выполним деление
Правило деления дробей с разными знаками
Частное от деления дробей с разными знаками есть отрицательная дробь, модуль которой равен частному модулей делимого и делителя.
Выполним деление
Из правил деления дробей с любыми знаками следует, что их можно делить по тем же правилам, что и целые числа. То есть мы можем сначала определять знак результата, а потом выполнять действия с модулями.
Выполним деление
Дополнительный материал
Решение задачи
Решение
Найдём, сколько автомобиль проехал за второй час. Известно, что в 2 раза меньше, чем за первый, значит, путь за первый час разделим на 2.
Найдём общую часть пути за два часа.
Для этого сложим части пути за первый и за второй час.
Разбор заданий тренировочного модуля
№ 1. Разместите нужные подписи под изображениями.
Какие действия изображены?
Варианты ответов:
деление дробей с одинаковыми знаками
деление дробей с разными знаками
деление дроби на целое число
Для ответа на вопрос задания, обратимся к теоретическому материалу урока.
Правильный ответ
№ 2. Вставьте в текст нужные слова.
Частное двух дробей есть дробь, … которой равен … числителя первой дроби и … второй, а знаменатель – произведению знаменателя первой дроби и числителя второй дроби.
Варианты слов для вставки:
числитель
произведению
частному
сумме
разности
знаменателя
Для ответа на вопрос задания, обратимся к теоретическому материалу урока.
Правильный ответ:
Частное двух дробей есть дробь, числитель которой равен произведению числителя первой дроби и знаменателя второй, а знаменатель – произведению знаменателя первой дроби и числителя второй дроби.
Тип лекции: ключевая; Время чтения: 15 минут;
Цель: понять, что такое дробь, где применяется и как с ней работать.
Узнаем, что такое наибольший общий делитель, наименьшее общее кратное и применяется. Обсудим, почему при делении на дробь её нужно перевернуть и умножить, а также почему при делении на 0 получается бесконечность. Разберем пару простых задач на процент и как решать их в одно действие.
Что такое дробь
В лекции про числа обсуждали, что существуют исчисляемые предметы, такие как дом, автомобиль, велосипед и другие. При делении этих предметов они теряют свои свойства: автомобиль без колес не поедет, а жить в доме без крыши – некомфортно. С другой стороны существуют неисчисляемые предметы, которые не потеряют свои свойства при делении: вода, воздух, пицца, молоко и очарование =)
Дроби – способ описать части неисчисляемого предмета.
Возьмем пиццу, пицца – неисчисляемый предмет, потому что ее можно разделить на кусочки и каждый кусочек будет обладать вкусом.
Например, пицца – состоит из 8 кусочков, 1 кусочек забрали, как описать это на языке математики?
Пицца – это 7/8, где 8 – сколько кусочков в целом предмете, 7 – сколько кусочков сейчас.
Дробь – это другая запись деления, имеет тот же смысл.
Определение дроби
Дробь – это запись из двух чисел, разделенных чертой. Верхнее число называют числителем, нижнее – знаменателем. Это понадобится, чтобы понимать математические определения.
Обратите внимание, что знаменатель не может быть равен нулю, мы поговорим об этом ниже, на самом деле делить на 0 можно и это будет равно бесконечности. Если можно делить на 0, значит может быть и дробь со знаменателем 0.
Читается дробь как “числитель знаменательных”: 3/4 – “три четвертых”; 2/3 – “две третьих”; 1/2 – “одна вторая” и т.д.
Дробь можно представить в виде круга поделенного на сектора: нижнее число (знаменатель) показывает на сколько секторов поделен целый круг, верхнее число (числитель) показывает сколько секторов круга взяли.
Обратите внимание, когда числитель больше знаменателя, значит взяли больше чем 1 круг. Здесь подошли к понятию правильной и неправильной дроби.
Дроби бывают правильные и неправильные.
Правильные дроби – в которых знаменатель больше числителя.
Неправильные дроби – в которых числитель больше знаменателя. Неправильная дробь выражает число больше единицы и ее можно представить в виде правильной дроби, для этого нужно вычислить целую часть, а остаток представить в виде дроби.
Действия с дробями
Дроби можно преобразовывать в разный вид, это нужно для того, чтобы сравнивать и складывать их. Преобразование дроби строится на свойствах умножения и деления: a × 1 = a; b/b = 1;
Сначала возьмем свойство a × 1 = a, вместо а подставим дробь 2/3, потому а – это переменная и можно подставить вместо нее все что угодно, получим: 2/3 × 1 = 2/3.
Теперь вместо 1 подставим деление любого числа самого на себя, для начала возьмем 2/2; 1 = 2/2;
Подставим в выражение: 2/3 × 2/2 = 2/3; Пока от такой записи мало пользы, но что если 2/2 представить в виде действий умножения и деления?
2/3 × 2 ÷ 2;
Разберемся сначала с умножением: 2/3 × 2 – то есть у нас есть 2 части, неважно третьих или автомобиля, просто две каких то части, что будет, когда мы возьмем их дважды? Будет 4 части, в нашем случае 4 третьих части: 2/3 × 2 = 4/3;
Теперь поговорим о делении: в выражении осталось 4/3 ÷ 2; Не важно что, что-то разделили на 3 части, а затем каждую получившуюся часть разбили еще на 2 части, то есть всего получилось 6 частей. Отсюда 4/3 ÷ 2 = 4/6;
Именно отсюда следует закон: при умножении дробей числители перемножаются и знаменатели перемножаются. Чуть ниже мы покажем как это выглядит графически, пока продолжим разговор про преобразование дробей.
Выражение 2/3 × 2/2 = 2/3 можно представить как 2/3 × 2/2 = 4/6;
То есть 2/3 = 4/6; Это одно и то же количество, просто представленное разными размерами кусочков. Ниже можно наглядно рассмотреть, как происходит изменение размера кусочков при умножении на разные числа.
Умножение дробей
Выше мы разобрали, почему при перемножении дробей числители перемножаются между собой и знаменатели перемножаются между собой. Графически умножение дробей можно представить так:
Вот так выглядит неполное преобразование или умножение дробей.
Сложение и сравнение дробей
Дробь – это части, чтобы их сравнить или сложить, нужно привести их к одинаковому размеру: “привести к общему знаменателю”
Выше разбирали, как происходит изменение размеров дробей. Технически нужно числитель и знаменатель одной дроби умножить на знаменатель другой дроби и наоборот. Так дроби будут состоять из одинаковых частей. Когда получили части одинакового размера, их легко можно складывать, вычитать и сравнивать.
Есть проблема, если попытаться сложить 1/231 и 1/84 получатся громоздкие, неудобные числа:
1/231 + 1/84 = ?;
1/231 × 84/84 = 84/19404;
1/84 × 231/231 = 231/19404;
84/19404 + 231/19404 = 315/25200;
Но можно проще:
1/231 + 1/84 = 4/924 + 11/924 = 15/924 = 5/308;
Это возможно благодаря наибольшему общему делителю (НОД) и наименьшему общему кратному (НОК), о них мы поговорим ниже.
Наибольший общий делитель (НОД) и Наименьшее общее кратное (НОК)
Все целые числа подразделяются на простые числа и составные числа.
Простые числа – делятся только на самих себя и на единицу: 2, 3, 5, 7, 11, 13 и так далее. Нет конца простым числам, они нам нужны для поиска НОД и НОК, но также участвуют в алгоритмах генерации псевдослучайных чисел, в алгоритмах шифрования.
Составные числа – получаются путем перемножения простых чисел.
Чтобы найти НОД и НОК, нужно разложить числа на множители.
Как раскладывать на множители
Возьмем дробь 84/231, до этого мы преобразовывали дроби в сторону увеличения числителя и знаменателя, но как преобразовать дробь в сторону уменьшения числителя и знаменателя? В этом поможет наибольший общий делитель.
Нужно разложить на множители все интересующие нас числа: 84 и 231. Поочередно делим число на простые числа. Если не делится без остатка, берем следующее простое число, иначе использованное простое число – множитель нашего числа. Результат деления по этому же механизму делим на простые числа.
Разложим 84 на множители:
- 84 делится на 2? – да, добавляем 2 в список множителей. 84 ÷ 2 = 42;
- 42 делится на 2? – да, добавляем 2 в список множителей. 42 ÷ 2 = 21;
- 21 делится на 2? – нет, на 3? – да, добавляем 3 в список множителей.
21 ÷ 3 = 7; - 7 – это простое число, то есть делится только само на себя и на единицу. Добавляем 7 в список множителей и завершаем.
Получилось: 84 = 2 × 2 × 3 × 7;
Разложим 231 на множители:
- 231 делится на 2? – нет, на 3? – да, добавляем 3 в список множителей.
231 ÷ 3 = 77; - 77 делится на 2? – нет, на 3? – нет, на 5? – нет, на 7? – да, добавляем 7 в список множителей. 77 ÷ 7 = 11;
- 11 – это простое число, то есть делится только само на себя и на единицу. Добавляем 11 в список множителей и завершаем.
Получилось: 231 = 3 × 7 × 11;
Даже большие числа без труда раскладываются на множители.
Как найти НОД на основе множителей
Наибольший общий делитель – самое больше число, которое без остатка поделит указанные числа.
Технически НОД – это произведение общих множителей.
231 = 3 × 7 × 11; 84 = 2 × 2 × 3 × 7; Общие множители: 3 и 7;
НОД(84, 231) = 3 × 7 = 21;
Графически это выглядит так:
Как найти НОК на основе множителей
НОК – это произведение всех множителей, но общие множители берутся единожды.
Хотим сложить две дроби: 1/231 и 1/84, нужно найти общий знаменатель. Для этого возьмем наименьшее число, которое делится на оба знаменателя. Точнее возьмем наименьшее общее кратное.
231 = 3 × 7 × 11; 84 = 2 × 2 × 3 × 7; Общие множители: 3 и 7, значит их возьмем только единожды;
НОК(84, 231) = 3 × 7 × 2 × 2 × 11 = 924;
Каждую дробь умножим на множители, которых нет в текущем числе, но есть в другом числе.
Графически это выглядит так:
НОД и НОК – это инструменты для преобразования дробей. Однако это не единственная область применения.
Почему при делении дробь переворачивается
Существует 2 объяснения.
Графический способ
Деление можно представить в виде вопроса: “если разобьем по столько то, сколько получим”.
Например, возьмем число 6, если разобьем
- по 3 кусочка, получим 2 части;
- по 2 кусочка, получим 3 части;
- по 1 кусочку, получим 6 частей;
- по половинке кусочка (1/2), получим 12 частей; то есть в 2 раза больше, чем изначальное число (6), или 6 ÷ 1/2 = 6 × 2;
Переформулирование вопроса
Действие это вопрос, помните? Сколько будет если число разделить на другое число, например 6 ÷ 3; Здесь ответ очевиден: 2.
Но здесь 6 ÷ 1/2 неочевидно, что должно получиться. Давайте переформулируем вопрос: сколько раз нужно взять половинку (1/2), чтобы получилось 6?
1/2 × ? = 6; Теперь ответ очевиден: 12
Вспоминайте взаимосвязь умножения и деления из лекции про базовые математические операции и их свойства
Почему на 0 делить нельзя или почему при делении на 0 получается бесконечность?
Результат неочевиден: 1 ÷ 0 = ? Можно делить единицу на числа приближающиеся к нулю и заметить закономерность.
Для начала возьмем число меньше единицы, например 1/10:
1 ÷ 1/10 дробь при делении переворачивается 1 × 10/1 = 10;
- 1/100:
1 ÷ 1/100 → 1 × 100/1 = 100; - 1/1000:
1 ÷ 1/1000 → 1 × 1000/1 = 1000; - 1/10000:
1 ÷ 1/10000 → 1 × 10000/1 = 10000;
Закономерность очевидна: чем меньше число, на которое делим, тем больше результат, потому при делении на 0, результат будет где-то невообразимо далеко.
Процент и промилле
Процент и промилле – это те же дроби и они подчиняются тем же правилам, что и обычные дроби.
Один процент (%) – это 1/100;
Один промилле (‰) – это 1/1000;
Задачи на процент
Разберем пару задач с использованием процентов.
Задача 1. Сколько процентов от прибыли
Прибыль компании за неделю 180 000 рублей, а за день составила 28 800 рублей, сколько процентов от прибыли в неделю сделали за день.
- Надо узнать сколько составляет 1%: 180 000 – это то, с чем сравниваем, значит это 100%. 1% = 180 000/100 = 1 800.
- Нужно целевую сумму (28 800) разделить на размер 1%, чтобы узнать сколько процентов в этой сумме: 28 800 / 1% = 28 800 / 1 800 = 16%
Ответ: 28 800 это 16% от 180 000
Запишем в одно действие:
28 800 ÷ (180 000 / 100) = 28 800 × 100 / 180 000 = 28 800 / 180 000 × 100;
Можно отбросить × 100 и получим 28 800 ÷ 180 000 = 0,16
0,16 – это называют процентом в виде доли.
Таким образом задача на процент сократилась до одного действия.
Задача 2. Сколько прибыли по проценту
На счете в банке 12 334 рублей, за год банк выплатил 11,4% от суммы счета. Каков размер счета на конец года?
- Узнаем сколько составляет 1%: 12 334 / 100 = 123,34
- Умножим сумму одного процента на размер выплаты в %:
123,34 × 11,4% = 1 406,07 - Прибавляем сумму на начало года и сумму процентов:
12 334 + 1 406,07 = 13 740,07
Ответ: 12 334 + 11,4% = 13 740,07
Запишем в одно действие:
12 334 + 12 334 / 100 × 1,4; создадим скобку:
12 334 + 12 334 / 100 × 1,4 = 1 (12 334+ 12 334 / 100 × 1,4);
вынесем 12 334 за скобку:
1 (12 334 + 12 334 / 100 × 1,4) = 12 334 (1 + 1/100 × 1,4) =
12 334 (1 + 1,4/100) = 12 334 (1 + 0,014) =
12 334 × 1,014
Снова пришли к решению в одно действие.
Закономерность: чтобы узнать результат после увеличения числа на %, достаточно число × (1 + % в виде доли):
100 увеличили на 24% = 100 × (1 + 0,24) = 100 × 1,24 = 124;
100 увеличили на 5% = 100 × (1 + 0,05) = 100 × 1,05 = 105;
100 увеличили на 275% = 100 × (1 + 2,75) = 100 × 3,75 = 375;
Закономерность: чтобы узнать результат после уменьшения числа на %, достаточно число × (1 – % в виде доли):
100 уменьшили на 24% = 100 × (1 – 0,24) = 100 × 0,76 = 76;
100 уменьшили на 5% = 100 × (1 – 0,05) = 100 × 0,95 = 95;
100 уменьшили на 54% = 100 × (1 – 0,54) = 100 × 0,46 = 46;
Задача 3. С подвохом
Товар стоит 100 рублей, накрутка продавца составляет 15%. Сколько процентов составила накрутка от результирующей стоимости товара?
Важный момент: процент берется от какой-то величины, вначале это
100 рублей, то есть результирующая стоимость товара по закономерностям из предыдущих задач: 100 × (1 + 0,15) = 100 × 1,15 = 115;
А накрутка 15% = 100 × 0,15 = 15 рублей.
Сколько процентов составила накрутка от результирующей стоимости товара?
15 / 115 ≈ 0,13 = 13%
Ответ: накрутка от результирующей стоимости товара составила 13%
Вывод
Процент и промилле – это те же дроби и они подчиняются тем же правилам, что и обычные дроби.
Многие задачи можно решать в одно действие, достаточно представить процент в виде доли.
Процент и промилле можно выразить в виде доли:
например, 45% (45 процентов) – это 0,45, а 45‰ (45 промилле) – это 0,045.
Заключение
Дроби – способ описать части неисчисляемого предмета. Технически, дробь – это запись из двух чисел, разделенных чертой. Верхнее число называют числителем, нижнее – знаменателем. Это понадобится, чтобы понимать математические определения. Знаменатель – это размер частей, числитель – количество частей.
Правильные дроби – в которых знаменатель больше числителя.
Неправильные дроби – в которых числитель больше знаменателя.
Дробь – это части, чтобы их сравнить или сложить, нужно привести их к одинаковому размеру: “привести к общему знаменателю”.
Умножение дробей можно представить в виде поочередных операций умножения и деления. При делении на дробь ее нужно перевернуть и умножить на получившуюся дробь.
Наибольший общий делитель (НОД) и наименьшее общее кратное (НОК) – инструменты для преобразования дробей. Чтобы найти НОД и НОК, нужно разложить число на простые множители.
Простые числа – делятся только на самих себя и на единицу.
Составные числа – получаются путем перемножения простых чисел.
Процент и промилле – это те же дроби и они подчиняются тем же правилам, что и обычные дроби.
Один процент (%) – это 1/100;
Один промилле (‰) – это 1/1000;
Если есть вопросы, задавайте в комментариях. Ставьте палец вверх, если понравилось.
Копирование приветствуется и вознаграждается по закону кармы. Пусть знания будут доступны каждому человеку.
Фото автора Polina Tankilevitch: Pexels
#математика просто #математика #дроби #наибольший общий делитель #нод #наименьшее общее кратное #нок #сложение дробей #умножение дробей #деление дробей
С дробями можно выполнять все действия, в том числе и деление. Данная статья показывает деление обыкновенных дробей. Будут даны определения, рассмотрены примеры. Подробно остановимся на делении дробей на натуральные числа и наоборот. Будет рассмотрено деление обыкновенной дроби на смешанное число.
Деление обыкновенных дробей
Деления является обратным умножению. При делении неизвестный множитель находится при известном произведении и другого множителя, где и сохраняется его данный смысл с обыкновенными дробями.
Если необходимо произвести деление обыкновенной дроби ab на cd, тогда для определения такого числа нужно произвести умножение на делитель cd, это даст в итоге делимое ab. Получим число и запишем его ab·dc, где dc является обратным cd числу. Равенства можно записать при помощи свойств умножения, а именно: ab·dc·cd=ab·dc·cd=ab·1=ab, где выражение ab·dc является частным от деления ab на cd.
Отсюда получим и сформулируем правило деления обыкновенных дробей:
Чтобы разделить обыкновенную дробь ab на cd, необходимо делимое умножить на число, обратное делителю.
Запишем правило в виде выражения: ab:cd=ab·dc
Правила деления сводятся к умножению. Чтобы придерживаться его, нужно хорошо разбираться в выполнении умножения обыкновенных дробей.
Перейдем к рассмотрению деления обыкновенных дробей.
Выполнить деление 97 на 53. Результат записать в виде дроби.
Решение
Число 53 – это обратная дробь 35. Необходимо использовать правило деления обыкновенных дробей. Это выражение запишем так: 97:53=97·35=9·37·5=2735.
Ответ: 97:53=2735.
При сокращении дробей следует выделять целую часть, если числитель больше знаменателя.
Разделить 815:2465. Ответ записать в виде дроби.
Решение
Для решения нужно перейти от деления к умножению. Запишем это в такой форме: 815:2465=2·2·2·5·133·5·2·2·2·3=133·3=139
Необходимо произвести сокращение, а это выполняется следующим образом: 8·6515·24=2·2·2·5·133·5·2·2·2·3=133·3=139
Выделяем целую часть и получаем 139=149.
Ответ: 815:2465=149.
Деление необыкновенной дроби на натуральное число
Используем правило деления дроби на натуральное число: чтобы разделить ab на натуральное число n, необходимо умножить только знаменатель на n. Отсюда получим выражение: ab:n=ab·n.
Правило деления является следствием правила умножения. Поэтому представление натурального числа в виде дроби даст равенство такого типа: ab:n=ab:n1=ab·1n=ab·n.
Рассмотрим данное деление дроби на число.
Произвести деление дроби 1645 на число 12.
Решение
Применим правило деления дроби на число. Получим выражение вида 1645:12=1645·12.
Произведем сокращение дроби. Получим 1645·12=2·2·2·2(3·3·5)·(2·2·3)=2·23·3·3·5=4135.
Ответ: 1645:12=4135.
Деление натурального числа на обыкновенную дробь
Правило деления аналогично правилу деления натурального числа на обыкновенную дробь: чтобы разделить натуральное число n на обыкновенную ab, необходимо произвести умножение числа n на обратное дроби ab.
Исходя из правила, имеем n:ab=n·ba, а благодаря правилу умножения натурального числа на обыкновенную дробь, получим наше выражение в виде n:ab=n·ba. Необходимо рассмотреть данное деление на примере.
Делить 25 на 1528.
Решение
Нам необходимо переходить от деления к умножению. Запишем в виде выражения 25:1528=25·2815=25·2815. Сократим дробь и получим результат в виде дроби 4623.
Ответ: 25:1528=4623.
Деление обыкновенной дроби на смешанное число
При делении обыкновенной дроби на смешанное число легко можно свети к делению обыкновенных дробей. Нужно совершить перевод смешанного числа в неправильную дробь.
Разделить дробь 3516 на 318.
Решение
Так как 318 – смешанное число, представим его в виде неправильной дроби. Тогда получим 318=3·8+18=258. Теперь произведем деление дробей. Получим 3516:318=3516:258=3516·825=35·816·25=5·7·2·2·22·2·2·2·(5·5)=710
Ответ: 3516:318=710.
Деление смешанного числа производится таким же образом, как и обыкновенных.
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Обыкновенные дроби
- Деление обыкновенных дробей
Примеры:
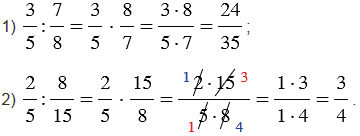
Обратите внимание, если возможно, то прежде, чем перемножить числа, выполняем сокращение (такой ход действий облегчит вычисления).
Деление смешанных чисел
Примеры:
Обратите внимание, если возможно, то прежде, чем перемножить числа, выполняем сокращение (такой ход действий облегчит вычисления).
Деление на натуральное число
При делении дроби на натуральное число, учитываем то, что любое натуральное число можно представить в виде дроби со знаменателем 1, затем пользуемся правилом деления дробей.
Примеры:
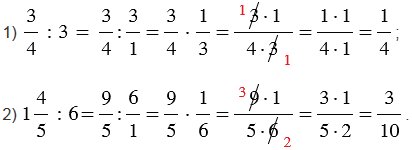
Обратите внимание, если возможно, то прежде, чем перемножить числа, выполняем сокращение (такой ход действий облегчит вычисления).
Нахождения числа по его дроби
Чтобы найти число по данному значению его дроби, надо это значение разделить на дробь
Примеры:
1) Найдите число, если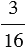 
данного числа равны 27:
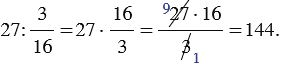
2) Найдите число, если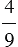 
данного числа равны 
:
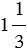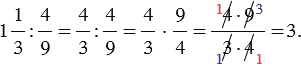
Советуем посмотреть:
Доли. Обыкновенные дроби
Сравнение дробей
Делители и кратные
Признаки делимости на 10, на 5 и на 2
Четные и нечетные числа
Признаки делимости на 9 и на 3
Простые и составные числа
Разложение на простые множители
Наибольший общий делитель
Наименьшее общее кратное
Деление и дроби
Сложение и вычитание дробей с одинаковыми знаменателями
Смешанное число
Сложение и вычитание смешанных чисел
Основное свойство дроби
Решето Эратосфена
Приведение дробей к общему знаменателю
Сравнение, сложение и вычитание дробей с разными знаменателями
Умножение обыкновенных дробей
Обыкновенные дроби
Правило встречается в следующих упражнениях:
6 класс
Номер 459,
Мерзляк, Полонский, Якир, Учебник
Номер 462,
Мерзляк, Полонский, Якир, Учебник
Номер 513,
Мерзляк, Полонский, Якир, Учебник
Номер 516,
Мерзляк, Полонский, Якир, Учебник
Номер 568,
Мерзляк, Полонский, Якир, Учебник
Номер 579,
Мерзляк, Полонский, Якир, Учебник
Задание 478,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 655,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 714,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1330,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
7 класс
Номер 4,
Мерзляк, Полонский, Якир, Учебник
Номер 34,
Мерзляк, Полонский, Якир, Учебник
Номер 75,
Мерзляк, Полонский, Якир, Учебник
Номер 125,
Мерзляк, Полонский, Якир, Учебник
Номер 348,
Мерзляк, Полонский, Якир, Учебник
Номер 527,
Мерзляк, Полонский, Якир, Учебник
Номер 618,
Мерзляк, Полонский, Якир, Учебник
Номер 792,
Мерзляк, Полонский, Якир, Учебник
Номер 1118,
Мерзляк, Полонский, Якир, Учебник
Номер 1119,
Мерзляк, Полонский, Якир, Учебник
8 класс
Номер 13,
Мерзляк, Полонский, Якир, Учебник
Номер 91,
Мерзляк, Полонский, Якир, Учебник
Номер 118,
Мерзляк, Полонский, Якир, Учебник
Номер 135,
Мерзляк, Полонский, Якир, Учебник
Номер 205,
Мерзляк, Полонский, Якир, Учебник
Номер 223,
Мерзляк, Полонский, Якир, Учебник
Номер 278,
Мерзляк, Полонский, Якир, Учебник
Номер 315,
Мерзляк, Полонский, Якир, Учебник
Номер 354,
Мерзляк, Полонский, Якир, Учебник
Номер 482,
Мерзляк, Полонский, Якир, Учебник
