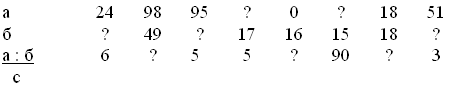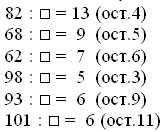Как найти делитель при делении с остатком

Как найти делитель при делении с остатком

Главная цель урока: познакомить с правилом
нахождения неизвестного делителя при делении с
остатком.

Образовательные цели:


  • повторить способы записи частного;
  • повторить названия компонентов действия
    деления;
  • повторить правило нахождения неизвестного
    делителя при делении нацело;
  • составить формулу нахождения неизвестного
    делителя при делении с остатком;
  • формировать умение сравнивать, выделять
    главное;
  • учить устанавливать причинно-следственные
    связи, обобщать, делать выводы;
  • закреплять вычислительные навыки;
  • закреплять решение текстовых задач на деление с
    остатком;
  • формировать умение целенаправленно работать в
    парах.

Воспитательные цели:


  • воспитывать умение слушать одноклассников,
    высказывать свою точку зрения и обосновывать её;
  • воспитывать интерес к математике.

Развивающие цели:


  • развивать рефлексию.

Оздоровительные цели:


  • профилактика утомления, нарушения осанки.

Оборудование:


  • карточки с числами;
  • схематическое изображение темы урока;
  • формула нахождения неизвестного делителя при
    делении с остатком;
  • распечатки для самостоятельной работы;
  • карточки с условными знаками для проведения
    рефлексии;
  • индивидуальные текстовые карточки для
    проведения рефлексии.

Ход урока

1. Организационный момент.

Эмоциональный настрой на урок

– Сегодня у нас много гостей на уроке.
Повернитесь, поздоровайтесь и улыбнитесь им. Вот
видите, и они вам улыбнулись. В классе стало уютно
от ваших улыбок.

2. Чистописание.

На доске написана цифра 9.

– Сегодня на уроке мы с вами будем повторять
написание цифры 9.

– Напишите три цифры.

– Оцените свою работу. Если вы считаете, что все
три цифры написали каллиграфически верно,
поставьте на полях тетради знак плюс, если нет –
знак минус.

3. Актуализация знаний.

“Разминка для головы и рук”

– Что движется быстрее скорости света?

– Мне интересно будет сегодня на уроке
наблюдать, как движутся ваши мысли. Не прячьте их.

18 : 9 2 27 : 9 3

– Что записано на доске?

– Прочитайте выражения разными способами.

– Найдите закономерность записи чисел и
выражений.

– Какое деление выполнили?

– Продолжите закономерность до конца строчки.

– Что общего во всех выражениях?

– Как найти неизвестный делитель?

– Найдите компоненты действия деления.

– Какой компонент неизвестен в первом примере?

На доске представлена таблица. У каждого
учащегося на парте карточка с числом, которое
является значением одного из выражений. Всем
учащимся необходимо выполнить устные вычисления
и прикрепить свою карточку в нужное место
таблицы. Примеры решаются по порядку, карточки
прикрепляются по мере решения примеров.

Разминка закончилась.

4. Сообщение темы и задач урока.

– Теперь нам надо узнать тему нашего урока.

На доске открывается схематическое
изображение темы урока.

– Какое деление сегодня мы будем выполнять на
уроке?

– Какие компоненты при делении с остатком умеем
находить?

– Какой компонент будем сегодня учиться
находить?

– Задача нашего урока составить формулу
нахождения неизвестного делителя при делении с
остатком.

5. Этап “открытия” нового знания.

На доске открывается запись.

– Подумайте, как мы будем находить неизвестный
делитель?

– Можем ли мы использовать формулу нам уже
известную?

– Почему?

– Давайте уберём остаток. Как это сделать?

86 – 5 = 81

– Теперь можем воспользоваться уже известной
нам формулой?

– Воспользуйтесь.

81 : 9 = 9

– Проверьте себя.

9 · 9 + 5 = 86

– Можем ли мы теперь ответить на главный вопрос
урока?

– Как найти неизвестный делитель при делении с
остатком?

На доске открывается формула нахождения
неизвестного делителя при делении с остатком.

в = (а – ч ) : с

– Откройте учебники на стр. 61, найдите №122.

– Используя данную формулу, вставьте числа в
“окошки”.

– Считайте устно и комментируйте свой ответ.

6. Физкультурная минутка.

1) И.п.- сидя за партой, руки за голову. 1-2-руки
вверх, потянуться; 3-4-И.п.

2) И.п.- сидя за партой, ноги на ширину плеч, руки
на пояс. 1-2- наклон вправо; 3-4 – И.п. То же влево.

3) И.п. – сидя за партой. 1-2- встать, выпрямиться;
3-4 – И.п.

7. Закрепление пройденного материала.

– Что мы будем делать дальше на уроке, ведь на
главный вопрос урока мы дали ответ?

– Зачем нам тренироваться в решении примеров на
нахождение неизвестного делителя?

Учащиеся получают карточки для
самостоятельной работы.

– Найдите неизвестный делитель. Закройте
окошки.

– Выполненную работу передайте члену своей
пары. Оцените работы.

– При выполнениеиработы без ошибок, передайте
члену пары карточку со знаком плюс. При ошибках в
вычислениях передайте карточку со знаком минус.

– Покажите карточки.

На доске открываются значения выражений,
представленные на карточках.

6   7   8   15   19   14

– А теперь сравните свои результаты с
результатами на доске.

– Если результаты совпали, оставьте карточку со
знаком плюс, если нет, верните ее обратно члену
пары, который проверял вашу работу.

– Покажите карточки.

8. Повторение.

– Откройте учебник на стр.64.

– Прочитайте задачу № 28.

– Как вы думаете, почему именно данная задача
включена в урок?

– Что в задаче известно?

– Что значит “по 6 банок тушёнки”?

– Что надо узнать?

– Можем сразу ответить на вопрос задачи?

– Почему?

– Как узнать?

– Теперь можем ответить на поставленный вопрос?

– Что для этого нужно сделать?

– А как письменно оформить нашу мысль?

– Что мы записали?

– Прочитайте, как рассуждали при решении данной
задачи Миша и Маша.

– С чьим рассуждением совпадает наше?

– Кто прав: Маша и мы или Миша?

9. Подведение итогов урока. Домашнее задание.
Инструктаж его выполнения.

– Оцените себя и покажите, кто может
самостоятельно в домашнем задании найти
делитель при делении с остатком?

Учащиеся показывают карточки с условными
знаками: +,-, ?.

– Кому необходимо пользоваться формулой при
решении примеров на нахождение неизвестного
делителя при делении с остатком?

Учащиеся показывают карточки с условными
знаками: +,-, ?.

– В домашнем задании я предлагаю вам составить
примеры на деление с остатком с неизвестным
делителем. Напечатайте примеры, используя
компьютер. У вас получатся карточки для
самостоятельной работы. Мы будем использовать их
на следующих уроках.

-Урок окончен. Ваши мысли двигались
действительно быстрее скорости света. Мне было
интересно и комфортно на уроке.

– А как вы ощущали себя на уроке?

Каждый учащийся работает с индивидуальными
текстовыми карточками

– Выберите утверждение. Отметьте галочкой.

Ощущал себя на уроке:

  • хорошо;
  • уверенно;
  • смело;
  • гордо;
  • комфортно;
  • глупо;
  • неуверенно;
  • испуганно;
  • сердито;
  • грустно.

Спасибо.

Источник

Как найти делитель при делении с остатком?

Виктория Казакова



Знаток

(266),
на голосовании



7 лет назад

Дополнен 7 лет назад

И как найти неполное частное тоже при делении с остатком

Голосование за лучший ответ

657567654

Гуру

(4665)


7 лет назад

делить делимое на частное

Виктория КазаковаЗнаток (266)

7 лет назад

С остатком

657567654
Гуру
(4665)
делить делимое на частное и + остаток

Диана ТычинаУченик (102)

4 года назад

Прибавить остаток

Dasha )))

Знаток

(343)


6 лет назад

Делительным свойством

Диана Тычина

Ученик

(102)


4 года назад

Делимое разделить на неполное частное и прибавить остаток

Похожие вопросы

Источник

План урока

  • Понятие деления с остатком.
  • Сравнение остатка и делителя.
  • Правило нахождения делимого.

Цели урока

  • Знать понятия «неполное частное», «остаток».
  • Уметь делить с остатком.
  • Уметь решать задачи с помощью деления с остатком.

Разминка

  • Какие компоненты деления вы знаете?
  • Как найти делимое?
  • Как найти делитель?
  • Можно ли разделить число 8 на 3?

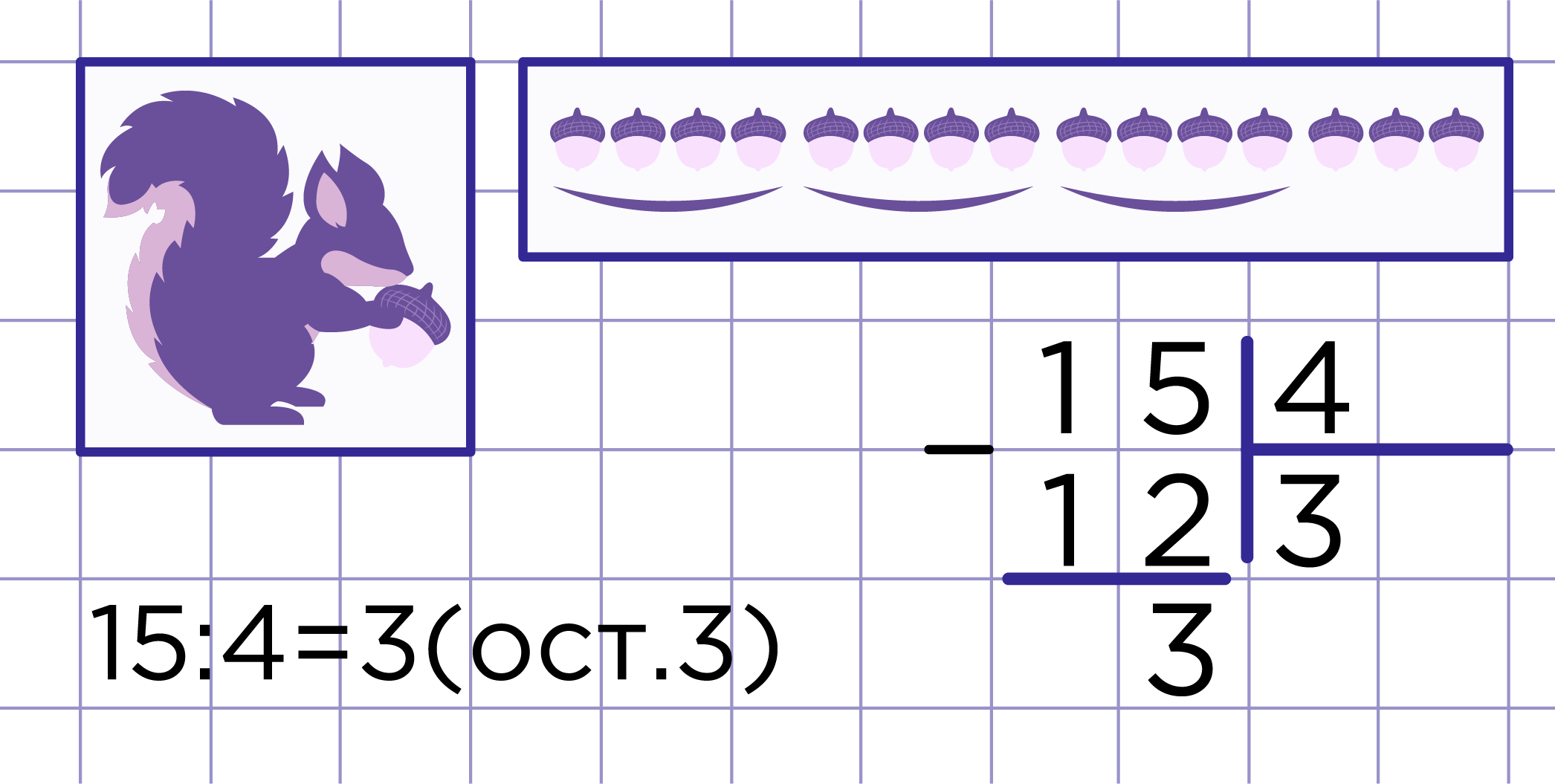
Как разделить число 15 на 4? Давайте решим задачу — разделите 15 орехов между 4 белками так, чтобы им досталось поровну орехов. 


Рис. 1

На рис.1 показано, что каждой белке достанется по 3 ореха, но при этом еще 3 ореха останется.  Можно записать следующее равенство: 

15 = 4 · 3 + 3;

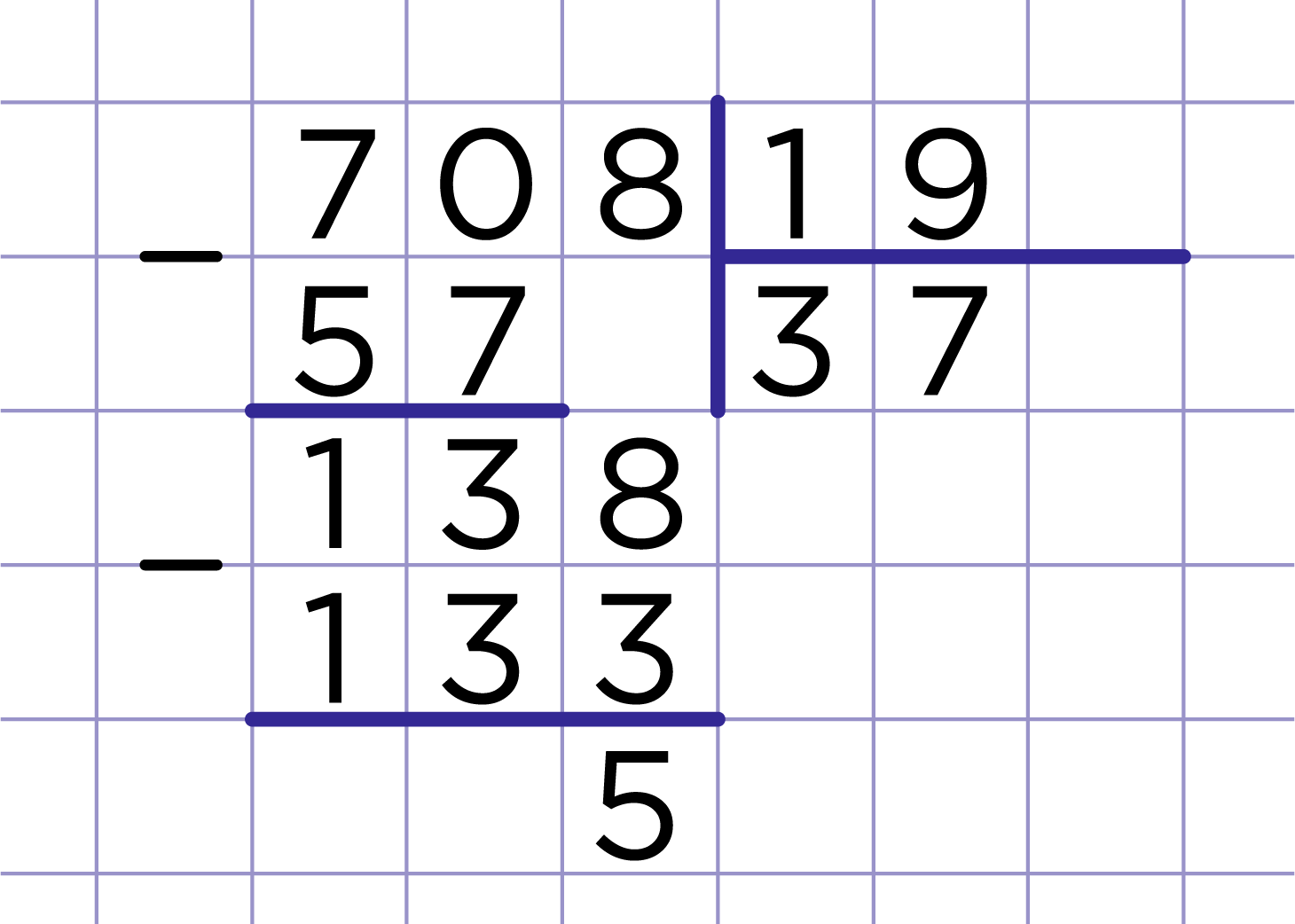
Рассмотрим еще один пример: 708 : 19 = 37 (ост. 5)


Рис. 2

Заметим, что 37 — это наибольшее число, произведение которого на 19 меньше делимого 708. Число 37 — неполное частное; число 5 — остаток.  

Остаток всегда меньше делителя:  5 < 19.

Чтобы найти делимое, нужно делитель умножить на неполное частное и прибавить остаток.

a = bq + r,  где a — делимое, b — делитель, q — неполное частное, r — остаток.

Может ли остаток быть равен нулю? Рассмотрим равенство: 34 = 17 · 2.

Можно равенство написать по-другому: 34 = 17 · 2 + 0. В таком случае говорят, что остаток равен нулю и число 34 делится нацело на число 17.

Оля разделила число 84 на некоторое число и получила остаток 4. Какое число делила Оля?

Решение

Найдем произведение неполного частного и делителя:

84 – 4 = 80.

Методом подбора найдем возможные делители числа 80.

80  = 80 · 1 = 40 · 2 = 20 · 4 = 16 · 5 = 10 · 8.

Так как остаток 4 должен быть меньше делителя, то делителем может быть любое из чисел 80, 40, 20, 16, 5, 10, 8.

Ответ: 80; 40; 20; 16; 5; 10; 8.

Выполните деление с остатком: 1) 48 : 5;   2) 678 : 24;   3) 882 : 40.

Найдите делимое, если делитель равен 12, неполное частное — 6, а остаток — 8.

Тетрадь стоит 16 р. Какое наибольшее количество тетрадей можно купить, имея 100 р.?

Петя разделил число 108 на некоторое число и получил остаток 10. На какое число делил Петя?

Контрольные вопросы

1. Как найти делимое (при делении с остатком)?

2. Может ли остаток быть больше делителя?

3. Что означает фраза «делится нацело»?

Итоги:

В случаях, когда одно число не делится нацело на другое, говорят о делении с остатком. Чтобы найти делимое, нужно неполное частное умножить на делитель и к произведению прибавить остаток. 

Ответы

Упражнение 1

1) 9 (ост. 3);   2) 28 (ост. 6);   3) 22 (ост. 2).

Упражнение 2

80.

Упражнение 3

6 тетрадей.

Упражнение 4

49, 14 или 98.

Источник

Деление c остатком — арифметическая операция, играющая большую роль в арифметике, теории чисел, алгебре и криптографии. Чаще всего эта операция определяется для целых или натуральных чисел следующим образом[1]. Пусть a и b — целые числа, причём bneq 0. Деление с остатком a («делимого») на b («делитель») означает нахождение таких целых чисел q и r, что выполняется равенство:

a=bcdot q+r

Таким образом, результатами деления с остатком являются два целых числа: q называется неполным частным от деления, а r — остатком от деления. На остаток налагается дополнительное условие: {displaystyle 0leqslant r<|b|,} то есть остаток от деления должен быть неотрицательным числом и по абсолютной величине меньше делителя. Это условие обеспечивает однозначность результатов деления с остатком для всех целых чисел, то есть существует единственное решение уравнения a=bcdot q+r при заданных выше условиях. Если остаток равен нулю, говорят, что a нацело делится на b.

Нахождение неполного частного также называют целочисленным делением, а нахождение остатка от деления называют взятием остатка или, неформально, делением по модулю (однако последний термин стоит избегать, так как он может привести к путанице с делением в кольце или группе вычетов по аналогии со сложением или умножением по модулю).

Примеры
Проверка: 78=33cdot 2+12.
Проверка: -78=33cdot (-3)+21.
Проверка: {displaystyle -9=1cdot (-13)+4.}
Проверка: {displaystyle 9=90cdot 0+9.}

Операция деления с остатком может быть определена не только для целых чисел, но и для других математических объектов (например, для многочленов), см. ниже.

Определение[править | править код]

Оставаясь строго в рамках натуральных чисел, приходится различать деление с остатком и деление нацело, поскольку нулевой остаток не является натуральным числом; кроме того, неполное частное при делении меньшего числа на большее должно равняться нулю, что тоже выводит за рамки натуральных чисел. Все эти искусственные ограничения неоправданно усложняют формулировки, поэтому в источниках обычно либо рассматривается расширенный натуральный ряд, включающий ноль[2], либо теория сразу формулируется для целых чисел, как указано выше[1].

Для вычисления неполного частного от деления a на положительное число b следует разделить (в обычном смысле) a на b и округлить результат до ближайшего целого в меньшую сторону:

{displaystyle q=leftlfloor {frac {a}{b}}rightrfloor ,} когда b>0.

где полускобки {displaystyle leftlfloor cdot rightrfloor } обозначают взятие целой части. Значение неполного частного q позволяет вычислить значение остатка r по формуле:

{displaystyle r=a-bcdot q.}

Для отрицательного делителя нужно округлять частное в большую сторону:

{displaystyle q=leftlceil {frac {a}{b}}rightrceil ,} когда b<0.

Операция «mod» и связь со сравнениями[править | править код]


Величина остатка может быть получена бинарной операцией «взятия остатка» от деления a на b, обозначаемой mod:

{displaystyle r=a{bmod {b}}.}

Не следует путать это обозначение с обозначением сравнения по модулю b. Формула для r влечёт выполнение сравнения:

{displaystyle requiv a{pmod {b}},}

однако обратная импликация, вообще говоря, неверна. А именно, это сравнение не подразумевает выполнения неравенства 0leqslant r<|b|, необходимого для того, чтобы r было остатком.

В программировании[править | править код]

Операция вычисления неполного частного и остатка в различных языках программирования

Язык Неполное
частное		 Остаток Знак остатка
ActionScript % Делимое
Ada mod Делитель
rem Делимое
Бейсик MOD Не определено
Си (ISO 1990) / % Не определено
Си (ISO 1999) / % Делимое[3]
C++ (ISO 2003) / % Не определено[4]
C++ (ISO 2011) / % Делимое[5]
C# / % Делимое
ColdFusion MOD Делимое
Common Lisp mod Делитель
rem Делимое
D / % Делимое[6]
Delphi div mod Делимое
Eiffel // \ Делимое
Erlang div rem Делимое
Euphoria remainder Делимое
Microsoft Excel (англ.) QUOTIENT() MOD() Делитель
Microsoft Excel (рус.) ЧАСТНОЕ() ОСТАТ()
FileMaker Div() Mod() Делитель
Fortran mod Делимое
modulo Делитель
GML (Game Maker) div mod Делимое
Go / % Делимое
Haskell div mod Делитель
quot rem Делимое
J |~ Делитель
Java / % Делимое[7]
Math.floorDiv Math.floorMod Делитель (1.8+)
JavaScript .toFixed(0) % Делимое
Lua % Делитель
Mathematica Quotient Mod Делитель
MATLAB idivide(?, ?, 'floor') mod Делитель
idivide rem Делимое
MySQL DIV MOD
%		 Делимое
Oberon DIV MOD +
Objective Caml mod Не определено
Pascal div mod Делимое[8]
Perl Нет % Делитель
PHP Нет[9] % Делимое
PL/I mod Делитель (ANSI PL/I)
Prolog (ISO 1995) mod Делитель
PureBasic / Mod
%		 Делимое
Python // % Делитель
QBasic MOD Делимое
R %/% %% Делитель
RPG %REM Делимое
Ruby / % Делитель
Scheme modulo Делитель
SenseTalk modulo Делитель
rem Делимое
Tcl % Делитель
Verilog (2001) % Делимое
VHDL mod Делитель
rem Делимое
Visual Basic Mod Делимое

Нахождение остатка от деления часто используется в компьютерной технике и телекоммуникационном оборудовании для создания контрольных чисел и получения случайных чисел в ограниченном диапазоне, например в конгруэнтном генераторе случайных чисел.

Обозначения операции взятия остатка в различных языках программирования представлены в таблице справа.
Например, в Паскале операция mod вычисляет остаток от деления, а операция div осуществляет целочисленное деление, при котором остаток от деления отбрасывается: 

78 mod 33 = 12
78 div 33 = 2

Знак остатка[править | править код]

Операция взятия остатка в языках программирования может возвращать отрицательный результат (для отрицательного делимого или делителя). Тут есть два варианта:

  • Знак остатка совпадает со знаком делимого: неполное частное округляет к нулю.
  • Знак остатка совпадает со знаком делителя: неполное частное округляет к -infty .

Если в языке есть оба типа остатков, каждому из них соответствует своя операция неполного частного. Обе операции имеют жизненный смысл.

Операция div в x86/x64 делит регистровую пару rdx:rax на любой другой регистр или число из памяти[10]. Неполное частное и остаток выходят по первому варианту — округляют к нулю.

Как запрограммировать, если такой операции нет?[править | править код]

Неполное частное можно вычислить через деление и взятие целой части: q=left[{frac {a}{b}}right], где [x], в зависимости от задачи, может быть «полом» или усечением. Однако деление здесь получается дробное, которое намного медленнее целого. Такой алгоритм используется в языках, в которых нет целых типов (отдельные электронные таблицы, программируемые калькуляторы и математические программы), а также в скриптовых языках, в которых издержки интерпретации намного превышают издержки дробной арифметики (Perl, PHP).

При отсутствии команды mod остаток программируется как a-qb.

Если b положительно, а знак r совпадает со знаком делимого, не определён или неизвестен, для нахождения минимального неотрицательного остатка можно воспользоваться формулой r'=(b+(aoperatorname {mod}b))operatorname {mod}b.

Неполное частное и неотрицательный остаток от деления на степень двойки 2^{n} — это битовый сдвиг {displaystyle agg n} (для чисел со знаком — арифметический) и {displaystyle aoperatorname {&} (2^{n}-1)}.

Обобщения[править | править код]

Вещественные числа[править | править код]

Если два числа a и b (отличное от нуля) относятся к множеству вещественных чисел, a может быть поделено на b без остатка, и при этом частное также является вещественным числом. Если же частное по условию должно быть целым числом, в этом случае остаток будет вещественным числом, то есть может оказаться дробным.

Формально:

если a,bin {mathbb {R}},bneq 0, то {displaystyle a=bq+r}, где 0leqslant r<|b|.
Пример

Деление 7,9 на 2,1 с остатком даёт:

{displaystyle leftlfloor {frac {7{,}9}{2{,}1}}rightrfloor =3} (неполное частное);
{displaystyle 7{,}9-3cdot 2{,}1=1{,}6} (остаток).

Гауссовы целые числа[править | править код]

Гауссово число — это комплексное число вида a+bi, где a,b — целые числа. Для них можно определить деление с остатком: любое гауссово число u можно разделить с остатком на любое ненулевое гауссово число v, то есть представить в виде:

u=vq+r,

где частное q и остаток r — гауссовы числа, причём |r|<|v|.
Однако, в отличие от целых чисел, остаток от деления определяется неоднозначно. Например, {displaystyle 7+2i} можно разделить на {displaystyle 3-i} тремя способами:

{displaystyle 7+2i=(3-i)(2+i)+i=(3-i)(1+i)+3=(3-i)(2+2i)+(-1-2i).}

Многочлены[править | править код]

При делении с остатком двух многочленов f(x) и g(x) для однозначности результата вводится условие: степень многочлена-остатка должна быть строго меньше степени делителя:

{displaystyle f(x)=q(x)g(x)+r(x)}, причём {displaystyle deg(r)<deg(g)}.
Пример
{frac {2x^{2}+4x+5}{x+1}}=2x+2 (остаток 3), так как: {displaystyle 2x^{2}+4x+5=(x+1)(2x+2)+3}.

См. также[править | править код]

  • Алгоритм Евклида
  • Делимость
  • Наибольший общий делитель
  • Непрерывная дробь
  • Сравнение по модулю

Примечания[править | править код]

  1. ↑ 1 2 Деление // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1979. — Т. 2.
  2. ↑ Потапов М. К., Александров В. В., Пасиченко П. И. Алгебра и анализ элементарных функций. М.: Наука, 1981, 560 с., С. 9.
  3. ↑ ISO/IEC 9899:TC2: When integers are divided, the result of the / operator is the algebraic quotient with any fractional part discarded. [This is often called «truncation toward zero».]; в списке изменений 1999→TC1 и TC1→TC2 данное изменение не числится.
  4. ↑ «ISO/IEC 14882:2003 : Programming languages — C++», 5.6.4: International Organization for Standardization, International Electrotechnical Commission, 2003. «the binary % operator yields the remainder from the division of the first expression by the second. …. If both operands are nonnegative then the remainder is nonnegative; if not, the sign of the remainder is implementation-defined».
  5. ↑ N3242=11-0012 (Working draft), текст совпадает с C99
  6. ↑ D language specification (англ.). dlang.org. Дата обращения: 29 октября 2017. Архивировано из оригинала 3 октября 2017 года.
  7. ↑ Арнолд, Кен, Гослинг, Дж., Холмс, Д. Язык программирования Java. — 3-е изд. — М., СПб., Киев: Вильямс, 2001. — С. 173—174. — ISBN 5-8459-0215-0.
  8. ↑ Стандарт 1973 года: div — division with truncation.
  9. ↑ PHP: Arithmetic Operators — Manual. Дата обращения: 27 ноября 2014. Архивировано 19 ноября 2014 года.
  10. ↑ DIV — Unsigned Divide
Источник

Деление с остатком.

Рассмотрим простой пример:
15:5=3
В этом примере натуральное число 15 мы поделили нацело на 3, без остатка.

Иногда натуральное число полностью поделить нельзя нацело. Например, рассмотрим задачу:
В шкафу лежало 16 игрушек. В группе было пятеро детей. Каждый ребенок взял одинаковое количество игрушек. Сколько игрушек у каждого ребенка?

Решение:
Поделим число 16 на 5 столбиком получим:

Деление с остатком
Мы знаем, что 16 на 5 не делиться. Ближайшее меньшее число, которое делиться на 5 это 15 и 1 в остатке. Число 15 мы можем расписать как 5⋅3. В итоге (16 – делимое, 5 – делитель, 3 – неполное частное, 1 — остаток). Получили формулу деления с остатком, по которой можно сделать проверку решения.

16=5⋅3+1

a=b⋅c+d
a – делимое,
b – делитель,
c – неполное частное,
d – остаток.

Ответ: каждый ребенок возьмет по 3 игрушки и одна игрушка останется.

Остаток от деления

Остаток всегда должен быть меньше делителя.

Если при делении остаток равен нулю, то это значит, что делимое делиться нацело или без остатка на делитель.

Если при делении остаток больше делителя, это значит, что найденное число не самое большое. Существует число большее, которое поделит делимое и остаток будет меньше делителя.

Вопросы по теме “Деление с остатком”:
Остаток может быть больше делителя?
Ответ: нет.

Остаток может быть равен делителю?
Ответ: нет.

Как найти делимое по неполному частному, делителю и остатку?
Ответ: значения неполного частного, делителя и остатка подставляем в формулу и находим делимое. Формула:
a=b⋅c+d
(a – делимое, b – делитель, c – неполное частное, d – остаток.)

Пример №1:
Выполните деление с остатком и сделайте проверку: а) 258:7 б) 1873:8

Решение:
а) Делим столбиком:
Деленис с остатком 258:7

258 – делимое,
7 – делитель,
36 – неполное частное,
6 – остаток. Остаток меньше делителя 6<7.

Подставим в формулу и проверим правильно ли мы решили пример:
7⋅36+6=252+6=258

б) Делим столбиком:
Деление с остатком 1873:8

1873 – делимое,
8 – делитель,
234 – неполное частное,
1 – остаток. Остаток меньше делителя 1<8.

Подставим в формулу и проверим правильно ли мы решили пример:
8⋅234+1=1872+1=1873

Пример №2:
Какие остатки получаются при делении натуральных чисел: а) 3 б)8?

Ответ:
а) Остаток меньше делителя, следовательно, меньше 3. В нашем случае остаток может быть равен 0, 1 или 2.
б) Остаток меньше делителя, следовательно, меньше 8. В нашем случае остаток может быть равен 0, 1, 2, 3, 4, 5, 6 или 7.

Пример №3:
Какой наибольший остаток может получиться при делении натуральных чисел: а) 9 б) 15?

Ответ:
а) Остаток меньше делителя, следовательно, меньше 9. Но нам надо указать наибольший остаток. То есть ближайшее число к делителю. Это число 8.
б) Остаток меньше делителя, следовательно, меньше 15. Но нам надо указать наибольший остаток. То есть ближайшее число к делителю. Это число 14.

Пример №4:
Найдите делимое: а) а:6=3(ост.4) б) с:24=4(ост.11)

Решение:
а) Решим с помощью формулы:
a=b⋅c+d
(a – делимое, b – делитель, c – неполное частное, d – остаток.)
а:6=3(ост.4)
(a – делимое, 6 – делитель, 3 – неполное частное, 4 – остаток.) Подставим цифры в формулу:
а=6⋅3+4=22
Ответ: а=22

б) Решим с помощью формулы:
a=b⋅c+d
(a – делимое, b – делитель, c – неполное частное, d – остаток.)
с:24=4(ост.11)
(с – делимое, 24 – делитель, 4 – неполное частное, 11 – остаток.) Подставим цифры в формулу:
с=24⋅4+11=107
Ответ: с=107

Задача:

Проволоку 4м. нужно разрезать на куски по 13см. Сколько таких кусков получится?

Решение:
Сначала надо метры перевести в сантиметры.
4м.=400см.
Можно поделить столбиком или в уме получим:
400:13=30(ост.10)
Проверим:
13⋅30+10=390+10=400

Ответ: 30 кусков получиться и 10 см. проволоки останется.

Источник

Добавить комментарий