Рассмотрим два основных метода нахождения НОД двумя основными способами: с использованием алгоритма Евклида и путем разложения на простые множители. Применим оба метода для двух, трех и большего количества чисел.
Алгоритм Евклида для нахождения НОД
Алгоритм Евклида позволяет с легкостью вычислить наибольший общий делитель для двух положительных чисел. Формулировки и доказательство алгоритма Евклида мы привели в разделе «Наибольший общий делитель: определитель, примеры».
Суть алгоритма заключается в том, чтобы последовательно проводить деление с остатком, в ходе которого получается ряд равенств вида:
a=b·q1+r1, 0<r1<bb=r1·q2+r2, 0<r2<r1r1=r2·q3+r3, 0<r3<r2r2=r3·q4+r4, 0<r4<r3⋮rk-2=rk-1·qk+rk, 0<rk<rk-1rk-1=rk·qk+1
Мы можем закончить деление тогда, когда rk+1=0, при этом rk=НОД(a, b).
Найдите наибольший общий делитель чисел 64 и 48.
Решение
Введем обозначения: a=64, b=48.
На основе алгоритма Евклида проведем деление 64 на 48.
Получим 1 и остаток 16. Получается, что q1=1, r1=16.
Вторым шагом разделим 48 на 16, получим 3. То есть q2=3, а r2=0. Таким образом число 16 – это наибольший общий делитель для чисел из условия.
Ответ: НОД(64, 48)=16.
Чему равен НОД чисел 111 и 432?
Решение
Делим 432 на 111. Согласно алгоритму Евклида получаем цепочку равенств 432=111·3+99, 111=99·1+12, 99=12·8+3, 12=3·4.
Таким образом, наибольший общий делитель чисел 111 и 432 – это 3.
Ответ: НОД(111, 432)=3.
Найдите наибольший общий делитель чисел 661 и 113.
Решение
Проведем последовательно деление чисел и получим НОД(661, 113)=1. Это значит, что 661 и 113 – это взаимно простые числа. Мы могли выяснить это до начала вычислений, если бы обратились к таблице простых чисел.
Ответ: НОД(661, 113)=1.
Нахождение НОД с помощью разложения чисел на простые множители
Для того, чтобы найти наибольший общий делитель двух чисел методом разложения на множители, необходимо перемножить все простые множители, которые получаются при разложении этих двух чисел и являются для них общими.
Если мы разложим числа 220 и 600 на простые множители, то получим два произведения: 220=2·2·5·11 и 600=2·2·2·3·5·5. Общими в этих двух произведениях будут множители 2,2 и 5. Это значит, что НОД(220, 600)=2·2·5=20.
Найдите наибольший общий делитель чисел 72 и 96.
Решение
Найдем все простые множители чисел 72 и 96:
72361893122233
96482412631222223
Общими для двух чисел простые множители: 2, 2, 2 и 3. Это значит, что НОД(72, 96)=2·2·2·3=24.
Ответ: НОД(72, 96)=24.
Правило нахождения наибольшего общего делителя двух чисел основано на свойствах наибольшего общего делителя, согласно которому НОД(m·a1, m·b1)=m·НОД(a1, b1), где m– любое целое положительное число.
Нахождение НОД трех и большего количества чисел
Независимо от количества чисел, для которых нам нужно найти НОД, мы будем действовать по одному и тому же алгоритму, который заключается в последовательном нахождении НОД двух чисел. Основан этот алгоритм на применении следующей теоремы: НОД нескольких чисел a1, a2, …, ak равен числу dk, которое находится при последовательном вычислении НОД(a1, a2)=d2, НОД(d2, a3)=d3, НОД(d3, a4)=d4, …, НОД(dk-1, ak)=dk.
Найдите наибольший общий делитель четырех чисел 78, 294, 570 и 36.
Решение
Введем обозначения: a1=78, a2=294, a3=570, a4=36.
Начнем с того, что найдем НОД чисел 78 и 294: d2=НОД(78, 294)=6.
Теперь приступим к нахождению d3=НОД(d2, a3)=НОД(6, 570). Согласно алгоритму Евклида 570=6·95. Это значит, что d3=НОД(6, 570)=6.
Найдем d4=НОД(d3, a4)=НОД(6, 36). 36 делится на 6 без остатка. Это позволяет нам получить d4=НОД(6, 36)=6.
d4=6, то есть, НОД(78, 294, 570, 36)=6.
Ответ: НОД(78, 294, 570, 36)=6.
А теперь давайте рассмотрим еще один способ вычисления НОД для тех и большего количества чисел. Мы можем найти НОД, перемножив все общие простые множители чисел.
Вычислите НОД чисел 78, 294, 570 и 36.
Решение
Произведем разложение данных чисел на простые множители: 78=2·3·13, 294=2·3·7·7, 570=2·3·5·19, 36=2·2·3·3.
Для всех четырех чисел общими простыми множителями будут числа 2 и 3.
Получается, что НОД(78, 294, 570, 36)=2·3=6.
Ответ: НОД(78, 294, 570, 36)=6.
Нахождение НОД отрицательных чисел
Если нам приходится иметь дело с отрицательными числами, то для нахождения наибольшего общего делителя мы можем воспользоваться модулями этих чисел. Мы можем так поступить, зная свойство чисел с противоположными знаками: числа n и -n имеют одинаковые делители.
Найдите НОД отрицательных целых чисел −231 и −140.
Решение
Для выполнения вычислений возьмем модули чисел, данных в условии. Это будут числа 231 и 140. Запишем это кратко: НОД(−231, −140)=НОД(231, 140). Теперь применим алгоритм Евклида для нахождения простых множителей двух чисел: 231=140·1+91; 140=91·1+49; 91=49·1+42; 49=42·1+7 и 42=7·6. Получаем, что НОД(231, 140)=7.
А так как НОД(−231, −140)=НОД(231, 140), то НОД чисел −231 и −140 равен 7.
Ответ: НОД(−231, −140)=7.
Определите НОД трех чисел −585, 81 и −189.
Решение
Заменим отрицательные числа в приведенном перечне на их абсолютные величины, получим НОД(−585, 81, −189)=НОД(585, 81, 189). Затем разложим все данные числа на простые множители: 585=3·3·5·13, 81=3·3·3·3 и 189=3·3·3·7. Общими для трех чисел являются простые множители 3 и 3. Получается , что НОД(585, 81, 189)=НОД(−585, 81, −189)=9.
Ответ: НОД(−585, 81, −189)=9.
![]()
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Загрузить PDF
Загрузить PDF
Любое натуральное число можно разложить на произведение простых множителей. Если вы не любите иметь дело с большими числами, такими как 5733, научитесь раскладывать их на простые множители (в данном случае это 3 x 3 x 7 x 7 x 13). Подобная задача часто встречается в криптографии, которая занимается проблемами информационной безопасности. Если вы еще не готовы создать собственную систему безопасной электронной почты, для начала научитесь раскладывать числа на простые множители.
-

1
Узнайте, что такое разложение числа на множители. Разложение числа на произведение множителей представляет собой процесс его “разбиения” на более мелкие части. При перемножении эти части, или множители, дают первоначальное число.
- Например, число 18 можно разложить на следующие произведения: 1 x 18, 2 x 9, или 3 x 6.
-

2
Вспомните, что такое простые числа. Простое число делится без остатка лишь на два числа: на само себя и на 1. Например, число 5 можно представить в виде произведения 5 и 1. Это число нельзя разложить на другие множители. Цель разложения числа на простые множители заключается в том, чтобы представить его в виде произведения простых чисел. Это особенно удобно при операциях с дробями, так как позволяет сравнивать и упрощать их.[1]
-

3
Начните с исходного числа. Выберите составное число больше 3. Нет смысла брать простое число, так как оно делится лишь на само себя и единицу.
- Пример: разложим на произведение простых чисел число 24.
-

4
Разложим данное число на произведение двух множителей. Найдем два меньших числа, произведение которых равно исходному числу. Можно использовать любые множители, но проще взять простые числа. Один из хороших способов состоит в том, чтобы попробовать поделить исходное число сначала на 2, затем на 3, потом на 5 и проверить, на какие из этих простых чисел оно делится без остатка.
- Пример: если вы не знаете множителей для числа 24, попробуйте поделить его на малые простые числа. Так вы обнаружите, что данное число делится на 2: 24 = 2 x 12. Это хорошее начало.
- Поскольку 2 является простым числом, его хорошо использовать при разложении четных чисел.
-

5
Начните строить дерево множителей. Эта простая процедура поможет вам разложить число на простые множители.[2]
Для начала проведите от исходного числа две “ветки” вниз. На конце каждой ветки напишите найденные множители.- Пример:
- 24
- /
- 2 12
-

6
Разложите на множители следующую строку чисел. Взгляните на два новых числа (вторая строка дерева множителей). Оба ли они относятся к простым числам? Если одно из них не является простым, также разложите его на два множителя. Проведите еще две ветки и напишите два новых множителя в третьей строке дерева.
- Пример: 12 не является простым числом, поэтому его следует разложить на множители. Используем разложение 12 = 2 x 6 и запишем его в третьей строке дерева:
- 24
- /
- 2 12
- /
- 2 x 6
-

7
Продолжайте двигаться вниз по дереву. Если один из новых множителей окажется простым числом, проводите от него одну “ветку” и пишите на ее конце это же число. Простые числа не раскладываются на меньшие множители, поэтому просто переносите их на уровень ниже.
- Пример: 2 является простым числом. Просто перенесите 2 из второй в третью строку:
- 24
- /
- 2 12
- / /
- 2 2 6
-

8
Продолжайте раскладывать числа на множители, пока у вас не останутся одни простые числа. Проверяйте каждую новую строку дерева. Если хоть один из новых множителей не является простым числом, разложите его на множители и запишите новую строку. В конце концов у вас останутся одни простые числа.
- Пример: 6 не является простым числом, поэтому его также следует разложить на множители. В то же время 2 представляет собой простое число, и мы переносим две двойки на следующий уровень:
- 24
- /
- 2 12
- / /
- 2 2 6
- / / /
- 2 2 2 3
-

9
Запишите последнюю строку в виде произведения простых множителей. В конце концов у вас останутся одни простые числа. Когда это случится, разложение на простые множители завершено. Последняя строка представляет собой набор простых чисел, произведение которых дает исходное число.
- Проверьте ответ: перемножьте стоящие в последней строке числа. В результате должно получиться исходное число.
- Пример: в последней строке дерева множителей содержатся числа 2 и 3. Оба этих числа являются простыми, поэтому разложение завершено. Таким образом, разложение числа 24 на простые множители имеет следующий вид: 24 = 2 x 2 x 2 x 3.
- Порядок множителей не имеет значения. Разложение можно записать также в виде 2 x 3 x 2 x 2.
-

10
При желании упростите ответ с помощью степенной записи. Если вы знакомы с возведением чисел в степень, можно записать полученный ответ в более простом виде. Помните, что внизу записывается основание, а надстрочное число показывает, сколько раз это основание следует умножить на само себя.
- Пример: сколько раз встречается число 2 в найденном разложении 2 x 2 x 2 x 3? Три раза, поэтому выражение 2 x 2 x 2 можно записать в виде 23. В упрощенной записи получаем 23 x 3.
Реклама
-

1
Найдите наибольший общий делитель двух чисел. Наибольшим общим делителем (НОД) двух чисел называется максимальное число, на которое оба числа делятся без остатка. В приведенном ниже примере показано, как с помощью разложения на простые множители найти наибольший общий делитель чисел 30 и 36.
- Разложим оба числа на простые множители. Для числа 30 разложение имеет вид 2 x 3 x 5. Число 36 раскладывается на простые множители следующим образом: 2 x 2 x 3 x 3.
- Найдем число, которое встречается в обоих разложениях. Перечеркнем это число в обоих списках и напишем его с новой строки. Например, 2 встречается в двух разложениях, поэтому запишем 2 в новой строке. После этого у нас остается 30 =
2x 3 x 5 и 36 =2x 2 x 3 x 3. - Повторяйте это действие, пока в разложениях не останется общих множителей. В оба списка входит также число 3, поэтому в новой строке можно записать 2 и 3. После этого вновь сравните разложения: 30 =
2 x 3x 5 и 36 =2x 2 x3x 3. Как видно, в них не осталось общих множителей. - Чтобы найти наибольший общий делитель, следует найти произведение всех общих множителей. В нашем примере это 2 и 3, поэтому НОД равен 2 x 3 = 6. Это наибольшее число, на которое делятся без остатка числа 30 и 36.
-

2
С помощью НОД можно упрощать дроби. Если вы подозреваете, что какую-то дробь можно сократить, используйте наибольший общий делитель. По описанной выше процедуре найдите НОД числителя и знаменателя. После этого поделите числитель и знаменатель дроби на это число.[3]
В результате вы получите ту же дробь в более простом виде.- К примеру, упростим дробь 30/36. Как мы установили выше, для 30 и 36 НОД равен 6, поэтому поделим числитель и знаменатель на 6:
- 30 ÷ 6 = 5
- 36 ÷ 6 = 6
- 30/36 = 5/6
-

3
Найдем наименьшее общее кратное двух чисел. Наименьшее общее кратное (НОК) двух чисел — это наименьшее число, которое делится без остатка на оба данных числа. Например, НОК 2 и 3 является 6, поскольку это наименьшее число, которое делится на 2 и 3. Ниже приведен пример нахождения НОК с помощью разложения на простые множители:
- Начнем с двух разложений на простые множители. Например, для числа 126 разложение можно записать как 2 x 3 x 3 x 7. Число 84 раскладывается на простые множители в виде 2 x 2 x 3 x 7.
- Сравним, сколько раз каждый множитель встречается в разложениях. Выберите тот список, где множитель встречается максимальное число раз, и обведите это место. Например, число 2 встречается один раз в разложении для числа 126 и дважды в списке для 84, поэтому следует обвести 2 x 2 во втором списке множителей.
- Повторите это действие для каждого множителя. Например, 3 встречается чаще в первом разложении, поэтому следует обвести в нем 3 x 3. Число 7 встречается по одному разу в обоих списках, так что обводим 7 (неважно в каком списке, если данный множитель встречается в обоих списках одинаковое число раз).
- Чтобы найти НОК, перемножьте все обведенные числа. В нашем примере наименьшим общим кратным чисел 126 и 84 является 2 x 2 x 3 x 3 x 7 = 252. Это наименьшее число, которое делится на 126 и 84 без остатка.
-

4
Используйте НОК для сложения дробей. При сложении двух дробей необходимо привести их к общему знаменателю. Для этого найдите НОК двух знаменателей. Затем умножьте числитель и знаменатель каждой дроби на такое число, чтобы знаменатели дробей стали равны НОК. После этого можно сложить дроби.
- Например, необходимо найти сумму 1/6 + 4/21.
- С помощью приведенного выше метода можно найти НОК для 6 и 21. Оно равно 42.
- Преобразуем дробь 1/6 так, чтобы ее знаменатель равнялся 42. Для этого необходимо поделить 42 на 6: 42 ÷ 6 = 7. Теперь умножим числитель и знаменатель дроби на 7: 1/6 x 7/7 = 7/42.
- Чтобы привести вторую дробь к знаменателю 42, поделим 42 на 21: 42 ÷ 21 = 2. Умножим числитель и знаменатель дроби на 2: 4/21 x 2/2 = 8/42.
- После того как дроби приведены к одинаковому знаменателю, их можно легко сложить: 7/42 + 8/42 = 15/42.
Реклама
Примеры задач
- Попробуйте решить приведенные ниже задачи самостоятельно. Если вы считаете, что получили правильный ответ, выделите мышкой место после двоеточия в условии задачи. Последние задачи наиболее сложные.
- Найдите разложение на простые множители для числа 16: 2 x 2 x 2 x 2
- Запишите ответ в степенной форме: 24
- Найдите разложение на простые множители для числа 45: 3 x 3 x 5
- Запишите ответ в степенной форме: 32 x 5
- Найдите разложение на простые множители для числа 34: 2 x 17
- Найдите разложение на простые множители для числа 154: 2 x 7 x 11
- Найдите разложение на простые множители для чисел 8 и 40, а затем определите их наибольший общий делитель: разложение на простые множители числа 8 имеет вид 2 x 2 x 2 x 2; разложение на простые множители числа 40 имеет вид 2 x 2 x 2 x 5; НОД двух чисел 2 x 2 x 2 = 6.
- Найдите разложение на простые множители для чисел 18 и 52 и найдите их наименьшее общее кратное: разложение на простые множители числа 18 имеет вид 2 x 3 x 3; разложение на простые множители числа 52 имеет вид 2 x 2 x 13; НОК двух чисел составляет 2 x 2 x 3 x 3 x 13 = 468.
Советы
- Каждое число имеет характерное для него единственное разложение на простые множители. Неважно, каким образом вы находите это разложение, в конце должен получиться один и тот же ответ. Это называется основной теоремой арифметики.[4]
- Вместо того чтобы каждый раз переписывать простые числа в новой строке дерева множителей, можно оставлять их на месте и просто обводить. По окончании разложения в него войдут все обведенные простые множители.
- Всегда проверяйте полученный ответ. Вы можете допустить ошибку и не заметить этого.
- Будьте готовы к заданиям с подвохом. Если вас просят найти разложение на простые множители простого числа, нет необходимости проводить какие-либо вычисления.[5]
Например, для числа 17 разложением на простые множители будет 17; это число не раскладывается на другие простые множители. - Наибольший общий делитель и наименьшее общее кратное можно найти для трех и более чисел.
Реклама
Предупреждения
- Дерево множителей позволяет определить лишь простые, а не все возможные множители.
Реклама
Об этой статье
Эту страницу просматривали 8209 раз.
Была ли эта статья полезной?
В данном уроке мы рассмотрим такие понятия как делители и кратные.
Что такое делитель?
Мы знаем, что делитель это число, показывающее на сколько частей нужно разделить делимое. Например, в выражении 8 : 2 = 4, делителем является число 2. Это число показывает на сколько частей нужно разделить число 8. После разделения получается ответ 4. Как видно из примера, число 8 делится на число 2 без остатка. Говорят, что число 2 является делителем числа 8.
Пример 1. Число 2 является делителем числа 8, поскольку 8 делится на 2 без остатка:
8 : 2 = 4
Пример 2. Число 3 является делителем числа 9, поскольку 9 делится на 3 без остатка:
9 : 3 = 3
Пример 3. Число 4 не является делителем числа 10 поскольку 10 не делится на 4 без остатка:
10 : 4 = 2 (2 в остатке)
Определение. Делителем числа а называется число, на которое число а делится без остатка.
Данное определение содержит переменную a. Подставим вместо этой переменной любое число, например число 12 и прочитаем определение:
Делителем числа 12 называется число, на которое 12 делится без остатка.
Попробуем перечислить эти числа:
1, 2, 3, 4, 6, 12
Все эти числа являются делителями числа 12, поскольку число 12 делится на них без остатка. Покажем это:
12 : 1 = 12
12 : 2 = 6
12 : 3 = 4
12 : 4 = 3
12 : 6 = 2
12 : 12 = 1
Кратные числа
Если какое-нибудь число без остатка разделилось на другое, то его называют кратным этого числа. Например, 6 без остатка делится на 3. Поэтому 6 является кратным числа 3
6 : 3 = 2
Определение. Кратным числа а называется число, которое делится без остатка на а.
Данное определение содержит переменную a. Подставим вместо этой переменной любое число, например число 5 и прочитаем определение:
Кратным числа 5 называется число, которое делится без остатка на 5.
У любого числа бесконечно много кратных. Например, первыми кратными числа 5, являются числа 5, 10, 15, 20, 25. Все они кратны 5, поскольку делятся на 5 без остатка:
5 : 5 = 1
10 : 5 = 2
15 : 5 = 3
20 : 5 = 4
25 : 5 = 5
Признаки делимости чисел
Признаки делимости чисел используются для того, чтобы ускорить процесс деления чисел. Существует множество признаков делимости и других интересных алгоритмов, значительно ускоряющих решение и освобождающих от излишней волокиты. Рассмотрим наиболее популярные из них.
Признак делимости на 10
Любое число, которое оканчивается нулем, делится без остатка на 10. Чтобы получить частное, достаточно отбросить цифру 0 в делимом.
Например, 380 : 10 = 38. Мы просто отбросили последний ноль в числе 380.
В случае, если мы имеем выражение такого вида 385 : 10, то получится 38 и 5 в остатке, поскольку 380 : 10 = 38, а пятерка это остаток, который не разделился.
Таким образом, если число оканчивается цифрой 0, то оно делится без остатка на 10. Если же оно оканчивается другой цифрой, то оно не делится без остатка на 10. Остаток в этом случае равен последней цифре числа. Действительно, в примере 385 : 10 = 38 (5 в остатке), остаток равен последней цифре в числе 385, то есть пятерке.
Признак делимости на 5 и на 2
Любое число, которое оканчивается нулем, делится без остатка и на 5, и на 2.
Примеры:
10 : 5 = 2
100 : 5 = 20
100 : 2 = 50
Признак делимости на 5
Если число оканчивается цифрой 0 или 5, то оно делится без остатка на 5.
Примеры:
355 : 5 = 71
200 : 5 = 40
475 : 5 = 95
Признак делимости на 3
Число делится на 3, если сумма цифр этого числа делится на 3. Например, рассмотрим число 27, сумма его цифр 2 + 7 = 9. Девять, как мы знаем делится на 3, значит и 27 делится на 3:
27 : 3 = 9
Признак делимости на 9
Число делится на 9, если сумма его цифр делится на 9. Например, рассмотрим число 18. Сумма его цифр 1 + 8 = 9. Девять делится на девять, значит и 18 делится на 9
18 : 9 = 2
Рассмотрим число 846. Сумма его цифр 8 + 4 + 6 = 18. Восемнадцать делится на девять, значит и 846 делится на 9:
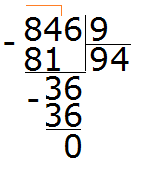
Чётные и нечётные числа
Чётным называется число, которое делится без остатка на 2. Например, число 20 является четным, поскольку оно делится без остатка на 2:
20 : 2 = 10
Нечётным называется число, если при его делении на 2, остаётся остаток 1. Например число 21 является нечетным, поскольку после его деления на 2 остается остаток 1:
21 : 2 = 10 (1 в остатке)
Как распознать чётное число от нечетного, не выполняя деления на 2? Очень просто. Из однозначных чисел чётными являются числа 0, 2, 4, 6, 8, а нечетными являются 1, 3, 5, 7, 9. Если число оканчивается чётной цифрой, то это число является чётным. Если число оканчивается нечетной цифрой, то это число является нечетным.
Например, число 308 чётно, поскольку оно оканчивается чётной цифрой. Число 1024 тоже четно, поскольку оканчивается четной цифрой.
А числа 305 и 1027 являются нечётными, поскольку они оканчиваются нечётными цифрами.
Простые и составные числа
Простым называется число, которое делится без остатка на единицу и на само себя. Другими словами, имеет только два делителя. Например, число 5 делится без остатка на единицу и на само себя:
5 : 1 = 5
5 : 5 = 1
Значит, число 5 является простым числом.
Составным же называется число, которое имеет больше двух делителей. Например, число 4 составное, поскольку у него больше двух делителей: 4, 2 и 1
4 : 4 = 1
4 : 2 = 2
4 : 1 = 4
Значит, число 4 является составным числом.
Разложение составного числа на простые множители
Любое составное число можно разложить на простые множители. Чем-то похожим мы занимались в уроке замены в выражениях. Из этого урока мы узнали, что любое число, входящее в выражение, можно заменить на то же самое, но записанное в другом виде.
Например, число 6 можно записать в виде суммы 4 + 2 или в виде частного 12 : 2 или в виде произведения 2 × 3. Последнюю запись 2 × 3 можно назвать разложением числа 6 на простые множители.
Суть разложения числа на простые множители заключается в том, чтобы представить это число в виде произведения нескольких простых множителей.
Разложим число 4 на простые множители. Для этого соберем данное число из других чисел, при этом соединим их знаком умножения (×). Число 4 состоит из чисел 2 и 2. Эти два числа и являются простыми множителями, из которых состоит число 4
4 = 2 × 2
Разложим на множители число 6. Число 6 можно собрать из чисел 2 и 3. Эти два числа и являются простыми множителями, из которых состоит число 6
6 = 2 × 3
Разложим на множители число 8. Это число можно разложить на множители 2 и 4, при этом множитель 4 можно разложить на два множителя: 2 и 2. Поэтому вместо четвёрки записываем её разложение:
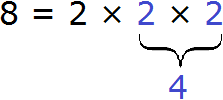
Большие числа раскладываются таким же образом. Сначала их раскладывают на большие множители, затем эти большие множители раскладывают на маленькие. И так до тех пор, пока каждый множитель не станет простым числом.
Например, разложим число 180 на простые множители. Число 180 это два множителя 18 и 10
180 = 18 × 10
Теперь раскладываем множители 18 и 10 на другие множители:
18 = 3 × 6
10 = 5 × 2
Теперь раскладываем выделенную синюю шестерку. Это последний большой множитель, который можно разложить на простые множители:
6 = 2 × 3
Теперь собираем все простые множители вместе:
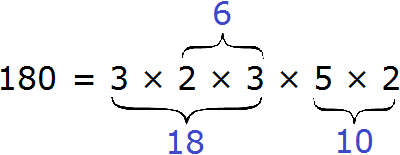
На множители можно разложить только составное число. Простое число на множители не раскладывается. Именно поэтому, когда разложение доходит до простых чисел, мы эти простые числа дальше не раскладываем.
Есть и второй способ разложения на простые множители. Он проще и хорошо подходит для больших чисел. Суть этого способа заключается в том, что сначала проводится вертикальная линия. Затем слева от этой линии записываются делимые, а справа — делители, которые впоследствии собирают во множители.
При разложении числа этим способом, используют признаки делимости, такие как: признаки делимости на 2, на 3, на 5 и другие.
Например, разложим предыдущее число 180 этим способом.
Проводим вертикальную линию и слева записываем первое делимое 180

Теперь применяем признаки делимости. В первую очередь проверяем делится ли 180 на 2. Если делится, то нужно записать эту двойку справа от вертикальной линии.
180 делится на 2, поскольку 180 оканчивается нулём. Записываем двойку справа от вертикальной линии:

Теперь делим 180 на 2 и получаем второе делимое 90. Записываем это делимое слева от вертикальной линии:
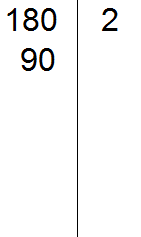
Теперь делим 90. Снова применяем признаки делимости. Проверяем делится ли 90 на 2.
90 делится на 2, поскольку 90 оканчивается нулём. Записываем двойку справа от вертикальной линии:
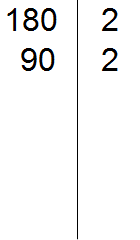
Теперь делим 90 на 2, получаем третье делимое 45. Записываем это делимое слева от вертикальной линии:
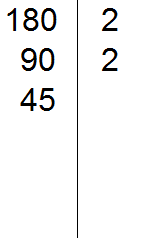
Теперь делим 45. Снова применяем признаки делимости. Проверяем делится ли 45 на 2.
45 на 2 не делится. Тогда проверяем делится ли 45 на 3.
45 делится на 3, поскольку сумма цифр 4 и 5 делится на 3. Записываем тройку справа от вертикальной линии:
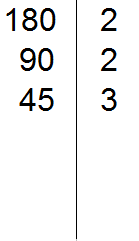
Делим 45 на 3, получаем четвёртое делимое 15. Записываем это делимое слева от вертикальной линии:
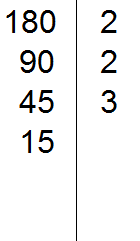
Теперь делим 15. Проверяем делится ли 15 на 2.
15 не делится на 2. Тогда проверяем делится ли 15 на 3.
15 на 3 делится, поскольку сумма цифр 1 и 5 делится на 3. Записываем тройку справа от вертикальной линии:
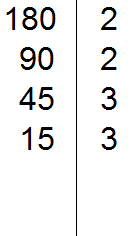
Делим 15 на 3, получаем пятое делимое 5. Записываем пятёрку слева от вертикальной линии:
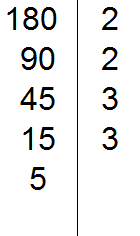
Теперь делим 5. Проверяем делится ли 5 на 2.
5 не делится на 2. Тогда проверяем делится ли 5 на 3.
5 не делится на 3. Тогда проверяем делится ли 5 на 5.
5 делится на 5. Записываем эту пятёрку справа от вертикальной линии:
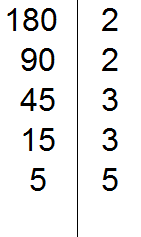
Делим 5 на 5, получаем шестое делимое 1. Записываем эту единицу слева от вертикальной линии:
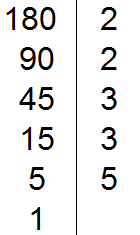
На этом деление завершается, поскольку мы достигли единицы. Делители, которые записывают справа от вертикальной линии должны быть простыми числами. Поэтому, когда делимое 5 не разделилось на 2, а затем не разделилось на 3, мы попробовали разделить его на 5, не пробуя разделить на 4, поскольку 4 является не простым, а составным числом.
Теперь переписываем в один ряд все делители, которые записаны справа от вертикальной линии. Они и будут разложением числа 180 на простые множители. Желательно записывать их, начиная с самых малых. Это позволяет упорядочить их по возрастанию:
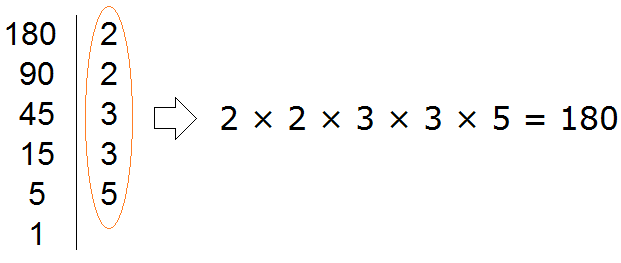
Не расстраивайтесь, если будете испытывать затруднения при разложении чисел на простые множители. Эта тема требует немного практики. Для тренировки можете разложить на простые множители следующие числа: 256, 378, 512.
Нахождение делителей числа
В начале данного урока было сказано, что делителем называется число, на которое другое число делится без остатка.
Например, число 2 является делителем числа 6, поскольку число 6 можно без остатка разделить на 2
6 : 2 = 3
Ещё делителем числа 6 является число 3
6 : 3 = 2
Ещё делителем числа 6 является число 1
6 : 1 = 6
Наконец, делителем числа 6 является само это число
6 : 6 = 1
Перечислим все делители числа 6
1, 2, 3, 6
Иногда возникает необходимость найти все делители какого-нибудь числа. Чтобы понять, как это делается, рассмотрим несколько примеров.
Пример 1. Найти делители числа 12
Во-первых, единица является делителем любого числа. Пусть и у нас первым делителем числа 12 будет 1

Теперь раскладываем число 12 на простые множители:

Получили разложение 2 × 2 × 3.
В процессе разложения числа 12 на простые множители, мы делили его на числа 2 и 3. На них число 12 разделилось без остатка, значит они тоже являются делителями числа 12. Внесём эти два числа в нашу таблицу делителей:
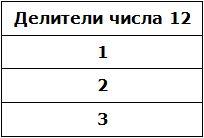
Чтобы получить остальные делители числа 12, нужно найти все возможные произведения его простых множителей между собой. Получаемые в результате ответы и будут остальными делителями числа 12.
Число 12 мы разложили на простые множители 2 × 2 × 3. Найдём все возможные произведения этих простых множителей между собой. Первое произведение это 2 × 2. Это произведение равно 4
2 × 2 = 4
Занесём число 4 в нашу таблицу делителей

Следующее возможное произведение из простых множителей числа 12 это произведение 2 × 3. Данное произведение равно 6. Занесём число 6 в нашу таблицу делителей:

Последнее возможное произведение из простых множителей числа 12 это произведение из всех его множителей, а именно 2 × 2 × 3. Это произведение равно 12. Занесём число 12 в нашу таблицу делителей:

Таким образом, делителями числа 12 являются числа 1, 2, 3, 4, 6, 12.
На основании приведённого примера можно сформировать правило для нахождения делителей числа:
Чтобы найти делители числа, нужно:
- записать в качестве первого делителя единицу;
- разложить исходное число на простые множители и выписать из полученных простых множителей те множители, которые являются делителями исходного числа (если множитель повторяется, то выписать его нужно только один раз);
- найти все возможные произведения полученных простых множителей между собой. Получаемые в результате ответы будут остальными делителями исходного числа.
Пример 2. Найти делители числа 6
Первым делителем числа 6 запишем единицу:
1
Теперь разложим число 6 на простые множители:
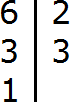
Выпишем из полученного разложения те множители, которые являются делителями числа 6. Видим, что это множители 2 и 3. Они будут следующими делителями числа 6. Допишем их к нашим делителям:
1, 2, 3
Теперь найдём все возможные произведения простых множителей числа 6. В данном случае имеется только одно произведение, а именно 2 × 3. Это произведение равно 6. Допишем число 6 к нашим делителям:
1, 2, 3, 6
Таким образом, делителями числа 6 являются числа 1, 2, 3, 6.
Задания для самостоятельного решения
Задание 1. Разложите число 256 на простые множители
Решение:
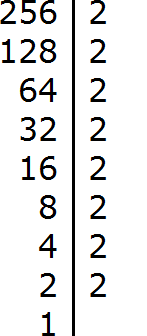
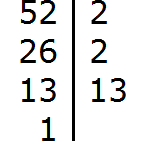
Задание 2. Разложите число 52 на простые множители
Решение:
Задание 3. Разложите число 98 на простые множители
Решение:
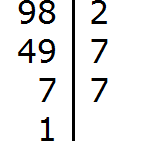
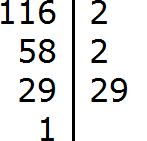
Задание 4. Разложите число 116 на простые множители
Решение:
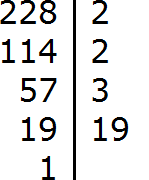
Задание 5. Разложите число 228 на простые множители
Решение:
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже


Здравствуйте, дорогие читатели! Как посчитать, сколько делителей у какого-нибудь числа? Если это число маленькое, то никаких сложностей не возникает. Например, для числа 10, мы легко можем найти все делители и посчитать их количество простым перебором. А вот как узнать, на какое количество различных чисел делится, например, число 720? Можно, конечно, опять же перебрать все делители, но это будет довольно трудоемко. При чем, 720 – еще и довольно маленькое число.
Сегодня, я Вам расскажу, как находить количество делителей любого натурального числа, зная всего лишь одну простую формулу.
На самом деле, наша сегодняшняя формула будет даже проще, чем те, которые изображены на картинке выше)
Вы находитесь на канале Trifler, где я разбираю интересные математические задачи, а также рассуждаю на некоторые околоматематические темы. Если Вы искренне увлечены математикой, но еще не подписаны на этот канал, то самое время это исправить! Подписаться
Чудо-формула
Ну что ж, пора переходить от разговоров к делу.
Мы знаем, что любое натуральное число можно представить в виде произведения простых чисел, которые являются его делителями. Так как один и тот же простой делитель может встречаться несколько раз, то любое натуральное числа можно записать так:
Если не совсем понятно, о чем идет речь, то потом посмотрите пример ниже. На самом деле, все очень просто.
Так вот, после того, как мы найдем такое представление числа n, количество его делителей можно будет посчитать по формуле:
Посмотрим, как все это считается на примере
Пример
Раскладываем это число на простые множители, чтобы получить нужное представление:
Теперь, запишем число 720 в каноническом виде:
Ну и все, остается только применить чудо-формулу:
Вот и все, получили, что у числа 720 имеется 30 различных натуральных делителей. Стоит сделать замечание:
По этой формуле мы считаем количество делителей вместе с единицей и самим числом.
Если Вам понравилась статья, то обязательно ставьте лайки и комментируйте ее. Это поспособствует тому, чтобы ее увидело много людей!
Читайте также ТОП-3 статьи, выпущенные в этом месяце на моем канале:
- Quincy: робот, который обучит Ваших детей математике, английскому и рисованию
- Почему вторая степень это квадрат, а третья – куб
- Необычное тригонометрическое уравнение
Содержание:
Делимость натуральных чисел
Делители и кратные натурального числа. простые числа
Посмотрите на рисунок 1. Вы видите, что 6 яблок разделили на 2 кучки по 3 яблока в каждой. Тут число 6 является делимым, число 2 — делителем, а число 3 — частным. Однако 6 яблок можно разделить и иначе — разложить их на 3 кучки по 2 яблока в каждой. Тогда для делимого 6 число 3 является делителем, а число 2 — частным. Это значит, что числа 2 и 3 являются делителями числа 6. В то же время число 6 является кратным для каждого из своих делителей — и для числа 2, и для числа 3. Делители и кратные являются натуральными числами.

Определение:
Делителем числа называется такое число, на которое делится данное число.
Kpaтным числа называется такое число, которое делится на данное число.
Пример:
Есть ли другие делители у числа 6? Да. Число 6 делится ещё на 1 и само на себя. Значит, всего у числа 6 есть четыре делителя: 1; 2;3;6.
Обратите внимание:
каждое натуральное число, начиная с числа 2. имеет по меньшей мере два делителя — число 1 и само это число. Другие делители находят по специальным правилам.
Пример:
Найдите все делители числа: 1) 7; 2) 12; 3)25.
Решение:
1) У числа 7 есть по меньшей мере два делителя — 1 и 7. Ни на одно другое натуральное число 7 не делится, поэтому у него всего два делителя: 1 и 7.
2) Число 12 имеет по меньшей мере два делителя — 1 и 2. Далее последовательно проверяем делимость числа 12 на натуральные числа от 2 до 11.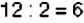
3) У числа 25 есть как минимум два делителя: 1 и 25 На 2, 3 и 4, а также на числа от 6 до 24 это число не делится. 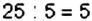 , поэтому число 5 является делителем числа 25, причём дважды. Однако равные делители учитываются только один раз. Значит, у числа 25 не четыре, а три делителя: 1; 5; 25.
, поэтому число 5 является делителем числа 25, причём дважды. Однако равные делители учитываются только один раз. Значит, у числа 25 не четыре, а три делителя: 1; 5; 25.
Запомните: Натуральное число, у которого есть только два делителя (1 и само число), называется простым. Натуральное число, у которого больше двух делителей, называется составным.
Например, 7 — простое число, а 12 и 25 — составные.
Пример:
Является ли 1 простым числом? А составным? Нет, поскольку у числа 1 только один делитель. Значит, число 1 особенное. Оно и не простое, и не составное.
Обратите внимание:
наименьшим простым числом является число 2.
Чтобы выписать некоторое количество простых чисел, можно воспользоваться способом, придуманным ещё в III в до н.э. Эратосфеном Киренским (27бг. до н. э. — 194 г. до н. э ). греческим математиком, астрономом, географом и поэтом. В честь учёного этот способ называется «решето Эратосфена». На рисунке (с. 4) вы видите, как находили простые числа от 2 до 50. Попробуйте самостоятельно объяснить, как это делали.
Признаки делимости на 2, 10, 5
Запишем натуральный ряд чисел:
1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12…
Умножим каждое число на 2. Получили ряд чисел, кратных числу 2:
2; 4; 6; 8; 10; 12; 14; 16; 18; 20; 22; 24…
Такие числа называют чётными. Их можно задать формулой:
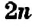 , где
, где 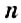 — некоторое натуральное число. Цифры О, 2, 4, 6, 8 считают чётными цифрами.
— некоторое натуральное число. Цифры О, 2, 4, 6, 8 считают чётными цифрами.
В натуральном ряде чётные числа чередуются с нечётными числами — они не делятся на 2. Например, числа 3, 5, 11 — нечётные. Их также можно задать формулой:
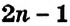 , где
, где 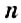 — некоторое натуральное число. Цифры 1, 3, 5, 7, 9 считают нечётными цифрами.
— некоторое натуральное число. Цифры 1, 3, 5, 7, 9 считают нечётными цифрами.
Пример:
Как выяснить, является ли чётным данное число? Для этого пользуются признаком делимости на 2.
Признак делимости на 2
На 2 делятся те и только те числа, запись которых заканчивается чётной цифрой.
Например, запись числа 538 заканчивается цифрой 8, которая является чётной, поэтому число 538 делится на 2. Действительно, 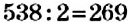 . А вот запись числа 537 закапывается нечётной цифрой 7, поэтому данное число не делится на 2.
. А вот запись числа 537 закапывается нечётной цифрой 7, поэтому данное число не делится на 2.
Опираясь на натуральный ряд чисел, запишем ряд чисел, кратных числу 10:
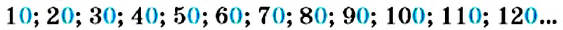
Как видим, запись каждого числа этого ряда заканчивается цифрой 0. Именно в этом и состоит признак делимости на 10.
Признак делимости на 10
На 10 делятся те и только те числа, запись которых заканчивается цифрой 0.
Например, число 1000 делится на 10, а число 1001 не делится.
Пример:
Можно ли считать признак делимости на 10 признаком делимости на 5? Нет, так как существуют числа, которые делятся на 5, но не делятся на 10. Например, число 2055.
Опираясь на натуральный ряд чисел, запишем ряд чисел, кратных числу 5:
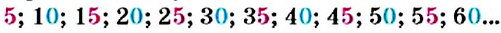
Как видим, запись каждого числа этого ряда заканчивается либо цифрой 5, либо цифрой 0. Именно в этом и состоит признак делимости на 5.
Признак делимости на 5
На 5 делятся те и только те числа, запись которых заканчивается либо цифрой 5, либо цифрой 0.
Например, число 85 делится на 5, а число 86 – не делится.
Пример:
Найдите все нечётные числа от 10 до 40, которые делятся на 5.
Решение:
Способ 1. Сначала выберем все нечётные числа от 10 до 40:
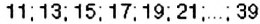 .
.
Применив к этим числам признак делимости на 5, получим искомые числа: 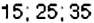 .
.
Способ 2. Искомые числа — нечётные и делятся на 5. Поэтому : среди них не должно быть чисел, запись которых заканчивается цифрой 0. поскольку такие числа — чётные. Итак, среди чисел от : 10 до 40 достаточно выбрать числа, запись которых заканчивается только цифрой 5. Отсюда искомым и будут числа: 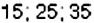 .
.
Обратите внимание:
среди чисел, делящихся на 5. чётные числа делятся и на 10. а нечётные — нет.
Признак делимости на 4. Число делится на 4 тогда и только тогда, когда на 4 делится число, образованное двумя последними цифрами данного числа. Например, число 3436 делится на 4, поскольку число 36 делится на 4.
Признак делимости на 8. Число делится на 8 тогда и только тогда, когда на 8 делится число, образованное тремя последними цифрами данного числа. Например, число 29176 делится на 8, поскольку число 176 делится на 8.
Признак делимости на 25. Число делится на 25 тогда и только тогда, когда на 25 делится число, образованное двумя последними цифрами данного числа Например, число 6575 делится на 25, поскольку число 75 делится на 25.
Признак делимости на 125. Число делится на 125 тогда и только тогда, когда на 125 делится число, образованное тремя последними цифрами данного числа. Например, число 36 375 делится на 125, поскольку число 375 делится на 125.
Признаки делимости на 9, 3
Запишем ряд чисел, кратных числу 9:
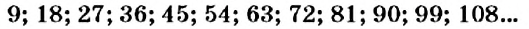 .
.
Как видим, признак делимости на 9 не связан с последней цифрой в записи числа. Он связан с сумой цифр в этой записи. Позже вы сможете это обосновать.
Признак делимости на 9
На 9 делятся те и только те числа, сумма цифр которых делится на 9.
Например, число 1476 делится на 9, поскольку 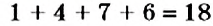 , а число 18 делится на 9. Число 1239 не делится на 9, поскольку
, а число 18 делится на 9. Число 1239 не делится на 9, поскольку 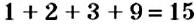 , а число 15 не делится на 9.
, а число 15 не делится на 9.
Пример:
Как выяснить, делится ли число на 3? Для этого пользуются признаком делимости на 3.
Признак делимости на 3
На 3 делятся те и только те числа, сумма цифр которых делится на 3.
Например, в числе 237 сумма цифр равна: 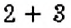
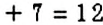 . Число 12 делится на 3, поэтому и число 237 делится на 3. Действительно,
. Число 12 делится на 3, поэтому и число 237 делится на 3. Действительно, 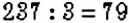 .
.
Пример:
Можно ли считать, что числа, которые делятся на 9, делятся и на 3? Да. Поскольку сумма цифр чисел, кратных числу 9, делится на 9, то она делится и на 3. Однако обратное утверждение не будет верным: числа, которые делятся на 3, не всегда делятся на 9. Например, числа 12, 33, 213 делятся на 3, но не делятся на 9.
Пример:
Найдите все трёхзначные числа, которые содержат цифры 5 и 1 и делятся на 9.
Решение:
Обозначим неизвестную цифру звездочкой. Сумма цифр искомого числа равна: 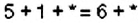 . Эта сумма должна делиться на 9, поэтому вместо звёздочки можно подставить только цифру 3. А далее из цифр 1, 3, 5 составляем все возможные трёхзначные числа: 135; 153; 315; 351; 513; 531.
. Эта сумма должна делиться на 9, поэтому вместо звёздочки можно подставить только цифру 3. А далее из цифр 1, 3, 5 составляем все возможные трёхзначные числа: 135; 153; 315; 351; 513; 531.
У вас мог возникнуть вопрос: «Как объяснить, почему сумма цифр в записи числа может показывать, делится ли число на 9?» Разберёмся на примерах.
Числа 99 и 999 делятся на 9, а числа 100 и 1000 на 9 не делятся. Представим эти числа в виде сумм:

Проанализируем полученные суммы. В столбике слева каждое слагаемое суммы делится на 9, а в столбике справа — нет. Вообще, если каждое слагаемое делится на данное число, то их сумма делится на данное число; если одно из слагаемых не делится на данное число, а сумма всех остальных слагаемых делится на данное число, то сумма не делится на данное число. Запишем число 351 в виде суммы разрядных слагаемых и преобразуем её:

В полученной сумме каждое слагаемое делится на 9, поэтому число 351 делится на 9. Как видим, результат зависит от последнего слагаемого, которое получили как сумму: 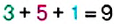 . Эта сумма — не что иное, как сумма цифр данного числа.
. Эта сумма — не что иное, как сумма цифр данного числа.
Разложение чисел на множители. Наибольший общий делитель
Вы знаете, что каждое натуральное число, большее 1, имеет несколько делителей, поэтому его можно представить в виде произведения своих делителей. Например: 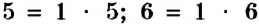 , или
, или 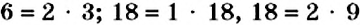 , или
, или 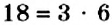 . О таких равенствах говорят, что данное число разложили на множители, а само равенство называют разложением числа на множители.
. О таких равенствах говорят, что данное число разложили на множители, а само равенство называют разложением числа на множители.
Число 5 — простое. Его можно разложить на множители только одним способом. Числа 6 и 18 — составные. Для них существует два и более разложений на множители. Однако эти разложения отличаются. В разложении 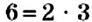 оба множителя являются простыми числами, а в разложении
оба множителя являются простыми числами, а в разложении 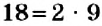 первый множитель — простое число, а второй — составное, и его тоже можно разложить на множители:
первый множитель — простое число, а второй — составное, и его тоже можно разложить на множители: 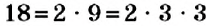 . А уже в этом разложении все множители являются простыми числами.
. А уже в этом разложении все множители являются простыми числами.
Определение:
Разложение числа на множители, в котором все множители — простые числа, называется разложением числа на простые множители.
Пример:
Является ли разложением на простые множители равенство 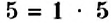 ? Нет. В этом разложении один из множителей не является простым. Это число 1. Однако будем считать, что для любого простого числа также можно записать разложение на простые множители. Для этого достаточно записать в разложении само это число. Например, для данного простого числа 5 получим такое разложение:
? Нет. В этом разложении один из множителей не является простым. Это число 1. Однако будем считать, что для любого простого числа также можно записать разложение на простые множители. Для этого достаточно записать в разложении само это число. Например, для данного простого числа 5 получим такое разложение: 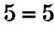 .
.
Пример:
Разложите на простые множители число 210.
Решение:
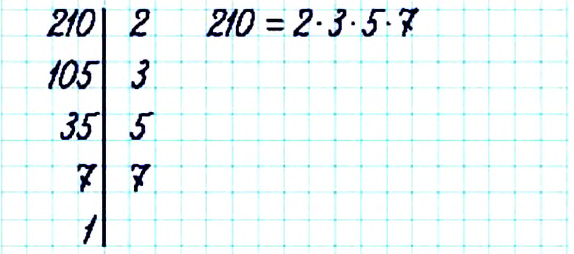
С помощью разложения числа на простые множители ищут общие делители двух чисел. Например, у чисел 12 и 30 есть два простых общих делителя — числа 2 и 3. Но числа 12 и 30 делятся и на число 6, то есть на произведение своих общих делителей. Число 6 — наибольшее число, на которое одновременно делится и число 12, и число 30. Такое число называют наибольшим общим делителем двух чисел 12 и 30.
 Записывают: НОД
Записывают: НОД 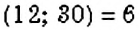 и говорят: «Наибольшим общим делителем чисел 12 и 30 является число 6».
и говорят: «Наибольшим общим делителем чисел 12 и 30 является число 6».
Пример:
Найдите НОД чисел 18 и 45.
Решение:
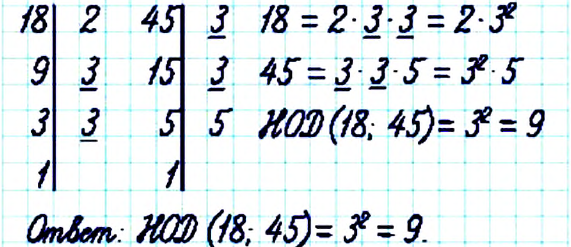
Определение:
Наибольшим общим делителем двух чисел называется наибольшее число, на которое делится каждое из данных чисел.
Правило нахождения НОД
Чтобы найти НОД двух чисел:
1) разложите данные числа на простые множители;
2) найдите произведение общих делителей данных чисел.
Пример:
Можно ли найти НОД двух чисел, не имеющих общих делителей, кроме числа 1? Да. Но НОД таких чисел равен 1.
Два числа, НОД которых равен 1, называют взаимно простыми. Например, 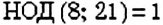 . Значит, числа 8 и 21 — взаимно простые. Два разных простых числа также являются взаимно простыми. Например,
. Значит, числа 8 и 21 — взаимно простые. Два разных простых числа также являются взаимно простыми. Например, 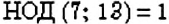 , поэтому простые числа 7 и 13 являются взаимно простыми.
, поэтому простые числа 7 и 13 являются взаимно простыми.
Пример:
Можно ли найти НОД нескольких чисел? Да. Для этого выполняют те же действия, что и в задаче 3, но для нескольких чисел. Например, найдём 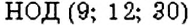 . Имеем:
. Имеем: 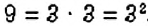 ,
, 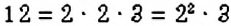 ,
, 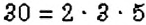 . Следовательно,
. Следовательно, 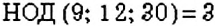 .
.
Интересный способ нахождения НОД двух чисел описал Евклид (около 365 – 300 лет до н. э.) в своей книге «Начала». В честь учёного этот способ называется «алгоритмом Евклида». Пусть нужно найти НОД двух чисел 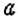 и
и 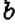 , где
, где 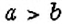 . Из данных чисел образуем пары:
. Из данных чисел образуем пары: 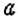 и
и 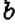 и
и 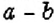 и
и 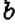 . Заметим, что НОД для каждой пары один и тот же:
. Заметим, что НОД для каждой пары один и тот же: 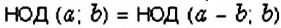 . Число
. Число 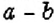 обозначим как
обозначим как 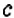 . Из чисел
. Из чисел 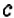 и
и 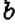 снова берём большее, пусть это будет число
снова берём большее, пусть это будет число 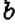 . Вычтем из большего числа меньшее:
. Вычтем из большего числа меньшее: 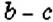 . Тогда имеем:
. Тогда имеем: 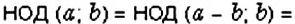
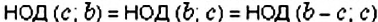 . Повторяем эту цепочку рассуждений, пока не получим пару одинаковых чисел
. Повторяем эту цепочку рассуждений, пока не получим пару одинаковых чисел 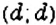 . Число
. Число 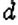 и есть НОД чисел
и есть НОД чисел 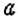 и
и 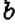 .
.
Например, 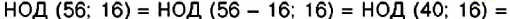
Наименьшее общее кратное
Найдём кратные числа 4. Для этого достаточно умножить число 4 на числа натурального ряда:
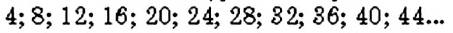
Аналогично найдём кратные числа 6:
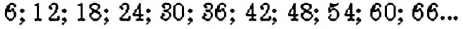
Среди кратных числа 4 и числа 6 есть такие числа, которые делятся на оба данных числа:
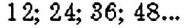
Эти числа являются общими кратными чисел 4 и 6. Наименьшим среди них является число 12. Это — наименьшее общее кратное двух чисел 4 и 6.
Записывают: 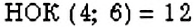 и говорят: «Наименьшим общим кратным чисел 4 и 6 является число 12».
и говорят: «Наименьшим общим кратным чисел 4 и 6 является число 12».
Определение:
Наименьшим общим кратным двух чисел называется наименьшее число, которое делится на каждое из данных чисел.
Общие кратные нескольких чисел можно находить при помощи разложений данных чисел на простые множители.
Пример:
Найдите НОК чисел 18 и 45.
Решение:
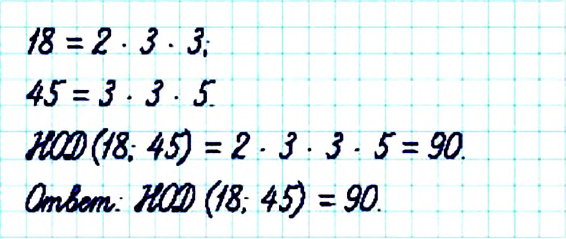
Правило находжения НОК
Чтобы найти НОК двух чисел:
- разложите данные числа на простые множители;
- запишите разложение одного из данных чисел;
- допишите к этому разложению такие множители из разложения другого числа, которые ещё не вошли в произведение;
- вычислите полученное произведение.
Пример:
Как найти НОК двух взаимно простых чисел? Нескольких чисел?
Поскольку у взаимно простых чисел нет других общих делителей, кроме 1, то НОК взаимно простых чисел равно их произведению. Например, 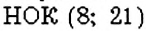
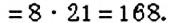
НОК нескольких чисел находят так же, как и двух чисел. Например, найдём 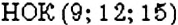 . Имеем:
. Имеем: 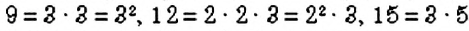 .
. 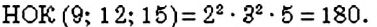
Оказывается, между НОК и НОД чисел 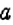 и
и 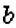 существует связь:
существует связь:
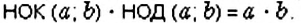
Например, для чисел 54 и 48 получим:
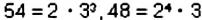 .
.
Отсюда 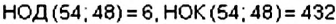 . А теперь воспользуемся формулой. Имеем:
. А теперь воспользуемся формулой. Имеем:
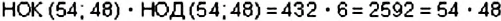 .
.
——–
Делимость натуральных чисел
В этом разделе рассматриваются важнейшие сведения из теории чисел. Это очень древняя и интересная математическая наука, которая исследует свойства натуральных чисел, связанные с их делением. Кратко основное содержание раздела выглядит так.
- Деление и делители числа.
- Признаки делимости на 10, 5 и 2.
- Признаки делимости на 3 и 9.
- Разложение чисел на простые множители.
- Наибольший общий делитель.
- Наименьшее общее кратное.
Эти темы часто используются в последующих разделах математики. В частности, без их знания невозможно успешно изучать обыкновенные дроби. Поэтому раздел 1 учебника можно считать введением к разделу 2.
Деление и делители числа
Складывать и умножать можно любые числа. Вычитание возможно лишь тогда, когда вычитаемое не больше уменьшаемого. Сложнее с делением. Деление – это действие, обратное умножению.
20 : 4 = 5, потому что 5*4 = 20.
Разделить одно число на другое — значит найти такое третье число, которое при умножении на второе дает первое число. То есть, если 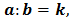 то
то 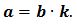
Вы уже знаете, что иногда при делении одного числа на другое получают неполное частное и остаток. Вы также знаете, что делить можно и дробные числа. В этом разделе мы будем рассматривать деление только натуральных чисел, причем без остатка.
Например, число 21 делится на 7. Говорят, что число 7 является делителем числа 21. Делителями числа 21 являются также числа 1, 3 и 21. Никакое другое число не является делителем числа 21.
Если 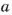 делится на
делится на 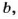 то число
то число 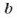 называют делителем числа
называют делителем числа 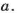
Например, число 22 имеет четыре делителя: 1,2,11 и 22;
- число 9 имеет три делителя: 1, 3 и 9;
- число 7 имеет два делителя: 1 и 7.
Число, которое имеет только два делителя, называется простым числом. Можно сказать и так. Число, которое делится только на 1 и само на себя, называется простым.
Простыми являются числа 2, 3, 5, 7, 11, 13, 17, 19, … . Простых чисел существует бесконечно много. Таблица простых чисел, меньших 1000, представлена на форзаце учебника.
Число, имеющее больше двух делителей, называется составным.
Простое 7 = 1-7.
Составное 14=1-2-7.
1 — не простое и не составное.
Составными, например, являются числа 4, (5, 8, 9, 10, 12, 14. Составных чисел также бесконечно много.
Число 1 имеет только один делитель: 1. Его не принято называть ни простым, ни составным числом.
В зависимости от количества делителей все натуральные числа делятся на три класса: простые числа, составные числа, число 1.
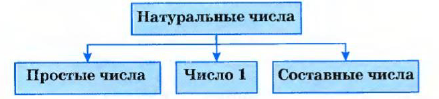
Если простые числа записать в порядке их возрастания, то образуется последовательность простых чисел:
2,3, 5, 7, 11, 13, 17…..
Последовательность простых чисел имеет много интересных свойств и тайн. Например, еще ученые Древней Греции заметили, что среди простых чисел много таких, разность которых равна 2, например: 3 и 5, 5 и 7, 11 и 13, 17 и 10 и т. д. Такие пары чисел называются простыми числами близнецами.
Уже более 25 веков математики пытаются выяснить, существуют ли наибольшие числа-близнецы, но и до сих пор ответа на этот вопрос мы не знаем.
Существует также много других проблем (еще не решенных задач), связанных с простыми числами.
Выполнение заданий:
Пример №1
Проверьте, является ли число 7 делителем числа 63. А числа 67?
Решение:
63 : 7 = 9, поэтому число 7 – делитель 63.
67:7 = 9 (остаток 4), поэтому 7 – не делитель числа 67.
Пример №2
Найдите наибольший делитель и наибольший простой делитель числа 20.
Решение:
Делителями числа 20 являются 1, 2, 4, 5, 10, 20. Наибольший из них – 20, наибольший простой делитель – 5.
Признаки делимости на 10, 5 и 2
Как узнать, делится ли то или иное число на 10? Очень легко. Нужно лишь посмотреть на его последнюю цифру. Если она 0, то данное число делится на 10. Если же последняя цифра не 0, то это число на 10 не делится. Два последние предложения можно заменить одним, которое называется признаком делимости чисел на 10.
На 10 делятся все те и только те числа, которые оканчиваются цифрой 0.
Используя этот признак, можно сразу (не выполняя деления) сказать, что числа 130, 3700, 4080 делятся на 10, а числа 83, 305, 1001 на 10 не делятся.
Признак делимости на 5 можно сформулировать так.
На 5 делятся все те и только те числа, которые оканчиваются цифрой 5 или 0.
Например, каждое из чисел 95, 375, 70, 4900 делится на 5, а каждою из чисел 37, 559, 5008 на 5 не делится. Убедитесь в этом, разделив каждое из этих чисел на 5.
На 2 делится каждое натуральное число, которое оканчивается цифрой 0, 2, 4, 6 или 8. Эти цифры называют четными. Поэтому признак делимости на 2 можно сформулировать так.
На 2 делятся все те и только те числа, которые оканчиваются четной цифрой.
Примеры чисел, которые делятся на 2:
0, 2, 4, 6, 8, 10, 12, 14, 16, 376, 11 108.
Числа, которые делятся на 2, называются четными.
Цифры 1, 3, 5, 7, 9 называются нечетными. Каждое натуральное число, которое оканчивается нечетной цифрой, – нечетное. Нечетное число не делится на 2. В зависимости отделимости на 2 все натуральные числа можно разбить на два класса: четные и нечетные числа.
11а координатном луче за каждым четным числом следует нечетное, а за каждым нечетным – четное (рис. 2).

Выполнение заданий:
Пример №3
Найдите наибольшее четное трехзначное число.
Решение:
Наибольшее трехзначное число 999 – нечетное. Ему предшествует четное число 998. Следовательно, наибольшее четное трехзначное число 998.
Пример №4
Сколько существует нечетных чисел, которые больше 90 и меньше 100?
Решение:
Такими являются числа 91,93, 95, 97 и 99. Их всего 5.
Пример №5
Докажите, что сумма двух нечетных чисел – число четное.
Решение:
Если числа 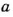 и
и 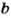 нечетные, то
нечетные, то 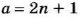 и
и 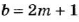 , где
, где 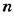 и
и 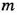 – некоторые натуральные числа.
– некоторые натуральные числа.
Тогда 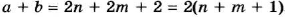 , а это число четное.
, а это число четное.
Признаки делимости на 3 и 9
Чтобы узнать, делится число на 3 или нет, находят его сумму цифр. Например, сумма цифр числа 21 204 равна 9, поскольку 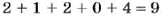 . Оказывается, что если сумма цифр числа делится на 3, то и само число делится на 3. Если же сумма цифр числа на 3 не делится, то и число на 3 не делится. Это признак делимости на 3.
. Оказывается, что если сумма цифр числа делится на 3, то и само число делится на 3. Если же сумма цифр числа на 3 не делится, то и число на 3 не делится. Это признак делимости на 3.
На 3 делятся все те и только те числа, сумма цифр которых делится на 3.
Примеры: Сумма цифр числа 31 104 равна 9, а 9 делится на 3, поэтому и число 31 104 делится на 3. Сумма цифр числа 5051 равна 11, она не делится на 3. Поэтому и число 5051 па 3 не делится. Проверьте!
Аналогично формулируется и признак делимости на 9.
На 9 делятся все те и только те числа, сумма цифр которых делится на 9.
Примеры: Число 5742 делится на 9, поскольку сумма его цифр 5 + 7 + 4 + 2 = 18, а 18 делится на 9. А число 5051 на 9 не делится, так как его сумма цифр 5 + 0 + 5+1 = 11, а 11 на 9 не делится.
Каждое число, которое делится на 9, называется кратным числа 9. Каждое число, которое делится на 3, называется кратным числа 3.
Вообще, если одно число делится на другое, то первое называется кратным другого.
3, 6, 9, 12, 15, 18, … – последовательность натуральных чисел, кратных 3. Таких чисел бесконечно много. Наименьшее из них число 3, наибольшего не существует.
Говорят: «кратное трех», но «кратно трем».
Если число 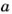 делится на
делится на 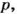 то
то 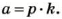 Тогда и
Тогда и 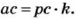 Здесь все буквы обозначают натуральные числа. Итак, если один из множителей делится на какое-то число, то и произведение этих множителей делится на это же число.
Здесь все буквы обозначают натуральные числа. Итак, если один из множителей делится на какое-то число, то и произведение этих множителей делится на это же число.
Если каждое из чисел 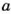 и
и 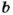 делится на
делится на 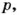 то
то 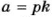 и
и 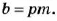 Поэтому
Поэтому 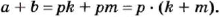 Число
Число 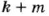 натуральное, тогда число
натуральное, тогда число 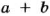 также делится на
также делится на 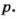 Следовательно, если каждое из двух слагаемых делится на какое-то число, то и их сумма делится па это число.
Следовательно, если каждое из двух слагаемых делится на какое-то число, то и их сумма делится па это число.
О признаках делимости на 4,6, 7,11,13 читайте на с. 37.
- Заказать решение задач по высшей математике
Выполнение заданий:
Пример №6
Какое утверждение верно:
а) если число делится на 9, то оно делится и на 3.
б) если число делится на 3, то оно делится и на 9?
Решение:
Если число делится на 9, то сумма его цифр делится на 9. Эта сумма делится и на 3. Поэтому первое утверждение верно.
Второе утверждение неверно. Например, 30 делится на 3, но не делится на 9.
Пример №7
Запишите наибольшее четырехзначное число, которое кратно 3, но не кратно 9.
Решение:
Наибольшее четырехзначное число 9999. Оно делится и на 9, и на 3. Если это число уменьшить на 3, то получим число 9996. Оно кратно 3, но не кратно 9.
Разложение чисел на простые множители
Какие простые числа нужно умножить, чтобы получить 15? Нетрудно догадаться, что такими числами являются 3 и 5. Следовательно, 15 = 3 • 5. Такое представление числа 15 называется его разложением на простые множители.
Другие примеры:
30 = 2 • 3 • 5; 45 = 3 • 3 • 5; 88 = 2 • 2 • 2 • 11.
Каждое составное число можно разложить на два или больше простых множителей.
Как это делать покажем на примере. Пусть нужно разложить па простые множители число 104. Пишем это число, и справа от него проводим вертикальную черту. По признаку делимости определяем, что число 104 делится на 2 – наименьшее простое число. За чертой пишем число 2, а 52 – частное отделения 104 на 2 – записываем под числом 104. То же самое делаем с частным 52 и новым частным 26. Разделив 26 на его наименьший делитель 2, получим простое число 13. Его пишем тоже справа от черты. 13 делится на 13. Частное равно 1. На этом процесс определения простых множителей числа 104 завершен. Все они записаны справа от черты. Итак, 104 = 2 • 2 • 2 • 13. Это и есть разложение числа 104 на простые множители.

В отдельных случаях разложение числа на простые множители можно упростить. Например, число 9000 на простые множители можно разложить так:
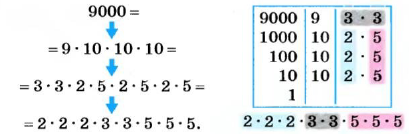
Число 9000 раскладывается на восемь простых множителей. Каждый из них является делителем числа 9000. Вообще, каждый из множителей, на какие раскладывается число а, является делителем этого числа.
Разных простых делителей число 9000 имеет три: 2, 3 и 5. А разных натуральных делителей это число имеет очень много: 1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 4500, 9000.
Как вы уже знаете, произведение 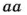 называют квадратом числа
называют квадратом числа 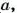 а произведение
а произведение 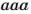 – кубом числа
– кубом числа 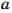 и обозначают
и обозначают 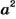 и
и 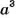 соответственно.
соответственно.
Аналогично, 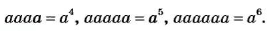
Такие произведения равных чисел называют соответственно четвертой, пятой, шестой степенью числа 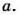
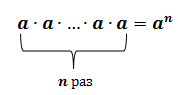 Произведение
Произведение 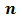 чисел, каждое из которых равно
чисел, каждое из которых равно 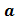 , называют
, называют 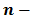 степенью числа
степенью числа 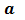 и обозначают символом
и обозначают символом 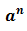 . Здесь
. Здесь 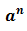 – степень,
– степень, 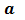 – основание степени,
– основание степени, 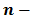 показатель степени.
показатель степени.
Используя понятие степени, разложение числа на простые множители можно записать короче:
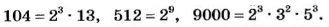
Разложить на простые множители числа, которые делятся на 2, 3, 5, 9, 10, сравнительно несложно. В иных случаях это бывает сделать сложно. Попытайтесь, например, разложить на простые множители число 323. Специалисты, которым часто приходиться заниматься разложением чисел на множители, пользуются специальными таблицами. Часть такой таблицы (для небольших чисел, которые не делятся на 2, 3, 5) представлена на форзаце учебника. Пользуясь этой таблицей, можно сразу записать: 323 = 17 • 19.
Выполнение заданий:
Пример №8
Можно ли разложить на простые множители число 1?
Решение:
Нет, нельзя. Каждое простое число больше 1. А произведение чисел, каждое из которых больше 1, не может равняться 1.
Пример №9
Можно ли равенство 17=1 • 17 считать разложением числа на простые множители?
Решение:
Нельзя. Хотя в произведении 1 • 17 каждое число множитель, но первое из них – число не простое.
Пример №10
Разложите на простые множители число 600.
Решение:
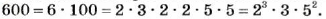
Пример №11
Разложите на простые множители число 266.
Решение:
Число 266 делится на 2, поэтому 266 = 2 • 133. Число 133 не делится ни на какое из чисел 2, 3, 5. Его нет и в таблице простых чисел. Ищем его в таблице разложения чисел на простые множители: 133 = 7 • 19. Следовательно, 266 = 2 • 7 • 19.
Пример №12
Какое наименьшее трехзначное число можно разложить на два одинаковых простых множителя?
Решение:
7 • 7 = 49 – число не трехзначное, 11 • 11 = 121 – трехзначное. Значит искомое число равно 121.
Наибольший общий делитель
Часто возникает необходимость находить общие делители двух или нескольких чисел. Попытаемся найти, например, общие делители чисел 30 и 45.
30 делится на: 1 , 2, 3 , 5 , 6, 10, 15 , 30;
45 делится на: 1 , 3 , 5 , 9, 15 , 45.
Числа 30 и 45 имеют четыре общих делителя: 1, 3, 5 и 15. Наибольшее из этих четырех чисел 15. Это – наибольший общий делитель чисел 30 и 45.
Наибольшим общим делителем (ПОД) нескольких чисел называется наибольшее число, на которое делится каждое из данных чисел.
Найдем, например, НОД (72, 84, 90). Разложим каждое из этих чисел на простые множители: 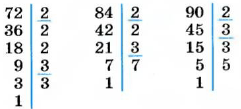
Числа 72, 84, 90 имеют два общих простых делителя: 2 и 3. Умножив их, получим:
НОД (72, 84, 90) = 2 • 3 = 6.
Чтобы найти наибольший общий делитель нескольких чисел, необходимо разложить их на простые множители и умножить все их общие множители.
Найдем НОД (65, 32). Поскольку
65 = 5 • 13, 32 = 2 • 2 • 2 • 2 • 2,
то числа 65 и 32 имеют только один общий делитель – число 1. Поэтому НОД (65, 32) = 1.
Два числа, наибольший общий делитель которых равен 1, называются взаимно простыми. Числа 65 и 32 взаимно простыми.
Замечание. Не путайте взаимно простые числа с простыми. Некоторое число может быть простым, но не взаимно простым. (Взаимно – значит с каким-то другим.) Взаимно простыми могут быть и составные числа.
Взаимно простыми могут быть не только два числа, но и три, и больше. Например, числа 8, 9 и 25 – взаимно простые. Эти три числа не только взаимно простые, но и попарно взаимно простые, поскольку каждые два из них -числа взаимно простые. А вот числа 6, 8 и 9 – взаимно простые, но не попарно взаимно простые, поскольку НОД (6, 8) = 2, НОД (6, 9) = 3.
Выполнение заданий:
Пример №13
Найдите НОД (72, 156).
Решение:
В разложениях чисел 72 и 156 на простые множители общими являются такие простые множители: 2, 2 и 3.
Поэтому 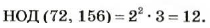
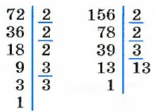
Пример №14
Какое наибольшее количество одинаковых букетов можно составить из 6 васильков и 9 ромашек?
Решение:
Необходимо найти наибольшее число, на которое делится 6 и 9, то есть наибольший общий делитель этих чисел. НОД (6, 9) = 3. Следовательно, можно составить 3 букета (рис. 6)

Наименьшее общее кратное
Запишем несколько натуральных чисел, которые делятся на 8: 8, 16, 24, 32, 40, 48, 56, 64, … .
Каждое из этих чисел кратно 8. Любое число, которое делится на 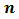 , называется кратным числа
, называется кратным числа 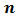 . Напомним, что речь идет только о натуральных числах и о делении без остатка.
. Напомним, что речь идет только о натуральных числах и о делении без остатка.
Числа, кратные 6,-это: 6, 12 , 18, 24 , 30, 36 , 42, 48…..
Числа, кратные 4, – это: 4,8, 12, 16, 20, 24 , 28, 32, 36 , … .
Общими кратными чисел 4 и 6 являются: 12, 24, 36 и много других чисел. Наибольшего общего кратного числа 6 и 4 не имеют. А наименьшее существует.
Наименьшим общим кратным (НОК) нескольких чисел называется такое наименьшее натуральное число, которое делится на каждое данное число. НОК (4, 6) = 12.
Наименьшее общее кратное двух чисел можно найти, разложив эти числа на простые множители. Найдем, например, НОК (72, 90). Для этого разложим числа 72 и 90 на простые множители. Их НОК должно содержать все простые множители числа 72 и все простые множители числа 90. Следовательно, 35 чтобы найти НОК (72, 90), необходимо простые множители числа 72 дополнить такими простыми множителями числа 90, которых нет в разложении числа 72. В данном случае к произведению 2 • 2 • 2 • 3 • 3 надо дописать множитель 5. Имеем: НОК (72, 90) = 2 • 2 • 2 • 3 • 3 • 5 = 72 • 5 = 360.
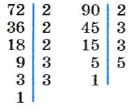
Наименьшее общее кратное двух взаимно простых чисел равно их произведению. Например, НОК (5, 8) = 40. Почему?
А как найти НOK трех чисел?
Чтобы найти наименьшее общее кратное чисел 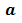 ,
, 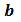 и
и 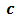 , надо простые множители числа
, надо простые множители числа 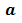 дополнить такими простыми множителями чисел
дополнить такими простыми множителями чисел 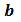 и
и 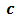 , которых в
, которых в 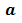 нет, и умножить их.
нет, и умножить их.
Найдем, например, НОК чисел 72, 90 и 80. Поскольку
72 = 2 • 2 • 2 • 3 • 3,
90 = 2 • 3 • 3 • 5,
80 = 2 • 2 • 2 • 2 • 5,
то НОК (72, 90, 80) = 2 • 2 • 2 • 3 • 3 • 5 • 2 = 720.
Рассмотрим пример. Пусть 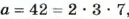 a
a 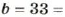
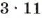 . Их произведение
. Их произведение 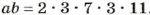 . Такое же и произведение НОД
. Такое же и произведение НОД 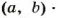 НОК
НОК 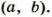 Проверьте! Это свойство верно для любых значений
Проверьте! Это свойство верно для любых значений 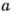 и
и 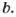 Произведение НОД и НОК двух натуральных чисел равно произведению этих чисел. Всегда НОД
Произведение НОД и НОК двух натуральных чисел равно произведению этих чисел. Всегда НОД 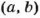 • НОК
• НОК 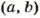 –
– 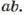
Поэтому, чтобы найти наименьшее общее кратное двух чисел, можно произведение этих чисел разделить на их наибольший общий делитель.
Из этого утверждения вытекают важные следствия:
- Если НОД
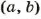 = 1, то НОК
= 1, то НОК 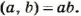
- Если число
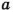 делится на
делится на 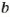 , то НОК
, то НОК 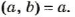
Выполнение заданий:
Пример №15
Найдите наибольшее двузначное число, кратное чисел 2 и 7.
Решение:
Если число 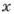 кратно 2 и 7, то
кратно 2 и 7, то 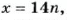 где
где 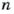 – число натуральное. Если
– число натуральное. Если 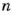 = 8, то
= 8, то 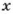 = 112 – не двузначное. Если
= 112 – не двузначное. Если 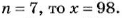
Ответ. 98.
Пример №16
Во время тренировки на стадионе два велосипедиста стартовали одновременно. Первый велосипедист проезжает полный круг за 75 с, а второй — за 100 с. Через какое время велосипедисты вновь встретятся на старте?
Решение:
Искомый интервал времени должен быть кратным чисел 75 и 100. Найдем НОК (75, 100).
75 = 3 • 5 • 5, 100 = 2 • 2 • 5 • 5. IIOK (75, 100) = 100 • 3 = 300. 300 с = 5 мин.
Следовательно, спустя 5 мин велосипедисты вновь встретятся на старте.
Исторические сведения:
Деление натуральных чисел некоторые ученые древности умели выполнять еще несколько тысячелетий назад. Это математическое действие тогда считалось наиболее трудным, поскольку люди не знали современных правил деления, а числа записывали не так, как их записывают теперь. Попытайтесь, например, разделить число 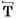 на число
на число 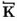 или
или 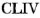 на
на 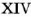 . Когда-то делили одно число на другое, используя камешки или косточки слив и т. и.
. Когда-то делили одно число на другое, используя камешки или косточки слив и т. и.
Признаки делимости на 2 и на 9 древнегреческие математики знали еще в III в. до н. э. Только формулировали их не так, как теперь. Издавна известны и другие признаки делимости.
На 4 делятся все те и только те числа, в которых две последние цифры выражают число, которое делится на 4.
На в делятся все те и только те числа, которые делятся и на 2, и на 3.
Интересный признак делимости на 7, 11 и 13. Пусть имеется какое-то число, например 1 057 958. Отделив три последние цифры, разобьем данное число на два меньших: 1057 и 958. Если разность образованных таким способом чисел делится на 7, 11 или 13, то и данное число делится соответственно на 7, 11 или 13. Поскольку разность 1057 – 958 равна 99, а 99 делится на 11 и не делится на 7 и 13, то и данное число делится на 11, но не делится на 7 и 13. Проверьте!
Простые числа были известны еще в VI в. до н. э. Евклид в III в. до н. э. доказал, что множество простых чисел бесконечно, то есть последовательность
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, … не имеет конца.
Интересный способ составления таблиц простых чисел предложил в III в. до н. э. Оратосфен. Выписав подряд все натуральные числа от 2 до какого-то 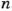 , он оставлял число 2 и вычеркивал после него все числа через одно (т. е. 4, 6, 8, …); оставлял число 3 и вычеркивал после него все числа через два (т. е. 6, 9, 12, …); оставлял число 5 и вычеркивал после него все числа через четыре (т. е. 10, 15, 20,…) и т. д. При этом некоторые числа вычеркивались два и больше раза. Все не вычеркнутые числа – простые. Эратосфен писал па доске, покрытой воском, и не вычеркивал числа, а прокалывал. После этого его доска была похожей на решето.
, он оставлял число 2 и вычеркивал после него все числа через одно (т. е. 4, 6, 8, …); оставлял число 3 и вычеркивал после него все числа через два (т. е. 6, 9, 12, …); оставлял число 5 и вычеркивал после него все числа через четыре (т. е. 10, 15, 20,…) и т. д. При этом некоторые числа вычеркивались два и больше раза. Все не вычеркнутые числа – простые. Эратосфен писал па доске, покрытой воском, и не вычеркивал числа, а прокалывал. После этого его доска была похожей на решето.
Отсеивание составных чисел образно показано па рисунке 11.
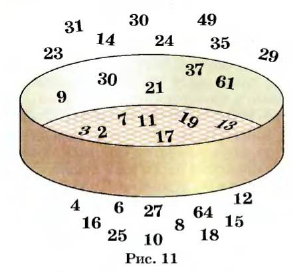
Поэтому такой способ составления таблиц простых чисел назвали «решетом Эратосфена». Ниже показано, как с помощью «решета Эратосфена» можно составить таблицу простых чисел, меньших 40.
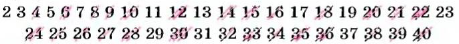
Раскладывать числа на простые множители древнегреческие математики умели еще в VI в. до н. э. Интересный способ нахождения НОД предложил Евклид. Пусть, надо найти НОД (517, 141). Для этот делим большее число на меньшее, меньшее – на полученный первый остаток, первый остаток – на второй и т. д. Последний отличный от 0 остаток – искомый НОД.
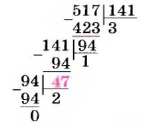
В данном примере НОД (517, 141) = 47. Математики и теперь часто используют этот способ, его называют алгоритмом Евклида.
Главное в разделе:
Если числа 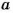 и
и 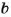 натуральные и
натуральные и 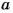 делится на
делится на 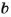 без остатка, то говорят, что
без остатка, то говорят, что 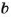 – делитель числа
– делитель числа 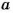 , а
, а 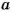 – кратное числа
– кратное числа 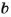 . Например, число 9 имеет три делителя: 1, 3 и 9. Кратных числа 9 бесконечно много: 9, 18, 27…..
. Например, число 9 имеет три делителя: 1, 3 и 9. Кратных числа 9 бесконечно много: 9, 18, 27…..
Каждое число, которое делится только на 1 и на само себя, называют простым. Если число имеет более двух делителей, его называют составным. Число 1 имеет только один делитель, оно – ни простое, ни составное.
2, 3, 5, 7, 11, 13, 17, 19, … – последовательность простых чисел. Простых чисел бесконечно много.
На 2 делятся все те и только те числа, которые оканчиваются четной цифрой. Четные цифры: 0, 2, 4, 6, 8. Все остальные цифры (1, 3, 5, 7, 9) – нечетные. Числа, которые делятся на 2, называются четными, а которые не делятся на 2, нечетными.
1, 3, 5, 7, 9, 11, 13,… – последовательность нечетных чисел;
0, 2, 4, 6, 8, 10, 12,… – последовательность четных чисел.
На 5 делятся все те и только те числа, которые оканчиваются цифрой 5 или 0.
На 10 делятся все те и только те числа, которые оканчиваются цифрой 0.
На 3 делятся все те и только те числа, сумма цифр которых делится на 3.
На 9 делятся все те и только те числа, сумма цифр которых делится на 9.
Если каждое слагаемое делится на некоторое число, то их сумма тоже делится на это число. Если хотя бы один из множителей делится на некоторое число, то и все произведение делится на это число.
Разложить число на простые множители – это значит представить его в виде произведения простых чисел. Например, 2 • 3 • 5 -разложение на простые множители числа 30.
Наибольшее число, на которое делится каждое из данных чисел, называется наибольшим общим делителем этих чисел (НОД). Чтобы найти НОД нескольких чисел, надо разложить их на простые множители и умножить все их общие множители. Два числа, НОД которых равен 1, называют взаимно простыми. Например, числа 15 и 32 – взаимно простые, потому что НОД (15, 32) =1.
Наименьшим общим кратным нескольких чисел (НОК) называют наименьшее натуральное число, которое делится на каждое из данных чисел. Чтобы найти НОК чисел 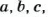 достаточно разложение на простые множители числа
достаточно разложение на простые множители числа 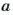 дополнить такими простыми множителями чисел
дополнить такими простыми множителями чисел 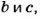 которых нет в разложении числа
которых нет в разложении числа 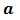 , и умножить их.
, и умножить их.
- Выражения и уравнения
- Линейное уравнение с одной переменной
- Целые выражения
- Одночлены
- Делимость чисел в математике
- Обыкновенные дроби
- Отношения и пропорции
- Рациональные числа и действия над ними
