Как найти делители числа информатика

Как найти делители числа информатика

На уроке рассмотрено решение 25 задания ЕГЭ по информатике: дается подробное объяснение и разбор заданий демонстрационных вариантов и досрочных экзаменов

Содержание:

  • Объяснение задания 25 ЕГЭ по информатике
    • Алгоритмизация и программирование
  • Решение 25 заданий ЕГЭ по информатике
    • Делители числа
    • Простые числа
  • Задания прошлых лет для тренировки (до 2021)
    • Задачи с поэлементной обработкой массива
    • Задачи на обработку элементов массива с последующей заменой
    • Задачи на обработку пар элементов массива (два подряд идущих)
    • Задачи на обработку трёх подряд идущих элементов массива (тройки элементов массива)
    • Задачи на поиск максимума, минимума элементов массива и другие
  • Решение 25 заданий ЕГЭ по информатике: более сложные задания

25-е задание: «Программная обработка целочисленной информации»

Уровень сложности

— высокий,

Требуется использование специализированного программного обеспечения

— да,

Максимальный балл

— 2,

Примерное время выполнения

— 20 минут.

  
Проверяемые элементы содержания: Умение создавать собственные программы (10–20 строк) для обработки целочисленной информации

Рекомендации по выполнению:

“В этом задании требуется написать фрагмент программы, реализующий простую обработку целочисленного массива. У экзаменуемых, хорошо освоивших технику программирования, это задание обычно не вызывает серьёзных затруднений, поскольку алгоритм обработки массива не относится к сложным”

Типичные ошибки и рекомендации по их предотвращению:

  • “в цикле происходит выход за границу массива;
  • не инициализируется или неверно инициализируется искомое значение;
  • исходный массив не изменяется;
  • изменяются не все требуемые элементы (например, только первый или последний из них);
  • отсутствует вывод ответа, или ответ выводится не полностью (например, только один элемент массива ввиду пропущенного цикла вывода элементов или операторных скобок);
  • используется переменная, не объявленная в разделе описания переменных;
  • не указано или неверно указано условие завершения цикла”

    • “Часто бывает, что увлекшись написанием решения, экзаменуемый совершает ошибки в простых ситуациях: организация ввода-вывода, описание и инициализация переменных, обработка массива (выход за границу) и т.д. Эти ошибки могут стоить Вам нескольких баллов, старайтесь их не допускать”

    ФГБНУ “Федеральный институт педагогических измерений”

    Алгоритмизация и программирование

    Для решения задания требуется вспомнить темы:

    • Одномерные массивы.
    • Двумерные массивы.

    Решение 25 заданий ЕГЭ по информатике

    Плейлист видеоразборов задания на YouTube:
    Задание демонстрационного варианта 2022 года ФИПИ

    Делители числа

    25_7:

    Напишите программу, которая ищет среди целых чисел, принадлежащих числовому отрезку [126849; 126871], числа, имеющие ровно 4 различных делителя.
    Выведите эти четыре делителя для каждого найденного числа в порядке возрастания.

    ✍ Решение:

      ✎ Решение (неоптимизированный вариант, метод полного перебора):

      PascalABC.net:

      1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

      begin
  var divCount := 4;
  for var n := 126849 to 126871 do
  begin
    var divs := new List<integer>; 
    for var d := 1 to n do
      if n mod d = 0 then begin
        divs.Add(d);      
        if divs.Count > divCount then break;
      end;
    if divs.Count = divCount then
    begin
      divs.Sort();
      Println(divs);
    end;
  end;
end.
      Python:

      1
2
3
4
5
6
7
8

      for n in range(126849,126871+1):
      divs = [] # чистим список делителей
      for d in range(1,n+1): #
        if n % d == 0:
          divs = divs + [d] # добавляем делитель в список
          if len(divs) > 4: break
      if len(divs) == 4:
        print(*divs)
      С++:

      ✎ Решение (оптимизированный вариант):

    • Будем использовать оптимизированный вариант программы, подходящий для «медленных» компьютеров. Для этого перебор делителей для числа n будем выполнять от 2 до √n, округлив его до ближайшего целого числа (не включая точный квадратный корень, если он существует):
      • вместо диапазона делителей [1; число]
использовать диапазон [1; округл(√n)]
    • При переборе делителей будем определять: если делитель – это точный квадратный корень(n), то в список делителей добавлять будем только сам делитель, если нет – то добавляем пару делителей (делитель и n // делитель):
      • Пример:
число 8 = 2 * 4
Достаточно рассмотреть цикл от 2 до округл(√8) (=2)
если 8 делится на 2 и 8/2 не равно 2, то делители: 2 и 4 (8/2)
      PascalABC.net:

      1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

      begin
  var divCount := 4;
  for var n := 126849 to 126871 do
  begin
    var divs := new List<integer>;
    var d := 1;
    while d * d <= n do  // можно цикл for var d := 1 to round(sqrt(n)) do
    begin
      if n mod d = 0 then begin
        divs.Add(d);      
        if d * d <> n then 
          divs.Add(n div d);
        if divs.Count > divCount then break;
      end;
      d := d+1;
    end;
    if divs.Count = divCount then
    begin
      divs.Sort();
      Println(divs);
    end;
  end;
end.
      Python:

      1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

      # import math # для квадратного корня числа (sqrt)
divCount = 4  # нужное количество делителей
for n in range(126849,126871 + 1):
  divs = [] # чистим список делителей
  d = 1
  #  вместо while можно цикл for d in range(1,round(math.sqrt(n))):
  while d*d <= n: # перебор делителей
    if n % d == 0:
      divs.append(d) # добавляем делитель в список
      if d != n//d: # если делитель - не точный квадратный корень n
        divs.append(n//d)
      if len(divs) > divCount: break
    d+=1
  if len(divs) == divCount:
    divs.sort()
    print(divs)
      С++:

      ✎ Решение: Генерация списка делителей.
      Общая идея:

    • Для каждого числа указанного диапазона генерируем список делителей.
    • Если длина списка равна четырем, выводим его.
      • PascalABC.net:

      		 Python:

      for n in range(126849, 126871+1):
  divs = [d for d in range(1, n+1) if n % d == 0] 
  if len(divs) == 4:
    print( *divs )
      С++:

    Ответ: 

    1 3 42283 126849
1 47 2699 126853
1 5 25373 126865
1 293 433 126869

    25_8:

    Напишите программу, которая ищет среди целых чисел, принадлежащих числовому отрезку [164700; 164752], числа, имеющие ровно 6 различных делителей.
    Выведите эти делители для каждого найденного числа в порядке возрастания.

    ✍ Решение:

      ✎ Решение (оптимизированный вариант):

      PascalABC.net:

      1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

      begin
  var divCount := 6;
  for var n := 164700 to 164752 do
  begin
    var divs := new List<integer>; 
    for var d := 1 to round(sqrt(n)) do
      if n mod d = 0 then begin
        divs.Add(d);      
        if d * d <> n then 
          divs.Add(n div d);
        if divs.Count > divCount then break;
      end;
    if divs.Count = divCount then
    begin
      divs.Sort();
      Println(divs);
    end;
  end;
end.
      Python:

      1
2
3
4
5
6
7
8
9
10
11
12
13

      import math # для квадратного корня sqrt
divCount = 6  # нужное количество делителей
for n in range(164700, 164752 + 1):
  divs = [] # чистим список делителей
  for d in range(1,round(math.sqrt(n))): # перебор делителей
    if n % d == 0:
      divs.append(d) # добавляем делитель в список
      if d != n//d:
        divs.append(n//d)
      if len(divs) > divCount: break
  if len(divs) == divCount:
    divs.sort()
    print(divs)
      С++:

      ✎ Решение: Генерация списка делителей.
      Общая идея:

    • Для каждого числа указанного диапазона генерируем список делителей.
    • Если длина списка равна четырем, выводим его.
      • PascalABC.net:

      		 Python:

      for n in range(164700, 164752+1):
    divs = [d for d in range(1, n+1) if n % d == 0] 
    if len(divs) == 6:
        print( *divs )
      С++:

    Ответ: 

    1 2 4 41177 82354 164708
1 3 9 18301 54903 164709
1 2 4 41179 82358 164716
1 2 4 41183 82366 164732

    25_9:

    Напишите программу, которая ищет среди целых чисел, принадлежащих числовому отрезку [190201; 190230], числа, имеющие ровно 4 различных делителя.
    Выведите эти четыре делителя для каждого найденного числа в порядке убывания.

    ✍ Решение:

      ✎ Решение (неоптимизированный вариант, метод полного перебора):

      PascalABC.net:

      1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

      begin
  var divs := new integer[4];
  for var n := 190201 to 190230 do
  begin
    var i := 0; // для индекса массива
    for var d := 1 to n do
    begin
      if n mod d = 0 then 
      begin
        if i < 4 then
          divs[i] := d;
        inc(i);
      end;
      if i > 4 then 
        break; 
    end;
    if i = 4 then begin
      println(divs.Reverse())
    end;
  end;
end.
      Python:

      1
2
3
4
5
6
7
8
9

      for n in range(190201,190230+1):
      divs = [] # чистим список делителей
      for d in range(1,n+1): #
        if n % d == 0:
          divs = divs + [d] # добавляем делитель в список
          if len(divs) > 4: break
      if len(divs) == 4:
        divs.reverse()
        print(*divs)
      С++:

      ✎ Решение (оптимизированный вариант):

      PascalABC.net:

      1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

      begin
  var divCount := 4;
  for var n := 190201 to 190230 do
  begin
    var divs := new List<integer>; 
    for var d := 1 to round(sqrt(n)) do
      if n mod d = 0 then begin
        divs.Add(d);      
        if d * d <> n then 
          divs.Add(n div d);
        if divs.Count > divCount then break;
      end;
    if divs.Count = divCount then
    begin
      divs.Sort();
      divs.Reverse();
      Println(divs);
    end;
  end;
end.
      Python:

      1
2
3
4
5
6
7
8
9
10
11
12
13
14

      import math # для квадратного корня sqrt
divCount = 4  # нужное количество делителей
for n in range(190201, 190230 + 1):
  divs = [] # чистим список делителей
  for d in range(1,round(math.sqrt(n))): # перебор делителей
    if n % d == 0:
      divs.append(d) # добавляем делитель в список
      if d != n//d:
        divs.append(n//d)
      if len(divs) > divCount: break
  if len(divs) == divCount:
    divs.sort()
    divs.reverse()
    print(divs)
      С++:

      ✎ Решение: Генерация списка делителей.
      Общая идея:

    • Для каждого числа указанного диапазона генерируем список делителей.
    • Если длина списка равна четырем, выводим его.
      • PascalABC.net:

      		 Python:

      for n in range(190201, 190230+1):
    divs = [d for d in range(1, n+1) if n % d == 0] 
    if len(divs) == 4:
        divs.reverse() # реверсируем (по убыванию)
        print( *divs )
      С++:

    Ответ: 

    190201 17291 11 1
190202 95101 2 1
190214 95107 2 1
190219 853 223 1
190222 95111 2 1
190223 17293 11 1
190227 63409 3 1
190229 14633 13 1

    Видеоразбор задания:

    📹 YouTube здесь
    📹 Видеорешение на RuTube здесь

    25_10:

    Напишите программу, которая ищет среди целых чисел, принадлежащих числовому отрезку [190201; 190280], числа, имеющие ровно 4 различных ЧЁТНЫХ делителя.
    Выведите эти четыре делителя для каждого найденного числа в порядке убывания.

    ✍ Решение:

      ✎ Решение (неоптимизированный вариант, метод полного перебора):

      PascalABC.net:

      1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

      begin
  var divs := new integer[4];
  for var n := 190201 to 190280 do
  begin
    var i := 0; // для индекса массива
    for var d := 1 to n do
    begin
      if (n mod d = 0) and (d mod 2 = 0) then 
      begin
        if i < 4 then
          divs[i] := d;
        inc(i);
      end;
      if i > 4 then 
        break; 
    end;
    if i = 4 then begin
      println(divs.Reverse())
    end;
  end;
end.
      Python:

      1
2
3
4
5
6
7
8
9

      for n in range(190201,190280+1):
      divs = [] # чистим список делителей
      for d in range(1,n+1): #
        if n % d == 0 and d%2==0:
          divs = divs + [d] # добавляем делитель в список
          if len(divs) > 4: break
      if len(divs) == 4:
        divs.reverse()
        print(*divs)
      С++:

      ✎ Решение: Генерация списка делителей.

      Общая идея:

    • Для каждого числа указанного диапазона генерируем список делителей.
    • Если длина списка равна четырем, выводим его.
      • PascalABC.net:

      		 Python:

      for n in range(190201, 190280+1):
    divs = [d for d in range(1, n+1) if n % d == 0 and d % 2 == 0] 
    if len(divs) == 4:
        divs.reverse()
        print( *divs )
      С++:

    Ответ: 

    190226 838 454 2
190234 17294 22 2
190238 2606 146 2
190252 95126 4 2
190258 758 502 2
190274 27182 14 2
190276 95138 4 2

    25_11:

    Напишите программу, которая ищет среди целых чисел, принадлежащих числовому отрезку [394441; 394505], числа, имеющие максимальное количество различных делителей. Если таких чисел несколько, то найдите минимальное из них.
    Выведите количество делителей найденного числа и два наибольших делителя в порядке убывания.

    ✍ Решение:

      ✎ Решение (неоптимизированный вариант, метод полного перебора):

      PascalABC.net:

      1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

      begin
  var max := 0;
  var divsMax := new List<integer>; 
  for var n := 394441 to 394505 do
  begin
    var divs := new List<integer>; 
    for var d := 1 to n do
      if n mod d = 0 then 
        divs.Add(d);      
    if divs.Count > max then 
    begin
      max := divs.Count;
      divsMax := divs;
    end;
  end;
  divsMax.Reverse();
  print(max, divsMax[0], divsMax[1])
end.
      Python:

      1
2
3
4
5
6
7
8
9
10
11
12

      maxim = 0  # нужное количество делителей
divsMax = []
for n in range(394441, 394505 + 1):
  divs = [] # чистим список делителей
  for d in range(1,n+1): # перебор делителей
    if n % d == 0:
      divs.append(d) # добавляем делитель в список
  if len(divs) > maxim: 
    maxim = len(divs)
    divsMax = divs
divsMax.reverse()
print(maxim,divsMax[0],divsMax[1])
      С++:

      ✎ Решение (Генерация списка делителей):

      PascalABC.net:
      Python:

      1
2
3
4
5
6
7
8
9

      maxim=0
divsmax=[]
for n in range(394441, 394505+1):
    divs = [d for d in range(1, n+1) if n % d == 0] 
    if len(divs) > maxim:
        maxim = len(divs)
        divsmax = divs # сохраняем делители для числа с макс кол-вом дел-ей
divsmax.reverse()
print(maxim, divsmax[0], divsmax[1])
      С++:

    Ответ: 48 394450 197225

    Видео

    Простые числа

    25_12:

    Напишите программу, которая ищет среди целых чисел, принадлежащих числовому отрезку [3532000; 3532160], простые числа.
    Выведите все найденные простые числа в порядке убывания, слева от каждого числа выведите его номер по порядку.

    ✍ Решение:

      ✎ Решение (неоптимизированный вариант, метод полного перебора):

      PascalABC.net:

      1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

      begin
  var count := 0;
  for var n := 3532160 downto 3532000 do // цикл с конца 
  begin
    var flag := true; 
    for var d := 2 to n - 1 do // перебор делителей, начиная с двух до n-1
    begin
      if n mod d = 0 then begin // есть делитель помимо единицы и самого n
        flag := false; // число не простое     
        break;
      end;
    end;
    if flag = true then // если число простое
    begin
      inc(count);
      Println(count, n);
    end;
  end;
end.
      Python:

      1
2
3
4
5
6
7
8
9
10

      count = 0
for n in range(3532160, 3532000-1, -1): # цикл с конца и с шагом (-1) 
  flag = True
  for d in range(2, n): # перебор делителей, начиная с двух
    if n % d == 0: # есть делитель помимо единицы и самого n
      flag = False # число не простое
      break
  if flag == True: # число простое
    count+=1
    print(count , n)
      С++:

      ✎ Решение (оптимизированный вариант):

      PascalABC.net:

      1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

      begin
  var count := 0;
  for var n := 3532160 downto 3532000 do // цикл с конца 
  begin
    var flag := true; 
    var d := 2;
    while d * d <= n - 1 do // перебор делителей, начиная с двух
    begin
      if n mod d = 0 then begin // есть делитель помимо единицы и самого n
        flag := false;  // число не простое    
        break;
      end;
      d := d + 1;
    end;
    if flag = true then // если число простое
    begin
      inc(count);
      Println(count, n);
    end;
  end;
end.
      Python:

      1
2
3
4
5
6
7
8
9
10
11
12

      count = 0
for n in range(3532160, 3532000-1, -1): # цикл с конца и с шагом (-1) 
      flag = True
      d = 2
      while d*d <= n-1: # перебор делителей, начиная с двух
            if n % d == 0: # есть делитель помимо единицы и самого n
                  flag = False # число не простое
                  break
            d+=1
      if flag == True: # число простое
            count+=1
            print(count , n)
      С++:

    Ответ:

    1  3532147
2  3532121
3  3532103
4  3532091
5  3532049
6  3532033
7  3532021
8  3532019
9  3532007

    Задания прошлых лет для тренировки (до 2021)

    Задачи с поэлементной обработкой массива

    25_1: ЕГЭ по информатике 2017 года (один из вариантов со слов выпускника):

    Дан целочисленный массив из 20 элементов. Элементы массива могут принимать целые значения от 0 до 10 000 включительно. Опишите на естественном языке или на одном из языков программирования алгоритм, позволяющий найти и вывести количество элементов массива НЕ кратных 3.

    Исходные данные объявлены так, как показано ниже. Запрещается использовать переменные, не описанные ниже, но использовать все описанные переменные не обязательно.

    1
2
3
4
5
6
7
8

    const N = 20;
var i,j,k:integer;
a:array [1..N] of integer; 
begin
for i:=1 to N do 
  readln(a[i]); 
…
end.

    ✍ Решение:

    Рассмотрим заданный фрагмент решения:

    • в цикле со счетчиком i запрашиваются значения элементов массива, т.е. формируется массив;
    • из постановки задания видим, что необходимо найти количество чего-то, это значит, что нужно использовать переменную счетчик;
    • объявлены три целочисленных переменных: i, j, k; переменная i использована в первом цикле, значит для счетчика можно взять переменную k;
    • счетчик всегда нужно обнулять, поэтому следующим оператором будет:
    • определим, количество чего нам необходимо считать: количество элементов массива не кратных 3. Кратность можно определить через остаток от деления: если значение элемента массива при делении на 3 в остатке не возвращает 0, значит элемент не кратен трем;
    • остаток при делении в паскале — оператор mod. Поскольку необходимо просмотреть каждый элемент массива, то это нужно делать в цикле for;
    • переменная i уже использована в первом цикле for, значит, для очередного цикла возьмем неиспользованную переменную j:
      • for j:=1 to N do
  if a[j] mod 3 <> 0 then
    • если условие истинно (т.е. нашелся элемент массива, не кратный трем), то увеличиваем счетчик:
    • после цикла остается вывести значение счетчика, т.е. вывести количество элементов массива не кратных 3:

    Результат:

    k:=0;
for j:=1 to N do
  if a[j] mod 3 <> 0 then
    inc(k);
writeln(k);

    Смотрите видео с подробным объяснением и разбором данного 25 задания:

    📹 YouTube здесь
    📹 Видеорешение на RuTube здесь

    Задачи на обработку элементов массива с последующей заменой

    25_3: Решение 25 задания ЕГЭ по информатике Демоверсия 2018:

    Дан целочисленный массив из 30 элементов. Элементы массива могут принимать целые значения от 0 до 10000 включительно. Опишите на одном из языков программирования алгоритм, который находит количество элементов массива, больших 100 и при этом кратных 5, а затем заменяет каждый такой элемент на число, равное найденному количеству. Гарантируется, что хотя бы один такой элемент в массиве есть. В качестве результата необходимо вывести измененный массив, каждый элемент массива выводится с новой строчки.

    Например, для массива из шести элементов: 4 115 7 195 25 106
    программа должна вывести числа 4 2 7 2 25 106

    Исходные данные объявлены так, как показано ниже на примерах для некоторых языков программирования. Запрещается использовать переменные, не описанные ниже, но разрешается не использовать некоторые из описанных переменных.

    Паскаль:

    1
2
3
4
5
6
7
8
9
10

    const
N = 30;
var
a: array [1..N] of longint;
i, j, k: longint;
begin
	for i := 1 to N do
		readln(a[i]);
	...
end.

    В качестве ответа Вам необходимо привести фрагмент программы, который должен находиться на месте многоточия. Вы можете записать решение также на другом языке программирования (укажите название и используемую версию языка программирования, например Free Pascal 2.6). В этом случае Вы должны использовать те же самые исходные данные и переменные, какие были предложены в условии.

    Похожие задания для тренировки

    ✍ Решение:

      Решение на языке Паскаль:

      1
2
3
4
5
6
7
8
9

      k := 0;
for i := 1 to N do
	if (a[i] > 100) and (a[i] mod 5 = 0) then
		k:=k+1;
for i := 1 to N do begin
	if (a[i] > 100) and (a[i] mod 5 = 0) then
		a[i] := k;
writeln(a[i])
end

    25_6:

    Дан массив, содержащий неотрицательные целые числа. Необходимо вывести:

  • максимальный чётный элемент, если количество чётных элементов не меньше, чем нечётных;
  • максимальный нечётный элемент, если количество нечётных эле-ментов больше, чем чётных.

    • Например, для массива из шести элементов: 4 6 12 17 3 8
    ответом будет 12 — наибольшее чётное число, поскольку чётных чисел в этом массиве больше

    Исходные данные объявлены так, как показано ниже. Запрещается использовать переменные, не описанные ниже, но разрешается не использовать некоторые из описанных переменных.

    Python:

    1
2
3
4
5
6

    # допускается также использовать
# целочисленные переменные j, k, m
a = []
n = 2000 // менять значение n нельзя
for i in range(0, n):
  a.append(int(input()))

    ✍ Решение:

      Решение на языке Python:

      1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

      a = []
n = 2000 // менять значение n нельзя
for i in range(0, n):
    a.append(int(input()))
j = 0 
k = 0 
m = 0 
for i in range(0, n):
	if a[i]%2 == 0:
		j+=1
	else:
		k+=1
if k>j:
	j = 0
	for i in range(0, n):
		if a[i]>j and a[i] % 2 != 0:
			j = a[i]
	print(j)
else:
	for i in range(0, n):
		if a[i]>m and a[i] % 2 == 0:
			m = a[i]
	print(m)

    Задачи на обработку пар элементов массива (два подряд идущих)

    25_4:

    Дан целочисленный массив из 40 элементов. Элементы массива могут принимать целые значения от 0 до 10 000 включительно. Опишите на естественном языке или на одном из языков программирования алгоритм, позволяющий найти и вывести количество пар элементов массива, в которых одно из чисел двузначное. В данной задаче под парой подразумевается два подряд идущих элемента массива.

    Например, для массива из семи элементов: 13; 323; 12; 33; 117 — ответ: 4.

    Исходные данные объявлены так, как показано ниже. Запрещается использовать переменные, не описанные ниже, но разрешается не использовать некоторые из описанных переменных.

    1
2
3
4
5
6
7
8
9
10

    const
  N = 40;
var
  a: array [1..N] of integer;
  i, j, k: integer;
begin
  for i := 1 to N do 
    readln(a[i]);
  ...
end.

    ✍ Решение:
     

      1
2
3
4
5

      k := 0;
for i := 1 to N - 1 do
 if ((a[i] < 100) and (a[i] > 9)) or ((a[i + l] < 100) and (a[i + 1] > 9)) then 
      inc(k);
writeln(k);

    25_5:

    Дан целочисленный массив из 20 элементов. Элементы массива могут принимать целые значения от -10 000 до 10 000 включительно. Опишите алгоритм, позволяющий найти и вывести количество пар элементов массива, в которых сумма элементов делится на 2, но не делится на 4. В данной задаче под парой подразумевается два подряд идущих элемента массива.

    Исходные данные объявлены так, как показано ниже. Запрещается использовать переменные, не описанные ниже, но разрешается не использовать некоторые из описанных переменных.

    Python:

    1
2
3
4
5
6
7

    #  допускается также использовать
#  две целочисленные переменные
#  j и k
a = []
n = 20
for i in range(0, n):
  a.append(int(input()))

    ✍ Решение:

      Проанализируем данный фрагмент кода на языке Python:

    • В первой строчке кода объявляется список а. Дальше, идет объявление переменной n = 20, она отвечает за размер массива.

      • При решении такого рода задач, необходимо помнить, что массив в Python — это список и это динамический тип данных. Кроме того, нумерация элементов массива начинается с 0.

    • Ниже мы видим инициализацию списка а. Мы должны дописать код дальнейшей программы, который последует после заполнения списка пользователем.
    • Итак, по условию мы должны находить пары элементов, сумма которых делится на 2, но не делится на 4, причем парами считаются соседние элементы, например: a[0] и a[1], a[1] и a[2].
    • Мы можем узнать, делится ли данный элемент на число, если остаток от деления на него равен 0, и не делится — в противном случае. Тогда сумма соседних элементов при делении на 2 должна давать остаток 0, а при делении на 4 наоборот — отличный от 0.
    • Введем цикл, который будет перебирать все элементы массива, считать сумму соседей и проверять истинность условия.
      • for i in range(0, n-1):
    j = a[i] + a[i+1]
    if j%2 == 0 and j%4 != 0:

      Так как мы рассматриваем элемент a[i + 1], значит, цикл должен работать до n — 1, чтобы не выйти за границы диапазона массива.

    • Когда мы определились с условием, за счетчик возьмем переменную k, которую допустимо брать исходя из комментариев к программе.
      • ...
 if j%2 == 0 and j%4 != 0:
        k+=1
    • Мы добавили допустимую переменную j, чтобы условный оператор выглядел компактнее.
    • Однако задача еще не решена. Во-первых, мы должны до цикла инициализировать счетчик k = 0. Так как иначе Python выдаст ошибку.

      • Дело в том, что мы пытаемся присвоить переменной k его же значение, но на 1 больше, но интерпретатор «не встречал» раньше переменной k, из-за чего возникает ошибка.

    • Кроме того, добавим вывод результата после цикла.
    • Таким образом, правильный вариант с учетом доработок:
      • a = []
n = 20
for i in range(0, n):
  a.append(int(input()))
k = 0
for i in range(0, n - 1):
    j = a[i] + a[i + 1]
    if j%2 == 0 and j%4 != 0:
        k += 1
print(k)

    Задачи на обработку трёх подряд идущих элементов массива (тройки элементов массива)

    25_2:

    Дан целочисленный массив из 40 элементов. Элементы массива могут принимать целые значения от 0 до 10 000 включительно. Опишите на естественном языке или на одном из языков программирования алгоритм, позволяющий найти и вывести количество троек элементов массива, состоящих из равных между собой чисел. В данной задаче под тройкой подразумевается три подряд идущих элемента массива.

    Например, для массива из семи элементов: 2; 2; 2; 4; 4; 4; 4 — ответ: 3.

    Исходные данные объявлены так, как показано ниже. Запрещается использовать переменные, не описанные ниже, но разрешается не использовать некоторые из описанных переменных.

    1
2
3
4
5
6
7
8
9
10

    const
  N=40;
var
  a: array[1..N] of integer;
  i, j, k:integer;
begin
  for i:=1 to N do
    readln(a[i]);
  ...
end.

    ✍ Решение:

    • из постановки задания видим, что необходимо искать количество чего-то, это значит, что нужно использовать переменную счетчик; возьмем для нее объявленную переменную k;
    • счетчик всегда нужно сначала обнулять, поэтому следующим оператором будет:
    • определим, количество чего нам необходимо считать: количество троек элементов массива, состоящих из равных между собой чисел. Т.е. необходимо сравнивать между собой каждые три подряд идущих элемента массива, например так:
      • if (a[i]=a[i+1]) and (a[i]=a[i+2]) then
    inc(k);
    • inc(k) — оператор, увеличивающий счетчик k на единицу;
    • условие необходимо выполнять в цикле, так как нужно проверить все элементы массива; цикл со счетчиком необходимо организовать от 1 до N-2, в противном случае индексы элементов a[i+2] выйдут за границы диапазона массива (например, при i = 40, получим … a[40+2], а 42-го элемента массива не существует, поэтому цикл надо делать до i = 38, т.е. N-2).

    Результат:

    for i:=1 to N-2 do
    if (a[i]=a[i+1]) and (a[i]=a[i+2]) then
      inc(k);
writeln(k);

    Более подробное объяснение предлагаем посмотреть на видео:

    📹 YouTube здесь
    📹 Видеорешение на RuTube здесь

    Задачи на поиск максимума, минимума элементов массива и другие

    Источник

    На этой странице вы узнаете

    • Как быстро работает программа?
    • Есть ли смысл перебирать делители после корня?
    • Что количество делителей может сказать о самом числе?

    Гадание на кофейной гуще или на картах Таро? Может, на ромашке? Хотя лучше не доверять свои отношения цветку. Наша судьба — только в наших руках. А судьба чисел предопределена заранее. Сегодня мы будем предсказывать их жизнь и судьбу по делителям. Но главная проблема — найти эти делители.

    Постановка проблемы. Переборное решение

    Встречали ли вы странных персонажей в задачах, которым резко понадобилось купить 50 арбузов? А что подумаете, если ваш учитель математики задаст найти число, у которого 50 делителей?

    Поиск делителей в математике не самый сложный процесс. Есть разные способы: разложение на простые множители, обычный перебор и так далее. Сложность задания будет зависеть от самого числа. Довольно быстро получится найти делители числа 24 — число небольшое, красивое, удобное. Нахождение делителей числа 1234567 займет гораздо больше времени.

    Я предлагаю включить компьютер, открыть среду разработки и заставить код сделать за нас всю работу.

    Идея в следующем:

    1. Создадим список, в который мы сохраним все делители числа.
    2. С помощью цикла for переберем все числа из диапазона от 1 до самого числа.
    3. Если в переборе мы нашли такое число, которое является делителем исходного — остаток от деления будет равен 0 — сохраним это число в список.

    В итоге мы получим список всех делителей исходного числа.

    number = 1234567
dels = []

for i in range(1, number + 1):
	if number % i == 0:
		dels.append(i)

print(dels)
_____________________________________________________________________
Вывод: [1, 127, 9721, 1234567]

    У этого метода есть очень большая проблема — время его работы.

    Программа выполняет команды очень быстро, но не бесконечно быстро.

    Как быстро работает программа?

    Время работы программы можно измерить. Например, Sublime Text 3 занимается этим автоматически. И он помог посчитать, что программа выше выполнилась за 0.2 секунды. Давайте постепенно повышать ставки и смотреть, сколько времени понадобится этой же программе для поиска делителей других чисел:
    — число 1234567 — 0.2 секунды;
    — число 12345670 — 0.9 секунды;
    — число 123456700 — 8.0 секунд;
    — число 1234567000 — 115.7 секунд.

    С числом 1234567 программа сделала 1234567 шагов цикла for, и справилась неимоверно быстро. Но чем больше ей придется выполнять команд, тем дольше придется работать.

    Замеры времени зависят от многих факторов, например, мощности компьютера. Но мы можем повысить эффективность работы программы. 

    Ускоренный перебор делителей

    Идея ускоренного перебора делителей заключается в том, что, найдя один делитель, мы сразу можем подобрать второй — его пару.

    Возьмем число 24. Найдя его делитель 2, мы сразу можем сказать, что у 24 есть еще один делитель — 12, потому что 12 = 24 / 2. Интересная мысль? Давайте ее развивать.

    Найдем по такой логике все делители числа 16.

    1. Самый простой делитель числа — 1. И по этой логике сразу найдем второй делитель — само число 16, так как 16 / 1 = 16.
    1. Проверим число 2. Это делитель, так что сразу найдем его пару: 16 / 2 = 8.
    1. Проверяем число 3 — это не делитель, его просто пропускаем.
    1. При проверке числа 4 мы столкнемся с интересной ситуацией. Его парой будет 16 / 4 = 4 — то же самое число, а мы ищем различные пары. Значит, у корня числа пары не будет: найдя корень, мы найдем только один делитель.

    Если мы продолжим перебор, числа 5, 6 и 7 — не будут делителями. А за ними — 8, делитель, который мы уже нашли.

    Есть ли смысл перебирать делители после корня?

    Нет. Найдя “маленький” делитель, при ускоренном переборе мы можем найти его пару, которая будет “большим” делителем. Перебирая делители, рано или поздно мы дойдем до корня числа, у которого нет пары. Перебирая числа после корня, мы будем находить только “большие” делители, которые уже нашли в паре с “маленькими”.

    Если у числа целого корня нет, перебираем до его округленного вниз значения.
    Нам нет смысла перебирать числа после корня, так что будем перебирать до предельно близкого к нему значения, но не больше.

    Логика программы будет такой:

    1. Перебираем числа от 1 до корня исходного числа.
    2. Если мы нашли корень числа, добавляем в список делителей только его.
    3. Если мы нашли не корень, а обычный делитель — добавляем в список сразу пару делителей.

    Пример реализации ускоренного перебора делителей для числа 1234567000:

    number = 1234567000
dels = []

for i in range(1, int(number ** 0.5) + 1):
	if i * i == number:
		dels.append(i)
	elif number % i == 0:
		dels.append(i)
		dels.append(number // i)

print(len(dels))
_____________________________________________________________________
Вывод: 64

    Эта программа нашла все делители числа и выдала их количество — 64. А на ее работу ушло меньше секунды.

    Но и это не панацея. Что, если нам придется проверить делители сразу нескольких чисел? Например, мы хотим найти все числа, у которых ровно 7 делителей, в диапазоне от 1 до 10000. 

    Программу надо немного модифицировать:

    1. заведем переменную-счетчик, которая будет считать подходящие числа;
    2. number сделаем перебираемой переменной по нужному диапазону с помощью цикла for;
    3. ускоренный перебор будет внутри перебора number;
    4. в конце каждого шага цикла проверяем — если делителей у числа ровно 7, то увеличиваем наш счетчик на 1.

    Теперь программа будет выглядеть следующим образом:

    count = 0
for number in range(1, 10000):
	dels = []

	for i in range(1, int(number ** 0.5) + 1):
		if i * i == number:
			dels.append(i)
		elif number % i == 0:
			dels.append(i)
			dels.append(number // i)

	if len(dels) == 7:
		count += 1

print(count)
_____________________________________________________________________
Вывод: 2

    Эта программа работала всего 0.2 секунды. Звучит неплохо, но давайте снова поднимать ставки:

    1. диапазон 1 — 10000 — 0.2 секунды;
    2. диапазон 1 — 100000 — 2.6 секунды;
    3. диапазон 1 — 1000000 — 80.2 секунды.

    Время снова увеличивается очень быстро. Что можно с этим сделать? 

    Еще более ускоренный перебор делителей

    Не считаем, что не нужно

    Обратите внимание — программа выше нашла среди чисел 1–10000 всего 2 числа, имеющих ровно 7 делителей. А сколько же у остальных? Может быть и больше, может быть и меньше. Например, у числа 9864 делителей аж 24 штуки. Стоило ли тратить время на поиск их всех, если количество делителей больше 7?

    Конечно, нет. Как только мы нашли 8 штук, мы уже можем понять, что анализировать число далее нам неинтересно. Значит, нужно остановить работу цикла.

    Команда break полностью останавливает работу цикла.

    Мы можем модернизировать нашу последнюю программу: если в переборе делителей мы увидим, что их больше семи, завершаем цикл командой break.

    count = 0
for number in range(1, 10000):
	dels = []

	for i in range(1, int(number ** 0.5) + 1):
		if i * i == number:
			dels.append(i)
		elif number % i == 0:
			dels.append(i)
			dels.append(number // i)
		if len(dels) > 7:
			break

	if len(dels) == 7:
		count += 1

print(count)

    При этом завершится именно цикл перебора делителей i, так как break находится именно в нем, а цикл перебора number продолжит свою работу.

    Давайте произведем замеры еще раз:

    1. диапазон 1-10000 — 0.2 секунды;
    2. диапазон 1-100000 — 2.1 секунды;
    3. диапазон 1-1000000 — 53.5 секунды.

    В последнем случае мы сэкономили около трети от времени работы программы. Но и это не предел.

    Не считаем, что не нужно 2.0

    Вернемся на несколько абзацев выше, когда мы искали делители числа 16. Мы нашли 5 делителей — 2 пары и 1 корень, который не даст пару. Это справедливо для любого числа: целый корень не будет давать пару ни с каким другим числом, а все остальные делители — будут. 

    Что количество делителей может сказать о числе?

    Если у числа есть целый корень, количество делителей числа будет нечетным, так как корень не даст пару ни с кем.
    Если же у числа целого корня нет — количество его делителей будет четным, так как все делители будут иметь пару.

    Нам нужны числа, у которых ровно 7 делителей. Следовательно, нам нужны числа, у которых есть целый корень. Это можно проверить, вычислив точный корень числа и его округленное значение. Если они совпадут, значит, округлять корень было некуда и он целый. 

    Но как пропускать числа, которые нам не нужны?

    Команда continue останавливает работу текущего шага цикла и сразу переходит к следующему.

    Если мы найдем число number, у которого нет целого корня, мы можем применить команду continue: данный шаг цикла перебора number завершается, и мы сразу перейдем к следующему.

    Включить эту проверку в программу можно следующим образом:

    count = 0
for number in range(1, 10000):
	if number ** 0.5 != int(number ** 0.5):
		continue

	dels = []

	for i in range(1, int(number ** 0.5) + 1):
		if i * i == number:
			dels.append(i)
		elif number % i == 0:
			dels.append(i)
			dels.append(number // i)
		if len(dels) > 7:
			break

	if len(dels) == 7:
		count += 1

print(count)

    Снова посмотрим на время работы программы при разных диапазонах:

    1. диапазон 1-100000 — 0.1 секунды;
    2. диапазон 1-1000000 — 0.5 секунды;
    3. диапазон 1-10000000 — 4.5 секунды;
    4. диапазон 1-100000000 — 44.4 секунды.

    А делители — это вообще для чего? А таблицы со временем — это точно важно? Может, подождать проще, чем учить все это?

    Нахождению делителей чисел посвящена задача 25 ЕГЭ, и без этих теоретических знаний решить ее крайне сложно. Что же касается времени работы, то за ним приходится следить внимательнейшим образом, ведь в задачах могут встречаться ситуации, когда надо найти делители для сотен миллионов чисел за раз!

    Зная все особенности ускорения перебора делителей и поиска чисел с конкретными делителями, за считанные секунды можно решать задачи огромных диапазонов. 

    Фактчек

    • Ускоренный перебор делителей подразумевает нахождение делителей попарно, при этом перебирать делители достаточно только до корня числа.
    • Команда break полностью останавливает работу цикла, а команда continue завершает работу лишь текущего шага цикла, перенося нас сразу на следующий.
    • Если у числа есть целый корень, количество делителей числа будет нечетным, так как корень не даст пару ни с кем. Если же у числа целого корня нет — количество его делителей будет четным, так как все делители будут иметь пару.

    Проверь себя

    Задание 1.
    Для чего нужен ускоренный перебор делителей?

    1. Обычный перебор слишком скучный
    2. Для большей точности вычислений
    3. Для ускорения работы программы

    Задание 2.
    Найдите количество делителей числа 2568568668.

    1. 5
    2. 6
    3. 7
    4. 8

    Задание 3.
    Найдите, сколько чисел из диапазона от 2000 до 1002000 имеют ровно 5 делителей.

    1. Ни одного
    2. 1
    3. 10
    4. 8

    Ответы: 1. — 3; 2. — 3; 3. — 4.

    Источник

    Всем привет! Добрались мы до 25 задания из ЕГЭ по информатике 2023.

    Рассмотрим типовые задачи, а так же новые формулировки 25 задания из ЕГЭ по информатике 2023.

    Приступаем к первой классической задаче.

    Задача (ЕГЭ по информатике, Демо 2022)

    Пусть M – сумма минимального и максимального натуральных делителей
    целого числа, не считая единицы и самого числа. Если таких делителей
    у числа нет, то значение M считается равным нулю.

    Напишите программу, которая перебирает целые числа, бо́льшие 700 000,
    в порядке возрастания и ищет среди них такие, для которых значение M
    оканчивается на 8. Выведите первые пять найденных чисел
    и соответствующие им значения M.

    Формат вывода: для каждого из пяти таких найденных чисел в отдельной
    строке сначала выводится само число, затем – значение М.
    Строки выводятся в порядке возрастания найденных чисел.

    Количество строк в таблице для ответа избыточно.

    ЕГЭ по информатике демоверсия 2022 - задание 25

    Решение:

    На ЕГЭ по информатике 2023 удобно писать программы на языке Python.

    import math
count=0
for i in range(700001, 800000):

    b=0
    
    for j in range(2, int(math.sqrt(i)) + 1):
        if i%j==0:
            b=i//j
            break
    
    
    if  b==0: M=0
    else: M=j+b

    if M!=0 and M%10==8:
        count=count+1
        print(i, M)

    if count==5: break

    В данной программе перебираются числа в цикле for, начиная с 700001.

    Переменная b — считается наибольшим делителем числа i. Затем, с помощью ещё одного цикла for перебираются числа с 2 до корня числа i (включительно). Ищем тем самым наименьший делитель.

    Если до корня числа включительно не встретился ни один делитель, значит, у числа нет делителей, кроме 1 и самого числа.

    ЕГЭ по информатике демоверсия 2022 - задание 25 поиск делителей

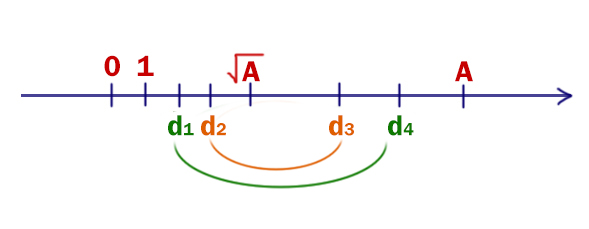
    Пусть у нас есть число A. Если у этого числа есть делитель d1, то он находится до корня этого числа. А вот то число (так же делитель d4), на которое умножается d1, чтобы получить A, будет находиться после корня A.

    Получается, что у каждого делителя есть своя пара. У единицы – это само число. Причём один делитель из пары находится до корня, другой после корня. Исключением будет тот случай, когда из числа А извлекается целый корень. Тогда для этого корня не будет пары (парой и будет само это число √A * √A = A).

    Таким образом, первый найденный делитель будет являться наименьшим делителем. А вот делительный, который находится в паре с наименьшим делителем, будет наибольшим.

    После того, как мы нашли наименьший делитель (он будет сидеть в переменной j) и наибольший делитель b, выходим из второго цикла for.

    Если переменная b осталась равна нулю, то, значит, у числа i нет указанных делителей, и переменная M должна равняться 0. Если b не равна нулю, то M=j+b.

    Проверить, на что оканчивается число, можно узнав остаток от деления числа на 10.

    Переменная count следит, чтобы было распечатано ровно 5 чисел, которые удовлетворяют условию задачи.

    Ответ:

    700005 233338
    700007 100008
    700012 350008
    700015 140008
    700031 24168

    Задача (Стандартная)

    Напишите программу, которая перебирает целые числа, большие 550 000, в порядке возрастания и ищет среди них такие, для которых наибольший натуральный делитель, не равный самому числу, не является простым числом.

    Программа должна найти и вывести первые 6 таких чисел и соответствующие им значения упомянутых делителей.

    Формат вывода: для каждого из 6 таких найденных чисел в отдельной строке сначала выводится само число, затем упомянутый делитель. Строки выводятся в порядке возрастания найденных чисел.

    Например, для числа 105 наибольший натуральный делитель 35 не является простым, для числа 15 наибольший натуральный делитель 5 — простое число, а для числа 13 такого делителя не существует.

    ЕГЭ по информатике демоверсия 2022 - задание 25

    Решение:

    Здесь мы ищем наибольший делитель числа, как и в прошлом решении.

    import math

def Pr(x):
    for i in range(2, int(math.sqrt(x))+1):
        if x%i==0: return False
    return True


count=0
for i in range(550001, 1000000):

    b=0
    
    for j in range(2, int(math.sqrt(i)) + 1):
         if i%j==0:
            b=i//j
            break


    if not(Pr(b)):
        count=count+1
        print(i, b)

    if count==6: break

    Чтобы проверить число, является ли оно простым, напишем функцию Pr(). Там мы проходим до корня числа. Если не встретился не один делитель, значит, число простое — возвращаем True. Если до корня хотя бы один делитель встретили — возвращаем False.

    Ответ:

    550002 275001
    550004 275002
    550005 183335
    550008 275004
    550010 275005
    550011 183337

    Задача (Ровно 4 различных делителя)

    Напишите программу, которая ищет среди целых чисел, принадлежащих числовому отрезку [258274; 258297], числа, имеющие ровно 4 различных делителя. Выведите для каждого найденного числа два наибольших делителя в порядке возрастания.

    Решение:

    import math

for i in range(258274, 258298):
    a=[]
    for j in range(1, int(math.sqrt(i))+1):
        if i%j==0:
            a.append(j)
            b=i//j
            if j!=b:
                a.append(b)

    if len(a)==4:
        a.sort()
        print(a[2], a[3])

    Здесь для каждого числа i заводим массив a, где будем сохранять все его делители. Идём как всегда до корня. Если мы нашли делитель, мы добавляем его в массив a c помощью команды append и ищем его “брата”. Второй делитель (“брат”) не должен равняться самому делителю j, т.к. нам сказали, что все делители должны быть различны. Одинаковые делители j и b могут получится, если из нашего числа i извлекается целый корень. Ведь для делителя √i является парой этот же делитель ( √i* √i=i).

    После прохождения внутреннего цикла (с переменной j) в массиве a будут сидеть все делители числа i. Если их ровно 4, то сортируем массив a и выводим на экран два наибольших.

    Ответ:

    15193 258281
    1427 258287
    1493 258289
    36899 258293
    51659 258295

    Задача (Крепкий орешек)

    Назовём нетривиальным делителем натурального числа его делитель, не равный единице и самому числу. Найдите все натуральные числа, принадлежащие отрезку [4234679; 10157812] и имеющие ровно три нетривиальных делителя. Для каждого найденного числа запишите в ответе само число и его наибольший нетривиальный делитель. Найденные числа расположите в порядке возрастания.

    Решение:

    import math

for i in range(4234679, 10157813):
    if int(math.sqrt(i))**2 == i:
        a=[]
        for j in range(2, int(math.sqrt(i))+1):
            if i%j==0:
                a.append(j)
                b=i//j
                if j!=b:
                    a.append(b)
        if len(a)==3:
            a.sort()
            print(i, a[2])

    Как у нас могут быть три различных нетривиальных делителя, когда делители идут, как мы выяснили, парами? Это может быть, когда существует целый корень из этого числа. Тогда в паре два числа будут одинаковыми (√i* √i = i). Поэтому в этой задаче нас интересуют числа из которых извлекается елый корень.

    Если этим рассуждением не воспользуемся, то программа будет считать очень долго, потому что здесь диапазон и сами числа очень большие.

    Далее, решаем, как и в прошлый раз.

    Ответ:

    4879681 103823
    7890481 148877

    Задача (ЕГЭ по информатике, 20.06.22)

    Назовём маской числа последовательность цифр, в которой также могут встречаться следующие символы:

    — символ “?” означает ровно одну произвольную цифру;

    — символ “*” означает любую последовательность цифр произвольной длины; в том числе “*” может задавать и пустую последовательность.

    Например, маске 123*4?5 соответсвуют числа 123405 и 12300405.

    Среди натуральных чисел, не превышающих 108, найдите все числа, соответствующие маске 1234*7, делящиеся на 141 без остатка.

    В ответе запишите в первом столбце таблицы все найденные числа в порядке возрастания, а во втором столбце — соответствующие им результаты деления этих чисел на 141.

    Решение:

    Здесь самый главный момент заключается в том, что есть верхняя граница 108. Т.е. самое большое число, которое нужно рассмотреть 1234[999]7 <= 108 = 100000000. Нижняя граница тоже задана, когда вместо звёздочки ни одной цифры не будет 12347.

    i=12347

#Вместо звёздочки ноль разрядов
if i%141==0:
    print(i, i//141)

#Вместо звёздочки один разряд
for x in '0123456789':
    s = '1234' + x + '7'
    i=int(s)
    if i%141==0:
        print(i, i//141)

#Вместо звёздочки два разряда
for x in '0123456789':
    for y in '0123456789':
        s = '1234' + x + y + '7'
        i=int(s)
        if i%141==0:
            print(i, i//141)

#Вместо звёздочки три разряда
for x in '0123456789':
    for y in '0123456789':
        for z in '0123456789':
            s = '1234' + x + y + z + '7'
            i = int(s)
            if i%141==0:
                print(i, i//141)

    Таким образом, нужно рассмотреть, когда вместо звёздочки ноль разрядов, один разряд, два разряда и три разряда.

    Каждый разряд перебираем как цифры (символы). Формируем строку s, а затем её переводим в тип int.

    Когда два разряда или три разряда нужно перебирать строку с помощью вложенных циклов.

    Ответ:

    1234737 8757
    12341307 87527
    12342717 87537
    12344127 87547
    12345537 87557
    12346947 87567
    12348357 87577
    12349767 87587

    Источник

    Слайд 1

    Решение задачи 25 ЕГЭ Тема : Обработка целых чисел. Проверка делимости Что проверяется: Умение создавать собственные программы (10–20 строк) для обработки целочисленной информации. Дрынова Светлана Викторовна

    Слайд 2

    Что нужно знать : можно использовать простой перебор без оптимизации; пусть необходимо перебрать все целые числа на отрезке [ a ; b ] и подсчитать, для скольких из них выполняется некоторое условие; общая структура цикла перебора записывается так ( Python ): count = 0 for n in range(a, b+1): if условие выполнено : count += 1 print( count ) проверку условия удобно оформить в виде функции, возвращающей логическое значение ( True / False ), но можно этого и не делать

    Слайд 3

    проверить делимость числа n на число d можно с помощью операции взятия остатка от деления n на x : если остаток равен 0, число n делится на x нацело проверка делимости на языке Python выглядит так: if n % d == 0: print (“Делится”) else : print (“Не делится”) для определения числа делителей натурального числа n можно использовать цикл, в котором перебираются все возможные делители d от 1 до n , при обнаружении делителя увеличивается счётчик делителей: count = 0 for d in range(1, n+1): if n % d == 0: count += 1 print ( count ) # вывести количество делителей

    Слайд 4

    перебор делителей можно оптимизировать, учитывая, что наименьший из пары делителей, таких что a  b = n , не превышает квадратного корня из n ; нужно только аккуратно обработать случай, когда число n представляет собой квадрат другого целого числа (можно не оптимизировать для нахождения количества делителей); если требуется определить не только количество делителей, но и сами делители, нужно сохранять их в массиве в языке Python удобно использовать динамический массив: сначала он пуст, а при обнаружении очередного делителя этот делитель добавляется в массив: divs = [] for d in range (1, n +1): # перебор всех возможных делителей if n % d == 0: # если нашли делитель d divs . append ( d ) # то добавили его в массив

    Слайд 5

    простое число n делится только на 1 и само на себя, причём единица не считается простым числом; таким образом, любое простое число имеет только два делителя для определения простоты числа можно считать общее количество его делителей; если их ровно два, то число простое, если не два – не простое: nDel = 0 # количество делителей числа for d in range (1, n +1): # все возможные делители if n % d == 0: nDel += 1 # нашли ещё делитель if nDel == 2: print( ” Число простое ” ) else: print ( “Число составное” )

    Слайд 6

    работу программы можно ускорить: если уже найдено больше двух делителей, то число не простое и можно досрочно закончит работу цикла с помощью оператора break : nDel = 0 # количество делителей числа for d in range (1, n +1): # все возможные делители if n % d == 0: nDel += 1 # нашли ещё делитель if nDel > 2: # уже не простое число break # досрочный выход из цикла if nDel == 2: print ( “Число простое” ) else : print ( “Число составное” ) другой вариант – считать количество делителей числа на отрезке [2; n– 1]; как только хотя бы один такой делитель будет найден, можно завершить цикл, потому что число явно не простое:

    Слайд 7

    Задача 1. Напишите программу, которая ищет среди целых чисел, принадлежащих числовому отрезку [174457; 174505], числа, имеющие ровно два различных натуральных делителя, не считая единицы и самого числа. Решение 1. Для того чтобы вообще избавиться от работы с дробными числами, удобно заменить условие d <= sqrt (n) на равносильное условие, использующее только целые значения: d*d <= n ; при этом, правда, придётся заменить цикл for на while и вручную увеличивать переменную d в конце каждой итерации цикла divCount = 2 # нужное количество делителей for n in range (174457, 174505+1): divs = [] d = 2 while d*d <= n: if n % d == 0: divs.append ( d ) if n//d > d: divs.append ( n//d ) if len ( divs ) > divCount : break d += 1 if len ( divs ) == divCount : print ( * divs )

    Слайд 8

    Решение 2. Так как здесь нам нужно выводить все делители, кроме единицы и самого числа, в цикле перебора делителей начинаем с 2 и включаем  N, если очередной делитель d –это точный квадратный корень, добавляем в список делителей только один делитель, если нет – то добавляем пару делителей ( d , x // d ): from math import sqrt divCount = 2 # нужное количество делителей for n in range(174457, 174505+1): divs = [] q = int (sqrt(n)) for d in range(2,q+1): if n % d == 0: if d == n//d: divs = divs + [d] else: divs = divs + [d, n//d] if len ( divs ) > divCount : break if len ( divs ) == divCount : print( * divs )

    Слайд 9

    Решение 3. Можно построить массив делителей на языке Python можно и с помощью генератора списка: for n in range ( 174457; 174505 +1): divs = [d for d in range(1, n+1) if n % d == 0] if len ( divs ) = = 2 : print( * divs ) Аналогично можно построить массив делителей, удовлетворяющих заданному условию, например, всех чётных делителей: for n in range( 174457 , 174457 +1): divs = [d for d in range(1, n+1) if n % d == 0 and d % 2 == 0 ] if len ( divs ) == 4 : print( * divs )

    Слайд 10

    Решение 4. ещё один вариант программы (с функцией, которая возвращает массив делителей): def allDivisors (n): divs = [] for d in range(1,n+1): if n % d == 0: divs.append (d) return divs for n in range( 174457; 174505 +1): divs = allDivisors (n) if len ( divs ) == 2 : print( * divs )

    Слайд 11

    Решение 5. (программа без массива): учитывая, что в этой задаче нас интересуют только два делителя, можно вместо массива использовать две дополнительных переменные for i in range (174457, 174505+1): k = 0; for j in range (2, i ): if i % j == 0: k = k + 1; if k == 1: d1 = j if k == 2: d2 = j if k == 2: print( d1, d2 )

    Слайд 12

    Задача 2.Напишите программу, которая ищет среди целых чисел, принадлежащих числовому отрезку [3532000; 3532160], простые числа. Выведите все найденные простые числа в порядке возрастания, слева от каждого числа выведите его номер по порядку. from math import sqrt count = 0 for n in range(3532000, 3532160+1): prime = True for d in range(2, round(sqrt(n))): if n % d == 0: prime = False break if prime: count += 1 print( count, n ) Решение 1.

    Слайд 13

    Решение 2. компактное решение, использующее встроенную функцию all – она возвращает логическое значение T rue , если все элементы переданного ей списка равны T ru e ; возвращает F alse , если хотя бы один из них равен F alse ( если у ‘n’ нет делителей от 2 до корня из n т.е. все ‘d’ дают остаток отличный от нуля): count=0 for n in range(3532000,3532160+1): if all( n%d !=0 for d in range(2,round(n**0.5)+1) ): count+=1 print ( count,n )

    Слайд 14

    Решение 3. вариант с функцией isPrime , которая возвращает логическое значение True (истина) для простых чисел и False (ложь) для составных: from math import sqrt def isPrime (n): for d in range(2, round(sqrt(n)+1) ): if n % d == 0: return False return True count = 0 for n in range(3532000, 3532160+1): if isPrime (n): count += 1 print( count, n )

    Источник

    Оглавление:

    • 1 Задача — Вывести количество делителей и делители числа
      — программирование на Pascal, Си, Кумир, Basic-256, Python

      • 1.1 Pascal
      • 1.2 Язык Си
      • 1.3 Python
      • 1.4 Basic-256

    Задача — Вывести количество делителей и делители числа
    — программирование на Pascal, Си, Кумир, Basic-256, Python

    В введенном промежутке натуральных чисел найти те, количество делителей у которых не меньше введенного значения. Для найденных чисел вывести на экран количество делителей и все делители.

    Пользователь вводит числовой промежуток — минимальное (a) и максимальное (b) числа. После этого запрашивается искомое количество делителей.

    Во внешнем цикле перебираются натуральные числа от a до b. При этом в конце каждой итерации a увеличивается на 1, тем самым приближаясь к b.

    В теле внешнего цикла вводится счетчик (m) количества делителей очередного натурального числа. Далее во внутреннем цикле перебираются числа (i) от 1 до a. Если i делит нацело a, то счетчик увеличивается на 1.

    После этого значение счетчика сравнивается с требуемым количеством делителей. Если у очередного натурального числа не меньше делителей, чем требуется, то оно и количество делителей выводятся на экран. После этого в цикле снова ищутся делители, но теперь уже они просто выводятся на экран.

    Pascal

    var
    a,b,n,m,i: word;

    begin
    write(‘Числовой промежуток: ‘);
    readln(a,b);
    write(‘Количество делителей не менее… ‘);
    readln(n);
    while a <= b do begin
    m := 0;
    for i:=1 to a do
    if a mod i = 0 then m := m + 1;
    if m >= n then begin
    write(a,’ — ‘, m,’ — ‘);
    for i:=1 to a do
    if a mod i = 0 then write(i,’ ‘);
    writeln;
    end;
    a := a + 1;
    end;
    end. Числовой промежуток: 21 44
    Количество делителей не менее… 5
    24 — 8 — 1 2 3 4 6 8 12 24
    28 — 6 — 1 2 4 7 14 28
    30 — 8 — 1 2 3 5 6 10 15 30
    32 — 6 — 1 2 4 8 16 32
    36 — 9 — 1 2 3 4 6 9 12 18 36
    40 — 8 — 1 2 4 5 8 10 20 40
    42 — 8 — 1 2 3 6 7 14 21 42
    44 — 6 — 1 2 4 11 22 44

    Язык Си

    #include <stdio.h>
    main() {
    unsigned int a,b,m,n,i;
    printf(«Числовой промежуток: «);
    scanf(«%d%d»,&a,&b);
    printf(«Минимальное количество делителей: «);
    scanf(«%d»,&n);
    while (a <= b) {
    m = 0;
    for (i=1; i<=a; i++)
    if (a%i == 0) m += 1;
    if (m >= n) {
    printf(«%d — %d — «, a, m);
    for (i=1; i<=a; i++)
    if (a%i == 0) printf(«%d «, i);
    printf(«n»);
    }
    a += 1;
    }
    } Числовой промежуток: 343 434
    Минимальное количество делителей: 20
    360 — 24 — 1 2 3 4 5 6 8 9 10 12 15 18 20 24 30 36 40 45 60 72 90 120 180 360
    420 — 24 — 1 2 3 4 5 6 7 10 12 14 15 20 21 28 30 35 42 60 70 84 105 140 210 420
    432 — 20 — 1 2 3 4 6 8 9 12 16 18 24 27 36 48 54 72 108 144 216 432

    Python

    a = int(input(«Минимум: «))
    b = int(input(«Максимум: «))
    n = int(input(«Минимальное количество делителей: «))
    while a <= b:
    m = 0
    for i in range(1,a+1):
    if a%i == 0:
    m += 1
    if m >= n:
    print(a,’-‘,m,end=’ — ‘)
    for i in range(1,a+1):
    if a%i == 0:
    print(i,end=’ ‘)
    print()
    a += 1 Минимум: 45
    Максимум: 66
    Минимальное количество делителей: 7
    48 — 10 — 1 2 3 4 6 8 12 16 24 48
    54 — 8 — 1 2 3 6 9 18 27 54
    56 — 8 — 1 2 4 7 8 14 28 56
    60 — 12 — 1 2 3 4 5 6 10 12 15 20 30 60
    64 — 7 — 1 2 4 8 16 32 64
    66 — 8 — 1 2 3 6 11 22 33 66

    Basic-256

    input «Минимум: «, a
    input «Максимум: «, b
    input «Минимальное количество делителей: «, n
    while a <= b
    m = 0
    for i=1 to a
    if a%i = 0 then m = m + 1
    next i
    if m >= n then
    print a + » — » + m + » — «;
    for i=1 to a
    if a%i = 0 then print i + » «;
    next i
    print
    endif
    a = a + 1
    endwhile Минимум: 150
    Максимум: 177
    Минимальное количество делителей: 12
    150 — 12 — 1 2 3 5 6 10 15 25 30 50 75 150
    156 — 12 — 1 2 3 4 6 12 13 26 39 52 78 156
    160 — 12 — 1 2 4 5 8 10 16 20 32 40 80 160
    168 — 16 — 1 2 3 4 6 7 8 12 14 21 24 28 42 56 84 168

    Did you find apk for android? You can find new Free Android Games and apps.

    Источник

    Добавить комментарий