-
Кольцо с единицей
Из определения
кольца не вытекает существование или
отсутствие в нем единицы е. Но, как
было доказано в алгебре на I
курсе, если в кольце К единичный
элемент существует, то только один. В
нулевом кольце
![]()
,
состоящем только из одного нуля, элемент
0 одновременно является и единицей,
т.к.
![]()
.
Определение.
Нулевое кольцо К, в котором есть
единичный элемент е, называется
кольцом с единицей.
Примерами колец
с единицей являются: кольцо целых чисел
Z; кольцо рациональных
чисел Q; кольцо
действительных чисел R;
кольцо комплексных чисел С; кольцо
матриц n-го порядка над
полями R, Q,
C, единицей этих
колец является матрица

Примерами кольца,
в котором нет единицы, служит кольцо
целых чисел, кратных произвольно
выбранному натуральному числу m>1;
в частности, нет единицы в кольце четных
целых чисел.
Пусть К –
произвольное кольцо с единицей е.
Для всякого отличного от нуля элемента
а
К
справедливы равенства

Отсюда следует,
что
![]()
.
Если для элемента
а
К
в кольце К существует обратный
элемент а-1, то только один.
Элемент е является обратным для
самого себя. Из равенства
![]()
следует, что элемент – е также
является обратным для самого себя.
Элемент 0 не имеет обратного элемента,
т.к.
![]()
для любого а
К.
Если для а
К
в кольце К существует обратный
элемент а-1, то а , по
определению делителей элемента кольца,
является делителем e,
т.к.
![]()
.
Поэтому можно
принять такое определение.
Определение
2. Элемент а, для которого в
кольце К существует обратный элемент
а-1, называется обратимым
или делителем единицы.
Пример.
Кольцо Z является
самым простым примером коммутативного
кольца, в котором только 1 и -1 являются
делителями единицы.
Теорема 3. Множество
К* всех делителей единицы
кольца К является группой по
умножению.
□ Пусть элементы
![]()
,
т.е. являются делителями единицы е.
Значит
и
![]()
,
а это значит, что а-1 и ab
тоже являются делителями е, а, значит,
содержатся в К*, е также
содержится в К*. Поэтому
К* является мультипликативной
группой.
Группа К*
называется группой делителей единичного
элемента, или группой обратимых
элементов кольца К.■
-
Делители нуля. Область целостности
Пусть К –
произвольное кольцо. Для
![]()
выполняется равенство
![]()
.
Следовательно, каждый элемент кольца
является делителем нуля. Но в теории
колец принимают следующее определение
делителей нуля.
Определение
3. Элементы а
и b
кольца К
называются делителями
нуля, если
![]()
и
![]()
,
но ab=0,
при этом а
называется левым,
а b
– правым
делителем нуля.
В коммутативных
кольцах очевидно, что понятия левого и
правого делителей нуля совпадают.
Пример 1.
В качестве кольца К рассмотрим
кольцо классов вычетов Zm,
где m – некоторое составное
целое число, например,
![]()
.
Тогда классы вычетов
![]()
и
![]()
отличные от нулевого класса
![]()
,
а их произведение равно нулевому классу:
![]()
.
Следовательно, классы
и
являются делителями нуля
в кольце Zm.
Пример 2.
В кольце Rn
матриц n-го порядка
(![]()
)
с действительными элементами матрицы
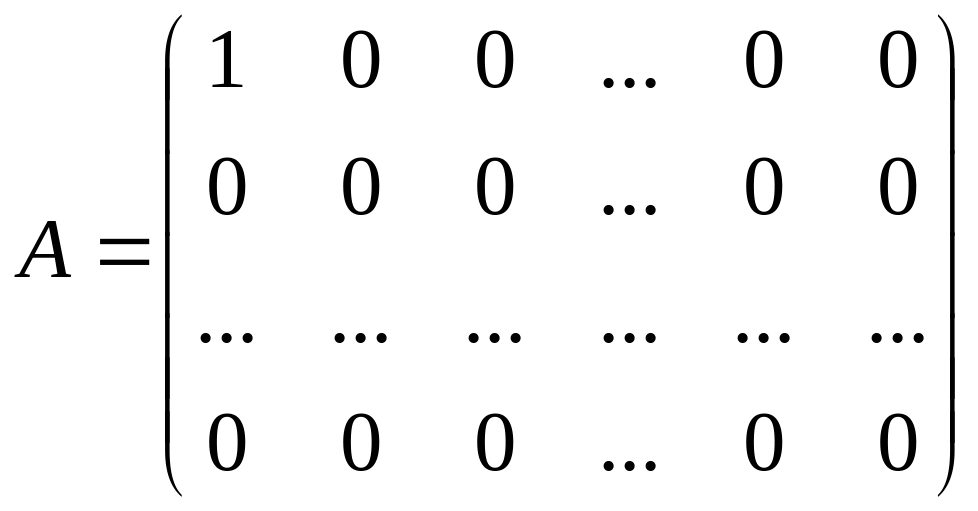
и

являются делителями
в кольце Rn.
Определение
4. Коммутативное кольцо с единицей,
в котором нет делителей нуля, называется
областью целостности.
Пример 1.
Очевидно, что всякое числовое кольцо
является областью целостности.
Пример 2.
Областью целостности является всякое
поле Р, т.к.
![]()
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Обратимый элемент — элемент кольца с единицей, для которого существует обратный элемент относительно умножения. Другое название — делитель единицы. Также, в основном в переводах с английского, встречается название единица, что может вызывать путаницу с единичным элементом (в английских источниках используются два разных термина: unit element и Identity element[1]).
Иначе говоря, элемент кольца 

где 
Множество всех обратимых элементов кольца образует мультипликативную группу, называемую группой обратимых элементов (реже группой единиц). Эта группа всегда непустая, так как содержит как минимум единицу кольца.
Ассоциированные элементы[править | править код]
Если 



Обычно термин делитель единицы и понятие ассоциированного элемента употребляются для областей целостности.
Группа единиц[править | править код]
Обратимые элементы кольца R образуют группу U(R) по умножению, группу единиц кольца R. Другие общепринятые обозначение — R×, R* и E(R) (от немецкого Einheit).
В коммутативном кольце R группа единиц U(R) действует на R посредством умножения. Орбиты этих действий называются множествами ассоциированных элементов; другими словами, имеется отношение эквивалентности ~ на R, называемое ассоциированностью, где
- r ~ s
означает, что существует единица u, такая, что r = us.
Можно показать, что U — это функтор из категории колец в категорию групп: каждый гомоморфизм колец f : R → S порождает гомоморфизм групп U(f) : U(R) → U(S), поскольку f отображает единицы в единицы.
Кольцо R является телом тогда и только тогда, когда U(R) = R {0}.
Примеры[править | править код]
- В кольце целых чисел два делителя единицы: +1 и −1.
- В кольце вычетов по модулю m обратимыми элементами являются вычеты, взаимно простые с модулем m. Они образуют мультипликативную группу кольца вычетов.
- В кольце гауссовых целых чисел четыре делителя единицы:
.
- В кольце многочленов над полем любой ненулевой элемент поля коэффициентов (как многочлен нулевой степени) является делителем единицы.
Примечания[править | править код]
- ↑ Сравните Unit divisor Архивная копия от 19 декабря 2021 на Wayback Machine и Unital ring Архивная копия от 19 декабря 2021 на Wayback Machine
Литература[править | править код]
- Ван дер Варден Б. Л. Алгебра. — М.: Наука, 1975.
- Зарисский О., Самюэль П. Коммутативная алгебра. — М.: ИЛ, 1963. — Т. 1.
- Ленг С. Алгебра. — М.: Мир, 1967.
Кольца, тела, поля
Определение 2.5. Кольцом называют алгебру сигнатура которой состоит из двух бинарных и двух нульарных операций, причем для любых
выполняются равенства:
1) ;
2) ;
3) ;
4) для каждого существует элемент
, такой, что
;
5) ;
6) ;
7) .
Операцию называют сложением кольца, операцию умножением кольца, элемент
— нулем кольца, элемент
— единицей кольца.
Равенства 1–7, указанные в определении, называют аксиомами кольца. Рассмотрим эти равенства с точки зрения понятия группы и моноида.
Аксиомы кольца 1-4 означают, что алгебра , сигнатура которой состоит только из операций сложения кольца
и нуля кольца
, является абелевой группой. Эту группу называют аддитивной группой кольца
и говорят также, что по сложению кольцо есть коммутативная (абелева) группа.
Аксиомы кольца 5 и 6 показывают, что алгебра , сигнатура которой включает только умножение кольца
и единицу кольца
, есть моноид. Этот моноид называют мультипликативным моноидом кольца
и говорят, что по умножению кольцо есть моноид.
Связь между сложением кольца и умножением кольца устанавливает аксиома 7, согласно которой операция умножения дистрибутивна относительно операции сложения.
Учитывая сказанное выше, отметим, что кольцо — это алгебра с двумя бинарными и двумя нульарными операциями , такая, что:
1) алгебра — коммутативная группа;
2) алгебра — моноид;
3) операция (умножения кольца) дистрибутивна относительно операции
(сложения кольца).
Замечание 2.2. В литературе встречается иной состав аксиом кольца, относящихся к умножению. Так, могут отсутствовать аксиома 6 (в кольце нет 1) и аксиома 5 (умножение не ассоциативно). В этом случае выделяют ассоциативные кольца (к аксиомам кольца добавляют требование ассоциативности умножения) и кольца с единицей. В последнем случае добавляются требования ассоциативности умножения и существования единицы.
Определение 2.6. Кольцо называют коммутативным, если его операция умножения коммутативна.
Пример 2.12. а. Алгебра есть коммутативное кольцо. Отметим, что алгебра
кольцом не будет, поскольку
— коммутативный моноид, но не группа.
б. Рассмотрим алгебру с операцией
сложения по модулю
и
(умножения по модулю
). Последняя аналогична операции сложения по модулю
равно остатку от деления на
числа
. Эта алгебра есть коммутативное кольцо, которое называют кольцом вычетов по модулю
.
в. Алгебра — коммутативное кольцо, что следует из свойств пересечения и симметрической разности множеств.
г. Пример некоммутативного кольца дает множество всех квадратных матриц фиксированного порядка с операциями сложения и умножения матриц. Единицей этого кольца является единичная матрица, а нулем — нулевая.
д. Пусть — линейное пространство. Рассмотрим множество всех линейных операторов, действующих в этом пространстве.
Напомним, что суммой двух линейных операторов и
называют оператор
, такой, что
Произведением линейных операторов и
называют линейный оператор
, такой, что
для любого
.
Используя свойства указанных операций над линейными операторами, можно показать, что множество всех линейных операторов, действующих в пространстве , вместе с операциями сложения и умножения операторов образует кольцо. Нулем этого кольца служит нулевой оператор, а единицей — тождественный оператор.
Это кольцо называют кольцом линейных операторов в линейном пространстве .
Основные аксиомы и тождества кольца
Аксиомы кольца называют также основными тождествами кольца. Тождество кольца — это равенство, справедливость которого сохраняется при подстановке вместо фигурирующих в нем переменных любых элементов кольца. Основные тождества постулируются, и из них затем могут быть выведены как следствия другие тождества. Рассмотрим некоторые из них.
Напомним, что аддитивная группа кольца коммутативна и в ней определена операция вычитания.
Теорема 2.8. В любом кольце выполняются следующие тождества:
1) ;
2) ;
3) .
Докажем тождество . Запишем для произвольного а:
Итак, . Последнее равенство можно рассматривать как уравнение в аддитивной группе кольца относительно неизвестного элемента
. Так как в аддитивной группе любое уравнение вида
имеет единственное решение
, то
. Тождество
доказывается аналогично.
Докажем теперь тождество . Имеем
откуда . Точно так же можно доказать, что
.
Докажем третью пару тождеств. Рассмотрим первое из них. С учетом доказанного выше имеем
т.е. тождество справедливо. Второе тождество этой пары доказывается аналогично.
Следствие 2.1. В любом кольце справедливо тождество .
Указанное следствие вытекает из второго тождества теоремы 2.8 при и
.
Первые два тождества из доказанных в теореме 2.8 выражают свойство, называемое аннулирующим свойством нуля в кольце. Третья же пара тождеств указанной теоремы выражает свойство дистрибутивности операции умножения кольца относительно операции вычитания. Таким образом, производя вычисления в любом кольце, можно раскрывать скобки и менять знаки так же, как и при сложении, вычитании и умножении действительных чисел.
Кольца и делители нуля
Ненулевые элементы и
кольца
называют делителями нуля, если
или
. Пример кольца с делителем нуля дает любое кольцо вычетов по модулю
, если
— составное число. В этом случае произведение по модулю
любых
и
, дающих при обычном перемножении число, кратное
, будет равно нулю. Например, в кольце вычетов по модулю 6 элементы 2 и 3 являются делителями нуля, поскольку
. Другой пример дает кольцо квадратных матриц фиксированного порядка (не меньшего двух). Например, для матриц второго порядка имеем
При отличных от нуля и
приведенные матрицы являются делителями нуля.
По умножению кольцо является только моноидом. Поставим вопрос: в каких случаях кольцо по умножению будет группой? Прежде всего заметим, что множество всех элементов кольца, в котором , не может образовывать группы по умножению, так как нуль не может иметь обратного. Действительно, если предположить, что такой элемент
существует, то, с одной стороны,
, а с другой —
, откуда
. Это противоречит условию
. Таким образом, поставленный выше вопрос можно уточнить так: в каких случаях множество всех ненулевых элементов кольца образует группу по умножению?
Если в кольце имеются делители нуля, то подмножество всех ненулевых элементов кольца не образует группы по умножению уже хотя бы потому, что это подмножество не замкнуто относительно операции умножения, т.е. существуют ненулевые элементы, произведение которых равно нулю.
Кольцо, в котором множество всех ненулевых элементов по умножению образует группу, называют телом, коммутативное тело — полем, а группу ненулевых элементов тела (поля) по умножению — мультипликативной группой этого тела (поля). Согласно определению, поле есть частный случай кольца, в котором операции обладают дополнительными свойствами. Выпишем все свойства, выполнение которых требуется для операций поля. Их еще называют аксиомами поля.
Поле есть алгебра , сигнатура которой состоит из двух бинарных и двух нульарных операций, причем справедливы тождества:
1) ;
2) ;
3) ;
4) для каждого существует элемент
, такой, что
;
5) ;
6) ;
7) ;
8) для каждого , отличного от
, существует элемент
, такой, что
;
9) .
Пример 2.13. а. Алгебра есть поле, называемое полем рациональных чисел.
б. Алгебры и
есть поля, называемые полями действительных и комплексных чисел соответственно.
в. Примером тела, не являющегося полем, может служить алгебра кватернион.
Итак, мы видим, что известным законам сложения и умножения чисел соответствуют аксиомы поля. Занимаясь числовыми расчетами, мы “работаем в полях”, а именно имеем дело преимущественно с полями рациональных и вещественных чисел, иногда “переселяемся” в поле комплексных чисел.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Простейшие свойства делимости в коммутативном кольце.
Пусть  — коммутативное кольцо и а, b — его элементы.
— коммутативное кольцо и а, b — его элементы.
ОПРЕДЕЛЕНИЕ. Элемент b называется делителем а, а элемент а — кратным b, если в  существует такой элемент с, что
существует такой элемент с, что 
Запись  означает, что b есть делитель а. Запись
означает, что b есть делитель а. Запись  означает, что а делится на b, или а кратно b.
означает, что а делится на b, или а кратно b.
Элемент с называется общим делителем а и b, если  Аналогично определяется общий делитель нескольких элементов кольца.
Аналогично определяется общий делитель нескольких элементов кольца.
Элементы а и b кольца  называются ассоциированными в
называются ассоциированными в  , если а
, если а 
Элемент а называется обратимым в  или делителем единицы, если существует в
или делителем единицы, если существует в  такой элемент 6, что
такой элемент 6, что  в этом случае пишут
в этом случае пишут 
Делитель единицы делит любой элемент кольца. Если  — поле, то обратим любой его элемент, отличный от нуля.
— поле, то обратим любой его элемент, отличный от нуля.
Рассмотрим простейшие свойства делимости в коммутативном кольце.
ПРЕДЛОЖЕНИЕ 3.1. Отношение делимости в кольце рефлексивно и транзитивно, т.е. является предпорядком,
ПРЕДЛОЖЕНИЕ 3.2. Общий делитель двух или нескольких элементов кольца является делителем суммы и произведения этих элементов.
ПРЕДЛОЖЕНИЕ 3.3. Если элемент с делит хотя бы один из элементов  то он делит произведение этих элементов.
то он делит произведение этих элементов.
ПРЕДЛОЖЕНИЕ 3.4. Отношение ассоциированности в коммутативном кольце является отношением эквивалентности.
ПРЕДЛОЖЕНИЕ 3.5. Если а ассоциировано с b и  , то
, то 
Доказательство предложений 3.1-3.5 предоставляется читателю.
ПРЕДЛОЖЕНИЕ 3.6. В области целостности элементы а и b ассоциированы тогда и только тогда, когда существует такой обратимый в кольце элемент и, что 
Доказательство. Пусть  — область целостности и а, b — элементы, ассоциированные в
— область целостности и а, b — элементы, ассоциированные в  . Если один из элементов а, b равен нулю, то необходимо равен нулю и другой. Тогда
. Если один из элементов а, b равен нулю, то необходимо равен нулю и другой. Тогда 
Предположим, что  Тогда существуют такие ненулевые элементы и и v, что
Тогда существуют такие ненулевые элементы и и v, что  . Следовательно,
. Следовательно,  . Поскольку
. Поскольку  — область целостности и
— область целостности и  из последнего равенства следует, что
из последнего равенства следует, что  Таким образом, элемент и обратим в
Таким образом, элемент и обратим в  и
и 
Предположим теперь, что  где
где  — обратимый элемент кольца
— обратимый элемент кольца  тогда
тогда  Следовательно, а и b ассоциированы в
Следовательно, а и b ассоциированы в  .
.
ПРЕДЛОЖЕНИЕ 3.7. Пусть А — множество всех обратимых элементов коммутативного кольца  Тогда алгебра
Тогда алгебра  где
где  -унарная операция, ставящая в соответствие элементу а из А обратный элемент
-унарная операция, ставящая в соответствие элементу а из А обратный элемент  является группой.
является группой.
Доказательство предложения 3.7 предоставляется читателю.
Делитель единицы
- Делитель единицы
-
Делитель единицы — элемент
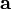 кольца, являющийся обратимым, то есть таким, что существует такой элемент b, что
кольца, являющийся обратимым, то есть таким, что существует такой элемент b, что 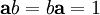 . Множество всех обратимых элементов кольца образует группу. Если
. Множество всех обратимых элементов кольца образует группу. Если 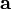 — единица, то элементы
— единица, то элементы  и
и 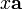 называются ассоциированными с x.
называются ассоциированными с x.Обычно понятия единицы и ассоциированного элемента употребляются для областей целостности.
Литература
- Ван дер Варден Б. Л. Алгебра — М.:, Наука, 1975.
- Зарисский О., Самюэль П. Коммутативная алгебра, т.1 — М.:, ИЛ, 1963.
- Ленг С. Алгебра — М.:, Мир, 1967.
Wikimedia Foundation.
2010.
Смотреть что такое “Делитель единицы” в других словарях:
-
ДЕЛИТЕЛЬ ЕДИНИЦЫ — элемент а кольца (коммутативного с единицей 1), для к рого существует обратный, т. е. такой элемент 6, что ab 1. В теории алгебраических чисел и алгебраических функций Д. е. наз. также единицами. O. A. Иванова … Математическая энциклопедия
-
Делитель (значения) — Делитель (математика) Наибольший общий делитель Делитель нуля в абстрактной алгебре Делитель единицы Делитель напряжения Делитель тока Делитель мощности Делитель комбинационное логическое устройство в электронике Делитель потока дроссельный или… … Википедия
-
Делитель — Делимость одно из основных понятий арифметики и теории чисел, связаное с операцией деления. Содержание 1 Определение 2 Обозначения 3 Связанные определения … Википедия
-
Наибольший общий делитель — Наибольшим общим делителем (НОД) для двух целых чисел m и n называется наибольший из их общих делителей.[1] Пример: для чисел 70 и 105 наибольший общий делитель равен 35. Наибольший общий делитель существует и однозначно определён, если хотя бы… … Википедия
-
Гауссовы целые числа — (гауссовы числа, целые комплексные числа) это комплексные числа, у которых как вещественная, так и мнимая часть целые числа. Введены Гауссом в 1825 году. Содержание 1 Определение и операции 2 Теория делимости … Википедия
-
Обратимый элемент — Не следует путать с единичным элементом. Обратимым элементом, а также единицей кольца или делителем единицы, называется всякий элемент кольца, для которого существует обратный элемент относительно умножения, то есть такой элемент , что , где e… … Википедия
-
АЛГЕБРАИЧЕСКОЕ ЧИСЛО — Ч комплексное (в частности, действительное) число, являющееся корнем многочлена с рациональными коэффициентами, из к рых не все равны нулю. Если Ч А. ч., то среди всех многочленов с рациональными коэффициентами, имеющих своим корнем, существует… … Математическая энциклопедия
-
Единица — 1) наименьшее из натуральных чисел n = 1. При умножении любого числа на 1 получается то же самое число. 2) Во множестве предметов или элементов, подвергающихся изучению, часто бывает определена какая либо операция (например, сложение или… … Большая советская энциклопедия
-
АРИФМЕТИКА — искусство вычислений, производимых с положительными действительными числами. Краткая история арифметики. С глубокой древности работа с числами подразделялась на две различные области: одна касалась непосредственно свойств чисел, другая была… … Энциклопедия Кольера
-
P-1 метод Полларда — (читается как п 1 метод Полларда) один из методов факторизации целых чисел. Метод был впервые опубликован британским математиком Джоном М. Поллардом в 1974 году в статье журнала Математические Труды Кэмбриджеского Философского… … Википедия

