Как найти delta a

Как рассчитать дельту

Четвертой буквой греческого алфавита, «дельтой», в науке принято называть изменение какой-либо величины, погрешность, приращение. Записывается этот знак различными способами: чаще всего в виде небольшого треугольника Δ перед буквенным обозначением величины. Но иногда можно встретить и такое написание δ, либо латинской строчной буквой d, реже латинской прописной – D.

Инструкция

Для нахождения изменения какой-либо величины вычислите или измерьте ее начальное значение (x1).

Вычислите или измерьте конечное значение этой же величины (x2).

Найдите изменение данной величины по формуле: Δx=x2-x1. Например: начальное значение напряжения электрической сети U1=220В, конечное значение – U2=120В. Изменение напряжения (или дельта напряжения) будет равно ΔU=U2–U1=220В-120В=100В

Для нахождения абсолютной погрешности измерения определите точное или, как его иногда называют, истинное значение какой-либо величины (x0).

Возьмите приближенное (при измерении – измеренное) значение этой же величины (x).

Найдите абсолютную погрешность измерения по формуле: Δx=|x-x0|. Например: точное число жителей города – 8253 жителя (х0=8253), при округлении этого числа до 8300 (приближенное значение х=8300). Абсолютная погрешность (или дельта икс) будет равна Δx=|8300-8253|=47, а при округлении до 8200 (х=8200), абсолютная погрешность – Δx=|8200-8253|=53. Таким образом, округление до числа 8300 будет более точным.

Для сравнения значений функции F(х) в строго фиксированной точке х0 со значениями этой же функции в любой другой точке х, лежащей в окрестностях х0, используются понятия «приращение функции» (ΔF) и «приращение аргумента функции» (Δx). Иногда Δx называют «приращением независимой переменной». Найдите приращение аргумента по формуле Δx=x-x0.

Определите значения функции в точках х0 и х и обозначьте их соответственно F(х0) и F(х).

Вычислите приращение функции: ΔF= F(х)- F(х0). Например: необходимо найти приращение аргумента и приращение функции F(х)=х˄2+1 при изменении аргумента от 2 до 3. В этом случае х0 равно 2, а х=3.
Приращение аргумента (или дельта икс) будет Δx=3-2=1.
F(х0)= х0˄2+1= 2˄2+1=5.
F(х)= х˄2+1= 3˄2+1=10.
Приращение функции (или дельта эф) ΔF= F(х)- F(х0)=10-5=5

Обратите внимание

Вычитать нужно не из большего числа меньшее, а из конечного значения (не важно: больше оно или меньше) начальное!

Полезный совет

При нахождении Δ все значения используйте только в одинаковых единицах измерения.

Источники:

• Справочник по математике для средних учебных заведений, А.Г. Цыпкин, 1983

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Математики любят греческие буквы и используют дельту заглавной буквы, которая выглядит как треугольник (∆), чтобы символизировать изменение. Когда дело доходит до пары чисел, дельта обозначает разницу между ними. Вы получаете эту разницу, используя основную арифметику и вычитая меньшее число из большего. В некоторых случаях числа располагаются в хронологическом порядке или в некоторой другой упорядоченной последовательности, и вам, возможно, придется вычесть большее из меньшего, чтобы сохранить порядок. Это может привести к отрицательному числу.

Абсолютная Дельта

Если у вас есть случайная пара чисел, и вы хотите узнать дельту – или разницу – между ними, просто вычтите меньшее из большего. Например, дельта между 3 и 6 составляет (6 – 3) = 3.

Если одно из чисел отрицательно, сложите два числа вместе. Операция выглядит следующим образом: (6 – {-3}) = (6 + 3) = 9. Легко понять, почему в этом случае дельта больше, если вы визуализируете два числа на оси x графика. Число 6 равно 6 единицам справа от оси, но отрицательное значение 3 равно 3 единицам слева. Другими словами, он дальше от 6, чем от положительного 3, который находится справа от оси.

Вам нужно запомнить некоторую арифметику вашей начальной школы, чтобы найти дельту между парой дробей. Например, чтобы найти дельту между 1/3 и 1/2, вы должны сначала найти общий знаменатель. Для этого умножьте знаменатели вместе, а затем умножьте числитель в каждой дроби на знаменатель другой дроби. В этом случае это выглядит так: 1/3 x 2/2 = 2/6 и 1/2 x 3/3 = 3/6. Вычтите 2/6 из 3/6, чтобы получить дельту, которая составляет 1/6.

Относительная дельта

Относительная дельта сравнивает разницу между двумя числами, A и B, в процентах от одного из чисел. Базовая формула A – B / A x100. Например, если вы зарабатываете 10 000 долларов в год и жертвуете 500 долларов на благотворительность, относительная дельта вашей зарплаты составляет 10 000 – 500/10 000 x 100 = 95%. Это означает, что вы пожертвовали 5 процентов своей зарплаты, а у вас осталось 95 процентов. Если вы зарабатываете 100 000 долларов в год и делаете то же самое пожертвование, вы сохранили 99, 5% своей зарплаты и пожертвовали только 0, 5% на благотворительность, что не очень впечатляет в момент налогообложения.

От дельты к дифференциалу

Вы можете представить любую точку на двумерном графике парой чисел, которые обозначают расстояние от точки до пересечения осей в направлениях x (горизонтальное) и y (вертикальное). Предположим, у вас есть две точки на графике, называемые точкой 1 и точкой 2, и эта точка 2 находится дальше от пересечения, чем точка 1. Дельта между значениями x этих точек – ∆ x – определяется как (x ₂ – x ₁), и y для этой пары точек равно (y ₂ – y ₁). Когда вы делите ∆y на ∆x, вы получаете наклон графика между точками, который говорит вам, как быстро x и y изменяются относительно друг друга.

Склон предоставляет полезную информацию. Например, если вы наносите время вдоль оси x и измеряете положение объекта при его перемещении в пространстве по оси Y, наклон графика показывает среднюю скорость объекта между этими двумя измерениями.

Скорость может быть не постоянной, и вы можете узнать скорость в определенный момент времени. Дифференциальное исчисление обеспечивает концептуальный трюк, который позволяет вам сделать это. Хитрость заключается в том, чтобы представить две точки на оси х и позволить им бесконечно сближаться. Отношение ∆y к ∆x – ∆y / ∆x – при приближении ∆x к 0 называется производной. Обычно это выражается как dy / dx или как df / dx, где f – алгебраическая функция, которая описывает граф. На графике, на котором время (t) отображается на горизонтальной оси, «dx» становится «dt», а производная dy / dt (или df / dt) является мерой мгновенной скорости.

Как рассчитать дельту между двумя числами

Как рассчитать дельту между двумя числами – Рецепты

Содержание

Математики любят греческие буквы, и они используют дельту заглавной буквы, которая выглядит как треугольник (∆), чтобы обозначить изменение. Когда дело доходит до пары чисел, дельта означает разницу между ними. Вы получаете эту разницу, используя простую арифметику и вычитая меньшее число из большего. В некоторых случаях числа расположены в хронологическом порядке или в другой упорядоченной последовательности, и вам, возможно, придется вычесть большее из меньшего, чтобы сохранить порядок. Это может привести к отрицательному числу.

Абсолютная дельта

Если у вас есть случайная пара чисел и вы хотите узнать дельту – или разницу – между ними, просто вычтите меньшее из большего. Например, дельта между 3 и 6 составляет (6 – 3) = 3.

Если одно из чисел отрицательное, сложите два числа. Операция выглядит так: (6 – <-3>) = (6 + 3) = 9. Легко понять, почему дельта больше в этом случае, если вы визуализируете два числа на оси x графика. Число 6 находится на 6 единиц справа от оси, а отрицательное 3 – на 3 единицы слева.Другими словами, она дальше от 6, чем положительная 3, которая находится справа от оси.

Чтобы найти дельту между парой дробей, вам нужно запомнить некоторые из школьных арифметических действий. Например, чтобы найти дельту между 1/3 и 1/2, вы должны сначала найти общий знаменатель. Для этого умножьте знаменатели вместе, а затем умножьте числитель каждой дроби на знаменатель другой дроби. В данном случае это выглядит так: 1/3 x 2/2 = 2/6 и 1/2 x 3/3 = 3/6. Вычтите 2/6 из 3/6, чтобы получить дельту, которая равна 1/6.

Относительная дельта

Относительная дельта сравнивает разницу между двумя числами, A и B, в процентах от одного из чисел. Основная формула – A – B / A x100. Например, если вы зарабатываете 10 000 долларов в год и жертвуете 500 долларов на благотворительность, относительная разница в вашей зарплате составляет 10 000–500 / 10 000 x 100 = 95%. Это означает, что вы пожертвовали 5 процентов своей зарплаты, и у вас все еще осталось 95 процентов. Если вы зарабатываете 100000 долларов в год и делаете такое же пожертвование, вы оставляете 99,5 процента своей зарплаты и жертвуете только 0,5 процента на благотворительность, что не столь впечатляюще с точки зрения налоговой отчетности.

От дельты к дифференциалу

Вы можете представить любую точку на двумерном графике парой чисел, которые обозначают расстояние от точки до пересечения осей в направлениях x (по горизонтали) и y (по вертикали). Предположим, у вас есть две точки на графике, называемые точкой 1 и точкой 2, и эта точка 2 находится дальше от пересечения, чем точка 1. Дельта между значениями x этих точек – ∆ x – задается выражением (x₂ – Икс₁), а ∆ y для этой пары точек есть (y₂ – у₁). Когда вы делите ∆y на ∆x, вы получаете наклон графика между точками, который показывает, насколько быстро x и y изменяются относительно друг друга.

Наклон дает полезную информацию. Например, если вы наносите время на ось x и измеряете положение объекта во время его перемещения в пространстве по оси y, наклон графика показывает вам среднюю скорость объекта между этими двумя измерениями.

Однако скорость может быть непостоянной, и вы можете узнать скорость в определенный момент времени. Дифференциальное исчисление предоставляет концептуальный трюк, который позволяет вам это делать. Уловка состоит в том, чтобы представить две точки на оси x и позволить им приблизиться друг к другу бесконечно близко. Отношение ∆y к ∆x – ∆y / ∆x – когда ∆x приближается к 0, называется производной. Обычно это выражается как dy / dx или как df / dx, где f – алгебраическая функция, описывающая график. На графике, на котором время (t) отложено по горизонтальной оси, «dx» становится «dt», а производная dy / dt (или df / dt) является мерой мгновенной скорости.

ru.mosg-portal.com

Что такое Дельта в математике? – Наука

Содержание:

По мере развития математики в течение истории математикам требовалось все больше и больше символов для представления чисел, функций, наборов и уравнений, которые выходили на свет. Поскольку большинство ученых имели некоторое понимание греческого языка, буквы греческого алфавита были легким выбором для этих символов. В зависимости от области математики или естественных наук, греческая буква «дельта» может символизировать различные понятия.

+ Изменить

Верхний регистр дельта (Δ) часто означает «изменение» или «изменение» в математике. Например, если переменная «x» обозначает движение объекта, то «Δx» означает «изменение в движении». Ученые часто используют это математическое значение дельты в физике, химии и технике, и оно часто встречается в словесных задачах.

дискриминантный

В алгебре дельта верхнего регистра (Δ) часто представляет дискриминант полиномиального уравнения, обычно это квадратное уравнение. Например, с учетом квадратичного ax² + bx + c дискриминант этого уравнения будет равен b² – 4ac, и будет выглядеть так: Δ = b² – 4ac. Дискриминант дает информацию о корнях квадратиков: в зависимости от значения Δ квадратик может иметь два действительных корня, один действительный корень или два комплексных корня.

В геометрии дельта в нижнем регистре (δ) может представлять угол в любой геометрической форме. Это потому, что геометрия имеет свои корни в работе Евклида в древней Греции, а затем математики отмечали свои углы греческими буквами. Поскольку буквы просто представляют углы, знание греческого алфавита и его порядка не является необходимым, чтобы понять их значение в этом контексте.

Частные производные

Производная функции является мерой бесконечно малых изменений в одной из ее переменных, а римская буква «d» представляет производную. Частичные производные отличаются от обычных производных тем, что функция имеет несколько переменных, но рассматривается только одна переменная: остальные переменные остаются фиксированными. Дельта в нижнем регистре (δ) представляет частные производные, поэтому частная производная функции “f” выглядит следующим образом: δf над δx.

Кронекер Дельта

Дельта в нижнем регистре (δ) также может иметь более специфическую функцию в продвинутой математике. Например, дельта Кронекера представляет собой взаимосвязь между двумя целочисленными переменными, которая равна 1, если две переменные равны, и 0, если они не равны. Большинству изучающих математику не придется беспокоиться об этих значениях дельты до тех пор, пока их обучение не станет очень продвинутым

Как рассчитать уравнение с дельта

1.3 РЕШЕНИЕ ТИПОВЫХ ЗАДАЧ ПО ТЕМЕ “ХИМИЧЕСКАЯ ТЕРМОДИНАМИКА И ТЕРМОХИМИЯ”
(для нехимических специальностей)

1. Рассчита й те Δ H o ₂₉₈ химическо й реак ц ии Na₂O(т) + H₂O(ж) → 2NaOH(т)
по значениям стандартных теплот образования веществ (, см. таблицу 1 приложения). Укажите тип реак ц и (экз о- или эндотермическая).

По данным таблицы 1 приложения, стандартные энтальпии образования Na₂O(т), H₂O(ж) и NaOH (т) при 298К равны соответственно –416, –286 и –427,8 кДж/моль. Используя следствие из закона Гесса, рассчитываем Δ H o ₂₉₈ химическо й реак ц ии :

Δ H o ₂₉₈ = 2( NaOH,т ) – [(Na₂O,т) + (H₂O,ж)] = 2 · (– 427,8) –
– [–416 + (–286)] = –153,6 кДж.

2. Определите, как изменяется энтропия при протекании химического процесса Na₂O(т) + H₂O(ж) → 2NaOH(т).

В данном процессе при взаимодействии 1 моль кристаллического и 1 моль жидкого вещества образуется 2 моль кристаллического вещества. Следовательно, система переходит в состояние с меньшим беспорядком, и энтропия уменьшается ( Δ S 0).

3. Рассчита й те величину Δ S o ₂₉₈ для про ц есса
Na₂O(т) + H₂O(ж) → 2NaOH(т), используя значения стандартных энтропи й веществ (см. таблицу 1 приложения).

Используя справочные данные: S o ( NaOH,т ) = 64,16 Дж/(моль · К),
S o (Na₂O,т) = 75,5 Дж/(моль · К), S o (H₂O,ж) = 70 Дж/(моль · К), рассчитываем Δ S o ₂₉₈ :

Δ S o ₂₉₈ = 2 · S o ( NaOH , т ) – [ S o (Na₂O, т ) + S o (H₂O, ж )] = 2 · 64,16 – (75,5 + 70) =
= – 17,18 Дж / К .

4. Рассчита й те изменение энергии Гиббса ( Δ G o ₂₉₈ ) для про ц есса
Na₂O(т) + H₂O(ж) → 2NaOH(т) по значениям стандартных энергий Гиббса образования веществ (см. таблицу 1 приложения). Возможно ли самопроизвольное протекание реакции при стандартных условиях и 298К ?

При стандартных условиях и T=298К Δ G o ₂₉₈ можно рассчитать как разность суммарной энергии Гиббса образования продуктов реакции и суммарной энергии Гиббса образования исходных веществ. Необходимые справочные данные: ( NaOH,т ) = –381,1 кДж/моль, (Na₂O) = –378 кДж/моль, (H₂O,ж) = –237 кДж/моль.

Δ G o ₂₉₈ = 2 · ( NaOH,т ) – [(Na₂O,т) + (H₂O,ж)] = 2 · (–381,1) –
– [–378 + (–237)] = –147,2 кДж.

Значение Δ G o ₂₉₈ отрицательно, поэтому самопроизвольное протекание реакции возможно.

Ответ: –147,2 кДж; возможно.

5. Определите, возможно ли при 95 o С самопроизвольное протекание про ц есса Na₂O(т) + H₂O(ж) → 2NaOH(т). Ответ обосну й те, рассчитав величину изменения энергии Гиббса при данно й температуре.

Переведем температуру в шкалу Кельвина: Т=273+95=368К. Для расчета Δ G o ₃₆₈ воспользуемся уравнением:

Воспользуемся изменениями энтальпии и энтропии, рассчитанными для данного процесса в предыдущих задачах. При этом величину изменения энтропии необходимо перевести из Дж /К в кДж/К, поскольку значения Δ H и Δ G обычно измеряют в кДж.

–17,18 Дж /К = –0,01718 кДж/К

Δ G o ₃₆₈ = –153,6 – 368 · (–0,01718) = –147,3 кДж.

Таким образом, Δ G o ₃₆₈ o С возможно.

Ответ: –147,3 кДж; возможно.

6. Составьте термохимическое уравнение реакции взаимодействия Na₂O(т) и H₂O(ж), если при этом образуется 1 моль NaOH (т). В ответе приведите количество теплоты, указанное в термохимическом уравнении.

Коэффициенты в термохимическом уравнении имеют смысл молей. Поэтому допустимы дробные значения коэффициентов. 1 моль гидроксида натрия может образоваться из 1/2 моля оксида натрия и 1/2 моля воды. В задании 1 (см. выше) рассчитано, что при образовании 2 моль NaOH в данной реакции выделяется 153,6 кДж теплоты ( Δ H o ₂₉₈ = –153,6 кДж). Поэтому при образовании 1 моль NaOH количество выделившейся теплоты будет в 2 раза меньше, т.е. 76,8 кДж. В термохимическом уравнении количество выделяющейся теплоты указывают со знаком “плюс”: 1/2 Na₂O(т) + 1/2 H₂O(ж) → NaOH (т) + 76,8 кДж.

[spoiler title=”источники:”]

http://ru.mosg-portal.com/delta-math-6678201-3602

http://www.chem-astu.ru/chair/study/genchem/r1_3.htm

[/spoiler]

Как рассчитать дельту между двумя числами

Математики любят греческие буквы, и они используют дельту заглавной буквы, которая выглядит как треугольник (∆), чтобы обозначить изменение. Когда дело доходит до пары чисел, дельта означает разницу м

Содержание

Математики любят греческие буквы, и они используют дельту заглавной буквы, которая выглядит как треугольник (∆), чтобы обозначить изменение. Когда дело доходит до пары чисел, дельта означает разницу между ними. Вы получаете эту разницу, используя простую арифметику и вычитая меньшее число из большего. В некоторых случаях числа расположены в хронологическом порядке или в другой упорядоченной последовательности, и вам, возможно, придется вычесть большее из меньшего, чтобы сохранить порядок. Это может привести к отрицательному числу.

Абсолютная дельта

Чтобы найти дельту между парой дробей, вам нужно запомнить некоторые из школьных арифметических действий. Например, чтобы найти дельту между 1/3 и 1/2, вы должны сначала найти общий знаменатель. Для этого умножьте знаменатели вместе, а затем умножьте числитель каждой дроби на знаменатель другой дроби. В данном случае это выглядит так: 1/3 x 2/2 = 2/6 и 1/2 x 3/3 = 3/6. Вычтите 2/6 из 3/6, чтобы получить дельту, которая равна 1/6.

Относительная дельта

От дельты к дифференциалу

Наклон дает полезную информацию. Например, если вы наносите время на ось x и измеряете положение объекта во время его перемещения в пространстве по оси y, наклон графика показывает вам среднюю скорость объекта между этими двумя измерениями.

Источник

Дельта Формула

Дельта Формула (Содержание)

Что такое Дельта Формула?

В мире опционов или деривативов термин «дельта» относится к изменению стоимости опциона вследствие изменения стоимости его базового запаса. Другими словами, дельта измеряет скорость изменения стоимости опциона по отношению к движению стоимости базовой акции. Поскольку дельта преимущественно используется для стратегий хеджирования, она также известна как коэффициент хеджирования. Формула для дельты может быть получена путем деления изменения стоимости опциона на изменение стоимости его базового запаса. Математически это представляется как

Примеры формулы дельты (с шаблоном Excel)

Давайте рассмотрим пример, чтобы лучше понять расчет Delta.

Давайте возьмем пример товара X, который торговался по 500 долларов на товарном рынке месяц назад, и опцион колл для товара торговался с премией в 45 долларов при цене исполнения в 480 долларов. Сейчас товар продается по цене 600 долларов, а стоимость опциона выросла до 75 долларов. Рассчитать дельту опциона колл на основе предоставленной информации.

Дельта Δ рассчитывается по формуле, приведенной ниже

Давайте возьмем другой пример эталонного индекса, который в настоящее время торгуется на уровне 8000 долларов, в то время как опцион пут на индекс торгуется на уровне 150 долларов. Если индекс торговался по 7800 долларов в месяц назад, тогда как опцион пут торговался по 200 долларов, рассчитайте дельту опциона пут.

Дельта Δ рассчитывается по формуле, приведенной ниже

объяснение

Формула для дельты может быть рассчитана с помощью следующих шагов:

Шаг 3: Затем рассчитайте изменение значения опции, вычтя начальное значение опции (шаг 1) из окончательного значения опции (шаг 2).

Шаг 6: Затем рассчитайте изменение стоимости базового запаса, вычтя его начальное значение (шаг 4) из его окончательного значения (шаг 5).

Шаг 7: Наконец, формула для дельты может быть получена путем деления изменения стоимости опциона (шаг 3) на изменение стоимости базового запаса (шаг 6), как показано ниже.

Актуальность и использование формулы Delta

Калькулятор формулы Delta

Вы можете использовать следующий Delta Calculator

Рекомендуемые статьи

Источник

Кумулятивная дельта

Кумулятивная дельта – в трейдинге это показание индикатора, который считает совокупную разницу между сделками, прошедшими по цене ASK и BID. Кумулятивная дельта показывает разницу между рыночными покупками и продажи.

Дельта – что это простыми словами

В физико-математической науке дельтой является функция, которая отображает разницу между двух и более переменных. Так же, дельтой называется четвёртая буква греческого алфавита, после альфы, беты и гаммы. Именно, исходя из этих истоков, функция дельты записывается в виде треугольника. «Δ»! В сфере трейдинга дельта, как и полагается её формуле, показывает разницу некоторых переменных. А вот разницу, каких именно переменных, это ещё тот вопрос, который требует детального рассмотрения.

Например, дельта по футпринт, показывает разницу рыночных контрактов на покупку и рыночных контрактов на продажу. Ключевым словом здесь выступает прилагательное «рыночных». По причине того, что Market ордера́, сводятся исключительно с Limit заявками, то системе учёта дельты, нет необходимости дублировать объём контрактов. Отсюда вытекает вполне рациональный вывод. Отдельные ячейки, внутри каждого кластера, отображают результат дельт, исключительно ордеров по рынку, они же Market orders!

Внимание! Рекомендую вам ознакомиться с механикой рынка, что бы понять понятие кумулятивной дельты.

В свою очередь гистограмма индикатора дельта, суммирует все рыночные ордера за определённый период времени. Например, если мы используем 15-ти минутный таймфрейм, то бары гистограммы индикатора, отображают общий результат дельты, Market ордеров за 15 минут. Разумеется, что в расчёт дельты, берутся всё те же рыночные ордера. И ровно так же, как и в случае с «кластер дельта», здесь значения дельт, могут быть как положительными, так и отрицательными.

Что же касается такой разновидности дельта индикатора как, «динамический дельта профиль», так здесь всё аналогично. За исключением того, что данный горизонтальный профиль, указывает на преимущество покупателей и продавцов по отдельному ценовому уровню. Да. Вы можете возразить: «Так ведь кластер дельта отвечает за аналогичные результаты»?!

Мы с вами не согласны, так как кластер дельта (дельта по футпринт), отображает результаты разности, лишь за выбранный период времени. То бишь, на 15-ти минутном таймфрейме, отображается дельта по каждому ценовому уровню, только в рамках этих 15-ти минут. Тогда как динамический дельта профиль, суммирует все значения дельт за установленный трейдером временной отрезок!

Кумулятивная дельта основы.

Для кумулятивной дельты имеет ли значение масштаб таймфрейма

Cumulative – переводится как, совокупный, суммарный или накопительный. Из этого определения сразу становится понятно, что данный тип индикатора дельта, что-то накапливает или суммирует. Совершенно верно. Функция дельта с прилагательным «кумулятивная», подразумевает накопление всех дельт, от каждого бара гистограммы за выбранный период времени. И абсолютно не важно, какой масштаб фрейма мы с вами используем при торговле. Вернее важно, но лишь отчасти. Чтобы прояснить картину, рассмотрим один и тот же пример в 2-х вариантах:

Предположим, один из участников рынка, анализирует колебания цен, используя кумулятивную дельту. Важным условием в данном примере, является то, что в качестве фильтра, он использует дневной параметр «накопления». При этом он оптимистично настроен, анализировать и торговать финансовый актив, исключительно на таймфрейме Н1. То есть, его гистограмма индикатора, учитывает «часовые» дельты, с началом открытия биржи.

Теперь представим, что внутридневной трейдер из другого подъезда, так же использует в своей торговле дневную «накопительную» дельту. То есть, его гистограмма индикатора, так же рассчитывает показатели дельт, с момента открытия рынка. И, разумеется, тоже с эффектом «накопления». Но теперь этот персонаж предпочитает работать на 15-ти минутном масштабе. Так, его индикатор кумулятивного эффекта, будет отображать суммируемые значения дельт, относительно его рабочего таймфрейма.

На выше представленном скриншоте, продемонстрированы 2 снимка, которые в точности иллюстрируют придуманные выше примеры. Вопрос; для системы учёта накопительного эффекта, есть ли разница в таймфреймах, для кумулятивной дельты, с охватом расчёта в 1 день? Ответ; и да – есть разница, и нет – не имеет значение для самого индикатора Daily Cumulative Delta! Проясним картину, для полного исключения возможных вопросов и вероятно наивных утверждений, типа: «Как такое вообще может быть»? «Да неее. Так не бывает»!

Накопительный эффект кумулятивной дельты.

Здесь на самом деле всё очень даже просто. Если мы рассматриваем накопительный эффект кумулятивной дельты, относительно заданного параметра, то есть дневного периода. То в этом случае, для самого индикатора, не имеет абсолютно никакого значения, какой масштаб фрейма отображается на данный момент времени. Что при фрейме в 1 час, что при масштабе 15-ти минутных свеч. Дневная кумулятивная дельта, всё равно будет производить расчёты за весь текущий день.

Источник

Примеры работы функции ДЕЛЬТА для сравнения двух чисел в Excel

Функция ДЕЛЬТА в Excel используется для проверки двух числовых значений и возвращает два возможных варианта:

Примеры использования функции ДЕЛЬТА в Excel

Пример 1. В таблице Excel указаны значения независимой координаты X и значения зависимых координат Y1 и Y2 для двух разных функций. Определить количество пар совпадающих значений.

Вид исходной таблицы данных:

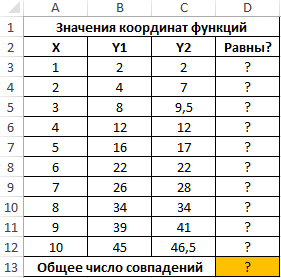
Для решения задачи сравним каждую пару значений зависимых координат Y1 и Y2 с помощью функции ДЕЛЬТА. В ячейке D3 запишем следующую формулу:

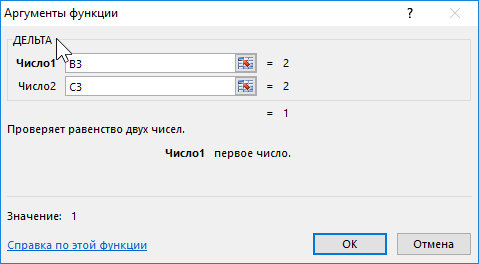
Полученное значение (1) свидетельствует о равенстве сравниваемых чисел. Протянем записанную в ячейке D3 формулу вниз до ячейки D12, чтобы автоматически рассчитать результаты для остальных значений Y1 и Y2:

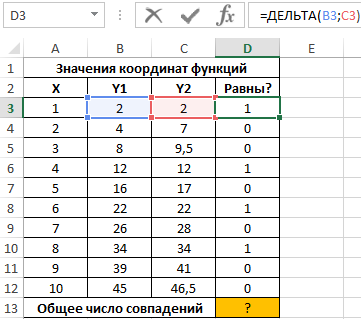
Для расчета числа пар совпадающих значений используем следующую функцию:

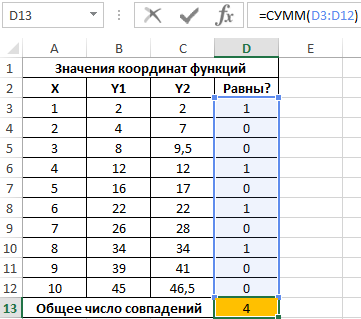
Всего 4 пары совпадений в значениях функций координат.

Калькулятор сроков возврата инвестиций в банковские депозиты

Пример 2. Реализовать калькулятор, который рассчитывает, сколько времени потребуется на получение определенной прибыли от депозита при известной начальной сумме вклада и годовой процентной ставки. Предусмотреть вывод сообщения об ошибке в случае, если одно или несколько исходных данных не указаны.

Вид формы для расчета:

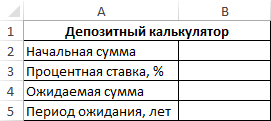
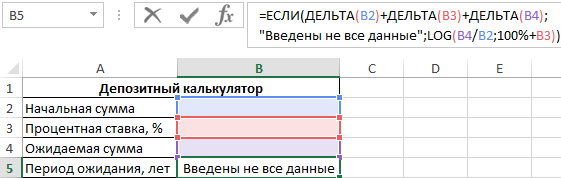
Поскольку для расчета используется логарифм из частного ожидаемой и начальной суммы с основанием в виде суммы депозита, выраженного в процентах (то есть 100%), и процентной ставки, то каждая ячейка из диапазона B2:B4 не должна являться пустой или принимать значение 0, поскольку логарифм нуля или логарифм с основанием 1 (100%) не может быть вычислен. Поэтому для расчетов используем следующую формулу:

В качестве проверочного выражения функции ЕСЛИ выступает значение, являющееся суммой возвращаемых результатов функциями ДЕЛЬТА. Последние сравнивают значения, содержащиеся в ячейках B2, B3 и B4 соответственно с 0 (второй аргумент явно не указан). Данный вариант записи соответствует логическому И (общий результат равен ИСТИНА, если все выражения, проверяемые функцией И, возвращают результат ИСТИНА). Полученное значение (0 или любое число от 1 до +∞) будет интерпретировано как ЛОЖЬ или ИСТИНА соответственно.

При незаполненных полях получим следующий результат:

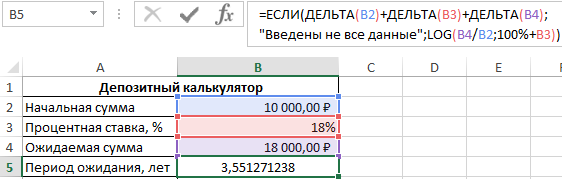
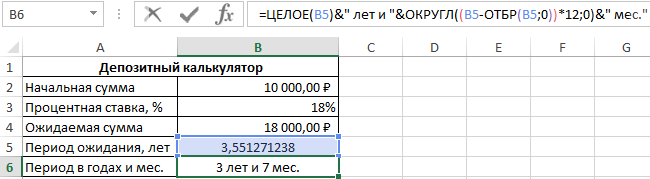
Напишем формулу для преобразования дробного числа в годы и месяцы:

В результате получим:

Расчет вероятности выпуска бракованной продукции на производстве в Excel

Пример 3. При изготовлении деталей на производственно-ремонтном заводе существует вероятность брака производимой продукции, которая равная коэффициенту 0,001. Определить, какая вероятность появления 10 выбракованных деталей (в этом случае вся партия считается браком) в партии из 35000 шт. Считается, что вероятностями ниже 10% можно пренебречь (то есть их приравнивают к нулю).

Вид исходной таблицы данных:

Для расчета используем следующую формулу:

Функция ОКРУГЛВНИЗ округляет до 0 все значения, которые меньше числа 0,01, то есть 10%-й вероятности. Функция ДЕЛЬТА принимает только один аргумент (выражение, полученное на основе формулы Пуассона для вычисления маловероятных случайных ситуаций), то есть сравнение выполняется с числом 0 (нуль).

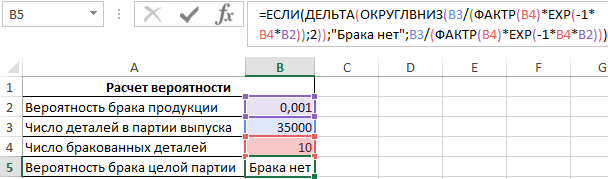
Если вычислять формулу поэтапно, будет видно, что вероятность по формуле Пуассона равна примерно 0,00974 число1 ;[число2])

Источник

Как работать с Дельтой?

Если говорить просто, то дельта – это разница между объёмами рыночных покупок и рыночных продаж за период времени. Этот термин вошёл в лексикон трейдеров в 2002 году, вместе с изобретением биржевого графика Футпринт и переходом трейдинга на цифровые платформы. Сегодня этот инструмент широко используется среди биржевых торговцев. В этой статье мы рассмотрим некоторые особенности этого индикатора и узнаем, как работать с Дельтой, чтобы улучшить торговую стратегию.

Дельта – суть и классификация

Чтобы понять суть термина Дельта, необходимо разобраться, из каких элементов она состоит. Известно, что на бирже есть, так называемые, агрессивные продавцы и агрессивные покупатели. Для упрощения классификации, сделки, которые инициируются агрессивными покупателями, торгуются по цене Ask, а сделки, проторгованные по инициативе агрессивных продавцов – по цене Bid.

Дельта же – это разница между этими двумя проторгованными объёмами. Чтобы рассчитать Дельту, необходимо от объёмов торговли по цене Ask отнять объёмы торговли по цене Bid. Дельта рассчитывается именно по рыночным, а не по лимитным ордерам, поскольку они бы только дублировали объёмы и усложнили задачу трейдеру.

Футпринт – детализация рынка

График Футпринт позволяет, образно говоря, препарировать каждый бар и увидеть, как изменялось значение Дельты внутри него. Для удобства визуализации, положительная Дельта (с преобладанием объёмов покупок) окрашивается зелёным цветом, причём, чем темнее оттенок, тем сильнее в конкретный момент были покупатели. Аналогично, отрицательная Дельта (с преобладанием объёмов продаж) на графике выкрашена в красный цвет, и чем темнее оттенок, тем интенсивнее велись продажи актива.

Что это знание даёт трейдеру? Возможность анализировать и делать более точные прогнозы. Поскольку поток ордеров и движение цены на рынке тесно взаимосвязаны, анализ графика Футпринт и Дельты может помочь трейдеру сориентироваться в текущей рыночной ситуации и принять верное решение.

Индикатор Дельта – читаем между строк

Увидеть индикатор Дельта можно в нижней части графика под каждым отдельным баром – н показывает суммарное значение Дельты для каждого из них. Также как и на графике Футпринт, здесь есть два цвета, показывающие преобладание отрицательного (продажи), либо положительного (покупки) потока ордеров.

Довольно часто именно индикатор Дельта позволяет внимательному трейдеру правильно интерпретировать рыночные движения, поскольку нередки случаи, когда при положительном потоке ордеров цена падает, а при отрицательном – растёт.

Подобные несостыковки ярко свидетельствуют о вмешательстве третьей силы – мощных рыночных игроков с большими капиталами. Если наблюдается падение цены при положительной Дельте, это означает, что крупный игрок защищает все свои рыночные продажи лимитными ордерами, тем самым без особых усилий и необходимости открывать дополнительные позиции толкает цену в нужном ему направлении.

Подобным образом действия биржевого крупняка прослеживаются и при преобладании отрицательной Дельты на растущей цене.

Внимательный взгляд на Дельту поможет трейдеру «читать между строк» — видеть поведение крупных игроков и замечать, а также прогнозировать истинный тренд, тогда как те, кто ориентируется исключительно на кривую цен, могут быть легко вытряхнуты из рынка.

Как работать с Дельтой – внимание к мелочам

Чтобы получить от этого ценного инструмента максимум пользы, нельзя пренебрегать показателями Дельты во время проведения технического анализа. При этом можно использовать и график Футпринт, и индикатор Дельта на каждом баре, и кумулятивную Дельту, отображающую суммарную Дельту за период времени, например, за торговую сессию.
Порой именно показатели Дельты способны дать трейдеру оптимальную точку для входа в рынок. К примеру, по длине отрицательной Дельты можно определить момент окончания периода накопления и войти в сделку прямо перед началом крупного восходящего тренда.

Чтобы научиться, как работать с Дельтой правильно и прибыльно для своей торговли, можно пройти курс в Школе трейдинга Александра Пурнова под руководством опытного наставника. Кроме того, после подписки на наш блог будут доступны ценные материалы на тематику трейдинга и финансов.

Источник