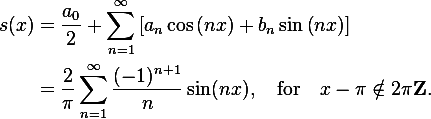Как найти дельта частота

Доброго времени суток.
Требуется помощь уважаемых радиолюбителей. Итак, постараюсь сформулировать вопрос:

Есть 2 синусоиды, скажем, 100мгц и 150мгц. Требуется определить дельту частот.
Порывшись в тех книжках, которые были у меня, найти ничего не удалось. Да и занятия в университете я посещал не слишком здорово, но, тем не менее, есть такая идея:

Из курса тригонометрии мы знаем, что sin(a-b) = sin(a)cos(b) – cos(a)sin(b). Получить косинусоиду из синусоиды, на сколько я могу помнить, не так уж и сложно. Останется перемножить их и вычесть. Таким образом мы получим синусоиду с частотой в разность частот a и b.

Вообще, данная задача ставится для того, чтобы по дельте частот определить скорость движущегося объекта(задача на эффект Допплера). Так что, осмелюсь задать еще один вопрос:

как имея синусоиду с частотой величиной в разницу двух частот(отправленной и полученной) определить саму величину (a-b)?
ведь все рассчеты производятся именно с этой величиной.
из моих догадок – перевести сигнал в цифру, а затем по его длительности уже вычислять нужные данные.
Надеюсь на вашу помощь. Заодно, на всякий случай, извиняюсь, если создал тему не в том разделе.

Чтобы описать колебательные процессы и отличить одни колебания от других, используют 6 характеристик. Они называются так (рис. 1):

• амплитуда,
• период,
• частота,
• циклическая частота,
• фаза,
• начальная фаза.

Такие величины, как амплитуду и период, можно определить по графику колебаний.

Начальную фазу, так же, определяют по графику, с помощью интервала времени (large Delta t), на который относительно нуля сдвигается начало ближайшего периода.

Частоту и циклическую частоту вычисляют из найденного по графику периода, по формулам. Они находятся ниже в тексте этой статьи.

А фазу определяют с помощью формулы, в которую входит интересующий нас момент времени t колебаний. Читайте далее.

Что такое амплитуда

Амплитуда – это наибольшее отклонение величины от равновесия, то есть, максимальное значение колеблющейся величины.

Измеряют в тех же единицах, в которых измерена колеблющаяся величина. К примеру, когда рассматривают механические колебания, в которых изменяется координата, амплитуду измеряют в метрах.

В случае электрических колебаний, в которых изменяется заряд, ее измеряют в Кулонах. Если колеблется ток – то в Амперах, а если – напряжение, то в Вольтах.

Часто обозначают ее, приписывая к букве, обозначающей амплитуду индекс «0» снизу.

К примеру, пусть колеблется величина ( large x ). Тогда символом ( large x_{0} ) обозначают амплитуду колебаний этой величины.

Иногда для обозначения амплитуды используют большую латинскую букву A, так как это первая буква английского слова «amplitude».

С помощью графика амплитуду можно определить так (рис. 2):

Что такое период

Когда колебания повторяются точно, изменяющаяся величина принимает одни и те же значения через одинаковые кусочки времени. Такой кусочек времени называют периодом.

Обозначают его обычно большой латинской буквой «T» и измеряют в секундах.

( large T left( c right) ) – период колебаний.

Одна секунда – достаточно большой интервал времени. Поэтому, хотя период и измеряют в секундах, но для большинства колебаний он будет измеряться долями секунды.

Чтобы по графику колебаний определить период (рис. 3), нужно найти два одинаковых значения колеблющейся величины. После, провести от этих значений к оси времени пунктиры. Расстояние между пунктирами – это период колебаний.

Период – это время одного полного колебания.

На графике период найти удобнее одним из таких способов (рис. 4):

Что такое частота

Обозначают ее с помощью греческой буквы «ню» ( large nu ).

Частота отвечает на вопрос: «Сколько полных колебаний выполняется за одну секунду?» Или же: «Сколько периодов умещается в интервал времени, равный одной секунде?».

Поэтому, размерность частоты — это единицы колебаний в секунду:

( large nu left( frac{1}{c} right) ).

Иногда в учебниках встречается такая запись ( large displaystyle nu left( c^{-1} right) ), потому, что по свойствам степени ( large  displaystyle frac{1}{c} = c^{-1} ).

Начиная с 1933 года частоту указывают в Герцах в честь Генриха Рудольфа Герца. Он совершил значимые открытия в физике, изучал колебания и доказал, что существуют электромагнитные волны.

Одно колебание в секунду соответствует частоте в 1 Герц.

[ large displaystyle boxed{ frac{ 1 text{колебание}}{1 text{секунда}} = 1 text{Гц} }]

Чтобы с помощью графика определить частоту, нужно на оси времени определить период. А затем посчитать частоту по такой формуле:

[ large boxed{ nu = frac{1}{T} }]

Существует еще один способ определить частоту с помощью графика колеблющейся величины. Нужно отмерить на графике интервал времени, равный одной секунде, и сосчитать количество периодов колебаний, уместившихся в этот интервал (рис. 5).

Что такое циклическая частота

Колебательное движение и движение по окружности имеют много общего – это повторяющиеся движения. Одному полному обороту соответствует угол (large 2pi) радиан. Поэтому, кроме интервала времени 1 секунда, физики используют интервал времени, равный (large 2pi) секунд.

Число полных колебаний для такого интервала времени, называется циклической частотой и обозначается греческой буквой «омега»:

( large displaystyle omega left( frac{text{рад}}{c} right) )

Примечание: Величину ( large omega ) так же называют круговой частотой, а еще — угловой скоростью (ссылка).

Циклическая частота отвечает на вопрос: «Сколько полных колебаний выполняется за (large 2pi) секунд?» Или же: «Сколько периодов умещается в интервал времени, равный (large 2pi) секунд?».

Обычная ( large nu ) и циклическая ( large omega ) частота колебаний связаны формулой:

[ large boxed{ omega = 2pi cdot nu }]

Слева в формуле количество колебаний измеряется в радианах на секунду, а справа – в Герцах.

Чтобы с помощью графика колебаний определить величину ( large omega ), нужно сначала найти период T.

Затем, воспользоваться формулой ( large displaystyle nu = frac{1}{T} ) и вычислить частоту ( large nu ).

И только после этого, с помощью формулы ( large omega = 2pi cdot nu ) посчитать циклическую ( large omega ) частоту.

Для грубой устной оценки можно считать, что циклическая частота превышает обычную частоту примерно в 6 раз численно.

Определить величину ( large omega ) по графику колебаний можно еще одним способом. На оси времени отметить интервал, равный (large 2pi), а затем, сосчитать количество периодов колебаний в этом интервале (рис. 6).

Что такое начальная фаза и как определить ее по графику колебаний

Отклоним качели на некоторый угол от равновесия и будем удерживать их в таком положении. Когда мы отпустим их, качели начнут раскачиваться. А старт колебаний произойдет из угла, на который мы их отклонили.

Такой, начальный угол отклонения, называют начальной фазой колебаний. Обозначим этот угол (рис. 7) какой-нибудь греческой буквой, например, (large varphi_{0} ).

(large varphi_{0} left(text{рад} right) ) — начальная фаза, измеряется в радианах (или градусах).

Начальная фаза колебаний – это угол, на который мы отклонили качели, перед тем, как их отпустить. Из этого угла начнется колебательный процесс.

Рассмотрим теперь, как величина (large varphi_{0} ) влияет на график колебаний (рис. 8). Для удобства будем считать, что мы рассматриваем колебания, которые происходят по закону синуса.

Кривая, обозначенная черным на рисунке, начинает период колебаний из точки t = 0. Эта кривая является «чистым», не сдвинутым синусом. Для нее величину начальной фазы (large varphi_{0} ) принимаем равной нулю.

Вторая кривая на рисунке обозначена красным цветом. Начало ее периода сдвинуто вправо относительно точки t = 0. Поэтому, для красной кривой, начавшей новый период колебаний спустя время (large Delta t), начальный угол (large varphi_{0} ) будет отличаться от нулевого значения.

Определим угол (large varphi_{0} ) с помощью графика колебаний.

Обратим внимание (рис. 8) на то, что время, лежащее на горизонтальной оси, измеряется в секундах, а величина (large varphi_{0} ) — в радианах. Значит, нужно связать формулой кусочек времени (large Delta t) и соответствующий ему начальный угол (large varphi_{0} ).

Как вычислить начальный угол по интервалу смещения

Алгоритм нахождения начального угла состоит из нескольких несложных шагов.

• Сначала определим интервал времени, обозначенный синими стрелками на рисунке. На осях большинства графиков располагают цифры, по которым это можно сделать. Как видно из рис. 8, этот интервал (large Delta t) равен 1 сек.
• Затем определим период. Для этого отметим одно полное колебание на красной кривой. Колебание началось в точке t = 1, а закончилось в точке t =5. Взяв разность между этими двумя точками времени, получим значение периода.

[large T = 5 – 1 = 4 left( text{сек} right)]

Из графика следует, что период T = 4 сек.

• Рассчитаем теперь, какую долю периода составляет интервал времени (large Delta t). Для этого составим такую дробь (large displaystyle frac{Delta t }{T} ):

[large frac{Delta t }{T} = frac{1}{4} ]

Полученное значение дроби означает, что красная кривая сдвинута относительно точки t = 0 и черной кривой на четверть периода.

• Нам известно, что одно полное колебание — один полный оборот (цикл), синус (или косинус) совершает, проходя каждый раз угол (large 2pi ). Найдем теперь, как связана найденная доля периода с углом (large 2pi ) полного цикла.

Для этого используем формулу:

[large boxed{ frac{Delta t }{T} cdot 2pi = varphi_{0} }]

(large displaystyle frac{1}{4} cdot 2pi = frac{pi }{2} =varphi_{0} )

Значит, интервалу (large Delta t) соответствует угол (large displaystyle frac{pi }{2} ) – это начальная фаза для красной кривой на рисунке.

• В заключение обратим внимание на следующее. Начало ближайшего к точке t = 0 периода красной кривой сдвинуто вправо. То есть, кривая запаздывает относительно «чистого» синуса.

Чтобы обозначить запаздывание, будем использовать знак «минус» для начального угла:

[large varphi_{0} = — frac{pi }{2} ]

Примечание: Если на кривой колебаний начало ближайшего периода лежит левее точки t = 0, то в таком случае, угол (large displaystyle frac{pi }{2} ) имеет знак «плюс».

Для не сдвинутого влево, либо вправо, синуса или косинуса, начальная фаза нулевая (large varphi_{0} = 0 ).

Для синуса или косинуса, сдвинутого влево по графику и опережающего обычную функцию, начальная фаза берется со знаком «+».

А если функция сдвинута вправо и запаздывает относительно обычной функции, величину (large varphi_{0} ) записываем со знаком «-».

Примечания:

1. Физики начинают отсчет времени из точки 0. Поэтому, время в задачах будет величиной не отрицательной.
2. На графике колебаний начальная фаза ( varphi_{0}) влияет на вертикальный сдвиг точки, из которой стартует колебательный процесс. Значит, можно для простоты сказать, что колебания имеют начальную точку.

Благодаря таким допущениям график колебаний при решении большинства задач можно изображать, начиная из окрестности нуля и преимущественно в правой полуплоскости.

Что такое фаза колебаний

Рассмотрим еще раз обыкновенные детские качели (рис. 9) и угол их отклонения от положения равновесия. С течением времени этот угол изменяется, то есть, он зависит от времени.

В процессе колебаний изменяется угол отклонения от равновесия. Этот изменяющийся угол называют фазой колебаний и обозначают (varphi).

Различия между фазой и начальной фазой

Существуют два угла отклонения от равновесия – начальный, он задается перед началом колебаний и, угол, изменяющийся во время колебаний.

Первый угол называют начальной ( varphi_{0}) фазой (рис. 10а), она считается неизменной величиной. А второй угол – просто ( varphi) фазой (рис. 10б) – это величина переменная.

Как на графике колебаний отметить фазу

На графике колебаний фаза (large varphi) выглядит, как точка на кривой. С течением времени эта точка сдвигается (бежит) по графику слева направо (рис. 11). То есть, в разные моменты времени она будет находиться на различных участках кривой.

На рисунке отмечены две крупные красные точки, они соответствуют фазам колебаний в моменты времени t1 и t2.

А начальная фаза на графике колебаний выглядит, как место, в котором находится точка, лежащая на кривой колебаний, в момент времени t=0. На рисунке дополнительно присутствует одна мелкая красная точка, она соответствует начальной фазе колебаний.

Как определить фазу с помощью формулы

Пусть нам известны величины (large omega) — циклическая частота и (large varphi_{0}) — начальная фаза. Во время колебаний эти величины не изменяются, то есть, являются константами.

Время колебаний t будет величиной переменной.

Фазу (large varphi), соответствующую любому интересующему нас моменту t времени, можно определить из такого уравнения:

[large boxed{ varphi = omega cdot t + varphi_{0} }]

Левая и правая части этого уравнения имеют размерность угла (т. е. измеряются в радианах, или градусах). А подставляя вместо символа t в это уравнение интересующие нас значения времени, можно получать соответствующие им значения фазы.

Что такое разность фаз

Обычно понятие разности фаз применяют, когда сравнивают два колебательных процесса между собой.

Рассмотрим два колебательных процесса (рис. 12). Каждый имеет свою начальную фазу.

Обозначим их:

( large varphi_{01}) – для первого процесса и,

( large varphi_{02}) – для второго процесса.

Определим разность фаз между первым и вторым колебательными процессами:

[large boxed{ Delta varphi = varphi_{01} —  varphi_{02} }]

Величина (large Delta varphi ) показывает, на сколько отличаются фазы двух колебаний, она называется разностью фаз.

Как связаны характеристики колебаний — формулы

Движение по окружности и колебательное движение имеют определенную схожесть, так как эти виды движения могут быть периодическими.

Поэтому, основные формулы, применимые для движения по окружности, подойдут так же, для описания колебательного движения.

• Связь между периодом, количеством колебаний и общим временем колебательного процесса:

[large boxed{ T cdot N = t }]

( large T left( c right) ) – время одного полного колебания (период колебаний);

( large N left( text{шт} right) ) – количество полных колебаний;

( large t left( c right) ) – общее время для нескольких колебаний;

• Период и частота колебаний связаны так:

[large boxed{ T = frac{1}{nu} }]

(large nu left( text{Гц} right) ) – частота колебаний.

• Количество и частота колебаний связаны формулой:

[large boxed{ N = nu cdot t}]

• Связь между частотой и циклической частотой колебаний:

[large boxed{ nu cdot 2pi = omega }]

(large displaystyle omega left( frac{text{рад}}{c} right) ) – циклическая (круговая) частота колебаний.

• Фаза и циклическая частота колебаний связаны так:

[large boxed{ varphi = omega cdot t + varphi_{0} }]

(large varphi_{0} left( text{рад} right) ) — начальная фаза;

(large varphi left( text{рад} right) ) – фаза (угол) в выбранный момент времени t;

• Между фазой и количеством колебаний связь описана так:

[large boxed{ varphi = N cdot 2pi }]

• Интервал времени (large Delta t ) (сдвигом) и начальная фаза колебаний связаны:

[large boxed{ frac{Delta t }{T} cdot 2pi = varphi_{0} }]

(large Delta t left( c right) ) — интервал времени, на который относительно точки t=0 сдвинуто начало ближайшего периода.

Гармонические колебания

На хабре было несколько статей по преобразованию Фурье и о всяких красивостях типа Цифровой Обработки Сигналов (ЦОС), но неискушённому пользователю совершенно не понятно, зачем всё это нужно и где, а главное как это применить.

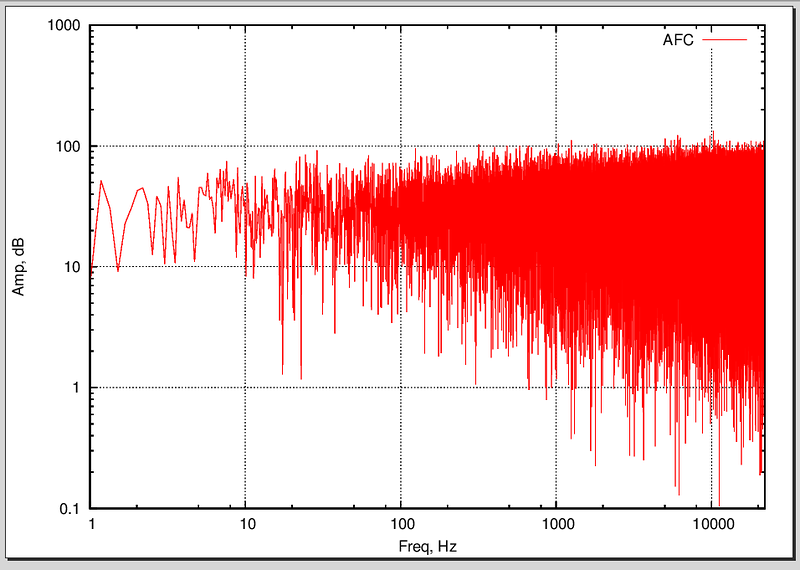
АЧХ шума.

Лично мне после прочтения этих статей (например, этой ) не стало понятно, что это и зачем оно нужно в реальной жизни, хотя было интересно и красиво.
Хочется не просто поглядеть красивые картинки, а так сказать, ощутить нутром, что и как работает. И я приведу конкретный пример с генерацией и обработкой звуковых файлов. Можно будет и послушать звук, и поглядеть его спектр, и понять, почему это так.
Статья не будет интересна тем, кто владеет теорией функций комплексной переменной, ЦОС и прочими страшными темами. Она скорее для любопытствующих, школьников, студентов и им сочувствующих :).

Сразу оговорюсь, я не математик, и многие вещи могу даже сказать неправильно (поправляйте личным сообщением), и данную статью пишу, опираясь на собственный опыт и собственное понимание текущих процессов. Если вы готовы, то поехали.

Пару слов о матчасти

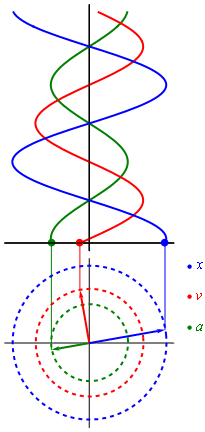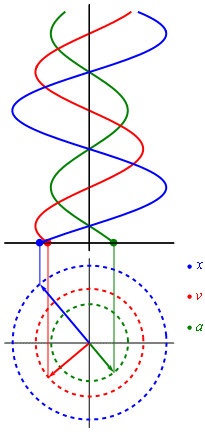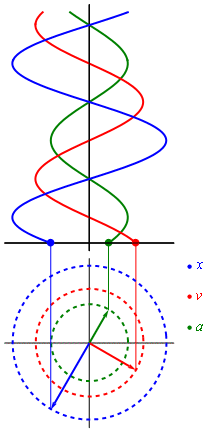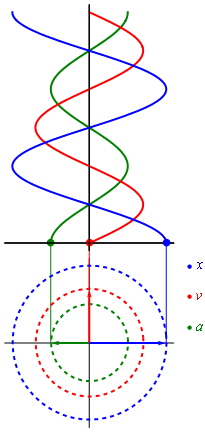
Если мы вспомним школьный курс математики, то для построения графика синуса мы использовали круг. В общем-то так и получается, что вращательное движение можно превратить в синусоиду (как и любое гармоническое колебание). Самое лучшая иллюстрация этого процесса приведена в википедии

Гармонические колебания

Т.е. фактически график синуса получается из вращения вектора, который описывается формулой:

f(x) = A sin (ωt + φ),

где A — длина вектора (амплитуда колебаний), φ — начальный угол (фаза) вектора в нулевой момент времени, ω — угловая скорость вращения, которая равна:

ω=2 πf, где f — частота в Герцах.

Как мы видим, что зная частоту сигнала, амплитуду и угол, мы можем построить гармонический сигнал.

Магия начинается тогда, когда оказывается, что представление абсолютно любого сигнала можно представить в виде суммы (зачастую бесконечной) различных синусоид. Иначе говоря, в виде ряда Фурье.
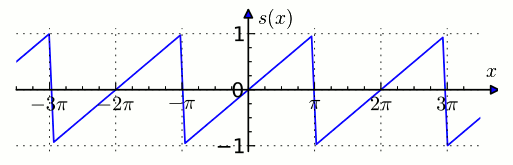
Я приведу пример из английской википедии. Для примера возьмём пилообразный сигнал.

Пилообразный сигнал

Его сумма будет представлена следующей формулой:

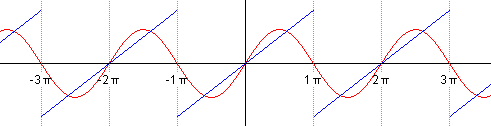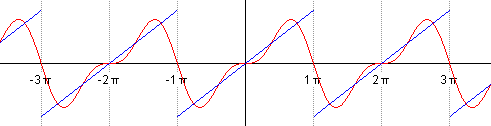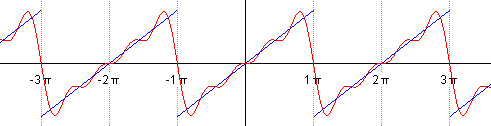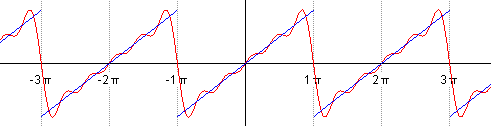
Если мы будем по очерёдно суммировать, брать сначала n=1, затем n=2 и т.д., то увидим, как у нас гармонический синусоидальный сигнал постепенно превращается в пилу:

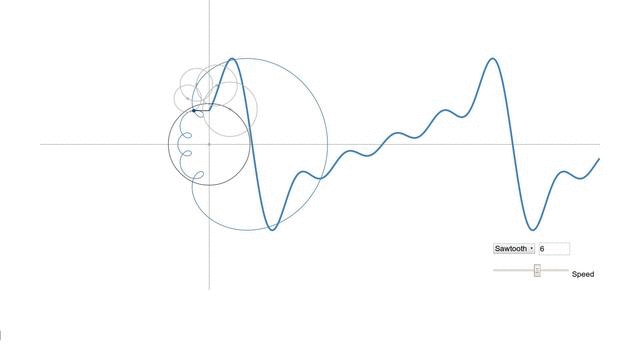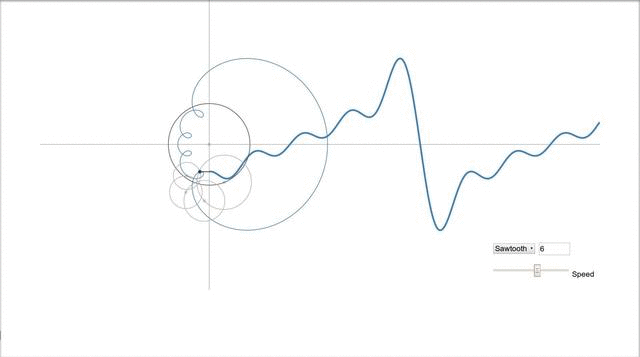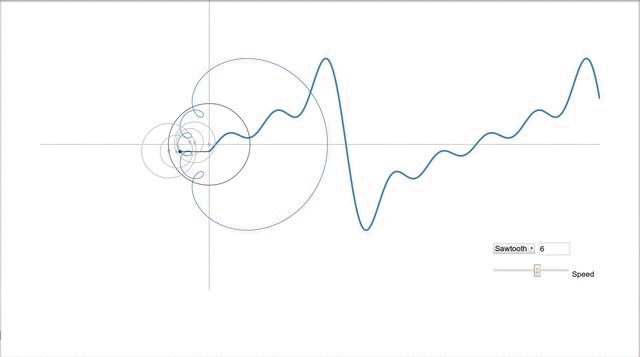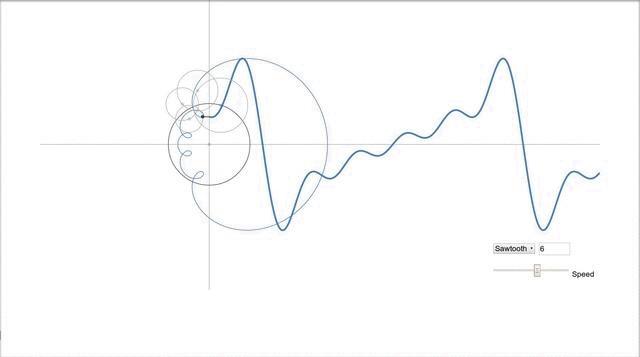
Наверное красивее всего это иллюстрирует одна программа, найденная мной на просторах сети. Выше уже говорилось, что график синуса является проекцией вращающегося вектора, а как же быть в случае более сложных сигналов? Это, как ни странно, проекция множества вращающихся векторов, а точнее их суммы, и выглядит это всё так:

Вектора рисуют пилу.

Вообще рекомендую сходить самим по ссылке и попробовать самим поиграться с параметрами, и посмотреть как меняется сигнал. ИМХО более наглядной игрушки для понимания я ещё не встречал.

Ещё следует заметить, что есть обратная процедура, позволяющая получить из данного сигнала частоту, амплитуду и начальную фазу (угол), которое называется Преобразование Фурье.

Разложение в ряд Фурье некоторых известных периодических функций (отсюда)

Я детально на нём останавливаться не буду, но покажу, как это можно применить по жизни. В списке литературы порекомендую то, где можно почитать подробнее о матчасти.

Переходим к практическим упражнениям!

Мне кажется, что каждый студент задаётся вопросом, сидя на лекции, например по матану: зачем мне весь этот бред? И как правило, не найдя ответа в обозримом будущем, к сожалению, теряет интерес к предмету. Поэтому я сразу покажу практическое применение данных знаний, а вы эти знания уже будете осваивать сами :).

Всё дальнейшее я буду реализовывать на сях. Делал всё, конечно, под Linux, но никакой специфики не использовал, по идее программа будет компилироваться и работать под другими платформами.

Для начала напишем программу для формирования звукового файла. Был взят wav-файл, как самый простой. Прочитать про его структуру можно тут.
Если кратко, то структура wav-файла описывается так: заголовок, который описывает формат файла, и далее идёт (в нашем случае) массив 16-ти битных данных (остроконечник) длиной: частота_дискретизации*t секунд или 44100*t штук.

Для формирования звукового файла был взят пример здесь. Я его немного модифицировал, исправил ошибки, и окончательная версия с моими правками теперь лежит на гитхабе тут

github.com/dlinyj/generate_wav

Сгенерируем двухсекундный звуковой файл с чистым синусом частотой 100 Гц. Для этого модифицируем программу таким образом:

#define S_RATE  (44100) //частота дискретизации
#define BUF_SIZE (S_RATE*10) /* 2 second buffer */
….

int main(int argc, char * argv[])
{
...
	float amplitude = 32000; //берём максимальную возможную амплитуду
	float freq_Hz = 100; //частота сигнала
	/* fill buffer with a sine wave */
	for (i=0; i<BUF_SIZE; i++)
	{

		buffer[i] +=(int)(amplitude * sin((float)(2*M_PI*i*freq_Hz/S_RATE))); 
	}
	write_wav("test.wav", BUF_SIZE, buffer, S_RATE);
 
	return 0;
}

Обращаю внимание, что формула чистого синуса соответствует той, о которой мы говорили выше. Амплитуда 32000 (можно было взять 32767) соответствует значению, которое может принимать 16-ти битное число (от минус 32767 до плюс 32767).

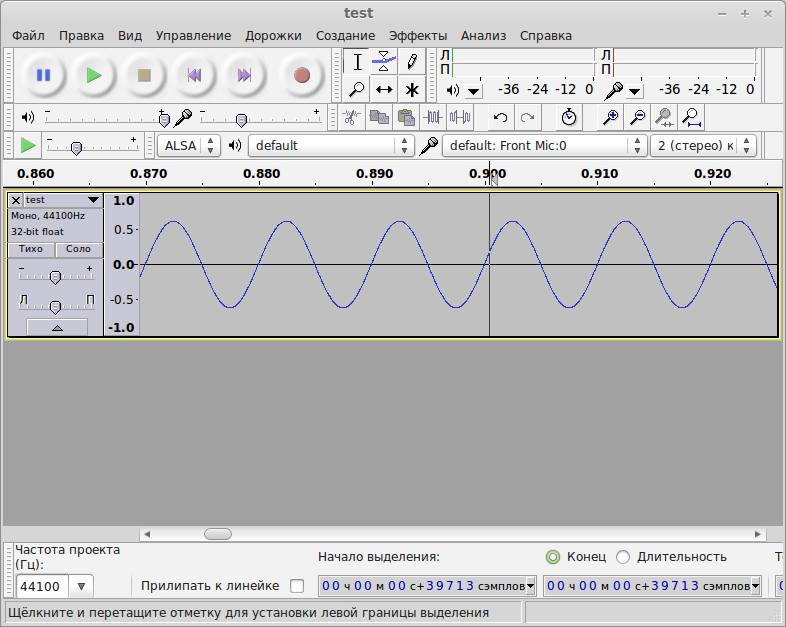
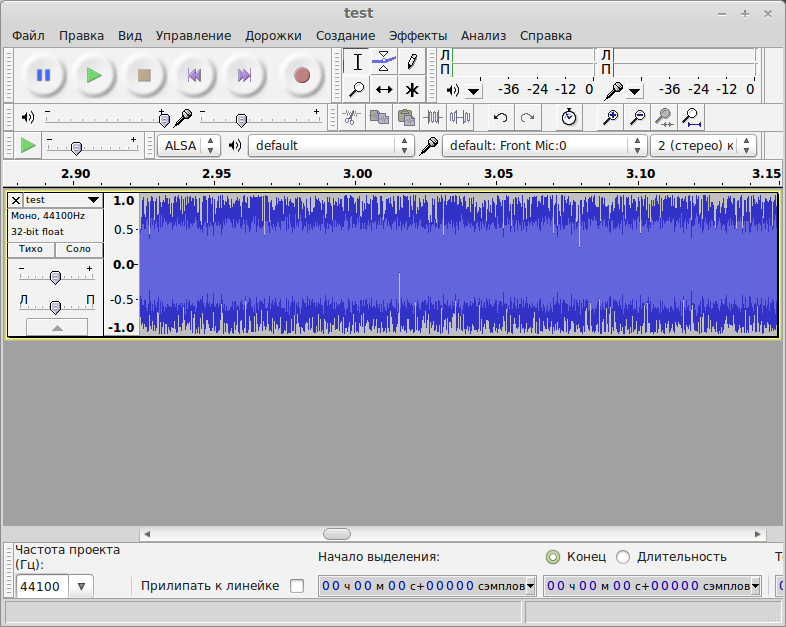
В результате получаем следующий файл (можно его даже послушать любой звуковоспроизводящей программой). Откроем данный файл audacity и увидим, что график сигнала в действительности соответствует чистому синусу:

Чистый ламповый синус

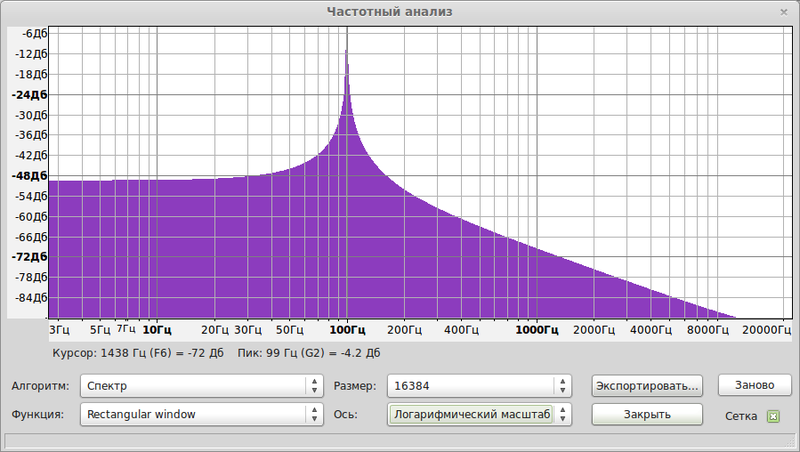
Поглядим спектр этого синуса (Анализ->Построить график спектра)

График спектра

Виден чистый пик на 100 Гц (логарифмический масштаб). Что такое спектр? Это амплитудно-частотная характеристика. Существует ещё фазочастотная характеристика. Если помните, выше я говорил, что для построения сигнала надо знать его частоту, амплитуду и фазу? Так вот, можно из сигнала получить эти параметры. В данном случае у нас график соответствий частот амплитуде, при чём амплитуда у нас не в реальных единицах, а в Децибелах.

Величина, выраженная в децибелах, численно равна десятичному логарифму безразмерного отношения физической величины к одноимённой физической величине, принимаемой за исходную, умноженному на десять.

В данном случае просто логарифм амплитуды, умноженный на 10. Логарифмический масштаб удобно использовать при работе с сигналами.

Мне, честно говоря, не очень нравится анализатор спектра в этой программе, поэтому я решил написать свой

с блекджеком и шлюхами

, тем более, что это несложно.

Пишем свой анализатор спектра

Здесь может быть скучно, поэтому можете перейти сразу к следующей главе.

Поскольку я прекрасно понимаю, что тут портянки кода размещать нет смысла, те, кому реально интересно — сами найдут и поковыряют, а тем, кому это неинтересно, будут скучать, то я остановлюсь только на основных моментах написания анализатора спектра wav-файла.

Во-первых, нам wav-файл необходимо читать. Там необходимо прочитать заголовок, чтобы понять, что содержит данный файл. Я не стал реализовывать море вариантов чтения данного файла, а остановился только на одном. Пример чтения файла был взят отсюда практически без изменений, ИМХО — отличный пример. Там же есть реализация на питоне.

Следующее, что нам нужно, это быстрое преобразование Фурье. Это то самое преобразование, которое позволяет получить из конечного набора точек

вектора

исходных сигналов. Пусть вас пока это не пугает, дальше я объясню.
Опять же, велосипед изобретать не стал, а взял готовый пример отсюда.

Я понимаю, что чтобы объяснить, как работает программа, надо объяснить, что такое быстрое преобразование Фурье, а это как минимум ещё на одну некислую статью.

Для начала алокируем массивы:

	c = calloc(size_array*2, sizeof(float)); // массив поворотных множителей
	in = calloc(size_array*2, sizeof(float)); //входный массив
	out = calloc(size_array*2, sizeof(float)); //выходной массив

Скажу лишь, что в программе мы читаем данные в массив длиной size_array (которое берём из заголовка wav-файла).

	while( fread(&value,sizeof(value),1,wav) ) {
		in[j]=(float)value;
		j+=2;
		if (j > 2*size_array)  break;
}

Массив для быстрого преобразования Фурье должен представлять собой последовательность {re[0], im[0], re[1], im[1],… re[fft_size-1], im[fft_size-1]}, где fft_size=1<< p — число точек БПФ. Объясняю нормальным языком:
это массив комплексных чисел. Я даже боюсь представить, где используется комплексное преобразование Фурье, но в нашем случае мнимая часть у нас равна нулю, а действительная равна значению каждой точке масива.
Ещё одна особенность именно быстрого преобразования Фурье, что оно обсчитывает массивы, кратные только степени двойки. В результате мы должны вычислить минимальную степень двойки:

int p2=(int)(log2(header.bytes_in_data/header.bytes_by_capture));

Логарифм от количество байт в данных, делённых на количество байт в одной точке.

После этого считаем поворотные множители:

fft_make(p2,c);// функция расчёта поворотных множителей для БПФ (первый параметр степень двойки, второй алокированный массив поворотных множителей). 

И скармливаем наш считанный массив в преобразователь Фурье:

fft_calc(p2, c,	in,	out, 1); //(единица означает, что мы получаем нормализованный массив).

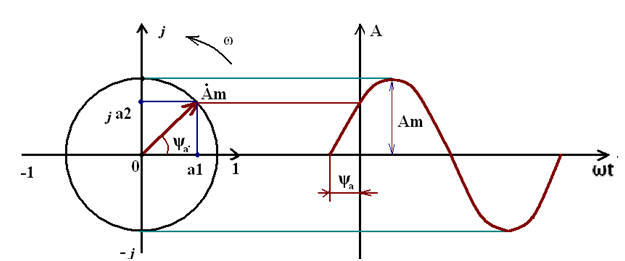
На выходе мы получаем комплексные числа вида {re[0], im[0], re[1], im[1],… re[fft_size-1], im[fft_size-1]}. Для тех, кто не знает, что такое комплексное число, поясню. Я не зря начал эту статью с кучи вращающихся векторов и кучи гифок. Так вот, вектор на комплесной плоскости определяется действительной координатой a1 и мнимой координатой a2. Или длиной (это у нас амплитуда Am) и углом Пси (фаза).

Вектор на комплексной плоскости

Обратите внимание, что size_array=2^p2. Первая точка массива соответствует частоте 0 Гц (постоянная), последняя точка соответствует частоте дискретизации, а именно 44100 Гц. В результате мы должны рассчитать частоту, соответствующей каждой точке, которые будут отличаться на частоту дельта:

double delta=((float)header.frequency)/(float)size_array; //частота дискретизации на размер массива.

Алокируем массив амплитуд:

	double * ampl;
	ampl = calloc(size_array*2, sizeof(double));

И смотрим на картинку: амплитуда — это длина вектора. А у нас есть его проекции на действительную и мнимую ось. В результате у нас будет прямоугольный треугольник, и тут мы вспоминаем теорему Пифагора, и считаем длину каждого вектора, и сразу пишем её в текстовый файл:

for(i=0;i<(size_array);i+=2) {
		fprintf(logfile,"%.6f %fn",cur_freq, (sqrt(out[i]*out[i]+out[i+1]*out[i+1])));
		cur_freq+=delta;
	}

В результате получаем файл примерно такого вида:

…
11.439514 10.943008
11.607742 56.649738
11.775970 15.652428
11.944199 21.872342
12.112427 30.635371
12.280655 30.329171
12.448883 11.932371
12.617111 20.777617
...

Окончательная версия программы обитает на гитхабе вот тут:
github.com/dlinyj/fft

Пробуем!

Теперь скармливаем получившейся программе тот звуковой файл синуса

./fft_an ../generate_wav/sin 100 Hz.wav 
format: 16 bits, PCM uncompressed, channel 1, freq 44100, 88200 bytes per sec, 2 bytes by capture, 2 bits per sample, 882000 bytes in data

chunk=441000
log2=18
size array=262144 
wav format
Max Freq = 99.928 , amp =7216.136

И получаем текстовый файл АЧХ. Строим его график с помощью гнуплота

Скрипт для построения:

#! /usr/bin/gnuplot -persist
set terminal postscript eps enhanced color solid
set output "result.ps"
#set terminal png size 800, 600
#set output "result.png"

set grid xtics ytics
set log xy
set xlabel "Freq, Hz" 
set ylabel "Amp, dB"

set xrange [1:22050]
#set yrange [0.00001:100000]

plot "test.txt" using 1:2 title "AFC" with lines linestyle 1

Обратите внимание на ограничение в скрипте на количество точек по X: set xrange [1:22050]. Частота дискретизации у нас 44100, а если вспомнить теорему Котельникова, то частота сигнала не может быть выше половины частоты дискретизации, следовательно сигнал выше 22050 Гц нас не интересует. Почему так, советую прочитать в специальной литературе.
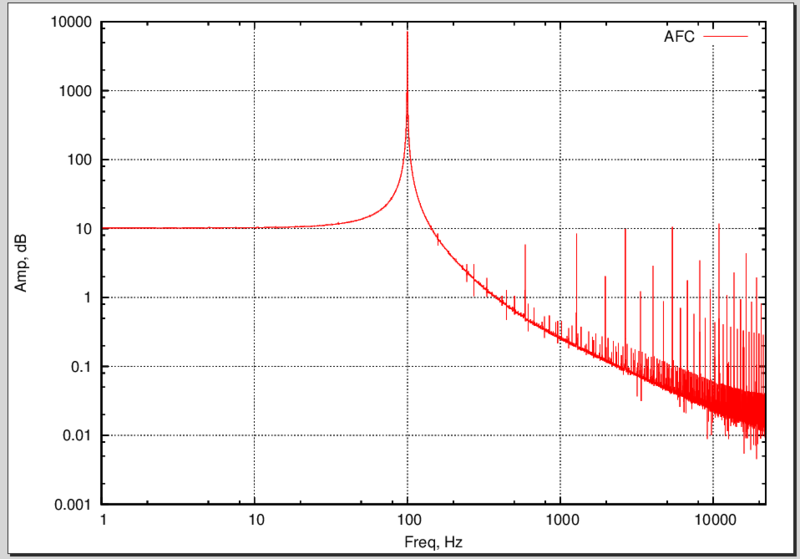
Итак (барабанная дробь), запускаем скрипт и лицезреем:

Спектр нашего сигнала

Обратите внимание на резкий пик на частоте 100 Гц. Не забывайте, что по осям — логарифмический масштаб! Шерсть справа, как я думаю, ошибки преобразования Фурье (тут на память приходят окна).

А давайте побалуем?

А давайте! Давайте поглядим спектры других сигналов!

Вокруг шум…

Для начала построим спектр шума. Тема про шумы, случайные сигналы и т.п. достойна отдельного курса. Но мы её коснёмся слегка. Модифицируем нашу программу генерации wav-файла, добавим одну процедуру:

double d_random(double min, double max)
{
    return min + (max - min) / RAND_MAX * rand();
}

она будет генерировать случайное число в заданном диапазоне. В результате main будет выглядеть так:

int main(int argc, char * argv[])
{
	int i;
	float amplitude = 32000;
	srand((unsigned int)time(0)); //инициализируем генератор случайных чисел
	for (i=0; i<BUF_SIZE; i++)
	{
		buffer[i] +=(int)amplitude*d_random(-1.0, 1.0); //nois		
	}
	write_wav("test.wav", BUF_SIZE, buffer, S_RATE);
 	return 0;
}

Сгенерируем файл, (рекомендую к прослушиванию). Поглядим его в audacity.

Сигнал в audacity

Поглядим спектр в программе audacity.

Спектр

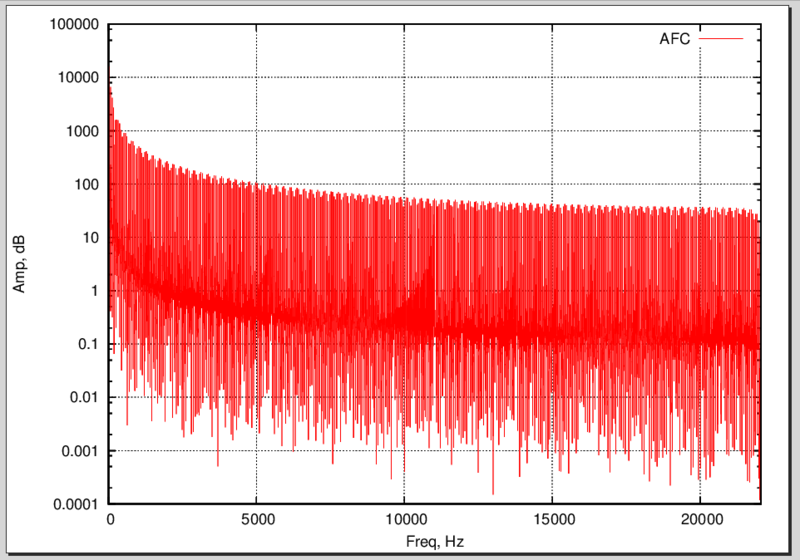
И поглядим спектр с помощью нашей программы:

Наш спектр

Хочу обратить внимание на очень интересный факт и особенность шума — он содержит в себе спектры всех гармоник. Как видно из графика, спектр вполне себе ровный. Как правило, белый шум используется для частотного анализа пропускной способности, например, аудиоаппаратуры. Существуют и другие виды шумов: розовый, синий и другие. Домашнее задание — узнать, чем они отличаются.

А компот?

А теперь давайте посмотрим другой интереснейший сигнал — меандр. Я там выше приводил табличку разложений различных сигналов в ряды Фурье, вы поглядите как раскладывается меандр, выпишите на бумажку, и мы продолжим.

Для генерации меандра с частотой 25 Гц мы модифицируем в очередной раз наш генератор wav-файла:

int main(int argc, char * argv[])
{
	int i;
	short int meandr_value=32767;
	/* fill buffer with a sine wave */
	for (i=0; i<BUF_SIZE; i++)
	{
		//meandr
		if (!(i%(S_RATE/((int)freq_Hz/2)))) {
			if (meandr_value==32767) {
				meandr_value=-32767;
			} else { 
				meandr_value=32767;
			}
		}
		buffer[i]=meandr_value;
	}
	write_wav("test.wav", BUF_SIZE, buffer, S_RATE);
	return 0;
}

В результате получим звуковой файл (опять же, советую послушать), который сразу надо посмотреть в audacity

Его величество — меандр или меандр здорового человека

Не будем томиться и поглядим его спектр:

Спектр меандра

Пока не очень что-то понятно, что такое… А давайте поглядим несколько первых гармоник:

Первые гармоники

Совсем другое дело! Ну-ка поглядим табличку. Смотрите-ка, у нас есть только 1, 3, 5 и т.д., т.е. нечётные гармоники. Мы так и видим, что у нас первая гармоника 25 Гц, следующая (третья) 75 Гц, затем 125 Гц и т.д., при этом у нас амплитуда постепенно уменьшается. Теория сошлась с практикой!
А теперь внимание! В реальной жизни сигнал меандра у нас имеет бесконечную сумму гармоник всё более и более высокой частоты, но как правило, реальные электрические цепи не могут пропускать частоты выше какой-то частоты (в силу индуктивности и ёмкости дорожек). В результате на экране осциллографа можно часто увидеть вот такой сигнал:

Меандр курильщика

Эта картинка прям как картинка из википедии, где для примера меандра берутся не все частоты, а только первые несколько.

Сумма первых гармоник, и как меняется сигнал

Меандр так же активно используется в радиотехнике (надо сказать, что — это основа всей цифровой техники), и стоит понимать что при длинных цепях его может отфильтровать так, что, родная мама не узнает. Его так же используют для проверки АЧХ различных приборов. Ещё интересный факт, что глушилки телевизоров работали именно по принципу высших гармоник, когда сама микросхема генерировала меандр десятки МГц, а его высшие гармоники могли иметь частоты сотни МГц, как раз на частоте работы телевизора, и высшие гармоники успешно глушили сигнал вещания телевизора.

Вообще тема подобных экспериментов бесконечная, и вы можете теперь сами её продолжить.

Рекомендации по прочтению

Книга

Для тех, кто нифига не понял, что мы тут делаем, или наоборот, для тех, кто понял, но хочет разобраться ещё лучше, а так же для студентам, изучающим ЦОС, крайне рекомендую эту книгу. Это ЦОС для чайников, которым является автор данного поста. Там доступным даже для ребёнка языком рассказываются сложнейшие понятия.

Заключение

В заключении хочу сказать, что математика — царица наук, но без реального применения многие люди теряют к ней интерес. Надеюсь, данный пост подстегнёт вас к изучению такого замечательного предмета, как обработка сигналов, и вообще аналоговой схемотехнике (затыкайте уши, чтобы не вытекали мозги!). 🙂
Удачи!

Как рассчитать дельту

Четвертой буквой греческого алфавита, «дельтой», в науке принято называть изменение какой-либо величины, погрешность, приращение. Записывается этот знак различными способами: чаще всего в виде небольшого треугольника Δ перед буквенным обозначением величины. Но иногда можно встретить и такое написание δ, либо латинской строчной буквой d, реже латинской прописной- D.

Для нахождения изменения какой-либо величины вычислите или измерьте ее начальное значение (x1).

Вычислите или измерьте конечное значение этой же величины (x2).

Найдите изменение данной величины по формуле: Δx=x2-x1. Например: начальное значение напряжения электрической сети U1=220В, конечное значение — U2=120В. Изменение напряжения (или дельта напряжения) будет равно ΔU=U2–U1=220В-120В=100В

Для нахождения абсолютной погрешности измерения определите точное или, как его иногда называют, истинное значение какой-либо величины (x0).

Возьмите приближенное (при измерении – измеренное) значение этой же величины (x).

Найдите абсолютную погрешность измерения по формуле: Δx=|x-x0|. Например: точное число жителей города — 8253 жителя (х0=8253), при округлении этого числа до 8300 (приближенное значение х=8300). Абсолютная погрешность (или дельта икс) будет равна Δx=|8300-8253|=47, а при округлении до 8200 (х=8200), абсолютная погрешность — Δx=|8200-8253|=53. Таким образом, округление до числа 8300 будет более точным.

Для сравнения значений функции F(х) в строго фиксированной точке х0 со значениями этой же функции в любой другой точке х, лежащей в окрестностях х0, используются понятия «приращение функции» (ΔF) и «приращение аргумента функции» (Δx). Иногда Δx называют «приращением независимой переменной». Найдите приращение аргумента по формуле Δx=x-x0.

Определите значения функции в точках х0 и х и обозначьте их соответственно F(х0) и F(х).

Вычислите приращение функции:ΔF= F(х)- F(х0). Например: необходимо найти приращение аргумента и приращение функции F(х)=х˄2+1 при изменении аргумента от 2 до 3. В этом случае х0 равно 2, а х=3.
Приращение аргумента (или дельта икс) будет Δx=3-2=1.
F(х0)= х0˄2+1= 2˄2+1=5.
F(х)= х˄2+1= 3˄2+1=10.
Приращение функции (или дельта эф) ΔF= F(х)- F(х0)=10-5=5

Источник

Дельта Формула

Дельта Формула (Содержание)

Что такое Дельта Формула?

В мире опционов или деривативов термин «дельта» относится к изменению стоимости опциона вследствие изменения стоимости его базового запаса. Другими словами, дельта измеряет скорость изменения стоимости опциона по отношению к движению стоимости базовой акции. Поскольку дельта преимущественно используется для стратегий хеджирования, она также известна как коэффициент хеджирования. Формула для дельты может быть получена путем деления изменения стоимости опциона на изменение стоимости его базового запаса. Математически это представляется как

• O _f = конечное значение опции
• O _i = начальное значение опции
• S _f = конечная стоимость базового запаса
• S _i = начальная стоимость базового запаса

Примеры формулы дельты (с шаблоном Excel)

Давайте рассмотрим пример, чтобы лучше понять расчет Delta.

Вы можете скачать этот шаблон Delta Formula Excel здесь — шаблон Delta Formula Excel

Формула Дельта — Пример № 1

Давайте возьмем пример товара X, который торговался по 500 долларов на товарном рынке месяц назад, и опцион колл для товара торговался с премией в 45 долларов при цене исполнения в 480 долларов. Сейчас товар продается по цене 600 долларов, а стоимость опциона выросла до 75 долларов. Рассчитать дельту опциона колл на основе предоставленной информации.

Дельта Δ рассчитывается по формуле, приведенной ниже

• Дельта Δ = (75–45 долл. США) / (600–500 долл. США)
• Дельта = 0, 30 $

Таким образом, дельта опциона составляет $ 0, 30, где положительный знак указывает на увеличение стоимости с увеличением базовой цены акции, которая является характеристикой опциона на покупку.

Формула Дельта — Пример № 2

Давайте возьмем другой пример эталонного индекса, который в настоящее время торгуется на уровне 8000 долларов, в то время как опцион пут на индекс торгуется на уровне 150 долларов. Если индекс торговался по 7800 долларов в месяц назад, тогда как опцион пут торговался по 200 долларов, рассчитайте дельту опциона пут.

Дельта Δ рассчитывается по формуле, приведенной ниже

• Дельта Δ = (150–200 долл. США) / (8 000–7 800 долл. США)
• Дельта Δ = — $ 0, 25

Таким образом, дельта опциона «пут» составляет — 0, 25 доллара США, где отрицательный знак указывает на уменьшение стоимости с увеличением базовой цены акции, которая является характеристикой опциона «пут».

объяснение

Формула для дельты может быть рассчитана с помощью следующих шагов:

Шаг 1: во- первых, рассчитайте начальную стоимость опциона, которая является премией, взимаемой за опцион. Обозначается O _i .

Шаг 2: Затем вычислите окончательное значение опции, которое обозначено O _f .

Шаг 3: Затем рассчитайте изменение значения опции, вычтя начальное значение опции (шаг 1) из окончательного значения опции (шаг 2).

Изменение значения опции, Δ _O = O _f — O _i

Шаг 4: Затем вычислите начальную стоимость базовой акции, которая может быть любой акцией компании, товарным индексом или эталонным индексом и т. Д. Он обозначается как S _i .

Шаг 5: Далее рассчитайте окончательную стоимость базового запаса, обозначенную S _f .

Шаг 6: Затем рассчитайте изменение стоимости базового запаса, вычтя его начальное значение (шаг 4) из его окончательного значения (шаг 5).

Изменение стоимости базового запаса, ΔS = S _f — S _i

Шаг 7: Наконец, формула для дельты может быть получена путем деления изменения стоимости опциона (шаг 3) на изменение стоимости базового запаса (шаг 6), как показано ниже.

Актуальность и использование формулы Delta

В мире опционов и деривативов концепция дельты (одного из греков) очень важна, поскольку она помогает оценить цену опциона и направление базовой акции. Дельта может иметь как положительные, так и отрицательные значения в зависимости от типа опции, с которой мы имеем дело, т. Е. Дельта может находиться в диапазоне от 0 до 1 для опций вызова, что означает, что значение опции вызова увеличивается с увеличением базового значения, в то время как оно может быть в диапазоне от -1 до 0 для опционов пут, что означает в точности противоположность опциону колл. Дельта часто используется в качестве стратегии хеджирования, когда управляющий портфелем намерен создать дельта-нейтральную стратегию, чтобы портфель практически не чувствовал к любому движению в основе. Таким образом, дельта является хорошим индикатором сообщества инвесторов.

Калькулятор формулы Delta

Вы можете использовать следующий Delta Calculator

Рекомендуемые статьи

Это руководство к Delta Formula. Здесь мы обсудим, как рассчитать Дельта вместе с практическими примерами. Мы также предоставляем Delta калькулятор с загружаемым шаблоном Excel. Вы также можете посмотреть следующие статьи, чтобы узнать больше —

1. Как рассчитать стоимость капитала по формуле?
2. EBITDA Formula
3. Расчет эффективной налоговой ставки
4. Примеры формулы корреляции

Источник

Как найти дельту напряжения

Доброго времени суток.
Требуется помощь уважаемых радиолюбителей. Итак, постараюсь сформулировать вопрос:

Есть 2 синусоиды, скажем, 100мгц и 150мгц. Требуется определить дельту частот.
Порывшись в тех книжках, которые были у меня, найти ничего не удалось. Да и занятия в университете я посещал не слишком здорово, но, тем не менее, есть такая идея:

Из курса тригонометрии мы знаем, что sin(a-b) = sin(a)cos(b) — cos(a)sin(b). Получить косинусоиду из синусоиды, на сколько я могу помнить, не так уж и сложно. Останется перемножить их и вычесть. Таким образом мы получим синусоиду с частотой в разность частот a и b.

Вообще, данная задача ставится для того, чтобы по дельте частот определить скорость движущегося объекта(задача на эффект Допплера). Так что, осмелюсь задать еще один вопрос:

как имея синусоиду с частотой величиной в разницу двух частот(отправленной и полученной) определить саму величину (a-b)?
ведь все рассчеты производятся именно с этой величиной.
из моих догадок — перевести сигнал в цифру, а затем по его длительности уже вычислять нужные данные.
Надеюсь на вашу помощь. Заодно, на всякий случай, извиняюсь, если создал тему не в том разделе.

Поставщик валерьянки для Кота

Ну и закрутили вопрос.
Можно было написать нужен доплеровский измеритель скорости и все.
Что бы получить разность частот эти сигналы нужно подать на нелинейный элемент, например диод, а на выходе поставить ФНЧ с частотой среза чуть больше предполагаемой разницы частот.
Дальше все это на частотометр.
В качестве нелинейного элемента лучше поставить специализированную микросхему смесителя, что бы на выходе «грязи» поменьше было.

Можно также подать на фазовый детектор и на выходе получить напряжение пропорциональное скорости объекта.
Техническую реализацию можно посмотреть в схеме какого либо охранного устройства на этом эффекте.
В интернете они есть..

Последний раз редактировалось VT1 Пн июл 19, 2010 14:25:27, всего редактировалось 1 раз.

JLCPCB, всего $2 за прототип печатной платы! Цвет — любой!

Зарегистрируйтесь и получите два купона по 5$ каждый:https://jlcpcb.com/cwc

спасибо большое. Как раз откопал у отца в пыльном ящике старый учебник по радиолокации и принялся за статью по допплеровским РЛС.

Готовых схем датчиков движения на УЗ и СВЧ(именно так звучало задание) — полно, но они не подходят по ряду причин:
например, дальность локации должна быть порядка 500-1000 метров, да и необходимо, вдобавок, определять расстояние до цели(уверен, что в этой книжке все рассматривается), но, все же, встанет вопрос как объеденить две системы.
Но, это будет несколько после)

Сборка печатных плат от $30 + БЕСПЛАТНАЯ доставка по всему миру + трафарет

Поставщик валерьянки для Кота

Так «гугл» предлагает вот это почитать.
Возможно книжки в интернете можно скачать.

Бартон Д. и Вард Г. Справочник по радиолокационным измерениям. Пер. с англ. под ред. М. М. Вейсбенна — М.: Сов. радио, 1976

Гришин Ю. П., Ипатов В. П., Казаринов Ю. М. Радиотехнические системы — 1990

Построение источников бесперебойного питания с двойным преобразованием, широко используемых в современных хранилищах данных, на базе карбид-кремниевых MOSFETs производства Wolfspeed позволяет уменьшить мощность потерь в них до 40%, а также значительно снизить занимаемый ими объем и стоимость комплектующих.

Кто сейчас на форуме

Сейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 10

Источник

Дельта и кумулятивная дельта: что это такое и чем они помогут внутридневному трейдеру?

Термин Дельта (англ. Delta) вошел в обиход трейдеров в далеком 2002 году, когда был изобретен революционный график Футпринт (англ. Footprint chart). Толчком для этого послужило повсеместное распространение информационных технологий и интернета, затронувшее и сферу трейдинга. Именно тогда доступ к данным о реальных объемах торговли на бирже перестал быть привилегией узкого круга участников рынка, а метод VSA (англ. Volume Spread Analysis — анализ объема и спреда) получил широкое распространение в среде ритейл трейдеров.

Сегодня ритейл трейдер, анализирующий, например, котировки валют Форекс (Forex), благодаря платформе ATAS может подкрепить свои решения торговыми объемами валютных фьючерсов (евро, британского фунта и других). Передовой, интуитивно понятный, а главное ставший доступным каждому, способ визуализации потока ордеров продолжает и по сей день помогать ритейл трейдерам выходить на новый профессиональный уровень.

Начни пользоваться ATAS абсолютно бесплатно! Первые две недели использования платформы дают доступ к полному функционалу с ограничением истории в 7 дней.

Расчет Дельты

Дельта представляет собой разницу между рыночными покупками и рыночными продажами по каждой цене (footprint delta), в каждой свече/баре (bar delta) или за период (cumulative delta — кумулятивная дельта).

Дельта рассчитывается путем вычитания объема контрактов, проторгованных по цене Bid из объема контрактов, проторгованных по цене Ask. В платформе ATAS сделками, совершенными по цене Ask, считаются сделки, инициированные «агрессивными» покупателями. Сделками же, совершенными по цене Bid, считаются сделки, инициированные «агрессивными» продавцами.

Таким образом, положительная Дельта отражает более высокий объем «агрессивных» покупок, прошедших по цене Ask в результате торговли решительно настроенных покупателей. В свою очередь отрицательная Дельта отражает более высокий объем «агрессивных» продаж, прошедших по цене Bid в результате торговли решительно настроенных продавцов.

Объем торговли по цене Ask — Объем торговли по цене Bid = Дельта

Для расчета Дельты вам потребуется знать следующие переменные: цена Bid, цена Ask, последняя цена по которой торговался инструмент, объем последней сделки и время ее заключения.

Например, представьте себе, что в определенный момент времени цена Bid фьючерса на нефть марки WTI = $63.50 за баррель, а цена Ask =$63.51 и по цене Ask совершается сделка на 25 контрактов. В результате этой сделки значение Дельты увеличится на 25. Сразу же после этого на рынке совершается вторая сделка на 10 контрактов, которая на этот раз уже проходит по цене Bid ($63.50). Это приведет к уменьшению Дельты на 10. Общее изменение Дельты за время совершения двух сделок составит +25-10 =+15.

Пожалуйста, помните, что Дельта рассчитывается как разница между объемом рыночных покупок и рыночных продаж. Из этого следует, что приведенный выше пример подразумевает, что первые 25 контрактов были куплены рыночным ордером по цене $63.51, а вторые 10 контрактов были проданы рыночным ордером по цене $63.50.

Расчет Дельты по рыночным, или как еще говорят «агрессивным», ордерам объясняется тем, что именно рыночные ордера двигают цену на рынке. Если немного углубиться в тему, то учитывать объемы лимитных ордеров в расчете Дельты нет необходимости. Ведь для заключения сделки, рыночному ордеру на покупку 25 контрактов потребуется лимитный ордер(а) на продажу 25 контрактов и дублировать эти объемы в показателях Дельты просто не имеет смысла.

Если сейчас вам это кажется немного сложным, не беспокойтесь. В данном вопросе вы сможете разобраться прочитав нашу статью «Механика рынка: Что нужно знать новичку о сведении ордеров», в которой данный аспект трейдинга подробно рассмотрен.

График Футпринт

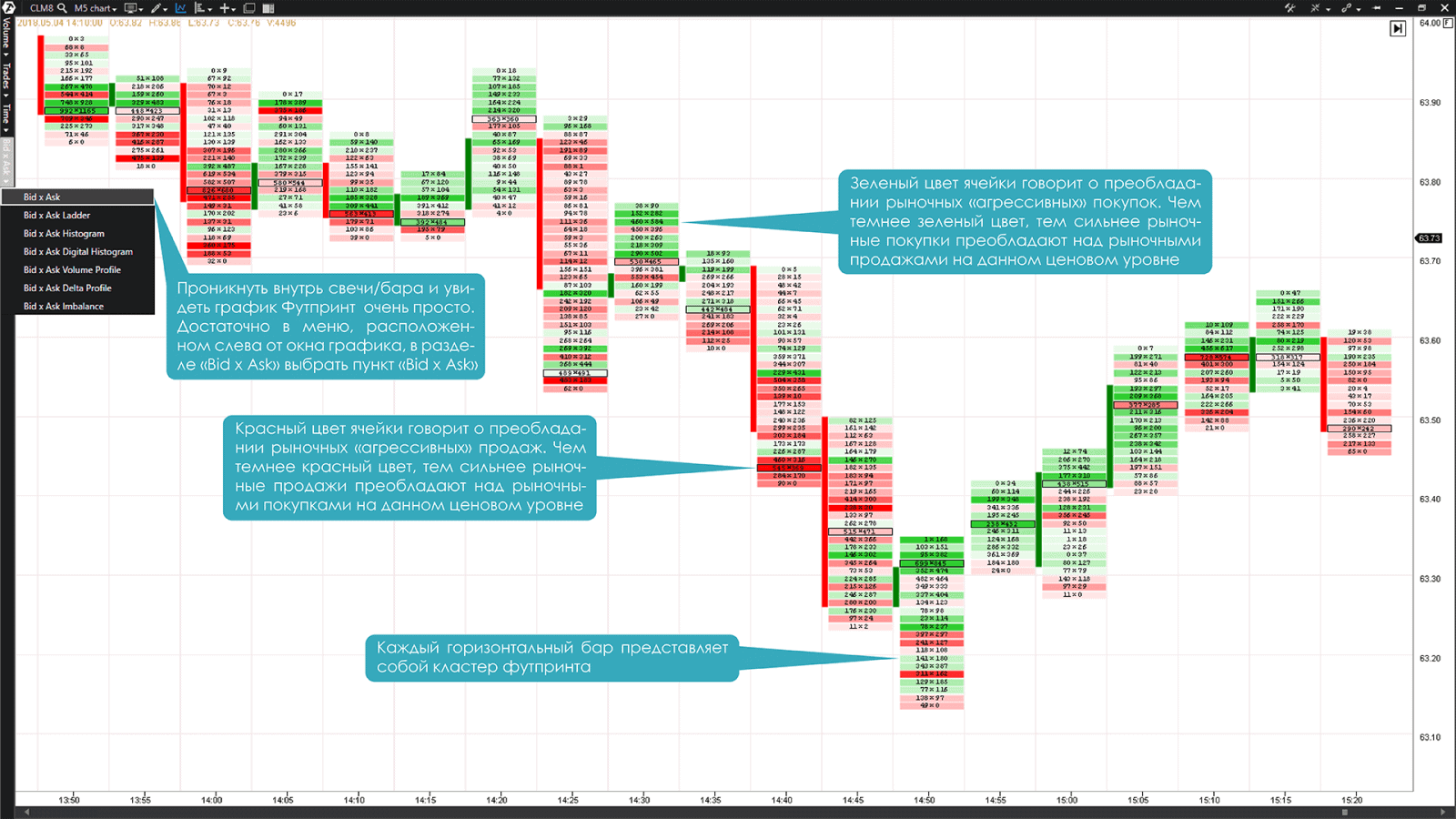
График Футпринт отражает положительное или отрицательное значение Дельты внутри каждой свечи как это видно на Графике №1. Ячейка Футпринта с положительной Дельтой отмечена зеленым цветом и характеризует «положительный» поток ордеров, в результате которого покупатели «агрессивнее» проявили себя на конкретном ценовом уровне. Ячейка Футпринта с отрицательной Дельтой отмечена красным цветом и характеризует «отрицательный» поток ордеров, в результате которого продавцы «агрессивнее» проявили себя на конкретном ценовом уровне.

График №1. 5-минутный таймфрейм фьючерса на нефть Light Sweet Crude Oil (тикер CL). График Футпринт Bid x Ask

На рынке существует высокая степень корреляции между направлением движения цены и потоком ордеров. Именно по этой причине график Футпринт платформы ATAS может стать ценным инструментом анализа текущей рыночной ситуации для проницательных трейдеров.

Индикатор Delta

Данный индикатор показывает суммарное значение Дельты для каждой свечи в виде вертикальной гистограммы в нижней части графика, причем не важно какой тип графика (фрейм) вы используете.

Бары индикатора Delta, могут быть как положительными, так и отрицательными. Положительная Дельта отмечена барами зеленого цвета и характерна для «положительного» потока ордеров, в результате которого покупатели «агрессивнее» проявили себя в конкретной свече. Отрицательная Дельта отмечена барами красного цвета и характерна для «отрицательного» потока ордеров, в результате которого продавцы «агрессивнее» проявили себя в конкретной свече.

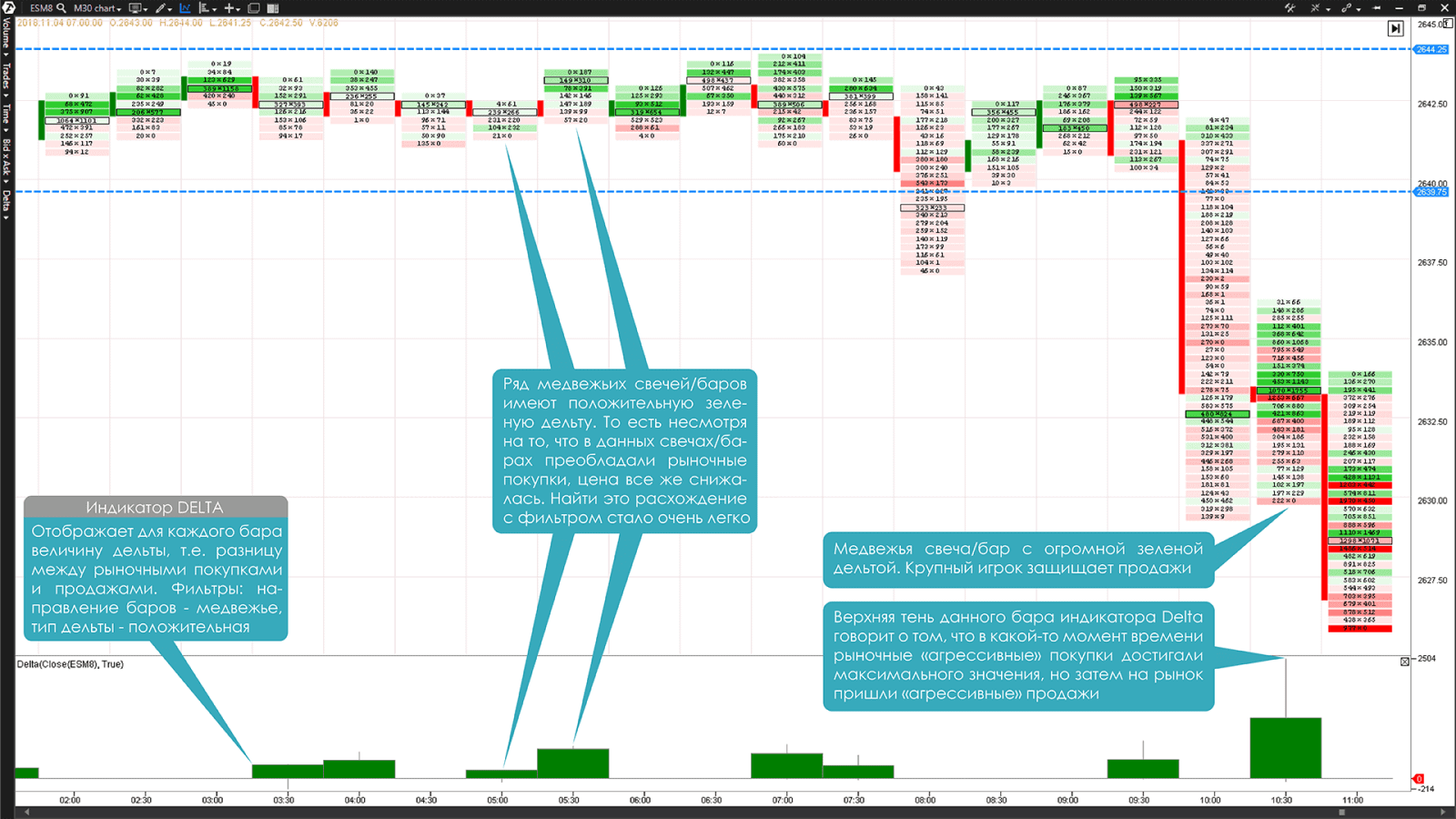
Одно из преимуществ баров индикатора Delta платформы ATAS состоит в том, что они позволяют трейдеру переключить внимание с анализа свечей графика Футпринт, внутри которых Дельта распределена по цене, на суммарный поток ордеров этих свечей. Этому можно найти хорошее применение сравнивая цвет бара индикатора Delta с направлением свечи графика Футпринт и находить расхождения. Вероятно, у вас может возникнуть вопрос, а разве может быть у растущей бычьей свечи отрицательная Дельта, и наоборот, у падающей медвежьей свечи положительная Дельта? Да может, и это встречается довольно часто.

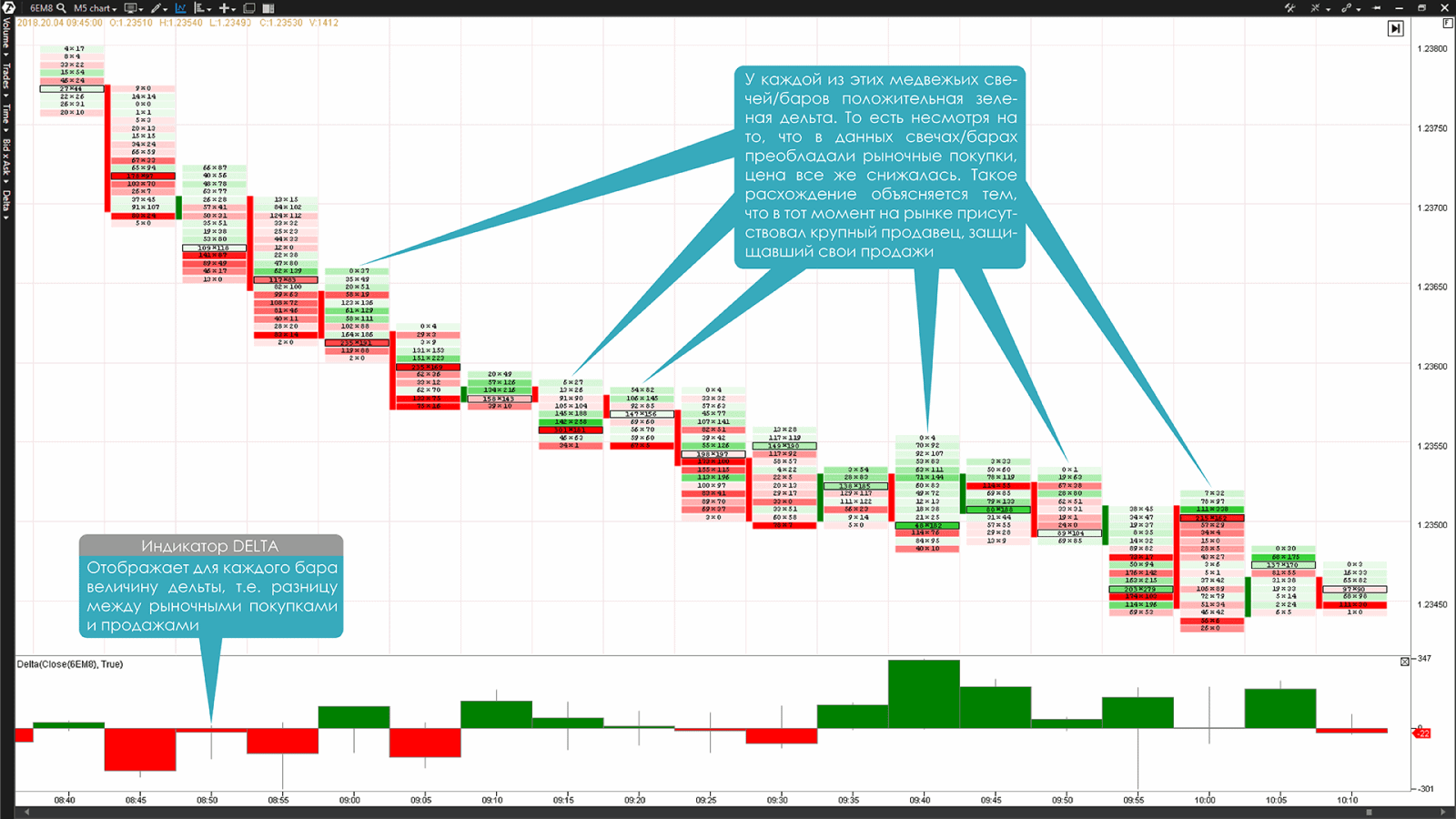
График №2. 5-минутный таймфрейм фьючерса на евро (тикер 6E). График Футпринт Bid x Ask и индикатор Delta в нижней части графика

Обратите внимание, что на Графике №2 у некоторых медвежьих свечей положительная зеленая Дельта. То есть несмотря на то, что в данных свечах преобладали рыночные покупки, цена все же снижалась. Такое расхождение объясняется тем, что на рынке в тот момент времени присутствовал крупный продавец, который открывая свои рыночные продажи, защищал их лимитными ордерами на продажу (англ. sell limit order).

В результате таких действий, все покупки, которые приходили в то время от «агрессивных» покупателей, пытавшихся сопротивляться нисходящему движению цены, исполнялись на защитных лимитных ордерах крупного продавца. Действуя таким образом, крупному продавцу, чтобы толкнуть цену в прибыльном для него направлении, не нужно было открывать крупных рыночных сделок на продажу.

Его продажи в значительной степени открывались на защитных лимитных ордерах, которые полностью поглощали все рыночные покупки. Стоит отметить, что цена продолжала снижаться еще и потому, что покупатели, в свою очередь, не стремились защитить свои рыночные покупки лимитными ордерами на покупку или же ставили их в недостаточном количестве для сдерживания продавцов.

Если вдруг выявление таких расхождений из общего потока рыночной информации кажется вам сложным, то платформа ATAS сможет максимально облегчить эту задачу. На Графике №3 фьючерса E-mini S&P 500, показатели индикатора Delta строятся с использованием двух фильтров: направление баров — медвежье , тип дельты — положительная .

График №3. 30-минутный таймфрейм фьючерса E-mini S&P 500 (тикер ES). График Футпринт Bid x Ask и индикатор Delta в нижней части графика с использованием фильтров

Пример на Графике №3 хорошо демонстрирует работу крупного продавца в период консолидации рынка в диапазоне цен от 2639.75 до 2644.25 а индикатор Delta, благодаря фильтрам, значительно облегчает нахождение расхождений.

В данном примере крупный игрок не пускал «агрессивных» покупателей выше уровня 2644.25 сдерживая их своими лимитными ордерами на продажу. Об этом нам говорит ряд медвежьих свечей с положительной Дельтой. Все рыночные покупки поглощались лимитными ордерами, расположенными у верхней границы консолидации.

Когда вы наблюдаете на рынке подобные ситуации помните, что часто они свидетельствуют о присутствии крупного, или как еще говорят, институционального игрока. Как вы уже наверняка знаете из наших предыдущих статей, только крупный игрок, в отличии от ритейл трейдеров, располагает достаточными финансовыми ресурсами для защиты своих открытых позиций. Уже два этих примера демонстрируют колоссальное преимущество торговли с использованием продвинутых инструментов анализа потока ордеров платформы ATAS.

Кумулятивная Дельта

Кумулятивная Дельта (англ. Cumulative Delta) — это накопительная дельта за определенный промежуток времени. Если обычная Дельта, которую мы рассматривали выше, показывает разницу между рыночными покупками и продажами для каждой свечи/бара, то кумулятивная Дельта отображает полную динамику баланса рыночных покупок и продаж начиная с определенного момента времени (с начала торговой сессии или контракта).

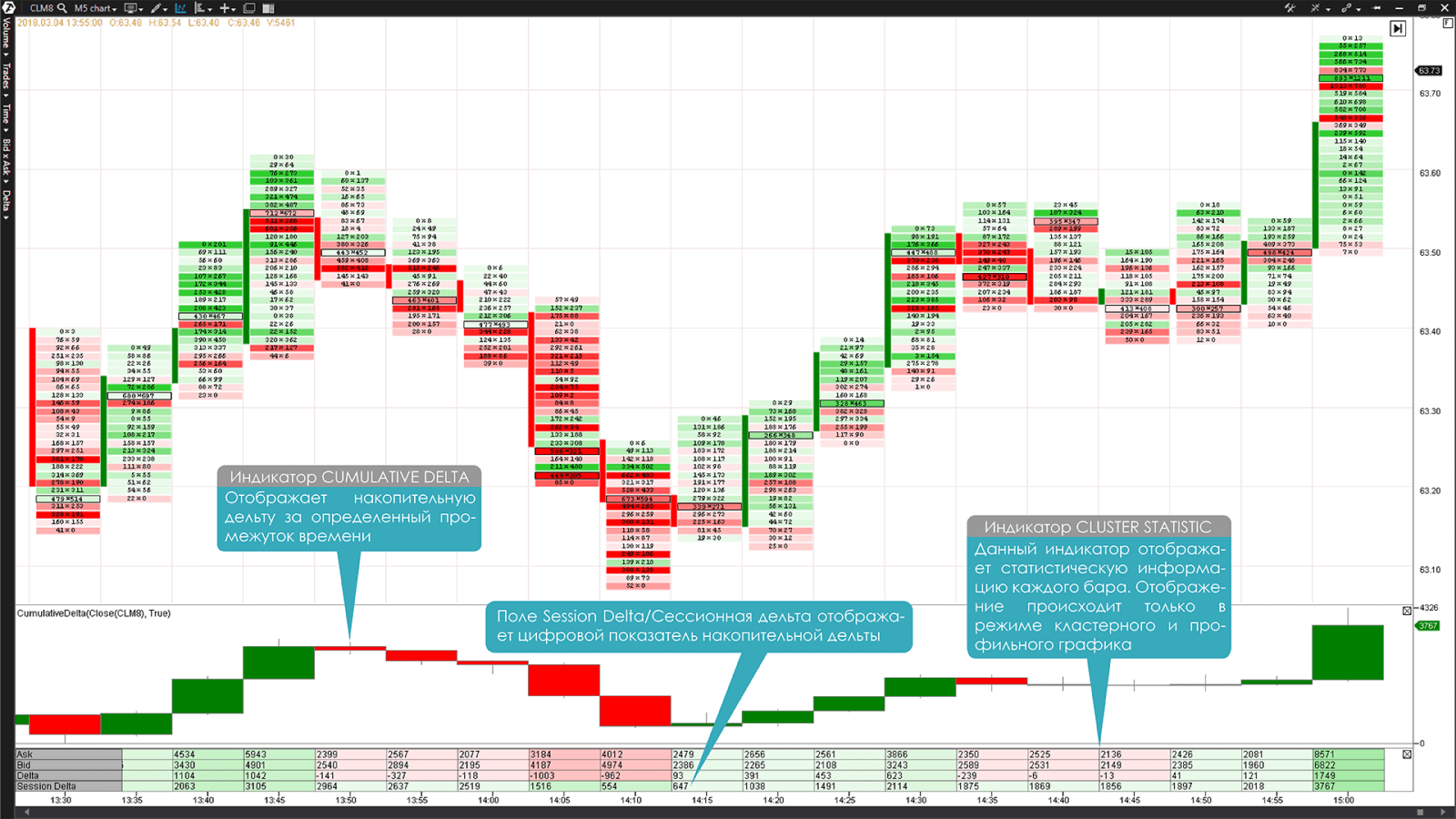
Таким образом кумулятивная Дельта позволяет увидеть более широкую картину Дельты, так как она может охватывать торговую сессию или же целый день. Поэтому не имеет значения какой фрейм или период вы используете для построения графика. Индикатор Cumulative Delta платформы ATAS подсчитывает накопительную Дельту и отображает ее текущий итоговый показатель в нижней части графика.

Помимо этого, показатель кумулятивной Дельты, как и другие подробные цифровые показатели Дельты можно вывести на график при помощи индикатора Cluster Statistic. В нем показатели кумулятивной Дельты будут выводиться в строке Session Delta.

Кумулятивная Дельта, может быть как положительной, так и отрицательной. Положительная кумулятивная Дельта окрашивается в зеленый цвет и характеризует «положительный» поток ордеров за торговую сессию, как результат более агрессивного поведения покупателей. Отрицательная кумулятивная Дельта окрашивается в красный цвет и характеризует «отрицательный» поток ордеров за торговую сессию, как результат более «агрессивного» поведения продавцов.

График №4. 5-минутный таймфрейм фьючерса на нефть Light Sweet Crude Oil (тикер CL). График Футпринт Bid x Ask и индикаторы Cumulative Delta и Cluster Statistic в нижней части графика

Одна из стратегий применения кумулятивной Дельты заключается в использовании ее для определения направления заключения сделки. Когда кумулятивная Дельта положительная, это говорит о доминировании «агрессивно» настроенных покупателей в течение торговой сессии. И наоборот, когда кумулятивная Дельта отрицательная, это значит, что в течение торговой сессии доминируют «агрессивно» настроенные продавцы. Это очень полезный аналитический инструмент для подтверждения направления движения цены.

В заключении статьи следует отметить, что Дельту, несмотря на все ее сильные стороны, следует использовать лишь в связке с другими торговыми элементами вашей торговой стратегии.

Внимание! Торговля на бирже сопряжена с финансовыми рисками и подходит не всем инвесторам. Данная публикация носит исключительно информационный характер. Проведение торговых операций на финансовых рынках может привести к получению убытков и потере инвестиционных средств. Перед использованием торговых идей убедитесь, что вы в полной мере осознаете все риски, а также обладаете соответствующими знаниями и опытом для торговли на бирже.

Понравилось? Расскажите друзьям:

Ответить

Добавить комментарий Отменить ответ

Другие статьи блога:

This site uses cookies. By continuing to browse the site, you are agreeing to our use of cookies.

Cookie и настройки приватности

Мы можем запросить сохранение файлов cookies на вашем устройстве. Мы используем их, чтобы знать, когда вы посещаете наш сайт, как вы с ним взаимодействуете, чтобы улучшить и индивидуализировать ваш опыт использования сайта.

Чтобы узнать больше, нажмите на ссылку категории. Вы также можете изменить свои предпочтения. Обратите внимание, что запрет некоторых видов cookies может сказаться на вашем опыте испольхования сайта и услугах, которые мы можем предложить.

These cookies are strictly necessary to provide you with services available through our website and to use some of its features.

Because these cookies are strictly necessary to deliver the website, refuseing them will have impact how our site functions. You always can block or delete cookies by changing your browser settings and force blocking all cookies on this website. But this will always prompt you to accept/refuse cookies when revisiting our site.

We fully respect if you want to refuse cookies but to avoid asking you again and again kindly allow us to store a cookie for that. You are free to opt out any time or opt in for other cookies to get a better experience. If you refuse cookies we will remove all set cookies in our domain.

We provide you with a list of stored cookies on your computer in our domain so you can check what we stored. Due to security reasons we are not able to show or modify cookies from other domains. You can check these in your browser security settings.

These cookies collect information that is used either in aggregate form to help us understand how our website is being used or how effective our marketing campaigns are, or to help us customize our website and application for you in order to enhance your experience.

If you do not want that we track your visit to our site you can disable tracking in your browser here:

We also use different external services like Google Webfonts, Google Maps, and external Video providers. Since these providers may collect personal data like your IP address we allow you to block them here. Please be aware that this might heavily reduce the functionality and appearance of our site. Changes will take effect once you reload the page.

Google reCaptcha Settings:

Vimeo and Youtube video embeds:

The following cookies are also needed — You can choose if you want to allow them:

Подробнее о нашей политике конфиденциальности и файлах cookies вы можете прочесть на странице Политики конфиденциальности.

Источник

➤ Adblock
detector