Содержание:
- Определение и формула длины волны
- Длина стоячей волны
- Длина бегущей волны
- Длина бегущей волны
- Длина электромагнитной волны
- Единицы измерения длины волны
- Примеры решения задач
Определение и формула длины волны
Определение
Длиной волны называют кратчайшее пространственное расстояние между ее точками, совершающими колебания в одной фазе.
Обозначают длину волны, чаще всего буквой $lambda$ .
Для синусоидальных волн $lambda$ – это расстояние, на которое волна распространяется за один период
(T). Длину волны в этом случае еще называют пространственным периодом. Тогда формулой длины волны можно считать выражение:
$$lambda=v T=frac{v}{nu}=frac{2 pi}{k}$$
где v – скорость распространения волны, $nu=frac{1}{T}$ – частота колебаний,
$k=frac{omega}{v}$ – волновое число,
$T=frac{2 pi}{omega}$ – период волны,
$omega$ – циклическая частота волны.
Длина стоячей волны
Длиной стоячей волны($lambda_{st}$) называют расстояние в пространстве между
двумя пучностями (или узлами):
$$lambda_{s t}=frac{pi}{k}=frac{lambda}{2}(2)$$
где $lambda$ – длина бегущей волны. Надо заметить, что расстояние между соседними пучностью и
узлом связывает равенство:
$$frac{lambda_{s t}}{2}=frac{lambda}{4}(3)$$
Длина бегущей волны
В бегущей волне длина волны связана с фазовой скоростью (vph) формулой:
$$lambda=frac{v_{p h}}{nu}(4)$$
Длина бегущей волны
Разность фаз и длина волны
Две точки волны находящиеся на расстоянии
$Delta x$ имеют при колебании разность
фаз ($Delta varphi$), которая равна:
$$Delta varphi=frac{2 pi Delta x}{lambda}(5)$$
Длина электромагнитной волны
Скорость распространения электромагнитных волн в вакууме равна скорости света в вакууме
($c approx 3 cdot 10^{8}$ м/с), следовательно, длина электромагнитной волны в
вакууме, может быть рассчитана при помощи формулы:
$$lambda=c T=frac{c}{nu}(6)$$
Длина электромагнитной волны в веществе равна:
$$lambda=frac{c}{n nu}(7)$$
где $n=sqrt{varepsilon mu}$ – показатель преломления вещества,
$varepsilon$ – диэлектрическая проницаемость вещества,
$mu$ – магнитная проницаемость вещества.
Отметим, что все рассматриваемые формулы относят к случаю T=const.
Единицы измерения длины волны
Основной единицей измерения длины волны в системе СИ является: [$lambda$]=м
В СГС: [$lambda$]=см
Примеры решения задач
Пример
Задание. Каково приращение длины электромагнитной волны, имеющей частоту v=1 МГц при ее переходе в немагнитную среду,
которая имеет диэлектрическую проницаемость $varepsilon$=2?
Решение. Так как речь в условии задачи идет о немагнитной среде, в которую переходит волна, то считаем магнитную
проницаемость вещества равной единице ($mu$=1).
Длина рассматриваемой нами волны в вакууме равна:
$$lambda_{1}=frac{c}{nu}(1.1)$$
Длина волны в веществе:
$$lambda_{2}=frac{c}{n nu}=frac{c}{sqrt{varepsilon mu} cdot nu}(1.2)$$
Используя выражения (1.1) и (1.2) найдем изменение длины волны:
$$Delta lambda=lambda_{2}-lambda_{1}=frac{c}{sqrt{varepsilon mu} cdot nu}-frac{c}{nu}=frac{c}{nu}left(frac{1}{sqrt{varepsilon mu}}-1right)$$
Проведем вычисления, если нам известно помимо данных приведенных в условии задачи, что
$c approx 3 cdot 10^{8}$ м/с- скорость света в вакууме, и v=1 МГц=106 Гц:
$$Delta lambda=frac{3 cdot 10^{8}}{10^{6}}left(frac{1}{sqrt{4 cdot 1}}-1right)=-1,5 cdot 10^{2}(mathrm{~m})$$
Ответ. Длина волны уменьшится на 150 м

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
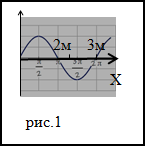
Задание. Какова длина плоской синусоидальной волны, которая распространяется по оси X. Две точки, которые
находятся на оси X расположенные на расстояниях 2 м и 3 м от источника совершают колебания с разностью фаз равной
$Delta varphi=frac{3 pi}{5}$ . Каким будет период колебаний в волне, если ее скорость в данной среде равна v=2м/с?
Решение. Сделаем рисунок.
Основой для решения задачи будет формула:
$$Delta varphi=frac{2 pi Delta x}{lambda}=frac{2 pileft(x_{2}-x_{1}right)}{lambda}(2.1)$$
Выразим из (2.1) искомую длину волны, получим:
$$lambda=frac{2 pileft(x_{2}-x_{1}right)}{Delta varphi}(2.2)$$
Период колебаний связан с длиной волны формулой:
$$T=frac{lambda}{v}(2.3)$$
C учетом (2.2), имеем:
$$T=frac{2 pileft(x_{2}-x_{1}right)}{Delta varphi v}$$
Проведем вычисления:
$$
begin{array}{c}
lambda=frac{2 pi(3-2)}{3 pi} cdot 5=frac{10}{3}(m) \
T=frac{10}{3 cdot 2}=1,67(c)
end{array}
$$
Ответ. $lambda approx 3,3 mathrm{~m} ; T approx 1,67 mathrm{c}$
Читать дальше: Формула количества теплоты.
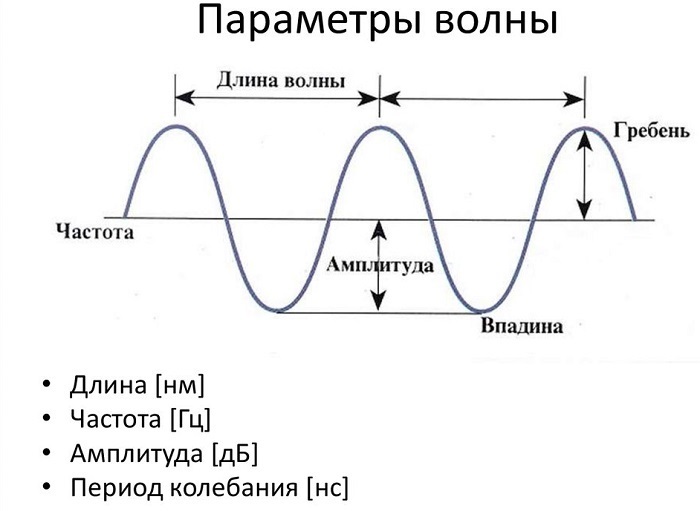
Длина волны – это расстояние между двумя последовательными пиками (гребнями) или впадинами. Самое высокое положение волны называется пиком. Самое нижнее положение волны называется впадиной.
Цикл – это полное колебание, например, кривая между двумя гребнями или двумя впадинами. Максимальное расстояние волны от равновесного положения называется амплитудой.
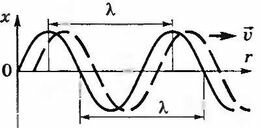
На рисунке показаны основные параметры волны, используемые в физике:
Определение и формула длины волн
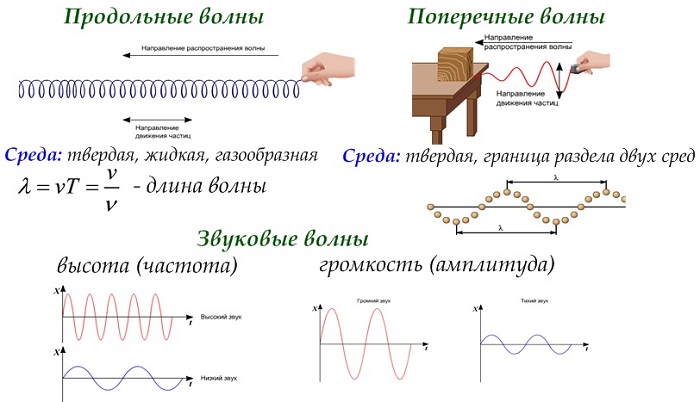
Волна – это возмущение, распространяющееся от точки, в которой она возникла, в окружающую среду. Такое возмущение переносит энергию без чистого переноса вещества.
Длина представляет собой фактическое расстояние, пройденное волной, которое не всегда совпадает с расстоянием среды, или частиц, в которых распространяется волна. Ее также определяют как пространственный период волнового процесса.
Греческая буква “λ” (лямбда) в физике используется для обозначения длины в уравнениях. Она обратно пропорциональна частоте волны.
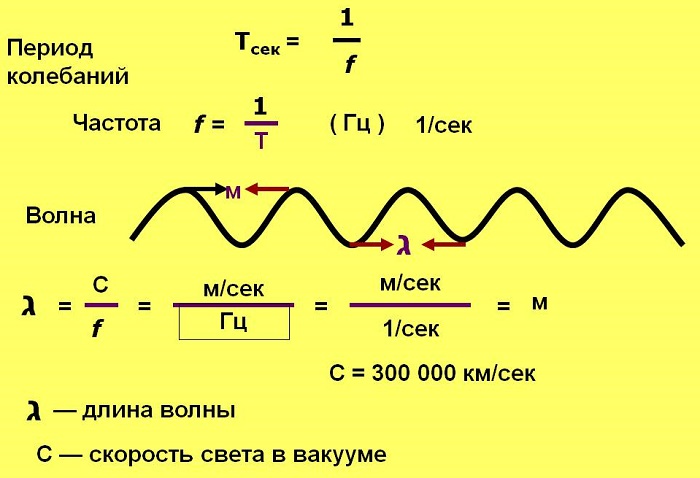
Период Т — время завершения полного колебания, единица измерения секунды (с).
Длинная волна соответствует низкой частоте, а короткая – высокой. Длина измеряется в метрах. Количество волн, излучаемых в каждую секунду, называется частотой и обратно пропорционально периоду.
У различных длин разная скорость распространения. Например, скорость света в воде равна 3/4 от скорости в вакууме.
Пространственный период волны – это расстояние, которое точка с постоянной фазой «пролетает» за интервал времени, соответствующий периоду колебаний.
Частота f — количество полных колебаний в единицу времени. Измеряется в Герцах (Гц).
При одном полном колебании в секунду f = 1 Гц; при 1000 колебаний в секунду f = 1 килогерц (кГц); 1 млн. колебаний в секунду f = 1 мегагерц (1 МГц).
Зная, что скорость света в вакууме с — 300 000 км/с, или 300 000 000 м/с, то для перевода длины волны в частоту нужно 3 х 108 м/с поделить на длину в метрах.
Единицы измерения длины волны λ – нанометры и ангстремы, где нанометр является миллиардной частью метра (1 м = 109 нм) и ангстрем является десятимиллиардной частью метра (1 м = 1010 А), то есть нанометр эквивалентен 10 ангстрем (1 нм = 10 А).
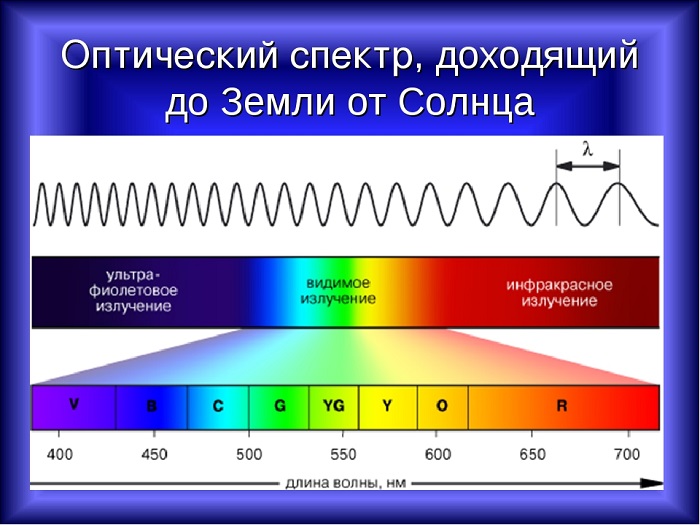
Свет, который исходит от Солнца, является электромагнитным излучением, которое движется со скоростью 300 000 км/с, но длина не одинакова для любого фотона, а колеблется между 400 нм и 700 нм. Длина световой волны влияет на цвет.
Белый свет разлагается на спектр различных цветных полос, каждая из которых определяется своей длиной волны. Таким образом, светом с наименьшей длиной является фиолетовый, который составляет около 400 нм, а светом с наибольшей длиной – красный, который составляет около 700 нм.
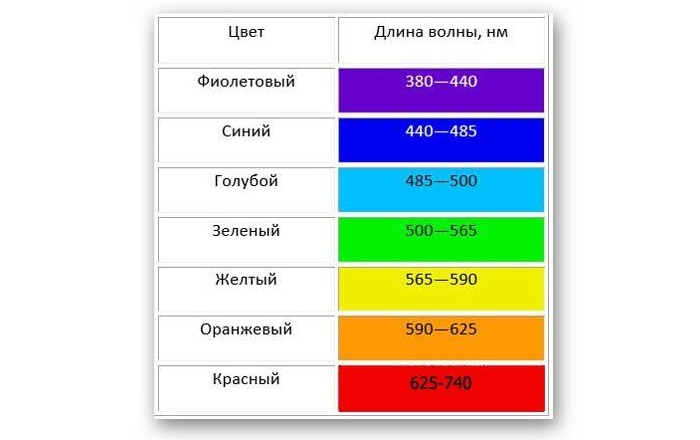
Таблица показывает длину волны в зависимости от цвета:
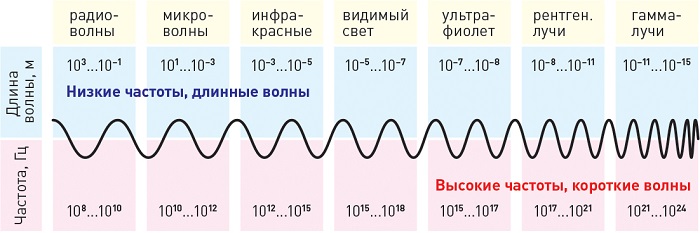
Излучения с длиной меньше фиолетового называются ультрафиолетовым излучением, рентгеновским и гамма-лучами в порядке уменьшения. Излучения больше красного называются инфракрасными, микроволнами и радиоволнами, в порядке возрастания.
Предельная дальность связи зависит от длины. Размеры антенны часто превышают рабочую длину радиоэлектронного средства.
Рисунок показывает длину волн и частоту (нм), исходящих от различных источников:
Примеры расчета длины волны для звуковых, электромагнитных и радиоволн
Задача №1
Скорость звука в воде 1450 м/с. На каком расстоянии находятся ближайшие точки, совершающие колебания в противоположных фазах, если частота колебаний равна 725 Гц?
Задача №2
Мимо неподвижного наблюдателя, стоящего на берегу озера, за 6 с. прошло 4 гребня волны. Расстояние между первым и третьим гребнями равно 12 м. Определить период колебания частиц волны, скорость распространения и длину волны.
Задача №3
Голосовые связки певца, поющего тенором (высоким мужским голосом), колеблются с частотой от 130 до 520 Гц. Определите максимальную и минимальную длину излучаемой звуковой волны в воздухе. Скорость звука в воздухе 330 м/с.
График волны функции (например, физической величины) y, распространяющейся вдоль оси Оx, построенный в фиксированный момент времени (t = const). Длина волны λ может быть измерена как расстояние между парой соседних максимумов y (x) либо минимумов, либо как удвоенное расстояние между соседними точками, в которых y = 0
Длина́ волны́ — расстояние между двумя ближайшими друг к другу точками в пространстве, в которых колебания происходят в одинаковой фазе[1][2].
Длина́ волны́ (в линии передачи) — расстояние в линии передачи, на котором фаза электромагнитной волны вдоль направления распространения меняется на 2π[3].
Длину волны можно также определить:
- как расстояние, измеренное в направлении распространения волны, между двумя точками в пространстве, в которых фаза колебательного процесса отличается на
;
- как путь, который проходит фронт волны за интервал времени, равный периоду колебательного процесса;
- как пространственный период волнового процесса.
Представим себе волны, возникающие в воде от равномерно колеблющегося поплавка, и мысленно остановим время. Тогда длина волны — это расстояние между двумя соседними гребнями волны, измеренное в радиальном направлении. Длина волны — одна из основных характеристик волны наряду с частотой, амплитудой, начальной фазой, направлением распространения и поляризацией. Для обозначения длины волны принято использовать греческую букву 
Как правило, длина волны используется применительно к гармоническому или квазигармоническому (например, затухающему или узкополосному модулированному) волновому процессу в однородной, квазиоднородной или локально однородной среде. Однако формально длину волны можно определить по аналогии и для волнового процесса с негармонической, но периодической пространственно-временной зависимостью, содержащей в спектре набор гармоник. Тогда длина волны будет совпадать с длиной волны основной (наиболее низкочастотной, фундаментальной) гармоники спектра.
Длина волны — пространственный период волнового процесса[править | править код]
Волна — колебательный процесс, развивающийся (распространяющийся) в пространстве и во времени, в связи с этим изменяющаяся в волновом процессе физическая величина является функцией пространственных координат и времени (то есть особого вида пространственно-временной функцией). Волновой процесс в частности может быть периодическим (например, гармоническим). По аналогии с периодом колебаний 





Связь с частотой[править | править код]
Получить соотношение, связывающее длину волны с фазовой скоростью 


Для электромагнитных волн в вакууме скорость 



Радиоволны делят на диапазоны по значениям длин волн, например, 10…100 м — декаметровые (короткие) волны, 1…10 м — метровые, 0.1…1,0 м — дециметровые и т. п. Механизмы и условия распространения радиоволн, степень проявления эффекта дифракции, отражающие свойства объектов, предельная дальность радиосвязи и радиолокации сильно зависят от длины волны. Как правило, габаритные размеры антенн сравнимы либо (справедливо всегда для антенн направленного действия) превышают рабочую длину волны радиоэлектронного средства. Магнитная антенна средневолнового радиоприёмника имеет габарит на порядки меньше длины волны, и при этом, тем не менее, обладает пространственной селективностью.
Длина волны в среде[править | править код]
В оптически более плотной среде (слой выделен тёмным цветом) длина электромагнитной волны сокращается. Синяя линия — распределение мгновенного (t = const) значения напряжённости поля волны вдоль направления распространения. Изменение амплитуды напряжённости поля, обусловленное отражением от границ раздела и интерференцией падающей и отражённых волн, на рисунке условно не показано.
Длина электромагнитной волны в среде короче, чем в вакууме:
- где
— показатель преломления среды;
— относительная диэлектрическая проницаемость среды;
— относительная магнитная проницаемость среды.
Величины 









Напротив, длина электромагнитной волны (поперечномагнитной, поперечноэлектрической) в волноводах может быть не только больше, чем в среде с тем же значением 

Волны де Бройля[править | править код]
Волнам де Бройля также соответствует определённая длина волны. Частице с энергией 

- частота:
- длина волны:
- где
— постоянная Планка.
Примеры[править | править код]
Приближённо, с погрешностью около 0,07 % рассчитать длину радиоволны в свободном пространстве можно так: 300 000 делим на частоту в килогерцах, получаем длину волны в метрах. Другой способ — запомнить какую-нибудь удобную пару 

Примеры характерных частот и длин волн: частоте 50 Гц (частота тока в электросети) соответствует длина радиоволны 6000 км; частоте 100 МГц (радиовещательный FM-диапазон) — 3 м; 900 (1800) МГц (мобильные телефоны) —
33,3 (16,7) см; 2,4 ГГц (Wi-Fi) — 12,5 см; 10 ГГц (бортовые радиолокационные станции системы управления вооружением современных самолётов-истребителей) — 3 см. Видимый свет представляет собой электромагнитное излучение c длинами волн от 380 до 780 нм[4].
Примечания[править | править код]
- ↑ Колебания и волны // Физика : Учебник для 11 класса общеобразовательных учреждений / Г. Я. Мякишев, Б. Б. Буховцев. — 12-е изд. — М. : Просвещение, 2004. — С. 121. — 336 с. — 50 000 экз. — ISBN 5-09-013165-1.
- ↑ Определение не вполне корректно, поскольку (1) в одинаковой фазе колебания происходят и на фронте волны, и расстояние между точками на фронте может быть произвольным, в том числе и нулевым; (2) чтобы расстояние между двумя точками равнялось длине волны, колебание должно происходить не в одинаковой фазе, а со сдвигом фаз в
, и расположены точки должны быть вдоль линии распространения
- ↑ ГОСТ 18238-72. Линии передачи сверхвысоких частот. Термины и определения.
- ↑ ГОСТ 7601-78. Физическая оптика. Термины, буквенные обозначения и определения основных величин Архивная копия от 23 марта 2013 на Wayback Machine
Литература[править | править код]
- Волны де Бройля / В. И. Григорьев // Вешин — Газли. — М. : Советская энциклопедия, 1971. — (Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров ; 1969—1978, т. 5).
- Длина волны // Дебитор — Евкалипт. — М. : Советская энциклопедия, 1972. — (Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров ; 1969—1978, т. 8).
Длина волны. Связь длины волны со скоростью ее распространения. Уравнение волны
Как уже отмечалось, возмущение, создаваемое колеблющимся в упругой среде телом, передается от одной точки среды к другой. Это происходит не мгновенно, а с определенной скоростью. Скоростью распространения волны называется физическая величина, определяемая расстоянием, которое проходит любая точка фронта волны за единицу времени. Вектор скорости (vec upsilon) направлен по нормали к волновой поверхности в сторону распространения волны и в однородной изотропной среде совпадает с направлением луча. Следует отличать скорость распространения волны от скорости колебания частиц среды около своих положений равновесия.
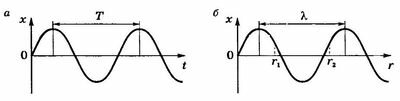
Пусть волна распространяется вдоль горизонтальной оси (например, вдоль упругого горизонтального шнура). В данный момент времени форма волны повторяется в пространстве вдоль шнура через определенные отрезки. На рисунке 15.7 показан профиль волны в определенный момент времени. С течением времени вся эта картина перемещается со скоростью (upsilon) слева направо (штриховая линия).
Расстояние между ближайшими точками, колеблющимися в одинаковых фазах (рис. 15.7), называется длиной волны. Длина волны (~lambda) равна расстоянию, на которое распространяется фронт волны за время, равное периоду (~T) колебаний источника волн[~lambda = upsilon T.]
Так как (T = frac{1}{nu};) (nu = frac{omega}{2 pi},) то скорость волны связана с частотой колебаний уравнением (~upsilon = lambda nu.) Отсюда (lambda = frac{upsilon}{nu} = frac{2 pi upsilon}{omega},) где (~omega) — циклическая частота колебаний, (~nu) и (~omega) зависят только от свойств источника волны.
При возникновении волн в среде их частота определяется частотой колебаний источника, а скорость распространения волны зависит от свойств среды. Поэтому волны одной и той же частоты имеют различную длину в разных средах.
Выведем уравнение плоской волны.
Пусть источник совершает гармонические колебания по закону
(~x = A sin omega t,)
где х — смещение, А — амплитуда, (~omega) — циклическая частота, t — время.
В точках, отстоящих на расстоянии r от источника, колебания частиц среды волнового фронта будут также гармоническими, с той же частотой, но будут отставать во времени от колебаний источника на (Delta t = frac{r}{upsilon}.)
Тогда смещение точки среды с координатой r в момент времени t
(x = A sin omega Bigr( t-frac{r}{upsilon} Bigl),) или (x = A sin Bigr( omega t-frac{omega r}{upsilon} Bigl).)
Это и есть уравнение плоской бегущей монохроматической волны (при этом предполагают, что затуханием волны в процессе ее распространения можно пренебречь). Смещение любой точки среды из равновесного положения при прохождении волны является функцией двух переменных: времени t и расстояния r до равновесного положения точки среды.
Из уравнения волны следует:
1. Амплитуда плоской незатухающей волны в данной точке среды постоянна и равна амплитуде колебаний источника.
2. Любая точка среды совершает гармонические колебания, начальная фаза которых зависит от удаления r данной точки от источника колебаний:
(~x = A sin(omega t + alpha),) где (alpha = -frac{omega r}{upsilon}.)
3. Положения колеблющихся точек среды в некоторый фиксированный момент времени описываются уравнением
(x = A sin Bigr( frac{omega r}{upsilon} + beta Bigl),) где (~beta = -omega t)
имеет разное значение в разные моменты времени.
На рисунке 15.8, б приведен график этой функции при t = 0, представляющий собой “моментальный снимок” волны, т.е. положение всех частиц среды, в которой распространяется волна, в момент времени t = 0 — график волны. В отличие от графика колебаний (рис. 15.8, а), который показывает зависимость смещения одной частицы от времени в данной точке среды, график волны (рис. 15.8, б) показывает зависимость смещения всех частиц среды из положения равновесия от расстояния г до источника колебаний в некоторый фиксированный момент времени.
Найдем разность фаз колебаний двух точек среды, находящихся на расстоянии (~Delta r = r_2 – r_1) друг от друга (рис. 15.8, б). Колебания этих точек описываются уравнениями:
(x_1 = A sin omega Bigr( t – frac{r_1}{upsilon} Bigl);) (x_2 = A sin omega Bigr( t – frac{r_2}{upsilon} Bigl).)
Разность фаз (Delta varphi_1 = varphi_1 – varphi_2) будет равна
(Delta varphi = omega Bigr( t – frac{r_1}{upsilon} Bigl) – omega Bigr( t – frac{r_2}{upsilon} Bigl) = frac{omega}{upsilon}(r_2-r_1) = frac{2 pi}{T upsilon}(r_2 – r_1) = frac{2 pi}{lambda} Delta r.)
Если две точки находятся на расстоянии (~Delta r = lambda,) то разность фаз колебаний этих точек (Delta varphi = 2 pi,) что соответствует данному выше определению длины волны.
Литература
Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — С. 428-430.
Обновлено: 23.05.2023
Характеристи́ческая ско́рость орбита́льного манёвра в астродинамике и ракетодинамике — изменение скорости космического аппарата, которое необходимо для выполнения орбитального манёвра (изменения траектории). Является скаляром и имеет размерность скорости. Обозначается в формулах как Δ v (дельта-v; произносится как де́льта-вэ́). В случае реактивного двигателя изменение скорости достигается путём выброса рабочего тела для производства реактивной тяги, которая и ускоряет корабль в космосе.
Сумма́рная характеристи́ческая ско́рость — сумма характеристических скоростей всех манёвров, необходимых для поддержания работоспособности космического аппарата или системы (орбитальной группировки) на протяжении всего периода эксплуатации [1] .
Содержание
T — мгновенная тяга двигателя, m — мгновенная масса корабля.
При отсутствии внешних сил (вакуум, гравитация небесных тел пренебрежимо мала, электромагнитные поля слабы):
где a — ускорение. Когда тяга приложена в постоянном направлении (без рысканья и тангажа), уравнение упрощается до
то есть просто до изменения скорости (относительно точки отчета в инерционной системе).
Орбитальные манёвры, как правило, выполняются выбросом из ракетного двигателя рабочего тела (газов) для создания противосилы, действующей на корабль. Значение этой силы равно
Vexh (от англ. exhaust ) — скорость истечения газа (рабочего тела). ρ — расход рабочего тела.
Ускорение (производная от скорости) v ˙ > корабля, вызванное этой силой, равно
где m — масса корабля.
Меняя переменную уравнения с времени t на массу корабля m , получаем:
Считая скорость истечения газа Vexh постоянной и независящей от остатков топлива, времени работы двигателя, это уравнение интегрируется в форму
Если, к примеру, 25 % начальной массы корабля — это топливо со скоростью истечения газов V e x h в районе 2100 м/с (обычное значение для гидразина), то достижимое для корабля полное изменение скорости равно:
Все приведённые формулы хорошо сходятся с реальностью для импульсных манёвров, характерных для химических реактивных двигателей (то есть с реакцией окисления горючего). Но для двигателей с малой тягой (например, ионных двигателей), а также двигателей, использующих электрические поля, солнечный ветер и т. п., эти упрощенные расчеты менее аккуратны, особенно если периоды работы двигателей (создания тяги) превышают несколько часов.
Также для химических двигателей с большой тягой действует эффект Оберта — включение ракетного двигателя при движении с высокой скоростью создаёт больше полезной энергии, чем такой же ракетный двигатель при медленной скорости. При движении с высокой скоростью топливо имеет больше кинетической энергии (она может даже превысить потенциальную химическую энергию), и эта энергия может использоваться для получения большей механической мощности.
| Манёвр | Требуемая Δ v за год [м/с] | |||
|---|---|---|---|---|
| Средняя | Макс. | |||
| Компенсация сопротивления атмосферы на высоте орбиты… |
400—500 км | 600 км | [2] | 0—400 |
Все скорости в таблице ниже указаны в км/с. Диапазоны скоростей указаны, так как Δ v вывода на орбиту зависит от места запуска на поверхности Земли и параметров переходных орбит.
Печатал насадку для пылесоса (в моделях выложил), скорость внешнего периметра выставил 30 мм/с.
Так при печати окружности поверхность стала неровной (шершавость), при переходе в овал начались микропаузы при переходе из одной арки в другую, и при печати больших овалов ситуация ухудшилась – несколько микропауз по арке. При микропаузе экструдер продолжает выдавливать пластик, поэтому идут утолщения по шву.
В марлине уменьшил количество расчетов сегментов с 200 до 120. Кстати, если слайсить такие вещи в Сликре – там еще хуже с этим делом.
Плата MEGA GT 2650.
Более менее печатает при снижении скорости внешнего периметра до 20 максимум.
Печатаю из Репитера.
Кто как решал такие проблемы и как увеличить скорость обработки gcoda – или уменьшить его размер/загруженность процессора.
Фото распечатанной насадки на пылесос в моделях.
Вопрос по физике:
Что такое дельта в физике, объясните пожалуйста самым обычным способом а то я в интернете нашел но нечего не понял? заранее спасибо
Ответы и объяснения 2
Дельта в физике означает приращение какой-либо величины. То есть разность СТАЛО минус БЫЛО (обычно речь идет о приращении величины за какой-то промежуток времени)
Пример. Скорость была v₁ = 4м/с а немного погодя стала v₂ = 6м/с. Тогда
Знаете ответ? Поделитесь им!
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
- Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
- Писать без грамматических, орфографических и пунктуационных ошибок.
Этого делать не стоит:
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Физика.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи – смело задавайте вопросы!
Физика — область естествознания: естественная наука о простейших и вместе с тем наиболее общих законах природы, о материи, её структуре и движении.
Греческой буквой Δ в науке принято обозначать разность между конечным и начальным значениями некой величины. Например, Δt – разность температур в начале и конце реакции или время, за которое выполнена работа. В некоторых случаях четвертую букву греческого алфавита заменяют прописной или строчной латинской d. Но латиницей в данном случае необходимо пользоваться осторожно, поскольку этой же буквой обозначаются и другие понятия.
- – измерительные приборы;
- – калькулятор.
Чтобы узнать, на сколько изменилась та или иная величина, нужно в первую очередь узнать начальное и конечное значение. Если речь идет о практической задаче, нужные параметры можно измерить. Нужный вам параметр можно в принципе назвать любой буквой, но лучше использовать принятые в науке обозначения. Допустим, вам нужно найти, насколько изменился объем вещества при нагревании. Результат первого измерения запишите как V1
Нередки задачи, когда необходимо вычислить дельту между фактическим и средним значением. Например, вам дана точка, которая поменяла свои координаты по двум осям. Обозначьте координаты как x1,x2, x3 и т. д. Найдите среднее значение. Затем вычислите разницу между полученным результатом и значением каждой координаты.
Если вам нужно вычислить приращение функции f(x), определите ее значение в жестко заданной точке — пусть это будет, например, х0. Чтобы вычислить дельту, вам необходимо сравнить значение функции в этой точке с ее же значением в любой другой точке по заданной оси. Для этого вычтите значение функции в точке х1 из ее же значения в точке х0. Это и будет Δf. Чтобы найти приращение аргумента, определите его значения в заданных точках и вычислите разность.
Буквой Δ обозначают и абсолютную погрешность. Она тоже представляет собой разность. За начальное и конечное значение принимаются истинное и приближенное значения. Величина дельты в данном случае соответствует классу точности прибора.
Буквой λ (лямбда) обозначается длина волны того или иного излучения. Эту величину можно измерить, можно рассчитать теоретически, а если излучение является видимым, то даже определить на глаз.
Чтобы рассчитать длину волны излучения, зная частоту и скорость распространения этого излучения, поделите вторую величину на первую. Если же вместо частоты известен период, умножьте его на скорость распространения излучения. Наконец, если известна циклическая частота излучения, умножьте скорость на 2π, а затем результат поделите на циклическую частоту.
Чтобы результат получился в системе СИ, предварительно переведите в нее же все величины из условия задачи. Затем переведите результат обратно в удобные для вас единицы.
Если излучение является световым, длину его волны в вакууме определите на глаз: красный – от 635 до 690 нм, оранжевый – 590, желтый – от 570 до 580, зеленый – от 510 до 520, синий – от 440 до 480, фиолетовый – от 380 до 400.
Имея специальный прибор – спектрометр, определить длину волны света можно точнее, чем на глаз. Если он является полихроматическим, определить его спектральный состав можно только с помощью этого прибора Для этого направьте световой поток во входное окно прибора. Он пройдет через щель, перпендикулярную призме, а затем и через саму призму, а затем попадет либо на шкалу, либо на линейку датчиков. Во втором случае, обработку результата измерения осуществит электронный блок прибора.
Для нахождения длины волны излучения дециметрового или сантиметрового диапазона подключите антенну к волномеру, после чего начните плавно менять ее размер. Когда он станет равен половине длины волны, показания волномера окажутся максимальными.
Направьте тонкий луч света строго перпендикулярно дифракционной решетке. На экране появится ряд пятен. Измерьте угол между воображаемой линией, продолжающей ход луча после решетки, линией, соединяющей точку входа луча в решетку с первым из пятен. Найдите синус этого угла, а затем умножьте на расстояние между двумя соседними линиями решетки. Получится длина волны, которая будет выражена в тех же единицах, что и расстояние между линиями.
На сколько легче поднимать в воде, чем в воздухе ведро с водой объемом V=10 л., масса ведра 1 кг. (Архимедовой силой, создаваемой воздухом можно прен … ебречь). Какую силу нужно приложить, чтобы поднять его?
№1. Какое количество теплоты выделилось при нагревании масла, объем которого 10 л, если температура изменилась от 30 0С до 60 0С. (Табличные значения: … плотность масла = 900кг/ м3; удельная теплоемкость масла = 1800Дж/ кг*0С ). Ответ дайте в кДж. ПЖ с проверкой едениц измерения
4. На какой глубине в пруду давление в 3 раза больше атмосферного? Плотность поды составляет 1000 кг/м³ (очитать Рo= 100000 Па; g = 9,8 Н/кг)
6. Масса пробкового спасательного круга ранна 10 кг. Опреден лите его подъемную силу в морской воде. Плотность морской по- ды составляет 1030 кг/м³, п … лотность пробки – 240 кг/м³ (считать В g=9,8 Н/кг)
Нижню частину сполучених посудин наповнили ртуттю. У ліве коліно налили гас, а в праве — воду, висота стовпчика якої 16 см. Якої висоти має бути стовп … чик гасу, щоб рівень ртуті в посудинах не змінився? У відповідь занести числове значення в одиницях СІ. *
задано направление линий магнитного поля прямого проводника с током (смотри рисунок). Определи направление тока в проводнике.
1. Определите объём стальной плиты, полностью погруженной в воду, если на неё действует выталкивающая сила 35 Н. 2. Вычислите архимедову силу, действ … ующую на брусок размером 2х10х4 см, если он наполовину погружен в Спирт. 3. Тело объёмом 4 дм имеет массу 4 кг. Утонет ли это тело в бензине? 4. Какой по весу груз сняли с парохода, если осадка его уменьшилась на 20 см? Площадь горизонтального сечения парохода на уровне воды 4000 м2. 5. По реке плывет льдина. Какая её часть погружена в воду, если Плотность льда 0,9г/см3 ? 6″. Полый цинковый шар, наружный объем которого 200 см, плавает в воде так, что половина его погружается в воду. Рассчитайте объём полости шара РЕШИТЕ ПОЖАЛУЙСТА. ДАЮ 20 БАЛЛОВ
Рассчитайте мощность насоса ,который за 2 минуты перекачивает 1200литров водоы на высоту 10 м.(ро воды =10куб кг/м3,g=10 Н/кг)
Дифракционная решетка – оптическое устройство, представляющее собой совокупность большого числа параллельных щелей, равноудаленных друг от друга.
Суммарная ширина щели и штриха (a+b=d) – период решетки.
! d=((a+b)*N)/N=C/N!, где С –ширина решетки, N -число штрихов на ней.
на нем: Л- линза; Р – решетка; Э – экран
Максимумы, которые образуются на экране, после интерференции вторичных волн, идущих от узких щелей, удовлетворяют условию:
!d*sin фи = k*лямбда! – формула дифракционной решетки.
фи – угол дифракции (угол отклонения от прямолинейного направления);
k – порядок спектра;
лямбда – длина волны света, освещающего решетку,
Дифракционные спектры для монохроматического света представляет собой чередование максимумов и минимумов по обе стороны от центрального механизма. Максимумы имеют цвет соответствующей длины света, освещающего решетку.
Если решетку освещать белым светом, то центральный максимум будет белым, а остальные будут представлять собой чередование цветных полос плавно переходящих друг в друга, т. к. sin фи= k*лямбда/d – зависит от длины волны света. D = к/t – угловая дисперсия решетки. R =k*N – разрешающая способность.
Диффузия в жидкости. Уравнение Фика. Уравнение диффузии для мембран.
Диффузия – самопроизвольное проникновение молекул одного вещества между молекулами других.
Явление диффузии – важный элемент диффракционирования мембран. При диффузии происходит перенос массы вещества. В биофизике это называется транспорт частиц. Основным уравнением диффузии является уравнение Фика:
где I – плотность частиц при диффузии в жидкость.
D – коэффициент диффузии.
Коэффициент 1/3 возник ввиду трехмерного пространства и хаоса в движении молекул (в среднем в каждом из 3-х направлений перемещается 1/3 часть всех молекул)
сигма – средняя длина свободного пробега молекул
тау -среднее время оседлой жизни молекул
С- массовая концентрация молекул
Х- перемещение молекул вдоль оси X
– градиент массовой концентрации
Уравнение диффузии можно записать в виде:
n – концентрация молекул.
Градиент концентрации
R- универсальная газовая постоянная; Т- абсолютная температура градиент химического потенциала,
Тогда
С – концентрация частиц. А Эйнштейн показал, что D пропорционально Т. Дня биологических мембран уравнение Фика имеет вид:
– концентрация молекул внутри клеток
– коэффициент проницаемости
l – толщина мембраны.
Дифракция света на щелях.
Дифракцией света называют явление отклонения света от прямолинейного распространения в среде с резкими неоднородностями.
Описать картину дифракции можно с учетом интерференции вторичных волн.
Рассмотрим дифракцию от узкой щели (АВ)
MN – непрозрачная преграда;
АВ=а – ширина щели;
АВ – часть волновой поверхности, каждая точка которой является источником вторичных волн, которые распространяются за щелью по разным направлениям. Линза соберет лучи А, А1 и В в точке О1 экрана.
АD – перпендикуляр к направлению пучка вторичных волн. Разбили ВD на отрезки =лямда/2.
АА1, А1В – зоны Френеля. Вторичные волны, идущие от двух соседних зон Френеля, не гасят друг друга, так как отличаются по фазе на пи. Число зон, укладывающихся в щели, зависит от длины волны лямда и угла альфа.
Если щель АВ разбить при построении на нечетное число зон Френеля, а ВD на нечетное число отрезков, равных лямда/2, то в точке О1 наблюдается максимум интенсивности света. ВD=а*sinα=+-(2k+1)*лямда/2.
Если щель разбить на четное число зон Френеля, то наблюдается минимум освещенности: а*sinα=+-2k*лямда/2=+-k*лямда.
Поэтому на экране получится система светлых (mах) и темных (min) полос симметричных относительно центра (альфа=треугольник – изменение) – наиболее яркой полосы.
Интенсивность остальных максимумов убывает с увеличением к.
3аконы излучения абсолютно чёрного тела (Стефана – Больцмана, Вина). Формула Планка. Использование термографии в диагностике.
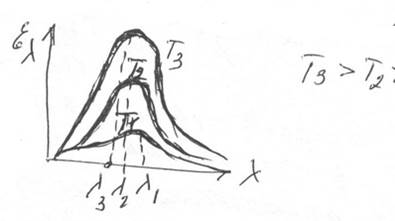
Излучение чёрного тела имеет сплошной спектр. Графически это выглядит для разных температур так:
Существует максимум спектральной светимости, который при повышении
температуры смещается в сторону коротких волн.
По мере нагревания чёрного тела его энергетическая светимость (Re)
увеличивается: Re = опред интеграл от 0 до бескон от Eлямда*dлямда
Стефан и Больцман установили, что Re=сигма*T^4
Сигма = 5,6696*10^-8 Вт/K*м^2 – постоянная Стефана-Больцмана,
T=t+273 – абсолютная (термодинамическая) температура по шкале
Кельвина. Все замечали это на практике, чем выше температура спирали, нагретой печи, тем больше они излучают тепла.
Планк получил формулу для спектральной плотности абсолютно черного тела (Eлямда) и серого тела (r лямда) (лямда-индекс): Eлямда=2п*h*c^2/лямда^5 * 1/exp[h*c/k*T*лямда-1]
альфа – коэффициент поглощения
h – постоянная Планка;
С – скорость света в вакууме;
лямда – длина волны;
k – постоянная Больцмана;
Т – абсолютная температура.
2 Затухающие колебания и декремент затухания. Апериодические колебания.
Свободные колебания (происходящие без внешнего воздействия периодически действующей силы) являются затухающими. График затухающих колебаний имеет вид:
Амплитуда колебаний с каждым разом убывает. Затуханию способствуют силы трения и сопротивления, возникающие в средах. Пусть r-коэффициент трения, характеризующий свойство среды оказывать сопротивление движению. Тогда БЕТТА= r/2m – коэффицент затухания.
Wo= корень(K/m) – циклическая частота собственных колебаний, тогда W^2=Wo^2-БЕТТА^2, где W – циклическая частота затухания колебаний.
Быстрота затухания колебаний определяется коэффициентом затухания. Уравнение затухающих колебаний имеет вид А=Ао*l в степени минус бета*t
Ao – первоначальная амплитуда, А-амплитуда затухающих через время t.
Лямда=lnA(t)/A(t+T)=lnAo*(e в степени минус бета*t)/Ao*e^-бета*(t+T)=ln(e^ бета*t) –логарифмический декрет затухания.
!Лямда=бета*Т!- связь логарифмического декремента затухания с коэффициентом затухания. При сильно затухании колебания становятся апериодическими (если бета^2>Wo^2)
№31 Импеданс полной цепи переменного тока. Сдвиг фаз. Резонанс напряжения.
Рассмотрим последовательно соединенные R, L, C.
При последовательном соединении:
1) Uвх=U0*cosW*t=Ur+Ul+Uc – входное напряжение.
2) I=I0*cos(W*t-фи) – сила тока в цепи.
Начертим векторную диаграмму:
Ur0 – совпадает по фазе с силой тока;
Ul0 – опережает на пи/2;
Uc0 – отстает от тока на пи/2.
По теореме Пифагора: (U0)^2=(U0r)^2+(U0l-U0c)^2
Сократив обе части уравнения на (I0)^2 получим выражение для полного сопротивления (Z):
Z=квадратный корень из (R^2+(W*L-1/W*c)^2) – импеданс.
Если сопротивление катушки Xl= W*L равно сопротивлению конденсатора Xc=1/W*c, то полное сопротивление Z=R; по закону Ома Iрез=U0/Z=U0/R (Iрез – резонансный ток) – сила тока резко возрастает – РЕЗОНАНС. При этом Ul=Uc>>U0 – резонанс напряжений. Это возможно, т.к. Ul и Uc сдвинуты по фазе между собой на пи:
При этом на резисторе R выделяется максимальное количество теплоты:
№32 Импенданс тканей организма. Эквивалентная Электрическая схема. Оценка жизнеспособности тканей и органов но частотной зависимости к углу сдвига фаз.
Ткани организма проводят как постоянный так и переменный ток. Биологическая мембрана а значит и весь организм обладает емкостным сопротивлением, т.к. обладают емкостью, т.е. способны
накапливать заряд. При пропускании через живые ткани переменного тока наблюдается отставание напряжения от тока. Омические емкостные свойства биологических тканей можно моделировать используя эквивалентные электрические схемы, при любых частотах зависимость сдвига фаз и импенданса от частоты выполняется для схемы
1/Zв2=1/Rв2+1/корень(R1 в2+1/Wв2*Св2)!, где Z-полное сопротивление данной цепи, с – ёмкость.
При малых частотах: Z=R2 При больших частотах: Zmin=(R1*R2)/(R1+R2).
Графическое изображение зависимости импенданса живой ткани от частоты переменного тока.
Сдвиг фаз между током и напряжением tg фи = R/Xc=RWC (1).
Частотная зависимость сдвига фаз живой ткани. При отмирании ткани натрий-калиевый канал биологических мембран разрушается, цитоплазма
клетки (проводник) соединяется с межклеточной
жидкостью(проводник) и емкостные свойства ткани уменьшаются, а это значит, что и импенданс (Z) и сдвиг фаз (фи) меньше зависят от частоты. Мёртвая ткань обладает лишь омическим сопротивлением (R), и не зависит от частоты. Диагностический метод, основанный на регистрации изменения импенданса тканей и сдвига фаз называется РЕОГРАФИЕЙ.
Читайте также:
- Как разобрать боковое зеркало инфинити qx56
- С чего подходят ступицы на оку
- Как поменять лампу ближнего света на ниссан мурано z50
- Не включается полный привод киа спортейдж 1
- Каско с выплатой наличными какие компании