![]() (кг/м3) – плотность
(кг/м3) – плотность
![]() (н/м3) – удельный вес
(н/м3) – удельный вес
![]()
ГИДРОСТАТИКА
р – давление или сжимающие напряжение (н/м2 = Па)
Свойства:
Давление всегда направлено к поверхности по внутренней нормали.
Действует одинаково по всем направлениям (не зависит от угла наклона площадки)
Основное уравнение гидростатики:
рА = ро + рв; рв = h·γ
рА – абсолютное давление;
ро – давление действующее на поверхность жидкости;
рв – весовое давление, т.е. давление столба жидкости.
рв = h·γ
h – глубина расположения точки;
γ – удельный вес жидкости.
При атмосферном давлении на поверхности:
рА = ра + ризб; ризб = hизб·γ
ра – атмосферное давление;
ризб – избыточное давление.
Выводы:
-
Закон Паскаля. Давление действующее на поверхность жидкости передается во все ее точки без изменения.
-
Любая горизонтальная плоскость проведенная в жидкости, является плоскостью равного давления.
-
Можем измерять величину давления эквивалентной ему высотой столба жидкости.
р = h·γ, отсюда h = р/γ
Например давление величиной в 1 атм. р = 1 кгс/см2 соответствует
h = 10 м вод. столба
Сила давления жидкости на плоскую поверхность
Р = рсS = hсγS (н)
рс = hсγ – давление в центре тяжести при атмосферном давлении на поверхности
рс = hсγ + рМ, либо рс = hсγ – рВАК
hс – глубина расположения центра тяжести поверхности (м);
S – площадь поверхности (м2).
Потенциальная энергия покоящейся жидкости величина постоянная, т.е. одинаковая для всех точек жидкости
Удельная энергия (напор) Э = Е/G = Е/mg (м)
Z + hп = НГС = Э = const
Z – геометрический напор;
hп – пьезометрический напор;
НГС –гидростатический напор или полная удельная потенциальная энергия жидкости.
ГИДРОДИНАМИКА
Уравнение неразрывности
Q = V1ω1 = V2ω2 = const
Q – расход жидкости (м3/с);
V – средняя скорость потока (м/с);
Ω – площадь живого сечения потока (м2).
Vi = Q / ωi – средняя скорость потока
Уравнение Бернулли для идеальной жидкости (при действии сил давления и сил тяжести)
![]()
где z – геометрический напор, м;
P/γ – приведенная пьезометрическая высота (если Р – абсолютное давление) или пьезометрическая высота (если Р – избыточное давление), м;
V2/2g – скоростной напор, м.
![]() – гидростатический напор,
– гидростатический напор,
удельная потенциальная энергия жидкости
НГС = Э – гидродинамический напор или полная удельная энергия
Уравнение Бернулли для реальной жидкости (с учетом сил трения (вязкости)).
![]()
Σh = hпот = hℓ + hм – потери энергии при движении жидкости от 1 до 2 сечений (м);
α= ЕКД /ЕКУ – коэффициент кинетический энергии (коэффициент Кориолиса);
hℓ – потери по длине.
![]() (м)
(м)
λ – коэффициент гидравлического трения f(Rе·Δ);
hм – потери на местных сопротивлениях.
![]() (м)
(м)
РЕЖИМЫ ДВИЖЕНИЯ
Число (критерий) Рейнольдса ![]()
Для кругло-цилиндрических труб ![]()
![]() (м)
(м)
RГ – гидравлический радиус;
ω – площадь живого сечения потока (м2);
Х – смоченный периметр.
Ламинарный режим: Rе < Rекр ≈ 2320
Эпюра скорости при ламинарном движении.
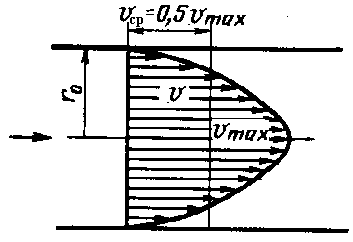
umax = 2V; α = 2; λ = f(Rе); λ = 64/Rе; hℓ = f (V1…1,4)
Турбулентный режим: Rе > Rекр
Профиль скорости при турбулентном движении
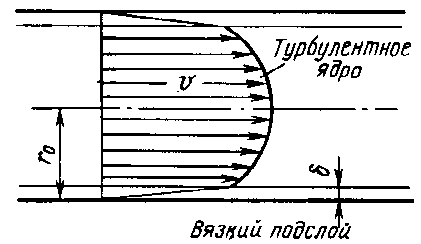
Толщина ламинарной пленки δ уменьшается с увеличением скорости V (числа Рейнольдса)
u ≈ V; α = 1…1,4
В турбулентном режиме имеется три вида трения:
Гидравлически гладкие русла
λ = f(Rе) λ = 0,3164/Rе0,25
Смешанное трение
λ = f(Rе;Δ)
![]()
Шероховатое трение, квадратичная область турбулентного режима
λ = f (Δ); λ = 0,11(Δ /d)0,25
hℓ = f (V1,7…2)
СКОРОСТЬ ДВИЖЕНИЯ (ИСТЕЧЕНИЯ ЧЕРЕЗ ОТВЕРСТИЯ И НАСАДКИ
![]() (м/с)
(м/с)
![]() – коэффициент скорости
– коэффициент скорости
Но – действующий (расчетный напор (м)
Расход жидкости
![]() (м3/с)
(м3/с)
μ = φε – коэффициент расхода;
ω – площадь проходного (живого) сечения потока (м2);
Но – действующий напор (м).
Основные буквенные обозначения, принятые в курсе гидравлики
|
C |
— |
скоростной |
|
D, |
— |
диаметр; |
|
|
— |
эквивалентный |
|
E |
— |
энергия; |
|
|
— |
модуль упругости; |
|
Eк |
— |
кинетическая |
|
Eп |
— |
потенциальная |
|
е |
— |
удельная энергия |
|
F |
— |
сила трения; |
|
Fr |
— |
число Фруда; |
|
G |
— |
вес (сила тяжести); |
|
g |
— |
ускорение силы |
|
H |
— |
геометрический |
|
|
— |
гидродинамический |
|
h |
— |
глубина потока; |
|
|
— |
заглубление |
|
hl |
— |
потери удельной |
|
hp |
— |
пьезометрическая |
|
|
— |
скоростной напор; |
|
hW |
— |
суммарные потери |
|
hм |
— |
метацентрическая |
|
|
— |
суммарные местные |
|
|
— |
глубина погружения |
|
|
— |
гидравлический |
|
|
— |
пьезометрический |
|
|
— |
момент инерции |
|
|
— |
момент инерции |
|
ie |
— |
средний |
|
ip |
— |
средний |
|
K |
— |
расходная |
|
L, |
— |
длина; |
|
|
— |
масса; |
|
n |
— |
коэффициент |
|
P |
— |
сила; |
|
Px |
— |
составляющая |
|
Py |
— |
составляющая |
|
Pz |
— |
составляющая |
|
P0 |
— |
сила внешнего |
|
P1 |
— |
сила избыточного |
|
p |
— |
давление в точке; |
|
pатм, |
— |
атмосферное |
|
p |
— |
полное давление |
|
|
— |
внешнее давление |
|
pм |
— |
избыточное или |
|
pвак |
— |
вакуум; |
|
Q |
— |
расход; количество |
|
q |
— |
удельный расход |
|
R |
— |
гидравлический |
|
r, |
— |
геометрический |
|
Re |
— |
число Рейнольдса; |
|
S |
— |
площадь соприкасания |
|
Sx |
— |
статический |
|
T, |
— |
время; |
|
|
— |
температура, |
|
|
— |
температура, |
|
u |
— |
местная скорость; |
|
|
— |
осредненная |
|
|
— |
пульсационная |
|
V |
— |
средняя скорость |
|
Vmin |
— |
минимальная |
|
Vдоп |
— |
допускаемая |
|
Vв. |
— |
верхняя критическая |
|
Vн. |
— |
нижняя критическая |
|
W |
— |
скоростная |
|
X, |
— |
проекции внешних |
|
hц., |
— |
глубина погружения |
|
z |
— |
геометрическая |
|
|
— |
коэффициент |
|
|
— |
коэффициент |
|
|
— |
угол в градусах; |
|
|
— |
угол в радианах; |
|
|
— |
удельный вес; |
|
|
— |
эквивалентная |
|
|
— |
толщина слоя; |
|
|
— |
коэффициент |
|
|
— |
коэффициент |
|
|
— |
смоченный |
|
|
— |
гидравлический |
|
|
— |
коэффициент |
|
|
— |
кинематический |
|
|
— |
плотность |
|
|
— |
удельная сила |
|
|
— |
коэффициент |
|
|
— |
площадь сечения |
|
|
— |
площадь живого |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 13 ноября 2019 года; проверки требуют 4 правки.
Формула Вейсбаха’[1] в гидравлике — эмпирическая формула, определяющая потери напора или потери давления при развитом турбулентном течении несжимаемой жидкости на гидравлических сопротивлениях (предложена Юлиусом Вейсбахом в 1855 году):
где
— потери напора на гидравлическом сопротивлении;
— коэффициент местного сопротивления (коэффициент потерь);
— средняя скорость течения жидкости;
— ускорение свободного падения;
- величина
называется скоростным (или динамическим) напором.
Формула Вейсбаха, определяющая потери давления на гидравлических сопротивлениях, имеет вид:
где
— потери давления на гидравлическом сопротивлении;
— плотность жидкости.
Формула Дарси — Вейсбаха[править | править код]
Если гидравлическое сопротивление представляет собой участок трубы длиной 


где
— коэффициент потерь на трение по длине (коэффициент Дарси).
Тогда формула Вейсбаха приобретает вид:
или для потери давления:
Последние две зависимости получили название формулы Дарси — Вейсбаха[2]. Предложена Ю. Вейсбахом (L. J. Weisbach, 1845) и А. Дарси (1857).
Если определяются потери на трение по длине для трубы некруглого поперечного сечения, то 
Следует отметить, что потери напора на гидравлических сопротивлениях не всегда пропорциональны скоростному напору.
Определение коэффициента потерь на трение по длине[править | править код]
Коэффициент 
Для ламинарного течения в гладких трубах с жёсткими стенками, коэффициент потерь на трение по длине определяется по формуле Пуазейля:
где
— число Рейнольдса.
Иногда для гибких труб в расчётах принимают
Для турбулентного течения существуют более сложные зависимости. Одна из наиболее часто используемых формул — это формула Блазиуса:
Эта формула даёт хорошие результаты при числах Рейнольдса, изменяющихся в пределах от критического числа Рейнольдса 

Для значений 

Для значений Рейнольдса больше 

Для гидравлически шероховатых труб коэффициент потерь на трение по длине определяется графически по эмпирическим зависимостям. Графики для определения коэффициента потерь на трение по длине для шероховатых труб можно посмотреть здесь (k — размер шероховатости, d — диаметр трубы).
Определение коэффициента Дарси для местных сопротивлений[править | править код]
Рис. 1. Гидравлический конфузор: 

Для каждого вида местных сопротивлений существуют свои зависимости для определения коэффициента 
К числу наиболее распространённых местных сопротивлений относятся внезапное расширение трубы, внезапное сужение трубы и поворот трубы.
1. При внезапном расширении трубы:
где 

2. При внезапном сужении трубы коэффициент Дарси определяется по формуле:
Рис. 2. Зависимость коэффициента Дарси от угла 
где 

3. При постепенном сужении трубы (конфузор):
где 

4. При резком (без закругления) повороте трубы (колено) коэффициент Дарси определяется по графическим зависимостям (рис. 2).
История[править | править код]
Исторически формула Дарси — Вейсбаха была получена как вариант формулы Прони.
См. также[править | править код]
- Гидравлические потери
- Формула Борда — Карно
- Формула Прони
- Формула Шези
Примечания[править | править код]
- ↑ Формула Вейсбаха Архивная копия от 1 марта 2011 на Wayback Machine в Физической энциклопедии
- ↑ Дарси-Вейсбаха формула Архивная копия от 16 марта 2012 на Wayback Machine в Физической энциклопедии
- ↑ М.П. Малков, И.Б. Данилов, А.Г. Зельдович, А.Б. Фрадков. Справочник по физико-техническим основам криогеники. — “Энергия”, 1973. — С. 242-243. — 392 с.
- ↑ Горшков-Кантакузен В. А. К вопросу вычисления коэффициента Дарси методом регрессионного анализа // Материалы XXI Международного симпозиума «Динамические и технологические проблемы механики конструкций и сплошных сред» имени А. Г. Горшкова, 16 – 20 февраля 2015, Вятичи.. — 2015. — № Том 1. — С. 59-60. — ISSN 978-5-906099-81-5.
- ↑ Горшков-Кантакузен В.А. Вычисление критерия Рейнольдса в рамках гемодинамики // Бюллетень НЦССХ им. А.Н. Бакулева “сердечно-сосудистые заболевания” : (Приложение). — май-июнь 2015. — № 3 Т.6. — С. С. 180. — ISSN 1810-0694.
Литература[править | править код]
- Гидравлика, гидромашины и гидроприводы: Учебник для машиностроительных вузов/ Т. М. Башта, С. С. Руднев, Б. Б. Некрасов и др. — 2-е изд., перераб. — М.: Машиностроение, 1982.
- Гейер В. Г., Дулин В. С., Заря А. Н. Гидравлика и гидропривод: Учеб для вузов. — 3-е изд., перераб. и доп. — М.: Недра, 1991.
- Горшков-Кантакузен В. А. К вопросу вычисления коэффициента Дарси методом регрессионного анализа // Материалы XXI Международного симпозиума «Динамические и технологические проблемы механики конструкций и сплошных сред» имени А. Г. Горшкова, 16 — 20 февраля 2015, Вятичи. Том 1 / МАИ. — М.: ООО «ТРП», 2015. С. 59-60
Формула Дарси — формула, определяющая потери напора или потери давления на гидравлических сопротивлениях:
где
- Δh — потери напора на гидравлическом сопротивлении;
- ξ — коэффициент потерь (коэффициент Дарси;
- V — средняя скорость течения жидкости;
- g — ускорение свободного падения;
- величина
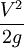 называется скоростным напором.
называется скоростным напором.
Формула Дарси, определяющая потери давления на гидравлических сопротивлениях, имеет вид:
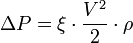
где
- ΔP — потери давления на гидравлическом сопротивлении;
- ρ — плотность жидкости.
Содержание
- 1 Формула Дарси-Вейсбаха
- 2 Определение коэффициента потерь на трение по длине
- 3 Определение коэффициента Дарси для местных сопротивлений
- 4 См. также
- 5 Литература
Формула Дарси-Вейсбаха
Если гидравлическое сопротивление представляет собой участок трубы длиной L и диаметром D, то коэффициент Дарси определяется следующим образом:
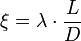
где λ — коэффициент потерь на трение по длине.
Тогда формула Дарси приобретает вид:
или для потери давления:
Последние две зависимости получили название формулы Дарси-Вейсбаха.
Если определяются потери на трение по длине для трубы некруглого поперечного сечения, то D представляет собой гидравлический диаметр.
Следует отметить, что потери напора на гидравлических сопротивлениях не всегда пропорциональны скоростному напору.
Определение коэффициента потерь на трение по длине
Коэффициент λ определяется по разному для разных случаев.
Для ламинарного течения в гладких трубах с жёсткими стенками, коэффициент потерь на трение по длине определяется по формуле:
где Re — число Рейнольдса.
Иногда для гибких труб в расчётах приниают
Для турбулентного течения существуют более сложные зависимости. Одна из наиболее часто используемых формул — это формула Блазиуса:
Эта формула даёт хорошие результаты при числах Рейнольдса, изменяющихся в пределах от критического числа Рейнольдса Reкр до значений Re = 105. Формула Блазиуса применяется для гидравлически гладких труб.
Для гидравлически шероховатых труб коэффициент потерь на трение по длине определяется графически по эмпирическим зависимостям. Графики для определения коэффициента потерь на трение по длине для шероховатых труб можно посмотреть здесь (k — размер шероховатости, d — диаметр трубы).
Определение коэффициента Дарси для местных сопротивлений
![]()
Рис. 1. Гидравлический конфузор: Q1 — поток жидкости в широком сечении трубы; Q2 — поток жидкости в узком сечении трубы
Для каждого вида местных сопротивлений существуют свои зависимости для определения коэффициента ξ.
К числу наиболее распространённых местных сопротивлений относятся внезапное расширение трубы, внезапное сужение трубы и поворот трубы.
1. При внезапном расширении трубы:
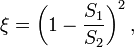
где S1 и S2 — площади поперечного сечения трубы, соответственно перед расширением и после него.
2. При внезапном сужении трубы коэффициент Дарси определяется по формуле:
![]()
Рис. 2. Зависимость коэффициента Дарси от угла δ поворота трубы
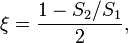
где S1 и S2 — площади поперечного сечения трубы, соответственно, перед сужением и после него.
3. При постепенном сужении трубы (конфузор):
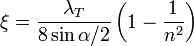 ,
,
где 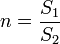 — степень сужения; λT — коэффициент потерь на трение по длине при турбулетном режиме.
— степень сужения; λT — коэффициент потерь на трение по длине при турбулетном режиме.
4. При резком (без закругления) повороте трубы (колено) коэффициент Дарси определяется по графическим зависимостям (рис. 2).
См. также
- Гидравлические потери
Литература
- Гидравлика, гидромашины и гидроприводы: Учебник для машиностроительных вузов/ Т.М. Башта, С.С. Руднев, Б.Б. Некрасов и др. — 2-е изд., перераб. – М.: Машиностроение, 1982.
- Гейер В.Г., Дулин В.С., Заря А.Н. Гидравлика и гидропривод: Учеб для вузов. — 3-е изд., перераб. и доп. — М.: Недра, 1991.
Данная справочная статья включает в себя 80% формул по гидравлике для студентов но и для инженеров можно подобрать формулы для выбора гидравлической машины (насоса) и гидропривода. Статья предназначена в основном для студентов высших технических учебных заведений и студентов технических, энергетических и некоторых строительных специализированных техникумов, изучающих общий курс гидравлики, гидравлических машин и гидравлического оборудования.
Возможно эта страница вам будет полезна:
Статья включает в себя простую теоретическую информацию, основные понятия и определения, формулы и значения экспериментальных формул, вспомогательные таблицы, графики и номограммы, необходимые для решения задач, расчета и выполнения графических работ. В некоторых разделах показана схема проектирования. Также полезно для инженеров и технологов, которые занимаются расчетами в области общей гидравлики, а также в области эксплуатации гидравлических машин и гидроприводов.














Системы единиц измерения
Согласно ГОСТ9867-61 и ГОСТ, проект «единица физической величины» вводится в качестве приоритетной системы единиц международных единиц измерения (си) во всех сферах науки, техники и народного хозяйства. В системе СИ имеется 6 основных единиц и дополнительных единицы, при расчете гидравлического давления, измеритель длины (м), масса-килограммы (кг), Время-секунды, температура-Кельвин.
Полученные единицы СИ, используемые для гидравлического расчета, приведены в таблице. Площадь Объем Скорость Ускорение Частота вращения Величина Размерность Единица наименование обозначение 1 3 4 i2 квадратный метр м2 № кубический метр м3 1, метр в секунду м/с 2 метр на секунду в квадрате м/с секунда в минус первой степени.
Угловая скорость 7-1 радиан в секунду рад/с Плотность Ла-з килограмм на кубическим метр кг/м Момент инерции площа- и ди фигуры метр в четвертой степени n1 Сила, сила тяжести (вес) -ньютон Давление, напряжение паскаль Па Модуль упругости Л17-2 паскаль Па Поверхностное натяжение- Н/м ньютон на. Метр Динамический коэффициент- Л Па вязкости паскаль-секунда Кинематический коэф- 1 м2/с коэффициент вязкости квадратный метр на секунду Удельный вес ныотон на кубический метр Н/м? Напор 1 метр м Массовый расход Д17-1 килограмм в секунду кг/с Объемный расход ит-1 кубический метр’в секунду М3/С Работа, энергия — 2 джоуль Дж Мощность ватт Вт.
Система Си использует кратные числа основания 10 и десятичных единиц исходного блока для представления больших или малых количеств машины. В гидравлическом калькуляторе множитель и его префикс перечислены в таблице. 11. 2.
Множитель Приставка наименование | обозначение Пример 106 мега м МЫ (меганьютон) 103 кило к кВт (киловатт) 101 дека да даН (деканьютон) 10-1 деци Д дм (дециметр) 10-2 санти с см (сантиметр) 10-3 МИЛЛИ м мм (миллиметр).
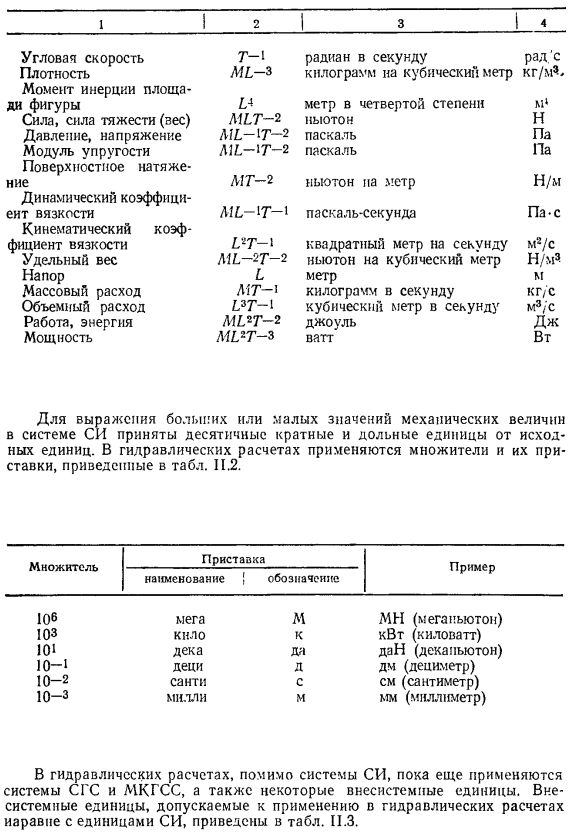
При расчете давления масла, помимо системы СИ, продолжают использоваться системы СГС и МКГСС, а также некоторые несистемные блоки. Вместе с блоком си в таблице приведены внесистемные блоки, которые могут быть использованы в гидравлических расчетах. Второй. 3.
Величина Единица Значение в наименование обозначение ницах СИ Длина сантиметр СМ 10-2 м Масса тонна т 103 кг грамм Г 10-3 кг Время минута [час мин ч 60 с 3600 с Площадь квадратный сантиметр см2 10–4 м2 градус о 0, 0175 рад Плоский угол минута / 2, 91 10–4 рад секунда ч 4, 85-10-6 рад Объем литр 1 кубический сантиметр Л см3 10-3 мз 10-6 мз.
Объемный расход литр в секунду л/с 10-3 м3/ с Частота вращения (оборот в секунду об/с i с-1 (оборот в минуту об/мни 1С-1 60 Работа, энергия киловатт-час кВт/ч 3, 6-106 Дж Скорость сантиметр в секунду см/с см/с2 10-2 м/с Ускорение сантиметр на секунду в квадрате 10-2 М/С2.
Плотность грамм на кубический г/см3 10-3 кг/м3 сантиметр п Динамический коэфф пуаз 0, 1 вязкости Кинематический коэффи- стокс Ст 10~м/с вязкости Единицы, допускавшиеся к применению до 1/1 1975 г. , приведены в табл. Ii. 4. Таблица /1. 4 Величина Единица наименование обозначение Сила, сила тяжести (нес) килограмм-сила к ГС килограмм-сила на квадратный сантиметр техническая атмосфера миллиметры водяного столба миллиметры ртутного столба К ГС/см2 Давление ат мм вод. ст. Мм рт. ст. Работа, энергия килограмм-сила-метр кгс м Мощность [килограмм-сила-метр в секунду [лошадиная сила кгс м/с л. с.
Показывает взаимосвязь между Си, icgss и единицами, наиболее часто используемыми в не системных системных гидравлических расчетах.
Величина Связь между единицами МКГСС я внесистемными и СИ Связь между единицами в системе СИ и МКГСС и внесистемными единицы в системе МКГСС и внесистемные значения в единицах СИ единицы в системе СИ значения в единицах МКГСС и внесистемных Масса 1 кгс-с2/м 9, 81 кг 1 кг 0, 102 кгс-с2/м Плотность 1 кгс-с2/м4 9, 81 кг/м 1 кг/м 0, 102 кгс с2/м Сила, силатяжес- (вес) 1 кгс 9, 81 Н 1 Н 0, 102 кгс Удельный вее 1 кгс/м8 9, 81 Н/мЗ 1 Н/м 0, 102 кгс/м’ Давление 1 кгс/м2 9, 81 Па 1 Па 0, 102 кгс/м2 1 кгс/см2= 98100 Па= 1 Па 1, 02-10-5 «=1 ат =98, 1кПа=0, 1 МПа кгс/см2=э -=1, 02-10-5 ат Работа, энергия 1 кгс-м 9, 81 Дж 1 Дж 0, 102 кгс-м Мощность 1 кгс-м/с 9, 81 Вт=0, 01 1 Вт 0, 102 кгс-м/с кВт Динамический коэффициент вязкости 1 кгс-с/м2 9, 81 Па-с 1 Па с 0, 102 кгс-с/м2
Определение жидкости, ее плотность, удельный и относительный вес
Жидкость —непрерывная среда, обладающая свойством текучести, т. е. Способная неограниченно изменять свою форму под действием сколь угодно малых сил, но в отличие от газа мало изменяющая свою плотность при изменении давления. В аэромеханике применяют термин «капельная жидкость» с целью подчеркнуть отличие жидкости от газа; газ в этих случаях называют «сжимаемой жидкостью».
Плотность р — масса жидкости в единице объема. Для однородной т жидкости р—, где т — масса жидкости в объеме v. Единицы измерения р в системе СГС — г/см3, в системе МКГСС — кгс-с2/м4, в системе СИ— кг/м . С Удельный (объемный) вес у— вес жидкости в единице объема: где О — вес жидкости. Единицы измерения у в системе СГС — дин/см3 г/см2-с2, в системе МКГСС—кгс/м3, в системе СИ—Н/м3=кг/м2-с2.
Удельный вес и плотность связаны между собой зависимостью у — где я = 9, 81 м/с2— ускорение свободного падения. Относительный вес б— безразмерная величина, равная отношению веса или массы данной жидкости к весу или массе дистиллированной воды, взятой в том же объеме при в Рв Плотность, так же как удельный и относительный веса жидкости, зависит от давления и температуры.
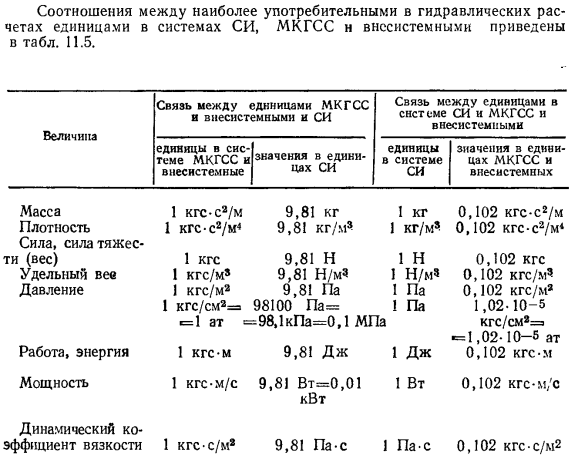
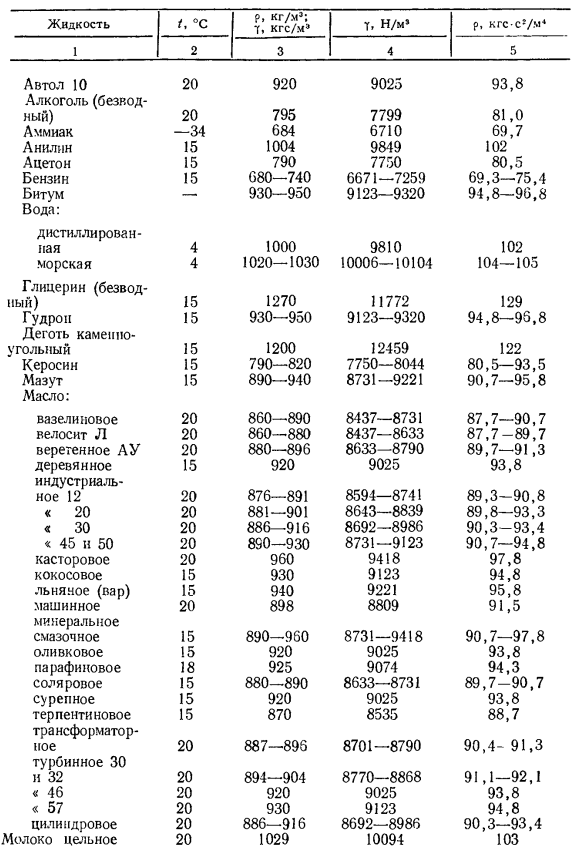
Значения плотности и удельного веса некоторых жидкостей при различных температурах и нормальном атмосферном давлении приведены в табл. 1. 1. [12. 77, 97, 116]. Плотности (р. Кг/м5) и удельные веса (у, кгс/м3) воды и ртути при различных температурах и нормальном атмосферном давлении показаны в табл. 1. 2, при температуре 0°С и различном давлении — в табл. 1. 3.
| Жидкость | Л °С | Р, кг/м3; Т, кгс/м | Т. Н/м* | р, кгс с’/ч4 |
| 1 | 2 | 3 | 4 | 5 |
| Автол 10 | 20 | 920 | 9025 | 93,8 |
| Алкоголь безводный | 20 | 795 | 7799 | 81,0 |
| Аммиак | —34 | 684 | 6710 | 69,7 |
| Анилин | 15 | 1004 | 9849 | 102 |
| Ацетон | 15 | 790 | 7750 | 80,5 |
| Бензин | 15 | 080-740 | 6671—7259 | 69,3-75,4 |
| Битум | — | 930—950 | 9123—9320 | 94,8—90,8 |
| Вода: | ||||
| дистиллированая | 1000 | 9810 | 102 | |
| морская | 4 | 1020—1030 | 10006-10104 | 104—105 |
| Глицерин безводный | 1270 | |||
| Гудрон | 15 | 930—950 | 9123—9320 | 94,8—96,8 |
| Деготь каменно | ||||
| угольный | 15 | 1200 | 12459 | 122 |
| Керосин | 15 | 790—820 | 7750-8044 | 80,5—93,5 |
| Мазут | 15 | 890—940 | 8731—9221 | 90,7—95,8 |
| Масло: | ||||
| вазелиновое | 20 | 860-890 | 8437—8731 | 87,7—90,7 |
| велосит Л | 20 | 860—880 | 8437—8633 | 87,7-89,7 |
| веретенное АУ | 20 | 880—896 | 8633-8790 | 89,7—91,3 |
| деревянное | 15 | 920 | 9025 | 93,8 |
| масло | 20 | 876—891 | а594—8741 | 89,3—90,8 |
| « 20 | 20 | 881—901 | 8643—8839 | 89,8—93,3 |
| « 30 | 20 | 886—916 | 8692-8986 | 90,3-93,4 |
| « 45 и 50 | 20 | 890—930 | 8731—9123 | 90,7—94,8 |
| касторовое | 20 | 960 | 9418 | 97,8 |
| кокосовое | 15 | 930 | 9123 | 94,8 |
| льняное (вар) | 15 | 940 | 9221 | 95,8 |
| машинное | 20 | 898 | 8809 | 91,5 |
| минеральное | ||||
| смазочное | 15 | 890-960 | 8731—9418 | 90,7—97,8 |
| оливковое | 15 | 920 | 9025 | 93,8 |
| парафиновое | 18 | 925 | 9074 | 94,3 |
| соляровое | 15 | 880-890 | 8633—8731 | 89,7-90,7 |
| сурепное | 15 | 920 | 9025 | 93,8 |
| терпентиновое | 15 | 870 | 8535 | 88,7 |
| трансформатор ное | 20 | 887—896 | 8701—8790 | 90,4- 91,3 |
| турбинное 30 | ||||
| и 32 | 20 | 894—904 | 8770—8868 | 91,1-92,1 |
| « 46 | 20 | 920 | 9025 | 93,8 |
| « 57 | 20 | 930 | 9123 | 94,8 |
| цилиндровое | 20 | 886—916 | 8692—8986 | 90,3—93,4 |
| Молоко цельное | 20 | 1029 | 10094 | 103 |
| 1 |
1 2 1 |
3 | 4 | 5 |
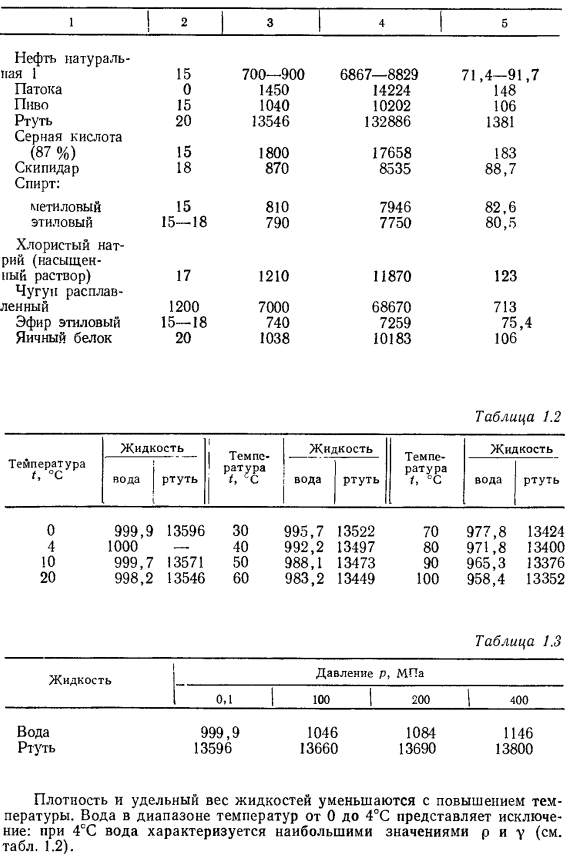
| Нефть натуральная | 15 | 700—900 | 6867—8829 | 71,4-91,7 |
| Патока | 0 | 1450 | 14224 | 148 |
| Пиво | 15 | 1040 | 10202 | 106 |
| Ртуть | 20 | 13546 | 132886 | 1381 |
| Серная кислота | ||||
| (87 о/0) | 15 | 1800 | 17658 | 183 |
| Скипидар | 18 | 870 | 8535 | 88,7 |
| метиловый | 15 | 810 | 7946 | 82,6 |
| этиловый | 15—18 | 790 | 7750 | 80,5 |
| Температура /, °С | Жидкость |
1 1 Тсмпс- 1 РатУРа |
Жидкость |
Температура и °с |
Жидкость |
| вода | ртуть | вода | ртуть | вода | ртуть |
| 0 | 999,9 | 13596 | 30 | 995,7 | 13522 |
| 4 | 1000 | — | 40 | 992,2 | 13497 |
| 10 | 999,7 | 13571 | 50 | 988,1 | 13473 |
| 20 | 998,2 | 13546 | 60 | 983,2 | 13449 |
| Жидкость | Давление р, | МПа | Спирт | ||
| Вода | 999,9 | 1046 | 1084 | 1146 | |
| Ртуть | 13596 | 13660 | 13690 | 13800 |
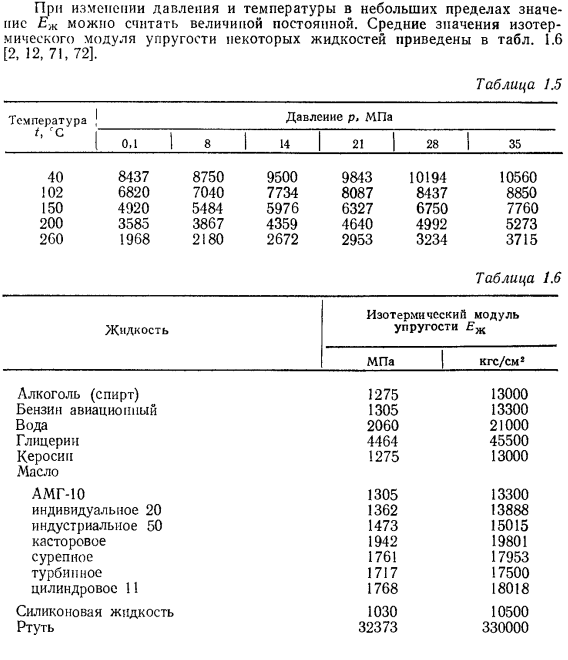
Плотность и удельный вес жидкостей уменьшаются с повышением температуры. Вода в диапазоне температур от 0 до 4°С представляет исключение: при 4СС вода характеризуется наибольшими значениями р и у (см. табл. 1.2).
Сжимаемость жидкостей
Сжимаемость-это свойство жидкости, которая изменяет свой объем под давлением. Сжимаемость жидкости характеризуется объемным коэффициентом сжимаемости, который представляет собой относительное изменение объема жидкости v0. Au 1 Л. С. .(1 .1 Знак минус формулы (1 .1) обусловлен тем, что положительному приращению давления соответствует отрицательное приращение (уменьшение) объема. Единицы системы МКГСС в 1 / ПА в системе СИ м2 / кгс .Часто он представлен см2 / кгс. Если приращение давления cp = p-p0 и изменение объема предполагается (1 .2 (1 .3
В уравнениях (1. 2) и (1. 3) v и v0-объем, а p и p0-плотность при давлениях p и p0 соответственно.
Людмила Фирмаль
Взаимное объемного коэффициента сжимаемости называется объемным модулем упругости жидкости Единицы Так же, как давления: кгс / м2, в системе МКГСС, Н / м2, в системе СИ или в Паскалях (па), кгс / см2 также часто используется. Жидкость ежа имеет значение температуры и давления р.
Существуют адиабатический модуль упругости и изотермический модуль упругости 1-й немного больше, чем 2-й, и, по-видимому, представляет собой переходный процесс сжатия жидкости, например, во время гидравлического удара в трубе внутри стола. 1. 4 значение изотермического модуля упругости Таблица 1.4 Давление р, МПа (1МПа=104 Па).
Если давление и температура изменяются в пределах небольшого предела, то значение h> k можно считать постоянной величиной. В таблице приведены средние значения изотермического модуля упругости некоторых жидкостей.
Температура Давление р. МПа
| 0.1 | 8 | 14 | 21 | 28 | | 35 | |
| 40 | 8437 | 8750 | 9500 | 9843 | 10194 | 10560 |
| 102 | 6820 | 7040 | 7734 | 8087 | 8437 | 8850 |
| 150 | 4920 | 5484 | 5976 | 6327 | 6750 | 7760 |
| 200 | 3585 | 3867 | 4359 | 4640 | 4992 | 5273 |
| 260 | 1968 | 2180 | 2672 | 2953 | 3234 | 3715 |
Таблица 1.6
Изотерма модуль упругости МПа кгс/см3
|
Алкоголь (спирт) |
1275 | 13000 |
|
Бензин авиационный |
1305 | 13300 |
| Вода | 2060 | 21000 |
| Глицерин | 4464 | 45500 |
| Керосин | 1275 | 13000 |
| АМГ-10 | 1305 | 13300 |
|
индивидуальное 20 |
1362 | 13888 |
|
индустриальное 50 |
1473 | 15015 |
| касторовое | 1942 | 19801 |
| сурепное | 1761 | 17953 |
| турбинное | 1717 | 17500 |
| цилиндровое 11 | 1768 | 18018 |
|
Силиконовая жидкость |
1030 | 10500 |
| Ртуть Масло | 32373 | 330000 |
Температурное расширение жидкостей
Тепловое расширение жидкости количественно характеризуется коэффициентом теплового расширения (3/, 1’0 относительное изменение с изменением температуры / ia gs: Коэффициент теплового расширения воды увеличивается с увеличением давления и температуры. Для большинства других капельных жидкостей он уменьшается с увеличением давления.
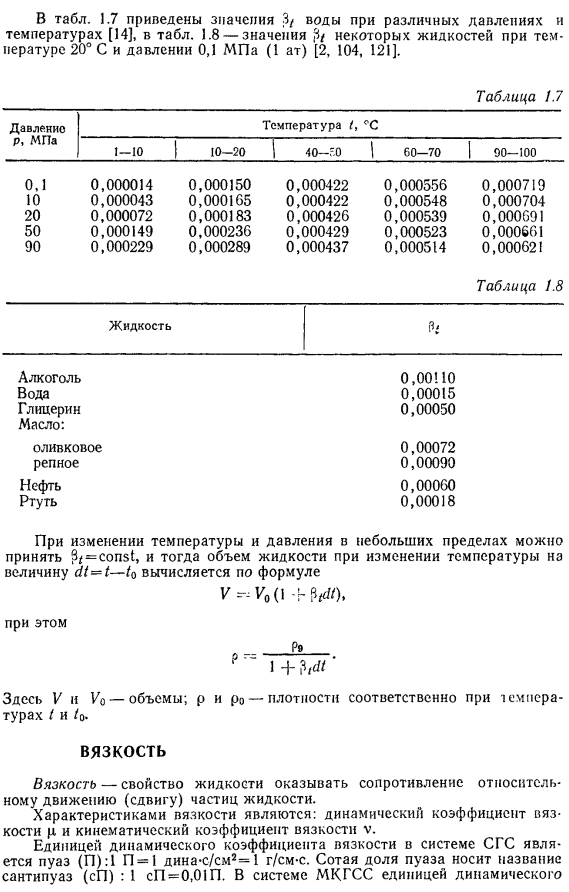
В табл. 1. 7 приведены значения 3/ воды при различных давлениях и температурах [14], в табл. 1. 8 —значения ^ некоторых жидкостей при температуре 20° С и давлении 0, 1 МПа (1 ат) [2, 104, 121]. Таблица 1. 7 Давление р, МГТа 1–10 10-20 Температура (, °С 40–-0 | 60–70 00-100 Жидкость Алкоголь Вода Глицерин.
Масло: оливковое репное Нефть Ртуть 0, 00! 10 0, 00015 0, 00050 0, 00072 0, 00090 0, 00060 0, 00018 При изменении температуры и давления в небольших пределах можно принять , и тогда объем жидкости при изменении температуры на величину (11 = 1–10 вычисляется по формуле при этом Рэ Н Здесь v и Уо — объемы; р и р0 — плотности соответственно при температурах.
Вязкость
Вязкость-это свойство жидкости, которая сопротивляется относительному движению (сдвигу) частиц жидкости. Вязкостными характеристиками являются коэффициент динамической вязкости c и коэффициент кинематической вязкости v. Единицей коэффициента кинематической вязкости системы ghs является pozzu, а 100/1 пор называется centipoise системы mkgss, а единицей коэффициента кинематической вязкости является kgf-s / m2.
Система Си-па-С. Соотношение между единицами таково: коэффициент кинематической вязкости единицами коэффициента кинематической вязкости системы СГС являются ход (СТ) или 1 см2 / с, а ССТ: 1 ССТ = 0, 01 С. В системах МКГСС и Си единицей коэффициента кинематической вязкости является м3/с: i м2 / с = 104st. As температура повышается, вязкость жидкости снижается. Влияние температуры на коэффициент динамической вязкости жидкости оценивается по формуле.
А индекс в зависимости от типа жидкости. Например, для масла его значение изменяется в пределах 0, 025-0, 035. Для смазочных и смазочных масел, используемых в механических и гидравлических системах, предложено уравнение[76], связанное с коэффициентом кинематической вязкости и температурой.
Коэффициент температурной кинематической вязкости при температуре 50 ° с. (Температура*- температура, необходимая для определения вязкости, °с; n-показатель степени, который изменяется от 1, 3 до 3, 5 или более в зависимости от значения УЗО. С достаточной точностью n может быть определено выражением n = 1. 50 + 2, 7.
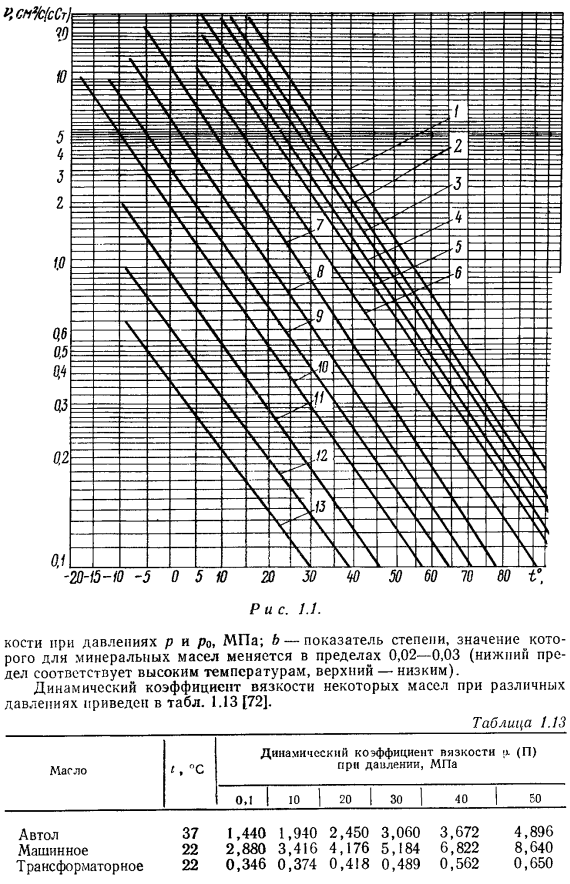
Величина n, зависящая от начальной вязкости v при 50°с, приведена в Таблице 1: 9 [76]. Значения динамических и кинематических коэффициентов вязкости для некоторых жидкостей приведены в таблице 1. 10 [47, 62, 116 температурная зависимость вязкости v некоторых смазочных масел приведена на Рис. 1. Т-следующее масло:/ — автол 18; 2-дизель Л; 3-цилиндр 11; 4-автол 10; 5-мотор Т; 6-мотор М; 7-промышленный 30 (машина л) ; 8-турбина л; 9-сепаратор; 10-промышленный 12 (шпиндель 2) ; 11-трансформатор; 12-Солер; 13-цикл.
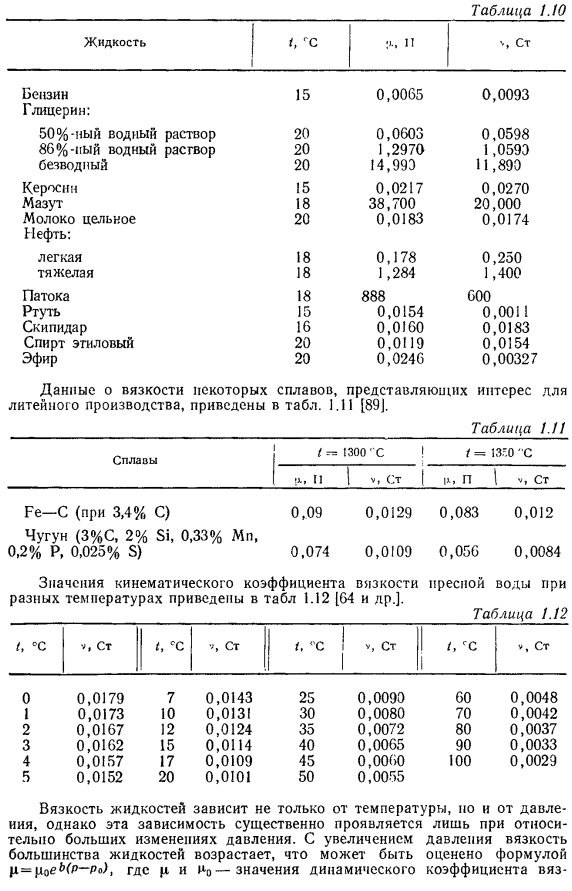
Данные о вязкости некоторых сплавов, представляющих интерес для литейного производства, приведены:
| Бензин | 15 | 0,0065 | 0,0093 |
| Глицерин: | |||
|
50%-иый водный раствор |
20 | 0,0603 | 0,0598 |
|
86%-пый водный раствор |
20 | 1,2970 | 1,059Э |
| безводный | 20 | 14,99Э | 11,890 |
| Керосин | 15 | 0,0217 | 0,0270 |
| Мазут | 18 | 38,700 | 20,000 |
| Молоко цельное | 20 | 0,0183 | 0,0174 |
| Нефть: | |||
| легкая | 18 | 0,178 | 0,250 |
| тяжелая | 18 | 1,284 | 1,400 |
| Патока | 18 | 888 | 600 |
| Ртуть | 15 | 0,0154 | 0,0011 |
| Скипидар | 16 | 0,0160 | 0,0183 |
| Спирт этиловый | 20 | 0,0119 | 0,0154 |
| Эфир | 20 | 0,0246 | 0,00327 |
Таблица 1.11 (= 13-0 С 300 «С Сплавы V, Ст ( IX, П 1 V, Ст
| 1, °С | V, Ст | 1, °С | V, Ст | (, °С | V, Ст |
1, СС 1 |
V, Ст |
| 0 | 0,0179 | 7 | 0,0143 | 25 | 0,0090 | 60 | 0,0048 |
| 1 | 0,0173 | 10 | 0,0131 | 30 | 0,0080 | 70 | 0,0042 |
| 2 | 0,0167 | 12 | 0,0124 | 35 | 0,0072 | 80 | 0,0037 |
| 3 | 0,0162 | 15 | 0,0114 | 40 | 0,0065 | 90 | 0,0033 |
| 4 | 0,0157 | 17 | 0,0109 | 45 | 0,00(Ю | 100 | 0,0029 |
| 5 | 0,0152 | 20 | 0,0101 | 50 | 0,0055 |
Вязкость жидкости зависит не только от температуры, но и от давления, эта зависимость проявляется только при относительно большом изменении pressure. As повышается давление, вязкость большинства жидкостей increases. It можно оценить по формуле m = tsob (p-p<). Где q и значение динамического коэффициента вязкости. Давление р и кости Р0, МПа; в-показатель, при котором значение минерального масла изменяется в пределах 0, 02-0, 03 (нижний предел соответствует высокой температуре, верхний предел соответствует низкой температуре).
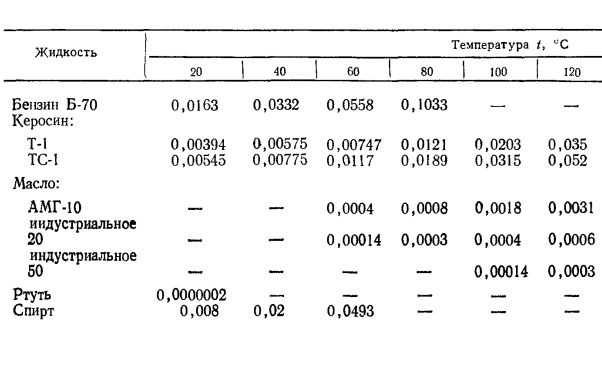
Коэффициенты динамической вязкости некоторых масел при различных давлениях приведены в таблице. 1. 13 [72]. В практических расчетах увеличение вязкости минерального масла, которое зависит от давления в интервале температур 20-60°с, получено из следующих приближенных данных[72]. Давление, МПа 7 15 20 40 00 Увеличение вязкости, начальный процент при атмосферном давлении 20-25 35-40 50-00 120-100 250-350.
Зависимость от давления р при увеличении вязкости минерального масла, используемого в гидросистеме, до 50 ППА может быть определена по приближенной эмпирической формуле= x (+cr). Р-давление, МПа. Коэффициент эксперимента по марке k-масла; для легкого масла^ 50 <15 cst) k −0. 02; для тяжелого масла (u5o> 15 cst) k = 0. 03. При давлении более 50 МПа нарушается линейная зависимость v от p, а при давлении 2000 МПа минерал затвердевает.
Во многих случаях вязкость жидкости, особенно масла, выражается в степени Энглера. Мощность Энглера — это отношение времени, которое вытекает из вискозиметра рыболова определенного количества образца u к времени, когда такое же количество дистиллированной воды вытекает из ta. 20 ° С: — значения вязкости некоторых материалов при степени Энглера Сидя при температуре 50°c дается
Масло Марка <Е&0
| Авиационное | МС-24 | 13-22 |
| Автомобильное | АКП-9,5 | Не менее 1,8 |
| * | АК-16 | 6,0 |
| Вазелиновое | Л | 1,40—1,72 |
| Велосинтетическое | Т | 1,29-1,40 |
| Веретенное | АУ | 2,05—2,26 |
| Индустриальное | 12 | 1,86-2,20 |
| * | 20 | 2,60—3,31 |
| * | 30 | 3,81—4,59 |
| * | 45 | 5,74-7,07 |
| * | 50 | 5,76-7,86 |
| Масло | АМГ-10 | 1,83 |
| Машинное | С | 5,5—7,0 |
| Приборное | мвп | 1,51 — 1,72 |
| Сепараторное | л | 1,60—1,93 |
| * | т | 2,2—2,5 |
| Трансформаторное | — | 1,8 |
| Турбинное | 22 | 2,9-3,2 |
| * | 30 | 3,9—4,4 |
| * | 40 | 6,0-6,5 |
| * | 57 | 7,5-8,0 |
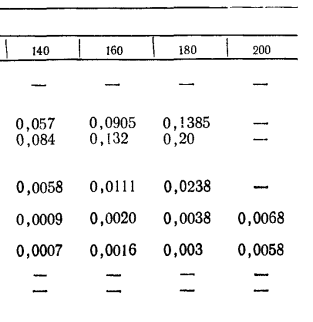
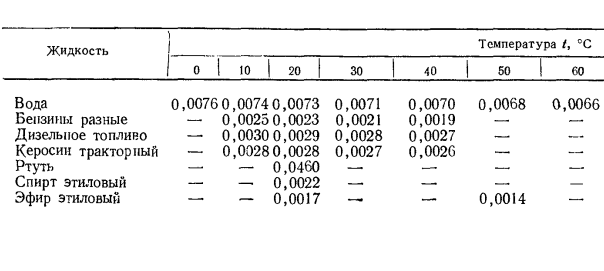
Расчет вязкости по Стоксу, выраженной в градусах Энглера, осуществляется по формуле 0. 0631. С v = 0. 073 ГЭ -^. (1. 4 В Соединенных Штатах единицы вязкости широко использовались в британских секундах saybolts, французских секундах redwood и градусах bar bay. Жидкость 20 1 40 Бензин Б-70 Керосин: Т-1 ТС-1 Масло: АМГ-10 индустриальное 20 индустриальное 50 Ртуть Спирт 0, 0163 0, 0332 0, 00394 0, 00545 0, 02 0, 0000002 0, 008
Парообразование
Испарение-это свойство сбрасывать жидкость и изменять состояние агрегации в газ. Испарение, которое происходит только на поверхности капающей жидкости, называется испарением. Испарение всей жидкости называется boiling. It происходит при определенной температуре в зависимости от давления. Давление, при котором жидкость кипит при данной температуре, является давлением насыщенного пара или давлением испарения rp. It называется п.
Его величина зависит от типа жидкости и ее температуры. Внутри таблицы. 1. 15 пн воды при различных температурах. (mpa) показывает значение другого жидкостного pn согласно температуре. Значения для (МПа) приведены в таблице. 1. 16 [12, 24, 115]. Если рабочая жидкость представляет собой многокомпонентную смесь различных минеральных масел, то расчет позволяет взять жидкость с большим значением Р.
К относительно низкой упругости относится силиконовое масло. Ниже приведено 1 давление насыщенного пара этой жидкости марки. Температура, °С25 65130200260 260 или выше Высокая скорость сатурации давления Пар п». Р, МПа 0, 00072 0, 001 0, 003 0, 007 увеличение 0, 007-0, 01 Силиконовая жидкость имеет сорт, давление паров которого в 5-10 раз превышает заданное значение.
| 1, СС | Рн.п» МПА |
1 | 1, С |
Рн.П’ МПа | 1 рн.п- МПа | Рн.п» МПа | ||
| 0 | 0,0006 | 25 | 0,0032 | 60 | 0,0202 | 90 | 0,0714 |
| 5 | 0,0009 | 30 | 0,0043 | 70 | 0,0317 | 100 | 0,1033 |
| 10 | 0,0012 | 40 | 0,0075 | 75 | 0,0392 | 125 | 0,2370 |
| 20 | 0,0024 | 50 | 0,0126 | 80 | 0,0482 | 150 | 0,4850 |
Растворимость газов в капельных жидкостях и пенообразование
Растворимость газа в капельной жидкости характеризуется коэффициентом растворения k. Коэффициент растворимости k рассчитывается при нормальных условиях 0°c и атмосферных ВИ. Давление), количество растворителя. Коэффициент растворения зависит не только от температуры и давления, но и от свойств жидкости и газа.
Растворимость газа в низковязких маслах выше, чем в высоковязких oils .As температура повышается, растворимость снижается slightly .As давление газа увеличивается, растворимость в жидкости увеличивается по линейному закону. Количество газа, которое может быть растворено перед каплей Полное насыщение выражается формулой yr =где p {и p-2- P1 Соответственно, начальное и конечное давление газа.
| Бензин | 0,2200 | веретенное АУ | 0,0759 |
|
Вода дистиллированная |
0,1600 | ГМЦ-2 | 0,1038 |
| Керосин | 0,1270 |
индустриальное 12 |
0,0759 |
| Масло: |
индустриальное 20 |
0,0755 | |
| АМГ-10 | 0,1038 | трансформаторное | 0,0828 |
| вазелиновое велосит | 0,0877 0,0959 |
Спирто-глицериновая смесь: |
56 |
Растворимость масла к сатурации воздуха зависит от плотности oil .As плотность увеличивается, растворимость уменьшается .Приведены данные о коэффициенте воздушного растворения некоторых жидкостей при температуре 20°С и давлении 0, 1 МПа .
Снижение давления в любой точке системы (всасывающая труба и др.) сопровождается выделением воздуха в виде мелких пузырьков и образованием bubbles .In кроме того, пузырьки образуются, когда воздух всасывается из негерметичных соединений в системе или когда жидкость смешивается в резервуаре с помощью свободной струи .Наличие пузырьков в жидкости значительно повышает сжимаемость, снижает ее плотность, что приводит к нарушению непрерывности движения .
Поверхностное натяжение и капиллярность
Поверхность капающей жидкости подвержена поверхностному натяжению, которое стремится придать объему жидкости сферическую форму и вызвать дополнительное давление. Здесь cg-коэффициент поверхностного натяжения, Н / м или кгс / м. G], а g2-главный радиус кривизны рассматриваемых элементов поверхности. Если поверхность жидкости представляет собой сферу или ее часть, то r равен r2-g, и Формула (1. 5) принимает вид: Р = — (1. 6
- Коэффициент поверхностного натяжения пропорционален плотности капельной жидкости и плотности газовой среды над жидкостью, которая уменьшается с увеличением температуры. Значение коэффициента поверхностного натяжения o (дан / м) для некоторых жидкостей выше < 7 / л. <5Э Рисунок 1. 2.
- Граница между воздухом и давлением 0, 1 МПа показана в таблице. 1. 18 [84, 107]. Для расплавленного чугуна при / = 1550°c, a = 0, 187-0, 190 дан / м для расплавленного немодифицированного чугуна при 1200-1450°c, o = 0, 0918-0, 102 дан / м. Избыточное давление Р, определяемое формулами (1. 5) и (1. 6), всегда направлено к центру кривизны поверхности.
- Наличие этого дополнительного давления является описанием капиллярности, и в открытой трубке малого диаметра с одним концом, погруженным в жидкость, последний устанавливается выше уровня с вогнутым мениском или ниже его с выпуклым мениском (рис. 1. 2).
При увлажнении жидкостью поверхности трубки образуется вогнутый мениск (рис. 1. 2, а) (вода-стекло и др.), а когда поверхность трубки жидкая и влажная, образуются выпуклые мениски (рис. 1. 2, б) (ртутное стекло и др.). Высота подъема жидкости в стеклянном капилляре диаметром si мм n (ММ) (при опускании ртути) определяется по формуле Один. (1-7
Высоту подъема (или падения) жидкости между параллельными стеклянными пластинами (расстояние составляет мм) можно определить по формуле: (1. 8 В формулах (1. 7) и (1. 8) k-экспериментальный коэффициент, имеющий следующее значение (мм2) : вода+30, ртуть-10. 1, спирт+11. 5, толуол+13.
Некоторые физические свойства жидкостей при
давлении 0,1 Мпа
|
Жидкость |
Температура, 0С |
Плотность, кг/м3 |
Удельный вес, Н/м3 |
Вязкость 104,м2/с |
|
|
Бензин |
авиационный |
20 |
739-780 |
7250-7652 |
0,49 для 20 0С |
|
автомобильный |
712-761 |
6980-7470 |
|||
|
Масло |
веретенное |
50 |
888-896 |
8711-8790 |
|
|
для (ГОСТ |
850 |
8340 |
|||
|
индустриальное общего назначения без присадок |
И-5А |
890 |
8731 |
0,04-0,06 |
|
|
И-8А |
900 |
8829 |
0,06-0,08 |
||
|
И-12А |
880 |
8633 |
0,10-0,14 |
||
|
И-20А |
885 |
8682 |
— |
||
|
И-25А |
890 |
8731 |
0,24-0,27 |
||
|
И-30А |
890 |
8731 |
0,28-0,33 |
||
|
И-40А |
895 |
8780 |
0,35-0,45 |
||
|
И—100А |
920 |
9025 |
0,90-1,18 |
||
|
соляровое |
20 |
885-902 |
8680-8850 |
||
|
трансформаторное |
50 |
886 |
8692 |
||
|
турбинное (ГОСТ 32-74) |
22 |
900 |
8829 |
||
|
30 |
900 |
8829 |
0,28-0,36 |
||
|
46 |
900 |
8829 |
0,44-0,48 |
Кинематическая вязкость масел при различных
температурах
|
Масло |
104, м2/с при 0С |
|||||||
|
100 |
50 |
10 |
0 |
-5 |
-10 |
|||
|
веретенное |
0,036 |
0,13 |
0,90 |
1,80 |
2,80 |
4,40 |
||
|
для |
0,047 |
0,11 |
0,30 |
0,44 |
0,54 |
0,67 |
||
|
индустриальное (ГОСТ 20799-75) |
И-20 |
0,048 |
0,18 |
1,13 |
2,75 |
4,20 |
6,40 |
|
|
И-45 |
0,081 |
0,42 |
5,01 |
11,90 |
19,50 |
59,90 |
||
|
И-50 |
0,085 |
0,50 |
8,33 |
22,90 |
41,70 |
83,80 |
||
|
трансформаторное |
0,030 |
0,09 |
0,05 |
0,89 |
1,24 |
1,77 |
||
|
турбинное (ГОСТ 32-74; 9972-74) |
ТП-22 |
0,060 |
0,22 |
2,13 |
4,76 |
7,73 |
9,10 |
|
|
ТП-22 (из |
0,050 |
0,21 |
1,72 |
3,75 |
5,68 |
25,30 |
||
|
ТП-30УТ |
0,060 |
0,42 |
3,59 |
8,63 |
14,40 |
33,10 |
||
Динамическая вязкость масел при различных
температурах
|
Жидкость |
0C |
10-1 Па с при давлении МПа |
|||||
|
0,1 |
10 |
20 |
30 |
40 |
50 |
||
|
Автол |
37 |
1,440 |
1,940 |
2,450 |
3,030 |
3,672 |
4,896 |
|
Машинное |
22 |
2,880 |
3,416 |
4,176 |
5,184 |
6,822 |
8,640 |
|
Трансформаторное |
22 |
0,346 |
0,374 |
0,418 |
0,489 |
0,562 |
0,650 |


| переменная | Формула слова с единицами | Упрощенная формула |
| Давление жидкости — P | (PSI) = сила (фунты) / площадь (кв. Дюймы) | P = F / A |
| Расход жидкости — Q | GPM = расход (галлоны) / единица времени (минуты) | Q = V / T |
| Жидкость в лошадиных силах — HP | Лошадиная сила = Давление (PSIG) x Расход (GPM) / 1714 | HP = PQ / 1714 |
Основные гидравлические формулы
| Формула для: | Формула слова: | Формула письма: |
| ДАВЛЕНИЕ ЖИДКОСТИ в фунтах на квадратный дюйм |
 |
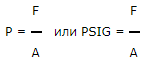 |
| СКОРОСТЬ ПОТОКА ЖИДКОСТИ в галлонах / минута |
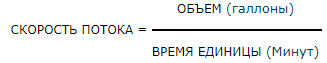 |
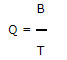 |
| ЖИДКОСТЬ В ЛОШАДИНОЙ СИЛЕ |
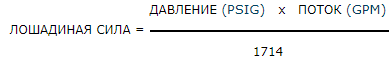 |
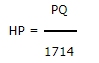 |
| СКОРОСТЬ через ТРУБОПРОВОД В Футах / Вторая Скорость |
 |
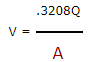 |
| СЖИМАЕМОСТЬ НЕФТИ Требуется масло Для достижения высокого давления |
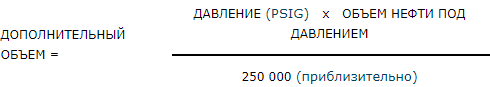 |
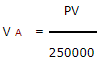 |
| Сжимаемость жидкости |
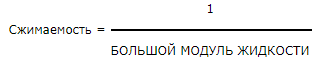 |
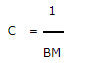 |
| ОСОБАЯ ГРАВИТАЦИЯ ЖИДКОСТИ |
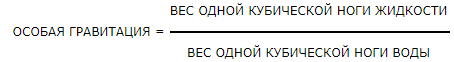 |
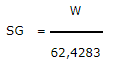 |
Соотношение давления, силы и лошадиных сил
Давление (фунт / кв.дюйм) = сила (фунты) / площадь (дюйм²)
Сила (фунты) = площадь (в ²) х давление (фунтов на квадратный дюйм)
Площадь (дюйм²) = сила (фунты) / давление (фунт / кв.дюйм)
Жидкость и мощность
Мощность жидкости Мощность (л.с.) = давление (фунт / кв.дюйм) х расход насоса (галлонов в минуту) / 1,714
Отношения крутящего момента и лошадиных сил
Крутящий момент (фунт-фут) = лошадиная сила (л.с.) x 5,252 / скорость (об / мин)
Лошадиная сила (л.с.) = крутящий момент (фут-фунт) х скорость (об / мин) / 5 252
Скорость (об / мин) = лошадиная сила (л.с.) x 5,252 / крутящий момент (фут-фунт)
Основные расчеты цилиндров:
Площадь поршневого цилиндра (дюйм²) = диаметр в квадрате x .7854
(Можно также использовать квадраты с радиусом 3,1416 х)
Площадь конца поршневого штока (торцевое кольцо) (дюйм²) = площадь поршневого цилиндра (дюйм²) — площадь штока (дюйм²)
Сила цилиндра (фунты) = давление (фунт / кв.дюйм) х площадь (дюйм²)
Скорость цилиндра (фут / мин) = 19,25 x скорость потока (галлонов в минуту) / площадь (дюйм²)
(Разделите на 60, чтобы преобразовать скорость в футы / с)
Скорость цилиндра (дюйм / мин) = скорость потока (куб. Дюйм / мин) / площадь (дюйм²)
(Обратите внимание, что 1 галлон США = 231 у.е.)
Время цилиндра (сек) = площадь (дюйм²) x ход цилиндра (дюйм) x .26 / расход (галлонов в минуту)
Расход цилиндра (галлонов в минуту) = 12 x 60 x скорость цилиндра (фут / с) x площадь (дюйм²) / 231
Объем цилиндра (галлоны) = площадь цилиндра (дюйм²) x ход цилиндра (дюйм) / 231
Основные расчеты гидравлического двигателя :
Крутящий момент двигателя (в фунтах) = давление (фунт / кв.дюйм) x рабочий объем двигателя (куб. Дюйм / об.) / 6,28
(Можно также использовать мощность (л.с.) х 63,025 / скорость (об / мин)
Скорость двигателя (об / мин) = 231 x скорость потока (галлонов в минуту) / рабочий объем двигателя (куб. Дюйм / об)
Мощность двигателя (л.с.) = крутящий момент (в фунтах) x скорость двигателя (об / мин) / 63 025
Расход двигателя (галлонов в минуту) = скорость двигателя (об / мин) х смещение двигателя (куб.см / об) / 231
Рабочий объем двигателя (куб. Дюйм / об.) = Крутящий момент (в фунтах) x 6,28 / давление (фунт / кв. Дюйм)
Основные расчеты насоса :
Расход на выходе насоса (галлонов в минуту) = частота вращения насоса (об / мин) x рабочий объем насоса (куб. Дюйм / об.) / 231
Скорость насоса (об / мин) = 231 x расход насоса (галлонов в минуту) / рабочий объем насоса (куб. Дюйм / об)
Мощность насоса (л.с.) = скорость потока (галлонов в минуту) х давление (фунт / кв.дюйм) / 1714 х коэффициент полезного действия насоса
(Можно также использовать мощность (л.с.) = крутящий момент (в фунтах) x скорость насоса (об / мин) / 63 025)
Крутящий момент насоса (в фунтах) = давление (фунт / кв.дюйм) х рабочий объем насоса (куб. Дюйм / об.) / 6,28
(Можно также использовать мощность (л.с.) х 63,025 / рабочий объем насоса (куб. Дюйм / об.)
Формула производства тепла : преобразование тепла в другие единицы
1 л.с. = 2545 БТЕ / ч = 42,4 БТЕ / мин = 33 000 фут. Фунтов / мин = 746 Вт
Лошадиная сила (л.с.) = давление (фунт / кв.дюйм) x расход (галлонов в минуту) / 1714 — BTU / час = 1½ x фунтов на кв. Дюйм х галлон
1 БТЕ / час = 0,0167 БТЕ / мин = .00039 л.с.
Пример: поток 10 галлонов в минуту через редукционный клапан с падением в 300 фунтов / кв. Дюйм = 1,75 л.с.
1.75 л.с. тепла = 4453 БТЕ / час = 105 БТЕ / мин = 57 750 футов. Фунтов / мин = 1305 Вт
- Большая часть этого тепла будет возвращена в резервуар.
- Обратите внимание, что тепло вырабатывается каждый раз, когда не производится механическая выходная работа.
Общая охлаждающая способность стального резервуара: HP (тепло) = .001 x TD x A
TD = разница температуры масла в резервуаре и окружающего воздуха
A = вся площадь поверхности резервуара в квадратных футах (включая дно, если оно поднято)
Общая информация и «Правила большого пальца» :
Оценка мощности привода насоса: 1 л.с. входного привода на каждый 1 галлон в минуту при производительности насоса 1500 фунтов / кв. Дюйм
Мощность на холостом ходу насоса: на холостом ходу и ненагруженном насосе потребуется около 5% от полной мощности л.с.
Объем резервуара (GALS) = длина (INS) x ширина (INS) x высота (INS) / 231
Сжимаемость масла: уменьшение объема приблизительно на 1/2% на каждые 1000 фунтов на квадратный дюйм давления
Сжимаемость воды: уменьшение объема приблизительно на 1/3% на каждые 1000 фунтов на квадратный дюйм давления
Мощность для нагрева гидравлического масла: каждый 1 ватт повышает температуру 1 галлона масла на 1 ° F в час
Указания по скорости потока в гидравлических линиях:
- От 2 до 4 футов / с = всасывающие линии
- От 10 до 15 футов / с = напорные линии до 500 фунтов на квадратный дюйм
- От 15 до 20 футов / с = напорные линии 500 — 3000 фунтов на квадратный дюйм
- 25 футов / с = напорные линии более 3000 фунтов на квадратный дюйм
- 4 фута / с = любые маслопроводы в системах подачи воздуха над маслом
Скорость потока нефти в трубе: скорость (фут / сек) = расход (галлонов в минуту) х. 3208 / внутренняя площадь трубы (кв. Дюймы)
Формулы площади круга:
- Площадь (кв. Дюймы) = π x r², где π (pi) = 3,1416 и r = радиус в дюймах в квадрате
- Площадь (кв. Дюймы) = π x d² / 4, где π (pi) = 3,1416 и d = диаметр в дюймах
- Окружность (ins) = 2 x π xr, где π (pi) = 3.1416, а r — радиус в дюймах
- Окружность (ins) = π xd, где π (pi) = 3.1416 и d = диаметр в дюймах
Часто используемые эквиваленты мощности жидкости :
Один галлон США равен:
- 231 кубический дюйм
- 3,785 литра (1 литр = 0,2642 доллара США)
- 4 кварта или 8 пинт
- 128 унций жидкости / 133,37 унции веса
- Вес 8,3356 фунтов
Одна лошадиная сила равна:
- 33 000 футов фунтов в минуту
- 550 футов в секунду
- 42,4 БТЕ / мин
- 2,545 БТЕ в час
- 746 Вт
- 0,746 кВт
На пси равняется:
- 0,0689 бар (1 бар = 14,504 фунтов на кв. Дюйм)
- 6,895 килопаскаля
- 2,0416 рт.ст. (дюймов ртутного столба)
- 27,71 ”воды
Одна атмосфера равна:
- 14,696 фунтов на квадратный дюйм
- 1,013 бар
- 29,921 рт.ст. (дюймов ртутного столба)
Эти страницы могут быть вам полезны:
- Задачи по гидравлике
- Решение задач по гидравлике
- Методические указания по гидравлике
- Примеры решения задач по гидравлике
- Учебник по гидравлике
- Сборник задач по гидравлике
- Курсовая работа по гидравлике








![{displaystyle lambda ={frac {0,316}{sqrt[{4}]{mathrm {Re} }}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d7df167d755f7538131ce1f05f4af4047b52e15c)





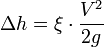
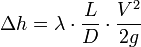
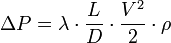
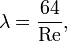
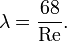
![lambda = frac{0,316}{sqrt[4]{mathrm{Re}}}.](http://dic.academic.ru/pictures/wiki/files/49/17f64e27c31fa4ba18d72540bdf11185.png)


