Перейти к содержанию
На чтение 3 мин Просмотров 3к.
Содержание
- Что ты хочешь узнать?
- Ответ
- Ответ
- Как найти дельта l в физике формула
- Использование [ править | править код ]
Что ты хочешь узнать?
Ответ
дельта это погрешность
- Комментарии
- Отметить нарушение
Ответ
приставка дельта означает изменение чего-либо . Например : если вначале скорость была 10 , а потом увеличилась до 15 , то дельта скорости будет равна 15-10
Как найти дельта l в физике формула
Автор Ѐасим задал вопрос в разделе Домашние задания
Формула вычисления дельта L по физике и получил лучший ответ
Ответ от Анастасия Терентьева[гуру]
как правило, дельта в физике чаще всего (а может даже и всегда) обозначает изменение чего – либо. L насколько я помню это длина. Значит дельта L обозначает изменение длины, и находится по формуле: L2 – L1
| Буква греческого алфавита дельта |
|---|
| Δδ |
| ◄ | ΐ | Α | Β | Γ | Δ | Ε | Ζ | Η | Θ | ► |
| ◄ | ΰ | α | β | γ | δ | ε | ζ | η | θ | ► |
Характеристики
Название
Δ: greek capital letter delta
δ: greek small letter delta
Юникод
Δ: U+0394
δ: U+03B4
HTML-код
Δ:
δ:
UTF-16
Δ: 0x394
δ: 0x3B4
Δ: %CE%94
δ: %CE%B4
Мнемоника
Δ: Δ
δ: δ
Δ , δ (название: де́льта, греч. δέλτα ) — 4-я буква греческого алфавита. В системе греческой алфавитной записи чисел имеет числовое значение 4. Происходит от финикийской буквы 
— делт, название которой означало «дверь» или «вход в палатку». От буквы дельта произошли латинская буква D и кириллическая Д. В древнегреческом языке дельта произносилась как взрывной [ d ], в современном греческом произносится как [ ð ] (английское th в слове this).
Использование [ править | править код ]
Прописная буква Δ используется как символ для обозначения:
- изменения или различия между значениями переменных (например, температуры: ΔT), обычно конечного;
- дифференциальногооператора Лапласа;
- любой из дельта-частиц в физике элементарных частиц;
- в электронике существует ΔΣ-модуляция;
- 4-й квадры в соционике;
- Плотность заряжания во внутренней баллистике.
Строчная буква δ используется как символ для обозначения:
- малого изменения значения переменной, точнее — обозначение неполного дифференциала (или вариации), в отличие от полного, обычно обозначаемого латинской буквой d;
- символа Кронекера в точных науках;
- G-дельта-множество;
- дельта-функции Дирака в математике;
- отклонения в инженерной механике;
- коэффициент общей полноты (в судостроении)
- в астрономии
- четвёртая по яркостизвезда в созвездии;
- одна из двух небесных координат — склонение
Также с греческой буквой сходны другие символы, употребляемые в математике:
Расим
Знаток
(338),
закрыт
5 месяцев назад
Анастасия Терентьева
Гуру
(4685)
9 лет назад
как правило, дельта в физике чаще всего (а может даже и всегда) обозначает изменение чего – либо. L насколько я помню это длина. Значит дельта L обозначает изменение длины, и находится по формуле: L2 – L1
Содержание:
При измерении разных физических величин мы получаем их числовые значения с определенной точностью. Например, при определении размеров листа бумаги (длины, ширины) мы можем указать их с точностью до миллиметра; размеры стола – с точностью до сантиметра, размеры дома, стадиона – с точностью до метра.
Нет необходимости указывать размеры стола с точностью до миллиметра, а размеры стадиона с точностью до сантиметра или миллиметра. Мы сами в каждой ситуации, опыте и эксперименте определяем, с какой точностью нам нужны данные физические величины. Однако очень важно оценивать, насколько точно мы определяем физическую величину, какую ошибку (погрешность) в ее измерении допускаем.
При измерении мы не можем определить истинное значение измеряемой величины, а только пределы, в которых она находится.
Пример:
Измерим ширину стола рулеткой с сантиметровыми и миллиметровыми делениями на ней (рис. 5.1). Значение наименьшего деления шкалы называют ценой деления и обозначают буквой С. Видно, что цена деления рулетки С = 1 мм (или 0,1 см).
Совместим нулевое деление рулетки с краем стола и посмотрим, с каким значением
шкалы линейки совпадает второй край стола (рис. 5.1). Видно, что ширина стола составляет чуть больше 70 см и 6 мм, или 706 мм. Но результат наших измерений мы запишем с точностью до 1 мм, то есть L = 706 мм.
Абсолютная погрешность измерения ∆ (ДЕЛЬТА)
Из рис. 5.1 видно, что мы допускаем определенную погрешность и определить ее «на глаз» достаточно трудно. Эта погрешность составляет не более половины цены деления шкалы рулетки. Эту погрешность называют погрешностью измерения и помечают ∆L («дельта эль»). В данном эксперименте ее можно записать
Сам результат измерения принято записывать таким образом: ширина стола L = (706,0 ± 0,5) мм, читают: 706 плюс-минус 0,5 мм. Эти 0,5 мм в нашем примере называют абсолютной погрешностью. Значения измеряемой величины (706,0 мм) и абсолютной погрешности (0,5 мм) должны иметь одинаковое количество цифр после запятой, то есть нельзя записывать 706 мм ± 0,5 мм.
Такая запись результата измерения означает, что истинное значение измеряемой величины находится между 705,5 мм и 706,5 мм, то есть 705,5 мм ≤ L ≤ 706,5 мм.
Относительная погрешность измерения ε (ЭПСИЛОН)
Иногда важно знать, какую часть составляет наша погрешность от значения
измеряемой величины. Для этого разделим 0,5 мм на 706 мм. В результате получим: 
. То есть наша ошибка составляет 0,0007 долю ширины стола, или 0,0007 · 100% = 0,07%. Это свидетельствует о достаточно высокой точности измерения. Эту погрешность называют относительной и обозначают греческой буквой (эпсилон):
(5.1)
Относительная погрешность измерения свидетельствует о качестве измерения. Если длина какогото предмета равна 5 мм, а точность измерения – плюс-минус 0,5 мм, то относительная погрешность будет составлять уже 10%.
Стандартная запись результата измерений и выводы
Таким образом, абсолютная погрешность в примере 5.1. составляет ∆L = 0,5 мм, а результат измерений следует записать в стандартном виде: L = (706,0 
0,5) мм – Опыт выполнен с относительной погрешностью 0,0007 или 0,07%.
На точность измерения влияет много факторов, в частности:
- При совмещении края стола с делением шкалы рулетки мы неминуемо допускаем погрешность, поскольку делаем это «на глаз» – смотреть можно под разными углами.
- Не вполне ровно установили рулетку.
- Наша рулетка является копией эталона и может несколько отличаться от оригинала.
Все это необходимо учитывать при проведении измерений.
Итоги:
- Измерения в физике всегда неточны, и надо знать пределы погрешности измерений, чтобы понимать, насколько можно доверять результатам.
- Абсолютную погрешность измерения можно определить как половину цены деления шкалы измерительного прибора.
- Относительная погрешность есть частное от деления абсолютной погрешности на значение измеряемой величины:
и указывает на качество измерения. Ее можно выразить в процентах.
Измерительные приборы
Устройства, с помощью которых измеряют физические величины, называют измерительными приборами.
Простейший и хорошо известный вам измерительный прибор — линейка с делениями. На ее примере вы видите, что у измерительного прибора есть шкала, на которой нанесены деления, причем возле некоторых делений написано соответствующее значение физической величины. Так, значения длины в сантиметрах нанесены на линейке возле каждого десятого деления (рис. 3.11). Значения же, соответствующие «промежуточным» делениям шкалы, можно найти с помощью простого подсчета.
Разность значений физической величины, которые соответствуютближайшим делениям шкалы, называют ценой деления прибора. Ёе находят так: берут ближайшие деления, возле которых написаны значения величины, и делят разность этих значений на количество промежутков между делениями, расположенными между ними.
Например, ближайшие сантиметровые деления на линейке разделены на десять промежутков. Значит, цена деления линейки равна 0,1 см = 1 мм.
Как определяют единицы длины и времени
В старину мерами длины служили большей частью размеры человеческого тела и его частей. Дело в том, что собственное тело очень удобно как «измерительный прибор», так как оно всегда «рядом». И вдобавок «человек есть мера всех вещей»: мы считаем предмет большим или малым, сравнивая его с собой.
Так, длину куска ткани измеряли «локтями», а мелкие предметы — «дюймами» (это слово происходит от голландского слова, которое означает «большой палец»).
Однако человеческое тело в качестве измерительного прибора имеет существенный недостаток: размеры тела и его частей у разных людей заметно отличаются. Поэтому ученые решили определить единицу длины однозначно и точно. Международным соглашением было принято, что один метр равен пути, который проходит свет в вакууме за 1/299792458 с. А секунду определяют с помощью атомных часов, которые сегодня являются самыми точными.
Можно ли расстояние измерять годами
Именно так и измеряют очень большие расстояния — например, расстояния между звездами! Но при этом речь идет не о годах как промежутках времени, а о «световых годах». А один световой год — это расстояние, которое проходит свет за один земной год. По нашим земным меркам это очень большое расстояние — чтобы убедиться в этом, попробуйте выразить его в километрах! А теперь вообразите себе, что расстояние от Солнца до ближайшей к нему звезды составляет больше четырех световых лет! И по астрономическим масштабам это совсем небольшое расстояние: ведь с помощью современных телескопов астрономы тщательно изучают звезды, расстояние до которых составляет много тысяч световых лет!
Что надо знать об измерительных приборах
Приступая к измерениям, необходимо, прежде всего, подобрать приборы. Что надо знать об измерительных приборах?
Минимальное (нижний предел) и максимальное (верхний предел) значения шкалы прибора — это пределы измерения. Чаще всего предел измерения один, но может быть и два. Например, линейка имеет один предел — верхний. У линейки на рисунке 32 он равен 25 см. У термометра на рисунке 33 два предела: верхний предел измерения температуры равен +50 °С; нижний -40 °С.
На рисунке 34 изображены три линейки с одинаковыми верхними пределами (25 см). По эти линейки измеряют длину с различной точностью. Наиболее точные результаты измерений дает линейка 7, наименее точные — линейка 3. Что же такое точность измерений и от чего она зависит? Для ответа на эти вопросы рассмотрим сначала понятие цена деления шкалы прибора.
Цена деления — это значение наименьшего деления шкалы прибора.
Как определить цену деления шкалы? Для этого необходимо:
- выбрать на шкале линейки два соседних значения, например 3 см и 4 см;
- подсчитать число делений (не штрихов!) между этими значениями; например, на линейке 1 (см. рис. 34) число делений между значениями 3 см и 4 см равно 10;
- вычесть из большего значения меньшее (4 см – 3 см = 1 см) и результат разделить на число делений.
Полученное значение и будет ценой деления шкалы прибора. Обозначим ее буквой С.
- Для линейки 1:
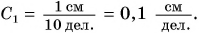
- Для линейки 2:
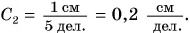
- Для линейки 3:
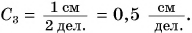
Точно так же можно определить и цену деления шкалы мензурок 1 и 2 (рис. 35). Цена деления шкалы мензурки 1:
Цена деления шкалы мензурки 2:
А какими линейкой и мензуркой можно измерить точнее?
Измерим один и тот же объем мензуркой 1 и мензуркой 2. Но показаниям шкал в мензурке 1 объем воды V = 35 мл; в мензурке 2 — V = 37 мл.
Понятно, что точнее измерен объем воды мензуркой 2, цена деления которой меньше 
Значит, чем меньше цена деления шкалы, тем точнее можно измерить данным прибором. Говорят: мензуркой 1 мы измерили объем с точностью до 5 мл (сравните с ценой деления шкалы 
), мензуркой 2 – с точностью до 1 мл (сравните с ценой деления 
). Точность измерения температуры термометрами 1 и 2 (рис. 36) определите самостоятельно.
Итак, любым прибором, имеющим шкалу, измерить физическую величину можно с точностью, не превышающей цены деления шкалы.
Линейкой 1 (см. рис. 34) можно измерить длину с точностью до 1 мм. Точность измерения длины линейками 2 и 3 определите самостоятельно.
Главные выводы:
- Верхний и нижний пределы измерения — это максимальное и минимальное значения шкалы прибора.
- Цена деления шкалы равна значению наименьшего деления шкалы.
- Чем меньше цена деления шкалы, тем точнее будут проведены измерения данным прибором.
Для любознательных:
В истории науки есть немало случаев, когда повышение точности измерений давало толчок к новым открытиям. Более точные измерения плотности азота, выделенного из воздуха, позволили в 1894 г. открыть новый инертный газ — аргон. Повышение точности измерений плотности воды привело к открытию в 1932 г. одной из разновидностей тяжелых атомов водорода — дейтерия. Позже дейтерий вошел в состав ядерного горючего. Оценить расстояния до звезд и создать их точные каталоги ученые смогли благодаря повышению точности при измерении положения ярких звезд на небе.
- Заказать решение задач по физике
Пример решения задачи
Для измерения величины угла используют транспортир. Определите: 1) цену деления каждой шкалы транспортира, изображенного на рисунке 38; 2) значение угла BАС, используя каждую шкалу; укажите точность измерения угла ВАС в каждом случае.
Решение:
1) Цена деления нижней шкалы:
Цена деления средней шкалы:
Цена деления верхней шкалы:
2) Определенный но нижней шкале с точностью до 10° 
определенный по средней шкале с точностью до 5° 
определенный по верхней шкале с точностью до 1° 
- Определение площади и объема
- Связь физики с другими науками
- Макромир, мегамир и микромир в физике
- Пространство и время
- Как зарождалась физика
- Единая физическая картина мира
- Физика и научно-технический прогресс
- Физические величины и их единицы измерения
Сила упругости. Закон Гука
- Виды деформаций
- Закон Гука
- Измерение силы с помощью динамометра
- Задачи
п.1. Виды деформаций
Под действием силы все тело или отдельные его части приходят в движение.
При движении одних частей тела относительно других происходит изменение формы и размеров.
Деформация – это изменение взаимного положения частиц тела, связанное с их перемещением друг относительно друга под действием приложенной силы, при котором тело изменяет свою форму и размеры.
 |
К простейшим видам деформации относятся:
|
Различают упругие (обратимые) и неупругие (необратимые) деформации.
Деформация является упругой, если, после прекращения действия вызвавших её сил, тело полностью восстанавливает свою форму и размеры.
Например, если немного согнуть школьную линейку, растянуть пружину или надавить на воздушный шарик, после прекращения действия силы линейка выпрямится, пружина сожмется, и шарик опять станет круглым. Эти деформации – упругие, они обратимы.
Если же приложенная сила окажется слишком большой, линейка сломается, пружина так и останется растянутой, а шарик лопнет. Эти деформации – неупругие, они необратимы.
Все здания и сооружения вокруг нас рассчитываются так, чтобы их «нагруженные» части испытывали только упругие деформации; это обеспечивает надёжность и долговечность конструкций.
Восстановление формы и размера тела при упругой деформации происходит под действием силы упругости, которая возникает благодаря межатомным и межмолекулярным взаимодействиям.
Сила упругости уравновешивает действие внешней силы и направлена в сторону, противоположную смещению частиц.
Например (см. рисунок):
- при растяжении сила упругости стремится сжать тело;
- при сжатии сила упругости стремится распрямить тело.
п.2. Закон Гука
 |
Проведем серию опытов с пружиной. Пусть при действии на пружину силой (F) мы получаем деформацию (удлинение) (Delta l). При этом в пружине возникают силы упругости, стремящиеся вернуть её в исходное положение, (overrightarrow{F_{text{упр}}}=-overrightarrow{F}). Если приложенную силу увеличить в 2 раза, то деформация также увеличится в 2 раза. Увеличение силы в 3 раза приводит к росту деформации в 3 раза и т.д. Опыты показывают, что во всех случаях деформация будет прямо пропорциональна приложенной силе. |
Следовательно, сила упругости также будет прямо пропорциональна деформации: $$ F_{text{упр}}simDelta l $$
Для каждого тела отношение силы упругости к величине деформации при малых упругих деформациях является постоянной величиной $$ k=frac{F_{text{упр}}}{Delta l}=const $$ которая называется коэффициентом упругости или жесткостью.
Жесткость тела зависит от формы, размеров и материала, из которого оно изготовлено.
В системе СИ жесткость измеряется в ньютонах на метр, (frac{text{Н}}{text{м}}).
Закон Гука
Сила упругости, возникающая во время упругой деформации тела, прямо пропорциональна удлинению (величине деформации): $$ F_{text{упр}}=kDelta l $$ Сила упругости всегда направлена противоположно деформации.
п.3. Измерение силы с помощью динамометра
 |
Динамометр– это прибор для измерения силы.
Простейший пружинный динамометр состоит из пружины с крючком и дощечки со шкалой (проградуированной в ньютонах). |
В технике используются динамометры более сложных конструкций.
Но принцип действия – использование закона Гука – во многих из них сохраняется.
п.4. Задачи
Задача 1. Резиновая лента удлинилась на 10 см под действием силы 50 Н. Какова жесткость ленты?
Дано:
(Delta l=10 text{см}=0,1 text{м})
(F=50 text{Н})
__________________
(k-?)
Жесткость ленты $$ k=frac{F}{Delta l} $$ $$ k=frac{50}{0,1}=500 left(frac{text{Н}}{text{м}}right) $$ Ответ: 500 Н/м
Задача 2. Под действием силы 300 Н пружина динамометра удлинилась на 0,6 см. Каким будет удлинение пружины под действием силы 700 Н? Ответ запишите в миллиметрах.
Дано:
(F_1=300 text{Н})
(Delta l_1=0,6 text{см}=6cdot 10^{-3} text{м})
(F_2=700 text{Н})
__________________
(Delta l_2-?)
Жесткость пружины begin{gather*} k=frac{F_1}{Delta l_1}=frac{F_2}{Delta l_2}Rightarrow Delta l_2=frac{F_2}{F_1}Delta l_1\[6pt] Delta l_2=frac{700}{300}cdot 6cdot 10^{-3}=14cdot 10^{-3} (text{м})=14 (text{мм}) end{gather*} Ответ: 14 мм
Задача 3. Пружина без груза имеет длину 30 см и коэффициент жесткости 20 Н/м. Найдите длину растянутой пружины, если на нее действует сила 5 Н. Ответ запишите в сантиметрах.
Дано:
(l_0=30 text{cм}=0,3 text{м})
(k=20 text{Н/м})
(F=5 text{Н})
__________________
(l-?)
Удлинение пружины под действием силы: $$ Delta l=frac Fk $$ Длина растянутой пружины begin{gather*} l=l_0+Delta l=l_0+frac Fk\[6pt] l=0,3+frac{5}{20}=0,3+0,25=0,55 (text{м})=55 (text{cм}) end{gather*} Ответ: 55 cм
Задача 4*. Грузовик взял на буксир легковой автомобиль массой 1,5 т с помощью троса. Двигаясь равноускоренно, они проехали путь 600 м за 50 с. На сколько миллиметров удлинился во время движения трос, если его жесткость равна (3cdot 10^5 text{Н/м})?
Дано:
(m=1,5 text{т}=1500 text{кг})
(s=600 text{м})
(t=50 text{c})
(v_0=0)
(k=3cdot 10^5 text{Н/м})
__________________
(Delta l-?)
Сила упругости, возникающая в тросе, уравновешивает силу тяги, передвигающую автомобиль с постоянным ускорением: $$ F_{text{упр}}=kDelta l=F_{text{т}}=ma $$ Перемещение из состояния покоя $$ s=frac{at^2}{2}Rightarrow a=frac{2s}{t^2} $$ Получаем: begin{gather*} kDelta l=mcdotfrac{2s}{t^2}Rightarrow Delta l=frac mkcdot frac{2s}{t^2}\[6pt] Delta l=frac{1500}{3cdot 10^5}cdot frac{2cdot 600}{50^2}=2,4cdot 10^{-3} (text{м})=2,4 (text{мм}) end{gather*} Ответ: 2,4 мм
Nechegoneznator
+20
Решено
5 лет назад
Физика
5 – 9 классы
Формула нахождения дельта эль
Смотреть ответ
Russsky
Мб Δt?
Nechegoneznator
Имеется в виду удлинение тела
Ответ проверен экспертом
3
(32 оценки)
39
Lika788778
5 лет назад
Светило науки – 3 ответа – 0 раз оказано помощи
дельта в физике чаще всего обозначает изменение чего – либо. L насколько я помню это длина. Значит дельта L обозначает изменение длины, и находится по формуле: L2 – L1
(32 оценки)
Остались вопросы?
Новые вопросы по предмету Физика
Помогите решить задачи.1)Автобус,двигаясь со скоростью 72км/ч,начинает тормозить с ускорением 3м/с2 и останавливается. Чему равно время торможе …
ДАЮ 60 БАЛЛОВШкольник решил испытать кастрюлю на плавучесть. Он поместил цилиндрическую кастрюлю массой 2.4 кг, высотой 30 см и площадью дна 8 …
Прямолинейное движение двух тел задано уравнениями x1(t) = k1t + b1 и x2(t) = k2t+ b2, где x1(t) и x2(t) – координаты в момент времени t первог …
СРОЧНО!! ДАЮ 30 БАЛЛОВЭкспериментатор Глюк добыл немного неизвестного науке вещества в твёрдомсостоянии, поместил его в калориметр и радостно н …
Движение точки на ободе колеса радиусом R, катящегося с угловой скоростью ω без скольжения по горизонтальной поверхности описывается уравнениям …
