Дельтообра́зный потенциа́л в ква́нтовой меха́нике — общее название профилей потенциальной энергии частицы, задаваемых выражениями с дельта-функцией Дирака. Такими профилями моделируется физическая ситуация, когда наличествуют очень узкие и острые максимумы или минимумы потенциала.
Простыми примерами подобных профилей являются дельтообразный туннельный барьер и дельтообразная квантовая яма вида 





В большинстве случаев при рассмотрении поведения частицы ищется решение одномерного стационарного уравнения Шрёдингера с соответствующим потенциалом. Обычно предполагается, что частица перемещается только вдоль направления 

Подход к решению уравнения Шрёдингера[править | править код]
Стационарное одномерное уравнение Шрёдингера для волновой функции 
,
где 



получится
.
Крупные значки 


и условие непрерывности плотности потока вероятности
.
Эти два условия актуальны вне зависимости от того, идёт ли речь о дельтообразном барьере или яме, а также (для ямы) от того, больше или меньше нуля величина энергии 

Коэффициенты прохождения и отражения[править | править код]
В этом разделе предполагается, что 
Барьер или яма делит пространство на две части (
,
,
где 







,
.
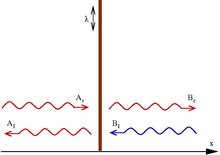
Туннелирование частицы через барьер в виде дельта-функции
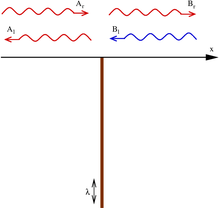
Прохождение частицы над ямой в виде дельта-функции
Пусть падающая частица приближается к барьеру слева (



.
В классическом случае частица с конечной энергией 
,
.
Здесь сразу три неожиданных, с классической точки зрения, результата. Во-первых, имеется ненулевая вероятность прохождения (коэффициент прохождения) для бесконечно высокого барьера. Во-вторых, поскольку формула вполне применима к отрицательным 



Дискретное состояние в дельтообразной яме[править | править код]
В этом разделе предполагается, что 

В обеих областях решение уравнения Шрёдингера, как и выше, может быть записано в виде суммы экспонент
,
,
где 

,
,
Из условий для 




,
то есть в дельтообразной яме существует ровно один уровень с выписанной энергией.
Практическая релевантность дельта-модели[править | править код]
Ситуация туннелирования через дельтообразный потенциал является предельным случаем туннелирования через прямоугольный барьер ширины 






Задача о туннелировании через дельтообразный барьер является стандартной модельной задачей квантовой механики. Она возникает, например, при описании токопереноса между двумя проводящими областями, на стыке которых самопроизвольно образуется тонкая окисная плёнка. Если толщина плёнки и её химический состав примерно известны, можно использовать модель прямоугольного или трапецеидального барьера. Однако в ряде случаев единственным выходом является привлечение модели дельтообразного потенциала.
Аналогично с задачей о дельтообразной яме: модель может использоваться в качестве грубого приближения. Значение 
Литература[править | править код]
- Ландау Л. Д., Лифшиц Е. М. Квантовая механика (нерелятивистская теория). — Издание 4-е. — М.: Наука, 1989. — 768 с. — («Теоретическая физика», том III). — ISBN 5-02-014421-5.
From Wikipedia, the free encyclopedia
In quantum mechanics the delta potential is a potential well mathematically described by the Dirac delta function – a generalized function. Qualitatively, it corresponds to a potential which is zero everywhere, except at a single point, where it takes an infinite value. This can be used to simulate situations where a particle is free to move in two regions of space with a barrier between the two regions. For example, an electron can move almost freely in a conducting material, but if two conducting surfaces are put close together, the interface between them acts as a barrier for the electron that can be approximated by a delta potential.
The delta potential well is a limiting case of the finite potential well, which is obtained if one maintains the product of the width of the well and the potential constant while decreasing the well’s width and increasing the potential.
This article, for simplicity, only considers a one-dimensional potential well, but analysis could be expanded to more dimensions.
Single delta potential[edit]

The time-independent Schrödinger equation for the wave function ψ(x) of a particle in one dimension in a potential V(x) is
where ħ is the reduced Planck constant, and E is the energy of the particle.
The delta potential is the potential
where δ(x) is the Dirac delta function.
It is called a delta potential well if λ is negative, and a delta potential barrier if λ is positive. The delta has been defined to occur at the origin for simplicity; a shift in the delta function’s argument does not change any of the following results.
Solving the Schrödinger equation[1][edit]
The potential splits the space in two parts (x < 0 and x > 0). In each of these parts the potential is zero, and the Schrödinger equation reduces to
this is a linear differential equation with constant coefficients, whose solutions are linear combinations of eikx and e−ikx, where the wave number k is related to the energy by
In general, due to the presence of the delta potential in the origin, the coefficients of the solution need not be the same in both half-spaces:
where, in the case of positive energies (real k), eikx represents a wave traveling to the right, and e−ikx one traveling to the left.
One obtains a relation between the coefficients by imposing that the wavefunction be continuous at the origin:
A second relation can be found by studying the derivative of the wavefunction. Normally, we could also impose differentiability at the origin, but this is not possible because of the delta potential. However, if we integrate the Schrödinger equation around x = 0, over an interval [−ε, +ε]:
In the limit as ε → 0, the right-hand side of this equation vanishes; the left-hand side becomes
because
Substituting the definition of ψ into this expression yields
The boundary conditions thus give the following restrictions on the coefficients
Bound state (E < 0)[edit]
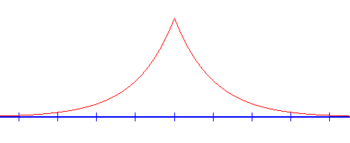
The graph of the bound state wavefunction solution to the delta function potential is continuous everywhere, but its derivative is not defined at x = 0.
In any one-dimensional attractive potential there will be a bound state. To find its energy, note that for E < 0, k = i√2m|E|/ħ = iκ is imaginary, and the wave functions which were oscillating for positive energies in the calculation above are now exponentially increasing or decreasing functions of x (see above). Requiring that the wave functions do not diverge at infinity eliminates half of the terms: Ar = Bl = 0. The wave function is then
From the boundary conditions and normalization conditions, it follows that
from which it follows that λ must be negative, that is, the bound state only exists for the well, and not for the barrier. The Fourier transform of this wave function is a Lorentzian function.
The energy of the bound state is then
Scattering (E > 0)[edit]

Transmission (T) and reflection (R) probability of a delta potential well. The energy E > 0 is in units of 
For positive energies, the particle is free to move in either half-space: x < 0 or x > 0. It may be scattered at the delta-function potential.
The quantum case can be studied in the following situation: a particle incident on the barrier from the left side (Ar). It may be reflected (Al) or transmitted (Br).
To find the amplitudes for reflection and transmission for incidence from the left, we put in the above equations Ar = 1 (incoming particle), Al = r (reflection), Bl = 0 (no incoming particle from the right) and Br = t (transmission), and solve for r and t even though we do not have any equations in t.
The result is
Due to the mirror symmetry of the model, the amplitudes for incidence from the right are the same as those from the left. The result is that there is a non-zero probability
for the particle to be reflected. This does not depend on the sign of λ, that is, a barrier has the same probability of reflecting the particle as a well. This is a significant difference from classical mechanics, where the reflection probability would be 1 for the barrier (the particle simply bounces back), and 0 for the well (the particle passes through the well undisturbed).
The probability for transmission is
Remarks and application[edit]
The calculation presented above may at first seem unrealistic and hardly useful. However, it has proved to be a suitable model for a variety of real-life systems.
One such example regards the interfaces between two conducting materials. In the bulk of the materials, the motion of the electrons is quasi-free and can be described by the kinetic term in the above Hamiltonian with an effective mass m. Often, the surfaces of such materials are covered with oxide layers or are not ideal for other reasons. This thin, non-conducting layer may then be modeled by a local delta-function potential as above. Electrons may then tunnel from one material to the other giving rise to a current.
The operation of a scanning tunneling microscope (STM) relies on this tunneling effect. In that case, the barrier is due to the air between the tip of the STM and the underlying object. The strength of the barrier is related to the separation being stronger the further apart the two are. For a more general model of this situation, see Finite potential barrier (QM). The delta function potential barrier is the limiting case of the model considered there for very high and narrow barriers.
The above model is one-dimensional while the space around us is three-dimensional. So, in fact, one should solve the Schrödinger equation in three dimensions. On the other hand, many systems only change along one coordinate direction and are translationally invariant along the others. The Schrödinger equation may then be reduced to the case considered here by an Ansatz for the wave function of the type 
Alternatively, it is possible to generalize the delta function to exist on the surface of some domain D (see Laplacian of the indicator).[2]
The delta function model is actually a one-dimensional version of the Hydrogen atom according to the dimensional scaling method developed by the group of Dudley R. Herschbach[3]
The delta function model becomes particularly useful with the double-well Dirac Delta function model which represents a one-dimensional version of the Hydrogen molecule ion, as shown in the following section.
Double delta potential[edit]

The symmetric and anti-symmetric wavefunctions for the double-well Dirac delta function model with “internuclear” distance R = 2
The double-well Dirac delta function models a diatomic hydrogen molecule by the corresponding Schrödinger equation:
where the potential is now
where 


Matching of the wavefunction at the Dirac delta-function peaks yields the determinant
Thus, 
which has two solutions 
The “+” case corresponds to a wave function symmetric about the midpoint (shown in red in the diagram), where A = B, and is called gerade. Correspondingly, the “−” case is the wave function that is anti-symmetric about the midpoint, where A = −B, and is called ungerade (shown in green in the diagram). They represent an approximation of the two lowest discrete energy states of the three-dimensional 
where W is the standard Lambert W function. Note that the lowest energy corresponds to the symmetric solution 
One of the most interesting cases is when qR ≤ 1, which results in 
See also[edit]
- Free particle
- Particle in a box
- Finite potential well
- Lambert W function
- Particle in a ring
- Particle in a spherically symmetric potential
- Quantum harmonic oscillator
- Hydrogen atom or hydrogen-like atom
- Ring wave guide
- Particle in a one-dimensional lattice (periodic potential)
- Hydrogen molecular ion
- Holstein–Herring method
- Laplacian of the indicator
- List of quantum-mechanical systems with analytical solutions
References[edit]
- ^ “quantum mechanics – Wave function with a delta potential”. Physics Stack Exchange. Retrieved 2021-03-29.
- ^ Lange, Rutger-Jan (2012), “Potential theory, path integrals and the Laplacian of the indicator”, Journal of High Energy Physics, 2012 (11): 1–49, arXiv:1302.0864, Bibcode:2012JHEP…11..032L, doi:10.1007/JHEP11(2012)032, S2CID 56188533
- ^ D.R. Herschbach, J.S. Avery, and O. Goscinski (eds.), Dimensional Scaling in Chemical Physics, Springer, (1992). [1]
- ^ T. C. Scott, J. F. Babb, A. Dalgarno and John D. Morgan III, “The Calculation of Exchange Forces: General Results and Specific Models”, J. Chem. Phys., 99, pp. 2841–2854, (1993).
- ^ van Dijk, W.; Kiers, K. A. (1992). “Time delay in simple one‐dimensional systems”. American Journal of Physics. American Association of Physics Teachers (AAPT). 60 (6): 520–527. Bibcode:1992AmJPh..60..520V. doi:10.1119/1.16866. ISSN 0002-9505.
- Griffiths, David J. (2005). Introduction to Quantum Mechanics (2nd ed.). Prentice Hall. pp. 68–78. ISBN 978-0-13-111892-8.
- For the 3-dimensional case look for the “delta shell potential”; further see K. Gottfried (1966), Quantum Mechanics Volume I: Fundamentals, ch. III, sec. 15.
External links[edit]
 Media related to Delta potential at Wikimedia Commons
Media related to Delta potential at Wikimedia Commons
В квантовой механике потенциал дельты является потенциальной ямой математически описывается дельта – функция Дирака – это обобщенная функция . Качественно он соответствует потенциалу, который везде равен нулю, кроме одной точки, где он принимает бесконечное значение. Это можно использовать для моделирования ситуаций, когда частица может свободно перемещаться в двух областях пространства с барьером между двумя областями. Например, электрон может почти свободно перемещаться в проводящем материале, но если две проводящие поверхности расположены близко друг к другу, граница раздела между ними действует как барьер для электрона, который можно аппроксимировать дельта-потенциалом.
Потенциал дельты также является предельным случаем из конечного потенциала скважины , которое получается , если один поддерживает продукт ширины скважины и потенциальные постоянная при уменьшении ширины колодца и увеличения потенциала.
В этой статье для простоты рассматривается только одномерная потенциальная яма, но анализ можно расширить до других измерений.
Единый дельта-потенциал

Не зависящее от времени уравнение Шредингера для волновой функции ψ ( x ) частицы в одном измерении в потенциале V ( x ) имеет вид
где ħ – приведенная постоянная Планка , а E – энергия частицы.
Дельта-потенциал – это потенциал
где δ ( x ) – дельта-функция Дирака .
Это называется дельта-потенциальной ямой, если λ отрицательно, и дельта-потенциальным барьером, если λ положительно. Для простоты определено, что дельта возникает в начале координат; сдвиг аргумента дельта-функции не меняет никаких результатов обработки.
Решение уравнения Шредингера
Потенциал разделяет пространство на две части ( x <0 и x > 0). В каждой из этих частей потенциальная энергия равна нулю, и уравнение Шредингера сводится к
это линейное дифференциальное уравнение с постоянными коэффициентами , чьи решения являются линейными комбинациями из электронной IKX и е – IKX , где волновое число K связан с энергией по
В общем, из-за наличия дельта-потенциала в начале координат коэффициенты решения не обязательно должны быть одинаковыми в обоих полупространствах:
где в случае положительных энергий (действительное k ) e ikx представляет волну, бегущую вправо, а e – ikx – волну, бегущую влево.
Связь между коэффициентами получается, предполагая, что волновая функция непрерывна в начале координат:
Второе соотношение можно найти, изучая производную волновой функции. Обычно мы могли бы также наложить дифференцируемость в начале координат, но это невозможно из-за дельта-потенциала. Однако, если мы проинтегрируем уравнение Шредингера вокруг x = 0 на интервале [- ε , + ε ]:
В пределе ε → 0 правая часть этого уравнения обращается в нуль; левая часть становится
потому что
Подставляя определение ψ в это выражение, получаем
Таким образом, граничные условия дают следующие ограничения на коэффициенты
Связанное состояние ( E <0)

График решения волновой функции связанного состояния для потенциала дельта-функции непрерывен всюду, но его производная не определена при x = 0.
В любом одномерном притягивающем потенциале будет связанное состояние . Чтобы найти его энергию, заметим, что для E <0, k = i √ 2 m | E | / ħ = iκ является мнимым, и волновые функции, которые колебались при положительных энергиях в приведенном выше вычислении, теперь являются экспоненциально возрастающими или убывающими функциями x (см. выше). Требование, чтобы волновые функции не расходились на бесконечности, исключает половину членов: A r = B l = 0. Тогда волновая функция равна
Из граничных условий и условий нормировки следует, что
откуда следует, что λ должно быть отрицательным, т. е. связанное состояние существует только для ямы, а не для барьера. Преобразование Фурье этой волновой функции является функцией Лоренца .
Тогда энергия связанного состояния равна
Рассеяние ( E > 0)

Вероятность прохождения ( T ) и отражения ( R ) дельта-потенциальной ямы. Энергия E > 0 выражается в единицах . Пунктиром: классический результат. Сплошная линия: квантовая механика.
Для положительных энергий частица может свободно перемещаться в любом полупространстве: x <0 или x > 0. Она может рассеиваться на потенциале дельта-функции.
Квантовый случай можно изучить в следующей ситуации: частица, падающая на барьер с левой стороны ( A r ) . Он может отражаться ( A l ) или передаваться ( B r ) . Чтобы найти амплитуды отражения и прохождения при падении слева, мы подставляем в приведенные выше уравнения A r = 1 (падающая частица), A l = r (отражение), B l = 0 (нет падающей частицы справа) и B r = t (передача), и решите относительно r и t, даже если у нас нет никаких уравнений относительно t . Результат
Из-за зеркальной симметрии модели амплитуды падения справа такие же, как и слева. В результате существует ненулевая вероятность
для отражения частицы. Это не зависит от знака λ , то есть барьер имеет такую же вероятность отражения частицы, как и яма. Это существенное отличие от классической механики, где вероятность отражения будет равна 1 для барьера (частица просто отскакивает назад) и 0 для ямы (частица проходит через яму без помех).
Таким образом, вероятность передачи равна
Замечания и применение
Представленный выше расчет на первый взгляд может показаться нереальным и малополезным. Однако она оказалась подходящей моделью для множества реальных систем.
Один из таких примеров касается границ раздела двух проводящих материалов. В объеме материалов движение электронов квазисвободно и может быть описано кинетическим членом в приведенном выше гамильтониане с эффективной массой m . Часто поверхности таких материалов покрыты оксидными слоями или не идеальны по другим причинам. Этот тонкий непроводящий слой можно затем смоделировать с помощью локального дельта-потенциала, как указано выше. Затем электроны могут туннелировать из одного материала в другой, вызывая ток.
Работа сканирующего туннельного микроскопа (СТМ) основана на этом туннельном эффекте. В этом случае барьер возникает из-за наличия воздуха между концом СТМ и нижележащим объектом. Прочность барьера связана с тем, что разделение тем сильнее, чем дальше друг от друга они находятся. Для более общей модели этой ситуации см. Конечный потенциальный барьер (QM) . Дельта-функция потенциального барьера является предельным случаем рассматриваемой здесь модели для очень высоких и узких барьеров.
Вышеупомянутая модель одномерная, а пространство вокруг нас – трехмерное. Таким образом, фактически следует решать уравнение Шредингера в трех измерениях. С другой стороны, многие системы изменяются только в одном направлении координат и трансляционно инвариантны в других направлениях. Тогда уравнение Шредингера может быть сведено к рассматриваемому здесь случаю с помощью анзаца для волновой функции данного типа .
В качестве альтернативы можно обобщить дельта-функцию, чтобы она существовала на поверхности некоторой области D (см. Лапласиан индикатора ).
Дельта – функция модель фактически является одномерной версия атома водорода в соответствии с размерным масштабированием метода , разработанного группой Дадли Р. Herschbach
дельты – функция модели становится особенно полезная при двухъямных моделях функции Дирака Delta , которая представляет собой одну -размерная версия иона молекулы водорода , как показано в следующем разделе.
Двойной дельта-потенциал

Симметричные и антисимметричные волновые функции для двухъямной модели дельта-функции Дирака с «межъядерным» расстоянием R = 2
Двухъямная дельта-функция Дирака моделирует двухатомную молекулу водорода с помощью соответствующего уравнения Шредингера:
где потенциал сейчас
где – «межъядерное» расстояние с пиками дельта-функции Дирака (отрицательными), расположенными в точке x = ± R / 2 (показано коричневым цветом на диаграмме). Принимая во внимание связь этой модели с ее трехмерным молекулярным аналогом, мы используем атомные единицы и набор . Вот формально регулируемый параметр. Из случая одной лунки мы можем вывести ” анзац ” для решения
Согласование волновой функции на пиках дельта-функции Дирака дает определитель
Таким образом, оказывается, что он определяется псевдоквадратичным уравнением
который имеет два решения . В случае равных зарядов (симметричный гомоядерный случай) λ = 1, и псевдоквадратичный сводится к
Случай «+» соответствует волновой функции, симметричной относительно средней точки (показанной красным на диаграмме), где A = B , и называется gerade . Соответственно, случай «-» – это волновая функция, которая антисимметрична относительно средней точки, где A = – B , и называется ungerade (показана зеленым на диаграмме). Они представляют собой приближение двух низших дискретных энергетических состояний трехмерного объекта и полезны при его анализе. Аналитические решения для собственных значений энергии для случая симметричных зарядов даются формулами
где W является стандартным Ламберта W функция . Обратите внимание, что самая низкая энергия соответствует симметричному решению . В случае неравных зарядов, и в этом отношении трехмерной молекулярной проблемы, решения даются путем обобщения W- функции Ламберта (см. Раздел об обобщении W-функции Ламберта и ссылки здесь).
Один из самых интересных случаев – это когда qR ≤ 1, что приводит к . Таким образом, имеется нетривиальное решение для связанного состояния с E = 0. Для этих конкретных параметров возникает много интересных свойств, одним из которых является необычный эффект, заключающийся в том, что коэффициент передачи равен единице при нулевой энергии.
Смотрите также
- Бесплатная частица
- Частица в коробке
- Конечная потенциальная яма
- W функция Ламберта
- Частица в кольце
- Частица в сферически-симметричном потенциале
- Квантовый гармонический осциллятор
-
Атом водорода или водородоподобный атом
- Кольцевой волновод
- Частица в одномерной решетке (периодический потенциал)
- Молекулярный ион водорода
- Метод голштинской селедки.
- Лапласиан индикатора
- Список квантово-механических систем с аналитическими решениями
использованная литература
-
^
«Квантовая механика – Волновая функция с дельта-потенциалом» . Обмен физическими стеками . Проверено 29 марта 2021 . - ^ Ланге, Рутгер-Ян (2012), «Теория потенциала, интегралы по траекториям и лапласиан индикатора», Journal of High Energy Physics , 2012 (11): 1–49, arXiv : 1302.0864 , Bibcode : 2012JHEP … 11 ..032L , DOI : 10.1007 / JHEP11 (2012) 032
- ^ DR Herschbach , JS Avery, and O. Goscinski (eds.), Dimensional Scaling in Chemical Physics , Springer, (1992). [1]
- ^ Т. С. Скотт, Дж. Ф. Бэбб, А. Далгарно и Джон Д. Морган III, «Расчет обменных сил: общие результаты и конкретные модели» , J. Chem. Phys. 99. С. 2841–2854, 1993.
- ^ W. ван Дейк и KA Kiers, “Время задержки в простых одномерных системах”, Am. J. Phys. , 60, стр 520-527, (1992),. DOI : 10.1119 / 1,16866 .
- Гриффитс, Дэвид Дж. (2005). Введение в квантовую механику (2-е изд.). Прентис Холл. С. 68–78. ISBN 978-0-13-111892-8.
- Для трехмерного случая ищите «потенциал дельта-оболочки»; далее см. K. Gottfried (1966), Quantum Mechanics Volume I: Fundamentals , ch. III, сек. 15.
внешние ссылки
-
 СМИ, связанные с потенциалом дельты на Викискладе?
СМИ, связанные с потенциалом дельты на Викискладе?
Задача о туннелировании через дельтообразный барьер это стандартная проблема из задачников по квантовой механике. Задача состоит в решении одномерного стационарного уравнения Шрёдингера с потенциалом в виде дельта-функции Дирака.
Решение
Стационарное одномерное уравнение Шрёдингера для волновой функции 
где 



дельтообразный потенциальный барьер с энергией 
Барьер делит пространство на две части (
,
где волновой вектор выражается из энергии как 

,
.
Второе из этих уравнений задаёт условие на разрыв производной при 
Коэффициенты прохождения и отражения
Здесь можно сравнить ситуацию с классическим случаем. в обоих случаях мы имеем свободную частицу, но в классическом случае частица с конечной энергией не может преодолеть бесконечный потенциальный барьер. Для дальнейшего решения квантовой задачи определим ситуацию следующим образом: частица на барьер падает слева (


Для определения амплитуд прохождения и отражения положим 




Неожиданный результат с классической точки зрения, то что имееется ненулевая вероятность или ненулевой коэффициент прохождения) для бесконечно высококо барьера
Этот эффект называется туннелированием.
В заключении приведём коэффициент отражения:
Эта страница использует содержимое раздела Википедии на русском языке. Оригинальная статья находится по адресу: Туннелирование через дельтообразный потенциал. Список первоначальных авторов статьи можно посмотреть в истории правок. Эта статья так же, как и статья, размещённая в Википедии, доступна на условиях CC-BY-SA .
Модель энергетического потенциала в квантовой механике
В квантовой механике дельта-потенциал представляет собой потенциальную яму, математически описываемую дельта-функцией Дирака – обобщенной функцией. Качественно он соответствует потенциалу, который везде равен нулю, кроме единственной точки, где он принимает бесконечное значение. Это можно использовать для моделирования ситуаций, когда частица может свободно перемещаться в двух областях пространства с барьером между двумя областями. Например, электрон может почти свободно перемещаться в проводящем материале, но если две проводящие поверхности расположены близко друг к другу, граница раздела между ними действует как барьер для электрона, который можно аппроксимировать дельта-потенциалом.
Дельта-потенциальная яма – это предельный случай конечной потенциальной ямы, который получается, если выдерживать произведение ширины ямы и постоянной потенциала при уменьшении ширины ямы и увеличении потенциала.
В этой статье для простоты рассматривается только одномерная потенциальная яма, но анализ можно расширить до других измерений.
Содержание
- 1 Единичный дельта-потенциал
- 1.1 Решение уравнения Шредингера
- 1.2 Связанное состояние (E < 0)
- _0) “>1.3 Рассеяние (E>0)
- 1.4 Замечания и применение
- 2 Двойной дельта-потенциал
- 3 См. Также
- 4 Ссылки
- 5 Внешние ссылки
Одинарный дельта-потенциал

Не зависящее от времени уравнение Шредингера для волновой функции ψ (x) частицы в одном измерении в потенциале V (x) равно
- – ℏ 2 2 md 2 ψ dx 2 (x) + V (x) ψ (x) Знак равно Е ψ (х), { Displaystyle – { гидроразрыва { hbar ^ {2}} {2m}} { гидроразрыва {d ^ {2} psi} {dx ^ {2}}} (х) + V (x) psi (x) = E psi (x) ~,}
где ħ – приведенная постоянная Планка, а E – энергия частицы
Дельта-потенциал – это потенциал
- V (x) = λ δ (x), { displaystyle displaystyle V (x) = lambda delta (x) ~,}
где δ (x) – дельта-функция Дирака..
Это называется дельта-потенциальной ямой, если λ отрицательно, и дельта-потенциальным барьером, если λ положительно. оштрафован на происхождение для простоты; сдвиг аргумента дельта-функции не меняет никаких результатов обработки.
Решение уравнения Шредингера
Потенциал разделяет пространство на две части (x < 0 and x>0). В каждой из этих частей потенциальная энергия равна нулю, и уравнение Шредингера сводится к
- d 2 ψ d x 2 = – 2 m E ℏ 2 ψ; { displaystyle { frac {d ^ {2} psi} {dx ^ {2}}} = – { frac {2mE} { hbar ^ {2}}} psi ~;}
это линейное дифференциальное уравнение с постоянными коэффициентами, решениями которого являются линейные комбинации e и e, где волновое число k связано с энергии на
- k = 2 m E ℏ. { displaystyle k = { frac { sqrt {2mE}} { hbar}} ~.}
В общем, из-за наличия дельта-потенциала в начале координат коэффициенты решения не обязательно должны быть то же самое в обоих полупространствах:
- ψ (x) = {ψ L (x) = A reikx + A le – ikx, если x < 0 ; ψ R ( x) = B r e i k x + B l e − i k x, if x>0, { displaystyle psi (x) = { begin { case} psi _ { mathrm {L}} (x) = A _ { mathrm {r}} e ^ {ikx} + A _ { mathrm {l}} e ^ {- ikx}, { text { if}} x <0;\psi _{mathrm {R} }(x)=B_{mathrm {r} }e^{ikx}+B_{mathrm {l} }e^{-ikx},{text{ if }}x>0, end {cases}}}
где в случае положительных энергий (действительный k), e представляет волну, бегущую вправо, а e – влево..
Можно получить соотношение между коэффициентами, наложив, что волновая функция будет непрерывной в начале координат,
- ψ (0) = ψ L (0) = ψ R (0) = A r + A l Знак равно В р + В l, { Displaystyle psi (0) = psi _ {L} (0) = psi _ {R} (0) = A_ {r} + A_ {l} = B_ {r} + B_ {l} ~,}
Второе отношение ca n можно найти, изучая производную волновой функции. Обычно мы также можем наложить дифференцируемость в начале координат, но это невозможно из-за дельта-потенциала. Однако, если мы проинтегрируем уравнение Шредингера вокруг x = 0, на интервале [−ε, + ε]:
- – ℏ 2 2 m ∫ – ϵ + ϵ ψ ″ (x) dx + ∫ – ϵ + ϵ V (x) ψ (x) dx = E ∫ – ϵ + ϵ ψ (x) dx. { displaystyle – { frac { hbar ^ {2}} {2m}} int _ {- epsilon} ^ {+ epsilon} psi ” (x) , dx + int _ {- epsilon } ^ {+ epsilon} V (x) psi (x) , dx = E int _ {- epsilon} ^ {+ epsilon} psi (x) , dx.}
В предел при ε → 0, правая часть этого уравнения обращается в нуль; левая сторона становится
- – ℏ 2 2 m [ψ R ′ (0) – ψ L ′ (0)] + λ ψ (0), { displaystyle textstyle – { frac { hbar ^ { 2}} {2m}} [ psi ‘_ {R} (0) – psi’ _ {L} (0)] + lambda psi (0),}
потому что
- ∫ – ϵ + ϵ ψ ″ (x) dx = [ψ ′ (+ ϵ) – ψ ′ (- ϵ)]. { displaystyle int _ {- epsilon} ^ {+ epsilon} psi ” (x) , dx = [ psi ‘({+ epsilon}) – psi’ ({- epsilon}) ].}
Подставляя определение ψ в это выражение, получаем
- – ℏ 2 2 mik (- A r + A l + B r – B l) + λ (A r + A l) = 0. { displaystyle – { frac { hbar ^ {2}} {2m}} ik (-A_ {r} + A_ {l} + B_ {r} -B_ {l}) + lambda (A_ {r} + A_ {l}) = 0 ~.}
Таким образом, граничные условия дают следующие ограничения на коэффициенты
- {A r + A l – B r – B l = 0; – A r + A l + B r – B l знак равно 2 m λ i k ℏ 2 (A r + A l). { displaystyle { begin {cases} A_ {r} + A_ {l} -B_ {r} -B_ {l} = 0; \ – A_ {r} + A_ {l} + B_ {r} – B_ {l} = { frac {2m lambda} {ik hbar ^ {2}}} (A_ {r} + A_ {l}) ~. End {ases}}}
Связанное состояние ( E < 0)
 График решения волновой функции связанного состояния для потенциала дельта-функции непрерывен всюду, но его производная не определена при x = 0.
График решения волновой функции связанного состояния для потенциала дельта-функции непрерывен всюду, но его производная не определена при x = 0.
В любом одномерном потенциале притяжения будет граница состояние. Чтобы найти его энергию, обратите внимание, что для E < 0, k = i√2m|E|/ħ = iκ is imaginary and the wave functions which were oscillating for positive energies in the calculation above, are now exponentially increasing or decreasing functions of x (see above). Requiring that the wave functions do not diverge at infinity eliminates half of the terms: Ar= B l = 0. Тогда волновая функция
- ψ (x) = {ψ L (x) = A le κ x, если x < 0 ; ψ R ( x) = B r e − κ x, if x>0. { displaystyle psi (x) = { begin {cases} psi _ { text {L}} (x) = A_ {l} e ^ { kappa x }, { text {if}} x <0;\psi _{text{R}}(x)=B_{r}e^{-kappa x},{text{ if }}x>0. end {cases}}}
Из граничных условий и условий нормализации следует, что
- {A l = В р = κ; κ = – м λ ℏ 2; { Displaystyle { begin {case} A_ {l} = B_ {r} = { sqrt { ka ppa}}; \ kappa = – { frac {m lambda} { hbar ^ {2}}} ~; end {cases}}}
откуда следует, что λ должно быть отрицательным, что связанное состояние существует только для ямы, а не для барьера. Преобразование Фурье этой волновой функции является функцией Лоренца.
. Тогда энергия связанного состояния равна
- E = – ℏ 2 κ 2 2 m = – m λ 2 2 ℏ 2. { displaystyle E = – { frac { hbar ^ {2} kappa ^ {2}} {2m}} = – { frac {m lambda ^ {2}} {2 hbar ^ {2}} }.}
Рассеяние (E>0)
 Вероятность прохождения (T) и отражения (R) дельта-потенциальной ямы. Энергия E>0 выражается в единицах
Вероятность прохождения (T) и отражения (R) дельта-потенциальной ямы. Энергия E>0 выражается в единицах
м λ 2 2 ℏ 2 { displaystyle { frac {m lambda ^ {2}} {2 hbar ^ {2}}} , !}

Для положительных энергий частица может свободно двигаться в любом полупространстве: x < 0 or x>0. Он может быть рассеян на потенциале дельта-функции.
Квантовый случай можно изучить в следующей ситуации: частица, падающая на барьер с левой стороны (A r). Он может быть отражен (A l) или передан (B r). Чтобы найти амплитуды отражения и пропускания при падении слева, мы положим в приведенные выше уравнения A r = 1 (падающая частица), A l = r (отражение), B l = 0 (нет входящей частицы справа) и B r = t (пропускание), и решите для r и t, даже если у нас нет никаких уравнений для t. Результат:
- t = 1 1 – m λ i ℏ 2 k { displaystyle t = { cfrac {1} {1 – { cfrac {m lambda} {i hbar ^ {2} k}}. }} , !}
- r = 1 я ℏ 2 км λ – 1 { displaystyle r = { cfrac {1} {{ cfrac {i hbar ^ {2} k} {m lambda} } -1}} , !}
Из-за зеркальной симметрии модели амплитуды падения справа такие же, как и слева. В результате существует ненулевая вероятность
- R = | г | 2 знак равно 1 1 + ℏ 4 К 2 м 2 λ 2 знак равно 1 1 + 2 ℏ 2 Е м λ 2. { displaystyle R = | r | ^ {2} = { cfrac {1} {1 + { cfrac { hbar ^ {4} k ^ {2}} {m ^ {2} lambda ^ {2} }}}} = { cfrac {1} {1 + { cfrac {2 hbar ^ {2} E} {m lambda ^ {2}}}}}. , !}
для частица для отражения. Это не зависит от знака λ, то есть барьер имеет такую же вероятность отражения частицы, как и яма. Это существенное отличие от классической механики, где вероятность отражения будет равна 1 для барьера (частица просто отскакивает) и 0 для ямы (частица проходит через яму без помех).
Таким образом, вероятность передачи составляет
- T = | т | 2 знак равно 1 – R = 1 1 + м 2 λ 2 ℏ 4 К 2 = 1 1 + м λ 2 2 ℏ 2 E { displaystyle T = | t | ^ {2} = 1-R = { cfrac {1 } {1 + { cfrac {m ^ {2} lambda ^ {2}} { hbar ^ {4} k ^ {2}}}}} = { cfrac {1} {1 + { cfrac { m lambda ^ {2}} {2 hbar ^ {2} E}}}} , !}
.
Замечания и применение
Представленный выше расчет сначала может показаться нереалистичным и вряд ли полезным. Однако она оказалась подходящей моделью для множества реальных систем.
Один из таких примеров касается границ раздела между двумя проводящими материалами. В основной массе материалов движение электронов квазисвободно и может быть описано кинетическим членом в приведенном выше гамильтониане с эффективной массой m. Часто поверхности таких материалов покрыты оксидными слоями или не идеальны по другим причинам. Этот тонкий непроводящий слой можно затем смоделировать с помощью локального дельта-функционального потенциала, как указано выше. Затем электроны могут туннелировать из одного материала в другой, вызывая ток.
Работа сканирующего туннельного микроскопа (СТМ) основана на этом туннельном эффекте. В этом случае барьер возникает из-за наличия воздуха между концом СТМ и нижележащим объектом. Прочность барьера связана с тем, что разделение тем сильнее, чем дальше друг от друга они находятся. Для более общей модели этой ситуации см. Конечный потенциальный барьер (QM). Дельта-функция потенциального барьера является предельным случаем рассматриваемой здесь модели для очень высоких и узких барьеров.
Вышеупомянутая модель одномерна, в то время как пространство вокруг нас трехмерно. Таким образом, фактически следует решать уравнение Шредингера в трех измерениях. С другой стороны, многие системы изменяются только вдоль одного координатного направления и трансляционно инвариантны относительно других. Уравнение Шредингера затем может быть сведено к рассмотренному здесь случаю с помощью анзаца для волновой функции типа Ψ (x, y, z) = ψ (x) ϕ (y, z) { displaystyle Psi ( x, y, z) = psi (x) phi (y, z) , !}
В качестве альтернативы можно обобщить дельта-функцию для существования на поверхности некоторой области D (см. Лапласиан индикатора ).
Модель дельта-функции на самом деле является одномерной версией атома водорода согласно методу размерного масштабирования, разработанному группой Дадли Р. Хершбаха Модель дельта-функции становится особенно полезной с двухъямной моделью дельта-функции Дирака, которая представляет одномерную версию иона молекулы водорода, как показано в следующем разделе.
Двойная дельта потенциал
 Симметричные и антисимметричные волновые функции для двухъядерной модели дельта-функции Дирака с «межъядерным» расстоянием R = 2.
Симметричные и антисимметричные волновые функции для двухъядерной модели дельта-функции Дирака с «межъядерным» расстоянием R = 2.
Двухъядерная дельта-функция Дирака моделирует диатомовые водоросли c молекулы водорода по соответствующему уравнению Шредингера:
- – ℏ 2 2 md 2 ψ dx 2 (x) + V (x) ψ (x) = E ψ (x) { displaystyle – { frac { hbar ^ {2}} {2m}} { frac {d ^ {2} psi} {dx ^ {2}}} (x) + V (x) psi (x) = E psi (x)}
где сейчас потенциал:
- V (x) = – q [δ (x + R 2) + λ δ (x – R 2)] { displaystyle V (x) = – q left [ delta left (x + { frac {R} {2}} right) + lambda delta left (x – { frac {R} {2}} right) right]}
где 0 < R < ∞ {displaystyle 0


- ψ (x) = A e – d | х + R 2 | + B e – d | х – R 2 | { Displaystyle psi (х) ~ = ~ Ae ^ {- d left | x + { frac {R} {2}} right |} + Be ^ {- d left | x – { frac {R } {2}} right |}}
Согласование волновой функции на пиках дельта-функции Дирака дает определитель:
- | q – d q e – d R q λ e – d R q λ – d | = 0, где E = – d 2 2. { displaystyle left | { begin {array} {cc} q-d qe ^ {- dR} \ q lambda e ^ {- dR} q lambda -d end {array}} right | = 0 quad { t_dv {where}} quad E = – { frac {d ^ {2}} {2}} ~.}
Таким образом, d { displaystyle d}
- d ± (λ) = 1 2 q (λ + 1) ± 1 2 {q 2 (1 + λ) 2 – 4 λ q 2 [1 – е – 2 d ± (λ) R]} 1/2 { displaystyle d _ { pm} ( lambda) ~ = ~ { textstyle { frac {1} {2}}} q ( lambda +1) pm { textstyle { frac {1} {2}}} left {q ^ {2} (1+ lambda) ^ {2} -4 , lambda q ^ {2} lbrack 1- e ^ {- 2d _ { pm} ( lambda) R}] right } ^ {1/2}}
, который имеет два решения d = d ± { displaystyle d = d _ { pm }}
- d ± = q [1 ± e – d ± R] { displaystyle d _ { pm} = q [ 1 pm e ^ {- d _ { pm} R}]}
Случай “+” соответствует волновой функции, симметричной относительно средней точки (показана красным на диаграмме), где A = B и называется Герад. Соответственно, случай «-» – это волновая функция, которая антисимметрична относительно средней точки, где A = –B, называется ungerade (показана зеленым на диаграмме). Они представляют собой приближение двух низших дискретных энергетических состояний трехмерного H 2 + { displaystyle H_ {2} ^ {+}}
- d ± = q + W (± q R e – q R) / R { displaystyle d _ { pm} = q ~ + ~ W ( pm qRe ^ {- qR}) / R}
где W – стандартная функция W Ламберта. Обратите внимание, что самая низкая энергия соответствует симметричному решению d + { displaystyle d _ {+}}
Один из наиболее интересных случаев – это когда qR ≤ 1, что приводит к d – = 0 { displaystyle d _ {-} = 0}
См. Также
Литература
- ^Ланге, Рутгер-Ян (2012), «Теория потенциала, интегралы по траекториям и лапласиан индикатора. “, Journal of High Energy Physics, 2012 (11): 1–49, arXiv : 1302.0864, Bibcode : 2012JHEP… 11..032L, doi : 10.1007 / JHEP11 (2012) 032
- ^DR Гершбах, И.С. Эйвери и О. Госцински (ред.), Масштабирование размеров в химической физике, Springer, (1992). [1]
- ^Т.К. Скотт, Дж. Ф. Бэбб, А. Далгарно и Джон Д. Морган III, «Расчет обменных сил: общие результаты и конкретные модели», Дж. Chem. Phys., 99, pp. 2841-2854, (1993). [2]
- ^У. ван Дейк и К. А. Кирс, “Задержка в простых одномерных системах”, Am. J. Phys., 60, стр. 520-527 (1992). [3]
- Гриффитс, Дэвид Дж. (2005). Введение в квантовую механику (2-е изд.). Прентис Холл. С. 68–78. ISBN 978-0-13-111892-8.
- Для трехмерного случая ищите «дельта-потенциал оболочки»; далее см. К. Готфрид (1966), Квантовая механика Том I: Основы, глава III, раздел 15.
Внешние ссылки
 Средства массовой информации, относящиеся к дельта-потенциалу на Wikimedia Commons
Средства массовой информации, относящиеся к дельта-потенциалу на Wikimedia Commons









![{displaystyle -{frac {hbar ^{2}}{2m}}[psi _{R}'(0)-psi _{L}'(0)]+lambda psi (0),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d3e5d47917c007c0516bd5ab616c7a94d2e8f7c0)
![{displaystyle int _{-varepsilon }^{+varepsilon }psi ''(x),dx=[psi '(+varepsilon )-psi '(-varepsilon )].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1bc4f99c244c1e61775376a2bd97017ae207ce7f)








![{displaystyle V(x)=-qleft[delta left(x+{frac {R}{2}}right)+lambda delta left(x-{frac {R}{2}}right)right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd5384118e4aa0ac7112305201d1a3e929301482)


![{displaystyle d_{pm }(lambda )={frac {1}{2}}q(lambda +1)pm {frac {1}{2}}left{q^{2}(1+lambda )^{2}-4lambda q^{2}left[1-e^{-2d_{pm }(lambda )R}right]right}^{1/2},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/049806acd696879ff372e46e924bc3693ba7b0ed)
![{displaystyle d_{pm }=qleft[1pm e^{-d_{pm }R}right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0ec7d8221ce4ffbd120343f1e3fcd30f5fea52a0)


![{ displaystyle int _ {- epsilon} ^ {+ epsilon} psi '' (x) , dx = [ psi '(+ epsilon) - psi' (- epsilon)].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ff2fa8ad12b015377c7e22ea015ce5ee3fb00310)
![{displaystyle Hpsi (x)=[-{frac {hbar ^{2}}{2m}}{frac {d^{2}}{dx^{2}}}+V(x)]psi (x)=Epsi (x),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc2dcaf235cacb91af4f8e8e20e6500ba81f7db2)











![{displaystyle textstyle -{frac {hbar ^{2}}{2m}}[psi '_{R}(0)-psi '_{L}(0)]+lambda psi (0),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4303c79a049714dd9f1cde212495da54ff8f6d86)
![{displaystyle int _{-epsilon }^{+epsilon }psi ''(x),dx=[psi '({+epsilon })-psi '({-epsilon })].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9b0c5ea0e70e99d056942b7806012a5c2afd96bc)








![{ displaystyle V (x) = - q left [ delta left (x + { frac {R} {2}} right) + lambda delta left (x - { frac {R} {2}} right) справа]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e1867499ffa5e0d70f1c59821968322c89f255b5)


![d _ { pm} ( lambda) ~ = ~ { textstyle { frac {1} {2}}} q ( lambda +1) pm { textstyle { frac {1} {2}}} left {q ^ {2} (1+ lambda) ^ {2} -4 , lambda q ^ {2} lbrack 1-e ^ {- 2d_ { pm} ( лямбда) R}] справа } ^ {1/2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/02509c77fbbd368bfbb4680bfed7062d06a7eedc)
![d _ { pm} = q [1 pm e ^ {- d _ { pm} R}]](https://wikimedia.org/api/rest_v1/media/math/render/svg/de3c25340e952fe2d73d65c9047a1eab7295c663)

