Как найти дельта сигма

Аналого-цифровое преобразование для начинающих

В этой статье рассмотрены основные вопросы, касающиеся принципа действия АЦП различных типов. При этом некоторые важные теоретические выкладки, касающиеся математического описания аналого-цифрового преобразования остались за рамками статьи, но приведены ссылки, по которым заинтересованный читатель сможет найти более глубокое рассмотрение теоретических аспектов работы АЦП. Таким образом, статья касается в большей степени понимания общих принципов функционирования АЦП, чем теоретического анализа их работы.

”

Введение

В качестве отправной точки дадим определение аналого-цифровому преобразованию. Аналого-цифровое преобразование – это процесс преобразования входной физической величины в ее числовое представление. Аналого-цифровой преобразователь – устройство, выполняющее такое преобразование. Формально, входной величиной АЦП может быть любая физическая величина – напряжение, ток, сопротивление, емкость, частота следования импульсов, угол поворота вала и т.п. Однако, для определенности, в дальнейшем под АЦП мы будем понимать исключительно преобразователи напряжение-код.

Понятие аналого-цифрового преобразования тесно связано с понятием измерения. Под измерением понимается процесс сравнения измеряемой величины с некоторым эталоном, при аналого-цифровом преобразовании происходит сравнение входной величины с некоторой опорной величиной (как правило, с опорным напряжением). Таким образом, аналого-цифровое преобразование может рассматриваться как измерение значения входного сигнала, и к нему применимы все понятия метрологии, такие, как погрешности измерения.

Основные характеристики АЦП

АЦП имеет множество характеристик, из которых основными можно назвать частоту преобразования и разрядность. Частота преобразования обычно выражается в отсчетах в секунду (samples per second, SPS), разрядность – в битах. Современные АЦП могут иметь разрядность до 24 бит и скорость преобразования до единиц GSPS (конечно, не одновременно). Чем выше скорость и разрядность, тем труднее получить требуемые характеристики, тем дороже и сложнее преобразователь. Скорость преобразования и разрядность связаны друг с другом определенным образом, и мы можем повысить эффективную разрядность преобразования, пожертвовав скоростью.

Типы АЦП

Существует множество типов АЦП, однако в рамках данной статьи мы ограничимся рассмотрением только следующих типов:

• АЦП параллельного преобразования (прямого преобразования, flash ADC)
• АЦП последовательного приближения (SAR ADC)
• дельта-сигма АЦП (АЦП с балансировкой заряда)

Существуют также и другие типы АЦП, в том числе конвейерные и комбинированные типы, состоящие из нескольких АЦП с (в общем случае) различной архитектурой. Однако приведенные выше архитектуры АЦП являются наиболее показательными в силу того, что каждая архитектура занимает определенную нишу в общем диапазоне скорость-разрядность.

Наибольшим быстродействием и самой низкой разрядностью обладают АЦП прямого (параллельного) преобразования. Например, АЦП параллельного преобразования TLC5540 фирмы Texas Instruments обладает быстродействием 40MSPS при разрядности всего 8 бит. АЦП данного типа могут иметь скорость преобразования до 1 GSPS. Здесь можно отметить, что еще большим быстродействием обладают конвейерные АЦП (pipelined ADC), однако они являются комбинацией нескольких АЦП с меньшим быстродействием и их рассмотрение выходит за рамки данной статьи.

Среднюю нишу в ряду разрядность-скорость занимают АЦП последовательного приближения. Типичными значениями является разрядность 12-18 бит при частоте преобразования 100KSPS-1MSPS.

Наибольшей точности достигают сигма-дельта АЦП, имеющие разрядность до 24 бит включительно и скорость от единиц SPS до единиц KSPS.

Еще одним типом АЦП, который находил применение в недавнем прошлом, является интегрирующий АЦП. Интегрирующие АЦП в настоящее время практически полностью вытеснены другими типами АЦП, но могут встретиться в старых измерительных приборах.

АЦП прямого преобразования

АЦП прямого преобразования получили широкое распространение в 1960-1970 годах, и стали производиться в виде интегральных схем в 1980-х. Они часто используются в составе «конвейерных» АЦП (в данной статье не рассматриваются), и имеют разрядность 6-8 бит при скорости до 1 GSPS.

Архитектура АЦП прямого преобразования изображена на рис. 1

Рис. 1. Структурная схема АЦП прямого преобразования

Принцип действия АЦП предельно прост: входной сигнал поступает одновременно на все «плюсовые» входы компараторов, а на «минусовые» подается ряд напряжений, получаемых из опорного путем деления резисторами R. Для схемы на рис. 1 этот ряд будет таким: (1/16, 3/16, 5/16, 7/16, 9/16, 11/16, 13/16) Uref, где Uref – опорное напряжение АЦП.

Пусть на вход АЦП подается напряжение, равное 1/2 Uref. Тогда сработают первые 4 компаратора (если считать снизу), и на их выходах появятся логические единицы. Приоритетный шифратор (priority encoder) сформирует из «столбца» единиц двоичный код, который фиксируется выходным регистром.

Теперь становятся понятны достоинства и недостатки такого преобразователя. Все компараторы работают параллельно, время задержки схемы равно времени задержки в одном компараторе плюс время задержки в шифраторе. Компаратор и шифратор можно сделать очень быстрыми, в итоге вся схема имеет очень высокое быстродействие.

Но для получения N разрядов нужно 2^N компараторов (и сложность шифратора тоже растет как 2^N). Схема на рис. 1. содержит 8 компараторов и имеет 3 разряда, для получения 8 разрядов нужно уже 256 компараторов, для 10 разрядов – 1024 компаратора, для 24-битного АЦП их понадобилось бы свыше 16 млн. Однако таких высот техника еще не достигла.

АЦП последовательного приближения

АЦП последовательного приближения реализует алгоритм «взвешивания», восходящий еще к Фибоначчи. В своей книге «Liber Abaci» (1202 г.) Фибоначчи рассмотрел «задачу о выборе наилучшей системы гирь», то есть о нахождении такого ряда весов гирь, который бы требовал для нахождения веса предмета минимального количества взвешиваний на рычажных весах. Решением этой задачи является «двоичный» набор гирь. Подробнее о задаче Фибоначчи можно прочитать, например, здесь: http://www.goldenmuseum.com/2015AMT_rus.html.

Аналого-цифровой преобразователь последовательного приближения (SAR, Successive Approximation Register) измеряет величину входного сигнала, осуществляя ряд последовательных «взвешиваний», то есть сравнений величины входного напряжения с рядом величин, генерируемых следующим образом:

1. на первом шаге на выходе встроенного цифро-аналогового преобразователя устанавливается величина, равная 1/2Uref (здесь и далее мы предполагаем, что сигнал находится в интервале (0 – Uref).

2. если сигнал больше этой величины, то он сравнивается с напряжением, лежащим посередине оставшегося интервала, т.е., в данном случае, 3/4Uref. Если сигнал меньше установленного уровня, то следующее сравнение будет производиться с меньшей половиной оставшегося интервала (т.е. с уровнем 1/4Uref).

3. Шаг 2 повторяется N раз. Таким образом, N сравнений («взвешиваний») порождает N бит результата.

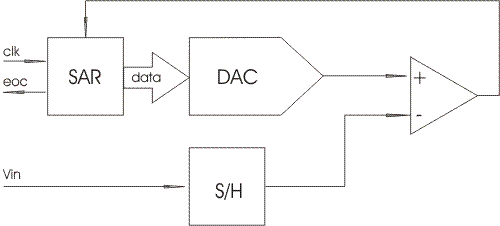
Рис. 2. Структурная схема АЦП последовательного приближения.

Таким образом, АЦП последовательного приближения состоит из следующих узлов:

1. Компаратор. Он сравнивает входную величину и текущее значение «весового» напряжения (на рис. 2. обозначен треугольником).

2. Цифро-аналоговый преобразователь (Digital to Analog Converter, DAC). Он генерирует «весовое» значение напряжения на основе поступающего на вход цифрового кода.

3. Регистр последовательного приближения (Successive Approximation Register, SAR). Он осуществляет алгоритм последовательного приближения, генерируя текущее значение кода, подающегося на вход ЦАП. По его названию названа вся данная архитектура АЦП.

4. Схема выборки-хранения (Sample/Hold, S/H). Для работы данного АЦП принципиально важно, чтобы входное напряжение сохраняло неизменную величину в течение всего цикла преобразования. Однако «реальные» сигналы имеют свойство изменяться во времени. Схема выборки-хранения «запоминает» текущее значение аналогового сигнала, и сохраняет его неизменным на протяжении всего цикла работы устройства.

Достоинством устройства является относительно высокая скорость преобразования: время преобразования N-битного АЦП составляет N тактов. Точность преобразования ограничена точностью внутреннего ЦАП и может составлять 16-18 бит (сейчас стали появляться и 24-битные SAR ADC, например, AD7766 и AD7767).

Дельта-сигма АЦП

И, наконец, самый интересный тип АЦП – сигма-дельта АЦП, иногда называемый в литературе АЦП с балансировкой заряда. Структурная схема сигма-дельта АЦП приведена на рис. 3.

Рис.3. Структурная схема сигма-дельта АЦП.

Принцип действия данного АЦП несколько более сложен, чем у других типов АЦП. Его суть в том, что входное напряжение сравнивается со значением напряжения, накопленным интегратором. На вход интегратора подаются импульсы положительной или отрицательной полярности, в зависимости от результата сравнения. Таким образом, данный АЦП представляет собой простую следящую систему: напряжение на выходе интегратора «отслеживает» входное напряжение (рис. 4). Результатом работы данной схемы является поток нулей и единиц на выходе компаратора, который затем пропускается через цифровой ФНЧ, в результате получается N-битный результат. ФНЧ на рис. 3. Объединен с «дециматором», устройством, снижающим частоту следования отсчетов путем их «прореживания».

Рис. 4. Сигма-дельта АЦП как следящая система

Ради строгости изложения, нужно сказать, что на рис. 3 изображена структурная схема сигма-дельта АЦП первого порядка. Сигма-дельта АЦП второго порядка имеет два интегратора и две петли обратной связи, но здесь рассматриваться не будет. Интересующиеся данной темой могут обратиться к [3].

На рис. 5 показаны сигналы в АЦП при нулевом уровне на входе (сверху) и при уровне Vref/2 (снизу).

Рис. 5. Сигналы в АЦП при разных уровнях сигнала на входе.

Более наглядно работу сигма-дельта АЦП демонстрирует небольшая программа, находящаяся тут: http://designtools.analog.com/dt/sdtutorial/sdtutorial.html.

Теперь, не углубляясь в сложный математический анализ, попробуем понять, почему сигма-дельта АЦП обладают очень низким уровнем собственных шумов.

Рассмотрим структурную схему сигма-дельта модулятора, изображенную на рис. 3, и представим ее в таком виде (рис. 6):

Рис. 6. Структурная схема сигма-дельта модулятора

Здесь компаратор представлен как сумматор, который суммирует непрерывный полезный сигнал и шум квантования.

Пусть интегратор имеет передаточную функцию 1/s. Тогда, представив полезный сигнал как X(s), выход сигма-дельта модулятора как Y(s), а шум квантования как E(s), получаем передаточную функцию АЦП:

Y(s) = X(s)/(s+1) + E(s)s/(s+1)

То есть, фактически сигма-дельта модулятор является фильтром низких частот (1/(s+1)) для полезного сигнала, и фильтром высоких частот (s/(s+1)) для шума, причем оба фильтра имеют одинаковую частоту среза. Шум, сосредоточенный в высокочастотной области спектра, легко удаляется цифровым ФНЧ, который стоит после модулятора.

Рис. 7. Явление «вытеснения» шума в высокочастотную часть спектра

Однако следует понимать, что это чрезвычайно упрощенное объяснение явления вытеснения шума (noise shaping) в сигма-дельта АЦП.

Итак, основным достоинством сигма-дельта АЦП является высокая точность, обусловленная крайне низким уровнем собственного шума. Однако для достижения высокой точности нужно, чтобы частота среза цифрового фильтра была как можно ниже, во много раз меньше частоты работы сигма-дельта модулятора. Поэтому сигма-дельта АЦП имеют низкую скорость преобразования.

Они могут использоваться в аудиотехнике, однако основное применение находят в промышленной автоматике для преобразования сигналов датчиков, в измерительных приборах, и в других приложениях, где требуется высокая точность. но не требуется высокой скорости.

Немного истории

Самым старым упоминанием АЦП в истории является, вероятно, патент Paul M. Rainey, «Facsimile Telegraph System,» U.S. Patent 1,608,527, Filed July 20, 1921, Issued November 30, 1926. Изображенное в патенте устройство фактически является 5-битным АЦП прямого преобразования.

Рис. 8. Первый патент на АЦП

Рис. 9. АЦП прямого преобразования (1975 г.)

Устройство, изображенное на рисунке, представляет собой АЦП прямого преобразования MOD-4100 производства Computer Labs, 1975 года выпуска, собранный на основе дискретных компараторов. Компараторов 16 штук (они расположены полукругом, для того, чтобы уравнять задержку распространения сигнала до каждого компаратора), следовательно, АЦП имеет разрядность всего 4 бита. Скорость преобразования 100 MSPS, потребляемая мощность 14 ватт.

На следующем рисунке изображена продвинутая версия АЦП прямого преобразования.

Рис. 10. АЦП прямого преобразования (1970 г.)

Устройство VHS-630 1970 года выпуска, произведенное фирмой Computer Labs, содержало 64 компаратора, имело разрядность 6 бит, скорость 30MSPS и потребляло 100 ватт (версия 1975 года VHS-675 имела скорость 75 MSPS и потребление 130 ватт).

Литература

W. Kester. ADC Architectures I: The Flash Converter. Analog Devices, MT-020 Tutorial. www.analog.com/static/imported-files/tutorials/MT-020.pdf
W. Kester. ADC Architectures II: Successive Approximation ADC. Analog Devices, MT-021 Tutorial. www.analog.com/static/imported-files/tutorials/MT-021.pdf
W. Kester. ADC Architectures III: Sigma-Delta ADC Basics. Analog Devices, MT-022 Tutorial. www.analog.com/static/imported-files/tutorials/MT-022.pdf
W. Kester. ADC Architectures IV: Sigma-Delta ADC Advanced Concepts and Applications. Analog Devices, MT-023 Tutorial. www.analog.com/static/imported-files/tutorials/MT-023.pdf

Предмет: Физика,


автор: romasmaha00

Очень срочно
Нужна формула для Δσ (дельта сигма)!!! ​

Ответы

Автор ответа: seahawks614

1

Ответ:

 = XnYn v XnCn–1 v YnCn–1, Cn = Xn ⊕ Yn ⊕ Cn–1 или же формула math>K=2^N</math

не знаю правильно написала или нет,но надеюсь,что верно(не помню т.к эту тему мы проходили в 9 классе,а нам ещё её и плохо объяснили)

---

romasmaha00:
Дуже дякую

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Геометрия,
автор: Aleks2475

Знайти довжину кола описаного навколо квадрата зі стороною 8см. а) 4√2π см; б) 8√2π см; в)10 см; г)8π см.

3 года назад

Предмет: Математика,
автор: Аноним

ПОМОГИТЕ пожалуйста СРОЧНО
​

3 года назад

Предмет: Другие предметы,
автор: NewSchoolBoy

Помогите срочно с 2 заданием дам 15 баллов

3 года назад

Предмет: Физика,
автор: bela200473

На каком участке дна сосуда гидростатического давления наименьшее?
A) CD
B) AB
C) BC

6 лет назад

Предмет: Алгебра,
автор: nanakiriya

Для того, чтобы сдать в срок книгу в библиотеку, ученик должен был прочитывать ежедневно 40 страниц, но он прочитывал в двое меньше, и потому ему пришлось отсрочить сдачу книги ещё на 10 дней. Сколько страниц в книге?

6 лет назад

Метод валентных связей

Метод валентных связей (локализованных электронных пар) предполагает, что каждая пара атомов в молекуле удерживается вместе при помощи одной или нескольких общих электронных пар.

Поэтому химическая связь представляется двухэлектронной и двухцентровой, т.е. локализована между двумя атомами. В структурных формулах соединений обозначается черточкой:

H-Cl, H-H, H-O-H

Рассмотрим в свете Метода ВС, такие особенности связи, как насыщаемость, направленность и поляризуемость.

Образование сигма-, пи- и дельта-связей

Валентность атома — определяется числом неспаренных (валентных) электронов, способных принять участие в образовании химической связи.

Валентность выражается небольшими целыми числами и равна числу ковалентных связей. Валентность элементов, проявляющуюся в ковалентных соединениях, часто называют ковалентностью.

Некоторые атомы имеют переменную валентность, например углерод в основном состоянии имеет 2 неспаренных электрона и будет двух валентен. При возбуждении атома, возможно распарить другие два спаренных электрона и тогда атом углерода станет четырех валентен:

Возбуждение атома до нового валентного состояния требует затраты энергии, которая компенсируется выделяемой при образовании связей энергией.

Взаимное перекрывание облаков, т.е. образование связи может происходить разными способами, ввиду их различной формы. Различают σ-, π- и δ-связи.

Как различить сигма-, пи- и дельта-связи?

Сигма – связи образуются при перекрывании облаков вдоль линии, проходящей через ядра атомов.

Пи – связи возникают при перекрывании облаков по обе стороны от линии, соединяющей ядра атомов.

Дельта – связи осуществляются при перекрывании всех четырех лопастей d – электронных облаков, расположенных в параллельных плоскостях.

σ– связь может возникнуть при перекрывании вдоль линии, соединяющей ядра атомов в следующих орбиталей:

s — s -, s — р-, р – р-, d — d -орбиталей , а также  d — s-, d — р– орбиталей. 

σ– связь обладает свойствами локализованной двухцентровой связи, каковой она и является.

π– связь может образовываться при перекрывании по обе стороны от линии, соединяющей ядра атомов следующих орбиталей:

р — р-, р — d-, d — d-, f — p-, f — d— и f — f— орбиталей.

Итак, s— элементы способны к образованию только σ– связи, 

р— элементы — σ– и π– связи, 

d— элементы — σ–, π– и δ‑ связи,  

f— элементы — σ– , π– , δ-связи.

При совместном образовании π– и σ- связей получается двойная связь.

Если же одновременно возникают две π–и σ- связь, то образуется тройная связь.

Количество возникших связей между атомами, называется кратностью связи.

Между двумя атомами может возникнуть только одна сигма-связь.

Направленность ковалентной связи

• При образовании связи с помощью  s — орбиталей, ввиду их сферической формы, не возникает какого-либо преимущественного направления в пространстве, для наиболее выгодного образования ковалентных связей.

• В случае же р – орбиталей, электронная плотность распределена неравномерно, поэтому возникает определенное направление, по которому образование ковалентной связи наиболее вероятно.

Гибридизация атомных орбиталей

Рассмотрим пример. Представим, что четыре атома водорода соединились с атомом углерода и образовалась молекула метана CH₄.

Рисунок показывает что происходит, но не объясняет, как ведут себя s-  и р— орбитали, при образовании таких соединений.

Хотя р— орбиталь имеет две части, развернутые друг относительно друга, но она может образовывать только одну связь. В итоге, можно предположить, что в молекуле метана один атом водорода присоединяется к 2s- орбитали углерода, остальные – к 2р— орбитали.

Тогда, каждый атом водорода будет находиться по отношению к другому под углом 90°, но это не так. Электроны отталкиваются друг от друга и расходятся на большее расстояние.

Что же на самом деле происходит?

Происходит гибридизация атомных орбиталей, в результате которой все орбитали объединяются, перестраиваются и образуют 4 эквивалентные гибридные орбитали, которые направлены к вершинам тетраэдра.

Гибридизация — это смешение различных атомных орбиталей (например, s и p) и образование одинаковых по форме и энергии гибридных орбиталей (например, sp, sp², sp³).

Типы гибридизации атомных орбиталей

sp³-гибридизация

В нашем примере, каждая из гибридных орбиталей содержит некий вклад 2s- орбитали и некоторые вклады  2р— орбиталей.

Поскольку 4 гибридные орбитали образованы одной 2s— и тремя 2р— орбиталями, то такой способ гибридизации называют sp³-гибридизацией.

Как видно из рисунка, конфигурация гибридных орбиталей позволяет четырем атомам вдорода образовать ковалентные связи с атомом углерода, при этом орбитали будут располагаться относительно друг друга под углом 109,5°.

Такой же тип гибридизации присутствует в таких молекулах, как , например, NH₃, H₂O.

На одной из sp³-гибридных орбиталей, в молекуле NH₃, находится неподеленная электронная пара, а три остальные орбитали используются для соединения с атомами водорода.

В молекуле H₂O неподеленными электронными парами заняты две гибридные орбитали атома кислорода, а две другие используются для связывания с атомами водорода.

sp²-гибридизация

Число гибридных орбиталей определяется числом одинарных связей, а также количеством неподеленных электронных пар в молекуле. Эти электроны находятся на гибридных орбиталях. Когда же происходит перекрывание негибридных орбиталей двух атомов, то образуется кратная связь. Например, в молекуле этилена связь реализуется следующим образом:

Плоское расположение трех связей вокруг каждого атома углерода дает основание предположить, что в данном случае имеет место sp²-гибридизация ( гибридные орбитали образованы одной 2s- и двумя 2р— орбиталями). При этом одна 2р— орбиталь остается неиспользованной (негибридной).

Орбитали будут располагаться относительно друг друга под углом 120°.

sp-гибридизация

Таким же образом, в молекуле ацетилена образуется тройная связь. В данном случае происходит sp-гибридизация атомов, т.е. гибридные орбитали образованы одной 2s- и одной 2р— орбиталями, а другие две 2р— орбитали являются негибридными.

Орбитали располагаются относительно друг друга под углом 180°

Ниже в таблице приведены примеры гибридных орбиталей, их геометрическое расположение .

Набор атомных орбиталей	Набор гибридных орбиталей	Геометрическое расположение гибридных орбиталей	Примеры
s,p	sp	Линейное (угол 180°)	Be(CH3)2, HgCl2 MgBr2, СаН2, ВаF2, C2H2
s,p,p	sp2	Плоское тригональное (угол 120°)	BF3,GaCl3, InBr3,TeI3, C2H4
s,p,p,p	sp3	Тетраэдрическое (угол 109,5°)	CH4, AsCl4—, TiCl4, SiCl4, GeF4
s,p,p,d	sp2d	Плоскоквадратнoe (угол 90°)	Ni(CO)4, [PdCl4]2—
s,p,p,p,d	sp3d	Тригонально-бипирамдальное (углы 120° и 90°)	PF5, PCl5, AsF5
s,p,p,p,d,d	sp3d2	Октаэдрическое (угол 90°)	SF6, Fe(CN)63-, CoF63-

Гибридные орбитали в пространстве располагаются различным образом:

Метод преобразования сигналов между цифровым и аналоговым

Дельта-сигма (ΔΣ; или сигма-дельта, ΣΔ) модуляция – это метод кодирования аналоговых сигналов в цифровых сигналов, как в аналого-цифровом преобразователе (АЦП). Он также используется для преобразования низкочастотных цифровых сигналов с большим числом битов в цифровые сигналы с более низким числом битов и более высокой частотой как часть процесса преобразования цифровых сигналов в аналоговые как часть цифро-аналогового преобразования. преобразователь (ЦАП).

В обычном АЦП аналоговый сигнал дискретизируется с частотой дискретизации и затем квантуется в многоуровневом квантователе в цифровой сигнал. Этот процесс вносит шум ошибки квантования. Первый шаг в дельта-сигма-модуляции – это дельта-модуляция. В дельта-модуляции кодируется изменение сигнала (его дельта), а не абсолютное значение. Результатом является поток импульсов, а не поток чисел, как в случае с импульсной кодовой модуляцией (ИКМ). При дельта-сигма-модуляции точность модуляции повышается путем пропускания цифрового выхода через 1-битный ЦАП и добавления (сигма) результирующего аналогового сигнала к входному сигналу (сигнал до дельта-модуляции), тем самым уменьшая ошибку, вносимую дельта-модуляция.

И АЦП, и ЦАП могут использовать дельта-сигма модуляцию. Дельта-сигма АЦП сначала кодирует аналоговый сигнал, используя высокочастотную дельта-сигма модуляцию, а затем применяет цифровой фильтр для формирования цифрового выходного сигнала с более высоким разрешением, но с более низкой частотой дискретизации. Дельта-сигма ЦАП кодирует цифровой входной сигнал высокого разрешения в сигнал с более низким разрешением, но с более высокой частотой дискретизации, который преобразуется в напряжения, а затем сглаживается аналоговым фильтром. В обоих случаях временное использование сигнала с более низким разрешением упрощает конструкцию схемы и повышает эффективность.

В первую очередь из-за своей экономической эффективности и меньшей сложности схемы, этот метод нашел все более широкое применение в современных электронных компонентах, таких как ЦАП, АЦП, синтезаторы частоты, импульсные источники питания. и контроллеры двигателей. Грубо-квантованный выход дельта-сигма-модулятора иногда используется непосредственно при обработке сигналов или как представление для хранения сигнала. Например, Super Audio CD (SACD) хранит выходной сигнал дельта-сигма-модулятора непосредственно на диске.

Содержание

• 1 Мотивация
• 2 Аналогово-цифровое преобразование
  • 2.1 Описание
  • 2.2 Анализ
  • 2.3 Практическая реализация
• 3 Улучшение разрешения и шума
  • 3.1 Примечания
• 4 Цифро-аналоговое преобразование
  • 4.1 Структуры прореживания
  • 4.2 Пример прореживания
• 5 Варианты
  • 5.1 Модулятор второго и более высокого порядка
  • 5.2 Трехуровневый квантователь и выше
• 6 Взаимосвязь до дельта-модуляции
• 7 Формулы теории квантования
• 8 Передискретизация
• 9 Именование
• 10 См. также
• 11 Ссылки
• 12 Внешние ссылки

Мотивация

Дельта-сигма Модуляция преобразует аналоговый сигнал напряжения в частоту импульсов или плотность импульсов, которую можно понимать как модуляция плотности импульсов (PDM). Последовательность положительных и отрицательных импульсов, представляющих биты с известной фиксированной скоростью, очень легко сгенерировать, передать и точно восстановить в приемнике, при условии только того, что можно восстановить синхронизацию и знак импульсов. Учитывая такую ​​последовательность импульсов от дельта-сигма модулятора, исходная форма волны может быть восстановлена ​​с достаточной точностью. Напротив, без преобразования в поток импульсов, а просто передачи аналогового сигнала напрямую, весь шум в системе будет добавлен к аналоговому сигналу, что снизит его качество. Использование PDM в качестве представления сигнала является альтернативой импульсно-кодовой модуляции (PCM), дискретизации и квантованию в многобитовый код со скоростью Найквиста.

Аналого-цифровое преобразование

Описание

Дельта-сигма или другой модулятор плотности импульсов или частотно-импульсный модулятор генерирует поток импульсов, в котором частота f импульсов в потоке пропорциональна аналоговому входному напряжению, v, так что f = k · v, где k – константа для конкретной реализации. Контур обратной связи отслеживает интеграл от v, и когда этот интеграл увеличивается на Δ, на что указывает интегральная форма сигнала, пересекающая пороговое значение, T, она вычитает Δ из интеграла от v, так что пилообразные формы комбинированной формы сигнала находятся между T и T – Δ.. На каждом шаге к потоку импульсов добавляется импульс.

Счетчик суммирует количество импульсов, которые происходят в заранее определенный период, P { displaystyle P}, так что сумма, Σ { displaystyle Sigma}, это п ⋅ е = к ⋅ п ⋅ v { displaystyle P cdot f = k cdot P cdot v}. В данной реализации k ⋅ P { displaystyle k cdot P}выбирается так, чтобы цифровое отображение счетчика Σ { displaystyle Sigma}, представляет собой отображение v { displaystyle v}с предварительно определенным коэффициентом масштабирования. Поскольку P { displaystyle P}может принимать любое расчетное значение, его можно сделать достаточно большим, чтобы обеспечить любое желаемое разрешение или точность.

Анализ

Рисунок 1: Блок-схема и формы сигналов для несинхронизированного преобразователя напряжения в частоту (левая часть) с подсчетом частоты (правая часть) составляют законченный аналого-цифровой преобразователь. Ограничение импульсов, возникающих через регулярные интервалы тактовых импульсов, преобразовало бы эту систему в сигма-дельта АЦП. Рисунок 1a: Эффект тактирующих импульсов

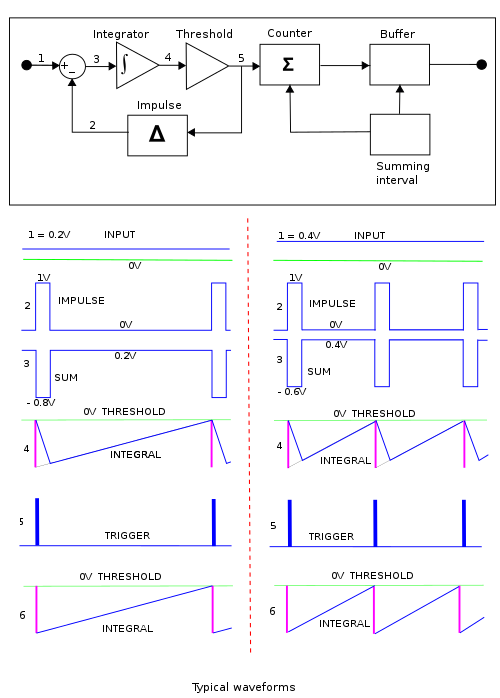
В целях введения рисунок 1 иллюстрирует концепцию отношения напряжения к напряжению. преобразование частоты в несинхронизированной форме, напоминающее дельта-сигма модуляцию, и называется асинхронной модуляцией, асинхронной дельта-сигма модуляцией или автономными модуляторами.

Ниже показаны формы сигналов в точках, обозначенных цифрами от 1 до 5 для входа 0,2 В в левом столбце и 0,4 В в правом столбце. Поток дельта-импульсов, генерируемых при каждом пересечении порога, показан в (2), а разница между (1) и (2) показана в (3). Эта разница интегрирована для получения формы сигнала (4). Детектор порога генерирует импульс (5), который начинается, когда форма сигнала (4) пересекает порог, и сохраняется до тех пор, пока форма сигнала (4) не упадет ниже порога. Порог (5) запускает генератор импульсов, чтобы произвести импульс фиксированной силы.

Интеграл (4) в правом столбце пересекает порог вдвое быстрее, чем в левом столбце. Таким образом частота импульсов увеличивается вдвое. Следовательно, счетчик увеличивается в два раза быстрее, чем справа; это удвоение частоты следования импульсов соответствует удвоению входного напряжения.

Построению форм сигналов, показанных в (4), помогают концепции, связанные с дельта-функцией Дирака в том смысле, что, по определению, все импульсы одинаковой силы производят одинаковый шаг при объединении. Затем (4) строится с использованием промежуточного шага (6), гипотетическая форма волны не в схеме, а в которой каждый интегрированный импульс идеальной дельта-функции интегрирован в шаг. Эффект конечной длительности фактического импульса построен в (4) путем проведения линии от основания импульсной ступени при нулевом напряжении до пересечения с линией затухания из (6) при полной длительности импульса.

В схеме за пределами цикла интервал суммирования является заранее определенным фиксированным временем, и по его истечении счет сохраняется, а буфер и счетчик сбрасываются. Затем буфер представляет последовательность цифровых значений, соответствующих квантованиям уровней аналогового сигнала в течение интервалов суммирования. Использование интервала суммирования – это способ (не обязательно идеальный способ) квантовать асинхронный поток импульсов в код; он будет иметь меньше ошибок квантования, если начало интервала синхронизировано с импульсом.

Преобразователи дельта-сигма дополнительно ограничивают работу генератора импульсов, так что начало импульса задерживается до следующего появления соответствующей границы тактового импульса. Эффект этой задержки показан на рисунке 1а для последовательности импульсов, которые возникают с номинальными интервалами 2,5 такта.

Практическая реализация

Рисунок 1b: принципиальная схема Рисунок 1c: Формы сигналов АЦП

Принципиальная схема реализации дельта-сигма модулятора показана на рисунке 1b, а соответствующие формы сигналов – на рисунке 1c. Формы сигналов, показанные на рисунке 1c, необычайно сложны, поскольку они предназначены для иллюстрации поведения контура в экстремальных условиях: V в насыщается при полном масштабе 1,0 В и насыщается при нуле. Также указано промежуточное состояние, V в при 0,4 В, где оно очень похоже на операцию, показанную на рисунке 1.

С верхней части рисунка 1c, формы сигналов, помечены, как они есть на принципиальной схеме:

• Часы
• (a) V в – это показано как изменяющееся от 0,4 В вначале до 1,0 В, а затем до нуля вольт, чтобы показать влияние на контур обратной связи.
• (b) Форма импульса, подаваемого на интегратор. Управление с помощью триггер выход (е) ниже.
• (с) Ток в конденсаторе, я с, является линейной суммой импульсов опорного напряжения разделенное на R и V в, деленное на R. Чтобы показать эту сумму как напряжение, строится произведение R × I c. Входной импеданс усилителя считается настолько высоким, что ток, потребляемый входом, не учитывается. Конденсатор подключается между отрицательной входной клеммой усилителя и его выходной клеммой. При таком подключении он обеспечивает отрицательную обратную связь вокруг усилителя. Изменение входного напряжения равно изменению выходного напряжения, деленному на коэффициент усиления усилителя. При очень высоком усилении усилителя изменением входного напряжения можно пренебречь, и поэтому входное напряжение поддерживается близким к напряжению на положительной входной клемме, которое в этом случае поддерживается на уровне 0 В. Поскольку напряжение на входной клемме равно 0 В, напряжение на R равно просто V в, так что ток в конденсаторе равен входному напряжению, деленному на сопротивление R.
• (d) Интеграл с отрицанием I c. Это отрицание является стандартным для интегратора операционного усилителя и возникает потому, что ток в конденсаторе на входе усилителя равен току на выходе конденсатора на выходе усилителя, а напряжение – это интеграл тока, деленный на емкость C.
• (e) Выход компаратора. Компаратор представляет собой усилитель с очень высоким коэффициентом усиления с его плюсовым входным выводом, подключенным для ссылки на 0,0 В. Когда отрицательный входной вывод становится отрицательным по сравнению с положительным выводом усилителя, выход насыщается положительным и, наоборот, отрицательным насыщением для положительного входа. Таким образом, выходные насыщается положительным всякий раз, когда интеграл (г) опускается ниже исходного уровня 0 В, а на выходе остается там до (г) идет положительным по отношению к опорному 0 V.
• (е) Импульсный таймер триггер, запускаемый положительным фронтом. Входная информация, подаваемая в D, передается в Q при появлении положительного фронта тактового импульса. Таким образом, когда выход компаратора (e) положительный, Q становится положительным или остается положительным на следующем положительном фронте тактового сигнала. Точно так же, когда (e) отрицательно, Q становится отрицательным на следующем положительном фронте тактового сигнала. Q управляет электронным переключателем, чтобы генерировать импульс тока (b) в интеграторе. Исследование формы сигнала (e) в течение проиллюстрированного начального периода, когда V в составляет 0,4 В, показывает (e) пересечение порога задолго до положительного фронта тактового импульса, так что имеется значительная задержка перед импульс начинается. После начала импульса происходит дальнейшая задержка, пока (d) поднимается обратно за порог. В это время на выходе компаратора (e) остается высокий уровень, но он становится низким перед следующим фронтом триггера, в этот момент импульсный таймер переходит в низкий уровень, чтобы следовать за компаратором. Таким образом, часы частично определяют продолжительность импульса. Для следующего импульса порог пересекает непосредственно перед фронтом триггера, поэтому компаратор только кратковременно дает положительный результат. V в (a) затем переходит на полную шкалу, + V ref, незадолго до окончания следующего импульса. В течение оставшейся части этого импульса ток конденсатора (c) стремится к нулю и, следовательно, крутизна интегратора на короткое время стремится к нулю. После этого импульса протекает полномасштабный положительный ток (c), и интегратор опускается с максимальной скоростью и, таким образом, пересекает порог задолго до следующего фронта запуска. На этом фронте начинается импульс, и ток V в теперь согласовывается с эталонным током, так что чистый ток конденсатора (c) равен нулю. Теперь интеграция имеет нулевой наклон и остается на отрицательном значении, которое было в начале импульса. Это приводит к тому, что импульсный ток остается включенным, потому что Q остается положительным, потому что компаратор остается положительным на каждом фронте запуска. Это согласуется с непрерывными, стыковочными импульсами, которые представляют полномасштабный входной сигнал. Затем V в (a) переходит в ноль, что приводит к тому, что текущая сумма (c) становится полностью отрицательной, а интеграл нарастает. Вскоре после этого он пересекает порог, и за ним, в свою очередь, следует Q, тем самым отключая импульсный ток. Конденсаторный ток (c) теперь равен нулю, поэтому интегральный наклон равен нулю, оставаясь постоянным на значении, которое он получил в конце импульса.
• (g) Счетный поток генерируется стробированием инвертированных часов с Q для создания этой формы сигнала. После этого интервал суммирования, сигма-счет и буферизованный счет производятся с использованием соответствующих счетчиков и регистров.

Улучшения разрешения и шума

Изучение рисунка 1c (g) показывает, что в потоке счетчика есть нулевые импульсы, когда входное напряжение равно нулю. Это условие может привести к тому, что высокочастотные компоненты сложного сигнала не будут разрешены. Этот эффект известен как интермодуляционные искажения (IMD). Одна из ловушек применения линейного анализа к нелинейной системе заключается в том, что IMD, поскольку это может быть следствием нелинейности, не присутствует в анализе. Чисто в иллюстративных целях способ смягчить это – добавить постоянное смещение 0,5 В к входному напряжению, чтобы оно теперь могло колебаться на +/- 0,5 В относительно смещения. Теперь это имеет нулевые импульсы в счетном потоке, когда входной сигнал составляет -0,5 В. Затем мы должны ограничить размах входного сигнала до +/- 0,4 В, скажем, так, чтобы минимальная частота счетного потока была больше нуля. Мы можем выбрать тактовую частоту так, чтобы минимальная частота счетного потока при -0,4 В была намного больше, чем частота Найквиста, так что разрешается даже самый высокий компонент входной частоты. Мы можем увеличить тактовую частоту еще выше до тех пор, пока фильтр нижних частот в достаточной степени не устранит пульсации, полностью восстанавливая входной сигнал. В этом иллюстративном обсуждении отфильтрованный сигнал также восстановит смещение, которое может быть устранено аналоговым сумматором, при этом сохраняя постоянную составляющую входного сигнала.

Примечания

Согласно Вули, основополагающая статья, объединяющая обратную связь с передискретизацией для достижения дельта-модуляции, была написана Ф. де Ягером в 1952 году.

Была разработана конфигурация дельта-сигма. Автор: Inose et al. в 1962 году для решения проблем точной передачи аналоговых сигналов. В этом приложении был передан поток импульсов, а исходный аналоговый сигнал восстановлен с помощью фильтра нижних частот после преобразования полученных импульсов. Этот фильтр нижних частот выполнял функцию суммирования, связанную с Σ. Они представили высоко математический подход к ошибкам передачи, применимый к потоку импульсов, но эти ошибки теряются в процессе накопления, связанном с Σ.

Для аналогового к применению цифрового преобразования каждому импульс в потоке счета является образцом среднего значения входного напряжения равного опорного напряжения разделить интервал между импульсами, Ts. Это потому, что это интегрирование формы входного сигнала по интервалу ts. Частотная область анализ сложной формы волны в этом интервале ts будет представлять ее как сумму константы, основной гармоники и гармоник, каждая из которых имеет точное целое число периодов в течение ts. Интеграл синусоидальной волны за один или несколько полных циклов равен нулю. Следовательно, интеграл входящей формы волны за интервал ts сводится к среднему значению за интервал. Подсчет N, накопленный в течение интервала суммирования, представляет N выборок среднего, а N, разделенное на счет, определяющий интервал суммирования, таким образом, является средним из средних и поэтому подвержен небольшому отклонению.

Цифроаналоговое преобразование

Как правило, ЦАП преобразует цифровое число N, представляющее некоторое аналоговое значение, в это аналоговое значение напряжения. Для преобразования цифровое число сначала загружается в счетчик. Затем счетчик ведет обратный отсчет до нуля с последовательностью импульсов, равным N. Каждому импульсу строки дается известный интеграл δ. Затем струна интегрируется, чтобы получить N.δ, сумму импульсов. Это необходимое аналоговое напряжение.

В некоторых приложениях, где аналоговый сигнал представлен серией цифровых чисел, требующих преобразования в частотно-модулированный поток, может быть достаточно взять поток импульсов (двух или трехуровневый), полученный в результате преобразования ЦАП. каждого числа N по очереди и применить этот поток через фильтр нижних частот непосредственно к выходу. Выходной сигнал до фильтрации будет грубо модулированным по частоте потоком с пакетами импульсов, пропорциональными по длине и количеству аналогу N, разделенных пустыми интервалами между пакетами.

Чтобы удалить пустые интервалы и улучшить шумовые характеристики, полное преобразование в аналоговое напряжение каждого последующего N с помощью ЦАП, описанного выше, может быть проведено в схеме выборки и удержания, а затем передано к дельта-сигма-преобразователю для создания потока непрерывных пакетов, частота каждого из которых пропорциональна его генерации N.

Структуры децимации

Концептуально простейшая структура децимации – это счетчик, который сбрасывается на ноль в начале каждого периода интегрирования, затем считывается в конце периода интегрирования.

Структура многокаскадного формирования шума (MASH) имеет свойство формирования шума и обычно используется в цифровых звуковых синтезаторах и синтезаторах частот с дробным N. Он состоит из двух или более каскадных переполненных аккумуляторов, каждый из которых эквивалентен сигма-дельта-модуляторам первого порядка. Выходы переноса объединяются посредством суммирования и задержек для получения двоичного выхода, ширина которого зависит от количества каскадов (порядка) MASH. Помимо функции формирования шума, у него есть еще два привлекательных свойства:

• простота реализации на аппаратном уровне; требуются только обычные цифровые блоки, такие как аккумуляторы, сумматоры и D-триггеры
• безоговорочно стабильные (нет контуров обратной связи снаружи аккумуляторы)

Очень популярной децимационной структурой является фильтр sinc. Для модуляторов второго порядка фильтр sinc3 близок к оптимальному.

Пример децимации

Давайте, например, имеем прореживающий фильтр 8: 1 и 1-битовый поток битов; если у нас есть входной поток типа 10010110, подсчитав количество единиц, мы получим 4. Тогда результат прореживания будет 4/8 = 0,5. Затем мы можем представить его 3-битным числом 100 (двоичным), что означает половину максимально возможного числа. Другими словами,

• частота дискретизации уменьшается в восемь раз.
• последовательная (1-битная) входная шина становится параллельной (3-битной) выходной шиной.

После применения прореживания и если передаются n-битовые коды, сигнал становится импульсной кодовой модуляцией. Прореживание сильно связано с дельта-сигма-модуляцией, но необходимо проводить различие.

Варианты

Есть много видов АЦП, которые используют эту дельта-сигма структуру. Приведенный выше анализ фокусируется на простейшем двухуровневом сигма-дельта АЦП 1-го порядка с равномерным прореживанием. Многие АЦП используют сигма-дельта-структуру sinc3 второго порядка с 5 уровнями. Во многом из того, что далее следует, используются загадочные сокращения с использованием символов, представляющих операционные функции с анализом, представленным в терминах преобразований Лапласа и т. Д. Это lingua franca индустрии передачи данных, и он не распространяется на широкую публику. Если требуется более полная документация по конкретному методу, не ищите ничего, кроме патентов. (Патентные эксперты обычно требуют полного раскрытия информации.) Прекрасная история – это «Эволюция аналого-цифровых преобразователей с передискретизацией» Брюса А. Вули, в которой есть много ссылок на соответствующие патенты.

Модулятор второго и высшего порядка

Рисунок 4: Блок-схема ΔΣ-модулятора второго порядка

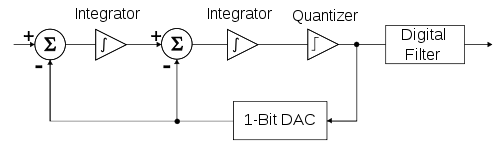
Количество интеграторов и, следовательно, количество контуров обратной связи указывает порядок модулятор ΔΣ; ΔΣ-модулятор второго порядка показан на рисунке 4. Модуляторы первого порядка безусловно стабильны, но для модуляторов более высокого порядка необходимо проводить анализ устойчивости.

Трехуровневый и более высокий квантователь

Модулятор также можно классифицировать по количеству битов, которые он имеет на выходе, что строго зависит от выхода квантователя. Квантователь может быть реализован с помощью N-уровневого компаратора, таким образом, модулятор имеет log 2 N-битный выход. У простого компаратора есть 2 уровня, как и у 1-битного квантователя; трехуровневый квантователь называется «1,5-битным квантователем»; 4-уровневый квантователь – это 2-битный квантователь; 5-уровневый квантователь называется «2,5-битным» квантователем.

Связь с дельта-модуляцией

Рисунок 2: Получение дельта-сигма из дельта-модуляции Рисунок 3: Пример дельта-сигма модуляция 100 отсчетов одного периода синусоидальной волны. 1-битные выборки (например, выход компаратора), наложенные синусоидальной волной. Высокий логический уровень (например, V CC) выборок представлен синим, а низкий логический уровень (например, -V CC) представлен белым.

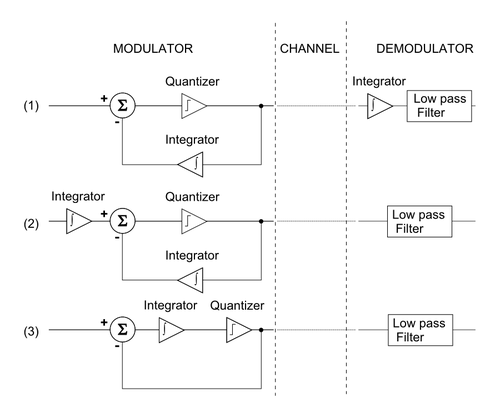
Дельта-сигма модуляция вдохновленные дельта-модуляцией, как показано на рисунке 2. Если квантование было однородным (например, если оно было линейным ), следующее было бы достаточным выводом эквивалентности:

1. Начните с блок-схемы дельта-модулятора / демодулятора.
2. Свойство линейности интегрирования, ∫ a + ∫ b = ∫ (a + b) { displaystyle scriptstyle int a , + , int b , = , int (a , + , b)}, позволяет перемещать интегратор, который восстанавливает аналоговый сигнал в секции демодулятора перед дельта-модулятором.
3. Опять же, свойство линейности интегрирования позволяет объединить два интегратора и получить блок-схему дельта-сигма модулятора / демодулятора.

Поскольку квантователь неоднороден, дельта-сигма вызвана дельта-модуляцией, но два работают по-разному.

Из первой блок-схемы на рисунке 2 интегратор в тракте обратной связи может быть удален, если обратная связь берется непосредственно со входа фильтра нижних частот. Следовательно, для дельта-модуляции входного сигнала u фильтр нижних частот видит сигнал

y DM = Quantize ⁡ (u – y DM). { displaystyle y _ { text {DM}} = int operatorname {Quantize} left (u-y _ { text {DM}} right). ,}

Однако сигма-дельта модуляция тот же входной сигнал помещается в фильтр нижних частот

y SDM = Quantize ⁡ (∫ (u – y SDM)). { displaystyle y _ { text {SDM}} = operatorname {Quantize} left ( int left (u-y _ { text {SDM}} right) right). ,}

В другом слова, дельта-сигма и дельта-модуляция меняют местами интегратор и квантователь. Чистый эффект представляет собой более простую реализацию, которая имеет дополнительное преимущество, заключающееся в формировании шума квантования вдали от сигналов, представляющих интерес (т. Е. Представляющие интерес сигналы фильтруются по нижним частотам, а шум квантования фильтруется по верхним частотам). Этот эффект становится более драматичным с увеличением передискретизации, что позволяет в некоторой степени программировать шум квантования. С другой стороны, дельта-модуляция одинаково формирует и шум, и сигнал.

Кроме того, квантователь (например, компаратор ), используемый в дельта-модуляции, имеет небольшой выходной сигнал, представляющий небольшой шаг вверх и вниз квантованного приближения входа, в то время как квантователь используется в дельта-сигма должен принимать значения за пределами диапазона входного сигнала, как показано на рисунке 3.

В общем, дельта-сигма имеет некоторые преимущества по сравнению с дельта-модуляцией:

• Структура упрощена как
  • необходим только один интегратор,
  • демодулятор может быть простым линейным фильтром (например, RC- или LC-фильтром) для восстановления сигнала, а
  • квантователь (например, компаратор) может иметь полный -масштабирование выходов
• Квантованное значение является интегралом разностного сигнала, что делает его менее чувствительным к скорости изменения сигнала.

Формулы теории квантования

Когда сигнал квантован, Результирующий сигнал имеет примерно статистику второго порядка сигнала с добавленным независимым белым шумом. Предполагая, что значение сигнала находится в диапазоне одного шага квантованного значения с равным распределением, среднеквадратичное значение этого шума квантования равно

erms = 1 Δ ∫ – Δ / 2 + Δ / 2 e 2 de Знак равно Δ 2 3 { Displaystyle е _ { mathrm {rms}} , = { sqrt {, { frac {1} { Delta}} int _ {- Delta / 2} ^ {+ Delta / 2} e ^ {2} , de ,}} = , { frac { Delta} {2 { sqrt {3}}}}}

На самом деле шум квантования, конечно,, не зависит от сигнала, и эта зависимость приводит к предельным циклам и является источником холостых тонов и структурного шума в сигма-дельта преобразователях.

Шум квантования можно уменьшить, увеличив коэффициент передискретизации (OSR), определенный как

OSR = fs 2 f 0 { displaystyle mathrm {OSR} , = , { frac {f_ {s }} {2f_ {0}}}}

где fs { displaystyle f _ { mathrm {s}}}– частота дискретизации, а 2 f 0 { displaystyle 2f_ {0}}равно коэффициент Найквиста.

RMS напряжение шума в пределах интересующего диапазона (f 0 { displaystyle f_ {0}}) можно выразить через OSR

n 0 = erms OSR { displaystyle mathrm {n_ {0}} , = , { frac {e_ {rms}} { sqrt { OSR}}}}

Передискретизация

Рис. 5: Кривые формирования шума и спектр шума в модуляторах ΔΣ первого, второго и третьего порядка. Полоса, представляющая интерес для преобразования, обозначена зеленым.

ΔΣ-модуляция – это метод передискретизации для уменьшения шума в интересующей полосе (зеленый на рисунке 5), который позволяет избежать использования высоких частот. -точные аналоговые схемы для сглаживающего фильтра. Общий шум квантования одинаков как в преобразователе Найквиста (желтый), так и в преобразователе передискретизации (синий), но он распределен по другому спектру. В преобразователях ΔΣ шум дополнительно снижается на низких частотах, что является полосой, в которой находится интересующий сигнал, и увеличивается на более высоких частотах, где он может быть отфильтрован. Этот метод известен как формирование шума.

Для дельта-сигма-модулятора первого порядка шум формируется фильтром с передаточной функцией H n (z) = [1 – z]. Предполагая, что частота дискретизации f s велика по сравнению с частотой сигнала, представляющего интерес, f 0, шум квантования в полосе частот полезного сигнала может быть аппроксимирован как:

n 0 знак равно e rms π 3 (2 f 0 τ) 3 2 { displaystyle mathrm {n_ {0}} = e _ { text {rms}} { frac { pi} { sqrt {3}}} , (2f_ {0} tau) ^ { frac {3} {2}}}.

Аналогично для дельта-сигма-модулятора второго порядка шум формируется фильтром с передаточной функцией H n (z) = [1 – z]. Шум внутриполосного квантования можно приблизительно рассчитать следующим образом:

n 0 = e rms π 2 5 (2 f 0 τ) 5 2 { displaystyle mathrm {n_ {0}} = e _ { text {rms}} { frac { pi ^ {2}} { sqrt {5}}} , left (2f_ {0} tau right) ^ { frac {5} {2}}}.

В целом, для модулятора ΔΣ N-го порядка дисперсия шума внутриполосного квантования равна:

n 0 = e rms π N 2 N + 1 (2 f 0 τ) 2 N + 1 2 { displaystyle mathrm {n_ {0}} = e _ { text {rms}} { frac { pi ^ {N}} { sqrt {2N + 1}}} , left (2f_ {0} tau right) ^ { frac {2N + 1} {2}}}.

Когда частота дискретизации удваивается, отношение сигнал-шум квантования улучшается на 6N + 3 дБ для модулятора ΔΣ N-порядка. Чем выше коэффициент передискретизации, тем выше отношение сигнал / шум и выше разрешение в битах.

Другим ключевым аспектом передискретизации является компромисс между скоростью и разрешением. Децимационный фильтр, установленный после модулятора, не только фильтрует весь дискретизированный сигнал в интересующей полосе частот (устраняя шум на более высоких частотах), но также снижает частоту сигнала, увеличивая его разрешение. Это достигается своего рода усреднением битового потока с более высокой скоростью передачи данных.

Именование

Впервые этот метод был представлен в начале 1960-х профессором Ясухико Ясуда, когда он был студентом Токийского университета. Название дельта-сигма происходит непосредственно от присутствия дельта-модулятора и интегратора, как впервые было введено Inose et al. в своей патентной заявке. То есть название происходит от интегрирования или суммирования разностей, которые в математике представляют собой операции, обычно связанные с греческими буквами сигма и дельта соответственно. Часто используются оба названия: сигма-дельта и дельта-сигма.

См. Также

Справочная информация

Внешние ссылки

Введение

Начнем с краткого исторического обзора. В 1939 году Джоном Ривзом из лаборатории Александра Г. Бэлла был изобретен способ преобразования и передачи аналоговых телефонных сигналов в виде дискретных импульсов, названный впоследствии импульсно-кодовой модуляцией (ИКМ). Позднее появилась идея передавать не абсолютное значение сигнала в каждый момент времени, а лишь его изменение относительно предыдущего значения (дифференциальная ИКМ — ДИКМ). Но ДИКМ была все еще многобитной системой. Следующим шагом по направлению к дельта-сигма модуляции стала разработка принципов дельта-модуляции, где изменение сигнала передается всего лишь 1 битом информации. С него и имеет смысл начать.

Дельта-модуляция

Рассмотрим блок-схему дельта-модулятора, изображенную на рис. 1. Принцип его действия можно описать следующим образом: на основании некоторого набора предыдущих выборок сигнала делается предположение о последующей. Затем предполагаемое значение сравнивается с фактическим и выносится решение о знаке их различия, что и является выходным сигналом.

Рис. 1. Блок-схема дельта-модулятора: ФНЧ — фильтр низких частот

Напряжение входного сигнала подается на вычитатель, где из него вычитается аппроксимирующее напряжение, созданное на основании предыдущих значений сигнала. Далее разность поступает на стробируе-мый компаратор, где сравнивается с нулевым уровнем. Таким образом, логическая единица на выходе компаратора означает, что эта разность положительна или что входной сигнал больше предполагаемого (аппроксимирующего), а логический ноль, соответственно, означает, что входной сигнал меньше аппроксимирующего. Далее последовательность нулей и единиц поступает на однобитный местный ЦАП, который обычно представляет из себя преобразователь уровней одно-полярного напряжения (лог. «0» и лог. «1») в двухполярное (±ипит). С выхода ЦАП сигнал поступает на вход интегратора, на выходе которого формируется аппроксимирующее напряжение, с заданной точностью повторяющее входное. Точность определяется частотой стробирования компаратора и шагом приращения напряжения в интеграторе. Схема приемной части состоит из однобитного ЦАП, интегратора и ФНЧ.

Эта схема имеет ряд существенных недостатков, которые препятствовали ее применению в аппаратуре аналогово-цифрового преобразования. Попытки ее модернизации привели к переходу от дельта-модуляции к дельта-сигма модуляции.

Дельта-сигма модуляция

Дельта-сигма модуляция обладает всеми достоинствами дельта-модуляции и в то же время лишена многих ее недостатков. Для того чтобы разобраться в ее структуре и понять, как был выполнен переход от схемы дельта-модулятора к схеме дельта-сигма модулятора (ДСМ), можно рассуждать следующим образом. Как известно, дельта-модулятор пригоден для работы только с хорошо коррелированными сигналами, поэтому для повышения кор-релированности входного сигнала его можно пропустить через интегратор, а на приемной стороне выходной преобразованный сигнал пропустить, соответственно, через дифференциатор (рис. 2).

Рис. 2. Переход от дельта-модулятора к дельта-сигма модулятору

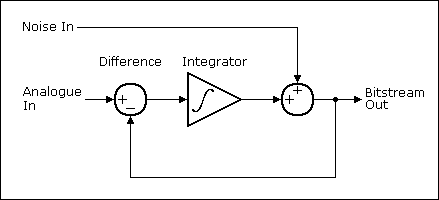
Поскольку разность интегралов равна интегралу разности, то два интегратора на входах вычитателя можно заменить одним на его выходе. Что касается дифференциатора на приемной стороне, то он вместе с приемным интегратором может быть исключен. Таким образом, схема ДСМ, изображенная на рис. 3, отличается от дельта-модулятора положением интегратора на передающей стороне и его отсутствием на приемной. Такое незначительное изменение в схеме значительно улучшило ее характеристики и, в частности, позволило достичь отношения сигнал/шум -120 дБ.

Рис. 3. Схема дельта-сигма модулятора

Рассмотрим работу схемы ДСМ. Когда образуется высококоррелированный сигнал, то коррелированными оказываются не только его отсчеты, но и ошибки при каждом квантовании. Следовательно, их легко предсказать и вычесть из сигнала, отправляемого на устройство квантования, прежде чем произойдет квантование. Хорошей оценкой текущей ошибки в таком случае выступает предшествующая ошибка. Предшествующая ошибка, образованная как разность между входом и выходом устройства квантования, помещается в схему задержки (триггер). Таким образом, в контуре обратной связи циркулирует сигнал ошибки.

Выходной сигнал ДСМ представляет собой однобитный поток импульсов. Рассмотрим его в терминах теории вероятности. Так, вероятность появления в потоке логической единицы P(1) и вероятность появления логического нуля P(0) связаны следующим выражением: P(0)+P(1) = 1. Более того, если на вход модулятора подается сигнал ж (ограниченный в динамическом диапазоне 0-1), то вероятность P(1) = х, а P(0) = (1-х). Иными словами, чем плотнее представлены импульсы определенной полярности в потоке, тем выше уровень сигнала в этот момент. Нулевой уровень сигнала кодируется одинаковой плотностью положительных и отрицательных импульсов. Импульсные последовательности при кодировании синусоидального напряжения представлены на рис. 4. Видно, что плотность положительных и отрицательных импульсов одинакова в точках, близких к 0, плотность отрицательных импульсов максимальна в точке -1, и плотность положительных импульсов максимальна в точке +1.

Рис. 4. Осциллограмма выходного сигнала дельта-сигма модулятора

Такие особенности позволяют кодировать в формате дельта-сигма модуляции сигналы с частотой от 0 до 100 кГц. В частности, прямоугольное аналоговое напряжение и уровни постоянного напряжения, последнее актуально при применении дельта-сигма модуляции в датчиках медленно меняющихся сигналов. Демонстрационные материалы из документа о формате дельта-сигма модуляции Square-wave reproduction, опублико

ванного на сайте фирмы Philips, результаты которых изображены на рис. 5, подтверждают вышесказанное. Здесь показано, как прямоугольное напряжение частотой 10 кГц проходит через цепь кодер-декодер в форматах ИКМ (16 бит, 44 кГц), ИКМ (24 бита, 96 кГц) и в формате дельта-сигма модуляции (2,8 МГц). Причем в ИКМ-формате на выходе получается сигнал синусоидальной формы, в то время как в формате дельта-сигма модуляции сигнал воспроизводится ближе всего к исходному.

Рис. 5. Результаты тестирования

Шумы

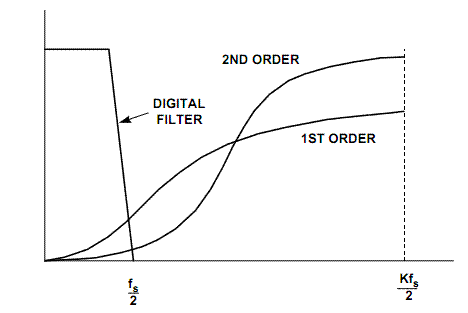
Исследование шумов в ДСМ заслуживает отдельного рассмотрения. Ведь методы достижения отношения сигнал/шум -120 дБ при разрядности 1 бит представляют известный интерес. В 1954 году С. Катлер из той же лаборатории Александра Бэлла предложил концепцию передискретизации и формирования спектра шума. Как известно, каждый дополнительный бит при преобразовании аналогового сигнала в цифровой добавляет 6 дБ к отношению сигнал/шум (рис. 6а). Одним из основополагающих принципов дельта-модуляции является превышение частоты Котельникова в К раз. При такой передискретизации эффективная разрядность, а соответственно, и отношение сигнал/шум, увеличивается согласно формуле К = 2^м, где К — коэффициент передискретизации, а N — количество дополнительных битов. Обычно применяется К = 64, и в этом случае эффективная разрядность будет 7 бит, а отношение сигнал/шум будет равно 42 дБ (рис. 6б). Однако передискретизация сама по себе не является эффективным средством. Дальнейшее подавление шума производится благодаря самой структуре дельта-сигма модулятора. В иностранной литературе часто применяется термин «нойзшейпинг», что означает формирование спектра шума. Чтобы понять, как именно происходит формирование, используем линеаризованную дискретную модель системы, в которой входной сигнал представлен последовательностью ж(п), выходной сигнал у(х) и шум квантования, вносимый компаратором и триггером, — е (п), что изображено на рис. 7.

Рис. 6. Спектры выходного сигнала

Рис. 7. Схема линеаризованной дискретной
модели системы

Рассмотрим Z-преобразование этой системы дельта-сигма модулятора:

Видно, что полезный сигнал Х(t) проходит эту цепь без изменений, с задержкой на 1 такт, в то время как для шума возникает препятствие в виде ФНЧ. Таким образом, осуществляется формирование спектра шума в дельта-сигма модуляторе. Интегратор в данном случае выступает в качестве ФНЧ для шумовой составляющей сигнала. Энергия шума сосредотачивается в области верхних частот, и большая ее часть может быть отфильтрована выходным ФНЧ (рис. 6в). Таким образом, в выходном сигнале после демодулирования дельта-сигма последовательности наблюдается намного более низкий уровень шума, чем можно было бы предполагать. Следующим шагом по улучшению параметров по шумам является повышение порядка модулятора. Следует особо отметить, что дельта-сигма АЦП с высочайшей (24 бита) эффективной разрядностью можно построить, всего лишь используя интегратор и стробируемый компаратор.

Информационные параметры

Еще одним важным на сегодня параметром сигнала является его информационная емкость. Здесь следует отметить, что сигнал в формате дельта-сигма модуляции не требует кадровой синхронизации, а значит, считывать его можно в любой момент времени в записи или в канале передачи. В этом его сходство с аналоговым сигналом. Еще одно важное его отличие — это факт одинаковой информационной емкости каждого бита в потоке, что повышает помехоустойчивость сигнала в формате дельта-сигма модуляции.

Оценим теперь информационные параметры сигнала. В качестве требуемого диапазона возьмем порог слышимости, принятый в различных стандартах звукозаписи, — 22 кГц. Частота Котельникова в ИКМ для такого диапазона, следовательно, будет равняться 44 кГц. Оверсэмплинг в формате дельта-сигма модуляции (например, SACD фирмы Sony) предполагает 64-кратное увеличение частоты Котельникова. Таким образом, получается, что частота дискретизации в формате дельта-сигма модуляции с овер-сэмплингом будет равна 2,82 МГц для передачи диапазона от 0 до 22 кГц. Учитывая, что передача цифровых сигналов в обоих форматах ведется в последовательном режиме, оценим количество бит в секунду. При последовательной передаче в формате ИКМ 44 кГц/16 бит поток равен 705 кБод, в формате дельта-модуляции — 2,8 мБод. Однако качество сигнала в формате дельта-модуляции 2,8 МГц приближается к качеству сигнала в формате ИКМ — 192 кГц/24 бита, поток которого составляет уже 4,8 мБод. Также следует учесть, что, в отличие от дельта-сигма модуляции, при передаче ИКМ-сигналов требуется жесткая кадровая синхронизация.

Применение

В настоящее время дельта-сигма модуляторы широко применяются в системах аналогово-цифрового и цифро-аналогового преобразования благодаря чрезвычайно простой архитектуре при высокой разрядности (как было сказано выше) и высокому отношению сигнал/шум. И хотя такие системы пользуются сейчас заслуженной популярностью, сама по себе дельта-сигма модуляция как метод передачи и хранения информации остается пока лишь вспомогательной, второстепенной технологией. Пожалуй, единственным примером полноценного использования дельта-сигма модуляции в области записи данных является разработка фирмы Sony под названием Super Audio Compact Disk (SACD), призванная заменить популярную, но уже устаревающую технологию Audio Compact Disk (Audio CD). Не вдаваясь в особенности этой технологии, скажем лишь, что информация на таком диске записана в формате дельта-сигма модуляции, что, по оценкам некоторых специалистов, обеспечивает более реалистичное звучание, чем при обычной, даже сверхвысококачественной записи в формате ИКМ. На рис. 8 приведены спектры шумов в различных форматах на выходе профессиональной звуковоспроизводящей аппаратуры. Нетрудно заметить, как энергия шума сосредоточена преимущественно в области частот более 20 кГц.

Рис. 8. Спектры шума в различных форматах

Однако как бы ни был хорош формат дельта-сигма модуляции, все существующие системы сбора, обработки и передачи информации предназначены для работы с сигналами в формате ИКМ. И даже в технологии SACD мастеринг записи и любые другие операции над записанными данными, вплоть до регулировки громкости, происходят в формате ИКМ. Это, конечно же, сводит на нет многие плюсы формата дельта-сигма модуляции и ставит под сомнение заявленный выигрыш в реалистичности записи. В настоящее время системы вида «АЦП-обработка, передача или хранение сигнала ЦАП» строятся так, как показано на рис. 9а.

Рис. 9. Структуры «кодер – ЦСП – декодер»:
ДСДМ — дельта-сигма демодулятор; ЦСП — цифровой сигнальный процессор

Сначала аналоговый сигнал поступает на дельта-сигма модулятор, преобразовывается в 1-битный цифровой поток, поступает на фильтр-преобразователь, который производит одновременно и цифровую фильтрацию высокочастотной шумовой составляющей сигнала, и преобразование в многоразрядный ИКМ-код. Обычно он строится по схеме, в англоязычной литературе именуемой Integrate and Dump (или, в переводе на русский, схема накопления и сброса), выполненной на двоичном счетчике и регистре. Далее многоразрядный ИКМ-код подвергается любым математическим операциям, передается по линии связи или сохраняется в памяти. При обратном преобразовании полученные отсчеты сигнала интерполируются и снова преобразовываются в битовый поток с помощью сложного цифрового ДСМ. Ну, а с его выхода сигнал поступает на демодулятор, который представляет собой фильтр нижних частот.

С появлением прецизионных и дешевых дельта-сигма АЦП и ЦАП возникает возможность избавиться от лишних ступеней преобразования форматов и перейти к новой схеме обработки и передачи сигналов уже без формата ИКМ. На рис. 9б изображена такая схема. Поток с выхода дельта-сигма модулятора поступает непосредственно на вход специального сигнального процессора (или ПЛИС) и на приемной стороне дельта-сигма ЦАП.

Однако попробуем разобраться, какие препятствия стоят на пути подобного упрощения системы, и рассмотрим их по порядку. Во-первых, пока не существует отработанных методов цифровой обработки дельта-сигма потоков для многих важных операций. Во-вторых, существующие методы не позволяют поддерживать качество обработанных с их помощью сигналов на приемлемом уровне. Иными словами, при выполнении каждой операции прямой обработки дельта-сигма сигналов существенно возрастает уровень шумов в сигнале.

Итак, какие же операции может выполнять разработчик над дельта-сигма сигналами? Одной из методик цифровой обработки дельта-сигма модулированных сигналов является так называемый метод Кувараса. Пусть Х_п и У_п — две синхронные дельта-сигма последовательности. Для их сложения используем полный двоичный одноразрядный сумматор, описываемый выражениями:

S = X_nY_n v X_nC_n–1 v Y_nC_n–1,
C_n = X_n ⊕ Y_n ⊕ C_n–1.

Видно, что кроме сумматора требуется еще элемент задержки на 1 такт, роль которого выполняет триггер. Таким образом, схема сумматора двух дельта-сигма потоков будет выглядеть, как показано на рис. 10.

Рис. 10. Сумматор дельта-сигма потоков

После демодулирования потока S_n получается сигнал, равный полусумме X_n и Y_n, который описывается следующим выражением:

S(t) = (x (t)+y (t))/2+(e₁(t)+e₂(t))/2,

где e₁(t) и e₂(t) — ошибки квантования сигналов x (t) и y (t). Уменьшить эти ошибки в k раз можно, подавая на тактовый вход триггера сигнал с частотой, в k раз превышающей f квантования. Однако следует учесть, что с каждым последующим сложением ошибка будет все больше возрастать, а значит, будет повышаться и уровень шумов.

Также, используя несколько вышеописанных сумматоров, базисные сигналы x (n), x(n) и нулевую дельта-сигма последовательность (101010___), можно построить умножитель ax(n), где 0 < a < 1, кратный 2ⁿ. Как можно заметить, умножение на коэффициент меньше 1 равносильно ослаблению сигнала. Но что делать, если сигнал необходимо усилить, то есть умножить его в 2, 3, 4 раза? В ходе анализа существующих научных работ по обработке сигналов в формате дельта-сигма модуляции выяснилось, что к настоящему моменту методы умножения на коэффициент больше 1 не публиковались. Автор берет на себя смелость высказать несколько собственных соображений по этому вопросу. Поскольку, как уже говорилось, уровень сигнала описывается плотностью импульсов, то, вероятно, умножение сигнала на коэффициент есть не что иное, как повышение плотности импульсов в n раз. Подобная задача решается с помощью схемы, изображенной на рис. 11, которая состоит из n D-триггеров и n-входового логического элемента «исключающее ИЛИ», таблица истинности которого приведена в таблице 1.

Таблица 1. Таблица истинности 3-входового элемента

X1	X2	X3	Y
0	0	0	0
0	0	1	1
0	1	0	1
0	1	1	0
1	0	0	1
1	0	1	0
1	1	0	0
1	1	1	1

Рис. 11. Схема умножителя на 3

Приведем наглядный пример. Когда в устройство попадают единичные импульсы, разделенные большим количеством нулевых, на выходе плотность единичных импульсов увеличивается в данном случае втрое. В дельта-сигма модуляции, как было сказано, уровень сигнала представляется плотностью единичных импульсов. Указанная схема моделировалась в различных компьютерных программах и показала свою работоспособность при сигналах малой амплитуды, симметричных относительно 0.

Следовательно, увеличивается и уровень сигнала в данном временном окне. Графики сигналов представлены на рис. 12. Красным цветом примерно обозначено соответствующее аналоговое напряжение.

Рис. 12. Графики входного и выходного сигналов умножителя

При реализации в ПЛИС семейства Spartan 3A обе рассмотренные схемы для обработки дельта-сигма потока требуют значительно меньше аппаратных ресурсов, чем подобные схемы для потока данных в формате ИКМ. Так, например, результаты моделирования двух указанных операций над сигналами S1 и S2 по формуле:

SUM = (3(S1+S2))/2

показаны в таблице 2. (Общие для обеих реализаций элементы в таблице не учтены.)

Таблица 2. Необходимые для различных форматов

Ресурс	ДСМ	ИКМ
FLIP-FLOPS	5	17
LOOK-UP TABLES	5	30
SLICES	4	18

Заключение

Таким образом, получается, что уже на простейших операциях видна значительная экономия ресурсов ПЛИС. Используя умножители, сумматоры и цепи D-триггеров в качестве элементов задержки, можно построить более сложные устройства обработки сигналов в формате дельта-сигма модуляции, которые требуют намного меньше ресурсов ПЛИС. Здесь необходимо учесть, что при увеличении числа операций над дельта-сигма сигналом из-за ошибок пропорционально падает и отношение сигнал/шум. Следовательно, реализация сложных многоступенчатых устройств обработки сигналов становится затруднительной. Это обстоятельство и является главным препятствием, которое необходимо преодолеть исследователям, чтобы формат дельта-сигма модуляции смог стать уверенным конкурентом для ИКМ в области обработки, хранения и передачи аналоговых сигналов.

Литература

1. Погрибной В. А. Дельта-модуляция в цифровой обработке сигналов. М.: Радио и связь, 1990.
2. Zrilich D. G. Circuits and Systems Based on Delta Modulation: Linear, Nonlinear and Mixed Mode Processing (Signais and Communication Technology). Springer, 2005.
3. Schreier R., Temes G. C. Understanding Delta-Sigma converters. Wiley, 2004.
4. Maloberti F., O’Leary P. Processing of signals in their oversampled domain. CICCAS, 1991.