Как найти дельта тау

Как рассчитать дельту

Четвертой буквой греческого алфавита, «дельтой», в науке принято называть изменение какой-либо величины, погрешность, приращение. Записывается этот знак различными способами: чаще всего в виде небольшого треугольника Δ перед буквенным обозначением величины. Но иногда можно встретить и такое написание δ, либо латинской строчной буквой d, реже латинской прописной – D.

Инструкция

Для нахождения изменения какой-либо величины вычислите или измерьте ее начальное значение (x1).

Вычислите или измерьте конечное значение этой же величины (x2).

Найдите изменение данной величины по формуле: Δx=x2-x1. Например: начальное значение напряжения электрической сети U1=220В, конечное значение – U2=120В. Изменение напряжения (или дельта напряжения) будет равно ΔU=U2–U1=220В-120В=100В

Для нахождения абсолютной погрешности измерения определите точное или, как его иногда называют, истинное значение какой-либо величины (x0).

Возьмите приближенное (при измерении – измеренное) значение этой же величины (x).

Найдите абсолютную погрешность измерения по формуле: Δx=|x-x0|. Например: точное число жителей города – 8253 жителя (х0=8253), при округлении этого числа до 8300 (приближенное значение х=8300). Абсолютная погрешность (или дельта икс) будет равна Δx=|8300-8253|=47, а при округлении до 8200 (х=8200), абсолютная погрешность – Δx=|8200-8253|=53. Таким образом, округление до числа 8300 будет более точным.

Для сравнения значений функции F(х) в строго фиксированной точке х0 со значениями этой же функции в любой другой точке х, лежащей в окрестностях х0, используются понятия «приращение функции» (ΔF) и «приращение аргумента функции» (Δx). Иногда Δx называют «приращением независимой переменной». Найдите приращение аргумента по формуле Δx=x-x0.

Определите значения функции в точках х0 и х и обозначьте их соответственно F(х0) и F(х).

Вычислите приращение функции: ΔF= F(х)- F(х0). Например: необходимо найти приращение аргумента и приращение функции F(х)=х˄2+1 при изменении аргумента от 2 до 3. В этом случае х0 равно 2, а х=3.
Приращение аргумента (или дельта икс) будет Δx=3-2=1.
F(х0)= х0˄2+1= 2˄2+1=5.
F(х)= х˄2+1= 3˄2+1=10.
Приращение функции (или дельта эф) ΔF= F(х)- F(х0)=10-5=5

Обратите внимание

Вычитать нужно не из большего числа меньшее, а из конечного значения (не важно: больше оно или меньше) начальное!

Полезный совет

При нахождении Δ все значения используйте только в одинаковых единицах измерения.

Источники:

• Справочник по математике для средних учебных заведений, А.Г. Цыпкин, 1983

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

1. Nauka.Club | Образовательный портал

2. Вопросы

3. 
   Как найти дельта t в физике

5.1. Понятие временных характеристик

Для оценки динамических
свойств системы и отдельных звеньев принято исследовать их реакцию на типовые
входные воздействия, которые наиболее полно отражают особенности реальных
возмущений. Во – первых, это позволяет сравнивать отдельные элементы между собой
с точки зрения их динамических свойств. Во – вторых, зная реакцию системы на типовые
воздействия, можно судить о том, как она будет вести себя при сложных изменениях
входной величины.

Наиболее распространенными типовыми воздействиями являются:
ступенчатое, импульсное и гармоническое воздействия. Любой сигнал
u(t), имеющий сложную форму, можно разложить на сумму типовых воздействий
u_i(t) и исследовать реакцию системы
на каждую из составляющих, а затем, пользуясь принципом суперпозиции, получить
результирующее изменение выходной величины y(t) суммируя полученные таким
образом составляющие выходного сигнала y_i(t).

Особенно важное значение в ТАУ придают ступенчатому воздействию 1(t) = . Все остальные воздействия
могут быть сведены к нему. Так, например, реальный импульсный сигнал может быть
представлен двумя ступенчатыми сигналами одинаковой величины, но противоположными
по знаку, поданными один за другим через интервал времени t
(рис.42).

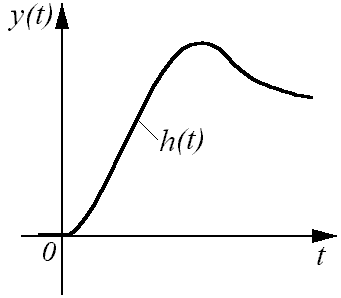
Зависимость изменения выходной величины системы от времени при
подаче на ее вход единичного ступенчатого воздействия при нулевых начальных условиях
называется переходной характеристикой и обозначается h(t).

Не менее важное значение в ТАУ уделяется импульсной переходной характеристике,
которая описывает реакцию системы на единичное импульсное воздействие при нулевых
начальных условиях, обозначают (t).
Единичный импульс физически представляет из себя очень узкий импульс, ширина
которого стремится к нулю, а высота – к бесконечности, ограничивающий единичную
площадь. Математически он описывается дельта – функцией d(t) = 1’(t).

Переходная
и импульсная переходная характеристики называются временными характеристиками.
Каждая из них является исчерпывающей характеристиками системы и любого ее звена
при нулевых начальных условиях. По ним можно однозначно определить выходную величину
при произвольном входном воздействии.

Зная передаточную функцию W(p) = K(p)/D(p), выражение для переходной
функции можно найти из формулы Хевисайда: , где p_k
– корни характеристического уравнения D(p) = 0. Взяв производную от переходной
функции можно получить выражение для импульсной переходной функции (t)
= h’(t).

5.2. Переходные характеристики элементарных
звеньев

Здесь мы рассмотрим только самые основные
звенья.

5.2.1. Безынерционное (пропорциональное,
усилительное) звено

Это звено, для которого
в любой момент времени выходная величина пропорциональна входной.

Его уравнение: y(t) = ku(t).

Передаточная функция: W(p) = k.

Переходная характеристика: h(t) = k1(t).

В ответ на единичное ступенчатое воздействие сигнал на выходе мгновенно достигает величины в k раз большей, чем на входе и сохраняет
это значение (рис.43). При k = 1 звено никак себя не проявляет, а при
k = – 1 – инвертирует входной сигнал.

Любое реальное звено обладает инерционностью, но с определенной
точностью некоторые реальные звенья могут рассматриваться как безынерционные,
например, жесткий механический рычаг, редуктор, потенциометр, электронный усилитель
и т.п.

5.2.2. Интегрирующее (астатическое) звено

Его
уравнение , или , или py = ku.

Передаточная
функция: W(p) = k/p.

Переходная характеристика: (рис.44).

При k = 1 звено представляет собой “чистый” интегратор
W(p) = 1/p. Интегрирующее звено неограниченно “накапливает”
входное воздействие. Примеры интегрирующих звеньев: электродвигатель, поршневой
гидравлический двигатель, емкость и т.п. Введение его в САУ превращает систему
в астатическую, то есть ликвидирует статическую ошибку.

5.2.3. Инерционное звено первого порядка
(апериодическое)

Уравнение динамики: , или Tpy + y = ku.

Передаточная
функция: W(p) = .

Переходная характеристика может быть получена с помощью формулы Хевисайда:

,

где p₁
= – 1/T – корень уравнения D(p) = Tp + 1 = 0; D’(p₁)
= T.

Переходная характеристика имеет вид экспоненты (рис.45), по
которой можно определить передаточный коэффициент k, равный установившемуся
значению h(t), и постоянную времени Т по времени t, соответствующему
точке пересечения касательной к кривой в начале координат с ее асимптотой. При
достаточно больших Т звено на начальном участке может рассматриваться
как интегрирующее, при малых Т звено приближенно можно рассматривать
как безынерционное. Примеры апериодического звена: термопара, электродвигатель,
четырехполюсник из сопротивления и емкости или сопротивления и индуктивности.

5.2.4. Инерционные
звенья второго порядка

Его уравнение: T₁²p²y
+ T₂py + y = ku.

Передаточная функция:
W(p) = .

Решение уравнения зависит
от соотношения постоянных времени T₁ и
T₂, которое определяет коэффициент затухания
r = . Можно записать W(p) = , где T = T₁.

Если r
1, то знаменатель W(p) имеет два вещественных корня p₁
и p2 и раскладывается на два сомножителя:

T₂p²
+ 2rTp + 1 = T²(p
– p₁).(p – p₂).

Такое звено можно разложить на два апериодических звена первого порядка, поэтому оно не является элементарным.

При r<1 корни полинома знаменателя W(p) комплексно
сопряженные: p_1,2 =
± j. Переходная
характеристика представляет собой выражение, характеризующее затухающий колебательный
процесс с затуханием
и частотой
(рис.46). Такое звено называется колебательным. При r = 0 колебания
носят незатухающий характер. Такое звено является частным случаем колебательного
звена и называется консервативным. Примерами колебательного звена могут
служить пружина, имеющая успокоительное устройство, электрический колебательный
контур с активным сопротивлением и т.п. Зная характеристики реального устройства
можно определить его параметры как колебательного звена. Передаточный коэффициент
k равен установившемуся значению переходной функции.

5.2.5. Дифференцирующее звено

Различают идеальное и реальное дифференцирующие звенья. Уравнение динамики
идеального звена: y(t) = , или y = kpu. Здесь выходная
величина пропорциональна скорости изменения входной величины. Передаточная функция:
W(p) = kp. При k = 1 звено осуществляет чистое дифференцирование
W(p) = p. Переходная характеристика: h(t) = k1’(t)
= d(t).

Идеальное дифференцирующее звено реализовать невозможно, так
как величина всплеска выходной величины при подаче на вход единичного ступенчатого
воздействия всегда ограничена. На практике используют реальные дифференцирующие
звенья, осуществляющие приближенное дифференцирование входного сигнала.

Его
уравнение: Tpy + y = kTpu.

Передаточная функция: W(p) = .

При малых Т
звено можно рассматривать как идеальное дифференцирующее. Переходную характеристики
можно вывести с помощью формулы Хевисайда:

,

здесь p₁
= – 1/T – корень характеристического уравнения D(p) = Tp + 1 = 0; кроме
того, D’(p₁) = T.

При подаче на вход единичного ступенчатого воздействия выходная величина оказывается ограничена
по величине и растянута во времени (рис.47). По переходной характеристике, имеющей
вид экспоненты, можно определить передаточный коэффициент k и постоянную
времени Т. Примерами таких звеньев могут являться четырехполюсник из сопротивления
и емкости или сопротивления и индуктивности, демпфер и т.п. Дифференцирующие звенья
являются главным средством, применяемым для улучшения динамических свойств САУ.

Кроме рассмотренных имеется еще ряд звеньев, на которых подробно
останавливаться не будем. К ним можно отнести идеальное форсирующее звено (W(p)
= Tp + 1, практически не реализуемо), реальное форсирующее звено (W(p)
= , при T₁
>> T₂), запаздывающее
звено (W(p) = e ^{– pT}),
воспроизводящее входное воздействие с запаздыванием по времени и другие.

Вопросы

1. Что
   называется и какие Вы знаете типовые входные воздействия? Для чего они нужны?
2. Что
   называется переходной характеристикой?
3. Что называется импульсной переходной
   характеристикой?
4. Что называется временными характеристиками?
5. Для
   чего служит формула Хевисайда?
6. Как получить кривую переходного процесса
   при сложной форме входного воздействия, если известна переходная характеристика
   звена?
7. Что называется безынерционным звеном, его уравнение динамики, передаточная
   функция, вид переходной характеристики?
8. Что называется интегрирующим звеном,
   его уравнение динамики, передаточная функция, вид переходной характеристики?
9. Что
   называется апериодическим звеном, его уравнение динамики, передаточная функция,
   вид переходной характеристики?
10. Что называется колебательным звеном, его
    уравнение динамики, передаточная функция, вид переходной характеристики?
11. Что
    называется консервативным звеном, его уравнение динамики, передаточная функция,
    вид переходной характеристики?
12. Почему не являются элементарными инерционные
    звенья второго порядка с коэффициентом затухания большим или равным единице?
13. Что
    называется идеальным дифференцирующим звеном? Почему его нельзя реализовать?
14. Что
    называется реальным дифференцирующим звеном, его уравнение динамики, передаточная
    функция, вид переходной характеристики?

Далее…

Основные (типовые) управляющие воздействия сау

При экспериментальном
и теоретическом исследовании автоматических
систем и их элементов используют ряд
стандартных сигналов, называемых
типовыми
воздействиями.
Эти воздействия описываются простыми
математическими функциями и легко
воспроизводятся при испытании систем.

Ступенчатое
воздействие
– это воздействие, которое мгновенно
возрастает от нуля до некоторого значения
и далее остается постоянным.

Ступенчатому
воздействию соответствует функция

При анализе и
расчете систем удобно использовать
ступенчатое воздействие, у которого
величина а₀ = 1.
Его называют единичным
ступенчатым воздействием
и обозначают 1(t).

Ступенчатое
воздействие чаще всего используют при
испытаниях и расчетах систем стабилизации,
так как эти воздействия наиболее близки
к реальным входным (задающим и возмущающим)
воздействиям систем стабилизации.

Импульсное
воздействие
представляет собой одиночный импульс
прямоугольной формы, имеющий достаточно
большую высоту и весьма малую
продолжительность (по сравнению с
инерционностью испытываемой системы).
Очевидно, что площадь такого импульса
всегда равна а₀.

При математическом
анализе автоматических систем используют
единичное
импульсное воздействие,
которое описывается так называемой
дельта–функцией

причем

Согласно этим
выражениям, дельта–функцию можно
рассматривать как импульс, имеющий
бесконечно большую высоту, бесконечно
малую длительность и единичную площадь.
Дельта–функцию можно определить также
как производную единичного скачка:

.

В качестве
стандартного гармонического
воздействия
используют обычно сигнал синусоидальной
формы, описываемый функцией

где А
– амплитуда сигнала;

– круговая частота,
рад/с;

Т
– период сигнала, с.

Гармонические
воздействия широко используются при
исследовании точности и устойчивости
как стабилизирующих, так следящих и
программных автоматических систем. Это
объясняется двумя обстоятельствами:
во–первых, реальные возмущения часто
имеют периодический характер и поэтому
могут быть представлены в виде суммы
гармонических составляющих; во–вторых,
математический аппарат анализа
автоматических систем хорошо разработан
именно для случая гармонических
воздействий.

Для следящих и
программных систем типовым является
линейное
воздействие

.

Коэффициент а₁
характеризует
скорость нарастания воздействия x(t).

Принцип суперпозиции для линейных систем

Для линейных систем
справедлив принцип суперпозиции
(наложения): реакция системы на несколько
одновременно действующих входных
воздействий равна сумме реакций на
каждое воздействие в отдельности.

Это позволяет
ограничиться изучением систем с одним
входом.

Временные характеристики сау

Наиболее наглядное
представление о динамических свойствах
элемента дает его переходная функция
(характеристика). Переходной
функцией h(t)
называют
изменение выходной величины y(t)
во времени, возникающее после подачи
на вход единичного ступенчатого
воздействия, при нулевых начальных
условиях.

Переходная функция
может быть задана в виде графика (тогда
она называется характеристикой) или в
формульном виде.
Переходная
функция h(t),
как и любое решение неоднородного
дифференциального уравнения имеет 2
составляющие: вынужденную
и свободную.Вынужденная
составляющая переходного
процесса представляет собой частное
решение исходного уравнения. При
ступенчатом воздействии вынужденная
составляющая равна установившемуся
значению выходной величины, которое
для статических элементов может быть
найдено непосредственно из дифференциального
уравнения (при нулевых производных):

.

Свободная
составляющая
может быть найдена как решение
соответствующего однородного
дифференциального уравнения в следующем
виде (при отсутствии одинаковых корней):

,

где
–
корни характеристического уравнения

– постоянные
интегрирования, зависящие от начальных
условий.

Характеристическое
уравнение, соответствующее
определенному дифференциальному
уравнению, представляет собой
алгебраическое уравнение, степень и
коэффициенты которого совпадают с
порядком и коэффициентами левой части
этого дифференциального уравнения. Для
дифференциального уравнения

характеристическое
уравнение имеет вид

где
– некоторое комплексное число, являющееся
решением (корнем), характеристического
уравнения.

Импульсной
переходной функцией (функцией веса)
(t)
называют изменение выходной величины
y(t),
возникающее после подачи на вход
дельта–функции, при нулевых начальных
условиях (см. рис.).

И

мпульсная переходная функция(t)
равна производной от переходной функции
h(t):

,

и наоборот,
переходная функция равна интегралу от
импульсной переходной:

Соседние файлы в папке ТАУ

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #