[Delta overline=left[xleft(t+Delta tright)-xleft(tright)right]overline+left[yleft(t+?tright)-yleft(tright)right]overline+left[zleft(t+?tright)-zleft(tright)right]overlineleft(5right).]
При прямолинейном движении вектор перемещения совпадает с соответствующим участком траектории и длина вектора перемещения равна пройденному точкой пути:
[left|Delta overlineright|=Delta s left(6right).]
Длину вектора перемещения (как и любого вектора) можно обозначать как $left|Delta overlineright|$ или просто $Delta r$ (без указания стрелки).
Если тело совершает несколько перемещений, то их можно складывать по правилам сложения векторов:
Если направление движения тела изменяется, то модуль вектора перемещения не равен пройденному телом пути.
Примеры задач на путь и перемещение
Задание: Мяч бросили вертикально вверх от поверхности Земли. Он долетел до высоты 20 м. и упал на Землю. Чему равен путь, который прошел мяч, каков модуль перемещения?
Решение: Сделаем рисунок.
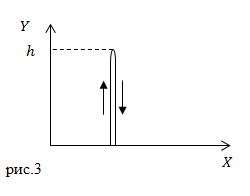
В нашей задаче мяч движется прямолинейно сначала вверх, затем вниз. Так как путь – длина траектории, то получается, что мяч дважды прошел расстояние h, следовательно:
Перемещение – направленный отрезок, соединяющий начальную точку и конечную при движении тела, но тело начало движение из той же точки, в которую вернулось, следовательно, перемещение мяча равно нулю:
Ответ: $ Путь Delta s=2h$. Перемещение $Delta r=0$
Задание: В начальный момент времени тело находилось в точке с координатами $(x_0=3;; y_0=1)$(см). Через некоторый промежуток времени оно переместилось в точку координаты которой ($x=2;;y=4$) (см). Каковы проекции вектора перемещения на оси X и Y?
Решение: Сделаем рисунок.
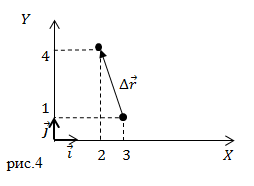
Радиус – вектор начальной точки запишем как:
Радиус – вектор конечной точки имеет вид:
Вектор перемещения представим как:
Из формулы видим, что:
[Delta r_x=-1;;Delta r_y=3. ]
Ответ: $Delta r_x=-1;;Delta r_y=3 $
Дельта-вектор в сверточных алгебрах

Омский государственный университет путей сообщения (ОмГУПС(ОмИИТ))
ДЕЛЬТА-ВЕКТОР В СВЕРТОЧНЫХ АЛГЕБРАХ
В математике и физике уже долгое время используется понятие дельта-функции. Это очень удобный математический объект, позволяющий эффективно решать большой круг научных задач. К сожалению, при работе с дельта-функцией возникают и серьезные проблемы. Например, нельзя перемножать дельта-функции. Дифференцирование дельта-функций также приводит к весьма неоднозначным результатам. Иногда применение дельта-функции является причиной появления нескольких взаимоисключающих решений для одной задачи.
В данной статье дельта-функция рассматривается немного под другим углом – это ни есть раз и навсегда заданная функция. Существуют пространства векторов, среди которых возможно найти вектор, обладающий всеми свойствами дельта-функции по отношению к векторам своего пространства.
Предположим, что задано пространство Гильберта  . Пусть
. Пусть  ,
,  и
и  – произвольные вектора пространства
– произвольные вектора пространства  , являющиеся действительными функциями переменной
, являющиеся действительными функциями переменной  , принадлежащей некому множеству
, принадлежащей некому множеству  .
.
 ,
,
где  . При этом, если
. При этом, если  – любой вектор пространства
– любой вектор пространства  , то и
, то и  , при любом
, при любом  .
.
Следовательно, на множестве  задано также и скалярное произведение двух векторов [1]:
задано также и скалярное произведение двух векторов [1]:
 . (1)
. (1)
Определим на базе скалярного произведения (1) двух произвольных векторов пространства Гильберта понятие свертки:
Определение 1: сверткой двух произвольных векторов пространства Гильберта является третий вектор этого же пространства, получаемый из следующего соотношения:
 . (2)
. (2)
Докажем для свертки свойство коммутативности.
Лемма 1. В отношении свертки двух произвольных векторов пространства Гильберта истинны следующие соотношения:
 .
.
 .
.
С учетом подстановки  и
и  имеем:
имеем:
 .
.
Что и требовалось доказать.
На базе введенного понятия свертки (2) определяем дельта-вектор пространства Гильберта.
Определение 2: дельта-вектором пространства Гильберта  , на котором определена свертка, называется такой вектор
, на котором определена свертка, называется такой вектор  , в отношении которого выполняется условие:
, в отношении которого выполняется условие:
 , (3)
, (3)
где  – любой вектор пространства
– любой вектор пространства  .
.
Теорема 1. Если в пространстве Гильберта, в котором определен ортогональный базис  и свертка, существует дельта-вектор, то этот вектор единственный и может быть вычислен по следующей формуле:
и свертка, существует дельта-вектор, то этот вектор единственный и может быть вычислен по следующей формуле:
 .
.
Доказательство. Пусть  – произвольный вектор пространства Гильберта. Имеем по определению дельта-вектора (3):
– произвольный вектор пространства Гильберта. Имеем по определению дельта-вектора (3):
 . (4)
. (4)
Разложим вектора  и
и  по базису
по базису  :
:
 ,
,
где  и
и  – коэффициенты разложения. С учетом равенства Парсеваля формула (4) преобразуется следующим образом:
– коэффициенты разложения. С учетом равенства Парсеваля формула (4) преобразуется следующим образом:
 .
.
Разложим по базису  и получим следующее:
и получим следующее:
 , (5)
, (5)
так как  – любой вектор, то коэффициенты
– любой вектор, то коэффициенты  – могут быть любыми, кроме того они независимы. Следовательно, равенство (5) может быть истинно только при условии
– могут быть любыми, кроме того они независимы. Следовательно, равенство (5) может быть истинно только при условии
 .
.
И так, любой вектор  раскладывается единственным образом в любом базисе:
раскладывается единственным образом в любом базисе:
 ,
,
а вектор  соответственно:
соответственно:
 .
.
Что и требовалось доказать.
Докажем некоторые свойства дельта-вектора пространства Гильберта.
Лемма 2: квадрат нормы (или энергия) дельта-вектора пространства Гильберта всегда равен  .
.
 .
.
 .
.
Вводим подстановку:  ,
,  :
:
 .
.
используем свойство коммутативности свертки:
 .
.
Что и требовалось доказать.
Рассмотрим другое важное свойство дельта-вектора – четность (симметричность). Для доказательства этого сначала докажем такое интересное свойство свертки:
Лемма 4: для любого произвольного  и
и  истинно следующее соотношение:
истинно следующее соотношение:
 .
.
Для доказательства в формулу:

введем подстановку:  ,
, 
 .
.
Исходя из определения дельта-вектора получаем:
 .
.
Что и требовалось доказать.
Теперь можно доказать четность дельта-вектора.
Лемма 5: для любого произвольного  истинно соотношение:
истинно соотношение:
 .
.
Как следствие Леммы 4, истинны утверждения, что
 .
.
Но из определения скалярного произведения:
 .
.
 .
.
Что и требовалось доказать.
Введем в рассматриваемое пространство понятие единичного вектора.
Определение 3: Единичным вектором  будем считать такой вектор, для которого справедливо соотношение:
будем считать такой вектор, для которого справедливо соотношение:
 .
.
Очевидно, что в рассматриваемом пространстве действительных функций, единичный вектор является действительной функцией  . Для дальнейшего описания свойств дельта-вектора введем понятие площади вектора.
. Для дальнейшего описания свойств дельта-вектора введем понятие площади вектора.
Определение 4: площадью вектора  пространства Гильберта, если в нем определен единичный вектор
пространства Гильберта, если в нем определен единичный вектор  является действительное число
является действительное число  , определяемое следующим соотношением:
, определяемое следующим соотношением:
 . (6)
. (6)
Докажем следующее свойство дельта-векотра.
Лемма 6. Площадь дельта-вектора всегда равна 1.
Найдем площадь дельта-вектора в соответствии с формулой (6):
 .
.
Что и требовалось доказать.
Теперь рассмотрим интерполяционные возможности дельта-вектора. Для этого предположим, что у нас имеется набор из  «смещенных» по оси
«смещенных» по оси  функций вида
функций вида  . Предположим, что функции
. Предположим, что функции  образуют полный ортогональный базис. В этом случае, по этим функциям возможно разложить любой вектор пространства
образуют полный ортогональный базис. В этом случае, по этим функциям возможно разложить любой вектор пространства  .
.
Теорема 2. Если в пространстве Гильберта возможно задать полный ортогональный базис размерности  состоящий из функций вида
состоящий из функций вида  , то любой вектор
, то любой вектор  этого пространства может быть однозначно восстановлен по своим значениям в точках
этого пространства может быть однозначно восстановлен по своим значениям в точках  .
.
Так как, функции  образуют полный ортогональный базис, то вектор
образуют полный ортогональный базис, то вектор  возможно разложить по этому базису:
возможно разложить по этому базису:
 , (7)
, (7)
где  – размерность базиса рассматриваемого пространства;
– размерность базиса рассматриваемого пространства;  – интервал значений
– интервал значений  . Остается только найти коэффициенты разложения по данному базису:
. Остается только найти коэффициенты разложения по данному базису:
 .
.
Таким образом, формула (7) принимает вид:
 . (8)
. (8)
Это означает, что имея только отсчеты вектора  в точках
в точках  возможно полностью восстановить весь вектор. Что и требовалось доказать.
возможно полностью восстановить весь вектор. Что и требовалось доказать.
Приведем пример пространства, в котором существует дельта-вектор. Таким пространством является множество всех функций со спектром, ограниченным отрезком  . Скалярным произведением векторов
. Скалярным произведением векторов  и
и  этого пространства выберем следующее известное соотношение [2]:
этого пространства выберем следующее известное соотношение [2]:
 .
.
Исходя из формулы (4) получим, что для дельта-вектора  данного пространства справедливо соотношение:
данного пространства справедливо соотношение:
 ,
,
где  – любой вектор рассматриваемого пространства. Данное соотношение – это классическая свертка двух функций
– любой вектор рассматриваемого пространства. Данное соотношение – это классическая свертка двух функций  и
и  . Сразу оговоримся, что классическая дельта-функция Дирака в данном случае дельта-вектором выступать не может, так как ее спектр не ограничен интервалом
. Сразу оговоримся, что классическая дельта-функция Дирака в данном случае дельта-вектором выступать не может, так как ее спектр не ограничен интервалом  и, следовательно, она не является вектором нашего пространства. Необходимо искать дельта вектор среди функций с ограниченным спектром.
и, следовательно, она не является вектором нашего пространства. Необходимо искать дельта вектор среди функций с ограниченным спектром.
Как известно из теории [2], классическая свертка во временной области соответствует перемножению спектров функций в спектральной области. Подберем такую функцию  , спектр
, спектр  которой в отношении спектра
которой в отношении спектра  любой функции рассматриваемого пространства обладает свойством:
любой функции рассматриваемого пространства обладает свойством:
 .
.
 .
.
А таким спектром обладает функция:
 . (9)
. (9)
Известно, что смещенные по оси времени на интервалы  функции вида (9) образуют полный ортогональный базис. Учитывая, что
функции вида (9) образуют полный ортогональный базис. Учитывая, что  , а
, а  , формула (8) приобретает вид широко известной интерполяционной формулы Котельникова [3]:
, формула (8) приобретает вид широко известной интерполяционной формулы Котельникова [3]:
 ,
,
где  .
.
В заключении приведем основные результаты, полученные в данной работе.
1. Дельта-функция Дирака не является уникальным математическим объектом. Существуют пространства Гильберта, в которых имеется вектор, обладающий свойствами дельта-функции в отношении всех векторов своего пространства.
2. Площадь дельта-вектора равна 1.
3. Квадрат нормы (энергия) дельта-вектора равна значению этого вектора в точке 0.
4. Если в пространстве Гильберта, в котором определен ортогональный базис и свертка, существует дельта-вектор, то этот вектор единственный и может быть стандартно вычислен из любого базиса этого пространства.
5. Дельта-вектор обладает свойством симметрии.
6. В пространстве функций, ограниченных по Котельникову существует дельта-вектор, определяемый формулой:
 .
.
1. Элементарное введение в абстрактную алгебру: М.:Мир, 1979.
2. Кудрявцев математического анализа (в двух томах): Учебник для студентов университетов и втузов. М.: Высш. школа, 1981.
3. Романюк цифровой обработки сигналов. М.:МФТИ, 2005.
[spoiler title=”источники:”]
http://www.webmath.ru/poleznoe/fizika/fizika_88_put_i_peremeshhenie.php
http://pandia.ru/text/78/392/89204.php
[/spoiler]
Таким образом, использование имитационного моделирования в совокупности с разработанным методом позволяет априорно определять расход электрической энергии на технологические процессы ремонта подвижного состава, повышая эффективность использования электрической энергии. Полученное таким способом значение расхода электрической энергии является технологически обоснованным, имеет слабую привязку к предыстории потребления и учитывает действительные характеристики исследуемого технологического процесса, режимы использования технологического оборудования.
Список литературы
1. Пашков, Д. В. Выявление отклонений параметров электропотребления в рамках исследуемого технологического процесса от оптимальных значений [Текст] / Д. В. Пашков, А. В. Пономарев // Обеспечение экономически целесообразных условий работы железных дорог на основе оптимизации режимов работы электротехнических комплексов: Межвуз. те-мат. сб. науч. тр. / Омский гос. ун-т путей сообщения. – Омск, 2008. – С. 55 – 58.
2. Пашков, Д. В. Повышение эффективности планирования и нормирования расхода электрической энергии на технологические нужды с применением имитационного моделирования [Текст] / Д. В. Пашков, А. В. Пономарев // Научные проблемы транспорта Сибири и Дальнего Востока. – 2009. – №№ 2. – С. 261 – 263.
3. Борщев, А. В. Применение имитационного моделирования в России – состояние на 2007 г. [Текст] / А. В. Борщев // Материалы 3-й всерос. науч.-практ. конф. по имитационному моделированию ИММОД 2007 / Центральный научно-исследовательский институт технологии судостроения. – СПб, 2007. – С. 11 – 16.
4. Сетевое планирование ремонта подвижного состава [Текст] / С. Г. Шантаренко, М. Ф. Капустьян и др. // Железнодорожный транспорт. – 2009. – N° 2. – С. 48, 49.
5. Орлов, А. И. Прикладная статистика [Текст] / А. И. Орлов. – М.: Экзамен, 2006. -672 с.
УДК 004.62:517.98
С. С. Грицутенко
ВВЕДЕНИЕ ПОНЯТИЯ «ДЕЛЬТА-ВЕКТОР» В ПРОСТРАНСТВЕ ГИЛЬБЕРТА ДЛЯ КОРРЕКТНОГО ПРЕДСТАВЛЕНИЯ ДАННЫХ В ИНФОРМАЦИОННЫХ СИСТЕМАХ
В статье вводится понятие дельта-вектора в пространстве Гильберта. Доказывается теорема, что таких векторов в каждом конкретном пространстве не может быть больше одного. Приводится формула для вычисления данного вектора в том случае, если он существует. Доказывается теорема о разложении остальных векторов пространства в ряд смещенных дельта-векторов и показывается взаимосвязь этой теоремы с теоремой Котельникова.
Железнодорожный транспорт является потребителем новейших достижений в фундаментальной науке, которая уделяет большое внимание общетехническим дисциплинам: связи, измерениям, системам управления и контроля. В настоящее время в перечисленных областях науки идет ревизия используемого математического аппарата, так как существующие методики уже не обеспечивают необходимой точности обработки сигналов. В данной статье рассматриваются новые математические подходы к представлению сигналов, позволяющие более адекватно строить алгоритмы связи и измерения.
В математике и физике используется понятие дельта-функции. Это очень удобный математический объект, позволяющий эффективно решать многие научные задачи. К сожалению, при работе с дельта-функцией возникают и серьезные проблемы. Например, нельзя пежмт
ремножать дельта-функции. Дифференцирование дельта-функций также приводит к весьма неоднозначным результатам. Иногда применение дельта-функции является причиной появления нескольких взаимоисключающих решений для одной задачи.
В данной статье дельта-функция рассматривается под другим углом – это не есть раз и навсегда заданная функция. Существуют пространства векторов, среди которых можно найти вектор, у которого есть все свойства дельта-функции по отношению к векторам своего пространства. Предположим, что задано пространство Гильберта Н. Пусть х (t), у (t) и г ) -произвольные векторы пространства Н, являющиеся действительными функциями переменной t, принадлежащей некому множеству Т :
{х,у (0, гН, (1)
где t е Т. При этом если х (t) – любой вектор пространства Н, то и х (t – т) е Н при любом теТ.
Следовательно, на множестве Н задано также и скалярное произведение двух векторов [1]:
(х(0, у(0). (2)
Определим на базе скалярного произведения (2) двух произвольных векторов пространства Гильберта понятие свертки.
Определение 1: сверткой двух произвольных векторов пространства Гильберта является третий вектор этого же пространства, получаемый из соотношения:
г (t) = х (t) • у (t) = (х (т), у (t -т)). (3)
Докажем для свертки свойство коммутативности.
Лемма 1. В отношении свертки двух произвольных векторов пространства Гильберта истинно соотношение:
х (^ у (г) = у (^ х (^. (4)
Действительно:
х ^ )• у ^) = (х (т), у ^-т)) = (у (t-т), х (т)). (5)
С учетом подстановки в уравнение (5) г = t – т и т = t – г имеем:
(у (t – т), х (т)) = (у (г), х (t – г)) = у (t) • х (t), (6)
что и требовалось доказать.
На базе введенного понятия свертки (3) определяем дельта-вектор пространства Гильберта.
Определение 2: дельта-вектором пространства Гильберта Н, на котором определена свертка, называется такой вектор 5(t), в отношении которого выполняется условие:
х (г ) = х ^ ) , (7)
где х (t) – любой вектор пространства Н.
Теорема 1. Если в пространстве Гильберта, в котором определены ортогональный базис {п (t)} и свертка, существует дельта-вектор, этот вектор единственный и может быть вычислен по формуле:
§(t) = Е п (t) п (0). (8)
Доказательство. Пусть х (t) – произвольный вектор пространства Гильберта. По определению дельта-вектора (7) имеем:
х (t) = х (t) • 5 (t) = (х (т), 5 (t -т)). (9)
Разложим векторы х(1) и 5(t) по базису {п (t)}:
х(т) = Хап (т); (10)
5(t-т) = XЬ (t)п (т)
где а. и Ь. – коэффициенты разложения. С учетом равенства Парсеваля формула (9) преобразуется следующим образом:
х(t) = (х(т),5(t-т)) = ХаЬ (t). (12)
Разложим выражение (12) по базису х(t) и получим следующее:
X ап (t )=Х аЬ< (t).
Так как х (t) – любой вектор, то коэффициенты {а. } могут быть любыми, кроме того, они независимы. Следовательно, равенство (13) может быть истинно только при условии, что
П (t ) = Ь (t). (14)
Таким образом, любой вектор 5(t -т) раскладывается единственным образом в любом базисе:
а вектор 5(t) соответственно
5(-т) = X П (t) П (т),
5( t )=5( t – 0 ) = Х п (t) П (0).
Докажем некоторые свойства дельта-вектора пространства Гильберта. Л е м м а 2: квадрат нормы (или энергия) дельта-вектора пространства Гильберта всегда равен 5(0):
Имеем:
|8( t 2 = 5( 0).
|5( t )| Г = (8( t), 5( t)),
вводим подстановку: / (-t) = 5 (t), / (t) = 5 (-):
(5( t), 5( t))=(5( t), / (-t))=(5( t), / (0 -1)).
используем свойство коммутативности свертки:
(8(0, / (0 – г)) = (/ (г), 5( 0 – г)) = /(0) = 5(-0) = 8( 0), (20)
что и требовалось доказать.
Рассмотрим другое важное свойство дельта-вектора – четность (симметричность). Для доказательства этого сначала докажем свойство свертки, представленной в лемме 3. Лемма 3: для любого произвольного х и Т истинно соотношение:
(х (г), 8(Т – г)) = (х (г), 8(г – Т)). (21)
В формулу (х (г), 8 (г – Т)) введем подстановку: г – Т = Т – т, г = 2Т -т:
(х (г), 8 (г – Т)) = (х (2Т -т), 8 (Т -т)). (22)
Исходя из определения дельта-вектора получаем:
( х ( 2Т-т), 8(Т-т))= х ( 2Т-Т) = х (Т) = (х (г), 8(Т-г)), (23)
что и требовалось доказать.
Теперь можно доказать четность дельта-вектора.
Лемма 4: для любого произвольного Т истинно соотношение:
8(Т) = 8(-Т). (24)
Как следствие леммы 3, истинны утверждения, что
(8(г), 8(г – Т)) = 8(Т); (25)
(8 (г – Т), 8( г)) = 8(-Т). (26)
Однако из определения скалярного произведения
(8(г),8(г -Т)) = (8(г -Т),8(г)), (27)
следовательно,
8(Т) = 8(-Т), (28)
что и требовалось доказать.
Введем в рассматриваемое пространство понятие единичного вектора. Определение 3: Единичным вектором е (г) будем считать такой вектор, для которого справедливо соотношение:
х (г ) = е (г) х (г). (29)
Очевидно, что в рассматриваемом пространстве действительных функций единичный вектор является действительной функцией е (г) = 1. Для дальнейшего описания свойств дельта-вектора введем понятие площади вектора.
Определение 4: площадью вектора х пространства Гильберта, если в нем определен единичный вектор е, является действительное число 5, определяемое соотношением:
5 = (е, х). (30)
Докажем следующее свойство дельта-вектора.
Лемма 5. Площадь дельта-вектора всегда равна 1.
Найдем площадь дельта-вектора в соответствии с формулой (30):
5 = (е (г), 8( г)) = (е (г), 8( 0 – г)) = е (0) = 1, (31)
что и требовалось доказать.
Теперь рассмотрим интерполяционные возможности дельта-вектора. Для этого предположим, что имеется набор из N «смещенных» по оси £ функций вида 5 (£ – пТ). Предположим, что функции 5(£ – пТ) образуют полный ортогональный базис. В этом случае по этим
функциям можно разложить любой вектор пространства Н.
Теорема 2. Если в пространстве Гильберта можно задать полный ортогональный базис размерности N, состоящий из функций вида 5(£ – пТ), то любой вектор х (£) этого пространства может быть однозначно восстановлен по своим значениям в точках £ = пТ.
Доказательство. Так как, функции 5(£ – пТ) образуют полный ортогональный базис, то
вектор х(£) можно разложить по этому базису:
п=М + N
х(0 = I Хп5(£ – пТ), (32)
где N – размерность базиса рассматриваемого пространства; [М, М + N] – интервал значений п.
Остается только найти коэффициенты разложения по данному базису:
1 / / ч ~чЧ 1 / / ч ~ чЧ 1
|5(0|Г (х (&), 5(£ – пТ)) = 8(0) (х (&), 5(пТ – £)) = 8(5) х (пТ) • (33)
Таким образом, формула (32) принимает вид:
1 п=М + N
х(£) = ^Т I х(пТ)5(£ – пТ). (34)
5( 0) п=М
Это означает, что имея только отсчеты вектора х (£) в точках £ = пТ, можно полностью
восстановить весь вектор, что и требовалось доказать.
Приведем пример пространства, в котором существует дельта-вектор. Таким пространством является множество всех функций со спектром, ограниченным отрезком [- О, О]. Скалярным произведением векторов х (£) и у () этого пространства выберем известное соотношение [2]:
(х(£), у(£))= I х(£) у(£) Л. (35)
Исходя из формулы (9) получим, что для дельта-вектора 5(£) данного пространства справедливо соотношение:
х (г) = | х (т) 5 (г – т) ¿т, (36)
где х (£) – любой вектор рассматриваемого пространства.
Соотношение (36) – классическая свертка двух функций – х (£) и 5(£). Сразу оговоримся, что классическая дельта-функция Дирака в данном случае дельта-вектором выступать не может, так как ее спектр не ограничен интервалом [-О, О], следовательно, она не является вектором нашего пространства. Необходимо искать дельта-вектор среди функций с ограниченным спектром.
Как известно из теории [2], классическая свертка во временной области соответствует перемножению спектров функций в спектральной области. Подберем такую функцию 5(£),
№ШЩ Ш20Т0
спектр Л(ю) которой в отношении спектра X (ю) любой функции рассматриваемого пространства имеет такое свойство:
X (ю) = Л(ю) X (ю). (37)
Очевидно, что
а такой спектр имеет функция
Г1, юс [-0,0];
Л(ю) = < (38)
5( t ) = ^ . (39)
Известно, что смещенные по оси времени на интервалы пТ = п функции вида (39)
образуют полный ортогональный базис. С учетом того, что 5 (0) = О, а N , формула (34) приобретает вид широко известной интерполяционной формулы Котельникова [3]:
х(t)= Х х(пТ) 51п 0(t” пТ) х(t) А ^() 0(1 – пТ) &
где Т = В заключение сформулируем основные выводы по проведенной работе.
1. Дельта-функция Дирака не является уникальным математическим объектом. Существуют пространства Гильберта, в которых имеется вектор, обладающий свойствами дельта-функции в отношении всех векторов своего пространства.
2. Площадь дельта-вектора равна единице.
3. Квадрат нормы (энергия) дельта-вектора равен значению этого вектора в точке 0.
4. Если в пространстве Гильберта, в котором определены ортогональный базис и свертка, существует дельта-вектор, этот вектор единственный и может быть стандартно вычислен из любого базиса этого пространства.
5. Дельта-вектор обладает свойством симметрии.
6. В пространстве функций, ограниченных по Котельникову, существует дельта-вектор, определяемый формулой (39).
7. Введение дельта-вектора в различные пространства Гильберта позволяет более адекватно строить информационные системы (в том числе и для железнодорожного транспорта), повышать точность обработки данных и уменьшать вероятность ошибки.
Список литературы
1. Фрид, Э. Элементарное введение в абстрактную алгебру [Текст] / Э. Фрид. -М.: Мир, 1979. – 260 с.
2. Кудрявцев, Л. Д. Курс математического анализа: в 2 т. [Текст] / Л. Д. Кудрявцев; Учебник. – М.: Высшая школа, 1981. – 2 т. – 584 с.
3. Романюк, Ю. А. Основы цифровой обработки сигналов: в 3 т. [Текст] / Ю. А. Рома-нюк / МФТИ. – М., 2005. – 3 т. – 332 с.
ЛИНЕЙНАЯ АЛГЕБРА ПРОСТРАНСТВО ГИЛЬБЕРТА СВЕРКА ДЕЛЬТА-ФУНКЦИЯ ТЕОРЕМА КОТЕЛЬНИКОВА linear algebra hilbert space convolution delta function kotelnikov theorem
Таким образом, использование имитационного моделирования в совокупности с разработанным методом позволяет априорно определять расход электрической энергии на технологические процессы ремонта подвижного состава, повышая эффективность использования электрической энергии. Полученное таким способом значение расхода электрической энергии является технологически обоснованным, имеет слабую привязку к предыстории потребления и учитывает действительные характеристики исследуемого технологического процесса, режимы использования технологического оборудования.
Список литературы
1. Пашков, Д. В. Выявление отклонений параметров электропотребления в рамках исследуемого технологического процесса от оптимальных значений [Текст] / Д. В. Пашков, А. В. Пономарев // Обеспечение экономически целесообразных условий работы железных дорог на основе оптимизации режимов работы электротехнических комплексов: Межвуз. те-мат. сб. науч. тр. / Омский гос. ун-т путей сообщения. – Омск, 2008. – С. 55 – 58.
2. Пашков, Д. В. Повышение эффективности планирования и нормирования расхода электрической энергии на технологические нужды с применением имитационного моделирования [Текст] / Д. В. Пашков, А. В. Пономарев // Научные проблемы транспорта Сибири и Дальнего Востока. – 2009. – №№ 2. – С. 261 – 263.
3. Борщев, А. В. Применение имитационного моделирования в России – состояние на 2007 г. [Текст] / А. В. Борщев // Материалы 3-й всерос. науч.-практ. конф. по имитационному моделированию ИММОД 2007 / Центральный научно-исследовательский институт технологии судостроения. – СПб, 2007. – С. 11 – 16.
4. Сетевое планирование ремонта подвижного состава [Текст] / С. Г. Шантаренко, М. Ф. Капустьян и др. // Железнодорожный транспорт. – 2009. – N° 2. – С. 48, 49.
5. Орлов, А. И. Прикладная статистика [Текст] / А. И. Орлов. – М.: Экзамен, 2006. -672 с.
УДК 004.62:517.98
С. С. Грицутенко
ВВЕДЕНИЕ ПОНЯТИЯ «ДЕЛЬТА-ВЕКТОР» В ПРОСТРАНСТВЕ ГИЛЬБЕРТА ДЛЯ КОРРЕКТНОГО ПРЕДСТАВЛЕНИЯ ДАННЫХ В ИНФОРМАЦИОННЫХ СИСТЕМАХ
В статье вводится понятие дельта-вектора в пространстве Гильберта. Доказывается теорема, что таких векторов в каждом конкретном пространстве не может быть больше одного. Приводится формула для вычисления данного вектора в том случае, если он существует. Доказывается теорема о разложении остальных векторов пространства в ряд смещенных дельта-векторов и показывается взаимосвязь этой теоремы с теоремой Котельникова.
Железнодорожный транспорт является потребителем новейших достижений в фундаментальной науке, которая уделяет большое внимание общетехническим дисциплинам: связи, измерениям, системам управления и контроля. В настоящее время в перечисленных областях науки идет ревизия используемого математического аппарата, так как существующие методики уже не обеспечивают необходимой точности обработки сигналов. В данной статье рассматриваются новые математические подходы к представлению сигналов, позволяющие более адекватно строить алгоритмы связи и измерения.
В математике и физике используется понятие дельта-функции. Это очень удобный математический объект, позволяющий эффективно решать многие научные задачи. К сожалению, при работе с дельта-функцией возникают и серьезные проблемы. Например, нельзя пе-
жмт
Ш20Т0
ремножать дельта-функции. Дифференцирование дельта-функций также приводит к весьма неоднозначным результатам. Иногда применение дельта-функции является причиной появления нескольких взаимоисключающих решений для одной задачи.
В данной статье дельта-функция рассматривается под другим углом – это не есть раз и навсегда заданная функция. Существуют пространства векторов, среди которых можно найти вектор, у которого есть все свойства дельта-функции по отношению к векторам своего пространства. Предположим, что задано пространство Гильберта Н. Пусть х (t), у (t) и г ) -произвольные векторы пространства Н, являющиеся действительными функциями переменной t, принадлежащей некому множеству Т :
{х,у (0, гН, (1)
где t е Т. При этом если х (t) – любой вектор пространства Н, то и х (t – т) е Н при любом теТ.
Следовательно, на множестве Н задано также и скалярное произведение двух векторов [1]:
(х(0, у(0). (2)
Определим на базе скалярного произведения (2) двух произвольных векторов пространства Гильберта понятие свертки.
Определение 1: сверткой двух произвольных векторов пространства Гильберта является третий вектор этого же пространства, получаемый из соотношения:
г (t) = х (t) • у (t) = (х (т), у (t -т)). (3)
Докажем для свертки свойство коммутативности.
Лемма 1. В отношении свертки двух произвольных векторов пространства Гильберта истинно соотношение:
х (^ у (г) = у (^ х (^. (4)
Действительно:
х ^ )• у ^) = (х (т), у ^-т)) = (у (t-т), х (т)). (5)
С учетом подстановки в уравнение (5) г = t – т и т = t – г имеем:
(у (t – т), х (т)) = (у (г), х (t – г)) = у (t) • х (t), (6)
что и требовалось доказать.
На базе введенного понятия свертки (3) определяем дельта-вектор пространства Гильберта.
Определение 2: дельта-вектором пространства Гильберта Н, на котором определена свертка, называется такой вектор 5(t), в отношении которого выполняется условие:
х (г ) = х ^ ) , (7)
где х (t) – любой вектор пространства Н.
Теорема 1. Если в пространстве Гильберта, в котором определены ортогональный базис {п (t)} и свертка, существует дельта-вектор, этот вектор единственный и может быть вычислен по формуле:
§(t) = Е п (t) п (0). (8)
Доказательство. Пусть х (t) – произвольный вектор пространства Гильберта. По определению дельта-вектора (7) имеем:
х (t) = х (t) • 5 (t) = (х (т), 5 (t -т)). (9)
Разложим векторы х(1) и 5(t) по базису {п (t)}:
х(т) = Хап (т); (10)
5(t-т) = XЬ (t)п (т)
(11)
где а. и Ь. – коэффициенты разложения. С учетом равенства Парсеваля формула (9) преобразуется следующим образом:
х(t) = (х(т),5(t-т)) = ХаЬ (t). (12)
Разложим выражение (12) по базису х(t) и получим следующее:
X ап (t )=Х аЬ< (t).
(13)
Так как х (t) – любой вектор, то коэффициенты {а. } могут быть любыми, кроме того, они независимы. Следовательно, равенство (13) может быть истинно только при условии, что
П (t ) = Ь (t). (14)
Таким образом, любой вектор 5(t -т) раскладывается единственным образом в любом базисе:
а вектор 5(t) соответственно
5(-т) = X П (t) П (т),
5( t )=5( t – 0 ) = Х п (t) П (0).
(15)
(16)
Докажем некоторые свойства дельта-вектора пространства Гильберта. Л е м м а 2: квадрат нормы (или энергия) дельта-вектора пространства Гильберта всегда равен 5(0):
Имеем:
|8( t 2 = 5( 0).
|5( t )| Г = (8( t), 5( t)),
(17)
(18)
вводим подстановку: / (-t) = 5 (t), / (t) = 5 (-):
(5( t), 5( t))=(5( t), / (-t))=(5( t), / (0 -1)).
используем свойство коммутативности свертки:
№ШЩ
шш
(8(0, / (0 – г)) = (/ (г), 5( 0 – г)) = /(0) = 5(-0) = 8( 0), (20)
что и требовалось доказать.
Рассмотрим другое важное свойство дельта-вектора – четность (симметричность). Для доказательства этого сначала докажем свойство свертки, представленной в лемме 3. Лемма 3: для любого произвольного х и Т истинно соотношение:
(х (г), 8(Т – г)) = (х (г), 8(г – Т)). (21)
В формулу (х (г), 8 (г – Т)) введем подстановку: г – Т = Т – т, г = 2Т -т:
(х (г), 8 (г – Т)) = (х (2Т -т), 8 (Т -т)). (22)
Исходя из определения дельта-вектора получаем:
( х ( 2Т-т), 8(Т-т))= х ( 2Т-Т) = х (Т) = (х (г), 8(Т-г)), (23)
что и требовалось доказать.
Теперь можно доказать четность дельта-вектора.
Лемма 4: для любого произвольного Т истинно соотношение:
8(Т) = 8(-Т). (24)
Как следствие леммы 3, истинны утверждения, что
(8(г), 8(г – Т)) = 8(Т); (25)
(8 (г – Т), 8( г)) = 8(-Т). (26)
Однако из определения скалярного произведения
(8(г),8(г -Т)) = (8(г -Т),8(г)), (27)
следовательно,
8(Т) = 8(-Т), (28)
что и требовалось доказать.
Введем в рассматриваемое пространство понятие единичного вектора. Определение 3: Единичным вектором е (г) будем считать такой вектор, для которого справедливо соотношение:
х (г ) = е (г) х (г). (29)
Очевидно, что в рассматриваемом пространстве действительных функций единичный вектор является действительной функцией е (г) = 1. Для дальнейшего описания свойств дельта-вектора введем понятие площади вектора.
Определение 4: площадью вектора х пространства Гильберта, если в нем определен единичный вектор е, является действительное число 5, определяемое соотношением:
5 = (е, х). (30)
Докажем следующее свойство дельта-вектора.
Лемма 5. Площадь дельта-вектора всегда равна 1.
Найдем площадь дельта-вектора в соответствии с формулой (30):
5 = (е (г), 8( г)) = (е (г), 8( 0 – г)) = е (0) = 1, (31)
что и требовалось доказать.
Теперь рассмотрим интерполяционные возможности дельта-вектора. Для этого предположим, что имеется набор из N «смещенных» по оси £ функций вида 5 (£ – пТ). Предположим, что функции 5(£ – пТ) образуют полный ортогональный базис. В этом случае по этим
функциям можно разложить любой вектор пространства Н.
Теорема 2. Если в пространстве Гильберта можно задать полный ортогональный базис размерности N, состоящий из функций вида 5(£ – пТ), то любой вектор х (£) этого пространства может быть однозначно восстановлен по своим значениям в точках £ = пТ.
iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
Доказательство. Так как, функции 5(£ – пТ) образуют полный ортогональный базис, то
вектор х(£) можно разложить по этому базису:
п=М + N
х(0 = I Хп5(£ – пТ), (32)
п = М
где N – размерность базиса рассматриваемого пространства; [М, М + N] – интервал значений п.
Остается только найти коэффициенты разложения по данному базису:
1 / / ч ~чЧ 1 / / ч ~ чЧ 1
х =
|5(0|Г (х (‘), 5(£ – пТ)) = 8(0) (х (‘), 5(пТ – £)) = 8(5) х (пТ) • (33)
Таким образом, формула (32) принимает вид:
1 п=М + N
х(£) = ^Т I х(пТ)5(£ – пТ). (34)
5( 0) п=М
Это означает, что имея только отсчеты вектора х (£) в точках £ = пТ, можно полностью
восстановить весь вектор, что и требовалось доказать.
Приведем пример пространства, в котором существует дельта-вектор. Таким пространством является множество всех функций со спектром, ограниченным отрезком [- О, О]. Скалярным произведением векторов х (£) и у () этого пространства выберем известное соотношение [2]:
¥
(х(£), у(£))= I х(£) у(£) Л. (35)
—¥
Исходя из формулы (9) получим, что для дельта-вектора 5(£) данного пространства справедливо соотношение:
¥
х (г) = | х (т) 5 (г – т) ¿т, (36)
—¥
где х (£) – любой вектор рассматриваемого пространства.
Соотношение (36) – классическая свертка двух функций – х (£) и 5(£). Сразу оговоримся, что классическая дельта-функция Дирака в данном случае дельта-вектором выступать не может, так как ее спектр не ограничен интервалом [-О, О], следовательно, она не является вектором нашего пространства. Необходимо искать дельта-вектор среди функций с ограниченным спектром.
Как известно из теории [2], классическая свертка во временной области соответствует перемножению спектров функций в спектральной области. Подберем такую функцию 5(£),
№ШЩ Ш20Т0
спектр Л(ю) которой в отношении спектра X (ю) любой функции рассматриваемого пространства имеет такое свойство:
X (ю) = Л(ю) X (ю). (37)
Очевидно, что
а такой спектр имеет функция
Г1, юс [-0,0];
Л(ю) = < (38)
5( t ) = ^ . (39)
Известно, что смещенные по оси времени на интервалы пТ = п функции вида (39)
образуют полный ортогональный базис. С учетом того, что 5 (0) = О, а N , формула (34) приобретает вид широко известной интерполяционной формулы Котельникова [3]:
х(t)= Х х(пТ) 51п 0(t” пТ) х(t) А ^() 0(1 – пТ) ‘
Т 2я
где Т = –
В заключение сформулируем основные выводы по проведенной работе.
1. Дельта-функция Дирака не является уникальным математическим объектом. Существуют пространства Гильберта, в которых имеется вектор, обладающий свойствами дельта-функции в отношении всех векторов своего пространства.
2. Площадь дельта-вектора равна единице.
3. Квадрат нормы (энергия) дельта-вектора равен значению этого вектора в точке 0.
4. Если в пространстве Гильберта, в котором определены ортогональный базис и свертка, существует дельта-вектор, этот вектор единственный и может быть стандартно вычислен из любого базиса этого пространства.
5. Дельта-вектор обладает свойством симметрии.
6. В пространстве функций, ограниченных по Котельникову, существует дельта-вектор, определяемый формулой (39).
7. Введение дельта-вектора в различные пространства Гильберта позволяет более адекватно строить информационные системы (в том числе и для железнодорожного транспорта), повышать точность обработки данных и уменьшать вероятность ошибки.
Список литературы
1. Фрид, Э. Элементарное введение в абстрактную алгебру [Текст] / Э. Фрид. -М.: Мир, 1979. – 260 с.
2. Кудрявцев, Л. Д. Курс математического анализа: в 2 т. [Текст] / Л. Д. Кудрявцев; Учебник. – М.: Высшая школа, 1981. – 2 т. – 584 с.
3. Романюк, Ю. А. Основы цифровой обработки сигналов: в 3 т. [Текст] / Ю. А. Рома-нюк / МФТИ. – М., 2005. – 3 т. – 332 с.
Путь и перемещение, теория и онлайн калькуляторы
Путь и перемещение
При своем движении материальная точка описывает некоторую линию, которую называют ее траекторией движения. Траектория может быть прямой линией, а может представлять собой кривую.
Путь
Определение
Путь – длина участка траектории, который прошла материальная точка за рассматриваемый отрезок времени. Путь – это скалярная величина.
При прямолинейном движении в одном направлении пройденный путь ($Delta s$) равен модулю изменения координаты тела. Так, если тело двигалось по оси X, то путь можно найти как:
[Delta s=left|x_2-x_1right|left(1right),]
где $x_1$ – координата начального положения тела; $x_2$ – конечная координата тела.
Его можно вычислить, если известен модуль скорости ($v=v_x$):
[Delta s=vt left(2right),]
где $t$ – время движения тела.
Графиком, который отображает зависимость пути от времени при равномерном прямолинейном движении, является прямая (рис.1). С увеличением величины скорости увеличивается угол наклона прямой относительно оси времени.
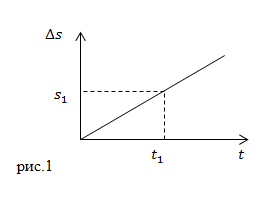
Если по графику $Delta s(t)$ необходимо найти путь, который проделало тело за время $t_1$, то из точки $t_1$ на оси времени проводят перпендикуляр до пересечения с графиком $Delta s(t)$. Затем из точки пересечения восстанавливают перпендикуляр к оси $Delta s$. На пересечении оси и перпендикуляра получают точку ${Delta s}_1$, которая соответствует пройденному пути за время от $t=0 c$ до $t_1$.
Путь не бывает меньше нуля и не может уменьшаться при движении тела.
Перемещение
Определение
Перемещением называют вектор, который проводят из начального положения движущейся материальной точки в ее конечное положение:
[Delta overline{r}=overline{r }left(t+Delta tright)-overline{r }left(tright)left(3right).]
Вектор перемещения численно равен расстоянию между конечной и начальной точками и направлен от начальной точки к конечной.
Приращение радиус-вектора материальной точки – это перемещение ($Delta overline{r}$).
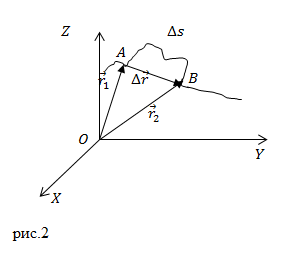
В декартовой системе координат радиус-вектор точки представляют в виде:
[overline{r }left(tright)=xleft(tright)overline{i}+yleft(tright)overline{j}+zleft(tright)overline{k}left(4right),]
где $overline{i}$, $overline{j}$,$ overline{k}$ – единичные орты осей X,Y,Z. Тогда $Delta overline{r}$ равен:
[Delta overline{r}=left[xleft(t+Delta tright)-xleft(tright)right]overline{i}+left[yleft(t+?tright)-yleft(tright)right]overline{j}+left[zleft(t+?tright)-zleft(tright)right]overline{k}left(5right).]
При прямолинейном движении вектор перемещения совпадает с соответствующим участком траектории и длина вектора перемещения равна пройденному точкой пути:
[left|Delta overline{r}right|=Delta s left(6right).]
Длину вектора перемещения (как и любого вектора) можно обозначать как $left|Delta overline{r}right|$ или просто $Delta r$ (без указания стрелки).
Если тело совершает несколько перемещений, то их можно складывать по правилам сложения векторов:
[Delta overline{r}=Delta {overline{r}}_1+Delta {overline{r}}_2+dots left(7right).]
Если направление движения тела изменяется, то модуль вектора перемещения не равен пройденному телом пути.
Примеры задач на путь и перемещение
Пример 1
Задание: Мяч бросили вертикально вверх от поверхности Земли. Он долетел до высоты 20 м. и упал на Землю. Чему равен путь, который прошел мяч, каков модуль перемещения?
Решение: Сделаем рисунок.
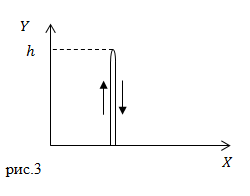
В нашей задаче мяч движется прямолинейно сначала вверх, затем вниз. Так как путь – длина траектории, то получается, что мяч дважды прошел расстояние h, следовательно:
[Delta s=2h.]
Перемещение – направленный отрезок, соединяющий начальную точку и конечную при движении тела, но тело начало движение из той же точки, в которую вернулось, следовательно, перемещение мяча равно нулю:
[Delta r=0.]
Ответ: $ Путь Delta s=2h$. Перемещение $Delta r=0$
Пример 2
Задание: В начальный момент времени тело находилось в точке с координатами $(x_0=3;; y_0=1)$(см). Через некоторый промежуток времени оно переместилось в точку координаты которой ($x=2;;y=4$) (см). Каковы проекции вектора перемещения на оси X и Y?
Решение: Сделаем рисунок.
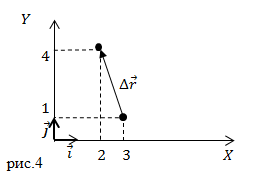
Радиус – вектор начальной точки запишем как:
[{overline{r }}_0left(tright)=x_0left(tright)overline{i}+y_0left(tright)overline{j}=3overline{i}+1overline{j}left(2.1right).]
Радиус – вектор конечной точки имеет вид:
[overline{r}left(tright)=xleft(tright)overline{i}+yleft(tright)overline{j}=2overline{i}+4overline{j}left(2.2right).]
Вектор перемещения представим как:
[Delta overline{r}=left[xleft(tright)-x_0left(tright)right]overline{i}+left[уleft(tright)-у_0left(tright)right]overline{j}=left[2-3right]+left[1-4right]overline{j}=-1overline{i}+3overline{j}(2.3).]
Из формулы видим, что:
[Delta r_x=-1;;Delta r_y=3. ]
Ответ: $Delta r_x=-1;;Delta r_y=3 $
Читать дальше: равнодействующая всех сил.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Любое тело, обладающее скоростью, обладает импульсом.
Скорость тела будет меняться, когда на него подействует сила и появится ускорение. Об этом сообщает второй закон Ньютона. А если изменяется скорость тела, то будет изменяться его импульс.
Второй закон Ньютона в импульсной форме описывает изменение импульса тела под действием силы.
Формула второго закона Ньютона в импульсной форме
Импульсная форма записи второго закона выглядит так:
[ large boxed{ overrightarrow{Delta p} = overrightarrow{ F cdot Delta t} } ]
Словами это выражение можно сформулировать так:
[ large boxed { text {Изменение импульса тела = импульсу силы }} ]
(overrightarrow{Delta p} left( text{кг} cdot frac{text{м}}{c}right) ) – вектор изменения импульса тела;
( overrightarrow{ F cdot Delta t} left( H cdot text{м} right) ) – вектор импульса силы;
Слева и справа в формуле находятся два вектора. Так как между ними записан знак равенства, значит у векторов (overrightarrow{Delta p} ) и ( overrightarrow{ F cdot Delta t} ) совпадают обе характеристики — направление и длина.
С помощью математики фразу «длины векторов равны» можно записать так:
( left| overrightarrow{Delta p} right | = left| overrightarrow{ F cdot Delta t} right | )
Как посчитать длину вектора, и как ее обозначать, читайте тут.
Пояснения и вывод формулы с помощью геометрии
Чтобы получить импульсный вид записи для второго закона, рассмотрим такую задачу.
Представим, что мы склонились над бильярдным столом и смотрим на него сверху. А в это время по столу катится бильярдный шар с какой-то постоянной скоростью.
Примечание: с постоянной скоростью, значит — с одной и той же скоростью. О такой скорости физики часто говорят «с неизменной скоростью», а математики применяют для нее запись ( vec{v} = const ).
Пусть для определенности масса шара равна двум килограммам.
( m = 2 left( text{кг} right) )
Пусть до того, как мы подействовали на шар, он двигался по столу в направлении, указанном на рисунке 1а. Шар вначале движется по горизонтали (рис. 1а), вектор начальной скорости обозначен ( vec{v_{0}} ).
Подействуем теперь на шар, ударив его кием под углом к начальной скорости. Направление, вдоль которого мы ударили, показано на рисунке 1б с помощью вектора силы ( vec{F} ) .
После удара шар будет катиться уже не по горизонтали на рисунке. Физики скажут: направление движения шара изменилось. Направление, в котором шар движется после удара, обозначено вектором ( vec{v} ) на рисунке 2в. Вектор ( vec{v} ) — конечная скорость шара.

Рис. 1. Направление движения шара а) — до удара, в) – после удара, б) – в эту сторону шар подтолкнули силой
Нам известны начальная и конечная скорости тела, а также, его масса. Мы можем вычислить импульс тела до удара (рис 2а), и после удара (рис 2б).
( m cdot vec{v_{0}} = vec{p_{0}}) – импульс тела до удара (начальный);
( m cdot vec{v} = vec{p}) – импульс тела после удара (конечный).

Рис. 2. Вектор скорости тела умножаем на скаляр — массу тела, получаем вектор импульса тела
Обратите внимание, что у векторов начального импульса ( vec{p_{0}}) и начальной скорости ( vec{v_{0}}) направления совпадают. Вектор конечного импульса ( vec{p}), так же, сонаправлен с вектором ( vec{v}) конечной скорости тела.
Для удобства совместим начала векторов ( vec{p_{0}}) и ( vec{p}) (рис. 3). Зададимся вопросом, как из вектора начального импульса ( vec{p_{0}}) получить конечный ( vec{p}) вектор?

Рис. 3. Начала векторов импульса тела до (черный) и после (красный) удара совмещены
Очевидно, нужно к вектору ( vec{p_{0}}) прибавить еще один вектор. Обозначим этот вектор ( overrightarrow{Delta p} ), он представлен на рисунке 4.

Рис. 4. К начальному вектору импульса прибавили вектор изменения импульса и получили конечный вектор импульса тела
Подробнее о том, как складывать векторы, написано тут.
Сумму можно записать так:
( vec{p_{0}} + overrightarrow{Delta p} = vec{p} )
Это уравнение записано в векторном виде. Стрелки над символами подчеркивают тот факт, что векторы складывают с помощью геометрии, то есть, учитывают их направления.
Выразим теперь вектор, обозначенный ( overrightarrow{Delta p} ). Для этого, из обеих частей уравнения вычтем вектор ( vec{p_{0}} ).
( overrightarrow{Delta p} = vec{p} — vec{p_{0}} )
Видно, что вектор ( overrightarrow{Delta p} ) – это разница между конечным ( vec{p} ) и начальным ( vec{p_{0}} ) векторами импульса тела.
Физики для вектора ( overrightarrow{Delta p} ) используют такое название:
( overrightarrow{Delta p} left( text{кг} cdot frac{text{м}}{c} right) ) – вектор изменения импульса тела.
Рассмотрим теперь совместно векторы ( overrightarrow{Delta p} ) и ( vec{F} ) на одном рисунке (рис. 5).

Рис. 5. Вектор изменения импульса тела сонаправлен с вектором силы, действующей на тело, длины векторов отличаются
Направления векторов совпадают, а длина – различается.
Примечание: Математики вместо выражения «длина вектора» употребляют термин «модуль вектора».
Предположим, у нас есть точный хронометр и мы измерили кусочек времени, в течение которого сила действовала на бильярдный шар.
Умножим теперь вектор ( vec{F} ) на этот промежуток времени ( Delta t ) — скаляр. Результат умножения представлен на рисунке 6.

Рис. 6. Вектор силы, действующей на тело, умножаем на скаляр – промежуток времени, в течение которого сила действовала, получили вектор импульса силы
Из рисунка 6 видно, что у векторов (overrightarrow{Delta p} ) и ( overrightarrow{ F cdot Delta t} ) совпадают не только направления, но и длины.
Если у векторов совпадают обе характеристики, то их можно приравнять. Подробнее о том, какие у векторов есть характеристики, написано тут.
[ large boxed{ overrightarrow{Delta p} = overrightarrow{ F cdot Delta t} } ]
Это выражение называют вторым законом Ньютона, записанным в импульсной форме.
Примечания
1). Сумму векторов
( vec{p_{0}} + overrightarrow{Delta p} = vec{p} )
можно теперь переписать в таком виде:
( vec{p_{0}} + overrightarrow{ F cdot Delta t} = vec{p} )
2). Складывать можно векторы, у которых размерность совпадает.
О сложении векторов простым языком написано тут.
Обратим внимание на размерность.
(overrightarrow{Delta p} left( text{кг} cdot frac{text{м}}{c}right) )
( overrightarrow{ F cdot Delta t} left( H cdot c right) )
На первый взгляд, она отличается, но с помощью простых преобразований можно показать, что
[ large 1 text{кг} cdot frac{ 1text{м}}{1 c} = 1 H cdot 1 c ]
Вывод формулы с помощью алгебры
Второй закон Ньютона в импульсной форме можно получить из алгебраических соображений.
Пусть для определенности векторы скоростей тела и вектор силы направлены вдоль одной прямой линии, т. е. движение прямолинейное.
Запишем второй закон Ньютона:
(displaystyle vec{a} = frac{vec{F}}{m})
Применим выражение для ускорения
(displaystyle vec{a} = frac{overrightarrow{Delta v}}{Delta t })
В этих уравнениях слева находится величина (vec{a}). Так как левые части уравнений равны, можно приравнять правые их части
(displaystyle frac{vec{F}}{m} = frac{vec{Delta v}}{Delta t })
Полученное выражение является пропорцией. Применив одно из свойств пропорции, получим такое выражение:
( overrightarrow{F cdot Delta t} = overrightarrow {Delta vcdot m} )
В правой части находится вектор (overrightarrow {Delta v} = vec {v} — vec {v_{0}} ) – это разница между конечной и начальной скоростью.
Преобразуем правую часть
(overrightarrow{Delta v}cdot m = left( vec {v} — vec {v_{0}} right) cdot m)
Раскрыв скобки, получим
(overrightarrow{Delta v}cdot m = vec {v} cdot m — vec {v_{0}} cdot m )
Вспомним обозначения:
(vec {v} cdot m = vec {p})
(vec {v_{0}} cdot m = vec {p_{0}} )
Подставляя их, получим
(overrightarrow{Delta v}cdot m = vec {p} — vec {p_{0}})
(vec {p} — vec {p_{0}}=overrightarrow{Delta p})
Или, сокращенно
(overrightarrow{Delta v}cdot m = overrightarrow{Delta p})
То есть, вектор (overrightarrow {Delta vcdot m}) – это вектор (overrightarrow {Delta p}).
Тогда второй закон Ньютона в импульсной форме запишем так
( overrightarrow{F cdot Delta t} = overrightarrow{Delta p})
