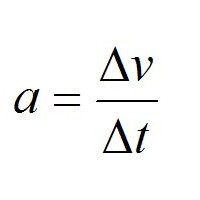Как найти дельту астрономия

From Wikipedia, the free encyclopedia

Orientation of astronomical coordinates

A star’s   galactic,   ecliptic, and   equatorial coordinates, as projected on the celestial sphere. Ecliptic and equatorial coordinates share the   March equinox as the primary direction, and galactic coordinates are referred to the   galactic center. The origin of coordinates (the “center of the sphere”) is ambiguous; see celestial sphere for more information.

Astronomical (or celestial) coordinate systems are organized arrangements for specifying positions of satellites, planets, stars, galaxies, and other celestial objects relative to physical reference points available to a situated observer (e.g. the true horizon and north to an observer on Earth’s surface).^[1] Coordinate systems in astronomy can specify an object’s position in three-dimensional space or plot merely its direction on a celestial sphere, if the object’s distance is unknown or trivial.

Spherical coordinates, projected on the celestial sphere, are analogous to the geographic coordinate system used on the surface of Earth. These differ in their choice of fundamental plane, which divides the celestial sphere into two equal hemispheres along a great circle. Rectangular coordinates, in appropriate units, have the same fundamental (x, y) plane and primary (x-axis) direction, such as an axis of rotation. Each coordinate system is named after its choice of fundamental plane.

Coordinate systems[edit]

The following table lists the common coordinate systems in use by the astronomical community. The fundamental plane divides the celestial sphere into two equal hemispheres and defines the baseline for the latitudinal coordinates, similar to the equator in the geographic coordinate system. The poles are located at ±90° from the fundamental plane. The primary direction is the starting point of the longitudinal coordinates. The origin is the zero distance point, the “center of the celestial sphere”, although the definition of celestial sphere is ambiguous about the definition of its center point.

Coordinate system[2]	Center point (origin)	Fundamental plane (0° latitude)	Poles	Coordinates	Primary direction (0° longitude)
Latitude	Longitude
Horizontal (also called alt–az or el-az)	Observer	Horizon	Zenith, nadir	Altitude (a) or elevation	Azimuth (A)	North or south point of horizon
Equatorial	Center of the Earth (geocentric), or Sun (heliocentric)	Celestial equator	Celestial poles	Declination (δ)	Right ascension (α) or hour angle (h)	March equinox
Ecliptic	Ecliptic	Ecliptic poles	Ecliptic latitude (β)	Ecliptic longitude (λ)
Galactic	Center of the Sun	Galactic plane	Galactic poles	Galactic latitude (b)	Galactic longitude (l)	Galactic Center
Supergalactic		Supergalactic plane	Supergalactic poles	Supergalactic latitude (SGB)	Supergalactic longitude (SGL)	Intersection of supergalactic plane and galactic plane

Horizontal system[edit]

The horizontal, or altitude-azimuth, system is based on the position of the observer on Earth, which revolves around its own axis once per sidereal day (23 hours, 56 minutes and 4.091 seconds) in relation to the star background. The positioning of a celestial object by the horizontal system varies with time, but is a useful coordinate system for locating and tracking objects for observers on Earth. It is based on the position of stars relative to an observer’s ideal horizon.

Equatorial system[edit]

The equatorial coordinate system is centered at Earth’s center, but fixed relative to the celestial poles and the March equinox. The coordinates are based on the location of stars relative to Earth’s equator if it were projected out to an infinite distance. The equatorial describes the sky as seen from the Solar System, and modern star maps almost exclusively use equatorial coordinates.

The equatorial system is the normal coordinate system for most professional and many amateur astronomers having an equatorial mount that follows the movement of the sky during the night. Celestial objects are found by adjusting the telescope’s or other instrument’s scales so that they match the equatorial coordinates of the selected object to observe.

Popular choices of pole and equator are the older B1950 and the modern J2000 systems, but a pole and equator “of date” can also be used, meaning one appropriate to the date under consideration, such as when a measurement of the position of a planet or spacecraft is made. There are also subdivisions into “mean of date” coordinates, which average out or ignore nutation, and “true of date,” which include nutation.

Ecliptic system[edit]

The fundamental plane is the plane of the Earth’s orbit, called the ecliptic plane. There are two principal variants of the ecliptic coordinate system: geocentric ecliptic coordinates centered on the Earth and heliocentric ecliptic coordinates centered on the center of mass of the Solar System.

The geocentric ecliptic system was the principal coordinate system for ancient astronomy and is still useful for computing the apparent motions of the Sun, Moon, and planets.^[3]

The heliocentric ecliptic system describes the planets’ orbital movement around the Sun, and centers on the barycenter of the Solar System (i.e. very close to the center of the Sun). The system is primarily used for computing the positions of planets and other Solar System bodies, as well as defining their orbital elements.

Galactic system[edit]

The galactic coordinate system uses the approximate plane of our galaxy as its fundamental plane. The Solar System is still the center of the coordinate system, and the zero point is defined as the direction towards the galactic center. Galactic latitude resembles the elevation above the galactic plane and galactic longitude determines direction relative to the center of the galaxy.

Supergalactic system[edit]

The supergalactic coordinate system corresponds to a fundamental plane that contains a higher than average number of local galaxies in the sky as seen from Earth.

Converting coordinates[edit]

Conversions between the various coordinate systems are given.^[4] See the notes before using these equations.

Notation[edit]

Hour angle ↔ right ascension[edit]

Equatorial ↔ ecliptic[edit]

The classical equations, derived from spherical trigonometry, for the longitudinal coordinate are presented to the right of a bracket; dividing the first equation by the second gives the convenient tangent equation seen on the left.^[5] The rotation matrix equivalent is given beneath each case.^[6] This division is ambiguous because tan has a period of 180° (π) whereas cos and sin have periods of 360° (2π).

Equatorial ↔ horizontal[edit]

Azimuth (A) is measured from the south point, turning positive to the west.^[7]
Zenith distance, the angular distance along the great circle from the zenith to a celestial object, is simply the complementary angle of the altitude: 90° − a.^[8]

In solving the tan(A) equation for A, in order to avoid the ambiguity of the arctangent, use of the two-argument arctangent, denoted arctan(x,y), is recommended. The two-argument arctangent computes the arctangent of y/x, and accounts for the quadrant in which it is being computed. Thus, consistent with the convention of azimuth being measured from the south and opening positive to the west,

,

where

.

If the above formula produces a negative value for A, it can be rendered positive by simply adding 360°.

^[a]

Again, in solving the tan(h) equation for h, use of the two-argument arctangent that accounts for the quadrant is recommended. Thus, again consistent with the convention of azimuth being measured from the south and opening positive to the west,

,

where

Equatorial ↔ galactic[edit]

These equations^[14] are for converting equatorial coordinates to Galactic coordinates.

are the equatorial coordinates of the North Galactic Pole and is the Galactic longitude of the North Celestial Pole. Referred to J2000.0 the values of these quantities are:

If the equatorial coordinates are referred to another equinox, they must be precessed to their place at J2000.0 before applying these formulae.

These equations convert to equatorial coordinates referred to B2000.0.

Notes on conversion[edit]

• Angles in the degrees ( ° ), minutes ( ′ ), and seconds ( ″ ) of sexagesimal measure must be converted to decimal before calculations are performed. Whether they are converted to decimal degrees or radians depends upon the particular calculating machine or program. Negative angles must be carefully handled; –10° 20′ 30″ must be converted as −10° −20′ −30″.
• Angles in the hours ( ^h ), minutes ( ^m ), and seconds ( ^s ) of time measure must be converted to decimal degrees or radians before calculations are performed. 1^h = 15°; 1^m = 15′; 1^s = 15″
• Angles greater than 360° (2π) or less than 0° may need to be reduced to the range 0°−360° (0–2π) depending upon the particular calculating machine or program.
• The cosine of a latitude (declination, ecliptic and Galactic latitude, and altitude) are never negative by definition, since the latitude varies between −90° and +90°.
• Inverse trigonometric functions arcsine, arccosine and arctangent are quadrant-ambiguous, and results should be carefully evaluated. Use of the second arctangent function (denoted in computing as atn2(y,x) or atan2(y,x), which calculates the arctangent of y/x using the sign of both arguments to determine the right quadrant) is recommended when calculating longitude/right ascension/azimuth. An equation which finds the sine, followed by the arcsin function, is recommended when calculating latitude/declination/altitude.
• Azimuth (A) is referred here to the south point of the horizon, the common astronomical reckoning. An object on the meridian to the south of the observer has A = h = 0° with this usage. However, n Astropy’s AltAz, in the Large Binocular Telescope FITS file convention, in XEphem, in the IAU library Standards of Fundamental Astronomy and Section B of the Astronomical Almanac for example, the azimuth is East of North. In navigation and some other disciplines, azimuth is figured from the north.
• The equations for altitude (a) do not account for atmospheric refraction.
• The equations for horizontal coordinates do not account for diurnal parallax, that is, the small offset in the position of a celestial object caused by the position of the observer on the Earth’s surface. This effect is significant for the Moon, less so for the planets, minute for stars or more distant objects.
• Observer’s longitude (λ_o) here is measured positively westward from the prime meridian; this is contrary to current IAU standards.

See also[edit]

• Apparent longitude
• Azimuth – Horizontal angle from north or other reference cardinal direction
• Barycentric celestial reference system – Celestial coordinate system
• Celestial sphere – Imaginary sphere of arbitrarily large radius, concentric with the observer
• International Celestial Reference System and Frame – Current standard celestial reference system and frame
• Orbital elements – Parameters that uniquely identify a specific orbit
• Planetary coordinate system – Coordinate system for planets
• Terrestrial reference frame – The reference frame as one views from earth

Notes[edit]

References[edit]

External links[edit]

• NOVAS, the United States Naval Observatory’s Vector Astrometry Software, an integrated package of subroutines and functions for computing various commonly needed quantities in positional astronomy.
• SOFA, the IAU’s Standards of Fundamental Astronomy, an accessible and authoritative set of algorithms and procedures that implement standard models used in fundamental astronomy.
• This article was originally based on Jason Harris’ Astroinfo, which comes along with KStars, a KDE Desktop Planetarium for Linux/KDE.

ΔT (дельта T, Delta T, delta-T, deltaT, или DT) — разница между земным временем (TT) и всемирным временем (UT), то есть разница между идеальным равномерно текущим временем, определенным по атомным часам, и «астрономическим временем», определённым по вращению Земли вокруг своей оси.

Тонкости определения[править | править код]

В литературе, выпущенной в разное время, могут встречаться немного отличающиеся определения ΔT (в зависимости от того, какая шкала равномерного времени была рекомендована для использования в астрономических расчетах в тот или иной период):

• ΔT=ET−UT (до 1984 года)
• ΔT=TDT−UT (с 1984 по 2001 годы)
• ΔT=TT−UT(с 2001 года по настоящее время).

Кроме того, под «Всемирным временем» может подразумеваться одна из его версий (UT0, UT1 и т. д.). Поэтому в специализированной литературе принято указывать, что имеется в виду под ΔT, например «TDT — UT1», что означает «Динамическое земное время минус Всемирное время версии UT1».

Несмотря на некоторые изменения в определении, физический смысл ΔT не меняется — это разница между идеальным равномерно текущим временем и «временем», определённым по вращению Земли (которое замедляется, причём неравномерно).

О неравномерности вращения Земли вокруг своей оси[править | править код]

Всемирное время (UT) является шкалой времени, основанной на суточном вращении Земли, которое не вполне равномерно на относительно коротких интервалах времени (от дней до столетий), и поэтому любые измерения времени, основанные на такой шкале, не могут иметь точность лучше чем 10⁻⁸. Однако основной эффект проявляется на больших временах: на масштабах столетий приливное трение постепенно замедляет скорость вращения Земли примерно на 2,3 мс/сутки/век. Однако есть и другие причины, изменяющие скорость вращения Земли. Самой важной из них являются последствия таяния материкового ледникового щита в конце последнего ледникового периода. Это привело к уменьшению мощной нагрузки на земную кору и послеледниковой релаксации, сопровождающейся распрямлением и поднятием коры в приполярных областях — процесс, который продолжается и сейчас и будет продолжаться пока не будет достигнуто изостатическое равновесие. Этот эффект послеледниковой релаксации приводит к перемещению масс ближе к оси вращения Земли, что заставляет её вращаться быстрее (закон сохранения углового момента). Полученное из этой модели ускорение составляет около −0,6 мс/сутки/век.
Таким образом, полное ускорение (на самом деле замедление) вращения Земли, или изменение длины средних солнечных суток составляет +1,7 мс/сутки/век. Эта величина хорошо соответствует среднему темпу замедления вращения Земли за последние 27 столетий^[1].

Земное время (TT) является теоретически равномерной временной шкалой, определенной так, чтобы сохранить непрерывность с предшествующей равномерной шкалой эфемеридного времени (ET). ET основана на независимой от вращения Земли физической величине, предложенной (и принятой к применению) в 1948—1952 годах^[2] с намерением получить настолько однородную и не зависящую от гравитационных эффектов временную шкалу, насколько это возможно было в то время. Определение ET опиралось на солнечные таблицы Ньюкома, интерпретированные новым образом, чтобы учесть определенные расхождения в наблюдениях^[3].

Таблицы Ньюкома служили основой для всех астрономических солнечных эфемерид с 1900 по 1983 год. Изначально они были выражены (и в таком виде опубликованы) в терминах среднего времени по Гринвичу и средних солнечных суток^[4]. однако позднее, в особенности в отношении периода с 1960 по 1983 год, они трактовались как выраженные в рамках ET^[5], в соответствии с принятым в 1948—1952 годах предложением о переходе к ET. В свою очередь ET могло теперь рассматриваться в свете новых результатов^[6] как шкала времени, максимально близкая к среднему солнечному времени на интервале 1750 и 1890 годы (с серединой около 1820 года), поскольку именно в этом интервале проводились наблюдения, на основании которых были составлены таблицы Ньюкома. Хотя шкала TT является строго однородной (основана на единице секунды СИ, и каждая секунда строго равна каждой другой секунде), на практике она реализуется как Международное атомное время (TAI) с точностью около 10⁻¹⁴.

Определение дельта Т из наблюдений[править | править код]

Время, определяемое положением Земли (точнее, ориентацией Гринвичского меридиана относительно фиктивного среднего Солнца), является интегралом от скорости вращения. При интегрировании с учётом изменения длины суток на +1,7 мс/сутки/век и выборе начальной точки в 1820 году (примерная середина интервала наблюдений, использованных Ньюкомом для определения длины суток), для ΔT получается в первом приближении парабола 31×((Год − 1820)/100)² в секунд. Сглаженные данные, полученные на основе анализа исторических данных о наблюдениях полных солнечных затмений дают значения ΔT около +16800 с в −500 году, +10600 с в 0, +5700 с в 500, +1600 с в 1000 и +180 с в 1500 годах.

Для времени после изобретения телескопа ΔT определяются из наблюдений покрытий звезд Луной, что позволяет получить более точные и более частые значения величины. Поправка ΔT продолжала уменьшаться после XVI века, пока не достигла плато +11±6 с между 1680 и 1866 года. В течение трех десятилетий до 1902 она оставалась отрицательной с минимумом −6,64 с, затем начала увеличиваться до +63,83 с в 2000 году.

В будущем ΔT будет увеличиваться с нарастающей скоростью (квадратично). Это потребует добавления все большего числа секунд координации к Всемирному координированному времени (UTC), поскольку UTC должно поддерживаться с точностью в одну секунду относительно равномерной шкалы UT1. (Секунда СИ, используемая сейчас для UTC, уже в момент принятия была немного короче, чем текущее значение секунды среднего солнечного времени.^[7])

Физически нулевой меридиан для Универсального времени оказывается почти всегда восточнее меридиана земного времени как в прошлом, так и в будущем. +16800 с или 4⅔ часа соответствуют 70° в.д. Это означает, что в −500 году вследствие более быстрого вращения Земли солнечное затмение происходило на 70° восточнее положения, которое следует из расчетов с использованием равномерного времени TT.

Все значения ΔT до 1955 года зависят от наблюдений Луны, связанных либо с затмениями, либо с покрытиями. Сохранение углового момента в Системе Земля-Луна требует, чтобы угловой момент Земли вследствие приливного трения передавался Луне, увеличивая её угловой момент, что означает, что её расстояние до Земли должно увеличиваться, что, в свою очередь, вследствие третьего закона Кеплера приводит к замедлению обращения Луны вокруг Земли. Приведенные выше значения ΔT предполагают, что ускорение Луны, связанное с этим эффектом составляет величину dn/dt = −26″/век², где n — средняя угловая сидерическая скорость Луны.
Это близко к лучшим экспериментальным оценкам для dn/dt, полученным в 2002 году: −25,858±0,003″/век²^[8], и поэтому оценки ΔT, полученные ранее исходя из значения −26″/век², принимая во внимание неопределенности и эффекты сглаживания в экспериментальных наблюдениях, можно не пересчитывать. В наше время UT определяется по измерению ориентации Земли по отношению к инерциальной системе отсчета, связанной с внегалактическими радиоисточниками, с поправкой на принятое соотношение между сидерическим и солнечным временем. Эти измерения, проводимые в нескольких обсерваториях, координируются Международной службой вращения Земли (IERS).

Величины дельта Т[править | править код]

Для 1900—1995 годов значения приведены согласно «Астрономия на персональном компьютере», четвёртое издание, 2002 год, Монтенбрук О., Пфеглер Т., для 2000 года — из английской Вики.

Год	дельта Т, с
1900	-2,72
1905	3,86
1910	10,46
1915	17,20
1920	21,16
1925	23,62
1930	24,02
1935	23,93
1940	24,33
1945	26,77
1950	29,15
1955	31,07
1960	33,15
1965	35,73
1970	40,18
1975	45,48
1980	50,54
1985	54,34
1990	56,86
1995	60,82
2000	63,83
2005	64,69
2010	66,07

Вычисление дельта Т[править | править код]

Приближенная формула для вычисления дельта Т[править | править код]

С 1972 года по наше время ΔT можно рассчитать зная количество секунд координации по формуле:

где
32,184 секунд — разница между TT и TAI,
10 секунд — разница между TAI и UTC на начало 1972 года,
N — количество введенных с 1972 года секунд координации.

Формула дает погрешность не более 0,9 секунд. Например, на начало 1995 года было введено 19 секунд координации и формула дает ΔT=61,184 секунд, что лишь на 0,364 секунды превышает табличное значение.

Точная формула для вычисления дельта Т[править | править код]

Из бюллетеня А (Bulletin — A) Службы вращения земли IERS можно узнать разность между TAI и UTC (зависит от количества секунд координации, величина меняется редко) и между UT1 и UTC (величина постоянно меняется, в бюллетене даётся на полночь ежесуточно), тогда дельта Т можно вычислить точно по формуле:

Приблизительная формула вычисления дельта Т на будущее[править | править код]

Рассчитать дельта Т на будущее можно только приблизительно, ввиду того, что изменение вращения Земли недостаточно изучено. Тем не менее для расчёта, например, пути прохождения тени от солнечного затмения или времени покрытия звёзд Луной делать хотя бы приблизительный расчёт необходимо. Фред Эспеньяк  (англ.) (рус. при расчёте солнечных затмений на период 2005—2050 годов пользовался формулой^[10]

где y — год, для которого определяется дельта Т.

См. также[править | править код]

Приливное ускорение

Примечания[править | править код]

• McCarthy, D.D. & Seidelmann, P.K. TIME: From Earth Rotation to Atomic Physics. Weinheim: Wiley-VCH. (2009). ISBN 978-3-527-40780-4
• Morrison, L.V. & Stephenson, F. R. «Historical values of the Earth’s clock error ΔT and the calculation of eclipses» (pdf, 862 KB), Journal for the History of Astronomy 35 (2004) 327—336.
• Stephenson, F.R. Historical Eclipses and Earth’s Rotation. Cambridge University Press, 1997. ISBN 0-521-46194-4

• Stephenson, F. R. & Morrison, L.V. «Long-term fluctuations in the Earth’s rotation: 700 BC to AD 1990». Philosophical Transactions of the Royal Society of London, Series A 351 (1995) 165—202. JSTOR link. Includes evidence that the ‘growth’ in Delta-T is being modified by an oscillation with a wavelength around 1500 years; if that is true, then during the next few centuries Delta-T values will increase more slowly than is envisaged.

Ссылки[править | править код]

• Robert van Gent. Delta T: Terrestrial Time, Universal Time and Algorithms for Historical Periods
• Felix Verbelen. Delta T
• Fred Espenak. Eclipse Predictions and Earth’s Rotation
• Polynomial expressions for Delta T (ΔT)
• IERS Rapid Service-Prediction Center Values for Delta T.

Обновлено: 23.05.2023

В данной статье поговорим о знаке Дельта – что он из себя представляет, в каких сферах применяется и для чего вообще используется. Также вы узнаете, как выглядит знак и как его можно вставить в текст в такой программе, какой является Ворд из Майкрософт Оффис.

Знак Дельта применяется во многих сферах жизнедеятельности, к примеру, в физике, текстовых редакторах, формулах и других сферах. Чаще всего именно при печати учебной литературы, докладов и других видов документов применяют знак дельта, который имеется в разных версиях ВОРД от Виндовс и других приложениях для создания документов текстового формата на ПК.

О происхождения знака

Буква, которая служит аналогом в русском алфавите – Д, а вот символ везде одинаков и изображается, как геометрическая фигура, а именно треугольник с равными сторонами (Δ). Эта версия является заглавной, прописная версия выглядит немного иначе, представляя собой кружок с хвостиком, похожий на обозначение в физике плотности (δ).

Где применяется данный символ?

Кроме использования в правописании греков, символ начали активно применять в математике, геометрии, алгебре, физике, химии и географии.

Поговорим отдельно о применении дельта в каждых научных сферах:

1. География. Дельта подразумевает в географическом смысле начальную часть реки, океана или моря, имеет смысловое, нежели символическое, буквенное понятие и восприятие. Почему именно область впадения реки принято так называть? Все просто, дело в форме данной области, если сделать снимок сверху, то отток реки будет иметь форму правильного треугольника, а символ дельта, как раз представляет собой такой геометрический объект. Ярчайшим представителем с выраженной дельтой является река Нил (Египет), которая впадает в Средиземное море, а также Амазонка с ее впадением в океан Атлантики.
2. Применение в математике, алгебре, геометрии. Очень часто знак применяют в математической сфере для таких целей, как: 1) Приращение аргумента подразумевает под дельтой измененную переменную. К примеру, сложим 5 и 4 в итоге получим число 9. Дельтой будет являться увеличение 5 на 4. 2) Применение в теории вероятности по системе Лапласа. Такой метод преподают в ВУЗах, а не школах и в нем используют такой знак. 3) А также символ применяется при обозначении прямой и обратной матриц. 4) Дельта, буква, применяемая в написании формул (как письменным методом, так и через компьютер);
3. Также в математике применяют прописную версию дельта. А именно, такой символ обозначает производную от числа. Обозначение выглядит следующим образом – δy/δx. 2) Используется для описания бесконечной функции-дельта. Бесконечная функция возможна, если все значения аргумента равны нулю. 3) При помощи δ еще обозначают символику Кронекера, символ равен всегда 1, при условии того, что все его индексы равны, либо нулевые при заданных условиях.
4. Физика, астрономия, космогония. Граничащие меж собой научные дисциплины, все особо важные и по-своему интересные, в каждой из дисциплин можно встретить знак дельта. В физике связь всех производных осуществляется при помощи формул с интеграцией. К примеру, формула скорости, которая выглядит следующим образом – δS к δt , является отношением одной части к другой. В данном случае расстояние, которое преодолел объект, соотносится со временем, затраченном на преодоление. Вторая производная – это ускорение, где тоже важна взаимосвязь одной составляющей формулы к другой. В космологии и астрономии применяют формулы, расчеты с данным символом, только в прописном варианте.

Поставь лайк, это важно для наших авторов, подпишись на наш канал в Яндекс.Дзен и вступай в группу Вконтакте

Занимаясь исследованиями космоса и неба, учёные установили, что всё вокруг находится в движении.
История возникновения системы координат началась ещё в древности.

Прежде всего, разработка системы координат связана с потребностью ориентирования на местности, и пониманием структуры небесной поверхности.

Небо над облаками

Для определения расположения и перемещения объектов человечество разработало целую систему методов и способов. Более того, придумали специальные числовые и символичные обозначения.

На самом деле, систем, определяющих точки положения объектов, несколько. Главным образом отличаются они выбором главной плоскости и пунктом отсчёта.
Так как, наблюдая с Земли, мы видим небо в виде сферы, то координаты в астрономии тоже сферические. Кроме того, они представляют некие дуги кругов сферы. Стоит отметить, что исчисляются они в градусах, иногда в часах.

Горизонтальная система координат

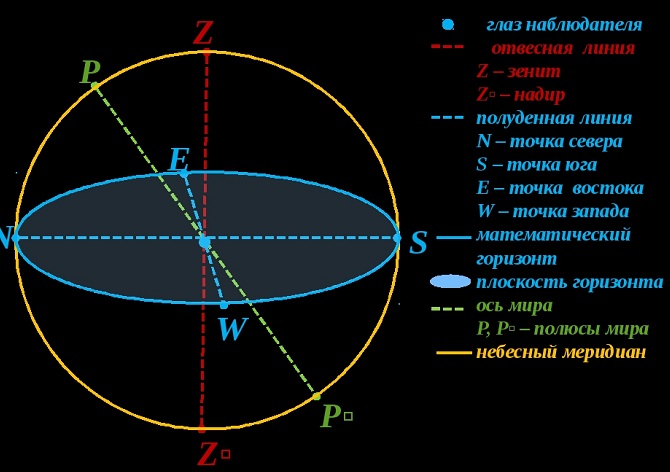
В ней математический горизонт выступает главной плоскостью. А полюса составляют зенит и надир.
Горизонтальной системой координат пользуются для наблюдений с Земли. Это возможно и невооружённым глазом, и с помощью телескопа. Наблюдают за звёздами и перемещением объектов на небе. Разумеется, что в рамках Солнечной системы.

Горизонтальная система координат

Разумеется, наблюдение и измерение происходит постоянно. Потому как движение небесных тел происходит непрерывно.

Некоторые определения системы координат

Отвесная линия представляет собой прямую, проходящую через центр неба. К тому же она совпадает с течением нити отвеса относительно точки наблюдения. Для наблюдателя данная прямая вертикально пересекает центр планеты и место наблюдения.

Зенит и надир это две противоположности. Как известно, отвесная линия пересекается с небом над головой наблюдателя-это и есть зенит. Собственно, надир оказывается полярной по диаметру точкой.

Математический горизонт является огромным кругом небесной сферической поверхности. Его область перпендикулярна отвесной линии. Что важно, он делит всю поверхность неба пополам. Более того, эти части называют видимой и невидимой для наблюдателя. Первая имеет верхнюю точку в зените, а вторая в надире.

Математический горизонт, Зенит и надир, Отвесная линия

В то же время, математический горизонт никогда не соответствует видимому горизонту. Так как, во-первых, поверхность Земли неровная. Как следствие, высшая точка наблюдения разная. А во-вторых, по причине искривления лучей в атмосфере нашей планеты.

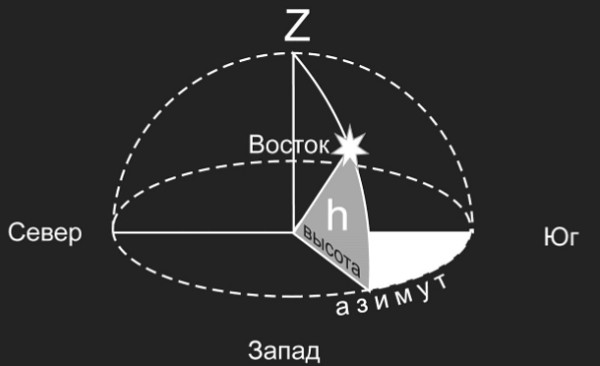
Горизонтальные координаты в астрономии составляют высота светила и зенитное расстояние. Помимо этого, есть ещё азимут.
Высота светила это дуга его вертикала от математического горизонта до направления на само светило. Границы высоты к зениту равны от 0° до +90°.и наоборот к надиру, то есть от 0° до — 90°.
Стоит отметить, что зенитное расстояние это дуга вертикала от зенита до светила. Кстати, рассчитывают зенитный отрезок от зенита к надиру в пределах от 0° до 180°.
Азимут, то есть дуга математического горизонта от южной точки до вертикали светила.
Притом азимут отсчитывают к западу от южной точки в пределах от 0° до 360°. А именно в сторону суточного вращения небесной сферы.

Азимут

Первая экваториальная система координат

За плоскую область в этой системе берётся поверхность экватора неба, а точка отчёта — Q. Помимо того, координаты представляют склонение и часовой угол.
Что такое склонение вы можете узнать тут.
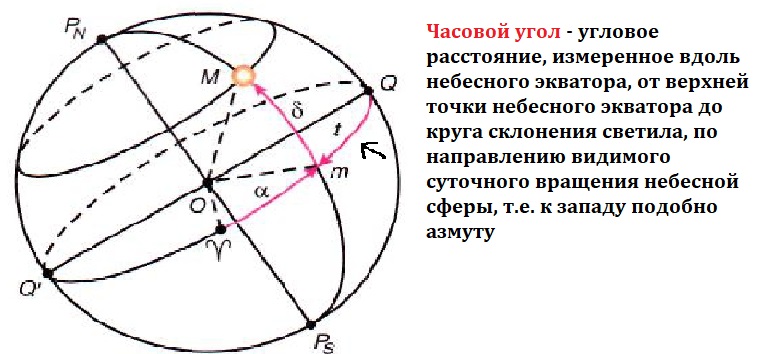
Часовым углом является дуга, которая расположена посередине небесного меридиана и кругом склонения. Граница его измерения от 0° до 360°.
Надо сказать, что применяется первая экваториальная система координат в связи с постоянным движением нашей планеты в течение суток. В связи с этим, местом отсчёта установили точку весеннего равноденствия. Так как она является постоянной относительно звёзд.

Часовой угол

Вторая экваториальная система координат

Что интересно, главная плоскость и точка отчёта аналогичны предыдущей системе. Но её координатами выступают склонение и прямое восхождение.
Подразумевается, что восхождение это дуга экватора неба, которая проходит от точки весеннего равноденствия до круга светила. Кроме того, измерение проходит в часовой мере. Однако, её отсчёт ведётся противоположно часовой стрелки.
Между тем, вторая система координат, характеризуется постоянными координатами звёзд. В противовес первой системе, движение Земли за сутки не влияет на них. Применяется она для определения перемещения небесных тел за год.

Вторая экваториальная система координат

Важно понимать, что координаты могут быть всегда разными. Поэтому существует множество задач. Их решение возможно с применением, подходящей отдельной ситуации, системой. Вообще, для решения задач и определении координат, очень часто чередуют системы.

Создание систем координат позволило учёным составить карту звёздного неба. Кроме того, обрисовалась определённая структура небесной системы. Что, в значительной мере, способствовало развитию астрономии и астрологии. Помимо того, экваториальные системы координат применяются во многих областях научной деятельности.

Звёздное небо

Очевидно, что разработка и внедрение определённых систем, составляет основу исследования космического пространства. Мы стараемся максимально приблизиться к его пониманию. Конечно, множество уже применяемых приёмов, расчётов и методов способствует расширению нашего кругозора.

ДЕ́ЛЬТА 2 , -ы, ж. Название четвертой буквы греческого алфавита.

Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека

Дельта — четвёртая буква греческого алфавита.

Дельта реки — низменность в низовьях реки, сложенная речными наносами.

Дельта — обозначение конечной разности при изменении какого-то параметра.

Дельта-функция — физико-математическая функция.

Дельта, Пенелопа (1874—1941) — греческая писательница, одна из первых литераторов-женщин в новогреческой литературе.

Дельта — одно из древних названий созвездия Треугольник.

Дельта Гудрем – австралийская певица и актриса

Дельта — штат в Нигерии.

Дельта — река на Аляске, США.

Дельта — ряд округов в США.

Дельта — комплекс защитных сооружений в дельте Рейна.

Дельта — посёлок в Красноярском районе Астраханской области.

ДЕ’ЛЬТА [дэ], ы, ж. 1. Название четвертой буквы греч. алфавита (Δ). 2. Устье реки, разветвляющейся на отдельные рукава (геогр.). Д. Волги.

де́льта

Делаем Карту слов лучше вместе

Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать Карту слов. Я отлично умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!

Спасибо! Я стал чуточку лучше понимать мир эмоций.

Вопрос: дружинный — это что-то нейтральное, положительное или отрицательное?

Откуда он пришел?

География

Широко используется данное понятие в географии. Здесь под этим термином скрывается область впадения реки в море или океан. Сверху она выглядит как треугольник. То есть аналогия здесь налицо, и подобное определение в этом случае более чем оправданно. Наиболее яркие примеры – это реки Нил (впадает в Средиземное море в северной части Африканского континента) или Амазонка (впадает в Атлантический океан и расположена в Южной Америке). С высоты птичьего полета места на стыке суши и воды этих двух великих рек действительно выглядят, как греческая буква Δ.

Математика

Значительно чаще и больше используется знак дельта в математике. Здесь он может обозначать следующее:

• Приращение аргументов. То есть за этим понятием скрывается величина, на которую изменилась переменная. Например, 2+3=5. В этом случае 2 увеличилась на 3. Это и есть Δ.
• Еще один случай, при котором используется эта буква греческого алфавита, – оператор Лапласа.
• Последний вариант, при котором используется Δ, – это обозначение определителя матрицы.

Это все справедливо для заглавной буквы. А вот с прописным символом ситуация аналогичная. Он может обозначать такое:

• В обозначении производной: δy/δx (аналогичным образом производная выглядит в физике, астрономии и космогонии).
• При описании дельта-функции, которая может быть равна бесконечности при аргументе ноль и нулю при всех остальных его значениях.
• С ее помощью обозначается символ Кронекера – δ_ij. Он равен единице при равенстве индексов и нулю во всех остальных случаях.

В общем, не так уж и редко в современной математике можно встретить этот символ.

Физика

Еще одна сфера, где эта греческая буква повсеместно используется, – это физика. Большая часть величин этой науки связаны между собой в виде интегралов и производных. Например, скорость – это отношение δS к δt, то есть пройденного расстояния ко времени, за которое оно преодолено. В свою очередь, производной второго порядка от скорости по времени будет ускорение. Это лишь один из примеров, который показывает то, насколько важна эта греческая буква для современной физики.

Астрономия и космогония

Не меньшее значение греческая δ имеет и для этих наук. Здесь опять-таки многие величины взаимосвязаны между собой с помощью интегралов и производных. Именно последнее понятие и обозначается прописной буквой дельта.

Любое приложение

Альтернативный вариант – буфер обмена

Таблица символов: оптимальное решение в любом случае

Подведем итоги: какой способ лучше?

Читайте также:

  

• Кто устанавливает нормативы по физкультуре в школе

  

• Положение о педагогическом классе в московской школе

  

• Роль воспитателя в организации музыкальной деятельности в доу

  

• Функции правоохранительной деятельности кратко

  

• Социально педагогические проблемы в сельской школе

Основные формулы школьного курса астрономии

1. Теоретическая разрешающая способность телескопа:

, где λ – средняя длина световой волны (5,5·10^-7 м), D – диаметр объектива телескопа, или , где D – диаметр объектива телескопа в миллиметрах.

2. Увеличение телескопа:

, где F – фокусное расстояние объектива, f – фокусное расстояние окуляра.

3. Высота светил в кульминации:

высота светил в верхней кульминации, кульминирующих к югу от зенита ( ):

, где  – широта места наблюдения,  – склонение светила;

высота светил в верхней кульминации, кульминирующих к северу от зенита ( ):

, где  – широта места наблюдения,  – склонение светила;

высота светил в нижней кульминации:

, где  – широта места наблюдения,  – склонение светила.

4. Астрономическая рефракция:

приближенная формула для вычисления угла рефракции, выраженного в секундах дуги (при температуре +10°C и атмосферном давлении 760 мм. рт. ст.):

, где z – зенитное расстояние светила (для z

5. Время:

звездное время:

, где  – прямое восхождение какого-либо светила, t – его часовой угол;

среднее солнечное время (местное среднее время):

T_m=T_+, где T_ – истинное солнечное время,  – уравнение времени;

всемирное время:

, где  – долгота пункта с местным средним временем T_m, выраженная в часовой мере, T₀ – всемирное время в этот момент;

поясное время:

, где T₀ – всемирное время; n – номер часового пояса (для Гринвича n=0, для Москвы n=2, для Красноярска n=6);

декретное время:

или

6. Формулы, связывающие сидерический (звездный) период обращения планеты T с синодическим периодом ее обращения S:

для верхних планет:

;

для нижних планет:

, где T_ – звездный период обращения Земли вокруг Солнца.

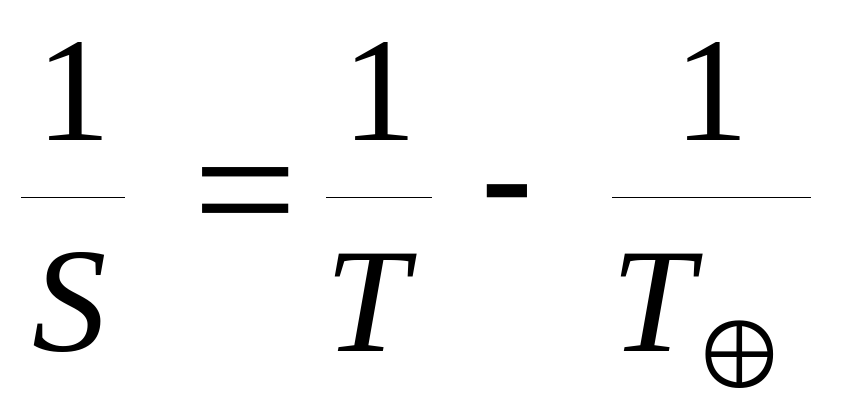
7. Третий закон Кеплера:

, где Т₁ и Т₂ – периоды обращения планет, a₁ и a₂ – большие полуоси их орбиты.

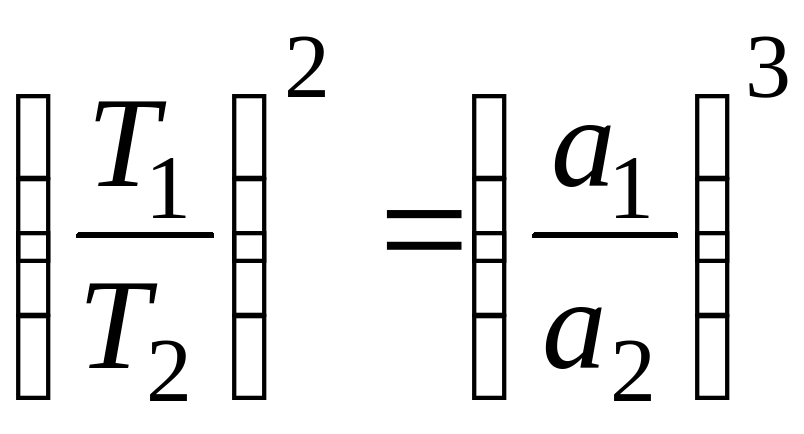
8. Закон всемирного тяготения:

, где m₁ и m₂ – массы притягивающихся материальных точек, r – расстояние между ними, G – гравитационная постоянная.

9. Третий обобщенный закон Кеплера:

, где m₁ и m₂ – массы двух взаимно притягивающихся тел, r – расстояние между их центрами, Т – период обращения этих тел вокруг общего центра масс, G – гравитационная постоянная;

для системы Солнце и две планеты:

, где Т₁ и Т₂ – сидерические (звездные) периоды обращения планет, М – масса Солнца, m₁ и m₂ – массы планет, a₁ и a₂ –большие полуоси орбит планет;

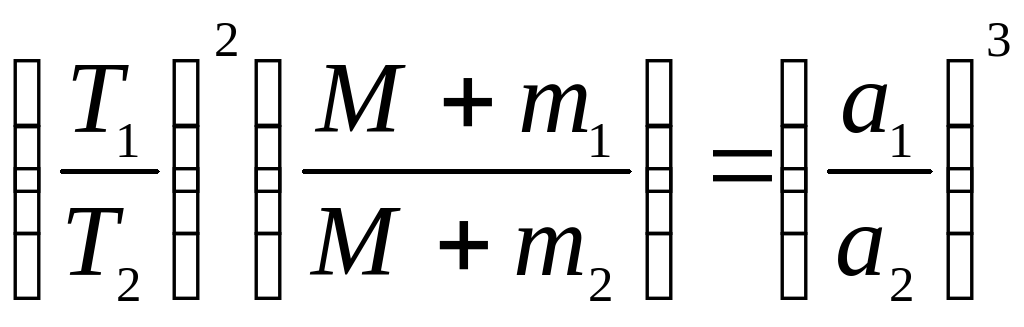
для систем Солнце и планета, планета и спутник:

, где M – масса Солнца; m₁ – масса планеты; m₂ – масса спутника планеты; Т₁ и a₁ – период обращения планеты вокруг Солнца и большая полуось ее орбиты; Т₂ и a₂ – период обращения спутника вокруг планеты и большая полуось его орбиты;

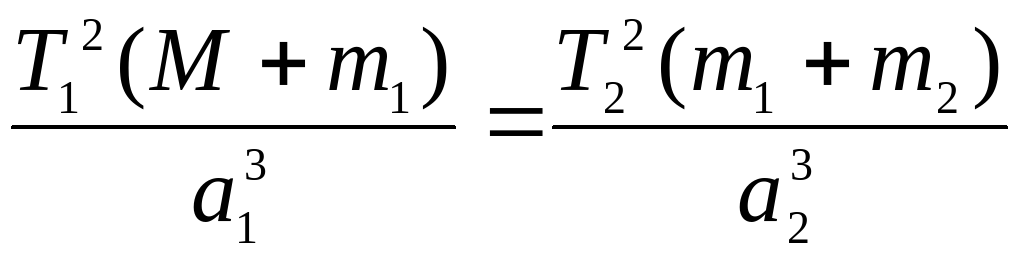
при M m₁, а m₁ m₂,

.

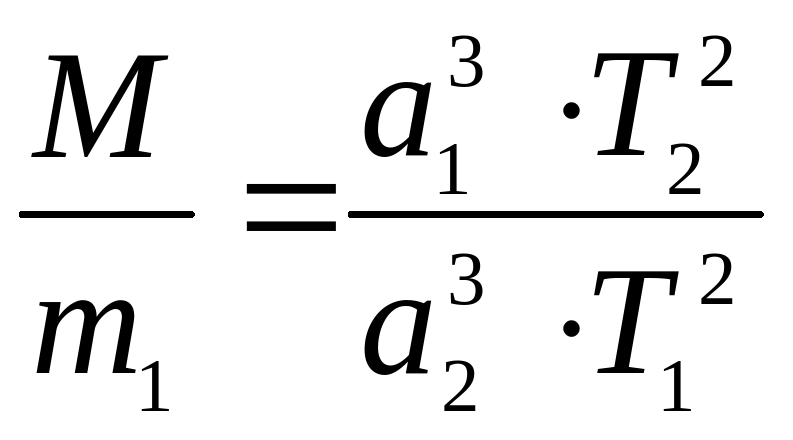
10. Линейная скорость движения тела по параболической орбите (параболическая скорость):

, где G – гравитационная постоянная, M – масса центрального тела, r – радиус-вектор избранной точки параболической орбиты.

11. Линейная скорость движения тела по эллиптической орбите в избранной точке:

, где G – гравитационная постоянная, M – масса центрального тела, r – радиус-вектор избранной точки эллиптической орбиты, a – большая полуось эллиптической орбиты.

12. Линейная скорость движения тела по круговой орбите (круговая скорость):

, где G – гравитационная постоянная, M – масса центрального тела, R – радиус орбиты, v_p – параболическая скорость.

13. Эксцентриситет эллиптической орбиты, характеризующий степень отклонение эллипса от окружности:

, где c – расстояние от фокуса до центра орбиты, a – большая полуось орбиты, b – малая полуось орбиты.

14. Связь расстояний перицентра и апоцентра с большой полуосью и эксцентриситетом эллиптической орбиты:

, , , где r_П – расстояния от фокуса, в котором находится центральное небесное тело, до перицентра, r_А – расстояния от фокуса, в котором находится центральное небесное тело, до апоцентра, a – большая полуось орбиты, e – эксцентриситет орбиты.

15. Расстояние до светила (в пределах Солнечной системы):

, где R_ – экваториальный радиус Земли, ρ₀– горизонтальный параллакс светила, выраженный в секундах дуги,

или , где D₁ и D₂ – расстояния до светил, ρ₁ и ρ₂ – их горизонтальные параллаксы.

16. Радиус светила:

, где ρ – угол, под которым с Земли виден радиус диска светила (угловой радиус), R_ – экваториальный радиус Земли, ρ₀– горизонтальный параллакс светила.

17. Расстояние до звезд:

в парсеках: , где  – годичный параллакс звезды, выраженный в радианах;

в астрономических единицах: , где  – годичный параллакс звезды, выраженный в секундах дуги;

в километрах: , где  – годичный параллакс звезды, выраженный в секундах дуги, a – средний радиус (большая полуось) земной орбиты.

18. Связь блеска звезды и ее звездной величины (формула Погсона):

, где I₁ – освещенность, создаваемая звездой, звездная величина которой равна m₁, и I₂ – освещенность, создаваемая другой звездой, звездная величина которой равна m₂.

19. Абсолютная звездная величина:

, где m – видимая звездная величина, R – расстояние до звезды в парсеках.

20. Закон Стефана–Больцмана:

ε=σT⁴, где ε – энергия, излучаемая в единицу времени с единицы поверхности, Т – температура (в кельвинах), а σ – постоянная Стефана–Больцмана.

21. Закон Вина:

, где λ_max – длина волны, на которую приходится максимум излучения абсолютно черного тела (в сантиметрах), Т – абсолютная температура в кельвинах.

22. Закон Хаббла:

, где v – лучевая скорость удаления галактики, c – скорость света, Δλ – доплеровское смещение линий в спектре, λ – длина волны источника излучения, z – красное смещение, r – расстояние до галактики в мегапарсеках, H – постоянная Хаббла, равная 75 км / (сМпк).

4

Содержание

Тонкости определения [ править | править код ]

В литературе, выпущенной в разное время, могут встречаться немного отличающиеся определения ΔT (в зависимости от того, какая шкала равномерного времени была рекомендована для использования в астрономических расчетах в тот или иной период):

• ΔT=ET−UT (до 1984 года)
• ΔT=TDT−UT (с 1984 по 2001 годы)
• ΔT=TT−UT(с 2001 года по настоящее время).

Кроме того, под «Всемирным временем» может подразумеваться одна из его версий (UT0, UT1 и т. д.). Поэтому в специализированной литературе принято указывать, что имеется в виду под ΔT, например «DTD — UT1», что означает «Динамическое земное время минус Всемирное время версии UT1».

Несмотря на некоторые изменения в определении, физический смысл ΔT не меняется — это разница между идеальным равномерно текущим временем и «временем», определённым по вращению Земли (которое замедляется, причём неравномерно).

О неравномерности вращения Земли вокруг своей оси [ править | править код ]

Всемирное время (UT) является шкалой времени, основанной на суточном вращении Земли, которое не вполне равномерно на относительно коротких интервалах времени (от дней до столетий), и поэтому любые измерения времени, основанные на такой шкале, не могут иметь точность лучше чем 1 : 10 8 . Однако основной эффект проявляется на больших временах: на масштабах столетий приливное трение постепенно замедляет скорость вращения Земли примерно на 2,3 мс/сутки/век. Однако есть и другие причины, изменяющие скорость вращения Земли. Самой важной из них являются последствия таяния материкового ледникового щита в конце последнего ледникового периода. Это привело к уменьшению мощной нагрузки на земную кору и послеледниковой релаксации, сопровождающейся распрямлением и поднятием коры в приполярных областях — процесс, который продолжается и сейчас и будет продолжаться пока не будет достигнуто изостатическое равновесие. Этот эффект послеледниковой релаксации приводит к перемещению масс ближе к оси вращения Земли, что заставляет её вращаться быстрее (закон сохранения углового момента). Полученное из этой модели ускорение составляет около −0,6 мс/сутки/век. Таким образом, полное ускорение (на самом деле замедление) вращения Земли, или изменение длины средних солнечных суток составляет +1,7 мс/сутки/век. Эта величина хорошо соответствует среднему темпу замедления вращения Земли за последние 27 столетий. [1]

Земное время (TT) является теоретически равномерной временной шкалой, определенной так, чтобы сохранить непрерывность с предшествующей равномерной шкалой эфемеридного времени (ET). ET основана на независимой от вращения Земли физической величине, предложенной (и принятой к применению) в 1948-52 [2] с намерением получить настолько однородную и не зависящую от гравитационных эффектов временную шкалу, насколько это возможно было в то время. Определение ET опиралось на солнечные таблицы (англ.) русск. Саймона Ньюкома (1895), интерпретированные новым образом, чтобы учесть определенные расхождения в наблюдениях. [3]

Таблицы Ньюкома служили основой для всех астрономических солнечных эфемерид с 1900 по 1983 год. Изначально они были выражены (и в таком виде опубликованы) в терминах среднего времени по Гринвичу и средних солнечных суток, [4] однако позднее, в особенности в отношении периода с 1960 по 1983 г., они трактовались как выраженные в рамках ET, [5] в соответствии с принятым в 1948-52 предложением о переходе к ET. В свою очередь, ET могло теперь рассматриваться в свете новых результатов [6] как шкала времени максимально близкая к среднему солнечному времени на интервале 1750 и 1890 (с серединой около 1820 года), поскольку именно в этом интервале проводились наблюдения, на основании которых были составлены таблицы Ньюкома. Хотя шкала TT является строго однородной (основана на единице секунды СИ, и каждая секунда строго равна каждой другой секунде), на практике она реализуется как Международное атомное время (TAI) с точностью около 1 : 10 14 .

Определение дельта Т из наблюдений [ править | править код ]

Время, определяемое положением Земли (точнее, ориентацией Гринвичского меридиана относительно фиктивного среднего Солнца), является интегралом от скорости вращения. При интегрировании с учётом изменения длины суток на +1,7 мс/сутки/век и выборе начальной точки в 1820 году (примерная середина интервала наблюдений, использованных Ньюкомом для определения длины суток), для ΔT получается в первом приближении парабола 31×((Год − 1820)/100)² в секунд. Сглаженные данные, полученные на основе анализа исторических данных о наблюдениях полных солнечных затмений дают значения ΔT около +16800 с в −500 году, +10600 с в 0, +5700 с в 500, +1600 с в 1000 и +180 с в 1500. Для времени после изобретения телескопа ΔT определяются из наблюдений покрытий звезд Луной, что позволяет получить более точные и более частые значения величины. Поправка ΔT продолжала уменьшаться после 16 века, пока не достигла плато +11±6 с между 1680 и 1866 года. В течение трех десятилетий до 1902 она оставалась отрицательной с минимумом −6,64 с, затем начала увеличиваться до +63,83 с в 2000 году. В будущем ΔT будет увеличиваться с нарастающей скоростью (квадратично). Это потребует добавления все большего числа секунд координации к Всемирному координированному времени (UTC), поскольку UTC должно поддерживаться с точностью в одну секунду относительно равномерной шкалы UT1. (Секунда СИ, используемая сейчас для UTC, уже в момент принятия была немного короче, чем текущее значение секунды среднего солнечного времени. [7] ) Физически нулевой меридиан для Универсального времени оказывается почти всегда восточнее меридиана Земного времени как в прошлом, так и в будущем. +16800 с или 4⅔ часа соответствуют 70° в.д. Это означает, что в −500 году вследствие более быстрого вращения Земли солнечное затмение происходило на 70° восточнее положения, которое следует из расчетов с использованием равномерного времени TT.

Все значения ΔT до 1955 года зависят от наблюдений Луны, связанных либо с затмениями, либо с покрытиями. Сохранение углового момента в Системе Земля-Луна требует, чтобы угловой момент Земли вследствие приливного трения передавался Луне, увеличивая её угловой момент, что означает, что её расстояние до Земли должно увеличиваться, что, в свою очередь, вследствие третьего закона Кеплера приводит к замедлению обращения Луны вокруг Земли. Приведенные выше значения ΔT предполагают, что ускорение Луны, связанное с этим эффектом составляет величину dn/dt = −26″/век², где n — средняя угловая сидерическая скорость Луны. Это близко к лучшим экспериментальным оценкам для dn/dt, полученным в 2002 году: −25,858±0,003″/век² [8] , и поэтому оценки ΔT, полученные ранее исходя из значения −26″/век², принимая во внимание неопределенности и эффекты сглаживания в экспериментальных наблюдениях, можно не пересчитывать. В наше время UT определяется по измерению ориентации Земли по отношению к инерциальной системе отсчета, связанной с внегалактическими радиоисточниками, с поправкой на принятое соотношение между сидерическим и солнечным временем. Эти измерения, проводимые в нескольких обсерваториях, координируются Международной службой вращения Земли (IERS).

Величины дельта Т [ править | править код ]

Для 1900—1995 годов значения приведены согласно «Астрономия на персональном компьютере», четвёртое издание, 2002 год, Монтенбрук О., Пфеглер Т., для 2000 года — из английской Вики.

Год	дельта Т
1900	-2,72
1905	3,86
1910	10,46
1915	17,20
1920	21,16
1925	23,62
1930	24,02
1935	23,93
1940	24,33
1945	26,77
1950	29,15
1955	31,07
1960	33,15
1965	35,73
1970	40,18
1975	45,48
1980	50,54
1985	54,34
1990	56,86
1995	60,82
2000	63,83
2005	64,69
2010	66,07

Вычисление дельта Т [ править | править код ]

Приближенная формула для вычисления дельта Т [ править | править код ]

С 1972 года по наше время ΔT можно рассчитать зная количество секунд координации по формуле:

Δ T ≃ 32,184 + 10 + N , <displaystyle Delta Tsimeq 32<,>184+10+N,>

где
32,184 секунд — разница между TT и TAI,
10 секунд — разница между TAI и UTC на начало 1972 года,
N — количество введенных с 1972 года секунд координации.

Формула дает погрешность не более 0,9 секунд. Например, на начало 1995 года было введено 19 секунд координации и формула дает ΔT=61,184 секунд, что лишь на 0,364 секунды превышает табличное значение.

Точная формула для вычисления дельта Т [ править | править код ]

Из бюллетеня А (Bulletin — A) Службы вращения земли IERS можно узнать разность между TAI и UTC (зависит от количества секунд координации, величина меняется редко) и между UT1 и UTC (величина постоянно меняется, в бюллетене даётся на полночь ежесуточно), тогда дельта Т можно вычислить точно по формуле:

Δ T = 32.184 s + ( T A I − U T C ) − ( U T 1 − U T C ) . <displaystyle Delta T=32.184s+(TAI-UTC)-(UT1-UTC).>

Приблизительная формула вычисления дельта Т на будущее [ править | править код ]

Рассчитать дельта Т на будущее можно только приблизительно, ввиду того, что изменение вращения Земли недостаточно изучено. Тем не менее для расчёта, например, пути прохождения тени от солнечного затмения или времени покрытия звёзд Луной делать хотя бы приблизительный расчёт необходимо. Фред Эспеньяк (англ.) русск. при расчёте солнечных затмений на период 2005—2050 годов пользовался формулой [10]

Δ T = 62 , 92 + 0 , 32217 ⋅ ( y − 2000 ) + 0 , 005589 ⋅ ( y − 2000 ) 2 , <displaystyle Delta T=62,92+0,32217cdot left(y-2000
ight)+0,005589cdot left(y-2000
ight)^<2>,>

где y — год, для которого определяется дельта Т.

Содержание

Тонкости определения [ править | править код ]

В литературе, выпущенной в разное время, могут встречаться немного отличающиеся определения ΔT (в зависимости от того, какая шкала равномерного времени была рекомендована для использования в астрономических расчетах в тот или иной период):

• ΔT=ET−UT (до 1984 года)
• ΔT=TDT−UT (с 1984 по 2001 годы)
• ΔT=TT−UT(с 2001 года по настоящее время).

Кроме того, под «Всемирным временем» может подразумеваться одна из его версий (UT0, UT1 и т. д.). Поэтому в специализированной литературе принято указывать, что имеется в виду под ΔT, например «DTD — UT1», что означает «Динамическое земное время минус Всемирное время версии UT1».

Несмотря на некоторые изменения в определении, физический смысл ΔT не меняется — это разница между идеальным равномерно текущим временем и «временем», определённым по вращению Земли (которое замедляется, причём неравномерно).

О неравномерности вращения Земли вокруг своей оси [ править | править код ]

Всемирное время (UT) является шкалой времени, основанной на суточном вращении Земли, которое не вполне равномерно на относительно коротких интервалах времени (от дней до столетий), и поэтому любые измерения времени, основанные на такой шкале, не могут иметь точность лучше чем 1 : 10 8 . Однако основной эффект проявляется на больших временах: на масштабах столетий приливное трение постепенно замедляет скорость вращения Земли примерно на 2,3 мс/сутки/век. Однако есть и другие причины, изменяющие скорость вращения Земли. Самой важной из них являются последствия таяния материкового ледникового щита в конце последнего ледникового периода. Это привело к уменьшению мощной нагрузки на земную кору и послеледниковой релаксации, сопровождающейся распрямлением и поднятием коры в приполярных областях — процесс, который продолжается и сейчас и будет продолжаться пока не будет достигнуто изостатическое равновесие. Этот эффект послеледниковой релаксации приводит к перемещению масс ближе к оси вращения Земли, что заставляет её вращаться быстрее (закон сохранения углового момента). Полученное из этой модели ускорение составляет около −0,6 мс/сутки/век. Таким образом, полное ускорение (на самом деле замедление) вращения Земли, или изменение длины средних солнечных суток составляет +1,7 мс/сутки/век. Эта величина хорошо соответствует среднему темпу замедления вращения Земли за последние 27 столетий. [1]

Земное время (TT) является теоретически равномерной временной шкалой, определенной так, чтобы сохранить непрерывность с предшествующей равномерной шкалой эфемеридного времени (ET). ET основана на независимой от вращения Земли физической величине, предложенной (и принятой к применению) в 1948-52 [2] с намерением получить настолько однородную и не зависящую от гравитационных эффектов временную шкалу, насколько это возможно было в то время. Определение ET опиралось на солнечные таблицы (англ.) русск. Саймона Ньюкома (1895), интерпретированные новым образом, чтобы учесть определенные расхождения в наблюдениях. [3]

Таблицы Ньюкома служили основой для всех астрономических солнечных эфемерид с 1900 по 1983 год. Изначально они были выражены (и в таком виде опубликованы) в терминах среднего времени по Гринвичу и средних солнечных суток, [4] однако позднее, в особенности в отношении периода с 1960 по 1983 г., они трактовались как выраженные в рамках ET, [5] в соответствии с принятым в 1948-52 предложением о переходе к ET. В свою очередь, ET могло теперь рассматриваться в свете новых результатов [6] как шкала времени максимально близкая к среднему солнечному времени на интервале 1750 и 1890 (с серединой около 1820 года), поскольку именно в этом интервале проводились наблюдения, на основании которых были составлены таблицы Ньюкома. Хотя шкала TT является строго однородной (основана на единице секунды СИ, и каждая секунда строго равна каждой другой секунде), на практике она реализуется как Международное атомное время (TAI) с точностью около 1 : 10 14 .

Определение дельта Т из наблюдений [ править | править код ]

Время, определяемое положением Земли (точнее, ориентацией Гринвичского меридиана относительно фиктивного среднего Солнца), является интегралом от скорости вращения. При интегрировании с учётом изменения длины суток на +1,7 мс/сутки/век и выборе начальной точки в 1820 году (примерная середина интервала наблюдений, использованных Ньюкомом для определения длины суток), для ΔT получается в первом приближении парабола 31×((Год − 1820)/100)² в секунд. Сглаженные данные, полученные на основе анализа исторических данных о наблюдениях полных солнечных затмений дают значения ΔT около +16800 с в −500 году, +10600 с в 0, +5700 с в 500, +1600 с в 1000 и +180 с в 1500. Для времени после изобретения телескопа ΔT определяются из наблюдений покрытий звезд Луной, что позволяет получить более точные и более частые значения величины. Поправка ΔT продолжала уменьшаться после 16 века, пока не достигла плато +11±6 с между 1680 и 1866 года. В течение трех десятилетий до 1902 она оставалась отрицательной с минимумом −6,64 с, затем начала увеличиваться до +63,83 с в 2000 году. В будущем ΔT будет увеличиваться с нарастающей скоростью (квадратично). Это потребует добавления все большего числа секунд координации к Всемирному координированному времени (UTC), поскольку UTC должно поддерживаться с точностью в одну секунду относительно равномерной шкалы UT1. (Секунда СИ, используемая сейчас для UTC, уже в момент принятия была немного короче, чем текущее значение секунды среднего солнечного времени. [7] ) Физически нулевой меридиан для Универсального времени оказывается почти всегда восточнее меридиана Земного времени как в прошлом, так и в будущем. +16800 с или 4⅔ часа соответствуют 70° в.д. Это означает, что в −500 году вследствие более быстрого вращения Земли солнечное затмение происходило на 70° восточнее положения, которое следует из расчетов с использованием равномерного времени TT.

Все значения ΔT до 1955 года зависят от наблюдений Луны, связанных либо с затмениями, либо с покрытиями. Сохранение углового момента в Системе Земля-Луна требует, чтобы угловой момент Земли вследствие приливного трения передавался Луне, увеличивая её угловой момент, что означает, что её расстояние до Земли должно увеличиваться, что, в свою очередь, вследствие третьего закона Кеплера приводит к замедлению обращения Луны вокруг Земли. Приведенные выше значения ΔT предполагают, что ускорение Луны, связанное с этим эффектом составляет величину dn/dt = −26″/век², где n — средняя угловая сидерическая скорость Луны. Это близко к лучшим экспериментальным оценкам для dn/dt, полученным в 2002 году: −25,858±0,003″/век² [8] , и поэтому оценки ΔT, полученные ранее исходя из значения −26″/век², принимая во внимание неопределенности и эффекты сглаживания в экспериментальных наблюдениях, можно не пересчитывать. В наше время UT определяется по измерению ориентации Земли по отношению к инерциальной системе отсчета, связанной с внегалактическими радиоисточниками, с поправкой на принятое соотношение между сидерическим и солнечным временем. Эти измерения, проводимые в нескольких обсерваториях, координируются Международной службой вращения Земли (IERS).

Величины дельта Т [ править | править код ]

Для 1900—1995 годов значения приведены согласно «Астрономия на персональном компьютере», четвёртое издание, 2002 год, Монтенбрук О., Пфеглер Т., для 2000 года — из английской Вики.

Год	дельта Т
1900	-2,72
1905	3,86
1910	10,46
1915	17,20
1920	21,16
1925	23,62
1930	24,02
1935	23,93
1940	24,33
1945	26,77
1950	29,15
1955	31,07
1960	33,15
1965	35,73
1970	40,18
1975	45,48
1980	50,54
1985	54,34
1990	56,86
1995	60,82
2000	63,83
2005	64,69
2010	66,07

Вычисление дельта Т [ править | править код ]

Приближенная формула для вычисления дельта Т [ править | править код ]

С 1972 года по наше время ΔT можно рассчитать зная количество секунд координации по формуле:

Δ T ≃ 32,184 + 10 + N , <displaystyle Delta Tsimeq 32<,>184+10+N,>

где
32,184 секунд — разница между TT и TAI,
10 секунд — разница между TAI и UTC на начало 1972 года,
N — количество введенных с 1972 года секунд координации.

Формула дает погрешность не более 0,9 секунд. Например, на начало 1995 года было введено 19 секунд координации и формула дает ΔT=61,184 секунд, что лишь на 0,364 секунды превышает табличное значение.

Точная формула для вычисления дельта Т [ править | править код ]

Из бюллетеня А (Bulletin — A) Службы вращения земли IERS можно узнать разность между TAI и UTC (зависит от количества секунд координации, величина меняется редко) и между UT1 и UTC (величина постоянно меняется, в бюллетене даётся на полночь ежесуточно), тогда дельта Т можно вычислить точно по формуле:

Δ T = 32.184 s + ( T A I − U T C ) − ( U T 1 − U T C ) . <displaystyle Delta T=32.184s+(TAI-UTC)-(UT1-UTC).>

Приблизительная формула вычисления дельта Т на будущее [ править | править код ]

Рассчитать дельта Т на будущее можно только приблизительно, ввиду того, что изменение вращения Земли недостаточно изучено. Тем не менее для расчёта, например, пути прохождения тени от солнечного затмения или времени покрытия звёзд Луной делать хотя бы приблизительный расчёт необходимо. Фред Эспеньяк (англ.) русск. при расчёте солнечных затмений на период 2005—2050 годов пользовался формулой [10]

Δ T = 62 , 92 + 0 , 32217 ⋅ ( y − 2000 ) + 0 , 005589 ⋅ ( y − 2000 ) 2 , <displaystyle Delta T=62,92+0,32217cdot left(y-2000
ight)+0,005589cdot left(y-2000
ight)^<2>,>

где y — год, для которого определяется дельта Т.

Дельта-4 — Дельта IV … Википедия

Дельта IV — Старт РН Дельта IV Медиум со спутником DSCS III B6 Общие сведения … Википедия

Дельта-2 — Дельта 2 … Википедия

ДЕЛЬТА — (греч.). Часть земли, находящаяся при устьях рек, между их рукавами; название это произошло оттого, что такой участок земли имеет обыкновенно форму греческой буквы дельты (?). Словарь иностранных слов, вошедших в состав русского языка. Чудинов… … Словарь иностранных слов русского языка

дельта — 1. ДЕЛЬТА [дэ], ы; ж. Устье большой реки с его разветвлениями на отдельные рукава и прилегающая к нему суша. Д. Волги. ◁ Дельтовый, ая, ое. Д ые отложения. ● От названия греческой буквы, в начертании имеющей форму треугольника. 2. ДЕЛЬТА [дэ], ы; … Энциклопедический словарь

ДЕЛЬТА — (греч. delta) 1) изменение цены опциона на будущую покупку или продажу акций, обусловленное изменением текущих цен акций. Обычно опцион на покупку имеет положительную Д., а опцион на продажу отрицательную. Это обусловлено тем, что если текущая… … Юридическая энциклопедия

ДЕЛЬТА — [от названия заглавной буквы греческого алфавита А (дельта)], низменность в низовьях крупных рек, впадающих, как правило, в море. Область аккумуляции,где откладываются аллювиальные наносы. Если энергия реки велика, то благодаря наносам дельта… … Экологический словарь

ДЕЛЬТА — ДЕЛЬТА, низменность в низовьях крупных рек, впадающих в мелководные участки моря или озера, образованная речными отложениями. Прорезана сетью рукавов и протоков. Название дельта происходит от заглавной буквы греческого алфавита D (дельта), по… … Современная энциклопедия

ДЕЛЬТА — низменность в низовьях крупных рек, впадающих в мелководные участки моря или озера, образованная речными отложениями. Прорезана сетью рукавов и протоков. Название дельта происходит от заглавной буквы дельта греческого алфавита, по сходству с… … Большой Энциклопедический словарь

ДЕЛЬТА — разветвление реки у ее устья на несколько рукавов, имеющее форму греческой буквы Δ (дельта). Образуется чаще в реках, впадающих во внутренние моря, где морские приливы слабы и не могут удалять из устья всех речных наносов; бывает также при… … Морской словарь