{mu = dfrac{F_{тр}}{mg}}
Ускорение свободного падения g
Приводим 2 варианта нахождения коэффициента трения – зная силу трения и массу тела или зная угол наклона. Для обоих вариантов вы найдете удобные калькуляторы и формулы для расчета.
Коэффициент трения представляет собой безразмерную скалярную величину, которая равна отношению силы трения между двумя телами и силы, прижимающей их друг к другу, во время или в начале скольжения.
Коэффициент трения чаще всего обозначают греческой буквой µ («мю»).
Следует помнить, что коэффициент трения (μ) величина безразмерная, то есть не имеет единицы измерения.
Коэффициент трения зависит от качества обработки трущихся поверхностей, скорости движения тел относительно друг друга и материала соприкасающихся поверхностей. В большинстве случаев коэффициент трения находится в пределах от 0,1 до 0,5 (см. таблицу).
Содержание:
- калькулятор коэффициента трения
- формула коэффициента трения через силу трения и массу
- формула коэффициента трения через угол наклона
- таблица коэффициентов трения
- примеры задач
Формула коэффициента трения через силу трения и массу
mu = dfrac{F_{тр}}{mg}
Fтр – сила трения
m – масса тела
g – ускорение свободного падения (в большинстве задач можно принять g=9.81 м/с²)
Формула коэффициента трения через угол наклона
mu = tg(alpha)
α – угол наклона
Таблица коэффициентов трения скольжения для разных пар материалов
| Трущиеся материалы (при сухих поверхностях) | Коэффициенты трения | |
|---|---|---|
| покоя | при движении | |
| Резина по сухому асфальту | 0,95-1,0 | 0,5-0,8 |
| Резина по влажному асфальту | 0,25-0,75 | |
| Алюминий по алюминию | 0,94 | |
| Бронза по бронзе | 0,20 | |
| Бронза по чугуну | 0,21 | |
| Дерево по дереву (в среднем) | 0,65 | 0,33 |
| Дерево по камню | 0,46-0,60 | |
| Дуб по дубу (вдоль волокон) | 0,62 | 0,48 |
| Дуб по дубу (перпендикулярно волокнам) | 0,54 | 0,34 |
| Железо по железу | 0,15 | 0,14 |
| Железо по чугуну | 0,19 | 0,18 |
| Железо по бронзе (слабая смазка) | 0,19 | 0,18 |
| Канат пеньковый по деревянному барабану | 0,40 | |
| Канат пеньковый по железному барабану | 0,25 | |
| Каучук по дереву | 0,80 | 0,55 |
| Каучук по металлу | 0,80 | 0,55 |
| Кирпич по кирпичу (гладко отшлифованные) | 0,5-0,7 | |
| Колесо со стальным бандажем по рельсу | 0,16 | |
| Лед по льду | 0,05-0,1 | 0,028 |
| Метал по аботекстолиту | 0,35-0,50 | |
| Метал по дереву (в среднем) | 0,60 | 0,40 |
| Метал по камню (в среднем) | 0,42-0,50 | |
| Метал по металу (в среднем) | 0,18-0,20 | |
| Медь по чугуну | 0,27 | |
| Олово по свинцу | 2,25 | |
| Полозья деревянные по льду | 0,035 | |
| Полозья обитые железом по льду | 0,02 | |
| Резина (шина) по твердому грунту | 0,40-0,60 | |
| Резина (шина) по чугуну | 0,83 | 0,8 |
| Ремень кожаный по деревянному шкиву | 0,50 | 0,30-0,50 |
| Ремень кожаный по чугунному шкиву | 0,30-0,50 | 0,56 |
| Сталь по железу | 0,19 | |
| Сталь(коньки) по льду | 0,02-0,03 | 0,015 |
| Сталь по райбесту | 0,25-0,45 | |
| Сталь по стали | 0,15-0,25 | 0,09 (ν = 3 м/с)
0,03 (ν = 27 м/с) |
| Сталь по феродо | 0,25-0,45 | |
| Точильный камень (мелкозернистый) по железу | 1 | |
| Точильный камень (мелкозернистый) по стали | 0,94 | |
| Точильный камень (мелкозернистый) по чугуну | 0,72 | |
| Чугун по дубу | 0,65 | 0,30-0,50 |
| Чугун по райбесту | 0,25-0,45 | |
| Чугун по стали | 0,33 | 0,13 (ν = 20 м/с) |
| Чугун по феродо | 0,25-0,45 | |
| Чугун по чугуну | 0,15 |
Примеры задач на нахождение коэффициента трения
Задача 1
Найдите коэффициент трения между полом и ящиком массой 20 кг, который равномерно двигают с силой 50 Н.
Решение
Для решения задачи воспользуемся формулой.
mu = dfrac{F_{тр}}{mg} = dfrac{50}{20 cdot 9.81} = dfrac{50}{196.2} approx 0.25484
Ответ: approx 0.25484
С помощью калькулятора удобно проверить ответ.
Задача 2
Найдите коэффициент трения если угол наклона 30°.
Решение
Для решения этой задачи воспользуемся второй формулой.
mu = tg(alpha) = tg(30°) approx 0.57735
Ответ: approx 0.57735
Проверим полученный ответ с помощью калькулятора .
1.
g – Ускорение свободного падения.
a – “Собственное” ускорение. Зависит от условий, например: Лифт спускается с ускорением 0,3 м/с²… В этом случае . Когда лифт начнёт подниматься(с тем же ускорением),
В первом случае, формула будет выглядеть вот так:
Во втором:
m – масса тела.
– векторы данных величин.
2.
Fтр= µmg
µ – коэффициент трения. Зависит от условий.
g – Ускорение свободного падения.
m – масса тела.
физика, напишите пожалуйста формулы по которым вы решали
Ученик
(177),
на голосовании
9 лет назад
Голосование за лучший ответ
Валентина Вавилова(Серкова)
Гений
(62183)
9 лет назад
1)Если движение равномерное, по сила упругости = силе трения.
Fупр=Fтр.
Fупр=k*dL. ( закон Гука)( k -жесткость, dL(дельта L) – удлинение пружины)
Fтр=м*m*g. ( м(мю) – коэффициент трения, m -масса,g -ускорение свободного падения).
k*dL=м*m*g. выразим удлинение
dL=м*m*g / k.
dL=0,3*2*10 / 100=0,06м. ( 6см).
2)По 2 закону Ньютона
m*a=Fтяг – Fтр.
Fтяг=m*a + м*m*g. ( a -ускорение. а=(v – v0) / t . a=( 30 – 0) / 20=1,5м/c^2).
Fтяг=1000*1,5 + 0,05*1000*10=2000H. ( 2кН).
3) По закону сохранения энергии: Потенциальная энергия в верхней точке = сумме кинетической энергии в нижней точке и работы силы сопротивления.
m*g*h = m*v^2 / 2 + Fc*h . ( Fc -сила сопротивления воздуха)
Fc=( m*g*h – m*v^2 / 2 ) / h
Fc= ( 65*10*10 – 65*(13^2) / 2 ) / 10=101H.
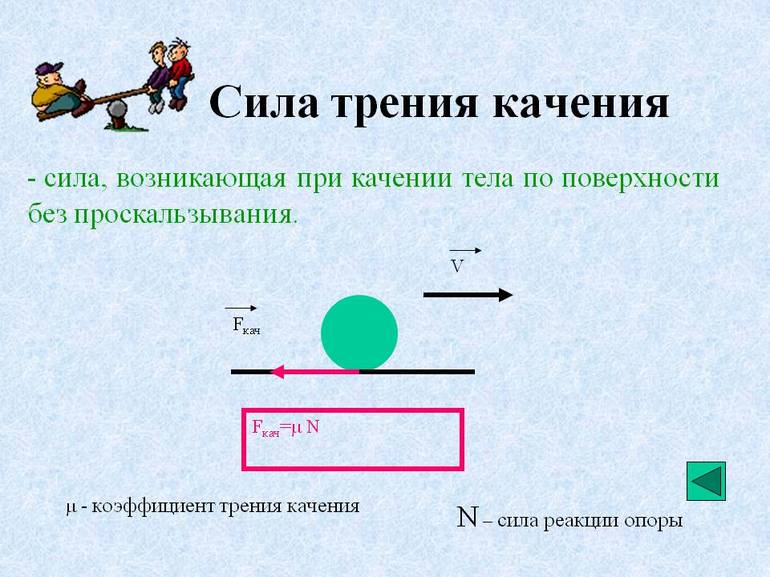
Общие сведения
Во время перекатывания тел возникает их взаимодействие. Описывается оно силой трения качения. Её существование возможно только при контакте поверхностей. При этом наряду с качением возникают силы покоя и скольжения. Объект, катящийся по другому телу, испытывает только трение, вызванное качением. По сравнению с другими силами оно небольшое, но при этом помогает осуществлять перемещение.
С физической точки зрения, трение представляет собой вектор, направление которого совпадает с линией, проходящей вдоль касательной трущихся поверхностей. Сила, измеряемая относительно перемещения соприкасающихся тел, называется внешней, а возникающая в области одного объекта, например, газа — внутренней.
Трение зависит от поверхности тел. Оно может быть сухим или вязким. В единицах СИ сила измеряется в ньютонах: [P]=H. Существует такое понятие, как адгезия, то есть способность тел «прилипать» друг к другу. Зависит она от шероховатости. Чем этот параметр больше, тем больше нужно затратить энергии для смещения поверхностей, но в то же время её затраты будут меньше для полного торможения.
Таким образом, трение может приносить как пользу, так и вред. С одной стороны, при работе за счёт силы происходит износ поверхностей, а с другой — выполняется торможение. Для уменьшения эффекта существуют несколько способов изменить трение: сгладить поверхности, сменить смазку, заменить скольжение качением.
Вычисление силы выполняют по формуле: F = k * N. Здесь:
- F — сила;
- K — коэффициент;
- N — реакция опоры.
Приложенное сопротивление направлено в противоположную сторону движения, при этом реакция силы опоры происходит перпендикулярно площади соприкосновения. Коэффициент является безразмерной величиной и не зависит от размера контакта. Если энергия движения совпадает по величине с трением, тело движется равномерно по прямой. Если же движущая сила будет меньше, объект остановится.
Основная формула силы трения учитывает различные моменты, оказывающие влияние на перемещение. Но при этом, если при соприкосновении с вращением не будет проскальзывания, формула изменится. В ней главную роль будет играть прижимающее давление.
Качение тела
Из названия силы можно сделать вывод, что сила качения возникает, когда одно тело перекатывается по поверхности другого. Например, езда с использованием колеса, работа подшипника. По сути, это явление, происходящее из-за деформации катка и опорной поверхности. При этом полагается, что тяговых и тормозных процессов нет.
Из-за того, что трение качения в несколько раз меньше скольжения, оно является довольно распространённым видом перемещения. Например, груз катить легче, чем тянуть. Это происходит из-за меньшего количества контактов с поверхностью. При этом отталкиваться от твёрдого тела проще, чем от мягкого.
Для определения процесса физики используют следующее объяснение: пусть имеется тело, которое располагается на опоре. Относительно неё происходит вращение. В любой выбранный момент времени на вращающийся объект будет действовать момент сил. При этом векторная сумма их будет равняться нулю: N + P +Ro = 0. Действующий момент состоит из внешней силы (P), прижимной (N) и реакции опоры (Ro).
Если сумма векторов равняется нулю, ось симметрии находится в равномерном и прямолинейном движении или остаётся в одном положении (неподвижная). Другими словами, вектор силы трения качения противодействует перемещению. Следовательно, прижимной момент уравновешивается реакцией опоры, а, точнее, её вертикальной составляющей. Внешняя же сила находится в равновесии с горизонтальной составляющей.
Равномерность обозначает, что воздействующие моменты компенсируют друг друга. А значит, формула для описания процесса будет выглядеть как Ft * R = N * f, где Ft — сила трения качения. Из этой формулы можно найти силу: Ft = f * N /R. Рассматриваемое воздействие прямо пропорционально произведению коэффициента трения и прижимной силы, обратно пропорционально радиусу катящегося тела. Фактически это и есть определение трения качения.
Правильность формулы подтверждают различные экспериментальные измерения. Действительно, при малой скорости качения процесс не зависит от неё. Когда же скорость возрастает до величин сопоставимых с деформацией в опоре, сопротивление движению становится пропорциональным её росту и влияние оказывает уже скольжение.
Момент и коэффициент
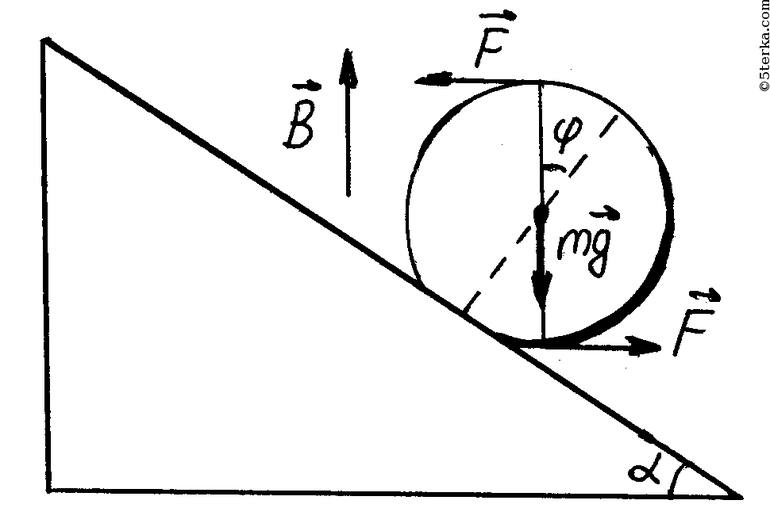
Пусть имеется цилиндр, расположенный на идеальной гладкой жёсткой поверхности. Какую бы силу Q ни приложили, уравновесить её можно только противодействующей энергией. Если же такой энергии нет, под действием Q цилиндр должен катиться. Но опыты показывают совершенно другое. Например, если подойти к многотонному грузовику и попробовать его толкнуть, он не покатится. Хотя теория утверждает обратное.
Но здесь дело в том, что поверхность считается идеальной. В момент времени на тело, кроме Q, действует равное ей сцепление. Эти силы будут уравновешенными. В вертикальной же плоскости на тело действует нормаль (N) и противодействующая ей сила равновесия (P).
На самом деле при прикосновении тело деформируется. Образуется впадина, при этом колесо всей своей тяжестью будет опираться на крайнюю правую точку деформированной поверхности. Момент сил здесь будет следующим:
- P — вес колеса, направленный вниз;
- N — момент нормали противоположный P;
- Q — импульс качения.
Перемещению препятствует равновесие пары PN. При этом плечо пары будет половиной размера, то есть возникает момент сил трения. Определяют его как эн делённое на дельту и называют моментом трения: Mтр = N * d. Эта формула совпадает по форме записи с законом Амонтона — Кулона. И там, и тут фигурирует величина опоры.
Становится очевидным, что R * Q = Mтр = P * d. Используя эту запись, можно обнаружить предельный импульс, который необходимо приложить к колесу, чтобы заставить его двигаться: Q = p d /R. При этом если колесо будет скользить, а не катиться, Q будет уже зависеть от трения: Q = P * f.
При сравнении двух формул видно, что d / r будет намного меньше f, поэтому качение произойдёт раньше. Это свойство как раз и используется в подшипниках. Нахождение коэффициента трения можно выполнить через момент трения качения и давление прижима: f = Mтр / N.
Он определяется следующими физическими интерпретациями:
- f равна длине линии, соединяющей прямые, вдоль которых создаются нормаль и давление вниз;
- для неидеализированных случаев мгновенный центр вращения сдвинут в сторону качения тела, при этом значение смещения равно коэффициенту трения.
Для мягкого дерева, катящегося по стали, коэффициент составляет 0,8 мм, стали по асфальту — 6 мм, железа по граниту — 2,1 мм. Это справочная величина, установленная экспериментально, которую не нужно вычислять самостоятельно.
Решение задач
При решении задач нужно помнить, что трение кручения зависит не только от свойств материалов, участвующих в движении, но и от радиуса. При этом часто областью деформации пренебрегают, так как величина смятия ничтожно мала, поэтому нахождение по формуле силы трения через массу при качении не выполняют.
Алгоритм решения примеров:
- Условия задачи изображают на рисунке. На нём показывают направление возможного перемещения до момента наступления равновесия.
- На чертеже рисуют момент трения противоположно движению, указывают вектор сцепления, направленный вдоль поверхности.
- Используя метод представления системы в виде отдельных тел, заменяют связи реакциями.
- Решают уравнения равновесия. Для этого проекции цилиндрических тел берут вдоль нормальной оси, а уравнение моментов составляют относительно точки соприкосновения.
- Изменяют направление возможного перемещения системы и движения момента качения. Находят второе условие равновесия.
Например, имеются 2 цилиндра с одинаковыми радиусами: R = 50 см. Их вес составляет соответственно 20 и 30 ньютон. Они соединены стержнем массой 40 ньютон. Первый цилиндр катится без сопротивления, а второй испытывает трение d = 2 мм. К первому кольцу приложена пара моментов, а к оси второго — нагрузка в 10 ньютон. Определить пределы изменения момента в условиях равновесия.
Для решения задачи нужно воспользоваться формулой: Мтр = N2 * d. Систему можно разбить на 3 тела. Связи заменить реакциями Fc1, N1, Fc2, N2. Внутренние связи обозначить x1, y1, x2, y2. При составлении системы нужно избегать уравнений с реакциями F. Равновесие для первого цилиндра можно определить из системы:
- Y ц = Y1 + N1 — G1 = 0;
- M ц = = X1 * R — M = 0.
Для второго колеса:
- Yi = Y2 + N2 — G2 — F sin45 = 0;
- M ц 2 = – X2 * R — M тр + F cos45 * R= 0.
Для стержня:
- Xi = – x 1 — x 2 = 0;
- Yi = -y — y2 — G3 = 0;
- Ma = =x2 * AB * sin30 — Y2 * AB * cos30 — G3 (AB/2) * cos 30 = 0.
Из решения системы можно определить, что М = (√3R FR √2 — d (G3 + 2G2 + FV2)) / (R (√3+d)). Все вычисления нужно делать в метрах. Подставив значения, заданные условием, можно вычислить, что М = 3,414. Нормальные реакции будут равны: N = 36,058 Н, N2 = 61,013 Н. Аналогичные вычисления выполняют и при изменении направления возможного перемещения. В ответе должно получиться, что M = 3, 66 Нм, N1 = 35.8 Н, Т2 = 61,3 Н. Таким образом, предел будет лежать в области от 3,414 Нм до 3, 66 Нм.
Сила трения. Коэффициент трения
- Причины возникновения трения
- Трение покоя
- Трение скольжения
- Трение качения
- Задачи
- Лабораторная работа №8. Измерение коэффициента трения скольжения
п.1. Причины возникновения трения
При движении одного тела по поверхности другого всегда возникает сила, направленная противоположно направлению скорости и замедляющая движение. Эта сила называется силой трения.
По своей природе сила трения отличается от силы тяготения и силы упругости, которые были рассмотрены в предыдущих параграфах.
Причины возникновения силы трения можно разделить на два класса: 1) шероховатость поверхностей контактирующих тел; 2) взаимное притяжение молекул при контакте.
Неровности поверхностей проявляются на макроуровне и видны невооруженным глазом или в оптический микроскоп. Их влияние можно уменьшить, если отполировать поверхности или нанести смазку.
Взаимное притяжение молекул проявляется на микроуровне и приводит к тому, что даже на идеально отполированных поверхностях не удается избежать трения, когда частицы одного тела перемещаются относительно частиц другого.
Сила трения – это сумма межмолекулярных сил, возникающих при деформациях и изломах контактирующих поверхностей за счет разрыва межмолекулярных связей.
Сила трения направлена вдоль поверхностей контактирующих тел.
Как и сила упругости, сила трения имеет электромагнитную природу и связана с межмолекулярным взаимодействием.
Но в отличие от силы упругости, причиной силы трения является разрыв межмолекулярных связей. Кроме того, если сила упругости всегда направлена перпендикулярно поверхностям контактирующих тел, то сила трения всегда направлена вдоль этих поверхностей.
В зависимости от характера движения контактирующих тел различают трение покоя, трение скольжения и трение качения.
п.2. Трение покоя
Сила трения, возникающая при относительной скорости двух контактирующих тел равной нулю, называется силой трения покоя.
Сила трения покоя равна по модулю приложенной силе и направлена в сторону, противоположную возможному движению тела, параллельно контактирующим поверхностям.
Если параллельно поверхности контакта на тело не действует сила, сила трения покоя равна нулю. Максимальное значение силы трения, при котором тело все ещё неподвижно, называется максимальной силой трения покоя.
Пример изменения силы трения покоя
 |
Сила трения покоя равна приложенной силе, которая все ещё не приводит тело в движение. Допустим, что мы прикладываем к шкафу последовательно силу 100 Н, 200 Н, 300 Н, и он начинает равномерно двигаться только при 300 Н. Как только тело начинает скользить, на него уже действует сила трения скольжения. Получаем: |
||
| Приложенная сила, Н | Движение | Сила трения покоя, Н | Сила трения скольжения, Н |
| 100 | Нет | 100 | – |
| 200 | Нет | 200 | – |
| 300 | Есть, равномерное | – | 300 |
п.3. Трение скольжения
Силу трения, возникающую в результате движения одного тела по поверхности другого, называют силой трения скольжения.
Сила трения скольжения всегда направлена в сторону, противоположную перемещению тела («тормозит» движение).
 |
Если тело расположено на горизонтальной опоре, сила тяжести (mg), действующая на него, равна по величине силе реакции опоры (N) (см. §22 данного справочника). Сила трения направлена противоположно силе тяги. |
Сила трения скольжения прямо пропорциональна силе реакции опоры: $$ F_{text{тр}}=mu N $$ Коэффициент (mu) называют коэффициентом трения скольжения; величина (mu) зависит от материала трущихся тел и состояния их поверхностей.
Значения коэффициентов трения скольжения для различных поверхностей приводятся в справочных таблицах.
При проектировании и разработке машин и механизмов коэффициенты трения скольжения для отдельных узлов определяются в специальных лабораториях.
п.4. Трение качения
Сила трения, возникающая при качении одного тела по поверхности другого, называется силой трения качения.
Сила трения качения значительно меньше силы трения скольжения.
 |
Уменьшение трения за счет качения используется в шариковых и роликовых подшипниках. Первый подшипник качения был установлен в опоре ветряка, построенного в Англии в 1780 г. Этот подшипник состоял из двух литых чугунных дорожек качения, между которыми находилось 40 чугунных шаров. Сегодня подшипники являются незаменимой деталью во всех подвижных конструкциях; они уменьшают износ трущихся деталей и снижают потери энергии на нагрев из-за трения. |
п.5. Задачи
Задача 1. Найдите коэффициент трения между шинами автомобиля и дорогой, если при равномерном движении по прямолинейному участку двигатель развивает силу тяги, равную 30 кН. Масса автомобиля 6 т.
Дано:
(m=6 text{т}=6cdot 10^3 text{кг})
(F_{text{тяги}}=30 text{кН}=3cdot 10^4 text{Н})
(gapprox 10 text{м/с}^2)
__________________
(mu-?)
Коэффициент трения $$ mu=frac{F_{text{тр}}}{N}. $$ При равномерном движении скорость постоянна и ускорение (overrightarrow{a}=0). По второму закону Ньютона, равнодействующая горизонтальных сил равна нулю $$ overrightarrow{F_{text{тр}}}+ overrightarrow{F_{text{тяги}}}=0. $$ Значит, сила трения и сила тяги равны по модулю: $$ F_{text{тр}}=F_{text{тяги}}. $$ Сила реакции горизонтальной опоры равна силе тяжести, действующей на автомобиль: $$ n=mg. $$ Получаем: $$ mu=frac{F_{text{тр}}}{N}= frac{F_{text{тяги}}}{mg}, mu=frac{3cdot 10^4}{6cdot 10^3cdot 10}=0,5. $$ Ответ: 0,5
Задача 2. Деревянный брусок массой 3 кг равномерно тянут по горизонтальной деревянной доске с помощью динамометра. Жесткость пружины динамометра равна 3 Н/см, коэффициент трения дерева об дерево 0,3. На сколько сантиметров растянется пружина?
Дано:
(m=3 text{кг})
(k=3frac{text{Н}}{text{см}}=frac{3 text{Н}}{0,01 text{м}}=300frac{text{Н}}{text{м}})
(mu=0,3)
(gapprox 10 text{м/с}^2)
__________________
(Delta l-?)
Показания динамометра – это сила упругости, равная силе тяги. При равномерном движении сила тяги равна по модулю силе трения. Поэтому begin{gather*} F_{text{упр}}=kDelta l=F_{text{тр}}=mu N=mu mgRightarrow kDelta l=mu mg end{gather*} Получаем: $$ Delta l=frac{mu mg}{k}, Delta l=frac{0,3cdot 3cdot 10}{300}=0,03 (text{м})=3 (text{см}) $$ Ответ: 3 см.
Задача 3. Автомобиль движется по горизонтальному участку дороги со скоростью 72 км/ч. Рассчитайте время торможения и тормозной путь до полной остановки, если коэффициент трения колес о дорогу равен 0,4.
Дано:
(v_1=72frac{text{км}}{text{ч}}=20frac{text{м}}{text{с}})
(mu=0,4)
(v_2=0)
(gapprox 10 text{м/с}^2)
__________________
(t, s-?)
Автомобиль тормозит за счет силы трения. По второму закону Ньютона begin{gather*} F_{text{тр}}=ma. end{gather*} С другой стороны на горизонтальной дороге $$ F_{text{тр}}=mu N=mu mg. $$ Получаем: $$ ma=mu mgRightarrow a=mu g. $$ По определению ускорения $$ a=frac{v_2-v_1}{t}. $$ Т.к. (v_2=0), ускорение отрицательное.
Модуль ускорения $$ |a|=frac{v_1}{t}=mu gRightarrow t=frac{v_1}{mu g} $$ Время торможения прямо пропорционально скорости и обратно пропорционально коэффициенту трения. $$ t=frac{20}{0,4cdot 10}=5 (text{с}) $$ Найдем тормозной путь $$ s=v_1t+frac{at^2}{2}=v_1t+ left(frac{overbrace{v_2}^{=0}-v_1}{t}right)frac{t^2}{2}=v_1t -frac{v_1t}{2}=frac{v_1t}{2}=frac{v_1t}{2}cdot frac{v_1}{mu g}=frac{v_1^2}{2mu g} $$ Тормозной путь прямо пропорционален квадрату(!) скорости и обратно пропорционален коэффициенту трения. $$ s=frac{20^2}{2cdot 0,4cdot 10}=50 (text{м}) $$ Ответ: 5 с; 50 м.
п.6. Лабораторная работа №8. Измерение коэффициента трения скольжения
Цель работы
Научиться измерять силу трения скольжения и определять коэффициент трения скольжения. Изучить зависимость коэффициента трения скольжения от материалов соприкасающихся тел и от площади опоры движущегося тела.
Теоретические сведения
 |
При (v=const) (равномерное движение) получаем По вертикали (moverrightarrow{g}=-overrightarrow{N}). Модули этих сил равны По горизонтали (overrightarrow{F_{text{тр}}}=-overrightarrow{F_{text{тяги}}}). Модули этих сил равны $$ F_{text{тяги}}=F_{text{тр}}=mu N=mu mg $$ |
Если тело перемещать с помощью динамометра, то сила упругости, возникающая в пружине, будет равна силе тяги. Т.е., сила тяги непосредственно измеряется динамометром.
В работе используются стандартные лабораторные грузики массой 100 г.
Измерив силу тяги и зная массу перемещаемого тела, рассчитываем коэффициент трения: $$ mu=frac{F_{text{тяги}}}{mg} $$
Для расчетов используем стандартное значение (g=9,80665 text{м/с}^2).
Погрешность для прямых измерений (F_{text{тяги}}) определяется как половина цены деления динамометра. Погрешность для массы определяется по маркировке грузиков и бруска, (Delta m=2 text{г}) для (m=100 text{г}), т.е. (delta_m=2text{%}).
Погрешность эксперимента (delta_e) рассчитывается как средняя арифметическая по результатам измерений и вычислений.
Приборы и материалы
Лабораторный динамометр на 5 Н; набор грузиков по 100 г; деревянный брусок с крючком 100 г; деревянная доска; наждачная бумага.
Ход работы
1. Прикрепите динамометр к бруску, положите доску горизонтально, поставьте брусок самой большой по площади гранью слева на доску.
2. Перемещая брусок слева направо по доске, добейтесь равномерного скольжения (со стабильными показаниями динамометра). Снимите показания динамометра и запишите.
3. Повторите эксперимент, нагружая брусок одним, двумя, тремя и четырьмя грузиками.
4. Рассчитайте коэффициент трения дерева об дерево, определите относительную и абсолютную погрешности эксперимента.
5. Повторите эксперимент, перемещая брусок по доске, обмотанной наждачной бумагой. Найдите коэффициент трения дерева об наждак, определите относительную и абсолютную погрешности эксперимента.
6. Снимите наждачную бумагу и повторите эксперимент для трения дерева об дерево. Однако на этот раз брусок должен опираться на меньшую по площади грань. Рассчитайте коэффициент трения дерева об дерево в этом случае.
7. Сравните полученные коэффициенты трения, сделайте выводы о зависимости коэффициента трения от материала соприкасающихся поверхностей и от площади опоры движущегося тела.
Результаты измерений и вычислений
Цена деления динамометра (d=0,1 text{Н}).
Таблица для расчета коэффициента трения скольжения дерева об дерево
| Опыт | (m, text{кг}) | (F_{text{тяги}}, text{Н}) | (mu=frac{F_{text{тяги}}}{mg}) | (Delta=|mu-mu_{text{ср}}|) | |
| 1 | Брусок | 0,1 | 0,3 | 0,306 | 0,026 |
| 2 | Брусок + 1 грузик | 0,2 | 0,7 | 0,357 | 0,025 |
| 3 | Брусок + 2 грузика | 0,3 | 1,0 | 0,340 | 0,008 |
| 4 | Брусок + 3 грузика | 0,4 | 1,3 | 0,331 | 0,001 |
| 5 | Брусок + 4 грузика | 0,5 | 1,6 | 0,326 | 0,006 |
| Всего | – | – | 1,660 | 0,065 |
Среднее значение коэффициента трения $$ mu_{text{ср}}=frac{1,660}{5}=0,332 $$ Среднее значение абсолютного отклонения $$ Delta =frac{0,065}{5}=0,013 $$ Относительная погрешность begin{gather*} delta=frac{0,013}{0,332}cdot 100text{%}approx 3,9text{%}\[7pt] mu_{text{дд}}=(0,332pm 0,013), delta_mu=3,9text{%} end{gather*}
Таблица для расчета коэффициента трения скольжения дерева об наждак
| Опыт | (m, text{кг}) | (F_{text{тяги}}, text{Н}) | (mu=frac{F_{text{тяги}}}{mg}) | (Delta=|mu-mu_{text{ср}}|) | |
| 1 | Брусок | 0,1 | 0,6 | 0,612 | 0,039 |
| 2 | Брусок + 1 грузик | 0,2 | 1,1 | 0,561 | 0,012 |
| 3 | Брусок + 2 грузика | 0,3 | 1,7 | 0,578 | 0,005 |
| 4 | Брусок + 3 грузика | 0,4 | 2,2 | 0,561 | 0,012 |
| 5 | Брусок + 4 грузика | 0,5 | 2,7 | 0,551 | 0,022 |
| Всего | – | – | 2,862 | 0,090 |
Среднее значение коэффициента трения $$ mu_{text{ср}}=frac{2,862}{5}approx 0,572 $$ Среднее значение абсолютного отклонения $$ Delta =frac{0,090}{5}=0,018 $$ Относительная погрешность begin{gather*} delta=frac{0,018}{0,572}cdot 100text{%}approx 3,1text{%}\[7pt] mu_{text{дн}}=(0,572pm 0,018), delta_mu=3,1text{%} end{gather*}
Таблица для расчета коэффициента трения скольжения дерева об дерево (узкая грань)
| Опыт | (m, text{кг}) | (F_{text{тяги}}, text{Н}) | (mu=frac{F_{text{тяги}}}{mg}) | (Delta=|mu-mu_{text{ср}}|) | |
| 1 | Брусок | 0,1 | 0,35 | 0,357 | 0,011 |
| 2 | Брусок + 1 грузик | 0,2 | 0,7 | 0,357 | 0,011 |
| 3 | Брусок + 2 грузика | 0,3 | 1,0 | 0,340 | 0,006 |
| 4 | Брусок + 3 грузика | 0,4 | 1,3 | 0,331 | 0,015 |
| 5 | Брусок + 4 грузика | 0,5 | 1,7 | 0,347 | 0,000 |
| Всего | – | – | 1,732 | 0,043 |
Среднее значение коэффициента трения $$ mu_{text{ср}}=frac{1,732}{5}approx 0,346 $$ Среднее значение абсолютного отклонения $$ Delta =frac{0,043}{5}approx 0,009 $$ Относительная погрешность begin{gather*} delta=frac{0,009}{0,346}cdot 100text{%}approx 2,5text{%}\[7pt] mu ‘_{text{дд}}=(0,346pm 0,009), delta_mu=2,5text{%} end{gather*}
Выводы
На основании проделанной работы можно сделать следующие выводы.
В работе исследовалась зависимость коэффициента трения скольжения от поверхностей, из которых изготовлены соприкасающиеся тела.
Для скольжения дерева об дерево был получен коэффициент begin{gather*} mu_{text{дд}}=(0,332pm 0,013), delta_mu=3,9text{%} end{gather*}
Для скольжения дерева об наждак был получен коэффициент begin{gather*} mu_{text{дн}}=(0,572pm 0,018), delta_mu=3,1text{%}\[7px] mu_{text{дн}}gt mu_{text{дд}} end{gather*}
Наждак является более шероховатой поверхностью и сила трения на ней больше.
Коэффициент трения скольжения сильно зависит от материалов соприкасающихся поверхностей.
Также в работе исследовалась зависимость коэффициента трения скольжения от площади опоры движущегося тела. Брусок выставлялся на более узкую грань, и изучалось скольжение дерева об дерево в этом случае. Был получен коэффициент begin{gather*} mu’_{text{дд}}=(0,346pm 0,009), delta_mu=2,5text{%} end{gather*} Поскольку begin{gather*} 0,319le mu_{text{дд}}le 0,345 0,337le mu’_{text{дд}}le 0,355 end{gather*} Полученные отрезки значений перекрываются.
Таким образом, в рамках погрешности эксперимента коэффициент трения скольжения не зависит от площади опоры движущегося тела.