Как найти дельту площади

Как рассчитать дельту

Четвертой буквой греческого алфавита, «дельтой», в науке принято называть изменение какой-либо величины, погрешность, приращение. Записывается этот знак различными способами: чаще всего в виде небольшого треугольника Δ перед буквенным обозначением величины. Но иногда можно встретить и такое написание δ, либо латинской строчной буквой d, реже латинской прописной – D.

Инструкция

Для нахождения изменения какой-либо величины вычислите или измерьте ее начальное значение (x1).

Вычислите или измерьте конечное значение этой же величины (x2).

Найдите изменение данной величины по формуле: Δx=x2-x1. Например: начальное значение напряжения электрической сети U1=220В, конечное значение – U2=120В. Изменение напряжения (или дельта напряжения) будет равно ΔU=U2–U1=220В-120В=100В

Для нахождения абсолютной погрешности измерения определите точное или, как его иногда называют, истинное значение какой-либо величины (x0).

Возьмите приближенное (при измерении – измеренное) значение этой же величины (x).

Найдите абсолютную погрешность измерения по формуле: Δx=|x-x0|. Например: точное число жителей города – 8253 жителя (х0=8253), при округлении этого числа до 8300 (приближенное значение х=8300). Абсолютная погрешность (или дельта икс) будет равна Δx=|8300-8253|=47, а при округлении до 8200 (х=8200), абсолютная погрешность – Δx=|8200-8253|=53. Таким образом, округление до числа 8300 будет более точным.

Для сравнения значений функции F(х) в строго фиксированной точке х0 со значениями этой же функции в любой другой точке х, лежащей в окрестностях х0, используются понятия «приращение функции» (ΔF) и «приращение аргумента функции» (Δx). Иногда Δx называют «приращением независимой переменной». Найдите приращение аргумента по формуле Δx=x-x0.

Определите значения функции в точках х0 и х и обозначьте их соответственно F(х0) и F(х).

Вычислите приращение функции: ΔF= F(х)- F(х0). Например: необходимо найти приращение аргумента и приращение функции F(х)=х˄2+1 при изменении аргумента от 2 до 3. В этом случае х0 равно 2, а х=3.
Приращение аргумента (или дельта икс) будет Δx=3-2=1.
F(х0)= х0˄2+1= 2˄2+1=5.
F(х)= х˄2+1= 3˄2+1=10.
Приращение функции (или дельта эф) ΔF= F(х)- F(х0)=10-5=5

Обратите внимание

Вычитать нужно не из большего числа меньшее, а из конечного значения (не важно: больше оно или меньше) начальное!

Полезный совет

При нахождении Δ все значения используйте только в одинаковых единицах измерения.

Источники:

• Справочник по математике для средних учебных заведений, А.Г. Цыпкин, 1983

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Математики любят греческие буквы и используют дельту заглавной буквы, которая выглядит как треугольник (∆), чтобы символизировать изменение. Когда дело доходит до пары чисел, дельта обозначает разницу между ними. Вы получаете эту разницу, используя основную арифметику и вычитая меньшее число из большего. В некоторых случаях числа располагаются в хронологическом порядке или в некоторой другой упорядоченной последовательности, и вам, возможно, придется вычесть большее из меньшего, чтобы сохранить порядок. Это может привести к отрицательному числу.

Абсолютная Дельта

Если у вас есть случайная пара чисел, и вы хотите узнать дельту – или разницу – между ними, просто вычтите меньшее из большего. Например, дельта между 3 и 6 составляет (6 – 3) = 3.

Если одно из чисел отрицательно, сложите два числа вместе. Операция выглядит следующим образом: (6 – {-3}) = (6 + 3) = 9. Легко понять, почему в этом случае дельта больше, если вы визуализируете два числа на оси x графика. Число 6 равно 6 единицам справа от оси, но отрицательное значение 3 равно 3 единицам слева. Другими словами, он дальше от 6, чем от положительного 3, который находится справа от оси.

Вам нужно запомнить некоторую арифметику вашей начальной школы, чтобы найти дельту между парой дробей. Например, чтобы найти дельту между 1/3 и 1/2, вы должны сначала найти общий знаменатель. Для этого умножьте знаменатели вместе, а затем умножьте числитель в каждой дроби на знаменатель другой дроби. В этом случае это выглядит так: 1/3 x 2/2 = 2/6 и 1/2 x 3/3 = 3/6. Вычтите 2/6 из 3/6, чтобы получить дельту, которая составляет 1/6.

Относительная дельта

Относительная дельта сравнивает разницу между двумя числами, A и B, в процентах от одного из чисел. Базовая формула A – B / A x100. Например, если вы зарабатываете 10 000 долларов в год и жертвуете 500 долларов на благотворительность, относительная дельта вашей зарплаты составляет 10 000 – 500/10 000 x 100 = 95%. Это означает, что вы пожертвовали 5 процентов своей зарплаты, а у вас осталось 95 процентов. Если вы зарабатываете 100 000 долларов в год и делаете то же самое пожертвование, вы сохранили 99, 5% своей зарплаты и пожертвовали только 0, 5% на благотворительность, что не очень впечатляет в момент налогообложения.

От дельты к дифференциалу

Вы можете представить любую точку на двумерном графике парой чисел, которые обозначают расстояние от точки до пересечения осей в направлениях x (горизонтальное) и y (вертикальное). Предположим, у вас есть две точки на графике, называемые точкой 1 и точкой 2, и эта точка 2 находится дальше от пересечения, чем точка 1. Дельта между значениями x этих точек – ∆ x – определяется как (x ₂ – x ₁), и y для этой пары точек равно (y ₂ – y ₁). Когда вы делите ∆y на ∆x, вы получаете наклон графика между точками, который говорит вам, как быстро x и y изменяются относительно друг друга.

Склон предоставляет полезную информацию. Например, если вы наносите время вдоль оси x и измеряете положение объекта при его перемещении в пространстве по оси Y, наклон графика показывает среднюю скорость объекта между этими двумя измерениями.

Скорость может быть не постоянной, и вы можете узнать скорость в определенный момент времени. Дифференциальное исчисление обеспечивает концептуальный трюк, который позволяет вам сделать это. Хитрость заключается в том, чтобы представить две точки на оси х и позволить им бесконечно сближаться. Отношение ∆y к ∆x – ∆y / ∆x – при приближении ∆x к 0 называется производной. Обычно это выражается как dy / dx или как df / dx, где f – алгебраическая функция, которая описывает граф. На графике, на котором время (t) отображается на горизонтальной оси, «dx» становится «dt», а производная dy / dt (или df / dt) является мерой мгновенной скорости.

При прямолинейном движении вектор перемещения совпадает с соответствующим участком траектории и длина вектора перемещения равна пройденному точкой пути:

[left|Delta overlineright|=Delta s left(6right).]

Длину вектора перемещения (как и любого вектора) можно обозначать как $left|Delta overlineright|$ или просто $Delta r$ (без указания стрелки).

Если тело совершает несколько перемещений, то их можно складывать по правилам сложения векторов:

Если направление движения тела изменяется, то модуль вектора перемещения не равен пройденному телом пути.

Примеры задач на путь и перемещение

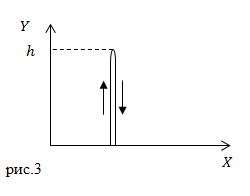
Задание: Мяч бросили вертикально вверх от поверхности Земли. Он долетел до высоты 20 м. и упал на Землю. Чему равен путь, который прошел мяч, каков модуль перемещения?

Решение: Сделаем рисунок.

В нашей задаче мяч движется прямолинейно сначала вверх, затем вниз. Так как путь – длина траектории, то получается, что мяч дважды прошел расстояние h, следовательно:

Перемещение – направленный отрезок, соединяющий начальную точку и конечную при движении тела, но тело начало движение из той же точки, в которую вернулось, следовательно, перемещение мяча равно нулю:

Ответ: $ Путь Delta s=2h$. Перемещение $Delta r=0$

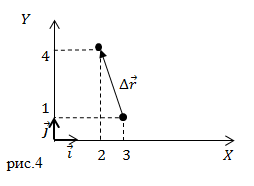
Задание: В начальный момент времени тело находилось в точке с координатами $(x_0=3;; y_0=1)$(см). Через некоторый промежуток времени оно переместилось в точку координаты которой ($x=2;;y=4$) (см). Каковы проекции вектора перемещения на оси X и Y?

Решение: Сделаем рисунок.

Радиус – вектор начальной точки запишем как:

Радиус – вектор конечной точки имеет вид:

Вектор перемещения представим как:

Из формулы видим, что:

[Delta r_x=-1;;Delta r_y=3. ]

Ответ: $Delta r_x=-1;;Delta r_y=3 $

Дельта-вектор в сверточных алгебрах

Омский государственный университет путей сообщения (ОмГУПС(ОмИИТ))

ДЕЛЬТА-ВЕКТОР В СВЕРТОЧНЫХ АЛГЕБРАХ

В математике и физике уже долгое время используется понятие дельта-функции. Это очень удобный математический объект, позволяющий эффективно решать большой круг научных задач. К сожалению, при работе с дельта-функцией возникают и серьезные проблемы. Например, нельзя перемножать дельта-функции. Дифференцирование дельта-функций также приводит к весьма неоднозначным результатам. Иногда применение дельта-функции является причиной появления нескольких взаимоисключающих решений для одной задачи.

В данной статье дельта-функция рассматривается немного под другим углом – это ни есть раз и навсегда заданная функция. Существуют пространства векторов, среди которых возможно найти вектор, обладающий всеми свойствами дельта-функции по отношению к векторам своего пространства.

Предположим, что задано пространство Гильберта . Пусть , и – произвольные вектора пространства , являющиеся действительными функциями переменной , принадлежащей некому множеству .

,

где . При этом, если – любой вектор пространства , то и , при любом .

Следовательно, на множестве задано также и скалярное произведение двух векторов [1]:

. (1)

Определим на базе скалярного произведения (1) двух произвольных векторов пространства Гильберта понятие свертки:

Определение 1: сверткой двух произвольных векторов пространства Гильберта является третий вектор этого же пространства, получаемый из следующего соотношения:

. (2)

Докажем для свертки свойство коммутативности.

Лемма 1. В отношении свертки двух произвольных векторов пространства Гильберта истинны следующие соотношения:

.

.

С учетом подстановки и имеем:

.

Что и требовалось доказать.

На базе введенного понятия свертки (2) определяем дельта-вектор пространства Гильберта.

Определение 2: дельта-вектором пространства Гильберта , на котором определена свертка, называется такой вектор , в отношении которого выполняется условие:

, (3)

где – любой вектор пространства .

Теорема 1. Если в пространстве Гильберта, в котором определен ортогональный базис и свертка, существует дельта-вектор, то этот вектор единственный и может быть вычислен по следующей формуле:

.

Доказательство. Пусть – произвольный вектор пространства Гильберта. Имеем по определению дельта-вектора (3):

. (4)

Разложим вектора и по базису :

,

где и – коэффициенты разложения. С учетом равенства Парсеваля формула (4) преобразуется следующим образом:

.

Разложим по базису и получим следующее:

, (5)

так как – любой вектор, то коэффициенты – могут быть любыми, кроме того они независимы. Следовательно, равенство (5) может быть истинно только при условии

.

И так, любой вектор раскладывается единственным образом в любом базисе:

,

а вектор соответственно:

.

Что и требовалось доказать.

Докажем некоторые свойства дельта-вектора пространства Гильберта.

Лемма 2: квадрат нормы (или энергия) дельта-вектора пространства Гильберта всегда равен .

.

.

Вводим подстановку: , :

.

используем свойство коммутативности свертки:

.

Что и требовалось доказать.

Рассмотрим другое важное свойство дельта-вектора – четность (симметричность). Для доказательства этого сначала докажем такое интересное свойство свертки:

Лемма 4: для любого произвольного и истинно следующее соотношение:

.

Для доказательства в формулу:

введем подстановку: ,

.

Исходя из определения дельта-вектора получаем:

.

Что и требовалось доказать.

Теперь можно доказать четность дельта-вектора.

Лемма 5: для любого произвольного истинно соотношение:

.

Как следствие Леммы 4, истинны утверждения, что

.

Но из определения скалярного произведения:

.

.

Что и требовалось доказать.

Введем в рассматриваемое пространство понятие единичного вектора.

Определение 3: Единичным вектором будем считать такой вектор, для которого справедливо соотношение:

.

Очевидно, что в рассматриваемом пространстве действительных функций, единичный вектор является действительной функцией . Для дальнейшего описания свойств дельта-вектора введем понятие площади вектора.

Определение 4: площадью вектора пространства Гильберта, если в нем определен единичный вектор является действительное число , определяемое следующим соотношением:

. (6)

Докажем следующее свойство дельта-векотра.

Лемма 6. Площадь дельта-вектора всегда равна 1.

Найдем площадь дельта-вектора в соответствии с формулой (6):

.

Что и требовалось доказать.

Теперь рассмотрим интерполяционные возможности дельта-вектора. Для этого предположим, что у нас имеется набор из «смещенных» по оси функций вида . Предположим, что функции образуют полный ортогональный базис. В этом случае, по этим функциям возможно разложить любой вектор пространства .

Теорема 2. Если в пространстве Гильберта возможно задать полный ортогональный базис размерности состоящий из функций вида , то любой вектор этого пространства может быть однозначно восстановлен по своим значениям в точках .

Так как, функции образуют полный ортогональный базис, то вектор возможно разложить по этому базису:

, (7)

где – размерность базиса рассматриваемого пространства; – интервал значений . Остается только найти коэффициенты разложения по данному базису:

.

Таким образом, формула (7) принимает вид:

. (8)

Это означает, что имея только отсчеты вектора в точках возможно полностью восстановить весь вектор. Что и требовалось доказать.

Приведем пример пространства, в котором существует дельта-вектор. Таким пространством является множество всех функций со спектром, ограниченным отрезком . Скалярным произведением векторов и этого пространства выберем следующее известное соотношение [2]:

.

Исходя из формулы (4) получим, что для дельта-вектора данного пространства справедливо соотношение:

,

где – любой вектор рассматриваемого пространства. Данное соотношение – это классическая свертка двух функций и . Сразу оговоримся, что классическая дельта-функция Дирака в данном случае дельта-вектором выступать не может, так как ее спектр не ограничен интервалом и, следовательно, она не является вектором нашего пространства. Необходимо искать дельта вектор среди функций с ограниченным спектром.

Как известно из теории [2], классическая свертка во временной области соответствует перемножению спектров функций в спектральной области. Подберем такую функцию , спектр которой в отношении спектра любой функции рассматриваемого пространства обладает свойством:

.

.

А таким спектром обладает функция:

. (9)

Известно, что смещенные по оси времени на интервалы функции вида (9) образуют полный ортогональный базис. Учитывая, что , а , формула (8) приобретает вид широко известной интерполяционной формулы Котельникова [3]:

,

где .

В заключении приведем основные результаты, полученные в данной работе.

1. Дельта-функция Дирака не является уникальным математическим объектом. Существуют пространства Гильберта, в которых имеется вектор, обладающий свойствами дельта-функции в отношении всех векторов своего пространства.

2. Площадь дельта-вектора равна 1.

3. Квадрат нормы (энергия) дельта-вектора равна значению этого вектора в точке 0.

4. Если в пространстве Гильберта, в котором определен ортогональный базис и свертка, существует дельта-вектор, то этот вектор единственный и может быть стандартно вычислен из любого базиса этого пространства.

5. Дельта-вектор обладает свойством симметрии.

6. В пространстве функций, ограниченных по Котельникову существует дельта-вектор, определяемый формулой:

.

1. Элементарное введение в абстрактную алгебру: М.:Мир, 1979.

2. Кудрявцев математического анализа (в двух томах): Учебник для студентов университетов и втузов. М.: Высш. школа, 1981.

3. Романюк цифровой обработки сигналов. М.:МФТИ, 2005.

[spoiler title=”источники:”]

http://www.webmath.ru/poleznoe/fizika/fizika_88_put_i_peremeshhenie.php

http://pandia.ru/text/78/392/89204.php

[/spoiler]

Как рассчитать дельту между двумя числами

Математики любят греческие буквы, и они используют дельту заглавной буквы, которая выглядит как треугольник (∆), чтобы обозначить изменение. Когда дело доходит до пары чисел, дельта означает разницу м

Содержание

Математики любят греческие буквы, и они используют дельту заглавной буквы, которая выглядит как треугольник (∆), чтобы обозначить изменение. Когда дело доходит до пары чисел, дельта означает разницу между ними. Вы получаете эту разницу, используя простую арифметику и вычитая меньшее число из большего. В некоторых случаях числа расположены в хронологическом порядке или в другой упорядоченной последовательности, и вам, возможно, придется вычесть большее из меньшего, чтобы сохранить порядок. Это может привести к отрицательному числу.

Абсолютная дельта

Чтобы найти дельту между парой дробей, вам нужно запомнить некоторые из школьных арифметических действий. Например, чтобы найти дельту между 1/3 и 1/2, вы должны сначала найти общий знаменатель. Для этого умножьте знаменатели вместе, а затем умножьте числитель каждой дроби на знаменатель другой дроби. В данном случае это выглядит так: 1/3 x 2/2 = 2/6 и 1/2 x 3/3 = 3/6. Вычтите 2/6 из 3/6, чтобы получить дельту, которая равна 1/6.

Относительная дельта

От дельты к дифференциалу

Наклон дает полезную информацию. Например, если вы наносите время на ось x и измеряете положение объекта во время его перемещения в пространстве по оси y, наклон графика показывает вам среднюю скорость объекта между этими двумя измерениями.

Источник

Дельта Формула

Дельта Формула (Содержание)

Что такое Дельта Формула?

В мире опционов или деривативов термин «дельта» относится к изменению стоимости опциона вследствие изменения стоимости его базового запаса. Другими словами, дельта измеряет скорость изменения стоимости опциона по отношению к движению стоимости базовой акции. Поскольку дельта преимущественно используется для стратегий хеджирования, она также известна как коэффициент хеджирования. Формула для дельты может быть получена путем деления изменения стоимости опциона на изменение стоимости его базового запаса. Математически это представляется как

Примеры формулы дельты (с шаблоном Excel)

Давайте рассмотрим пример, чтобы лучше понять расчет Delta.

Давайте возьмем пример товара X, который торговался по 500 долларов на товарном рынке месяц назад, и опцион колл для товара торговался с премией в 45 долларов при цене исполнения в 480 долларов. Сейчас товар продается по цене 600 долларов, а стоимость опциона выросла до 75 долларов. Рассчитать дельту опциона колл на основе предоставленной информации.

Дельта Δ рассчитывается по формуле, приведенной ниже

Давайте возьмем другой пример эталонного индекса, который в настоящее время торгуется на уровне 8000 долларов, в то время как опцион пут на индекс торгуется на уровне 150 долларов. Если индекс торговался по 7800 долларов в месяц назад, тогда как опцион пут торговался по 200 долларов, рассчитайте дельту опциона пут.

Дельта Δ рассчитывается по формуле, приведенной ниже

объяснение

Формула для дельты может быть рассчитана с помощью следующих шагов:

Шаг 3: Затем рассчитайте изменение значения опции, вычтя начальное значение опции (шаг 1) из окончательного значения опции (шаг 2).

Шаг 6: Затем рассчитайте изменение стоимости базового запаса, вычтя его начальное значение (шаг 4) из его окончательного значения (шаг 5).

Шаг 7: Наконец, формула для дельты может быть получена путем деления изменения стоимости опциона (шаг 3) на изменение стоимости базового запаса (шаг 6), как показано ниже.

Актуальность и использование формулы Delta

Калькулятор формулы Delta

Вы можете использовать следующий Delta Calculator

Рекомендуемые статьи

Источник

Кумулятивная дельта

Кумулятивная дельта – в трейдинге это показание индикатора, который считает совокупную разницу между сделками, прошедшими по цене ASK и BID. Кумулятивная дельта показывает разницу между рыночными покупками и продажи.

Дельта – что это простыми словами

В физико-математической науке дельтой является функция, которая отображает разницу между двух и более переменных. Так же, дельтой называется четвёртая буква греческого алфавита, после альфы, беты и гаммы. Именно, исходя из этих истоков, функция дельты записывается в виде треугольника. «Δ»! В сфере трейдинга дельта, как и полагается её формуле, показывает разницу некоторых переменных. А вот разницу, каких именно переменных, это ещё тот вопрос, который требует детального рассмотрения.

Например, дельта по футпринт, показывает разницу рыночных контрактов на покупку и рыночных контрактов на продажу. Ключевым словом здесь выступает прилагательное «рыночных». По причине того, что Market ордера́, сводятся исключительно с Limit заявками, то системе учёта дельты, нет необходимости дублировать объём контрактов. Отсюда вытекает вполне рациональный вывод. Отдельные ячейки, внутри каждого кластера, отображают результат дельт, исключительно ордеров по рынку, они же Market orders!

Внимание! Рекомендую вам ознакомиться с механикой рынка, что бы понять понятие кумулятивной дельты.

В свою очередь гистограмма индикатора дельта, суммирует все рыночные ордера за определённый период времени. Например, если мы используем 15-ти минутный таймфрейм, то бары гистограммы индикатора, отображают общий результат дельты, Market ордеров за 15 минут. Разумеется, что в расчёт дельты, берутся всё те же рыночные ордера. И ровно так же, как и в случае с «кластер дельта», здесь значения дельт, могут быть как положительными, так и отрицательными.

Что же касается такой разновидности дельта индикатора как, «динамический дельта профиль», так здесь всё аналогично. За исключением того, что данный горизонтальный профиль, указывает на преимущество покупателей и продавцов по отдельному ценовому уровню. Да. Вы можете возразить: «Так ведь кластер дельта отвечает за аналогичные результаты»?!

Мы с вами не согласны, так как кластер дельта (дельта по футпринт), отображает результаты разности, лишь за выбранный период времени. То бишь, на 15-ти минутном таймфрейме, отображается дельта по каждому ценовому уровню, только в рамках этих 15-ти минут. Тогда как динамический дельта профиль, суммирует все значения дельт за установленный трейдером временной отрезок!

Кумулятивная дельта основы.

Для кумулятивной дельты имеет ли значение масштаб таймфрейма

Cumulative – переводится как, совокупный, суммарный или накопительный. Из этого определения сразу становится понятно, что данный тип индикатора дельта, что-то накапливает или суммирует. Совершенно верно. Функция дельта с прилагательным «кумулятивная», подразумевает накопление всех дельт, от каждого бара гистограммы за выбранный период времени. И абсолютно не важно, какой масштаб фрейма мы с вами используем при торговле. Вернее важно, но лишь отчасти. Чтобы прояснить картину, рассмотрим один и тот же пример в 2-х вариантах:

Предположим, один из участников рынка, анализирует колебания цен, используя кумулятивную дельту. Важным условием в данном примере, является то, что в качестве фильтра, он использует дневной параметр «накопления». При этом он оптимистично настроен, анализировать и торговать финансовый актив, исключительно на таймфрейме Н1. То есть, его гистограмма индикатора, учитывает «часовые» дельты, с началом открытия биржи.

Теперь представим, что внутридневной трейдер из другого подъезда, так же использует в своей торговле дневную «накопительную» дельту. То есть, его гистограмма индикатора, так же рассчитывает показатели дельт, с момента открытия рынка. И, разумеется, тоже с эффектом «накопления». Но теперь этот персонаж предпочитает работать на 15-ти минутном масштабе. Так, его индикатор кумулятивного эффекта, будет отображать суммируемые значения дельт, относительно его рабочего таймфрейма.

На выше представленном скриншоте, продемонстрированы 2 снимка, которые в точности иллюстрируют придуманные выше примеры. Вопрос; для системы учёта накопительного эффекта, есть ли разница в таймфреймах, для кумулятивной дельты, с охватом расчёта в 1 день? Ответ; и да – есть разница, и нет – не имеет значение для самого индикатора Daily Cumulative Delta! Проясним картину, для полного исключения возможных вопросов и вероятно наивных утверждений, типа: «Как такое вообще может быть»? «Да неее. Так не бывает»!

Накопительный эффект кумулятивной дельты.

Здесь на самом деле всё очень даже просто. Если мы рассматриваем накопительный эффект кумулятивной дельты, относительно заданного параметра, то есть дневного периода. То в этом случае, для самого индикатора, не имеет абсолютно никакого значения, какой масштаб фрейма отображается на данный момент времени. Что при фрейме в 1 час, что при масштабе 15-ти минутных свеч. Дневная кумулятивная дельта, всё равно будет производить расчёты за весь текущий день.

Источник

Примеры работы функции ДЕЛЬТА для сравнения двух чисел в Excel

Функция ДЕЛЬТА в Excel используется для проверки двух числовых значений и возвращает два возможных варианта:

Примеры использования функции ДЕЛЬТА в Excel

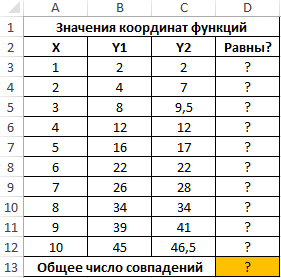
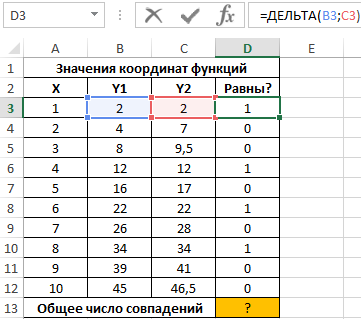
Пример 1. В таблице Excel указаны значения независимой координаты X и значения зависимых координат Y1 и Y2 для двух разных функций. Определить количество пар совпадающих значений.

Вид исходной таблицы данных:

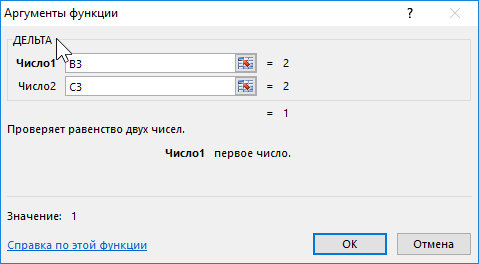
Для решения задачи сравним каждую пару значений зависимых координат Y1 и Y2 с помощью функции ДЕЛЬТА. В ячейке D3 запишем следующую формулу:

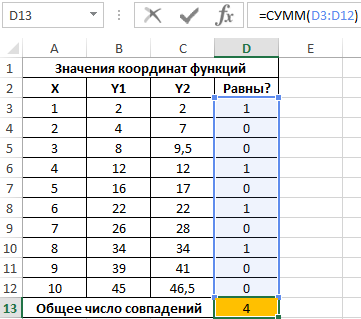
Полученное значение (1) свидетельствует о равенстве сравниваемых чисел. Протянем записанную в ячейке D3 формулу вниз до ячейки D12, чтобы автоматически рассчитать результаты для остальных значений Y1 и Y2:

Для расчета числа пар совпадающих значений используем следующую функцию:

Всего 4 пары совпадений в значениях функций координат.

Калькулятор сроков возврата инвестиций в банковские депозиты

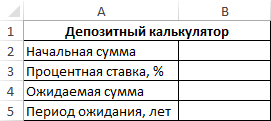
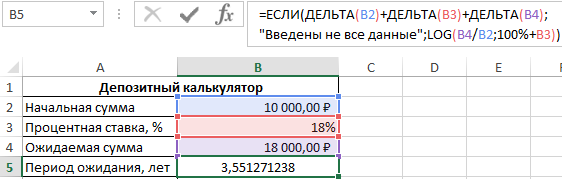
Пример 2. Реализовать калькулятор, который рассчитывает, сколько времени потребуется на получение определенной прибыли от депозита при известной начальной сумме вклада и годовой процентной ставки. Предусмотреть вывод сообщения об ошибке в случае, если одно или несколько исходных данных не указаны.

Вид формы для расчета:

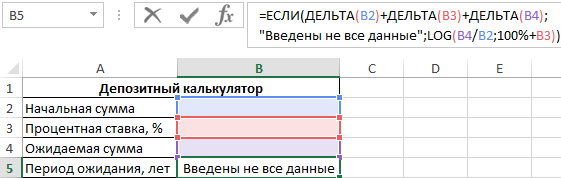
Поскольку для расчета используется логарифм из частного ожидаемой и начальной суммы с основанием в виде суммы депозита, выраженного в процентах (то есть 100%), и процентной ставки, то каждая ячейка из диапазона B2:B4 не должна являться пустой или принимать значение 0, поскольку логарифм нуля или логарифм с основанием 1 (100%) не может быть вычислен. Поэтому для расчетов используем следующую формулу:

В качестве проверочного выражения функции ЕСЛИ выступает значение, являющееся суммой возвращаемых результатов функциями ДЕЛЬТА. Последние сравнивают значения, содержащиеся в ячейках B2, B3 и B4 соответственно с 0 (второй аргумент явно не указан). Данный вариант записи соответствует логическому И (общий результат равен ИСТИНА, если все выражения, проверяемые функцией И, возвращают результат ИСТИНА). Полученное значение (0 или любое число от 1 до +∞) будет интерпретировано как ЛОЖЬ или ИСТИНА соответственно.

При незаполненных полях получим следующий результат:

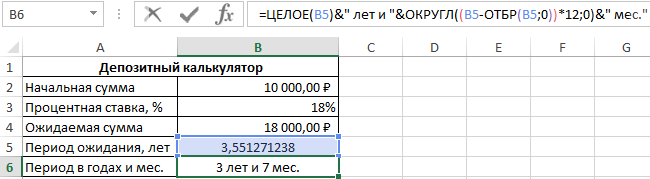
Напишем формулу для преобразования дробного числа в годы и месяцы:

В результате получим:

Расчет вероятности выпуска бракованной продукции на производстве в Excel

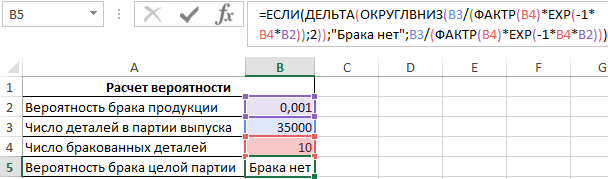
Пример 3. При изготовлении деталей на производственно-ремонтном заводе существует вероятность брака производимой продукции, которая равная коэффициенту 0,001. Определить, какая вероятность появления 10 выбракованных деталей (в этом случае вся партия считается браком) в партии из 35000 шт. Считается, что вероятностями ниже 10% можно пренебречь (то есть их приравнивают к нулю).

Вид исходной таблицы данных:

Для расчета используем следующую формулу:

Функция ОКРУГЛВНИЗ округляет до 0 все значения, которые меньше числа 0,01, то есть 10%-й вероятности. Функция ДЕЛЬТА принимает только один аргумент (выражение, полученное на основе формулы Пуассона для вычисления маловероятных случайных ситуаций), то есть сравнение выполняется с числом 0 (нуль).

Если вычислять формулу поэтапно, будет видно, что вероятность по формуле Пуассона равна примерно 0,00974 число1 ;[число2])

Источник

Как работать с Дельтой?

Если говорить просто, то дельта – это разница между объёмами рыночных покупок и рыночных продаж за период времени. Этот термин вошёл в лексикон трейдеров в 2002 году, вместе с изобретением биржевого графика Футпринт и переходом трейдинга на цифровые платформы. Сегодня этот инструмент широко используется среди биржевых торговцев. В этой статье мы рассмотрим некоторые особенности этого индикатора и узнаем, как работать с Дельтой, чтобы улучшить торговую стратегию.

Дельта – суть и классификация

Чтобы понять суть термина Дельта, необходимо разобраться, из каких элементов она состоит. Известно, что на бирже есть, так называемые, агрессивные продавцы и агрессивные покупатели. Для упрощения классификации, сделки, которые инициируются агрессивными покупателями, торгуются по цене Ask, а сделки, проторгованные по инициативе агрессивных продавцов – по цене Bid.

Дельта же – это разница между этими двумя проторгованными объёмами. Чтобы рассчитать Дельту, необходимо от объёмов торговли по цене Ask отнять объёмы торговли по цене Bid. Дельта рассчитывается именно по рыночным, а не по лимитным ордерам, поскольку они бы только дублировали объёмы и усложнили задачу трейдеру.

Футпринт – детализация рынка

График Футпринт позволяет, образно говоря, препарировать каждый бар и увидеть, как изменялось значение Дельты внутри него. Для удобства визуализации, положительная Дельта (с преобладанием объёмов покупок) окрашивается зелёным цветом, причём, чем темнее оттенок, тем сильнее в конкретный момент были покупатели. Аналогично, отрицательная Дельта (с преобладанием объёмов продаж) на графике выкрашена в красный цвет, и чем темнее оттенок, тем интенсивнее велись продажи актива.

Что это знание даёт трейдеру? Возможность анализировать и делать более точные прогнозы. Поскольку поток ордеров и движение цены на рынке тесно взаимосвязаны, анализ графика Футпринт и Дельты может помочь трейдеру сориентироваться в текущей рыночной ситуации и принять верное решение.

Индикатор Дельта – читаем между строк

Увидеть индикатор Дельта можно в нижней части графика под каждым отдельным баром – н показывает суммарное значение Дельты для каждого из них. Также как и на графике Футпринт, здесь есть два цвета, показывающие преобладание отрицательного (продажи), либо положительного (покупки) потока ордеров.

Довольно часто именно индикатор Дельта позволяет внимательному трейдеру правильно интерпретировать рыночные движения, поскольку нередки случаи, когда при положительном потоке ордеров цена падает, а при отрицательном – растёт.

Подобные несостыковки ярко свидетельствуют о вмешательстве третьей силы – мощных рыночных игроков с большими капиталами. Если наблюдается падение цены при положительной Дельте, это означает, что крупный игрок защищает все свои рыночные продажи лимитными ордерами, тем самым без особых усилий и необходимости открывать дополнительные позиции толкает цену в нужном ему направлении.

Подобным образом действия биржевого крупняка прослеживаются и при преобладании отрицательной Дельты на растущей цене.

Внимательный взгляд на Дельту поможет трейдеру «читать между строк» — видеть поведение крупных игроков и замечать, а также прогнозировать истинный тренд, тогда как те, кто ориентируется исключительно на кривую цен, могут быть легко вытряхнуты из рынка.

Как работать с Дельтой – внимание к мелочам

Чтобы получить от этого ценного инструмента максимум пользы, нельзя пренебрегать показателями Дельты во время проведения технического анализа. При этом можно использовать и график Футпринт, и индикатор Дельта на каждом баре, и кумулятивную Дельту, отображающую суммарную Дельту за период времени, например, за торговую сессию.
Порой именно показатели Дельты способны дать трейдеру оптимальную точку для входа в рынок. К примеру, по длине отрицательной Дельты можно определить момент окончания периода накопления и войти в сделку прямо перед началом крупного восходящего тренда.

Чтобы научиться, как работать с Дельтой правильно и прибыльно для своей торговли, можно пройти курс в Школе трейдинга Александра Пурнова под руководством опытного наставника. Кроме того, после подписки на наш блог будут доступны ценные материалы на тематику трейдинга и финансов.

Источник