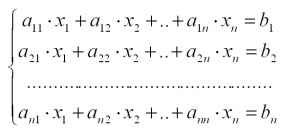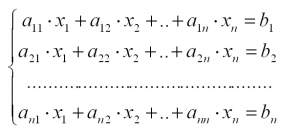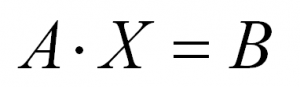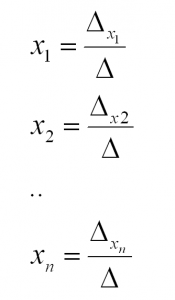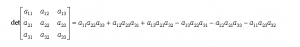Как найти дельту по методу крамера

Метод Крамера. Примеры решения систем линейных алгебраических уравнений методом Крамера.

Метод Крамера предназначен для решения тех систем линейных алгебраических уравнений (СЛАУ), у которых определитель матрицы системы отличен от нуля. Естественно, при этом подразумевается, что матрица системы квадратна (понятие определителя существует только для квадратных матриц). Решение системы уравнений методом Крамера проходит за три шага простого алгоритма:

1. Составить определитель матрицы системы (его называют также определителем системы), и убедиться, что он не равен нулю, т.е. $Deltaneq 0$.
2. Для каждой переменной $x_i$($i=overline{1,n}$) необходимо составить определитель $Delta_{x_i}$, полученный из определителя $Delta$ заменой i-го столбца столбцом свободных членов заданной СЛАУ.
3. Найти значения неизвестных по формуле $x_i=frac{Delta_{x_{i}}}{Delta}$ ($i=overline{1,n}$).

Перед переходом к чтению примеров рекомендую ознакомиться с правилами вычисления определителей второго и третьего порядка, изложенными здесь.

Пример №1

Решить СЛАУ $left{begin{aligned}
& 3x_1+2x_2=-11;\
& -x_1+5x_2=15.
end{aligned}right.$ методом Крамера.

Решение

Матрица системы такова: $ A=left( begin{array} {cc} 3 & 2\ -1 & 5 end{array} right)$. Определитель этой матрицы:

$$Delta=left| begin{array} {cc} 3 & 2\ -1 & 5 end{array}right|=3cdot 5-2cdot(-1)=17.$$

Как вычисляется определитель второго порядка можете глянуть здесь.

Так как определитель системы не равен нулю, то продолжаем решение методом Крамера. Вычислим значения двух определителей: $Delta_{x_1}$ и $Delta_{x_2}$. Определитель $Delta_{x_1}$ получаем из определителя $Delta=left| begin{array} {cc} 3 & 2\ -1 & 5 end{array}right|$ заменой первого столбца (именно этот столбец содержит коэффициенты при $x_1$) столбцом свободных членов $left(begin{array} {c} -11\ 15end{array}right)$:

$$
Delta_{x_1}=left|begin{array}{cc}-11&2\15&5end{array}right|=-55-30=-85.
$$

Аналогично, заменяя второй столбец в $Delta=left|begin{array}{cc}3&2\-1&5end{array}right|$ столбцом свободных членов, получим:

$$
Delta_{x_2}=left|begin{array} {cc} 3 & -11\ -1 & 15end{array}right|=45-11=34.
$$

Теперь можно найти значения неизвестных $x_1$ и $x_2$.

$$x_1=frac{Delta_{x_1}}{Delta}=frac{-85}{17}=-5;;x_2=frac{Delta_{x_2}}{Delta}=frac{34}{17}=2.$$

В принципе, можно ещё проверить, правильно ли решена система методом Крамера. Подставим в заданную СЛАУ $x_1=-5$, $x_2=2$:

$$left{begin{aligned}
& 3x_1+2x_2=3cdot(-5)+2cdot{2}=-11;\
& -x_1+5x_2=-(-5)+5cdot{2}=15.
end{aligned}right.$$

Проверка пройдена, решение системы уравнений методом Крамера найдено верно. Осталось лишь записать ответ.

Ответ: $x_1=-5$, $x_2=2$.

Пример №2

Решить СЛАУ $
left{begin{aligned}
& 2x_1+x_2-x_3=3;\
& 3x_1+2x_2+2x_3=-7;\
& x_1+x_3=-2.
end{aligned} right.$, используя метод Крамера.

Решение

Определитель системы:

$$Delta=left| begin{array} {ccc} 2 & 1 & -1\ 3 & 2 & 2 \ 1 & 0 & 1 end{array}right|=4+2+2-3=5.$$

Как вычисляется определитель третьего порядка можете глянуть здесь.

Заменяя первый столбец в $Delta$ столбцом свободных членов, получим $Delta_{x_1}$:

$$
Delta_{x_1}=left| begin{array} {ccc} 3 & 1 & -1\ -7 & 2 & 2 \ -2 & 0 & 1 end{array}right|=6-4-4+7=5.
$$

Заменяя второй столбец в $Delta$ столбцом свободных членов, получим $Delta_{x_2}$:

$$
Delta_{x_2}=left| begin{array} {ccc} 2 & 3 & -1\ 3 & -7 & 2 \ 1 & -2 & 1 end{array}right|=-14+6+6-7-9+8=-10.
$$

Заменяя третий столбец в $Delta$ столбцом свободных членов, получим $Delta_{x_3}$:

$$
Delta_{x_3}=left| begin{array} {ccc} 2 & 1 & 3\ 3 & 2 & -7 \ 1 & 0 & -2 end{array}right|=-8-7-6+6=-15.
$$

Учитывая все вышеизложенное, имеем:

$$
x_1=frac{Delta_{x_1}}{Delta}=frac{5}{5}=1;; x_2=frac{Delta_{x_2}}{Delta}=frac{-10}{5}=-2; ; x_3=frac{Delta_{x_3}}{Delta}=frac{-15}{5}=-3.
$$

Метод Крамера завершён. Можно проверить, верно ли решена система уравнений методом Крамера, подставив значения $x_1=1$, $x_2=-2$ и $x_3=-3$ в заданную СЛАУ:

$$left{begin{aligned}
& 2x_1+x_2-x_3=2cdot{1}+(-2)-(-3)=3;\
& 3x_1+2x_2+2x_3=3cdot{1}+2cdot(-2)+2cdot(-3)=-7;\
& x_1+x_3=1+(-3)=-2.
end{aligned} right.$$

Проверка пройдена, решение системы уравнений методом Крамера найдено верно.

Ответ: $x_1=1$, $x_2=-2$, $x_3=-3$.

Пример №3

Решить СЛАУ $left{begin{aligned}
& 2x_1+3x_2-x_3=15;\
& -9x_1-2x_2+5x_3=-7.
end{aligned}right.$ используя метод Крамера.

Решение

Матрица системы $ left( begin{array} {ccc} 2 & 3 & -1\ -9 & -2 & 5 end{array} right) $ не является квадратной. Однако это вовсе не означает, что решение системы уравнений методом Крамера невозможно. Преобразуем заданную СЛАУ, перенеся переменную $x_3$ в правые части уравнений:

$$

left { begin{aligned}
& 2x_1+3x_2=x_3+15;\
& -9x_1-2x_2=-5x_3-7.

end{aligned} right.

$$

Теперь матрица системы $ left( begin{array} {cc} 2 & 3 \ -9 & -2 end{array} right) $ стала квадратной, и определитель её $Delta=left| begin{array} {cc} 2 & 3\ -9 & -2 end{array}right|=-4+27=23$ не равен нулю. Применим метод Крамера аналогично предыдущим примерам:

$$
begin{aligned}
& Delta_{x_1}
=left| begin{array} {cc} x_3+15 & 3\ -5x_3-7 & -2 end{array}right|
=-2x_3-30-left(-15x_3-21right)
=13x_3-9;\
\
& Delta_{x_2}
=left| begin{array} {cc} 2 & x_3+15\ -9 & -5x_3-7 end{array}right|
=-10x_3-14-left(-9x_3-135right)
=-x_3+121.
end{aligned}
$$

$$
x_1=frac{Delta_{x_1}}{Delta}=frac{13x_3-9}{23};;
x_2=frac{Delta_{x_2}}{Delta}=frac{-x_3+121}{23}.
$$

Ответ можно записать в таком виде: $left{begin{aligned}
& x_1=frac{13x_3-9}{23};\
& x_2=frac{-x_3+121}{23};\
& x_3in R.
end{aligned}right.$ Переменные $x_1$, $x_2$ – базисные (в иной терминологии – основные), а переменная $x_3$ – свободная (в иной терминологии – неосновная). Проверка, при необходимости, проводится так же, как и в предыдущих примерах.

Примечание

В подобных примерах возможна ситуация, когда после переноса переменной (или переменных) в правые части уравнений, определитель системы равняется нулю. В этом случае можно перенести в правую часть иную переменную (или переменные). Например, рассмотрим СЛАУ
$left{begin{aligned}
& 2x_1-5x_2+10x_3=14;\
& -4x_1+10x_2-7x_3=5.
end{aligned}right.$. Если перенести в правые части уравнений $x_3$, получим: $
left{begin{aligned}
&2x_1-5x_2=-10x_3+14;\
&-4x_1+10x_2=7x_3+5.
end{aligned}right.$. Определитель данной системы $Delta=left| begin{array} {cc} 2 & -5\ -4 & 10 end{array}right|=20-20=0$. Однако если перенести в правые части уравнений переменную $x_2$, то получим систему $
left{begin{aligned}
&2x_1+10x_3=5x_2+14;\
&-4x_1-7x_3=-10x_2+5.
end{aligned}right.$, определитель которой $Delta=left| begin{array} {cc} 2 & 10\ -4 & -7 end{array}right|=-14+40=26$ не равен нулю. Дальнейшее решение аналогично рассмотренному в примере №3.

Пример №4

Решить СЛАУ

$$left{begin{aligned}
&x_1-5x_2-x_3-2x_4+3x_5=0;\
&2x_1-6x_2+x_3-4x_4-2x_5=0; \
&-x_1+4x_2+5x_3-3x_4=0.
end{aligned}right.$$

методом Крамера.

Решение

Матрица системы $left(begin{array} {ccccc} 1 & -5 & -1 & -2 & 3 \
2 & -6 & 1 & -4 & -2 \
-1 & 4 & 5 & -3 & 0
end{array}right)$ не является квадратной. Преобразуем заданную СЛАУ, перенеся переменные $x_4$, $x_5$ в правые части уравнений, и применим метод Крамера:

$$
left{begin{aligned}
& x_1-5x_2-x_3=2x_4-3x_5;\
& 2x_1-6x_2+x_3=4x_4+2x_5; \
& -x_1+4x_2+5x_3=3x_4.
end{aligned}right.$$

$$
begin{aligned}
& Delta
=left| begin{array} {ccc} 1 & -5 & -1\ 2 & -6 & 1\-1 & 4 & 5 end{array}right|
=19;\
\
& Delta_{x_1}
=left| begin{array} {ccc} 2x_4-3x_5 & -5 & -1\ 4x_4+2x_5 & -6 & 1\3x_4 & 4 & 5 end{array}right|
=-17x_4+144x_5;\
\
& Delta_{x_2}
=left| begin{array} {ccc} 1 & 2x_4-3x_5 & -1\ 2 & 4x_4+2x_5 & 1\-1 & 3x_4 & 5 end{array}right|
=-15x_4+41x_5;\
\
& Delta_{x_3}
=left| begin{array} {ccc} 1 & -5 & 2x_4-3x_5\ 2 & -6 & 4x_4+2x_5\-1 & 4 & 3x_4 end{array}right|
=20x_4-4x_5.
end{aligned}
$$

Ответ таков: $left{begin{aligned}
& x_1=frac{-17x_4+144x_5}{19};\
& x_2=frac{-15x_4+41x_5}{19};\
& x_3=frac{20x_4-4x_5}{19}; \
& x_4in R; ; x_5in R.
end{aligned}right.$ Переменные $x_1$, $x_2$, $x_3$ – базисные, переменные $x_4$, $x_5$ – свободные.

Естественно, что применение метода Крамера в случаях вроде того, что рассмотрен в примере №4, не всегда оправдано с точки зрения временных затрат. Мы ведь не можем гарантировать, что после переноса каких-либо переменных в правые части уравнений, определитель системы не будет равен нулю. А перебирать различные варианты – слишком долгий процесс. Гораздо удобнее в таком случае применить метод Гаусса. Я привёл пример №4 лишь с одной целью – показать, что метод Крамера применим вне зависимости от содержимого правых частей уравнений заданной СЛАУ (числа, переменные, функции – не имеет значения). Главное, чтобы определитель матрицы системы был отличен от нуля.

Метод Крамера. Примеры решения систем линейных алгебраических уравнений методом Крамера.

Метод Крамера предназначен для решения тех систем линейных алгебраических уравнений (СЛАУ), у которых определитель матрицы системы отличен от нуля. Естественно, при этом подразумевается, что матрица системы квадратна (понятие определителя существует только для квадратных матриц). Решение системы уравнений методом Крамера проходит за три шага простого алгоритма:

1. Составить определитель матрицы системы (его называют также определителем системы), и убедиться, что он не равен нулю, т.е. $Deltaneq 0$.
2. Для каждой переменной $x_i$($i=overline<1,n>$) необходимо составить определитель $Delta_$, полученный из определителя $Delta$ заменой i-го столбца столбцом свободных членов заданной СЛАУ.
3. Найти значения неизвестных по формуле $x_i=frac<Delta_>><Delta>$ ($i=overline<1,n>$).

Перед переходом к чтению примеров рекомендую ознакомиться с правилами вычисления определителей второго и третьего порядка, изложенными здесь.

Матрица системы такова: $ A=left( begin 3 & 2\ -1 & 5 end right)$. Определитель этой матрицы:

$$Delta=left| begin 3 & 2\ -1 & 5 endright|=3cdot 5-2cdot(-1)=17.$$

Как вычисляется определитель второго порядка можете глянуть здесь.

Так как определитель системы не равен нулю, то продолжаем решение методом Крамера. Вычислим значения двух определителей: $Delta_$ и $Delta_$. Определитель $Delta_$ получаем из определителя $Delta=left| begin 3 & 2\ -1 & 5 endright|$ заменой первого столбца (именно этот столбец содержит коэффициенты при $x_1$) столбцом свободных членов $left(begin -11\ 15endright)$:

Аналогично, заменяя второй столбец в $Delta=left|begin3&2\-1&5endright|$ столбцом свободных членов, получим:

Теперь можно найти значения неизвестных $x_1$ и $x_2$.

В принципе, можно ещё проверить, правильно ли решена система методом Крамера. Подставим в заданную СЛАУ $x_1=-5$, $x_2=2$:

Проверка пройдена, решение системы уравнений методом Крамера найдено верно. Осталось лишь записать ответ.

$$Delta=left| begin 2 & 1 & -1\ 3 & 2 & 2 \ 1 & 0 & 1 endright|=4+2+2-3=5.$$

Как вычисляется определитель третьего порядка можете глянуть здесь.

Заменяя первый столбец в $Delta$ столбцом свободных членов, получим $Delta_$:

$$ Delta_=left| begin 3 & 1 & -1\ -7 & 2 & 2 \ -2 & 0 & 1 endright|=6-4-4+7=5. $$

Заменяя второй столбец в $Delta$ столбцом свободных членов, получим $Delta_$:

$$ Delta_=left| begin 2 & 3 & -1\ 3 & -7 & 2 \ 1 & -2 & 1 endright|=-14+6+6-7-9+8=-10. $$

Заменяя третий столбец в $Delta$ столбцом свободных членов, получим $Delta_$:

$$ Delta_=left| begin 2 & 1 & 3\ 3 & 2 & -7 \ 1 & 0 & -2 endright|=-8-7-6+6=-15. $$

Учитывая все вышеизложенное, имеем:

Метод Крамера завершён. Можно проверить, верно ли решена система уравнений методом Крамера, подставив значения $x_1=1$, $x_2=-2$ и $x_3=-3$ в заданную СЛАУ:

Проверка пройдена, решение системы уравнений методом Крамера найдено верно.

Решить СЛАУ $left <begin& 2x_1+3x_2-x_3=15;\ & -9x_1-2x_2+5x_3=-7. endright.$ используя метод Крамера.

Матрица системы $ left( begin 2 & 3 & -1\ -9 & -2 & 5 end right) $ не является квадратной. Однако это вовсе не означает, что решение системы уравнений методом Крамера невозможно. Преобразуем заданную СЛАУ, перенеся переменную $x_3$ в правые части уравнений:

Теперь матрица системы $ left( begin 2 & 3 \ -9 & -2 end right) $ стала квадратной, и определитель её $Delta=left| begin 2 & 3\ -9 & -2 endright|=-4+27=23$ не равен нулю. Применим метод Крамера аналогично предыдущим примерам:

Ответ можно записать в таком виде: $left <begin& x_1=frac<13x_3-9><23>;\ & x_2=frac<-x_3+121><23>;\ & x_3in R. endright.$ Переменные $x_1$, $x_2$ – базисные (в иной терминологии – основные), а переменная $x_3$ – свободная (в иной терминологии – неосновная). Проверка, при необходимости, проводится так же, как и в предыдущих примерах.

Матрица системы $left(begin 1 & -5 & -1 & -2 & 3 \ 2 & -6 & 1 & -4 & -2 \ -1 & 4 & 5 & -3 & 0 endright)$ не является квадратной. Преобразуем заданную СЛАУ, перенеся переменные $x_4$, $x_5$ в правые части уравнений, и применим метод Крамера:

Естественно, что применение метода Крамера в случаях вроде того, что рассмотрен в примере №4, не всегда оправдано с точки зрения временных затрат. Мы ведь не можем гарантировать, что после переноса каких-либо переменных в правые части уравнений, определитель системы не будет равен нулю. А перебирать различные варианты – слишком долгий процесс. Гораздо удобнее в таком случае применить метод Гаусса. Я привёл пример №4 лишь с одной целью – показать, что метод Крамера применим вне зависимости от содержимого правых частей уравнений заданной СЛАУ (числа, переменные, функции – не имеет значения). Главное, чтобы определитель матрицы системы был отличен от нуля.

Заметили ошибку, опечатку, или некорректно отобразилась формула? Отпишите, пожалуйста, об этом в данной теме на форуме (регистрация не требуется).

Метод Крамера решения систем линейных уравнений

Формулы Крамера

Метод Крамера основан на использовании определителей в решении систем линейных уравнений. Это значительно ускоряет процесс решения.

Метод Крамера может быть использован в решении системы стольких линейных уравнений, сколько в каждом уравнении неизвестных. Если определитель системы не равен нулю, то метод Крамера может быть использован в решении, если же равен нулю, то не может. Кроме того, метод Крамера может быть использован в решении систем линейных уравнений, имеющих единственное решение.

Определение. Определитель, составленный из коэффициентов при неизвестных, называется определителем системы и обозначается (дельта).

Определители

получаются путём замены коэффициентов при соответствующих неизвестных свободными членами:

;

.

Формулы Крамера для нахождения неизвестных:

.

Найти значения и возможно только при условии, если

.

Этот вывод следует из следующей теоремы.

Теорема Крамера . Если определитель системы отличен от нуля, то система линейных уравнений имеет одно единственное решение, причём неизвестное равно отношению определителей. В знаменателе – определитель системы, а в числителе – определитель, полученный из определителя системы путём замены коэффициентов при этом неизвестном свободными членами. Эта теорема имеет место для системы линейных уравнений любого порядка.

Пример 1. Решить систему линейных уравнений:

. (2)

Согласно теореме Крамера имеем:

Итак, решение системы (2):

Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором, решающим методом Крамера.

Три случая при решении систем линейных уравнений

Как явствует из теоремы Крамера, при решении системы линейных уравнений могут встретиться три случая:

Первый случай: система линейных уравнений имеет единственное решение

(система совместна и определённа)

*

Второй случай: система линейных уравнений имеет бесчисленное множество решений

(система совместна и неопределённа)

* ,

** ,

т.е. коэффициенты при неизвестных и свободные члены пропорциональны.

Третий случай: система линейных уравнений решений не имеет

*

** .

Итак, система m линейных уравнений с n переменными называется несовместной, если у неё нет ни одного решения, и совместной, если она имеет хотя бы одно решение. Совместная система уравнений, имеющая только одно решение, называется определённой, а более одного – неопределённой.

Примеры решения систем линейных уравнений методом Крамера

Пусть дана система

.

На основании теоремы Крамера

………….
,

где
–

определитель системы. Остальные определители получим, заменяя столбец с коэффициентами соответствующей переменной (неизвестного) свободными членами:

Пример 2. Решить систему линейных уравнений методом Крамера:

.

Решение. Находим определитель системы:

Следовательно, система является определённой. Для нахождения её решения вычисляем определители

По формулам Крамера находим:

Итак, (1; 0; -1) – единственное решение системы.

Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором, решающим методом Крамера.

Если в системе линейных уравнений в одном или нескольких уравнениях отсутствуют какие-либо переменные, то в определителе соответствующие им элементы равны нулю! Таков следующий пример.

Пример 3. Решить систему линейных уравнений методом Крамера:

.

Решение. Находим определитель системы:

Посмотрите внимательно на систему уравнений и на определитель системы и повторите ответ на вопрос, в каких случаях один или несколько элементов определителя равны нулю. Итак, определитель не равен нулю, следовательно, система является определённой. Для нахождения её решения вычисляем определители при неизвестных

По формулам Крамера находим:

Итак, решение системы – (2; -1; 1).

Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором, решающим методом Крамера.

Применить метод Крамера самостоятельно, а затем посмотреть решения

Пример 4. Решить систему линейных уравнений:

.

Пример 5. Решить систему линейных уравнений методом Крамера:

.

К началу страницы

Пройти тест по теме Системы линейных уравнений

Продолжаем решать системы методом Крамера вместе

Как уже говорилось, если определитель системы равен нулю, а определители при неизвестных не равны нулю, система несовместна, то есть решений не имеет. Проиллюстрируем следующим примером.

Пример 6. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Определитель системы равен нулю, следовательно, система линейных уравнений либо несовместна и определённа, либо несовместна, то есть не имеет решений. Для уточнения вычисляем определители при неизвестных

Определители при неизвестных не равны нулю, следовательно, система несовместна, то есть не имеет решений.

Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором, решающим методом Крамера.

В задачах на системы линейных уравнений встречаются и такие, где кроме букв, обозначающих переменные, есть ещё и другие буквы. Эти буквы обозначают некоторое число, чаще всего действительное. На практике к таким уравнениям и системам уравнений приводят задачи на поиск общих свойств каких-либо явлений и предметов. То есть, изобрели вы какой-либо новый материал или устройство, а для описания его свойств, общих независимо от величины или количества экземпляра, нужно решить систему линейных уравнений, где вместо некоторых коэффициентов при переменных – буквы. За примерами далеко ходить не надо.

Пример 7. Решить систему линейных уравнений методом Крамера:

Здесь a – некоторое вещественное число. Решение. Находим определитель системы:

Находим определители при неизвестных

По формулам Крамера находим:

,

.

Следующий пример – на аналогичную задачу, только увеличивается количество уравнений, переменных, и букв, обозначающих некоторое действительное число.

Пример 8. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Находим определители при неизвестных

По формулам Крамера находим:

,

,

.

И, наконец, система четырёх уравнений с четырьмя неизвестными.

Пример 9. Решить систему линейных уравнений методом Крамера:

.

Внимание! Методы вычисления определителей четвёртого порядка здесь объясняться не будут. За этим – на соответствующий раздел сайта. Но небольшие комментарии будут. Решение. Находим определитель системы:

Небольшой комментарий. В первоначальном определителе из элементов второй строки были вычтены элементы четвёртой строки, из элементов третьей строки – элементы четвёртой строки, умноженной на 2, из элементов четвёртой строки – элементы первой строки, умноженной на 2. Преобразования первоначальных определителей при трёх первых неизвестных произведены по такой же схеме. Находим определители при неизвестных

Для преобразований определителя при четвёртом неизвестном из элементов первой строки были вычтены элементы четвёртой строки.

По формулам Крамера находим:

,

,

,

.

Итак, решение системы – (1; 1; -1; -1).

Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором, решающим методом Крамера.

Самые внимательные, наверное, заметили, что в статье не было примеров решения неопределённых систем линейных уравнений. А всё потому, что методом Крамера решить такие системы невозможно, можно лишь констатировать, что система неопределённа. Решения таких систем даёт метод Гаусса.

Онлайн калькулятор. Решение систем линейных уравнений методом Крамера

Используя этот онлайн калькулятор для решения систем линейных уравнений (СЛУ) методом Крамера, вы сможете очень просто и быстро найти решение системы.

Воспользовавшись онлайн калькулятором для решения систем линейных уравнений методом Крамера, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на решения систем линейных уравнений, а также закрепить пройденный материал.

Решить систему линейных уравнений методом Крамера

Изменить названия переменных в системе

Заполните систему линейных уравнений:

Ввод данных в калькулятор для решения систем линейных уравнений методом Крамера

• В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.
• Для изменения в уравнении знаков с “+” на “-” вводите отрицательные числа.
• Если в уравнение отсутствует какая-то переменная, то в соответствующем поле ввода калькулятора введите ноль.
• Если в уравнение перед переменной отсутствуют числа, то в соответствующем поле ввода калькулятора введите единицу.

Например, линейное уравнение x ₁ – 7 x ₂ – x ₄ = 2

будет вводится в калькулятор следующим образом:

Дополнительные возможности калькулятора для решения систем линейных уравнений методом Крамера

• Между полями для ввода можно перемещаться нажимая клавиши “влево”, “вправо”, “вверх” и “вниз” на клавиатуре.
• Вместо x ₁, x ₂, . вы можете ввести свои названия переменных.

Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.

[spoiler title=”источники:”]

http://function-x.ru/systems_kramer.html

http://ru.onlinemschool.com/math/assistance/equation/kramer/

[/spoiler]

В данной статье мы разберем, как найти неизвестные переменные по методу Крамера и опишем решение систем линейных уравнений.

Метод Крамера предназначен для того, чтобы решать системы линейных алгебраических уравнений (СЛАУ), в которых число неизвестных переменных равняется числу уравнений, а определитель основной матрицы не равен нулю.

Метод Крамера — вывод формул

Матричный вид записи такой системы линейных уравнений:

AX=B, где A=a11a12⋯a1na21a22⋯a2n⋮⋮⋮⋮an1an2⋯ann— основная матрица системы, в которой ее элементы — это коэффициенты при неизвестных переменных;

B=b1b2⋮bn — матрица-столбец свободных членов;

X=x1x2⋮xn— матрица-столбец неизвестных переменных.

После того как мы найдем неизвестные переменные x1, x2, …, xn, матрица X=x1x2⋮xn становится решением системы уравнений, а равенство AX=B обращается в тождество.

Метод Крамера основан на 2-х свойствах определителя матрицы:

• Определитель квадратной матрицы A=aij, i=1, 2, …, n; j=1, 2, …, n равняется сумме произведений элементов какой-либо строки (столбца) на их алгебраические дополнения:

a11a12⋯a1na21a22⋯a2n⋮⋮⋮⋮an1an2⋯ann=ap1×Ap1+ ap2×Ap2+…+apn×Apn=a1q×A1q+ a2q×A2q+…+anq×Anq

• Сумма произведений какой-либо строки (столбца) квадратной матрицы на алгебраические дополнения соответствующие элементы другой матрицы равняется нулю:

ap1×Ap1+ ap2×Ap2+…+apn×Apn=0a1q×A1q+ a2q×A2q+…+anq×Anq=0

p=1, 2, …, n, q=1, 2, …, n p не равно q

Приступаем к нахождению неизвестной переменной x1:

• Умножаем обе части первого уравнения системы на А11, обе части второго уравнения на А21и т.д. Таким образом, мы умножаем уравнения системы на соответствующие алгебраические дополнения 1-го столбца матрицы А:

A11a11x1+A11a12x2+…+A11a1nxn=A11b1A21a21x1+A21a22x2+…+A21x2nxn=A21b2⋯An1an1x1+An1an2x2+…+An1annxn=An1bn

• Складываем все левые части уравнения системы, сгруппировав слагаемые при неизвестных переменных  , и приравниваем получившуюся сумму к сумме всех правых частей уравнения:

x1(A11a11+A21a21+…+An1an1)++x2(A11a12+A21a22+…+An1an2)++…++xn(A11a1n+A21a2n+…+An1ann)==A11b1+A21b2+…+An1bn

Если воспользоваться свойствами определителя, то получится:

А11а11+А21а21+…+Аn1an1=АА11а12+А21а22+…+Аn1аn2=0⋮A11a1n+A21a2n+…+An1ann=0

A11b1+A21b2+…+An1bn=b1a12⋯a1nb2a22⋯a2n⋮⋮⋮⋮bnan2⋯ann

Предыдущее равенство будет иметь следующий вид:

x1A=b1a12⋯a1nb2a22⋯a2n⋮⋮⋮⋮bnan2⋯ann.

Откуда

x1=b1a12⋯a1nb2a22⋯a2n⋮⋮⋮⋮bnan2⋯annA

Таким же образом находим все оставшиеся неизвестные переменные.

Если обозначить

∆=b1a12⋯a1nb2a22⋯a2n⋮⋮⋮⋮bnan2⋯ann, ∆x1=b1a12⋯a1nb2a22⋯a2n⋮⋮⋮⋮bnan2⋯ann,

∆x2=b1a12⋯a1nb2a22⋯a2n⋮⋮⋮⋮bnan2⋯ann, … ∆xn=b1a12⋯a1nb2a22⋯a2n⋮⋮⋮⋮bnan2⋯ann.

то получаются формулы для нахождения неизвестных переменных по методу Крамера:

x1=∆x1∆, x2=∆x2∆, …, xn=∆xn∆.

Алгоритм решения СЛАУ методом Крамера

• Необходимо вычислить определитель матрицы системы и убедиться, что он не равен нулю.
• Найти определители

∆x1=b1a12⋯a1nb2a22⋯a2n⋮⋮⋮⋮bnan2⋯ann

∆x2=b1a12⋯a1nb2a22⋯a2n⋮⋮⋮⋮bnan2⋯ann

⋮

∆xn=b1a12⋯a1nb2a22⋯a2n⋮⋮⋮⋮bnan2⋯ann

Эти определители являются определителями матриц, которые получены из матрицы А путем замены k-столбца на столбец свободных членов.

• Вычислить неизвестные переменные при помощи формул:

x1=∆x1∆, x2=∆x2∆, …, xn=∆xn∆.

• Выполнить проверку результатов: если все определители являются тождествами, то решение найдено верно.

Примеры решения СЛАУ методом Крамера

Метод Крамера

Одним из методов решения систем линейных уравнений является метод Крамера. Используется для нахождения решения систем, в которых количество строк равно количеству неизвестных. То есть для квадратных систем уравнений. Основан он на вычислении определителей матрицы: основного и дополнительных, получающихся замещением одного из столбца основного определителя на столбец свободных членов системы алгебраических уравнений. Рассмотрим сам алгоритм метода Крамера и примеры с решением.

Дано СЛАУ $ begin{cases} a_{11}x_1+a_{12}x_2+a_{13}x_3 = b_1\a_{21}x_1+a_{22}x_2+a_{23}x_3 = b_2\a_{31}x_1+a_{32}x_2+a_{33}x_3=b_3 end{cases} $

Найти неизвестные $ begin{pmatrix}x_1\x_2\x_3 end{pmatrix} $

Алгоритм решения заключается в том, что  составляется из системы матрица $ A = begin{pmatrix} a_{11}&a_{12}&a_{13}\a_{21}&a_{22}&a_{23}\a_{31}&a_{32}&a_{33} end{pmatrix} $ и столбец свободных членов $ B = begin{pmatrix} b_1\b_2\b_3 end{pmatrix} $

Далее вычисляется основной определитель матрицы $ Delta = |A| $ и дополнительные $ Delta_i $, получающиеся из основного определителя путем поочередного замещения столбцов на столбец свободных членов$ begin{pmatrix}b_1\b_2\b_3 end{pmatrix} $

Если получается $ Delta = 0 $, тогда система не может быть решена методом Крамера! 

В итоге по формуле метода Крамера находим неизвестные в системе линейных уравнений: $$ x_1 = frac{Delta_1}{Delta}, x_2 = frac{Delta_2}{Delta}, x_3 = frac{Delta_3}{Delta} $$

Примеры с решением

Пример 1

Решить систему линейных уравнений методом Крамера: $$ begin{cases} 3x_1+x_2+2x_3 = 4\-x_1+2x_2-3x_3 = 1\-2x_1+x_2+x_3=-2 end{cases} $$

Решение

Составляем матрицу $ A = begin{pmatrix} 3&1&2\-1&2&-3\-2&1&1 end{pmatrix}  $ и выписываем столбец свободных членов $ b = begin{pmatrix} 4\1\-2 end{pmatrix} $ Вычисляем главный определитель матрицы: $$ Delta = |A| = begin{vmatrix} 3&1&2\-1&2&-3\-2&1&1 end{vmatrix} = 6 + 6 -2 +8 + 1 + 9 = 28 $$ Замечаем, что  $ Delta = 28 ne 0 $, то систему можно решить методом Крамера. Вычисляем первый дополнительный определитель  $ Delta_1 $. Подставляем столбец свободных членов $ b = begin{pmatrix} 4\1\-2 end{pmatrix} $ на место первого столбца в основной матрице: $$ Delta_1 = begin{vmatrix} 4&1&2\1&2&-3\-2&1&1 end{vmatrix} = 8 +6 +2 + 8 -1 +12 = 35 $$ Аналогично вычислим $ Delta_2 $: $$ Delta_2 = begin{vmatrix} 3&4&2\-1&1&-3\-2&-2&1 end{vmatrix} = 3 + 24 + 4 +4 -18 +4 = 21 $$ Точно также находим $ Delta_3 $: $$ Delta_3 = begin{vmatrix} 3&1&4\-1&2&1\-2&1&-2 end{vmatrix} = -12 -2 -4 +16 -3 -2 = -7 $$ По формуле Крамера: $$ x_1 = frac{Delta_1}{Delta} = frac{35}{28} = frac{5}{4} $$ $$ x_2 = frac{Delta_2}{Delta} = frac{21}{28} = frac{3}{4} $$ $$ x_3 = frac{Delta_3}{Delta} = frac{-7}{28} = -frac{1}{4} $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$ x_1 = frac{5}{4}; x_2 = frac{3}{4}; x_3 = -frac{1}{4} $$

Пример 2

Решить систему уравнений методом Крамера: $$ begin{cases} x+y-2z = 2\2x-3y-z = 1\x-4y+z=3 end{cases} $$

Решение

Попробуем  решить методом Крамера. Найдем основной определитель системы уравнений: $$ Delta = begin{vmatrix} 1&1&-2\2&-3&-1\1&-4&1 end{vmatrix} = -3 -1 +16 -6 -4 -2 = 0 $$ Внимание! Получили $ Delta = 0 $, а это означает, что данную систему нельзя решить методом Крамера. Алгоритм завершает  свою работу. Советуем воспользоваться другим методом для решения, например, матричным  методом или Гаусса.

Ответ

Метод Крамера нельзя применить к данной системе линейных уравнений

Методы Крамера и Гаусса – одни из самых популярных методов решения СЛАУ. К тому же, в ряде случаев целесообразно использовать именно конкретные методы. Сессия близка, и сейчас самое время повторить или освоить их с нуля. Сегодня разбираемся с решением методом Крамера. Ведь решение системы линейных уравнений методом Крамера – весьма полезный навык.

Системы линейных алгебраических уравнений

Система линейных алгебраических уравнений – система уравнений вида:

Набор значений x, при котором уравнения системы обращаются в тождества, называется решением системы,  a и b – вещественные коэффициенты. Простенькую систему, состоящую из двух уравнений с двумя неизвестными, можно решить в уме либо выразив одну переменную через другую. Но переменных (иксов) в СЛАУ может быть гораздо больше двух, и здесь простыми школьными манипуляциями не обойтись. Что же делать? Например, решать СЛАУ методом Крамера!

Итак, пусть система состоит из n уравнений с n неизвестными.

Такую систему можно переписать в матричном виде

Здесь A – основная матрица системы, X и B, соответственно, матрицы-столбцы неизвестных переменных и свободных членов.

Решение СЛАУ методом Крамера

Если определитель главной матрицы не равен нулю (матрица невырожденная), систему можно решать по методу Крамера.

Согласно методу Крамера, решение находится по формулам:

Здесь дельта – определитель главной матрицы, а дельта x n-ное – определитель, полученный из определителя главной матрицы путем заменой n-ного столбца на столбец свободных членов.

А теперь о том, как посчитать определитель. Например, определитель матрицы третьего порядка, который чаще всего встречается на практике, вычисляется по формуле:

В этом и заключается вся суть метода Крамера. Подставляя найденные по вышеприведенным формулам значения x в искомую систему, убеждаемся в правильности (или наоборот) нашего решения. Чтобы Вы быстрее уловили суть, приведем ниже пример подробного решения СЛАУ методом Крамера:

Даже если у Вас не получится с первого раза, не расстраивайтесь! Немного практики, и Вы начнете щелкать СЛАУ как орешки. Более того, сейчас совершенно необязательно корпеть над тетрадью, решая громоздкие выкладки и исписывая стержень. Можно легко решить СЛАУ методом Крамера в режиме онлайн, лишь подставив в готовую форму коэффициенты. Испробовать онлайн калькулятор решения методом Крамера можно, к примеру,  на этом сайте.

А если система оказалась упорной и  не сдается, Вы всегда можете обратиться за помощью к нашим авторам, например, чтобы купить конспект. Будь в системе хоть 100 неизвестных, мы обязательно решим ее верно и точно в срок!